3. The Jungle Tale and the Market Tale
An exercise in rhetoric
This chapter summarizes the very first lectures in two Introductory Economics courses. One lecture is from the Introduction to the Jungle Economy course. This is a unique course that you cannot learn anywhere else. I will ask you to imagine that you are listening to it in the straw huts of Lubungulu University, located deep in the thick, dark, green jungle. The purpose of this lecture is to present the basic idea of the jungle economy. The second lecture launches the Introduction to the Market Economy course. There is no need to travel to a far-off, exotic venue in order to attend this course. It is a course that anyone can take as part of the curriculum in the nearest Department of Economics, assuming, of course, that he is accepted into this prestigious club. Many people cram for this course, believing that it is essential for reaching the top. Some regard it as a guide to the economic galaxies – the nearby galaxy where we live, and the distant galaxy, where they would like us to live. The goal of this lecture is to present the basic idea of the market economy.
In both of these lectures, I will follow economic tradition and demonstrate the ideas via models – tales or fables. I will try to present the models precisely, with each claim accompanied by a real proof. But I will not use formal language, which would indeed make the models easier to understand for the few who are familiar with this language, but would pose an impenetrable barrier for all the rest.
Throughout this chapter, we will skip back and forth between the two lectures: jungle, market, jungle, market, and so on. You can consult two means of illustration – one for the jungle model and one for the market model – that are posted on the book’s website. When we are done, you will be asked a somewhat banal question: what are the similarities and differences between the two?
First lesson in the introduction to jungle economics course
Ladies and gentlemen, distinguished students, welcome to the first lecture in the Introduction to Jungle Economics course. In this lecture, we will study the principles of the economic system practiced in our society. We will see how an iron hand – not an invisible one – leads to an efficient result without the need for government intervention.
You know that you have come to the most popular course at the Lubungulu Jungle University. All of you passed the JAT (Jungle Aptitude Test) before being accepted to the class. You all excelled in marksmanship and pushups. But the truth is that the principles we will discuss are simple, and the abilities you have demonstrated are not essential for understanding the course material. Take a good look at the man on your right, and then on your left; because next year both of them will be here as well.
What is economics? I do not pose this question because it is important for me to put something into your heads that is not there, but rather to remove something that already is there. I assume that you have drawn your impressions about the field of economics primarily from the economics sections of the daily newspapers. However, academic economics does not deal with boring tables and gossip you are accustomed to calling economics. Our main task is to study the social mechanisms that determine what goods are available to us and that allocate them among individuals. If you hope the course will help you succeed in the complex environment of the jungle, I am afraid you are in for a disappointment. We, the teachers at the Jungle University, do not engage in professional training. We place the practical matters in the trusty hands of our brave military heroes. I am convinced that you jungle cadets will know how to conduct your lives successfully thanks to your common sense. You have come this far because you and your forefathers survived the hardships of the world. There is no useful advice that I, whose attention is entirely devoted to academic issues, can offer you. The aim of the courses in our research university is purely and simply to satisfy your curiosity, to enrich your language and to introduce you to new, unfamiliar ways of thinking.
Common interests and conflicts of interests intermingle in the jungle experience. There are things we can achieve only through collaboration: nearly every act of production requires a series of coordinated activities conducted by many people. It is vital for all of us to mobilize for defend and conquer missions. Nonetheless, the resources available to any society, even a flourishing society like ours, are limited. Everyone seeks to receive as much as possible of what he likes. And, often, what one person likes others also like.
In our view, economics is no more than a tool that helps us to achieve common objectives and to overcome conflicts of interests. Our economic perspective is part of our broader social and political outlook. We are aware of the fact that some countries try to separate economics and politics. Economic questions that ought to be decided democratically via the political system are treated there as if they were professional matters and are deferred to experts to decide. We believe this is a ploy that serves the stronger members of society (including, just by chance, the community of experts). In this course, we will see that our economic system brings order to the chaos, leads to an effective allocation of what we have, and enables us to realize our aspirations for territorial expansion.
There are no invisible hands in the jungle. Everything is clear and simple. Our economic system was designed based on an understanding of human nature. We are aware of the aggression inherent in each of us. We are not ashamed to admit that we believe in anarchist philosophies. Actually, our cultural heroes are anarchist philosophers. Our slogans are: “We owe each other nothing” and “Men merely use each other as tools.” Our flourishing and prosperous jungle culture does not suppress man’s drives. We encourage aggression and harness it for the just and eternal struggle of the tribe against the enemies who rise up against us and seek to annihilate us. We also know how to channel these aggressive impulses to lubricate the wheels of the social and economic order. And if you become faint-hearted and start having doubts about our use of the aggressive instinct, remember that you cannot argue with success. Just look at the prosperity our economic system has brought us.
In the lecture today, we will see that recognizing that each individual should grab what he can with “a strong hand and an outstretched arm” brings about an efficient outcome, prevents (or at least reduces) the need for wasteful and corrupt government intervention and frees us of the central planning mechanisms that have failed time and again throughout human history.
In the best economic tradition, we will understand the economic mechanism of the jungle via a model, which we will affectionately call the jungle tale.
First lesson in the introduction to market economics course
Ladies and gentlemen, distinguished students, welcome to the first lecture in the Introduction to Market Economics course. In this lecture we will study the principles of the market economy. We will see how an invisible hand leads to an efficient result in a competitive environment, without the need for government intervention.
I salute you for being accepted into the economics program, the most popular in our university. You are here thanks to your wonderful achievements in the SAT (Scholastic Assessment Test), which predicts – among other things – your ability to succeed in multiple-choice tests, a skill that is essential for the final exam in the course. The Introduction to Market Economics (or Principles as it is commonly named) is a challenging course. As Paul Samuelson used to say: “Take a good look at the man on your right, and then on your left; because next year one of you won’t be here.”
We cannot start the lecture without first saying something about the question, what is economics? Economics deals with individuals’ and society’s decision making processes. It examines how people make decisions. For example, should we send our son to university or buy him a car? Should we develop the health system or build highways? Should we enjoy more leisure time or try to increase our earnings? Economics helps us to best exploit our limited resources. It enables us to anticipate the changes engendered by government measures or environmental change. Economics has something to say about almost every issue, public or private. Economics will help us to conduct our lives rationally.
We act with the awareness that in our society there are common interests as well as conflicts of interests. In order to realize the aspirations of prosperity and growth, we all need to work vigorously and harmoniously to increase production. However, the resources available to any society, even a prosperous society like ours, are limited; and everyone wants to receive more and work less. The market economy is designed to promote common interests and deal with conflicting ones.
Our economic system is based on an understanding of human nature. We, in the advanced world, are aware of the selfishness inherent in each of us and harness it to the achievement of economic prosperity. Our system channels individuals’ desire for wealth so that it serves as the fuel that powers the economic order. As Adam Smith said: “Every individual … [is] led by an invisible hand to promote an end which was no part of his intention. Nor is it always the worse for the society that it was no part of it. By pursuing his own interest he frequently promotes that of the society more effectually than when he really intends to promote it” (The Wealth of Nations, Book 4, Chapter 2).
In today’s lecture, we will see how the realization that each individual should strive to obtain maximal wealth for himself without considering others results in an efficient outcome, prevents (or at least reduces) the need for wasteful and corrupt government intervention, and frees us of the mechanisms of central planning that have proved throughout history to be dangerous. The course also has practical objectives. After completing your studies, most of you will become economists, managers, merchants and bankers. Understanding the market mechanism will help you to succeed in whatever path you choose. The course will help you to think intelligently about economic questions that trouble the public. How unfortunate it is that economic affairs are left in the hands of populist politicians and not in the hands of professional economists capable of implementing what the course teaches and putting the world to rights.
In the best of economic tradition, we will present the economic mechanism of the market via a model which we will call the market model.
The jungle tale
The territory controlled by our tribe is divided into a number of homesteads, inhabited by our notables, the heroic warriors whose courage enabled us to conquer our homeland. The number of heroes is equal to the number of homesteads. Each homestead can accommodate one hero, and each hero occupies only one homestead. The homesteads differ from each other. Each hero ranks the homesteads according to his own individual preferences. One might think that the conflict of interests between the heroes would generate chaos: a number of heroes might claim the same homestead, arguing “I deserve it” or “I was here first” or “God promised me this homestead” or “my ancestors were here 3,000 years ago.” In this lecture, we will see how the laws of the jungle allocate homesteads among the heroes.
Let’s say that the tribe has six homesteads. One of them has oil and one includes a beach. One has a vineyard and there is a thick forest in another. The tomb of King Gulu I is located in one distant homestead and the big city homestead incorporates the famous nightclub Desire. The six heroes, A, B, C, D, E, F, will settle in the homesteads. In the table below, each column shows one hero’s ranking of the homesteads (in declining order). In a moment, we will explain the meaning of the number that appears in the table under each hero. At this stage, you can ignore the asterisks.
The Jungle Model
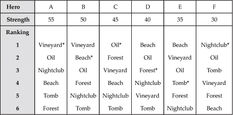
It is impossible to satisfy the wishes of all of the heroes. Two of them put the Vineyard homestead at the top of the list, and two have set their sights on the Beach homestead, but there is only one Vineyard homestead and only one Beach homestead. It is true that C snorts oil fumes, while A only ranks the Oil homestead in second place. But if A receives the oil fields, perhaps this will resolve the well-known centuries-old conflict between A and B over the wine country and bring peace to the residents of the jungle.
A mechanism is needed to allocate the homesteads and we can envisage many such mechanisms. One mechanism is the lottery. The homesteads are raffled between the heroes. They might grumble about the result of the lottery, but they cannot change it, even by consent. This mechanism is known to us from biblical times: “Notwithstanding the land shall be divided by lot; according to the names of the tribes of their fathers they shall inherit. According to the lot shall their inheritance be divided between the more and the fewer” (Numbers 26:55–56). When Joshua conducts this lottery in the biblical tale, God was also in the picture. But we’ll disregard this fine detail. In any case, here in the jungle, we cannot accept the idea that a toss of the coin will determine who wins the land flowing with milk and honey, and who gets stuck with the desert wasteland. Here, we have a Basic Law of Good Reasons: every public decision must be predicated on appropriate and well-formulated reasons. The casting of lots is not listed in the Book of Good Reasons and Joshua’s mechanism would not meet the criteria of the Supreme Court. Moreover, there are likely to be many dissatisfied individuals after the lottery who would be happy to engage in “swaps” between them if they could. Just imagine if the one who is allocated the Beach homestead cannot swim and the one who gets the Forest homestead is afraid of bears.
Another mechanism is an organizing committee. The elders of the tribe sit in the center of the village and members of the tribe come before them, one after the other, and report on their needs and aspirations. The honorable elders search (perhaps via the biological supercomputer we invented recently) for the best match of individuals and homesteads, for the glory of the tribe and to fulfill the vision of the prophets of efficiency. But here in the jungle we have little enthusiasm for organizing committees. We know that each committee of this type will turn us all into cheats and will corrupt our elders. And we believe not only in the Covenant of Thugs, but also in the values of the Movement for Quality Government.
And now we come to the mechanism that drives our prosperous economy. The allocation of homesteads in our society is dictated by the relative strength of the heroes. The balance of strength between any pair of heroes is defined unequivocally: either the first is stronger than the second, or the second is stronger than the first. In addition, we assume that if one hero is stronger than a second hero, and the second hero is stronger than a third hero, then the first hero is necessarily stronger than the third. In the table, the numbers assigned to the heroes are the strength indices. The numbers themselves have no significance beyond the fact that the higher the number, the stronger the hero.
The strength ranking of the heroes is known to all the jungle residents. All of the heroes are prepared to make unbridled use of their strength. The fact that one hero is stronger than a second hero means just one thing: the stronger one can grab any homestead held by the weaker one. There are no ownership contracts in the jungle. A hero can hold a homestead, but has no rights protecting him against someone who wants it. In our economy, unlike in a market economy, an exchange does not require a meeting of interests. One person, with one strong wish, is sufficient for a homestead to change hands. When a hero wants the homestead of someone who is weaker than him, he approaches him, greets him politely, and the two confirm their relative strength. In the worst case, they exchange a number of polite blows and the weaker one leaves the place submissively. Our inspiration for acting this way comes from nature – after all, we are part of it. In nature, it is enough for the stronger animal to remind the weaker one of the balance of strength between them to make the weaker one leave the nest or abandon the prey it is holding.
In our tale, as in a real jungle, the heroes cannot forge alliances to fight shoulder to shoulder for the interests of the members of the alliance. In the absence of a legal option to sign binding agreements, they find it impossible to organize into groups, even though they realize that they would benefit from forming such a coalition. In addition, we also have an antitrust law that prohibits individuals from organizing with the aim of exercising force against other heroes.
Like any tale, the jungle tale does not describe reality exactly as it is, but it simplifies what is complex and omits certain factors so that we can understand the operating principles of the jungle economy. In the tale, for example, the balance of strength decides every conflict between two heroes: in attack, the strong hero banishes the weaker hero from his homestead; and in defense, he prevents the weaker hero from expelling him from his home. In real life, on the other hand, things are a bit more complex. There is uncertainty, and sometimes David strikes down Goliath…
Another realistic factor that is not included in the model is that each evacuation of a homestead entails costs for both the one who is evicted and the one who expels him. These costs sometimes prevent a strong hero from exploiting his advantage over a weaker one. Some of the costs are real, such as removal costs. In addition, sometimes the weaker hero makes an error in judgment and rejects the demand of the stronger one and in the ensuing conflict the stronger one also pays a price and makes sacrifices. Some of the costs are mental ones: our warrior heroes are all sensitive souls, who experience profound discomfort when they are compelled to expel someone weak from the homestead he occupies.
In summary, the jungle tale begins with a presentation of the heroes and the homesteads, a description of the strength ranking and a list of each hero’s preferences regarding the homesteads.
The market tale
The territory controlled by our society is divided into homesteads. A number of traders operate in the market, and each one owns a different homestead. There is no ownerless homestead. The ownership of a homestead cannot be divided among several traders, and each trader can own only one homestead. The homesteads differ from each other and each trader ranks the homesteads in a way that reflects his own preferences.
Let’s say there are six homesteads in the market and six traders. In the following table, each column represents a trader. The homestead he owns at the beginning of trading appears at the top of the column, with his homestead rankings listed below it – in declining order. At this stage, you can disregard the asterisks and the row of prices.
The Market Model
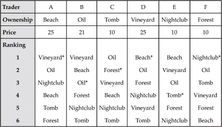
One might think that the process of allocating the homesteads is very chaotic, with several traders descending upon one trader and demanding that he swaps with them, making such claims as: “I deserve it,” or “I have more to offer you,” or “I came to you first,” or “I’m the man, and if you don’t comply with my demand I’ll kick you out.” In this lecture, we will see how the market mechanism imposes order on trading and leads to a stable and efficient allocation of homesteads.
Our economy sanctifies the concept of ownership. Owning a homestead means that no one is allowed to take the homestead from the owner against his will. This is not a jungle! A strong desire on one side is not sufficient for an exchange to be transacted. Each transaction requires a meeting of interests between two traders. Mankind has come a long way from the laws of the jungle to laws of ownership and contracts. The first commandment in our constitution is that no one has the right to impose anything on another person, and certainly no one is allowed to take something from someone else by force. Everything is conducted politely even though each trader is closely accompanied by an attorney. Each person is free to do what he wants… within the framework of budget constraints, of course.
We are aware that the concept of ownership in our model is simplistic. Sometimes there are disputes over ownership, resulting in violence between the rivals. Our legal system is designed to prevent situations in which two people try to occupy the same homestead, with each person insisting “It’s mine.”
In our model, the traders act as individuals. They are not allowed to form themselves into a group that coordinates the activity of its members in the market in order to obtain better assets. Such unions are also prohibited in real life by antitrust laws – laws that we enforce… sometimes.
The model ignores the existence of transaction costs. These include real costs – legal expenses and the costs of moving from one homestead to another; and mental costs – the traders are sensitive people and the heart of a trader cringes when he takes part in a deal that greatly improves his own situation but leaves his counterpart with only a small return. An expansion of the model to take into account the transaction costs would take us beyond the scope of this introductory lecture.
In summary, the presentation of the market model begins with introducing the traders and homesteads, a listing of homestead ownership, and a ranking of each trader’s homestead preferences.
Solution of the jungle tale
Every tale seeks an ending. The conclusion of the jungle tale must be an allocation – that is, a description of which hero holds which homestead. There are many possible allocations, with the number increasing rapidly as the number of heroes grows. When there are only six homesteads and six heroes in the jungle, there are 720 possible allocations. We are interested in possible endings in which the force that might generate instability is neutralized – that is, no hero has an interest in exploiting his strength against those who are weaker than him.
A trumpet blast and we will unveil the solution concept that guides us in selecting the tale’s ending.
Definition: We say that an allocation of the homesteads to the heroes is a jungle equilibrium if no hero prefers a homestead held by a weaker hero. In other words, in an allocation that is not an equilibrium, there is a hero who has his eyes on a homestead that is held by a weaker hero and is therefore up for grabs for him.
In general, after we define an equilibrium concept in economics, we verify that the requirements included in the definition are not so severe as to preclude any ending to the tale. Here as well, we are interested in proving that regardless of the heroes’ preferences and the balance of strength between them, the jungle tale has a jungle equilibrium. Claims of this type are called existence theorems. Advanced mathematical tools are sometimes used in proving these theorems, but in the model of the jungle we need only basic logical deductions.
Jungle Claim 1: For each beginning of the jungle tale, the tale has an ending that is a jungle equilibrium.
Proof: We will prove the claim by constructing an algorithm that will always lead to a jungle equilibrium. The algorithm is no more than a tool for proving the claim. It is an imaginary process and does not purport to describe the jungle dynamics.
We summon the heroes, one after another – from the strongest to the weakest. First, we enable the strongest to choose one out of all the homesteads. Then we call upon the second strongest hero and allow him to choose any homestead, except the one already chosen by the stronger hero. And we continue onward: at each stage, we call upon the next hero in the ranking of strength and let him choose from among the homesteads that were not selected in the earlier stages by the stronger contenders. Each hero chooses the homestead that he considers the best one for him among those still available.
The allocation resulting from the application of this algorithm is necessarily a jungle equilibrium. Why? The algorithm allocates to each hero the homestead he considers the best of those that have not been taken by those stronger than him. In other words, the hero regards his homestead as preferable to any of the homesteads allocated via the algorithm to those who are weaker than him. Therefore, no hero has an interest in attacking a weaker hero. It is definitely possible that there are homesteads that he would prefer to the one the algorithm allotted to him, but these are held by stronger heroes, so he cannot seize them.
Let’s apply the algorithm in the proof to the example of the six homesteads. Hero A is called first and chooses Vineyard. Hero B is called next. He would have liked to take Vineyard, but this homestead is already held by A. Of the homesteads that remain after A’s selection, Hero B chooses Beach. Hero C will take the homestead that he ranks highest, Oil, since it was not allocated in the first two stages. Hero D can choose one of the three homesteads that remain after the three stronger heroes took Vineyard, Beach and Oil, and he decides to settle for Forest. Hero E will take Tomb and the weakest hero, F, is left with only one “choice,” Nightclub, the only homestead that was not taken by one of the others. Fortunately for him, this homestead happens to be his heart’s desire. The allocation of the homesteads is marked by asterisks in the table in the jungle model.
Now we know that the jungle model always has at least one ending that can withstand the forces threatening to undermine its stability. But an additional danger threatens the solution concept: perhaps there are too many possible endings that comply with the definition of jungle equilibrium. This would make the solution concept uninteresting. But there is no need to worry: whatever the heroes’ preferences and balance of strength might be, there is exactly one equilibrium. This equilibrium will depend, of course, on the balance of strength and how the heroes rank the homesteads.
Jungle Claim 2: For each beginning, the jungle tale has only one ending that is a jungle equilibrium.
Proof: To prove that there is only one allocation that constitutes a jungle equilibrium, we will show that in this equilibrium each hero must hold the homestead allotted to him by the algorithm from the proof of Jungle Claim 1.
First, we will demonstrate that this is true with respect to the strongest hero. According to the jungle equilibrium, this hero does not prefer a homestead held by any other hero to the one he owns. Hence, in equilibrium, of all of the homesteads in the jungle he necessarily holds the one that he prefers. This is also the homestead the algorithm allocates to him. In order to see that in equilibrium all the other heroes also hold the homesteads allocated to them by the algorithm, we will use the method called proof by induction.
Inductive step: If, in equilibrium, each of the N strongest heroes holds the homestead the algorithm allocated to them, then this is also true for the (N+1)th hero in the hierarchy of strength.
Proof of the argument by induction: Let’s assume that in equilibrium each of the N strongest heroes holds the homestead the algorithm allocated to him. It follows that the homesteads that remain available after the algorithm has allotted N homesteads to the N strongest heroes are in equilibrium in the hands of the weaker ones. According to the definition of the jungle equilibrium, the (N+1)th hero prefers the homestead he possesses in equilibrium to all of the homesteads held by those weaker than him. Therefore, in equilibrium, of all the homesteads the algorithm did not allocate to the N strongest heroes, he holds the homestead he prefers, and it is precisely the homestead the algorithm has allocated to him. Since we have proven that, in equilibrium, the strongest hero holds the homestead the algorithm has allotted to him, it follows by induction that this is true for the second hero, the third hero, and thus for all the heroes.
Let’s summarize: the concept of the jungle equilibrium predicts a single ending for each jungle tale.
Solution of the market tale
Let’s go back and look at the example of the six homesteads. There are many barter transactions that would improve on the starting positions of the traders. Which of these transactions will be executed? It is worthwhile for C and E to swap Tomb and Nightclub. Will they indeed do so? Will B, who owns the Oil homestead, trade it with E for Nightclub (despite the fact that Nightclub is less preferable to B than his current holding) because he plans to make a trade with D subsequently in which he will receive Nightclub, his greatest dream, in exchange for Vineyard? The traders D and E compete to obtain the Beach homestead owned by A. Trader D can offer A the Vineyard homestead and E can offer Nightclub. Will the fact that D has more to offer help him get the Beach?
The solution of the model of the market must describe who ultimately owns each homestead. We believe in a solution concept called competitive equilibrium, whose definition is based on the concept of price. A sign is posted next to each homestead. When the traders wake for a morning of commerce, they see on each sign a number called a price. The prices on the signs comprise a price list. It functions like a traffic sign. At some of the turnoffs from the road, signs are posted that restrict the passage of certain types of vehicles. Every driver knows that he is allowed to turn only at an exit that does not have a sign restricting entry to his vehicle. Of the permitted turnoffs, he will choose the one that is best for him. Similarly, a trader knows that he cannot obtain a homestead whose price is higher than the price of his own, and he chooses the one he most prefers from among the homesteads within his price range.
Not every set of prices posted on signs will direct the flow of commerce without collisions. It is very possible that a certain homestead will be sought by more than one trader. We are looking for a set of prices that will steer commerce in such a way that each homestead will be the right one for only one trader. The fateful hour has arrived. The clamor of Wall Street can be heard in the background, creating a festive atmosphere as the moment when we announce the central concept of the lecture approaches.
Definition: A set of prices is called a set of competitive equilibrium prices if it satisfies the following requirement: for each homestead, there is exactly one trader who regards it as the best among the homesteads whose price is not higher than the price of the one he owns at the start of trading. The allocation that results from the traders’ choices is called a competitive equilibrium.
In the table in the market tale section, one price list is displayed. In each column in the table, an asterisk marks the homestead the respective trader seeks to purchase given the price list. Trader A can acquire any homestead and he chooses Vineyard. Trader B would like to acquire Beach and Vineyard, but their prices are higher than that of his initial homestead. He has no alternative but to settle for the Oil homestead. Trader C, who owns the Tomb homestead, can only trade it for Forest or Nightclub, and the Forest homestead is higher in his preferences. Similarly, D would like the Beach, E wants the Tomb and F seeks Nightclub. Thus we find that for each homestead there is exactly one trader who is interested in it at the given price. We have found a competitive equilibrium
Underlying the definition of competitive equilibrium, we have a story about the way prices change: in a situation in which more than one trader would like a certain homestead, its price rises; and when no trader wants it, the price goes down. One can imagine an announcer declaring the prices, revising them, and revising again and again… until, wonder of wonders, each homestead has a single trader who is still interested in it and can afford it. But there are only a few markets that have such an announcer. In the absence of an announcer, the long arm of the invisible hand operates, steering the prices toward competitive equilibrium.
Does a competitive equilibrium always exist? The following claim states that whatever the traders’ preferences and the initial state of ownership, there is always at least one equilibrium.
Market Claim 1: A competitive equilibrium always exists.
Proof: We will prove the claim by constructing an algorithm that always leads to a competitive equilibrium.
We will call a “cycle” any sequence of traders in which each trader prefers most the homestead of the trader who follows him in the series, with the last trader preferring the homestead of the first trader. How do we know that such a cycle exists? We will arbitrarily choose one of the traders,(let us call him Trader 1). The homestead he prefers most is the homestead belonging to a trader called Trader 2. Trader 2 prefers most the homestead of Trader 3 and Trader 3 prefers most the homestead of Trader 4. We will continue on until we again reach a trader who has already appeared in the chain. For example, if Trader 4 prefers the homestead of Trader 2, then we identify the cycle: Trader 2 → Trader 3 → Trader 4 → Trader 2. If Trader 4 prefers his own homestead, we get a so-called degenerate cycle: Trader 4 → Trader 4. We will assign a single arbitrary price to each of the homesteads owned by the traders in the cycle.
We will continue the algorithm without the homesteads whose prices we just set and without their initial owners. At every stage, we will identify a cycle of traders in which each trader regards the homestead held by the next trader in the cycle as the best of the homesteads that were not allocated during the earlier stages. We will assign to the homesteads of the traders in the cycle a lower price than the prices assigned to the homesteads in the earlier stages. We will allocate the homesteads whose prices we just set and their initial owners and we will continue this as long as traders and homesteads remain.
The algorithm can progress in various ways, but eventually it has to end because at each stage at least one trader leaves the cycle (when he is allocated a homestead). In this way, we will create a series of cycles of trade and will assign prices to each of the homesteads. We assigned an identical price to each of the homesteads whose owners are in the same cycle. We assigned a lower price to a cycle we found at a later stage.
We will prove that this set of prices is one of competitive equilibrium. Given a set of prices, we will see that each homestead has a single trader who would like it.
A trader whose initial homestead is assigned price P considers purchasing a homestead from among the group of homesteads whose prices are not higher than P – that is, all of the homesteads whose owners were not involved in the previous cycles of trade. The algorithm built the series of cycles such that his preferred homestead, among those left in his cycle, is the one that belonged to the next trader in the cycle of trade at the start of trading. Thus, each homestead has a single trader who would like it: the trader who appears before its owner in the current cycle of trade.
We will illustrate the algorithm with the example of the six homesteads: A is most interested in the homestead of D, who is most interested in that of A. Therefore, A→ D→ A is a cycle of trade: each of the traders in the cycle is most interested in the homestead of the trader who comes after him. We will arbitrarily determine that the price of each of the two homesteads they own, Vineyard and Beach, is 25. After removing these two homesteads and their owners, we are left with four traders (B, C, E, F) and four homesteads (Oil, Tomb, Nightclub and Forest).
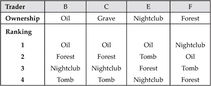
We will continue in the same way. Among the homesteads that remain, Trader B is most interested in Oil, the homestead he already possesses. Therefore, B → B is a cycle. We will assign Oil a price of 21. Finally, we will identify the cycle of trade C → F → E → C. Of the remaining homesteads, C prefers the homestead of F, who follows him in the cycle; F prefers the homestead of E, who prefers that owned by C. We will set the price of Forest, Nightclub and Tomb (the homesteads owned by these traders) at 10 (or any number less than 21)… and we have finished.
The wealth of a trader in the market means his ability to choose a homestead from among many. The source of the wealth in the market is based on a meeting of interests among the traders. For example, A is very interested in D’s homestead and D is very interested in A’s. Their homesteads have a relatively high price. On the other hand, the fact that there is someone (F) who wants E’s homestead very much does not guarantee that E will be wealthy; the market price of E’s homestead may be low because there is no one who really wants F’s homestead.
There are many price systems that have competitive equilibrium. Nonetheless, the following claim shows that the market model still has a single ending.
Market Claim 2: All competitive equilibria result in the same allocation (the proof of this claim is more complex than the other proofs in this chapter and the reader who is interested can find it in my article with Michele Piccione, “Equilibrium in the Jungle”).
How impressive! The competitive equilibrium provides a single prediction of the final allocation of homesteads, an allocation that depends, of course, on the initial ownership of the homesteads and the traders’ preferences.
The efficiency of the jungle equilibrium
The jungle equilibrium makes the use of force unnecessary. In equilibrium, no hero can or wants to take over a homestead held by another hero.
In our jungle, a hero’s takeover of another hero’s homestead by force is a legitimate action, but – unlike in the market – there are no mechanisms that allow a group of individuals to trade homesteads of their own volition. It is easy to imagine the unrest in the jungle if a number of heroes were to discover that they could enhance their situation if they adopted foreign ways and agreed among themselves on a round of homestead swaps. If they did this, the masses would accuse the economic system of the jungle of inefficiency and would demand reforms. The next claim shows that there is no reason for concern. Before formulating it, we will present one definition: an allocation is efficient if there is no cycle of homestead swaps between some of the heroes that would enhance the situation of all of those participating in the swap.
Jungle Claim 3: The jungle equilibrium is an efficient allocation.
Proof: We start with a situation in which each hero possesses the homestead allocated to him in the jungle equilibrium.
Let’s look at any cycle of homestead swaps and focus on the strongest hero in the cycle. The homestead the hero holds after the swap is different from the one he held before the swap. Therefore, in equilibrium, the homestead must have been held by one of the heroes weaker than him, as our hero is the strongest one participating. This homestead is necessarily less preferable for him than the homestead he possessed when in equilibrium: otherwise, he would have taken it over and the initial allocation would not have been an equilibrium.
Let’s summarize: After the jungle reaches equilibrium, any cycle of homestead swaps would worsen the situation of at least one of the participating heroes. Therefore, the allocation of the jungle equilibrium is efficient.
Until now, we assumed that each hero is concerned only with the homestead he owns and does not care which ones the other heroes own. In reality, the situation is sometimes different and the location of each hero affects the welfare of another hero. For example, we all want the strongest ones to live in the outlying areas so they can protect us from our enemies. A matter of concern for many of us is who lives in the neighboring homestead. In the language of economists, we say this is a situation where externalities exist. In such circumstances, the jungle equilibrium may not have the attribute of efficiency.
We will illustrate this point with an example:
Consider a jungle that has three heroes: A, B and C, and three homesteads: Beach, Forest and Oil. There are six possible allocations of homesteads to heroes. Let’s say that Hero A is stronger than Hero B, and Hero B is stronger than Hero C. The table below shows how the three heroes rank the six possible allocations. Each allocation is denoted by a threesome. For example, the threesome (Forest, Oil, Beach) denotes the allocation in which A settles in Forest, B in Oil and C in Beach.
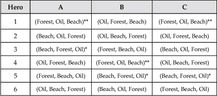
Note that Hero C is primarily concerned with the homestead he receives. On the other hand, Heroes A and B also attribute importance to the homestead in which the other heroes settle. Each of them wants the other to settle in the Oil homestead.
The definition of equilibrium in the jungle with externalities is a bit subtle. The hero who sets out to grab a different homestead must take into consideration not only which homestead to choose; he must consider also how the displaced hero will react. Here, we’ll assume that the evicted hero moves to the homestead of the hero who evicted him. Thus, we’ll say that the allocation is a jungle equilibrium if there is no hero who prefers the allocation that would result from an exchange of homesteads with a weaker hero. For example, the allocation marked in the table with two asterisks (**) is not a jungle equilibrium. B could impose a swap with C and the result of this exchange (Forest, Beach, Oil) is ranked higher by B than the allocation marked by two asterisks.
The allocation marked with one asterisk (*) is an equilibrium allocation, but it is not an efficient allocation: the three heroes prefer the allocation with the two asterisks. It is possible to implement a more efficient allocation, but in order to do this the government would need to declare the Beach homestead a closed military area and use its power to ensure the allocation of Beach to C.
Yes, we are proud that the anarchy of the jungle usually leads to an efficient allocation, but we recognize that there are circumstances in which government intervention is necessary.
The efficiency of competitive equilibrium
Competitive equilibrium is defined by the existence of a price list in which each homestead has a single trader who is interested in acquiring it and able to do so. We will now see that the action of the invisible hand which leads to a competitive equilibrium also achieves the virtue of Pareto efficiency: there is no other allocation of homesteads to traders that would benefit some of them without being detrimental to any others. (Incidentally, under the conditions of the model, this characteristic is equivalent to what we called efficiency in the jungle.) Achieving Pareto efficiency is a central goal of our economy. An allocation that is not Pareto efficient is not a good allocation because it is possible to improve the welfare of at least some of the individuals without this coming at the expense of one of the other individuals. The following statement (which is called in the economic literature the first fundamental theorem of welfare economics) stipulates that the market mechanism achieves the ideal of efficiency.
Market Claim 3: The allocation in a competitive equilibrium is Pareto efficient.
Proof: We’ll start with a competitive equilibrium allocation. Let’s consider some other allocation. We’ll call a trader differentiated if he receives two different homesteads in the two allocations. We will focus on differentiated Trader X, who possesses the most expensive of the homesteads held by the differentiated traders in equilibrium. In the new allocation, he received a homestead held in equilibrium by another differentiated trader, Y, and the price of the homestead Y held in equilibrium is not higher than the price of the homestead X held in equilibrium (because X is the richest of the differentiated traders). Consequently, given equilibrium prices, X could have acquired the homestead assigned to him in the new allocation but nonetheless refrained from doing so. This means that he values this homestead less than the homestead he held in equilibrium.
Let’s summarize: After the market reaches competitive equilibrium, any other allocation, even if it is advantageous to some of the traders, is detrimental to at least one of the others. Therefore, the allocation of competitive equilibrium is Pareto efficient.
There is usually no need for the government to intervene and disrupt the market forces from doing their work. But we realize that there are exceptional situations in which Pareto efficiency is not achieved and there are grounds for considering government intervention in the market mechanism, for instance by offering benefits to traders to settle in sensitive regions. These situations might arise, for example, when there are traders who care not only about their own location, but also about the location of the other traders. In the language of economists, we say that this is a situation in which externalities are present. In such a case, there is room for payment to traders who settle in sensitive regions. We will elaborate in another course.
We noted that sometimes competitive equilibrium does not lead to efficiency, but we forgot to teach this fact to the devoted supporters of the market economy, who continue to cite the first fundamental theorem of welfare economics without mentioning that its conclusion is based on the assumption that an individual’s welfare depends solely on the homestead he obtains.
Summary of the first lecture on the jungle economy
I hope that the first lecture was not too intensive, despite the fact that I crammed a summary of the entire course into it. Before I conclude the lecture, allow me to make a few more comments.
Yes, we are proud of the fact that our economic system compensates the strongest heroes, and that the weaker ones receive only the stronger ones’ leftovers. Our economic system encourages people not to be weaklings. The School of Economics is named after mighty Samson. Our business school awards the MBA degree to those who have specialized in taking over the assets of others in elegant and original ways. Our best people devote their energies to the army, security, and the construction of walls and fences, and do not waste their talents on luftgeschäft, pie in the sky ideas.
It is true that in order for the jungle economy to function, the heroes need to clearly identify who is stronger than whom. In the jungle, Valentine’s Day is the Festival of Strength and not of love. On that day, all of the heroes gather and wrestle until they collapse from exhaustion, or… until night falls. At night, fatigued but standing proud, the heroes line up in a row in the moonlight, ranked from strongest to weakest. At first glance, it seems like a meaningless ancient pagan ritual. But we, the economists, have discovered the logic behind this tradition: its objective is to let all the heroes know who is strong and who is weak in the jungle. In this way, our economy can function without unnecessary friction. You see, economics has just as much to say about anthropological issues as it has to contribute to so-called economic issues.
True, the use of power to grease the wheels of our economy sometimes leaves victims in its wake. Our heroes are also human and sometimes make mistakes. A weak hero sometimes gets confused, fails to recognize his weakness, and resists when a stronger hero demands that he evacuate his homestead. A commotion ensues and the stronger hero must resort to force – reasonable force, of course – to remind the weaker hero of his inferior standing. In the language of economists, we call the damages incurred in such clashes transaction costs. We will remember the victims of the jungle economy, upon whose backs the system was built, and continue on.
Of course, we understand the feelings of the social lobby which is frustrated that the jungle economy is liable to generate an unfair allocation. Those who have asthma or who suffer from humidity in the summer prefer to live far from the sea. If the asthmatic is weaker, the outcome of the jungle economy will be unjust. Alas, the jungle is green, but it is not the Garden of Eden.
To summarize the first lecture in the Introduction to Jungle Economics course: we showed that the laws of the jungle lead to a stable and efficient outcome, without markets, without money, without commercial law and almost without the need for government intervention.
Summary of the first lecture in the market economy
I know that the first lecture of the course was quite a load. No wonder. My colleagues say, with a wink, that the Introduction to Market Economics course contains all the ideas an economist really needs to understand. Before I conclude the lecture, I would like to add a few more points.
Some argue against us that our system encourages people to be greedy and hedonistic. That is not true. We have a marginal influence on the nature of human beings. Human beings bring credit to evolution. By nature, they always aspire to obtain the best of what is possible. Many people engage in a feverish search for business opportunities. When someone is ready to sell something at a low price and someone else is willing to buy it at a high price, there will always be someone who immediately identifies the opportunity to buy from the former and sell to the latter.
A system of prices can be created without the need for a centralized mechanism to manage commerce. You will ask: how does the market arrive at equilibrium prices? This mystery is the magic behind our economic system.
The commerce in the market entails transaction costs – the time and effort needed to identify and execute a transaction. But these are negligible costs that we can ignore, and we can move on.
We will sadly note the sense of frustration among members of the social lobby, who argue that the laws of the marketplace ignore considerations of fairness. If someone who suffers from asthma and someone who is allergic to sweat in the summer would benefit by living in a homestead far from the sea, but the desirable homestead is owned by a wimp who happened to inherit it from his parents, then the outcome of the market is unjust. Yes, alas, the market is only almost the Garden of Eden.
To summarize the first lecture on the market economy, we will say only: behold, look and see how great are the wonders of the market.
End
The presentation of the two Introduction to Economics lectures is over. In one lecture, the model of the market took center stage. It is a familiar model that is taught in every Department of Economics. It is conventionally regarded as a basis for understanding the economic world in which we live, even though it is quite unrealistic, imaginary, does not provide an explanation for the wonder of equilibrium prices, and its predictive qualities are limited. The other lecture focused on the model of the jungle, a model that does not appear in the textbooks and seems to be taken from a Walt Disney movie, completely detached from the developed world in which we live.
Is the jungle economy relevant only to cultures that are far from us in place and time? I’m afraid not. Here is a scenario that does not sound imaginary to me at all: as a result of climate change and the proliferation of nuclear weapons, the great Gog and Magog apocalypse erupts. The survivors do not need any consumer product except for a magic capsule called manna that falls from heaven every morning. Some people are unfortunate and nothing good ever falls upon them from above. Others are lucky, groaning under mountains of manna. In this post-traumatic world, those who lack manna try to use physical force to take what they need to subsist from those who have an abundance of manna. The market mechanism cannot be used for an exchange of goods because in this world there are no goods other than manna. At most, the market mechanism can regulate the barter of manna and strength; the owners of manna pay some of those who lack manna to physically protect them. A version of the jungle model would describe this world better than the model of the market.
But even without such a horrible scenario, the jungle model is more relevant to our world than might appear at first glance. Physical strength constitutes an influential factor also in the contemporary economy. Property crimes are aggressive actions in which assets are transferred from individuals to individuals. The bully in the prison cell gets the best bed and this is also true in many decent families. Strength played an important role in the allocation of assets in regimes that have collapsed. Nations have robbed and continue to rob other nations by exercising military power.
But when we speak about the use of force as a factor that determines the distribution of goods in a society, we are referring not only to military power. In our world, it is not uncommon for people to use gentle force to allocate goods, and in some cases we do not even see anything wrong with this. The power of rank determines the parking arrangements even at universities. The power of seniority determines priority in awarding special privileges in elite army units and in nursing homes. The power of persuasion leads participants in negotiations to agree to what they are not interested in. And let’s not forget the power of attraction, male or female, that drives the process of allocating men to women and vice versa. Let’s say He-1 is with She-1 and He-2 is with She-2. But now He-1 prefers She-2 to his present partner, bless her soul, and He-1 is more attractive than He-2. So He-1 appears before She-2, exercises his manly powers – and the deal is closed. I shudder at the thought of using the market mechanism to make matches between the sexes.
The models presented in the two Introduction to Economics lectures are nothing but fables. Neither of them describes reality, but both of them still describe something from reality. Neither of them provides an unequivocal argument in favor or against this or that economic system, but studying both of them together helps to some extent in understanding economic mechanisms.
I have attempted to present the two models, side by side, as symmetrically as possible. My main objective was to promote a critique of the way in which we teach economics in universities. The study of economics conventionally focuses on the market model which quickly captivates the hearts of the students, not as a result of empirical evidence or following proper discussion — these are usually absent. Students of economics are enchanted by the elegance of the market model, by its decisiveness, and by its ability to predict, whether correctly or erroneously. In this chapter, I have tried to emphasize how easy it is to impress students, by using similar tools and employing rhetorical ploys with a different economic system, a system that is not to my liking either.



