3. Why Is the World so Irrational?
The Al-Qassam Brigade is about killing, being killed, and the celebration of killing. None of this killing seems to serve any strategic plan, except as blind revenge, an expression of religious hysteria, and as a placeholder for a viable program for creating a Palestinian state. In short, the Al-Qassam Brigade can best be described as a psychotic death cult. Sharkansky, 2002
One of the most frustrating experiences for a working economist is to be confronted by a psychologist, political scientist – or even in some cases Nobel Prize winning economist – to be told in no uncertain terms “Your theory does not explain X – but X happens in the real world, so your theory is wrong.” The frustration revolves around the fact that the theory does predict X and you personally published a paper in a major journal showing exactly that. One cannot intelligently criticize – no matter what one’s credentials – what one does not understand. We have just seen that standard mainstream economic theory explains a lot of things quite well. Before examining criticisms of the theory more closely it would be wise to invest a little time in understanding what the theory does and does not say.
The point is that the theory of “rational play” does not say what you probably think it says. At first glance, it is common to call the behavior of suicide bombers crazy or irrational – as for example in the Sharkansky quotation at the beginning of the chapter. But according to economics it is probably not. From an economic perspective suicide need not be irrational: indeed a famous unpublished 2004 paper by Nobel Prize winning economist Gary Becker and U.S. Appeals Court Judge Richard Posner called “Suicide: An Economic Approach” studies exactly when it would be rational to commit suicide.
The evidence about the rationality of suicide is persuasive. For example, in the State of Oregon, suicide is legal. It cannot, however, be legally done in an impulsive fashion: it requires two oral requests separated by at least 15 days plus a written request signed in the presence of two witnesses, at least one of whom is not related to the applicant. While the exact number of people committing suicide under these terms is not known, it is substantial. Hence – from an economic perspective – this behavior is rational because it represents a clearly expressed preference.
What does this have to do with suicide bombers? If it is rational to commit suicide, then it is surely rational to achieve a worthwhile goal in the process. Eliminating ones enemies is – from the perspective of economics – a rational goal. Moreover, modern research into suicide bombers (see Kix [2010]) shows that they exhibit exactly the same characteristics of isolation and depression that leads in many cases to suicide without bombing. That is: leaning to committing suicide they rationally choose to take their enemies with them.
The Prisoner’s Dilemma and the Fallacy of Composition
Much of the confusion about what economics does and does not say revolves around the distinction between individual self interest and what is good for society. If people are so rational how can we have war and crime and poverty and other social ills? Why do bad things happen to societies made up of rational people? The place to start understanding this non-sequiter is with the most famous of all games, the Prisoner’s Dilemma game.
The Prisoner’s Dilemma is a game so popular Google shows over 564,000 web pages devoted to it. As this game has two players it can conveniently be described by a matrix, with the choices of the first player labeling the rows, and the choices of the second player labeling the columns. Each entry in the matrix represents a possible outcome – we specify the feeling players have about that outcome by writing two numbers representing the utility or payoff to the first and second player respectively.
In the original Prisoner’s Dilemma the two players are partners in a crime who at the onset of the game have been captured by the police and placed in separate cells. As is the case in every crime drama on television, each prisoner is offered the opportunity to confess to the crime. The matrix of payoffs can be written as
Not confess |
Confess |
|
Not confess |
10,10 |
–9,20 |
Confess |
20,–9 |
2,2 |
Prisoner’s Dilemma Payoffs
Each player has two possible actions – to Confess or to Not confess. The row labels represent possible choices of action by the first player “Player 1.” The column labels those of the second player “Player 2.” The numbers in the matrix represent payoffs also called utility. The first number applies to player 1, and the second to player 2. Higher numbers means the player likes that outcome better. Thus if player 2 chooses not to confess, then player 1 would rather confess than not, as represented by the fact that the payoff 20 is larger than the payoff 10. This reflects the fact that the police have offered him a good deal in exchange for his confession. By way of contrast, player 2 would prefer that player 1 not confess, as represented by the fact that the payoff –9 is smaller than the payoff 10. This reflects the fact that if his partner confesses but he does not, he is going to spend a substantial amount of time in prison.
We will go through the rest of the payoffs in a bit, but first – what do these numbers really mean? I want to emphasize that “utility” numbers are not meant to represent some sort of units of happiness that could be measured in the brain. Rather, economists recognize that players have preferences among the different things that can happen and are able to rank them. Assigning a utility of 10 to player 1 when the outcome is Not Confess/Not Confess and 20 when it is Confess/Not Confess is just a way of saying “Player 1 prefers the outcome Confess/Not Confess to the outcome Not Confess/Not Confess.”
More broadly, if certain regularities in preferences are true – for example they satisfy transitivity meaning that if you prefer apples to oranges and oranges to pears, then you also prefer apples to pears – then we can find numbers that represent those preferences in the sense that the analyst can determine which decision the player will make by comparing the utility numbers. However, while these utility numbers exist in the brain of the analyst we do not care whether or not they exist in the brain of the person.
The meaning of the utility numbers in the Prisoner’s Dilemma game is this: if neither suspect confesses, they go free, and split the proceeds of their crime which we represent by 10 units of utility for each suspect. Alternatively, if one prisoner confesses and the other does not, the prisoner who confesses testifies against the other in exchange for going free and having some other charges dismissed and prefers this to simply splitting the proceeds of the crime. We represent this with a higher level of utility: 20. The prisoner who did not confess goes to prison, represented by a low utility of –9. Similarly, if both prisoners confess, then both are given a reduced term, but both are convicted, which we represent by giving each 2 units of utility: better than not confessing when you are ratted out, but not as good as going free.
This game is fascinating for a variety of reasons. First, it is a simple representation of a variety of important strategic situations. For example, instead of Confess/Not confess we could label the choices “contribute to the common good” and “behave selfishly.” This captures a variety of circumstances economists describe as public goods problems, for example the construction of a bridge. It is best for everyone if the bridge is built, but best for each individual if someone else builds the bridge. Similarly this game could describe two firms competing in the same market, and instead of Confess/Not confess we could label the choices “set a high price” and “set a low price.” Naturally it is best for both firms if they both set high prices, but best for each individual firm to capture the market by setting a low price while the opposition sets a high price. This is a critical feature of game theory: many apparently different circumstances – prisoners in jail; tax-payers voting on whether to build a bridge; firms competing in the market – give rise to similar strategic considerations. To understand one is to understand them all.
A second feature of the Prisoner’s Dilemma game is that it is easy to find the Nash equilibrium, and it is self-evident that this is how intelligent individuals should behave. No matter what a suspect believes his partner is going to do, it is always best to confess. If the partner in the other cell is not confessing, it is possible to get 20 instead of 10. If the partner in the other cell is confessing, it is possible to get 2 instead of –9. In other words – the best course of play is to confess no matter what you think your partner is doing. This is the simplest kind of Nash equilibrium. When you confess – even not knowing whether or not your opponent is confessing – that is the best you can do. This kind of Nash equilibrium – where the best course of play does not depend on beliefs about what the other player is doing – is called a dominant strategy equilibrium. In a game with a dominant strategy equilibrium we expect learning to take place rapidly – perhaps even instantaneously.
The striking fact about the Prisoner’s Dilemma game and the reason it exerts such fascination is that each player pursuing individually sensible behavior leads to a miserable social outcome. The Nash equilibrium results in each player getting only 2 units of utility, much less than the 10 units each that they would get if neither confessed. This highlights a conflict between the pursuit of individual goals and the common good that is at the heart of many social problems.
Pigouvian Taxes
Now let us return to question raised in the traffic game: what good does Nash equilibrium do us if we cannot figure out what it is? The answer is straightforward: the traffic game is like the Prisoner’s Dilemma. Each commuter by choosing to drive – rather than, for example, taking the bus – derives an individual advantage by getting to work faster and more conveniently. She also inflicts a cost – called by economists a negative externality – on everyone else by making it more difficult for them to get to work. In other words, the private value of each commuter is higher than the social value of driving. Hence, as in the Prisoner’s Dilemma game, the Nash equilibrium is not for the common good: Nash equilibrium results in too many people driving – everyone would be better off if fewer people commuted by car and chose alternatives such as living closer to work, implementing car pools, or occasionally taking the bus or telecommuting.
Economists have understood the solution to this problem since Pigou’s work in 1920. If we set a corrective tax – known as Pigouvian tax in honor of this French economist – and charge each commuter for the cost that they impose on others (and therefore we internalize this external cost), then Nash equilibrium will result in social efficiency. In this example social efficiency differs from the solely private interaction because of the fact that commuters do not consider the cost of congestion on other drivers. In the Prisoner’s Dilemma above, by choosing to confess you cause a loss of 19 to your opponent – the external effect. If we charge a Pigouvian tax of 19 for confessing the payoffs become
Not confess |
Confess |
|
Not confess |
10, 10 |
–9,1 |
Confess |
1,–9 |
–17, –17 |
Payoffs in Prisoner’s Dilemma with Pigouvian Tax
In this case the best thing to do irrespectively of your beliefs about your opponents’ actions – the dominant strategy – is to Not confess, and everyone gets 10 instead of 2. Notice that in this example – in the resulting equilibrium – nobody actually pays the tax.
To implement a Pigouvian tax in the traffic game is not so difficult. In some circumstances it may be hard to compute the costs imposed on others. But not so in the traffic game where traffic engineers can easily do simulations to calculate the additional commuting time from each additional commuter and economists can give a relatively accurate assessment of the social cost of the lost time based on prevailing wage rates. Moreover, with modern technology, it is quite feasible to charge commuters based on congestion and location – this is done using cameras and transponders already in cities such as London.
Given that the social gain from reducing commuting time dwarfs such things as the cost of fighting a war in Afghanistan, why do not large U.S. cities charge commuters a congestion tax? Unfortunately there is another game involved – the political game. As we observed in our analysis of voting, the benefit of voting is very small when the chances of changing the outcome are small. So voters are rationally going to avoid incurring the large cost of investigating the quality of political candidates through their platforms. This is particularly the case for something like commuting – although the total benefits are large, they are spread among a very large number of people. Since voters do not spend much effort monitoring politicians, politicians have a lot of latitude in what they do – and therefore voters quite rationally distrust them.
Voters are especially suspicious of offers by politicians to raise their taxes. Those who lean left notice that a commuter tax will favor the rich – who can afford the toll – at the expense of the poor – who would be forced into public transportation. The right leaners oppose additional taxes because they are afraid the government will squander the proceeds. In the end both parties collaborate to prevent an efficient solution to the problem of congestion. The obvious compromise is to charge a commuting fee and use the revenue to reduce the local sales tax – which also disproportionately falls on the poor. However: who in the world would believe a politician’s promise that this is what she will do?
Many solutions to economic problems are obvious. For example: virtually all economists favor raising the gas tax – this serves as a tax on pollution, and whatever one’s views of global warming, raising the gas tax is much more desirable than mandating fuel efficiency standards for cars, which is what we currently do. Unfortunately we do not yet have a good recommendation for what to do about the problem of voters who rationally invest little in monitoring politicians and the politicians of both parties who are rationally bought and paid for by special interests. As Winston Churchill said in a speech in the House of Commons in 1947.
No one pretends that democracy is perfect or all-wise. Indeed, it has been said that democracy is the worst form of government except all those other forms that have been tried from time to time.
The Repeated Prisoner’s Dilemma
The outcome of the Prisoner’s Dilemma is counterintuitive. If a prisoner rats out his partner should he not fear future retaliation? That depends on whether he is likely to meet the partner in the future or not. Implicit in the original formulation of the problem is that the prisoners will not meet in the future. In many practical situations this is not the case.
A simple model game theorists use for studying this problem is that of the repeated game. Suppose that after the first game ends, and the suspects either are freed or are released from jail, they will play the same game one more time. In this case – the first time the game is played – the suspects may reason that they should not confess because if they do their partner will follow suit when the game is played again. Strictly speaking, this conclusion is not valid, since in the second game both suspects will confess no matter what happened in the first game. However, repetition opens up the possibility of being rewarded or punished in the future for current behavior, and game theorists have provided a number of theories to explain the obvious intuition that if the game is repeated often enough, the suspects ought to cooperate rather than confess.
To analyze a repeated game we must consider the fact that the utilities or payoffs are received at different time periods. As a rule payoffs you receive in the future are worth less than those you receive today – “a bird in the hand” and all that. The standard model that economists use is that of discounting the future. More formally, the discount factor is a positive number less than one that is used to weight payoffs received in the “next period.” As an example, take the discount factor to be ¾. Suppose that 20 is received today and 12 next period. Then the present value consists of the 20 today plus ¾ of the 12 tomorrow, that is, 20 + 9 = 29. Notice that the discount factor depends – among other things – on the amount of time between “periods.” The longer the time considered between time periods, the smaller the discount factor.
A fundamental fact about Nash equilibrium in a repeated game is that while there can be more equilibria than in the one-shot game – the game played once – there can never be fewer. That is: suppose that all players follow the strategy of playing as they would in the one-shot game no matter what their opponents do. Since it was best for each player to play that way when the game was played once, it is still best when the game is played over and over again.
There are two different kinds of repeated game: there are games that are repeated with a definite ending. For example, the game may be played once, or twice, or four times – or any finite number of times. And there are games with an indefinite ending – for example every time the game is played, say, there might be a 50% chance it will be played again and a 50% chance it will end.
In the Prisoner’s Dilemma it makes quite a bit of difference whether there is a definite or indefinite ending. If there is a definite ending, then the last time the game is played everyone knows it is being played only once: thus both players confess no matter what has gone before – they not expect to interact ever again. But now think of the next to last period: everyone anticipates that no matter what happens today, tomorrow everyone will confess. Hence you might as well confess today since failing to do so will not result in favorable consideration by your partner next time around. A moment of reflection should convince you that the same is no true in the next-to-next to last period and so forth, working backwards to the first game. Consequently both players always confess.
The situation changes when there is an indefinite ending. Suppose the discount factor is  – you can think of the discount factor as the probabilistic ending. For simplicity, limit attention to three strategies in the repeated game which we label Grim, Not Confess and Confess. Not Confess means just that: don’t confess ever. Similarly Confess means always confess no matter what. Grim is trickier: don’t confess the first time you play, then starting the second time the game is played do whatever the other player did the first time the game was played. If your opponent plays Grim like you neither player ever confesses. The same happens if your opponent plays Not Confess, but if he plays Confess, then you also confess beginning in the second period.
– you can think of the discount factor as the probabilistic ending. For simplicity, limit attention to three strategies in the repeated game which we label Grim, Not Confess and Confess. Not Confess means just that: don’t confess ever. Similarly Confess means always confess no matter what. Grim is trickier: don’t confess the first time you play, then starting the second time the game is played do whatever the other player did the first time the game was played. If your opponent plays Grim like you neither player ever confesses. The same happens if your opponent plays Not Confess, but if he plays Confess, then you also confess beginning in the second period.
Let us compute the payoffs – in present value – when neither player ever confesses. In every period each player gets 10. This must be properly discounted, as a result the present value in this case is 10 + (9/10) 10 + (9/10)2 10 + … = 100. Here I am using the property of geometric sums that says that  with 0 < r < 1. More interesting is the case where a player choosing Grim meets an opponent playing Confess. The grim player gets –9 + (9/10) 2 + (9/10)2 2 + … = 9 and the confessor gets 20 + (9/10)2 + (9/10)2 2 + … = 38. The complete payoffs to all the different of combinations is shown in the matrix below:
with 0 < r < 1. More interesting is the case where a player choosing Grim meets an opponent playing Confess. The grim player gets –9 + (9/10) 2 + (9/10)2 2 + … = 9 and the confessor gets 20 + (9/10)2 + (9/10)2 2 + … = 38. The complete payoffs to all the different of combinations is shown in the matrix below:

Simplified Repeated Prisoner’s Dilemma Payoffs
To find the Nash equilibrium, we start by asking the hypothetical question: if your opponent played Grim (Not Confess, Confess respectively), what would you like to do? If you thought your opponent was playing Grim, you would like to either play Grim or to Not Confess as this would result in a payoff of 100 rather than 38. This is marked with an asterisk in the matrix, and is called by game theorists a best response. If you think your opponent is not confessing, you would like to Confess and get 200, and you would also like to Confess and get 20 if your opponent is confessing. The Nash equilibria are the mutual best responses where both players are playing best responses to each other at the same time – the cells in the matrix with two asterisks. As you can see there are two pure strategy Nash equilibria – we leave the third Nash equilibrium using randomization for later analysis. As we observed – the original Nash equilibrium of the one-shot game at Confess-Confess is still a Nash equilibrium. Further there is an additional Nash equilibrium: Grim-Grim. If your opponent is playing Grim you do not want to cross her by confessing – the gain of 20 for one period is more than offset by the fact that you will lose 8 every period forever after.
Does that sound a bit theoretical? In 2005 Pedro Dal Bo took the Prisoner’s dilemma theory to the laboratory. He had players play the one-shot game. He had them play for two periods and for four periods (without any discounting). And then he had them play an indefinite ending – he had them play “dice games” where at the end of each round a dice was used to determine whether play would continue. He studied games where the chance of continuing was ½ and also games where it was ¾. To give players a chance to “learn their way to equilibrium” each player played 10 of these repeated games. The table below reports how often players succeeded in cooperating (not confessing) based on the type of game and how experienced players were.
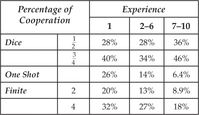
Percentage of Cooperation
Recall the predictions of the theory. In the one-shot and finite games players should not cooperate. Inexperienced players do cooperate in violation of the theory. This had also been remarked on by earlier investigators who concluded the theory was deficient. However, as players become more experienced their willingness to cooperate declines dramatically. Even when the game is repeated four times, cooperation falls to 18%, less than is the case in any game with inexperienced players. By way of contrast, in the dice games there are equilibria where players do not cooperate, but also equilibria in which they do. Here – in comparison to the finite length games – cooperation rather than diminishing over time actually increases over time. When there is a ¾ chance the game will continue – meaning on average the game will last four periods – experienced players cooperate 46% of the time.
Altruism and the Prisoner’s Dilemma
The theory of Nash equilibrium does not perfectly describe how people played in Dal Bo’s experiment. Some cooperation is taking place with relatively experienced players even when the game has a definite ending. This is not completely unexpected as in laboratory experiments about 10–20% of the participants are not paying attention to the instructions and play in a way unpredictable by any theory, rational or behavioral. The presence of a modest number of foolish players is a topic we will take up later. For the moment notice that the 18% of experienced cooperators during four period games cannot easily be dismissed as “inattentive.”
What conclusion can we reach about these “irrational” cooperators? One possibility is that they engage in a kind of magical reasoning that “if I cooperate then my opponent will cooperate,” or “the only way we can beat this dilemma is if we both cooperate so I better cooperate.” However, unless players are mind readers, this reasoning is wrong: there can be no causal link between what you do in the privacy of your own computer booth, and your unknown opponent does in hers. Experienced players have had ample opportunity to learn the fallacy of this reasoning, so it is difficult to explain their play this way.
A more likely explanation is players are rational and altruistic in the technical sense that they care not only about their own monetary payoff, but also that of their opponent. It is, after all, our common experience that some people are sometimes altruistic and as we shall see, we observe altruism in many other laboratory experiments.
A second possibility is that players have not completely learned the equilibrium. That is, if players start out cooperating in hopes of eliciting future cooperation, the first thing they will discover is that it is a mistake to cooperate in the fourth period. After players stop cooperating in the fourth period they will then discover it is a mistake to cooperate in the third period – and it may take a while before they stop cooperating in the first period. The fact that this can take a long while was first shown in simulations by John Nachbar in 1989.
What can we say about these two explanations? Economists have studied altruism for many years – it was central to Barro’s 1984 study of who bears the burden of taxes, for example. Yet while it is certainly real it is often ignored by economists because it is quantitatively small. People do give to charities, but for example in the United States – which has the highest rate of giving – only about 2.2–2.3% of Gross Domestic Product (GDP) is given. Moreover some of this is not strictly speaking “charitable” but rather fee for services, such as the 35% of donations that are given to religious organizations (GivingUSA, 2009). Further, as we shall see, in experiments where we can measure the relative contribution of “behavioral” preferences such as altruism and imperfect learning, imperfect learning is two to three times more important.
Despite the fact that it is unimportant in many settings, a little bit of altruism can go a long way – for example, a willingness to be altruistic only in the final period of a repeated game can dramatically change the strategic nature of the game. A player who is willing to cooperate in the final period can hold that out as a prospective reward to a not so altruistic opponent, and so get them to cooperate. This sort of altruism – kind to those people who are kind to you – is called reciprocal altruism. It is present in Dal Bo’s experiment. From his data we can look at the final period of the two period games with a definite ending. Against an experienced player (one who has already engaged in six or more matches) if you cheat in the first period probability of getting cooperation in the final period is only 3.2% – much less than the 6.4% chance of finding an experienced cooperative opponent in the one-shot game. On the other hand, if you cooperate the chance of getting cooperation in the final round jumps to 21% - much higher than the 6.4% cooperation in the one-shot case.
Reciprocal cooperation is interesting and much studied for two reasons: first, because in games taking place over time it has a big impact on equilibrium outcomes. Second, because it is difficult to distinguish from strategic non-altruistic behavior. That is: did I take care of my aged parent because I am altruistic or because I want to get an inheritance? Even in the experimental laboratory we must worry that the students who are the experimental subjects get together and share experiences afterwards. If I am a poor liar, I may be reluctant to behave selfishly in fear that I may spill the beans to my friends, and so earn their disrespect – a fate fare worse than losing a few dollars in the laboratory.
Although altruism has been studied by economists for many years, the social preferences of fairness and reciprocal altruism have not been as thoroughly examined, and are a major subject of current research interest by economists such as Rabin [1993], Levine [1998], Fehr and Schmidt [1999], Bolton and Ockenfels [2000], Gul and Pesendorfer [2004], and Cox, Friedman and Sadiraj [2008].
Do Better People Make a Better Society?
We can demonstrate some of the power and meaning of game theory by considering the following statement: “If we were all better people the world would be a better place.” This may seem to be self-evidently true. Or you may recognize that as a matter of logic this involves the fallacy of composition: just because a statement applies to each individual person it need not apply to the group. Game theory can give precise meaning to the statement of both what it means to be better people and what it means for the world to be a better place, and so makes it possible to prove or disprove the statement.
A sensible meaning of “being a better person” is to obey the biblical injunction to “love your neighbor as yourself” – that is, to be altruistic. If I truly value you – my neighbor – as myself, then I should place the same value on your utility as on my own: simply adding the two together. Hence if my selfish utility is 20 and yours is –9, my “altruistic utility” is just the sum of the two, that is to say, 11. If we begin with the payoffs in the Prisoner’s Dilemma game above, we may proceed in this way to compute the payoffs in the Biblical Game:
Not confess |
Confess |
|
Not confess |
20*,20* |
11*,11 |
Confess |
11,11* |
4,4 |
Biblical Game Payoffs
This game is easy to analyze: it has a dominant strategy equilibrium. No matter what you do and what I think you will do, the best thing for me to do is not to confess. For that reason the Nash equilibrium is that neither of us confesses and consequently we both get 10 – clearly a better outcome than the original equilibrium outcome of the Prisoner’s Dilemma game where we each get 2. As a result it seems if we were perfect people the world would be a better place.
The assertion, however, was not “if we were all perfect people the world would be a better place,” but rather “if we were all better people the world would be a better place.” A simple example adapted from Martin Osborne’s [2003] textbook illustrates the basic concept. Consider the Bus Seating Game. There is only one vacant bench on a bus and two passengers. If both passengers sit on the bench, both receive 2. If both stand, both receive 1 as it is less pleasant to stand than to sit. If one sits and one stands, the sitting passenger gets 3 as it is more pleasant to sit by one’s self than to share a bench, and the standing passenger gets 0 as it is more pleasant to share the discomfort of standing than to watch someone else seated in comfort. The payoff matrix of this game is given below:
Sit |
Stand |
|
Sit |
2*,2* |
3*,0 |
Stand |
0,3* |
1,1 |
Bus Seating Game Payoffs
Here it is a dominant strategy for each passenger to sit and the dominant strategy equilibrium is Sit/Sit. Moreover, this is a desirable outcome – Pareto efficient in the sense that it cannot be improved on for both players – in that both players get 2 rather than one. In other words, by making one player better off we will be making the other player worse off.
Next suppose that rather than love our neighbor as ourselves, we are excessively altruistic, caring only about the comfort of our fellow passengers. In this Polite Bus Seating Game the payoffs are:
Sit |
Stand |
|
Sit |
2,2 |
0,3* |
Stand |
3*,0 |
1*,1* |
Polite Bus Seating Game Payoffs
In this game it is dominant for both passengers to stand – that is the Nash equilibrium is Stand/Stand – and both get 1 rather than 2. By excessive altruism, a game with a socially good dominant strategy equilibrium – Sit/Sit – is converted into a Prisoner’s Dilemma type of situation with a socially bad dominant strategy equilibrium.
Now you may feel this is unfair: perhaps excessive politeness and caring only about other people and not ourselves is perhaps not what we mean by “being a better person” and certainly is not very realistic. But the central idea – that the changes in payoffs due to greater altruism can change incentives in such a way so as to lead to a less favorable equilibrium is true more broadly. If we consider situations in which players have more than two strategies, we can cause a switch to a less favorable equilibrium with a more sensible and moderate interpretation of what it means to be a “better person.” The game we will use to illustrate this is a variant on the repeated Prisoner’s Dilemma game with discount factor  that we studied earlier. There we considered three strategies: Not Confess ever, always Confess and Grim. In this game, instead of Grim, there is a strategy called Tough. This is similar to Grim, except that if you play Tough you get a bonus of 15 at a cost to your opponent of 35. Hence the Tough Game has payoff matrix given by:
that we studied earlier. There we considered three strategies: Not Confess ever, always Confess and Grim. In this game, instead of Grim, there is a strategy called Tough. This is similar to Grim, except that if you play Tough you get a bonus of 15 at a cost to your opponent of 35. Hence the Tough Game has payoff matrix given by:
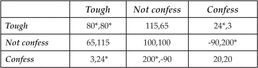
Tough Game Payoffs
Using the tool of best-responses, we see that this game has a unique Nash equilibrium of Tough-Tough giving both players 80. We can easily show this is the only possible equilibrium using a method called iterated dominance. Notice that Not confess is dominated by Tough, since no matter what the other player is doing, Tough always does better. Hence we throw out the strategy of Not confess and get a smaller game presented below:
Tough |
Confess |
|
Tough |
80,80 |
24,3 |
Confess |
3,24 |
20,20 |
Reduced Tough Game Payoffs
In this reduced game, we see that Tough-Tough is a dominant strategy equilibrium: this procedure of eliminating dominated strategies is called iterated dominance, and experimental evidence suggests that players learn their way to equilibrium without much difficulty in such games.
The Tough Game is very different than the Prisoner’s Dilemma game: while the unique equilibrium is not quite the best possible – players get 80 rather than the 100 they would get if the both played Not confess it is still quite a bit better than the 20 they each get from Confessing. In this sense the Tough Game is very like the Bus Seating Game in that the equilibrium is rather good for both players.
What happens if we “become better people?” Let us now take the reasonable interpretation that while I care about you, I am not completely altruistic. Suppose in particular that I place a weight of two on my selfish utility and a weight of one on yours. So, for example, in the Tough Game, if I get 65 and you get 15 then in the Altruistic Tough Game I get 2 × 65 + 115 = 245. The payoffs in the Altruistic Tough Game can be computed as:
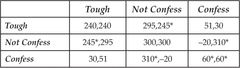
Altruistic Tough Game Payoffs
What happens? Using the tool of the best-response – look at those cells in the matrix with two asterisks – we see that the only equilibrium is the one in which both player Confess. When we compare the Tough Game to the Altruistic Tough Game, we see that greater altruism has disrupted the Tough-Tough equilibrium by causing players to generously switch to Not confess in order to give 55 to their opponent at a cost of only 5 to themselves. Unfortunately this does not result in an equilibrium: when both players are Not confessing they are still selfish enough to prefer to Confess.
Our conclusion? Far from making us better off, when we both become more altruist and more caring about one another, instead of us both getting a relatively high utility each period of 8, the equilibrium is disrupted, and we wind up in a situation in which we both get a utility each period of only 2. Notice how we can give a precise meaning to the “world being a better place.” If we both receive a utility of 2 per period rather than both receiving a utility of 8 per period, we agree the world is a worse place regardless of how altruistic or selfish we happen to be – or even how concerned about fairness we might be.
The key to game theory and to understanding why better people may make the world a worse place is to understand the delicate balance of equilibrium. It is true that if we simply become more caring and nothing else happens the world will at least be no worse. However: if we become more caring we will wish to change how we behave. In this example in which we both try to do this at the same time, the end result will make us all worse off.
We can put this in the context of day-to-day life: if we were all more altruistic we would choose to forgive and forget more criminal behavior – to turn the other cheek. The behavior of criminals has a complication though. More altruistic criminals would choose to commit fewer crimes. However, as crime is not punished so severely, they would be inclined to commit more crimes. If in the balance more crimes are committed, the world could certainly be a worse place. Our example shows how this might work.
The example of the Tough Game is very simple and not especially realistic. It is based on a 2008 academic paper by Hwang and Bowles. If you know some basic calculus the paper is very readable. They provide a much more persuasive and robust example tightly linked to experimental evidence showing how altruism can hurt cooperation.
Is Compromise Good?
The Tough Game illustrates a situation where the extremes are better than the intermediate case. If people are completely selfish the world is reasonably good; if they are completely altruistic it is even better, but if they are neither completely selfish nor completely altruistic then the world is a miserable place. Situations where a compromise is worse than either extreme are not so uncommon in economic analysis. Two important practical examples are the cases of bank regulation and of health insurance.
In the case of bank regulation, we have a system where deposits are insured by the Federal Government, which also oversees bank portfolios to ensure that banks do not engage in overly risky behavior. Some economists argue that a system without regulation and insurance would be a superior system. Others think the regulatory regime is better. Yet all economists agree that a system in which deposits are guaranteed – either explicitly through an insurance agency such as the FDIC or implicitly through “too big to fail” – and bank portfolios are not regulated would be a disaster. Then banks would acquire portfolios that promised a high rate of return but also a high risk of getting wiped out. Depositors and issuers of short- term bonds would head for the banks that offered the highest returns – knowing that the U.S. Treasury and Federal Reserve System will bail them out if things go south. Which of course eventually they will – leaving the taxpayer holding the bag. Does that sound familiar? It has happened twice in the last quarter century – during the Savings and Loan crisis of the late 1980s, and again in the crisis of 2008. Beware when bankers or other crony capitalists appear before Congress or State Legislatures arguing the merits of “deregulation.” What they mean is that they should be allowed to do whatever they want – especially paying themselves huge salaries for doing it – but that when things go wrong taxpayers should pay for all the losses.
Economists are not perfect people – like anyone else we put more weight on our own selfish interest than the common good. Because of this I am sure that some economists have managed to argue that this kind of “partial deregulation” is a good idea. However no economist who is not being paid to do so would argue for such a policy, and even those who do know better.
A similar problem arises with respect to health insurance. It is popular to argue that insurance companies should not be allowed to discriminate based on whether people are sick. After all, what good is insurance that you can’t have when you need it? However: if the decision to participate in health insurance is voluntary, then in such a system nobody would buy insurance until they were sick – meaning that there would be no health insurance at all. Economists refer to this as “adverse selection” – only the bad risks choose to get insured. Therefore we can have a system that excludes people based on pre-existing conditions, and we can have a system that does not discriminate but in which coverage is mandatory. Certainly the system that is halfway in between does not work. The reason that employer based health insurance works is because coverage is mandatory – if you work for that employer you must accept their health insurance. Indeed, as health care costs rise eventually only sick people will choose to work for firms that offer health insurance, while the healthy will choose to earn a substantially higher wage working for a firm that does not offer insurance. When that happens, the employer-based system will break down.
Bank Runs and the Crisis
The financial market meltdown in October 2009 has convinced many that markets are irrational, and rational models are doomed to failure. Only behavioral models recognizing the emotional “animal spirits” of investors can hope to capture the events that occur during a full blown financial panic. Most of this sentiment springs, however, from confusion about what rationality is and what rational models say.
Is it irrational to run for the exit when someone screams that the movie theater is on fire? Let’s analyze this problem using the tools of rational game theory. There are effectively two options: to exit in an orderly fashion, or to rush for the exit. To keep things simple, we’ll put your choice on the vertical and what everyone else does on the horizontal in the payoff matrix of this game. If everyone else is orderly and you rush, you get to the exit first, so are sure of escaping the fire. Let’s give this 10 units of utility. If you exit in an orderly way, you may not be first, consequently there is a chance – say 10% – you will be caught in the fire. Let’s assign that event a utility of 9. If everyone rushes and you are orderly, then you are likely not to escape – let’s assign that a utility of 0. If you rush along with everyone else, then you have a chance of escape – but less than if everyone exits in an orderly way, so let’s say that has a utility of 5. The table below shows your payoffs in this game:
Everyone else |
||
You |
Orderly |
Rush |
Orderly |
9 |
0 |
Rush |
10 |
5 |
Fire in the Theater Payoffs
This is simply a variation of the Prisoner’s Dilemma game. No matter what you think everyone else is doing – the dominant strategy for you is to rush. Of course in the resulting equilibrium everyone gets 5, while if they all exited in an orderly way they would all get 9.
Notice that the theory of rational play has no problem explaining the fact that everyone rushes for the exits – indeed that is exactly what the theory predicts. Nowhere do we model the very real sick feeling of panic that people feel as they rush for the exits. That is a symptom of being in a difficult situation, not an explanation of why people behave as they do. It isn’t paranoia if they are really out to get you.
The situation in a market panic is similar. Suppose you turn on the television and notice the Chairman of the Federal Reserve Board, hands trembling slightly, giving a speech indicating that the financial sector is close to meltdown. It occurs to you that when this happens, stocks will not have much value. Naturally you wish to sell your stocks – and to do so before they fall in price, which is to say, to sell before everyone else can rush to sell. Thus there is a “panic” as everyone rushes to sell. Individual behavior here is rational – and unlike the rushing to the exits where more lives would be spared if the exodus was orderly, in the stock market there is no real harm if people rush to sell rather than selling in an orderly way.
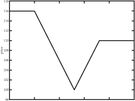
Panel (b): Theoretically Predicted Price Path
In some circumstances people overdo it – and the price drops so much that it bounces right back up as soon as people get their wits back. Perhaps this is due to irrationality? Not at all – there is a beautiful paper written in 2009 by Lasse Pedersen analyzing the so-called “quant event” of August 3–14 2007, where prices did exactly that. The first figure above shows the minute by minute real market price and the second figure shows prices computed from the theory. The two figures speak for themselves. The key thing to understand is that the theory is of pure rational expectations – irrationality, psychology, and “behavioral” economics do not enter the picture.
The same idea applies to bank runs. If you think your bank is going to fail taking your life savings with it, it is perfectly rational to try to get your money out as quickly as you can. If everyone does that it pretty much guarantees the bank will fail. A formal model of bank runs along these lines was first proposed by Diamond and Dybvig in the prestigious Journal of Political Economy in 1983. And no, I’m not picking some obscure paper that nobody in economics has paid any attention to – according to Google there have been 3,639 follow up papers. So far nobody has pointed out any facts or details about the financial crisis that is inconsistent with or fails to be predicted by these models of rational behavior.
Rational Expectations and Crashes
One problem with defending economics in public forums is that people you don’t know write you emails. The most common theme is “You guys didn’t predict the crisis so you are useless.” I’m not entirely clear on why the only possible use of economics should be to predict crises, but I can at least sympathize with the idea that failing to predict a giant crisis is a huge failure.
But is it? Step back a moment. Suppose that we could. We’d run a big computer program that all economists agreed was right, and everyone else believed, and it would tell us “Next week the stock market will fall 20%.” What would you do? Knowing the stock market will drop 20% next week, would you wait until next week to sell? Of course not, you’d want to dump your stocks before everyone else did. And when everyone tried to do that the stock market would drop by 20% – but not next week, it would happen right now. You don’t wait until you feel the flames before you rush for the theater exits.
Put another way, there is an intrinsic interaction between the forecaster and the forecast – at least if the forecaster is believed. Predicting economic activity isn’t like predicting the weather. Whether or not there is going to be a hurricane doesn’t depend on whether or not we think there is going to be a hurricane. Whether or not there is going to be an economic crisis depends on whether or not we think there is going to be one. And this is why the economics profession came to adopt the rational expectations model. Unlike behavioral models – which treat economic activity like hurricanes – the rational expectations model captures the intrinsic connection between the forecaster and the forecast. In fact one description of a model of rational expectations is that it describes a world where the forecaster has no advantage in making forecasts over anyone else in the economy – which if people believe his forecasts will have to be the case.
Did you get that? When people speak of “self-fulfilling prophecies” they aren’t talking about models of irrational behavior. Models of irrational behavior do not predict that there can be “self-fulfilling prophecies.” Only models of rational behavior do.
Let’s look at the criticism of the economics profession for having failed to predict the crisis more closely. One articulate critic of modern economics is a Nobel Prize winning economist – a New York Times columnist by the name of Paul Krugman who wrote in 2009 about
…the profession’s blindness to the very possibility of catastrophic failures in a market economy. During the golden years, financial economists came to believe that markets were inherently stable – indeed, that stocks and other assets were always priced just right. There was nothing in the prevailing models suggesting the possibility of the kind of collapse that happened last year.
But is that true? Some years earlier, in 1979, an economist wrote a paper called “A Model of Balance-of-Payments” showing how under perfect foresight crises are ubiquitous when speculators swoop in and sell short. The paper is deficient in that it supposes that crises are perfectly foreseen and – as indicated above – this cannot lead to catastrophic drops in prices. However, the paper is not obscure, there having been some 2,354 follow-on papers, including a beautiful paper written in 1983 by Steve Salant. Salant uses the tools of modern economics, in which the fundamental forces driving the economy are not perfectly foreseen, to show how rational expectations lead to speculation and unexpected yet catastrophic price drops. Lest you think that this 27 year old paper is lost in the mists of time… in 2001 I published a paper with Michele Boldrin entitled “Growth Cycles and Market Crashes.” The message was most assuredly not that the “kind of collapse that happened last year” is impossible or even unlikely.
Despite the fact that the idea of the Salant paper is integral to most modern economic models, it still never fails to surprise non-economists when market crises do occur. It has happened in England, Mexico, Argentina, Israel, Italy, Indonesia, Malaysia, Russia, and of course more than once in the United States. Perhaps policy makers and ordinary citizens should pay more attention to economists? The plaintiveness and whining when it happens are always the same: for example, in 1992, nine years after the Salant paper, Erik Ipsen reported in the New York Times that
Sweden’s abandonment Thursday of its battle to defend the krona, in a grudging capitulation to currency speculators, bodes ill for Europe’s other weak currencies and threatens to send new waves of turbulence through the European Monetary System.
The central bank, which jacked interest rates to an astronomical 500 percent to stave off devaluation during the European currency crisis in September, raised rates to 20 percent Thursday morning, from 11.5 percent, in a last attempt to bolster the krona, only to concede defeat hours later.
“The speculative forces just proved too strong,” Prime Minister Carl Bildt said in announcing that Sweden would let the krona float.
Those who forget history are doomed to repeat it. Oh, by the way – the author of that 1979 paper pointing out the ubiquity of crises? Paul Krugman.
The Economic Consequences of John Maynard Keynes
We have got quite a bit of mileage from variations of the theme of running for the exits – from the Prisoner’s dilemma game. But this is not the only game fraught with economic consequence. The coordination game – introduced by Thomas Schelling in 1960 – is another simple model with significant ramifications.
In the story told by Schelling, two strangers are told to meet in New York City on a specific day, but are unable to communicate with each other about the meeting place. Bear in mind that Schelling was writing in 1960, when the modern cell phone was not even a gleam in the science fiction novelists’ eye. It turns out that most people manage to say “noon in Grand Central station,” meaning that they mostly succeed in meeting each other.
To analyze this game theoretically, let’s imagine that the only other possible meeting place is Times Square. Specifically, we’ll suppose that the game matrix is a slight variation on the game analyzed by Schelling:
Grand Central |
Times Square |
|
Grand Central |
3*,3* |
0,0 |
Times Square |
0,0 |
2*,2* |
Schelling’s Meeting Game Payoffs
Here if they miss connections they get nothing, but we assume that since Times Square is more crowded than Grand Central, that they get slightly less – two instead of three – if they try to meet there.
This game is very different than the prisoner’s dilemma in that the interests of the two players are perfectly aligned – I would like to coordinate with you to meet at the same place. In particular, altruism or “goodness” has no role to play in this game. You might think that is pretty much the end of the story, but analysis of Nash equilibrium shows it is not. If you think the other person is going to Times Square – you should do the same. As a result the game has two rather than one pure-strategy Nash equilibrium, one where they meet at Grand Central and one where they meet in Times Square. There is also a Nash equilibrium involving randomization – I will talk about this later.
“This is silly,” you say, obviously Grand Central is better, we’ll meet there. And economists and game theorist agree. Alternatively suppose that it is much worse to be in Grand Central by yourself than in Times Square, so that the payoffs are really.
Grand Central |
Times Square |
|
Grand Central |
3*,3* |
–10,0 |
Times Square |
0,–10 |
2*,2* |
Grand Central Meeting Game Payoffs
Now are you so sure it is a good idea to go to Grand Central? After all if you are wrong about the other person you’ll be stuck with –10, while if you go to Times Square and the other person doesn’t show up you at least get 0. Similarly the other person reasoning the same way may also head to Times Square…. Then, in fact the relevant Nash equilibrium of this game may be Times Square/Times Square. This is worse than meeting in Grand Central – both get 2 instead of 3, and it is called a coordination failure equilibrium.
There is a theory of these coordination failure equilibria – but the concept of risk dominance that is used to analyze it and the probabilistic theory of learning that was created by Kandori, Mailath and Rob, and by Peyton Young in 1993 is too mathematical and complex to describe here. However – if you are a fan of the idea that economics spends too much time on rationality and not enough time on evolution, let me point out that these famous and highly cited articles employ…an evolutionary model.
That is digressive. The key point is that insofar as anybody has been able to make head or tails out of the confusing jumble of thought found in John Maynard Keyes General Theory of Employment, Interest and Money, it is the idea that there can be a coordination failure. That is, firms don’t produce because they don’t think anybody will buy their products, and consumers don’t buy because they don’t have any money because firms won’t employ them. There is no doubt that this makes logical sense – enough so that current pundits such as the ubiquitous Professor Krugman still wish to convince us that Keynes makes sense. The fact that nobody has been able to make sense out of Keynes isn’t because of ill-will or lack of effort on the part of the economics profession, however. Google shows some of the articles I’ve discussed with as many as several thousand citations; Keynes book, on the other hand, garners over ten thousand – and those are only the citations available by computer, which, since the book was published in 1936, misses most of them.
No, the problem with Keynes isn’t that it is impossible to construct a plausible yet logical model of what he had in mind. It’s just that every attempt to construct such a model has fallen victim of the evidence. First of all, if coordination failure was that easy, we would see it all the time – yet we’ve only had one Great Depression. At the time of the Great Depression, of course, models of the ubiquity of great depressions were very popular. For example, the leading growth model at that time was the Harrod-Domar model that said that the capitalist economy teetered on the razor’s edge, ready to fall into depression at an instant notice. It is perhaps unfortunate that the model was created between 1939 and 1946 – immediately proceeding one of the longest unbroken spells of growth and prosperity in history.
There have been valiant attempts – for example Leijonhufvud’s 1973 notion that there is a “classical corridor” in which as long as only moderately bad things happen, the economy behaves classically as predicted by some of the very early rational expectations models. However if something big and bad enough occurs – the collapse of the housing market? – then we are thrust into a Keynesian world of coordination failure.
The key problem is that Keynesian models are extremely delicate – writing in 1992 Jones and Manuelli show that coordination failure can occur only under very implausible assumptions about the economy. More to the point – there simply isn’t any empirical evidence pointing to coordination failure. We are rebounding from the current crisis – the theory of Keynes says we should not be doing so. Additionally modern analysis of the Great Depression, such as that of Cole and Ohanian [2004] suggests that the prolonged length of the depression was due more to bad government policies – the crony capitalism of the New Deal, for example – than to an intrinsic inability of a capitalist economy to right itself.




