Economic theory works some of the time. But perhaps not always? There is an experimental literature that argues there are gross violations of economic theory. Since these failures are not with the theory of Nash equilibrium, I will explain an important variation – the notion of subgame perfect equilibrium. How well does the theory of subgame perfection do in the laboratory? In three games – a public goods game called Best-shot, a bargaining game called Ultimatum and the game of Grab-a-dollar the simple theory with selfish players fails.
Subgame Perfection
Our notion of a game is a matrix game in which players simultaneously choose actions one time and one time only. Situations like this are rare outside the laboratory. The “real” theory of games has long-since incorporated both the presence of time – and that ubiquitous phenomenon known as uncertainty. Often when I am teaching a course and I get to this point, I say “now we start the real theory of games.” So let us begin.
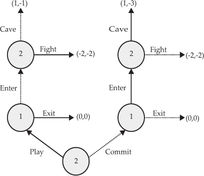
A “real” game involves players taking moves. Some may be simultaneous, in other cases we get to make choices after observing what other people have done. For example, we generally buy groceries after the store has posted the prices. To keep things easy, focus on sequential move games – although the complete theory allows both simultaneous and sequential moves. We model sequential moves by a game tree, a diagram of circles and arrows, with the circles indicating that a player is making a move, and the arrows the options available to that player. Below is illustrated a simple and famous example, the Selten Game:
Selten Game Tree
In this simple game player 1 moves first. Her decision node is represented by the circle labeled with her name “1.” She has two choices represented by arrows: to Enter the market or Exit the market. If she exits, the game ends and everyone gets a payoff of zero. If she enters, player 2 gets to move, as represented by the circle labeled with “2.” Player 2 has two possible responses to entry: either to Fight, or to Cave. If he fights, everyone loses, as indicated by the numbers –2, –2 representing the payoff to player 1 and player 2 respectively. If he Caves, player 1 wins and gets 1, while player 2 loses and gets –1. Notice that for player 2 it is better to cave and avoid the fight. Note the sequential nature of this game – player 2 gets to play only if player 1 decides to enter.
There are two ways to play this game. One is to play it as described. The other is to make advance plans. The idea of advance plans, or strategies is the heart of game theory. A strategy is a set of instructions that you can give to a friend – or program on a computer – explaining how you would like to play the game. It is a complete set of instructions: it must explain how to play in every circumstance that can arise in the game. As you can imagine this may not be very practical: think of trying to write down instructions for a friend to play a chess game on your behalf. Chess has a myriad of possible configurations – and you have to tell your friend how to play in each possible situation. Of course the IBM Corporation did provide a very effective set of instructions to the computer Deep Blue – so effective that Deep Blue beat the human world chess champion in 1997. For the rest of us implementing complex and effective strategies may not be so practical, but regardless, the idea of a strategy is very useful conceptually.
In the Selten Game, each player has two strategies. Player 1 can either exit or enter, and player 2 can either fight or cave. Notice that player 2’s strategy is conceptually different from player 1’s. Player 1’s strategy is a definite decision to do something. Player 2’s strategy is hypothetical: “if I get to play the game, here is what I will do.”
Strategies are chosen in advance – and each player has to choose a strategy without knowing what the other player has chosen. Thus, when the game is described by means of strategies it is a matrix game: each player chooses a strategy, and depending on the strategies chosen, they get payoffs. The matrix that goes with the Selten Game is below:
Fight |
Cave |
|
Enter |
–2,–2 |
1*,–1* (SGP) |
Exit |
0*,0*(Nash) |
0,0* |
Selten Game Payoffs
Notice how when player 1 chooses to exit it doesn’t matter what player 2 does – in that case player 2 does not get the chance to play.
We can analyze this game using our usual tools of best-response and Nash equilibrium. As marked in the matrix: if player 2 is going to fight, it is best for player 1 to exit; if player 2 is going to cave it is best for player 1 to enter. If player 1 is going to enter, it is best for player 2 to cave. If player 1 is going to exit, players do not interact at all, so it doesn’t really matter what player 2 does: she is indifferent.
The game has two Nash equilibria – exit/fight labeled “Nash” and enter/cave labeled “SGP” for reasons to be explained momentarily. Here is the thing: exit/fight while a Nash equilibrium is not completely plausible. Player 1 may reason to herself – if I were to enter rather than exit, it would not be in player 2’s interest to fight. So I believe that if I enter he will cave. In conclusion I see that I should go ahead and enter.
The notion that player 1 should enter is captured by the notion of subgame perfect equilibrium. This insists that not only should the strategies form an equilibrium, but, since (or if!) we believe the theory of Nash equilibrium, in every subgame the strategies in that subgame should also form a Nash equilibrium. In the Selten Game, there is one subgame: the game in which player 1 had chosen to enter – the subgame is very simple, it just consists of player 2 choosing whether to fight or to cave. It can be represented in matrix form as
Fight |
Cave |
–2,–2 |
1,–1 |
Selten Subgame Payoffs
As there is only one player in this subgame, the Nash equilibrium is obvious –1 is better than –2 so player 2 should cave.
This analysis is fine as far as it goes. But if I were player 2 and was discussing the game with player 1 before we played I would say “Don’t you dare enter – if you do I will fight.” I would say this because if I could convince player 1 of my willingness to fight he wouldn’t enter, and I would get 0 instead of –1. In game theory this is called commitment or precommitment, and is of enormous importance.
A practical example of the Selten game is the game played by the United States and Soviet Union during the Cold War – with nuclear weapons. We may imagine that player 1 is the Soviet Union, and entry corresponds to “invade Western Europe,” while fight means that the United States will respond with strategic nuclear weapons – effectively destroying the entire world. Naturally if the Soviet Union were to take over Western Europe it would hardly be rational for the United States to destroy the world. On the other hand, by persuading the Soviet Union of our irrational willingness to do this, we prevented them (perhaps) from invading Western Europe. As Richard Nixon instructed Henry Kissinger to say to the Russians “I am sorry, Mr. Ambassador, but [the president] is out of control… you know Nixon is obsessed about Communism. We can’t restrain him when he is angry – and he has his hand on the nuclear button.”
From a game-theoretic point of view, the game with commitment is a different game than the game without. In the Stackelberg Game illustrated below player 2 moves first and chooses whether to play or commit. If he chooses to play then the original game is played. If he chooses to commit, then a different game is played with the same structure and in which one payoff has been changed: the payoff to cave which is now –3 rather than –1. That is, the role of the commitment is to make it more expensive to cave.
The dashed arrows in the diagram show how to analyze subgame perfection. We start at the end of the game and work backwards towards the beginning. This is called backward induction, dynamic programming, or recursive analysis, and is a method widely used by economists to analyze complex problems involving the passage of time. We already implicitly used this method when we examined the finitely repeated Prisoner’s Dilemma: there we noticed that the final time the game was played it was optimal to confess. Here in the play subgame if player 2 gets the move, it is best – as shown by the dashed arrow – to cave. Working backwards in time knowing player 2 will cave it is best for player 1 to enter. In the commit subgame if player 2 gets the move it is best to fight since caving is now expensive. That means that in the commit subgame player 1 should exit. Should player 2 commit? If he chooses to play we see that player 1 will enter, he will cave and get –1. If he chooses to commit player 1 will exit and he will get 0. Consequently it is better to commit.
The Stackelberg Game illustrates the two essential components of effective commitment. First, it must be credible. There is no point in my threatening to blow up a hand grenade because I don’t like the service at a restaurant – nobody will believe me. In the Stackelberg Game the commitment is credible because it changes the payoff to caving from –1 to –3. This could be because of simple pride – having said I am committed to fighting I may feel humiliated by caving. Or it could be due to a real physical commitment.
A good example of commitment is in the wonderful game-theoretic movie Dr. Strangelove. Here it is the Soviet Union attempting to make a commitment to keep the United States from attacking. To make fight credible they build a doomsday device. This is an automated collection of gigantic atomic bombs buried underground in the Soviet Union and protected against tampering. If their computers detect an attack on the Soviet Union the doomsday device will automatically detonate and destroy the world. Because the device is proof against tampering the threat is credible: if the United States attacks, nobody, American or Soviet, can prevent the doomsday device from detonating. Devices like this were seriously discussed during the Cold War – and similar devices known as deadman switches have been used in practical wartime circumstances. A deadman switch is a switch that goes off if you die – for example, you remove the pin from a hand grenade, but keep your finger on a spring-loaded trigger. If your enemy kills you, your hand releases the trigger and blows you both to kingdom come. The advantage of such a device is that your enemy is not so tempted to kill you.
One essential element of commitment is that it must be credible. The other is that your opponent must know you are committed. A deadman switch is useless if your enemy doesn’t know you have one. A secret doomsday device is equally useless – and that is the heart of the movie Dr. Strangelove. The Soviets – apparently not being very bright – activate their doomsday device on Friday with the intention of revealing it to the world on Monday. Unfortunately a mad U.S. general decides to attack the Soviet Union over the weekend… go watch the movie – Peter Sellers plays half a dozen characters and is great as all of them.
And as long as I am on the subject of Peter Sellers, let me mention another fine example of commitment – this from his excellent Pink Panther movies in which Sellers plays the bumbling Inspector Clouseau. Clouseau has an assistant named Kato who is even more bungling than Clouseau himself. In order to provide himself incentive to stay alert against attackers, Clouseau instructs Kato to attack him without warning whenever he is not expecting it. Kato does so – always at especially inopportune moments such as the middle of a phone call or during a particularly elegant dinner date. Naturally – as with all good commitment – after the fact Clouseau has no interest in fighting with Kato and invariably instructs Kato to go away. Kato, obedient servant that he is, stops fighting – at which point Clouseau sneakily restarts the fight and gives Kato a long lecture about remaining alert. That game-theoretic point is that with a commitment there is always a tension since there is always a temptation not to carry out the threat.
In the end it doesn’t matter whether commitments are completely credible – with a truly awful threat just a small chance it will be carried out is enough to serve as an effective deterrent. Thankfully we will never know if the threat of nuclear holocaust which prevented the Cold War from becoming hot was credible.
Best-Shot
In 1989 Glenn Harrison and Jack Hirshleifer examined subgame perfection in a public goods contribution game called Best Shot. There are two players – player 1 moves first and chooses how much to contribute to the common good. After seeing player 1’s contribution player 2 decides also how much to contribute. The public benefit is determined by the largest contribution between the two players – that greatest contribution brings a benefit to both players as shown in the table below:
Contribution |
Public Benefit |
$0.00 |
$0.00 |
$1.64 |
$1.95 |
$3.28 |
$3.70 |
$4.10 |
$4.50 |
$6.50 |
$6.60 |
Best Shot Public Benefit
We can analyze this using the tool of best response. If your opponent contributes nothing then selfish you get the difference between your benefit and your contribution as shown below – the best amount to contribute is $3.28 giving you a net private benefit of $0.42.
Contribution |
Net Private Benefit |
$0.00 |
$0.00 |
$0.31 |
|
$3.28 |
$0.42 |
$4.10 |
$0.40 |
$6.50 |
$0.10 |
Best Shot Private Benefit
On the other hand, if your opponent contributes something, your contribution only matters if you contribute more than her, and it is easy to check that it is never worth contributing anything. For example, if your opponent contributes $1.64 you get $1.95; if you contribute $1.64 you still get $1.95; if you contribute more than that your additional benefit is given by:
Contribution |
Additional Benefit |
$3.28 |
$1.75 |
$4.10 |
$2.55 |
$6.50 |
$4.65 |
Additional Benefit when Opponent Contributes $1.64
so that the additional benefit of contribution is always less than the amount you have to put in.
What does subgame perfection say about this game? If I contribute nothing, then it is best for my opponent to put in $3.28 giving me $3.70. If I contribute anything it is best for my opponent to put in nothing, so I should put in $3.28 giving me a net of $0.42. So it is in fact best for me as the first mover not to contribute and force my opponent to make the contribution. Moreover, when Harrison and Hirshleifer carried out this experiment in the laboratory this is more or less what they found.
In 1992 Prasnikar and Roth carried out a variation on the Harrison and Hirshleifer experiment. They noticed that while Harrison and Hirshleifer had not told participants what the payoffs of their opponent were, they allowed them to alternate between being moving first and second, so implicitly allowed them to realize that their opponent had the same payoffs that they did. To understand more clearly what was going on Prasnikar and Roth forced players to remain in one player role for the entire ten times they got to play the game – that is they either moved first in all matches, or they moved second in all matches. They carried out the experiment under two different information conditions. In the full information condition players were informed of their own payoffs and that their opponent faced the same payoffs. In the partial information condition players were informed only of their own payoffs and were not told that their opponent faced the same payoffs.
In the full information treatment in the final eight rounds as the theory predicts the first mover never made a contribution. In the partial information treatment the bulk of matches also resulted in one player contributing $3.28 and the other $0.00 – but in over half of those matches the player who contributed the $3.28 was the first player rather than – as predicted by subgame perfection – the second player.
On the one hand this is a rather dramatic failure of the notion of subgame perfection. On the other hand – if players don’t know the payoffs of their opponent, they can hardly reason what their opponent will do in a subgame, so subgame perfection does not seem terribly relevant to a situation like this. Nor can we expect players necessarily to learn their way to equilibrium – if I move first and kick in $3.28 my opponent will contribute nothing – and I will never learn that had I not bothered to contribute my opponent would have put the $3.28 in for me. We will return to these learning theoretic considerations later.
If we view subgame perfection as a theory of what happens when players are fully informed of the structure of the game we should not expect the predictions to hold up when they are only half informed.
Information and Subgame Perfection
It is silly to expect subgame perfection when players have no idea what the motivations of their opponents might be. We might, however, hope that the predictions hold up when there is only a small departure from the assumption of perfect information about the game. Unfortunately the theory itself tells us that this is not the case.
In 1988 – before the Harrison and Hirshleifer paper was published – Drew Fudenberg, David Kreps and I conducted a theoretical study of the robustness of subgame perfect equilibrium to informational conditions. The main point can be illustrated in a simple variation of the Selten Game, the Elaborated Selten Game shown below.
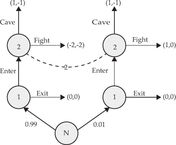
Elaborated Selten Game Tree
This diagram augments the earlier portraits of an extensive form game – that is, a game played over time – in two ways. First, it introduces an artificial player called Nature labeled N. Nature is not strategic but simply moves randomly. The moves of Nature are labeled with probabilities: in this game with probability 0.99 Nature chooses the Selten game. With probability 0.01 Nature chooses an alternative game. Player 1, who moves first, learns which game is being played. Player 2 who moves second does not. To represent player 2’s ignorance we draw a dashed line – an information set – connecting the two different nodes at which he might move. This means that while player 2 knows the probabilities with which Nature chooses the game that is played, he is uncertain about which one is actually being played. Notice how a game theorist approaches the issue of “not knowing what game we are playing” by explicitly introducing the possibility that there might be more than one game that can be played.
In this game particular strategies for the two players are shown by the red arrows. If Nature chooses the original game, player 1 exits – exactly what subgame perfection convinces us that player 1 should not do. If Nature chooses the alternative game player 1 enters. If player 2 gets the move he fights. Notice that the information set for player 2 means that player 2 – not knowing which eventuality holds – must fight regardless of which game is played.
The alternative game has payoffs similar to the Selten game, except that the payoffs to fight have been changed from (–2, –2) to (1, 0). Moreover, given the strategy of player 1, player 2 expects to play sometimes. What does player 2 think when he gets to play? Knowing player 1’s strategy, he knows that he is getting to play because Nature chose the alternative game. Hence he knows that it is better to fight than to cave. But player 1 in the alternative game understands that if she enters player 2 will fight – and she will get 1 rather than 0 by exiting so entering is in fact the right thing for player 1 to do. On the other hand in the original game she also knows if she enters player 2 will fight, so now exiting is the right move.
As it happens this Elaborated Selten Game is not usefully analyzed by subgame perfection – it has no subgames! Game theorists have introduced a variety of methods of bringing subgame perfection like arguments to bear on such games: sequential equilibrium, divine equilibrium, intuitive criterion equilibrium, proper equilibrium and hyperstable equilibrium are among the “refinements” of Nash equilibrium that game theorists have considered. However: the equilibrium we have described has the property that it is a strict Nash equilibrium meaning that no player is indifferent between their equilibrium strategy and any alternative. A strict Nash equilibrium is “all of the above:” it is subgame perfect, sequentially rational, divine, proper, hyperstable, and satisfies the intuitive criterion. In this sense the prediction of subgame perfection is not robust to the introduction of a small amount of uncertainty about the game being played: the equilibrium play that fails to be subgame perfect – exit by player 1 – appears as part of a strict and therefore robust Nash equilibrium. If players are a little unsure of what game they are playing it is merely glib to rule out this possibility. This major theoretical deficiency of the theory of subgame perfection helps explain why it does not do so well in practice.
Ultimatum Bargaining
One of the famous “failures” of economic theory is in the ultimatum bargaining game. Here one player proposes the division of an amount of money – often $10, and usually in increments of 5 cents – and the second player may accept, in which case the money is divided as agreed on, or reject, in which case neither player gets anything. If the second player is selfish, he must accept any offer that gives him more than zero. Given this, the first player should ask for – and get – at least $9.95. That is the reasoning of subgame perfect equilibrium. Notice, incidentally, that in this game players are fully informed about each other’s payoffs.
Not surprisingly this prediction – that the first player asks for and gets $9.95 – is strongly rejected in the laboratory. The table below shows the experimental results of Roth, Prasnikar, Okuno-Fujiwara and Zamir [1991]. The first column shows how much of the $10 is offered to the second player. (The data is rounded off.) The number of offers of each type is recorded in the second column, and the fraction of second players who reject is in the third column.
Amount of Offer |
Number of Offers |
Rejection Probability |
$3.00 or less |
3 |
66% |
$4.75 to $4.00 |
11 |
27% |
$5.00 |
13 |
0% |
U.S. $10.00 stake games, round 10 |
||
Ultimatum Bargaining Experimental Results
Notice that the results cannot easily be attributed to confusion or inexperience, as players have already engaged in 9 matches with other players. It is far from the case that the first player asks for and gets $9.95. Most ask for and get $5.00, and the few that ask for more than $6.00 are likely to have their offer rejected.
Looking at the data a simple hypothesis presents itself: players are not strategic at all they are “behavioral” and fair-minded and just like to split the $10.00 equally. Aside from the fact that this “theory” ignores slightly more than half the observations in which the two players do not split 50-50, it might be wise to understand whether the “economic theory” of rational strategic play has really failed here – and if so how.
The place to start is by looking at the rejections. Economic theory does not demand that players be selfish, although that may be a convenient approximation in certain circumstances, such as competitive markets. Yet it is clear from the rejections that players are not selfish. A selfish player would never reject a positive offer, yet ungenerous offers are likely to be rejected. Technically this form of social preference is called spite: the willingness to accept a loss in order to deprive the opponent of a gain. Once we take account of the spite of the second player, the unwillingness of the first player to make large demands becomes understandable.
There is a failure of the theory here, but it is not the fact that the players moving first demand so little. Indeed, from the perspective of Nash equilibrium rather than subgame perfection, practically anything can be an equilibrium: I might ask for only $4.00 thinking you will reject any less favorable offer – and you not expecting to ever be offered less than $6.00 can “hypothetically” reject all less favorable offers at no cost at all. This highlights a key fact about Nash equilibrium – the main problem with Nash equilibrium isn’t that it is so often wrong – it is that many times it has little to say. A theory that says “player 1 could offer $5.00… or $2.00… or $8.00” isn’t of that much use. Unfortunately the theory does say that all the player 1’s must make exactly the same offer as each other. Clearly that is not the case as about half the players offer $5.00 and about half offer less than that.
Recall our rationale for Nash equilibrium: it was a rationale of players learning how to expect their opponent to play. Here if I continually offer my opponent $5.00 I won’t learn that they would have been equally likely to accept an offer of $4.75. From the point of view of learning theory Nash equilibrium is problematic in a setting where not everything about your opponent is revealed after each match. We will return to this issue subsequently when we discuss learning theory.
To sum up, the experimental evidence is dramatic: the “theory” predicts the first mover asks for and gets $9.95 or more, while in the experiment nearly half the first movers ask for only $5.00. Yet on closer examination we see that the failure is not so dramatic. The “theory” in question is that of subgame perfection which we know not to be terribly robust. The assumption of selfishness fails, but that is not part of any theory of “rational” play. There is a failure, but it is a different – and more modest – failure. The robust theory of Nash equilibrium is on the one hand weak and tells us little about what sort of offers should be made. On the other hand it predicts all the first movers should make the same offers, and while 90% of them offer in the narrow range between $5.00 and $4.00, they do not all make the same offer.
In a sense the strongest test of subgame perfection is in a game lasting many rounds – can players indeed carry out many stages of recursive reasoning from the end of such a game? One such game is called Grab a Dollar. In this game there are two players and a dollar on the table between them. They take turns either passing or grabbing. Each time a player passes the money on the table is doubled. If as player grabs, she gets the money and the game ends. After a certain number of rounds specified in advance, there is a final round in which the player whose turn it is to move can either grab the money, or leave double the amount to her opponent.
What does subgame perfection say about such a game? Once again we use backward induction to solve the game. In the final round a selfish player should grab. Knowing your opponent will grab in the final round, the player moving next to last should grab right away, so on and so forth. We conclude that in the subgame perfect equilibrium the first player to moves grabs the dollar immediately. It is a little more difficult to show – but the same is true in Nash equilibrium as well.
In 1992 McKelvey and Palfrey tried a variant of this game in the laboratory. Rather than 100% of the money pile, the player who grabbed got only 80% while the loser got the remaining 20%. They also started with $0.50 rather than a dollar. Nevertheless both the subgame perfect equilibrium and indeed all Nash equilibria have the first player to grabbing the $0.50 right away rather than waiting and getting only $0.20 when her opponent grabs in the second round.
In the experiment there were four rounds: the game tree is illustrated below with the options labeled as G1, P1, G2, P2, G3, P3, G4, P4 for grabbing and passing on moves 1, 2, 3 or 4 respectively. Next to each option is shown the fraction of the players who chose that option in brackets. The failure of subgame perfection – and Nash equilibrium – is as dramatic, or perhaps more so, than in ultimatum bargaining. According the theory 100% of people should choose G1, while in fact only 8% of them do.
As in ultimatum bargaining, the place to begin to understand whether the theory has in fact “failed” – and if so, how – is in the final round. Notice that 18% of the player 2’s who make it to the final round choose P4 – that is to pass rather than to grab. There is no strategic issue that they face: the game is over – they must decide whether to take $3.20 leaving $0.80 to player 1, or whether to give up $1.60 in order to increase the payment to player 1 by $5.60. Apparently 18% of player 2’s are altruistic enough to choose the latter.
What may not be so obvious is that 18% of player 2’s giving money away at the end of the game changes the strategic nature of play quite a lot. What should a selfish player 1 do on the third move? If he grabs he gets $1.60. If he passes he has an 18% chance of getting $6.40 and an 82% chance of getting $0.80 – that means on average he can expect to earn slightly over $1.80 by passing. In other words – it is better to pass than to grab. The same is true for all the earlier moves – the best thing to do is to stay in as long as you can and hope if you are player 1 you have a kind player 2, and if you are player 2 that you make it to the last round where you can grab.
The puzzle here is not that players are not dropping out fast enough – it is that they are dropping out too soon! Yet perhaps that should not be such a puzzle from the perspective of learning theory: if I am one of the 8% of players who choose to drop out in the first round I will not have the chance to discover that 18% of player 2’s are giving money away in the final round.