The previous chapter discussed various irrationalities and biases alleged by behavioral economists. Much of the work in behavioral economics, however, has focused on the elements of time and uncertainty. Unlike the biases of the previous chapter – which generally attack issues that are not of great interest to economists – time and uncertainty lie at the very heart of modern economics. So let us examine these topics from the behavioral point of view.

Present Bias

As we said, in the idealized world usually studied by economists, there is no need for a single decision-maker ever to commit. In reality we often choose to make commitments to avoid future behavior we expect to find tempting but with bad long-term consequences: the drug addict who locks himself in a rehab center would be another obvious example. The long-term membership in a health club has a similar flavor. Skipping a workout can be tempting but has bad long-term consequences for health. Having to pony up $10 makes it easier to find excuses to avoid going.

There is little new under the sun: the economist Richard Strotz was studying problems of self-commitment in the rather mainstream Review of Economic Studies back in 1955. However the type of models he proposed were not widely used until the “behavioral economics revolution.” Two models that have come into widespread use are called respectively hyperbolic and quasi-hyperbolic discounting (also known as the beta-delta model) – as opposed to the more ordinary and familiar geometric sort of discounting. David Laibson’s [1997] paper examining the consequences of hyperbolic discounting models for consumption behavior – a topic of great interest to economists, although quite possibly nobody else – was published in the also mainstream Quarterly Journal of Economics and has been cited some 1543 times, so cannot be said to have been overlooked. The only problem with the model is that it predicts that present bias should not depend on whether or not the reward is uncertain. Unfortunately this is not the case.

Turning back to the data from Keren and Roelofsma [1995] as displayed in the table above – they examined what happened to preference reversals when there was only a 50% chance of getting the money.

A fair summary of the data is that when the chance of reward is only 50% people behave pretty much the same way with respect to both the present and future reward as they do with a certain future reward. If a non-standard model of discounting is needed to understand the first column, the standard model is needed to understand the second. This makes it hard to argue that the “behavioral” model is better than the standard one.

While it isn’t at all obvious that present bias has much to say about why we have economic crises or some countries are so poor, the topic has still gained the interest of economists, even economists such as the Princetonian pair Faruk Gul and Wolfgang Pesendorfer who are strongly declared opponents of any notion of behavioral. In 2001 the two wrote a paper proposing that people have preferences over menus – lists of which options will be available – that exhibit a preference for commitment. Dekel, Lipman and Rustichini proposed a similar model at about the same time. Variants of these models including models of internal conflict called self-control models are a major topic of ongoing research. For example, the enormously distinguished and mainstream economists Drew Fudenberg and David Levine wrote about self-control models in the American Economic Review in 2006 and again in Econometrica in 2012.

The fact is that a lot of behavior that is commonly thought to be impulsive – spur of the moment, giving in to temptation and taking immediate gratification at the expense of the future – is nothing of the sort. Gambling and sexual behavior are common examples of supposedly impulsive behavior. Nevertheless this so called “impulsive” behavior – giving in to temptation – is often anything but. Take Eliot Spitzer who lost his job as governor of New York because of his “impulsive” behavior in visiting prostitutes. The reality is that he paid months in advance (committing himself to seeing prostitutes rather than committing himself to avoiding them) and in one case flew a prostitute from Washington D.C. to New York – managing to violate Federal as well as State law in the process. Similarly, when Rush Limbaugh was discovered to be carrying large quantities of Viagra from the Dominican Republic it was widely suspected that he had gone there on a “sex vacation” – hardly something done impulsively at the last minute. Or perhaps a case more familiar to most of us – the Las Vegas102 vacation? This is planned well in advance and we spend months enjoying the anticipation of the rush of engaging in impulsive behavior. Of course, the more sensible among us may plan to limit the amount of cash we bring along.

The point here is simple: our “rational” self is not intrinsically in conflict with our impulsive self. The evidence is that our rational self often facilitates rather than overrides the activities of our impulsive self.

Procrastination

Prominent on Akerlof’s list of “behavioral” phenomena is procrastination. This is something we are all familiar with – but what is it exactly? When I quizzed a behavioral economist for examples he came up with the following list.

Here is the thing: none of these is the least irrational. In each case an unpleasant task is delayed until the deadline. But if the task is unpleasant and we are impatient – as economists assume we are – then the best thing to do is to wait until the deadline. In the folk story:

The king had a favorite horse that he loved very much. It was a beautiful and very smart stallion, and the king had taught it all kinds of tricks. The king would ride the horse almost every day, and frequently parade it and show off its tricks to his guards.

A prisoner who was scheduled to be executed soon saw the king with his horse through his cell window and decided to send the king a message. The message said, “Your Royal Highness, if you will spare my life, and let me spend an hour each day with your favorite horse for a year, I will teach your horse to sing.”

The king was amused by the offer and granted the request. So, each day the prisoner would be taken from his cell to the horse’s paddock, and he would sing to the horse “La-la-la-la” and would feed the horse sugar and carrots and oats, and the horse would neigh. And, all the guards would laugh at him for being so foolish.

One day, one of the guards, who had become somewhat friendly with the prisoner, asked him, “Why do you do such a foolish thing every day singing to the horse, and letting everyone laugh at you? You know you can’t teach a horse to sing. The year will pass, the horse will not sing, and the king will execute you.”

The prisoner replied, “A year is a long time. Anything can happen. In a year the king may die. Or I may die. Or the horse may die. Or… The horse may learn to sing.”

We previously discussed the DellaVigna and Malmendier [2006] study of health club memberships. They provide evidence that people pay extra to self-commit to exercising. They also discuss procrastination: the fact that people after they stop attending delay canceling their memberships. Unlike the example above there is no issue of delaying an unpleasant task until a deadline. So: is this the irrational procrastination Akerlof is concerned about? DellaVigna and Malmendier’s data shows that people typically procrastinate for an average of 2.3 months before canceling their self-renewing membership. The average amount lost is nearly $70 against canceling at the first moment that attendance stops.

Leaving aside the fact that it may take a while after last attending to make the final decision to quit the club, we are all familiar with this kind of procrastination. Why cancel today when we could cancel tomorrow instead? Or given the monthly nature of the charge, why not wait until next month. One behavioral interpretation of procrastination is that people are naïve in the sense that they do not understand that they are procrastinators. That is, they put off until tomorrow, believing they will act tomorrow, and do not understand that tomorrow they will face the same problem and put off again. There may indeed be some people that behave this way. But if we grant that people who put off cancellation are making a mistake, there are several kinds of untrue beliefs they might hold. One is that they falsely believe that they are not procrastinators. DellaVigna and Malmendier assert that canceling a membership is a simple inexpensive procedure. Supposing this to be true, it might be that people falsely believe that it will be a time consuming hassle. Foolishly they think canceling will involve endless telephone menus, employees who vanish in back rooms for long periods of time, and all the other things we are familiar with whenever we try to cancel an automatic credit card charge.

The question to raise about the “naïve” interpretation is this. Which is more likely: that people are misinformed about something they have observed every day for their entire lives (whether or not they are procrastinators) or something that they have observed infrequently and for which the data indicates costs may be high (canceling)? Learning theory suggests the latter – people are more likely to make mistakes about things they know little about. Behavioral economics argue the former is more likely.

Uncertainty surrounds us, and is central to modern economic models. People’s attitude towards risk and uncertainty is at the core of economic theory. Although behavioral economists sling around terms such as “loss aversion” to explain that the standard model is deficient deviations from the theory are in fact quite subtle, and indeed, impossible to understand without knowing something about the standard theory.

The basic economic theory of choice under uncertainty is called expected utility theory – the theory dates back to Daniel Bernoulli in 1738. However: utility theory is a construct. What is always fundamental in economics are preferences – in this case preferences between different risky prospects or lotteries.

For concreteness, suppose that there are four possible outcomes of equal probability. For example we might put four numbers in a hat and pull one out at random. Or we might flip two coins – this also leads to four equally probable outcomes: both coins heads, both tails, the first heads the second tails, and vice versa. One lottery might assign a certain amount of one dollar to each outcome. Another might assign a loss of two dollars to the first outcome and a gain of two dollars to the other three outcomes. Which would you choose? Or more relevant – does your choice depend on whether the outcome is determined by flipping two coins or drawing one of four numbers from a hat? Economists suspect it does not, and if it does not they say that your preferences satisfy the reduction of compound lotteries axiom. We also imagine that if you prefer lottery A to lottery B and B to C, then you prefer lottery A to C. This is called transitivity.

Now look at the table below with three equally likely outcomes

Finally, suppose that given three outcomes A, B and C, where A is better than B is better than C, we can find some probabilities between A and C that would leave you indifferent to B. That is, since B is in between A and C in your ranking, if you had a low enough probability of A and high enough probability of C, you should be willing to take that in place of B and vice versa. This is called the continuity axiom.

There are a number of possible explanations of the Allais paradox examined over the years by economists. Rubinstein [1988] and Leland [1994] suggest people might focus on the fact that a 1% chance of getting nothing is quite different than a 0% chance, but be less cognizant of the difference between 89% and 90%, while Andreoni and Sprenger [2010] presume that people perceive the probabilities zero and one quite differently than other probabilities. Machina [1982] suggests a systematic non-linearity of preference in probabilities. Behavioral economists and psychologists have their own theory – prospect theory – that we will come to shortly.

Risk Preferences: the Rabin Paradox

The Allais paradox is not widely viewed as an important deviation from the theory of expected utility by economists. The reason is that to get the paradox the numbers in the gambles must be very carefully chosen. As I mentioned, with my undergraduates the paradox vanished one day because the value of a million fell enough that they decided that it was worth giving up a sure million for a 10% chance at $5 million and an 89% chance of the $1 million despite the 1% risk of getting nothing. If we don’t craft the numbers just right, we don’t get a reversal. Typical economic choices don’t involve such carefully chosen numbers, so the paradox does not have much practical import.

This enormously higher risk aversion for small stakes gambles than for large stakes gambles was documented in a clever way by Matt Rabin. It poses an enormous challenge for economics and one that by and large economists have not attempted to address. It flavors laboratory research, which sometimes take as given the relatively low risk aversion observed for large stakes gambles and proceeds to ignore the fact that we know that for the small stakes gambles we observe in the laboratory people are far more risk averse. It poses also a difficult theoretical challenge since the existing theory of expected utility is not able to explain this enormous discrepancy. While several explanations have been offered, none has achieved widespread acceptance. The most widely used theory that can potentially explain the discrepancy is the psychological theory called prospect theory – which however is not widely used by economists.

Risk Preferences: Prospect Theory to the Rescue?

Because of the Allais and Rabin paradoxes psychologists widely regard the expected utility theory used by economists as nuts. As mentioned they also have a serious alternative called prospect theory. Prospect theory differs from expected utility theory in two ways. First, it allows for what is called a probability distortion. This says that people tend to exaggerate low probabilities. Second, it incorporates what is called a reference point. This says that people are not concerned with the effect of a gamble on some sort of measure of overall well-being, but rather with the gains and losses relative to a reference point. If I seem vague about what the reference point is there is a reason: it is treated as an unknown value that varies from setting to setting in an unexplained manner. From the perspective of an economist this is a bug that renders the theory unusable. A theory that says behavior depends on some unknown variable that changes in an unexplained way does not make very useful predictions.

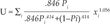
then the gambling behavior of these people is described by picking the gamble that yields the highest numerical value of the utility.

One issue with theories, however, is that they make a range of predictions – not only in the laboratory, but also outside the laboratory. Which would you rather have?

A. $5,000 for sure (or)

B. a 50–50 coin-flip between $9,700 dollars and nothing

People I have asked all prefer alternative A. However the utility function above yields a higher numerical value for option B, thus according to Bruhin, Fehr-Duda, and Epper, such an individual will choose B. As the “typical” person doesn’t do this, prospect theory is not without its own paradoxes.

Prospect theory is largely an empirical and experimental based theory. Many of the experiments on which it is based are for hypothetical money or for very small amounts of money. A question that is always important in this context – the more so given the Rabin paradox – is how the laboratory results reflect on real behavior. Indeed, it turns out that the empirical research underlying prospect theory is a case study in how problematic this can be. One of the main hypotheses in prospect theory is that people are risk averse for gains, but risk loving for losses. However: it isn’t all that easy to present people with the possibility of losses in the laboratory. We can’t easily force people to engage in gambles that involve them losing money. If we start them off with an initial stake that they can lose, we have to worry about the impact that stake has on their “reference point.” As a result experiments involving gains have typically been done for larger stakes than experiments involving losses and indeed most of the losses have been hypothetical rather than real. That raises the possibility that people aren’t risk averse for gains and risk loving for losses at all, but rather that they are risk loving for small (real) stakes and risk averse for (real) large stakes – quite different than is assumed in prospect theory.

In 2006 two clever investigators, Bosch-Domenech and Silvestre examined the possibility that risk aversion and risk loving are driven by the stakes rather than by gains and losses. To allow the possibility of substantial losses, they endowed subjects with money in one experiment, then – to avoid any possible effect of having given them money – they conducted the gambles in a second experiment several months later. What they found is that prospect theory is wrong: risk aversion and risk loving are in fact driven by stakes and not by losses and gains.

Interestingly there is evidence outside the laboratory that people are risk loving with respect to losses. For example: in the recent crisis, and historically as well, bankers have always appeared to be willing to gamble a small probability of a large loss for a modest increase in the average return. Prospect theory appears to predict this kind of behavior, and indeed we find Godlewski in 2007 proposing exactly this possibility. There are two problems with this analysis. First, as we just pointed out, laboratory data does not show that people are risk loving for substantial losses. Second, standard expected utility theory predicts that bankers should gamble on losses.

This notion that prospect theory is somehow needed to explain the gambling behavior of bankers is once again behavioral economics at its worst. Expected utility theory provides a simple and obvious explanation for what we see. Prospect theory is not needed here.

In summary, expected utility theory has its paradoxes. Prospect theory is an effort to explain those paradoxes. Unfortunately when subject to the same scrutiny as expected utility theory it has its own equally serious paradoxes.

It is worth mentioning also a related class of models called consumption lock-in models. These models are technically a bit different than habit formation models but have a very similar flavor: they assume that after you choose a particular level of consumption it is costly to adjust it right away, either up or down. These models also date back to 1990 when they were introduced by Grossman and Laroque. As Grossman and Laroque argued, while standard theory says that people ought to adjust their consumption in response to changes in stock market prices, nobody is terribly likely to sell their house and buy a slightly larger or smaller one in response to a modest change in stock prices (although they might skimp a bit on maintenance if prices fall).

In 2001 Gabaix and Laibson produced a very simple version of the consumption lock-in model showing that a lock-in of about a year and a half is what is needed to explain the equity premium. One advantage of these models over habit formation is that when combined with a model of self-control they can also produce the Rabin paradox: this was shown by Fudenberg and Levine in 2006.

The key thing to note is that these models were a response to a real problem that concerned economists. None of them are “behavioral” in the sense of Akerlof or Ariely, and indeed, nobody has come yet up with a sensible explanation of asset prices based on irrationality. Moreover: there is no shortage of explanations of the equity premium – explanations ranging from taxes to problems with the way the data were chosen have been proposed. Our problem is a surfeit of riches: we have too many explanations of the equity premium puzzle, not too few.

Notes