Nash equilibrium describes a situation in which players have identical and exactly correct beliefs about the strategies each player will choose. How and when might the players come to have correct beliefs, or at least beliefs that are close enough to being correct that the outcome corresponds to a Nash equilibrium? Fudenberg and Kreps, 1993
Do economists blindly assume that people are rational and have rational expectations? Ironically the notion of rational expectations that is widely attacked by non-economists as unrealistic is the least obnoxious of the assumptions about beliefs that economists make. The notion that would be attacked if the attackers had any idea what they were talking about is the idea of common knowledge. Common knowledge asserts that not only do I know what you are going to do and you know what I am going to do – but that I know that you know what I am going to do, and so forth and so on. To take a somewhat non-economic example, a husband and a wife love each other, and both know that the other loves them, and each knows that the other knows that they are loved and so forth and so on. In the case of a marriage this might indeed be true… but to take a more economic example – can this reasonably be believed to be true of stock traders? Rational expectations theory merely says that we share the same beliefs; common knowledge says that we have a mutual deep understanding of each others’ beliefs.
The further irony is that economists have not generally assumed either rational expectations or common knowledge for the last two decades. Rather, in modern theory, these are conclusions rather than assumptions – and conclusions that are only true under certain circumstances.
Game theory entered economics in a big way in the late 1970s and early 1980s. At that time the assumptions of rationality and common knowledge were taken for granted. From the standpoint of a science this is understandable: one walks before running, and there is little point in challenging assumptions before their implications are known. By the late 1980s – long before behavioral economics was in vogue – the inadequacy of the strong rationality assumptions underlying game theory was creating discontent among game theorists. In 1988 two top theorists, Drew Fudenberg and David Kreps, wrote a very influential – although never published – paper examining how equilibrium in games might arise from a process of boundedly rational learning rather than some sort of hyper-rational introspection. The theoretical work that flowered over the next two decades is now very much part of mainstream economics: in addition to economists, computer scientists have been very active in developing theories of learning in games.
I can hardly do justice to the subject of learning in games in a single chapter of a non-technical book. Yet from the perspective of someone who works on learning theory behavioral economics poses a great puzzlement. It talks extensively of biases and errors in decision making. However the great mystery to learning theorists is not why people learn so badly – it is why they learn so well.
Back up for a moment – behavioral economists, psychologists, economists and computer scientists model human learning by what can only be described as naïve and primitive models. Some of these models have various errors and biases built in. Even those models designed by computer scientists to make the best possible decisions cannot come close to the learning ability of the average human child – indeed, it is questionable that these models learn as well as the average chimpanzee or even rat.
The motivation for equilibrium models – and the rational expectations revolution – is simply that if we have to choose between our best models of learning and simply throwing in the towel and assuming that people learn perfectly – for most situations of interest to economists the assumption of perfect learning fits the facts far better than our best models of learning.
This is not to say that learning theory has not contributed to our understanding of economics. A fundamental tenet of learning theory is you can only learn to the extent that you have experience or other data to learn from. In the absence of information there is no reason to imagine that people are unbiased, or do not exhibit “irrational” or “behavioral” modes of decision making. In many ways the idea of incorrect beliefs is fundamental to learning theory – if beliefs were always correct there would be nothing to learn about.
To understand more clearly how learning theory helps us understand real behavior, let’s examine the central modification to equilibrium theory that arises from the theory of learning – the notion of self-confirming equilibrium.
Learning and Self-confirming Equilibrium
An important aspect of learning theory is the distinction between active learning and passive learning. We learn passively by observing the consequences of what we do simply by being there. However we cannot learn the consequences of things we do not do, so unless we actively experiment by trying different things, we may remain in ignorance.
In mainstream modern economic theory, a great deal of attention is paid to how players learn their way to “equilibrium” and what kind of equilibrium might result. It has long been recognized that players often have little incentive to experiment with alternative courses of action and may, as a result, get stuck doing less well than they would if they had more information. The concept of self-confirming equilibrium from Fudenberg and Levine [1993] captures that idea. It requires that beliefs be correct about the things that players see – but they may have incorrect beliefs about things they do not see.
We can illustrate this idea with the ultimatum bargaining game from Chapter 4. Recall that one player proposes the division of an amount of money – often $10, and usually in increments of 5 cents – and the second player may accept, in which case the money is divided as agreed on, or reject, in which case neither player gets anything. If the second player is selfish, he must accept any offer that gives him more than zero. Given this, the first player should ask for – and get – at least $9.95. That is the reasoning of subgame perfect equilibrium. As we observed the prediction that the first player asks for and gets $9.95 is strongly rejected in the laboratory.
Now let us apply the notion of self-confirming equilibrium to this game. Players know the consequences of the offer they make, but not the consequences of offers that they do not make. Using this concept we can distinguish between knowing losses, representing losses a player might reasonably know about, and unknowing losses that might be due to imperfect learning. We earlier computed (in Chapter 5) that in the Roth et al. [1991] data on average players are losing about $0.99 per game. Of that amount, $0.34 are knowing losses due to second players rejecting offers. The remaining $0.63 are due to the first mover making demands that are either too great and too likely to be rejected, or too small.1 Since the first mover only observes the consequences of the demand actually made, any loss due to making a demand that is too high or too low can be unknowing. Given that players only got to play ten times, it is not surprising that first movers did not have a good idea of the likelihood of different offers being accepted and rejected.
Notice that there is an important message here. Between social preferences – a major focus of behavioral economics – and learning – a major focus of mainstream economics – in the ultimatum bargaining experiment the role of learning is relatively more important than social preferences. In addition a reasonable measure of the failure of standard theory is not the $0.99 loss out of $10.00, but rather the $0.34 knowing loss.
Self-confirming Equilibrium and Economic Policy
The use of self-confirming equilibrium has become common in economics. A simple example adapted from Sargent, Williams and Zhao [2006a] by Fudenberg and Levine [2009] illustrates the idea and shows how it can be applied to concrete economic problems. Consider game between a government and a typical or representative consumer. First, the government chooses high or low inflation. Then consumers choose high or low unemployment. Consumers always prefer low unemployment. The government prefers low inflation to high inflation, but cares more about unemployment being low than about inflation. If we apply “full” rationality (subgame perfection), we may reason that the consumer will always choose low unemployment. The government recognizing this will always choose low inflation.
Suppose that the government believes incorrectly that low inflation leads to high unemployment – a belief that was widespread at one time. Since they care more about employment than inflation they will keep inflation high – and by doing so never learn that their beliefs about low inflation are false. This is a simple example of self-confirming equilibrium. Beliefs are correct about those things that are observed – high inflation – but not those that are not observed – low inflation.
Such a simple example cannot possibly do justice to the long history of inflation – for example in the United States. Some information about the consequences of low inflation is generated if only because inflation is accidentally low at times. Sargent, Williams and Zhao [2006a] show how a sophisticated dynamic model of learning about inflation enables us understand how U.S. Federal Reserve policy evolved post World War II to ultimately result in the conquest of U.S. inflation. More to the point, it also enables us to understand why it took so long – a cautionary note for economic policy makers.
Self-confirming Equilibrium and Economic Crises
While the current economic crisis is surprising and new to non-economists, it is much less so to economists who have observed and studied similar episodes throughout the world. Here too learning seems to play an important role. Prior to the current crisis Sargent, Williams and Zhao [2006b] examined a series of crises in Latin America from a learning theoretic point of view. They assume that consumers have short-run beliefs that are correct, but have difficulty correctly anticipating long run events (the collapse of a “bubble”). Periodic crises arise as growth that is unsustainable in the long run takes place, but consumers cannot correctly foresee that far into the future.
In talking about the crisis, there is a widespread belief that bankers and economists “got it wrong.” Economists anticipate events of this sort, but by their nature their timing is unpredictable. Bankers by way of contrast can hardly be accused of acting less than rationally. Their objective is not to preserve their banks or take care of their customers – it is to line their own pockets. They seem to have taken advantage of the crisis to do that very effectively. If you can pay yourself bonuses during the upswing, and have the government cover your losses on the downswing, there is not much reason to worry about the business cycle.
The Persistence of Superstition
What could be more irrational than superstition? If people are rational learners, won’t they learn that their superstitions are wrong? How can superstition persist in the face of evidence?
In fact no behavioral explanation is needed. Rational learning predicts the persistence of certain kinds of superstition. Take the code of Hammurabi2 as an example.
If anyone bring an accusation against a man, and the accused go to the river and leap into the river, if he sink in the river his accuser shall take possession of his house. But if the river prove that the accused is not guilty, and he escape unhurt, then he who had brought the accusation shall be put to death, while he who leaped into the river shall take possession of the house that had belonged to his accuser. (2nd law of Hammurabi)
As Fudenberg and Levine [2006] observe, this is puzzling to modern sensibilities for two reasons. First, it is based on a superstition that we do not believe to be true – we do not believe that the guilty are any more likely to drown than the innocent.3 Second, if people can be easily persuaded to hold a superstitious belief, why such an elaborate mechanism? Why not simply assert that those who are guilty will be struck dead by lightning?
Consider three different games. In the Hammurabi game the first player, a culprit, has to decide whether or not to commit a crime. He prefers to commit the crime if unpunished, but would not do so if he expects to be punished. If he does commit the crime a second player, a witness, must decide whether or not to correctly identify the culprit. The witness prefers to identify a particular enemy rather than the true culprit. After testifying, the accused objects, and the witness is tossed in the river – and most likely drowns.
In the game without the river, the witness simply identifies someone as the culprit and that person is punished.
Finally, in the lightning game, there is no witness, and the culprit – regardless of whether or not the crime was committed – has a small chance of being struck dead by lightning.
In each of these games a superstition can lead to a decision by the first player not to commit a crime. In the first game, the Hammurabi game, the witness believes that she will drown if she lies and survive if she tells the truth. She is definitely wrong: she will drown in both cases. However her beliefs lead her to tell the truth, and knowing this the culprit sensibly decides not to commit the crime. In the second game, the game without the river, the culprit believes that the witness will tell the truth. He is wrong: without any chance of punishment, the witness will lie and identify her enemy. Because of his wrong belief, however, the culprit will again choose not to commit the crime. In the third game, the lightning game, the culprit believes if he commits a crime he will be struck dead by lightning. He is wrong: he is very unlikely to be struck by lightning regardless of whether he commits a crime. Nevertheless, based on this wrong belief, he again optimally chooses not to commit the crime.
In each case the decision not to commit a crime is supported by a superstitious belief: a belief that is objectively false, a belief that evidence should show is false. What differentiates these games? When and why can superstition survive?
Take the lightning game first. From the perspective of Nash equilibrium, the culprit should know that the probability of being struck dead by lightning doesn’t depend on whether a crime is committed, so should commit the crime. From the standpoint of self-confirming equilibrium, however, if the culprit chooses not to commit the crime, his belief that he will be struck dead by lightning is purely hypothetical and is never confronted with evidence. Therefore the superstition is a self-confirming equilibrium, but not Nash.
While self-confirming equilibrium is a reasonable description of short-run behavior, it is an unlikely basis for a social norm. Over time some people will commit crimes for one reason or another, and of course they will not be struck dead by lightning. Hence we should not expect “being struck dead by lightning” to be the basis of criminal justice systems, and indeed, historically it does not seem to be so.
Let’s look at the game without the river next. Here it is a Nash equilibrium for the culprit not to commit the crime and the witness to tell the truth. Since the witness is never called upon to testify she is indifferent between telling the truth and lying, so it is “rational” to tell the truth. This equilibrium, while not merely self-confirming, but actually Nash, is no more plausible in the long-run than the lightning equilibrium. If people do occasionally commit crimes, the witness – being in fact called upon to testify – will lie, and eventually the superstition that witnesses tell the truth should die in the face of evidence.
In the game without the river, the superstition is consistent with Nash equilibrium, but not subgame perfection. This is relevant because Fudenberg and Levine [2006] show that when people are patient enough to try crimes to see if they “can get away with it” the kind of equilibrium that results is a sort of hybrid between subgame perfection and self-confirming equilibrium called subgame confirmed equilibrium. Basically this says that deviations from a Nash equilibrium into a particular subgame should result in a self-confirming equilibrium.
Let’s see how this theory works in the game with the river. Here the culprit is supposed to commit the crime only rarely to “see if he can get away with it.” He can’t in fact get away with it since the witness will tell the truth, so has no reason to commit the crime except for the purpose of learning. The witness tells the truth because she superstitiously believes she has a better chance of surviving the river if she does so. Since she doesn’t lie, she doesn’t learn that her belief about the river is wrong.
If the culprit commits crimes occasionally to see if “he can get away with it” why does the witness not lie occasionally to see if “she can get away with it?” Neither one expects to “get away with it” – but contemplates the possibility they might. The reason for experimenting is that if the belief of “not being able to get away with it” is wrong, then you will know that in the future that you can “get away with it.” Hence “trying it out to see” is an investment in the possibility of future benefits.
When do we invest in the future? If we are patient and the future rewards are not in the too distant future. For the culprit, the rewards are immediate: if you discover you can get away with murder, you can start on a life of crime straight away. It is different for the witness: we don’t expect to be called as a witness in a trial very frequently. Thus the benefit of “trying it out to see” is that at some far distant date in the future when called upon to testify again the witness can again lie. The return to the investment is too distant to be worth the trouble.
The bottom line here is that in the Hammurabi game with the river the superstition is about something that lies “off the equilibrium path.” That is to say, the superstition is about something that happens very infrequently when the social norm is adhered to. Hence it is not worth investing to see whether or not the superstition is wrong. According to learning theory superstitions of this type are far more robust than superstitions that we have reason to test every day. As Fudenberg and Levine say “Hammurabi had it exactly right: (our simplified interpretation of) his law uses the greatest amount of superstition consistent with patient rational learning.”
Self-Confirming, Nash Equilibrium and Agreeing to Disagree
Common knowledge can be puzzling even to economists. One particularly puzzling conclusion that (seemingly) derives from common knowledge is the no-trade theorem. The no-trade theorem says that in the absence of other reasons to trade, people should not trade merely based on informational differences. That is when you offer to bet that a particular horse will win at the race-track I should refuse the bet on the grounds that the only reason you are willing to make the offer is because you know something I don’t know. Put that way it seems pretty absurd.
Here is the thing: as Fudenberg and Levine [2005] point out, even in the absence of such rationality, there shouldn’t be trade based purely on informational differences. Learning theory alone gives rise to the no-trade theorem. If we are going to on average lose by trading then some of us must be losers – and eventually we should find that out and stop betting. Even in self-confirming equilibrium there can be no trade.
So: should we conclude that people are irrational because they bet on the ponies? Not necessarily. The theorem gives us two reasons why we may have information based trading. First, people may have some reason to trade. For example, at the race-track some people may simply enjoy betting. They happily lose money – and that money serves as incentive for everyone else to bet based on information differences. Second, there may indeed be a sucker born every minute. Over time they discover they are losers and stop betting, but new suckers arrive to take up the slack.
Keynes Beauty Contest
If John Maynard Keynes is not a hero to behavioral economists, he should be. Nobody believed more strongly that economics was governed by forces of irrationality than he. Stock markets, in particular, he believed were driven by mysterious animal spirits of investors.
Keynes theory of stock markets can be found in Chapter 12 of his 1936 General Theory. His notion was that investors want to buy stocks because they think that other investors like those stocks. He gives as an analogy his beauty contest game. In this game players must choose the most beautiful woman from six photographs. Players who pick the most popular face win. This in fact is a rather boring coordination game: every face is a Nash equilibrium. Whether this is really how stock markets work may be doubted: it is true that Keynes made a fortune for King’s College Cambridge through his stock market investments. It is equally true that at various times he also lost a fortune, so that if he had stepped down as Bursar at a different time his name would be as infamous there as it is today famous.
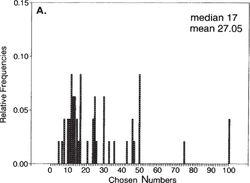
Be that as it may, in 1995 Rosemarie Nagel conducted some very influential experiments with a simple variation of Keynes beauty contest. In Nagel’s game, the players had to choose a number between 0 and 100. The players getting the closest to half the average value of the choices win. Like Keynes beauty contest, what you want to do in this game depends on what you think average opinion is. For example, if you think that people choose randomly, the average should be 50, so you would win by guessing 25. Unlike Keynes beauty contest, this game has a unique Nash equilibrium: it is pretty easy to see that any average greater than 0 can’t be an equilibrium since everyone would want to guess less. So everyone has to guess zero. The graph below is taken from Nagel’s paper and the dots show choices the third and fourth time the game was played.
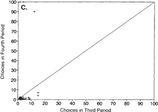
Nagel’s Beauty Contest Results
As you can see, the dots are in fact very close to the lower left corner where the theory of Nash equilibrium says they should be.4
What is interesting about this experiment is not that we find that experienced players get to Nash equilibrium. What is interesting is that the first time they played they did not get to Nash equilibrium. Nagel’s graph reproduced below shows the distribution of choices the first time players played the game.
Not exactly a Nash equilibrium. Since by now we hopefully know not to expect Nash equilibrium in first time play, what is the point? The point is that there is another theory – developed by economists – that does do a good job of explaining what is going on. The idea originates with Nagel, and is further developed by Stahl and Wilson [1994], with recent incarnations in the work of Costa-Gomes, Crawford and Broseta [2001] and Camerer, Ho and Chong [2004]. It has come to be called level-k theory.
The idea is relatively simple. People differ in their sophistication. Very naïve individuals – level-0 – play randomly. Less naïve individuals – level-1 – believe that their opponents are of level-0. In general higher level and more sophisticated individuals – level-k – believe that they face a mixture of less sophisticated individuals – people with lower levels of k. It turns out that a single common probability belief about the relative likelihood of degrees of sophistication can explain first time play in a variety of experimental games.
While it is impressive that such a simple theory can do a relatively good job of explaining first time play, the idea has yet to gain wide traction in economics. There are likely several reasons for this. First, the types of games in which the theory has been shown to work are relatively simple and unlike the kinds of situations economists are interested in. More to the point, in real markets – stock markets for example – participants are generally relatively experienced, so more likely to exhibit equilibrium behavior than level-k behavior. Still: in modern finance so called “noise traders” who are inexperienced and naïve despite being small in numbers play an important role both in the transmission of information through prices and in price fluctuations. Perhaps level-k theory will ultimately enable us to better model the behavior of these “noisy” individuals.
Behavioral economics seems to presume that we are most ignorant about the things we are the most familiar with. Despite a lifetime of evidence that we are procrastinators, we stubbornly stick to the belief that we are not. Despite our complete ignorance of the Becker-DeGroot-Marschak elicitation procedure and absence of experience with second price auctions, we comprehend that procedure perfectly, being confused only about how much we are willing to pay for a coffee mug.
Learning theory, by contrast, points the opposite direction. It says that things we are most likely to be mistaken about are the things we know the least about. This is not only common sense, but is supported by overwhelming evidence. If I drop this computer from my lap nobody will argue that it will fly to the ceiling rather than fall to the floor. We have a lifetime of evidence about the law of gravity – and I think we may reasonably say it is common knowledge. I know that you know that I know the law of gravity. By contrast, there is broad disagreement about the possibility and nature of life after death. Some disbelieve in the notion entirely. Others believe in heaven, or hell, or purgatory, or all three. Yet others believe we will be reincarnated as grasshoppers. Of course from a learning theoretic point of view this makes a great deal of sense: if you are reading this book it is unlikely that you are dead, and very few people have come back from the dead to relate their experiences.
Notes
1 The details of these calculations can be found in Fudenberg and Levine [1997].
2 The code of Hammurabi consists of 282 laws and was created circa 1750 B.C. It is the earliest known written legal code and was inscribed on stone.
3 A behavioralist might argue that if the superstition is believed, the guilty might be less inclined to try to swim, so that the superstition would be self-fulfilling. However, no such explanation is needed
4 I cherry-picked her data: she also reports experiments where you win by guessing 2/3rds the average and 4/3rds the average. These were much less close to a Nash equilibrium – although since people only got to play 4 times, it is hard to regard it as a meaningful violation of the idea that with enough experience players get to equilibrium.