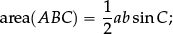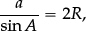IV. A sample curriculum for all—written from a humane mathematical viewpoint
What follows stems from an attempt to consider what a “humane mathematician and educator” might expect to see included at each Key Stage of a National Curriculum—under the assumption that:
•one would like to see number, measures and calculation grasped (in some sense) at primary level, with
•further work on number, together with algebra, geometry, and trigonometry being mastered by age 16 to a level that would allow those who proceed to further studies, in whatever subjects, to be in a position to use the mathematics they have learned.
In particular, the sample curriculum tries to set realistic (rather than ambitious) goals for primary mathematics. It also tries to restrict the extent of abstraction at Key Stage 3, on the assumption that for a significant group of pupils this material may form the core of work at secondary level (age 11–16), along with consolidation of material from upper primary school. More abstract material has been delayed wherever possible until Key Stage 4, where it serves as a transition from elementary mathematics to higher mathematics for all pupils who intend to proceed to further academic studies beyond age 16 (in any subject). Hence teachers may choose to blur the boundary between Key Stages 3 and 4 for many pupils, taking much longer to cover the listed Key Stage 3 material for some, while others may treat Key Stage 3 material more abstractly than is suggested here in preparation for Key Stage 4.
Having produced a Brief Version (which was already fairly detailed—see Section 2 below), we then drafted two further versions:
•a Fuller Version, which unpacked in greater detail some of the cryptic references we were advised might not be immediately understood; and
•a Very Brief Version (see Section 1 below) which rashly tried to compress the essence of each Key Stage into a single page.
We have chosen to reproduce here (and to improve) the Brief Version and the Very Brief Version, to provide an easily accessible reference for the reader of Parts I, II, and III. Some words that appear in bold type have a technical meaning that will have been explained in detail in Part II or Part III. If some aspect remains unclear, we recommend that readers refer to the Fuller Version, which is freely available at The De Morgan Forum.22
By the end of Year 2 pupils:
Counting, reading and recording number
•use the language for numbers and quantities in everyday settings
•count accurately; read, write and order numbers to at least 100; understand place value, know what each digit of any two-digit number represents, and know that the position of a digit determines its “value”
Recalling facts
•have instant recall of addition and subtraction facts for numbers to 10; have instant recall of ×2, ×5, ×10 multiplication tables, and derive corresponding division facts
•use the language for simple calculations in everyday settings
•carry out mental and informal written calculations using the four operations of addition, subtraction, multiplication and division
•recognise and use effectively the fact that subtraction is the inverse of addition, and in simple cases that division is the inverse of multiplication
•handle confidently two-digit addition and subtraction in standard written column format
Describing shapes and measuring
•recognise, name, and describe properties of common 2D and 3D shapes
•measure and draw straight lines accurate to the nearest centimetre; estimate lengths and other quantities; tell the time to the nearest quarter of an hour, compare durations using standard units, and order events chronologically; use measuring instruments to measure length (cm, m), weight (kg), capacity (l), reading and interpreting scales to the nearest labelled division; use money
Solving problems, reasoning, and using language and symbols
•apply their understanding of number and arithmetic to work with measures and to solve word problems
•use mathematical language accurately; read and interpret text, diagrams, and symbols when solving problems; record their results clearly; explain their methods and reasoning
By the end of Year 6 pupils:
Place value
•handle place value to represent and order numbers to 10 000 and beyond; extend this to negative integers and decimals; work with decimals and measures involving tenths, hundredths and thousandths; multiply and divide integers and decimals by 10, 100, 1000
•round integers, decimals and measures to the nearest “ten”, integer, or tenth
Recalling facts; correct use of language and symbols
•recall instantly addition and subtraction facts for numbers to 20; “know by heart” multiplication tables to 10 × 10 and corresponding division facts; factorise any two-digit integer; recognise primes and squares
•use mathematical language and notation correctly; understand that some statements are exact and can be clearly demonstrated
Structural arithmetic
•add and subtract positive and negative integers; multiply and divide positive integers; use place value and the structure of arithmetic to simplify calculations
•work flexibly with fractions and percentages; switch freely between equivalent fractions; add and subtract simple fractions
•understand the order of operations and the use of brackets
Calculating
•add and subtract any two two-digit integers mentally, and three-and four-digit integers using standard written column format
•multiply and divide mentally a two-digit integer by any one-digit integer; complete written short multiplication and division of three-digit and four-digit integers by numbers up to 12, and long multiplication of three-digit by two-digit integers
Geometry and measures
•copy simple figures; work with common 2D and 3D shapes; find unknown angles in simple figures; plot points with given coordinates
•measure and draw line segments accurate to the nearest millimetre and angles to the nearest degree; calculate reliably with standard measures; find the areas of rectangles and shapes made from rectangles, and the volumes of cuboids and shapes made from cuboids
•use and calculate with money; tell the time to the nearest minute; read scales—interpolating between marks; convert between related units
Solving problems
•tackle and solve word problems and simple multi-step problems involving numbers, measures, and shapes; make sensible estimates; make connections between topics; explain their reasoning
Key Stage 3 revisits important Key Stage 2 material—partly for revision, but mainly to reinterpret old material from a new “viewpoint” (extending the written algorithms to decimals, shifting the focus from bare hands mental methods to structural arithmetic and the simplification of expressions, etc.).
By the end of Year 9 pupils:
Place value
•handle place value to represent and order integers and decimals with up to six digits; multiply and divide by 10, 100, 1000
•work with decimals and measures involving up to four decimal places; write terminating decimals as fractions and vice versa, and know that some fractions have decimals that recur
•round numbers and measures freely and flexibly
Calculating
•use multiplication tables freely to multiply and divide mentally in context;
•compute with integers and decimals using standard column format
•compare and compute with fractions; work flexibly with fractions, ratios, percentages
Structural arithmetic
•use place value, factorisation, and the algebraic structure of arithmetic to simplify and to evaluate numerical expressions and calculations—including with fractions and negatives
•test for divisibility by 2, 3, 4, 5, 10; find HCFs and LCMs; factorise integers as a product of primes; recognise squares and cubes; find or estimate square roots
•represent numbers as powers—including simple fractional powers; work with powers of 10
•use the algebraic equivalence of expressions to simplify calculations
Simplification of algebraic expressions; solving linear equations
•use unknowns and variables in context (formulae); substitute values in expressions; use algebraic rules to simplify expressions and calculations—collect like terms, expand and factorise simple expressions; work with simple sequences
•set up and solve a single linear equation in one unknown in complete generality; use the rules of algebra to “change the subject of”, or to rearrange, equations and formulae; solve two simultaneous linear equations; solve linear inequalities in one unknown
Geometry and measures
•measure and draw accurately; read scales; change units; understand and use basic formulae; find lengths, areas, and volumes for common 2D or 3D shapes—including triangles, parallelograms, circles, cuboids, and prisms; calculate reliably with standard measures
•plot points in all four quadrants; find the midpoint of a line segment, and the distance between two given points; understand and work with linear equations and straight line graphs; interpret gradient as a ratio or rate; use trig ratios in right-angled triangles
•use basic ruler and compass constructions, parallels, angles in a triangle, angle-chasing, congruence; establish a preliminary basis for 2D Euclidean geometry; prove and use Pythagoras’ Theorem
Solving problems
•tackle and solve word problems and simple multi-step and inverse problems involving numbers, measures, symbols and shapes
•use the unitary method to solve proportion problems involving rates and ratios
•make sensible estimates
•make connections between topics; explain their reasoning
Key stage 4 revisits important Key Stage 3 material—partly as revision, but also to interpret it afresh. For some pupils, this re-working and strengthening of Key Stage 3 material (together with consolidation of Key Stage 2 material) will be their main goal at Key Stage 4; other pupils may supplement revision of Key Stage 3 material with a programme that covers selected parts of what is summarised here. Those who expect to continue to further academic studies beyond Key Stage 4 should aim to cover everything summarised here.
By the end of Year 11 pupils who complete the Key Stage 1–4 programme:
Number and measures
•handle (positive and negative) large numbers and decimals, with and without units, possibly expressed using powers or standard form
•move freely between fractions and decimals
•use rounding and exact arithmetic to work with approximations
•calculate probabilities in standard models; analyse sampled data
Calculating and simplifying
•compute with fractions; work flexibly with fractions, ratios, percentages
•solve problems involving proportion (including the unitary method)
•use algebraic structure and multiplication facts to simplify numerical expressions—including those involving fractions and powers
•calculate with surds and mixed surd expressions (without evaluating)
Algebra (expressions, formulae, equations, identities) and graphs
•use algebraic equivalence (including the index laws) to simplify expressions
•know, use, and rearrange standard formulae
•work in all four quadrants; work with equations of straight lines in 2D
•solve any linear equation or inequality in one unknown; solve any pair of simultaneous linear equations or inequalities in two unknowns; interpret the solutions graphically
•know and use standard quadratic identities; solve any quadratic equation or inequality; solve easy simultaneous equations—one linear and one quadratic; interpret solutions graphically
•understand linear and quadratic expressions in one variable as functions; sketch and analyse linear and quadratic graphs
Geometry
•use Pythagoras’ Theorem to solve problems in 2D and 3D; find lengths, surface areas, and volumes for common 2D and 3D shapes—including regular polygons
•use basic trigonometry and the Sine and Cosine rules to “solve triangles”
•understand and use basic ruler and compass constructions
•understand how congruence, parallels, and similarity provide a basis for Euclidean geometry; use these to derive results and to solve problems
•understand, prove, and use the basic properties of circles
•understand how scaling affects angles, lengths, areas, and volumes analyse standard 2D and 3D figures—including prisms, pyramids, cylinders, cones, spheres
Solving problems
•solve word problems and simple multi-step and inverse problems
•make connections between topics; write well-presented proofs; explain their reasoning
•calculate with standard and compound measures; work with “rates”
Breadth of study
1. During the Key Stage pupils should be taught the required Knowledge, Skills, and Understanding through:
practical activity, exploration and discussion | |
linking the language of mathematics with spoken and written English | |
learning key facts by heart; learning to store tens and units temporarily in the mind (including as intermediate outputs in a longer calculation) to support the development of mental calculation strategies | |
using mathematical ideas in practical activities, then recording these ideas using objects, pictures, diagrams, tables, words, and numbers | |
developing rich mental calculation strategies, and standard written procedures for addition and subtraction | |
drawing, measuring and estimating in a range of practical contexts |
Knowledge, Skills, and Understanding
Teaching should ensure that appropriate connections are made between the section Number and measures and the section Shape, space, and measures.
Ma1 Number and measures
1. Using and applying “Number and measures”
Pupils should:
explore, interpret, develop flexible approaches to, and persist with problems involving number and measures in a variety of forms |
Communicating
use correct language, symbols, and vocabulary associated with number and measures | |
explain and record methods and results in spoken, pictorial, and written form |
Reasoning
present results in an organised way; sort and classify numbers according to given criteria | |
understand that some statements are exact and can be clearly demonstrated |
2. Numbers and the number system
Pupils should: Counting
count reliably at first up to 20 objects, later extending counting to 100 and beyond (to 120 say), remaining secure across “tens boundaries” [e.g. from 19 to 20, or from 99 to 100]; recognise the invariance of quantity | |
estimate a number of objects that can be checked by counting; round two digit numbers to the nearest 10 |
The base 10 number system
understand the groupings into units and 10s (and later into 100s) that underpin place value; know what each digit represents (including 0 as a number, and as a placeholder), and how the “value” represented by each digit is determined by its position | |
read and write two-digit and three-digit numbers in figures and words | |
order two-digit numbers and position them on a number line; use =, <, and > and the associated language |
Number patterns and sequences
create, describe, and explore basic number patterns and sequences—including odd and even numbers, multiples of 2, multiples of 5, and multiples of 10 |
3. Calculation
Pupils should:
Number operations and the relationship between them
understand addition and use related vocabulary and notation; understand subtraction (as “take away” and as “difference”) and use the related vocabulary and notation; recognise that subtraction is the inverse of addition | |
identify and use the calculations needed to solve simple word problems and inverse problems [e.g. oral “I’m thinking of a number” problems] | |
understand simple instances of multiplication as repeated addition, and division as “grouping”, and as “sharing”; use the vocabulary and notation associated with multiplication and division; find one half, or one quarter of a familiar shape, or of a small set of objects |
Mental, informal, and standard written methods
develop instant recall of number facts; know addition and subtraction facts with totals less than 10, and use these to derive other facts; learn addition facts with totals up to 20 | |
know ×2, ×5, and ×10 multiplication tables, and derive the corresponding division facts; know the doubles of numbers to 20 and the corresponding halves | |
use practical and informal written methods to add and subtract two-digit numbers | |
develop mental methods which flexibly use known facts to calculate the answer to less familiar “sums” [e.g. working out 4 × 6 by doubling 2 × 6, or by doubling 4 × 3]; add 10 to any single digit number, then add and subtract a multiple of 10 to or from a two-digit number | |
make sense of number sentences involving all four operations | |
lay out and complete simple two-digit additions and subtractions in standard column format | |
use practical and informal written methods and related vocabulary to support multiplication and division, including calculations with remainder |
4. Solving numerical problems
Pupils should:
choose sensible calculation methods to solve simple word problems involving whole numbers—including problems involving money or measures, drawing on their understanding of arithmetical operations |
5. Processing, representing, and interpreting data
Pupils should:
solve suitable problems using simple lists, tables, and charts to sort, classify, and organise information; discuss the methods they use and explain what they find |
Ma2: Shape, space, and measures
1. Using and applying “Shape, space, and measures”
Pupils should:
follow instructions to construct simple 2D and 3D objects; represent 3D objects via 2D drawings |
Communicating
use correct language and vocabulary for shape, space, and measures | |
measure objects using ad hoc informal as well as standard measures; record measurements in ordered tables |
Reasoning
recognise simple spatial patterns and relationships; sort and classify shapes according to given criteria |
2. Understanding properties of shapes, position, and movement
Pupils should:
describe relationships using the language “larger – smaller”, “higher – lower”, “longer – shorter”, “above – below”, “left of – right of” | |
draw and describe properties of 2D and 3D shapes; recognise, name, and sort common 2D and 3D shapes—including triangles, rectangles (including squares), circles, cubes, cuboids, hexagons, pentagons, cylinders, pyramids, cones, and spheres | |
recognise right angles; understand whole turns, and quarter- and half-turns (clockwise and anticlockwise) |
3. Understanding measures
Pupils should:
use direct comparison to order objects by size, using appropriate language; put familiar events in chronological order | |
measure and draw straight lines accurate to the nearest centimetre | |
estimate, compare, and measure lengths, weights, and capacities; choose and use standard units (m, cm, kg, litre); compare durations (using seconds, minutes, hours, days); read and interpret numbers on scales to the nearest labelled division, interpreting the divisions between them; identify time intervals, including those that cross the hour |
Breadth of Study
1. During the Key Stage pupils should be taught the required Knowledge, Skills, and Understanding through:
extending place value to larger integers and to simple decimals | |
extending their understanding of the number system to include integers, fractions, and decimals | |
learning key facts by heart; learning to store hundreds, tens and units temporarily in the mind (including as intermediate outputs in a longer calculation) to support the development of mental calculation strategies | |
extending exact arithmetic to the standard written algorithms for integers and simple decimals | |
using structural arithmetic to calculate efficiently and to develop (pre-)algebraic thinking | |
drawing and measuring; using exact arithmetic to make good estimates when solving problems; recording results using words, pictures, numbers, diagrams, and tables (and symbols where appropriate) | |
linking the language of mathematics with spoken and written English using carefully crafted problems; solving word problems; establishing connections between number work, measures, geometry, and practical tasks; distinguishing between sensible and misleading uses of mathematics |
Knowledge, Skills, and Understanding
Teaching should ensure that appropriate connections are made between the section Number and measures and the section Geometry and measures.
Ma1 Number and measures
1. Using and applying “Number and measures”
Pupils should:
Solving problems
extract numerical, geometrical, and logical information from simple problems expressed in words | |
make connections; use integers, decimals, and fractions (and arithmetic) when solving problems involving measures, and in other settings | |
solve multi-step, and simple inverse problems | |
solve problems involving tables, lists, and information presented pictorially; | |
use knowledge of exact arithmetic to make good mental estimates |
Communicating
use notation, terminology, symbols, and language correctly | |
present results and solutions to problems clearly; explain reasoning, methods, and conclusions | |
interpret tables, lists, and charts; construct and interpret frequency tables |
Reasoning
present results in an organised way; sort and classify numbers and shapes according to given criteria | |
investigate apparent patterns; understand that some statements are exact and can be clearly explained |
2. Numbers and the number system
Pupils should:
Counting
count reliably beyond 100, passing smoothly from any given set of “90s” onto the next hundred | |
count on and back in steps of constant size, starting from any integer, extending to negative integers |
The base 10 number system
use place value in representing numbers first up to 1000, then up to 10 000 and beyond; extend to decimals with up to three decimal places |
Number patterns and sequences
recognise two- and three-digit multiples of 2, 5 and 10; find the factors of a given integer, and the common factors of two given integers; find the HCF and the LCM of two given integers; recognise prime numbers to 50, and square numbers to 10 × 10; find factor pairs and all the factors of any two-digit integer; double or halve any two-digit integer |
Integers
read, write (in figures and words), and order whole numbers to 10 000 | |
multiply, and divide, any integer by 10 or 100, and then by 1000; round integers to the nearest 10 or 100, and then 1000 | |
understand and use negative integers; order a given set of positive and negative integers |
Integers and decimals
use decimal notation for tenths, hundredths, and thousandths; order a set of numbers or measurements | |
compare and order integers and decimals in different contexts; locate integers (positive and negative), fractions, and decimals on the number line; use correctly the symbols =, ≠, <, ⩽, >, ⩾ | |
multiply and divide, any integer or decimal by 10 or 100; round integers and decimals to the nearest integer, to the nearest ten, and to the nearest tenth |
Fractions, percentages and ratio
understand fractions; locate fractions on a number line; find fractional parts of shapes or quantities | |
understand equivalent fractions; simplify by cancelling common factors | |
order simple fractions | |
understand percentage; use simple percentages for comparison; find fractions and percentages of whole number quantities, and express part of a given whole as a percentage; express one whole number quantity as a fraction of another | |
divide a given quantity into two parts in a given ratio (both part-to-part and part-to-whole); compare quantities in a given (external) ratio; solve simple problems involving ratios |
3. Calculation
Pupils should:
Number operations and the relationship between them
develop their understanding of the four number operations—including inverses, and operations with zero | |
find remainders after division; express a quotient as a fraction or decimal; relate | |
know and use the conventions for the order of operations; understand and use structural arithmetic to simplify calculations; write numerical expressions involving brackets; group related terms in a sum and related factors in a product to simplify, and hence evaluate, numerical expressions |
Mental methods
achieve instant recall of all addition and subtraction facts for integers up to 20 | |
add or subtract any pair of two-digit integers; handle suitable three-digit and four-digit additions and subtractions presented in written form | |
add and subtract positive and negative integers mentally | |
achieve instant recall of (i.e. know by heart) multiplication tables to 10 × 10 and use them to derive division facts | |
multiply and divide in the range 1 to 100, then for larger numbers | |
derive multiplication and division facts involving decimals | |
relate fractions to multiplication and division; work with simple quotients as fractions and as decimals; switch freely between equivalent fractions; add and subtract simple fractions by reducing to a common denominator |
Written methods
use the standard written method in column format to add and subtract three-digit positive integers, then four-digit positive integers; add and subtract numbers involving decimals | |
use the standard written method in column format for short multiplication (of two- and three-digit integers by a single digit multiplier), then long multiplication of two-digit and three-digit integers by two-digit multipliers; extend to simple decimal multiplication | |
use short division of two-digit and three-digit integers by numbers up to 12 | |
use approximations and other strategies to check that answers are reasonable |
Measures
calculate reliably with standard measures, money, and time; convert measures from one unit to a related unit | |
relate distance, time, and speed in uniform rectilinear motion; work with other simple rates and compound measures |
4. Solving numerical problems
Pupils should:
use the four number operations to solve word problems involving numbers, or money, or measures of length and area, mass, capacity, or time | |
solve multi-step and inverse problems with confidence | |
check that their results are reasonable; explain why their answers are correct |
5. Processing, representing, and interpreting data
Pupils should:
solve suitable problems using simple lists, tables, and charts to sort, classify, and organise information, discuss the methods they use, interpret their results, and explain what they find | |
explore the notions of “centre” and “spread” for numerical data sets |
1. Using and applying “Geometry and measures”
Pupils should:
Solving problems
recognise standard geometrical figures; use their properties to select and perform appropriate calculations; measure and draw accurately to construct 2D and 3D figures | |
use standard units of measurement and simple compound measures; convert reliably between related units |
Communicating
use geometrical notation, terminology, and symbols correctly; interpret solutions to problems involving geometrical figures and measures; organise work and record findings clearly |
Reasoning
analyse standard 2D and 3D figures; calculate efficiently and make simple deductions with angles, lengths, areas, volumes, time, and other measures |
2. Understanding properties of shape
Pupils should:
recognise right angles, perpendicular and parallel lines; know that angles at a point total 360°, that angles at a point on a straight line total 180°, and that angles in a triangle total 180° | |
describe relationships using the language “larger – smaller”, “higher – lower”, “longer – shorter”, “above – below”, “left of – right of”, “top – bottom”, “in front of – behind”, “closer – further away”, “between” | |
talk clearly about common 2D and 3D shapes; visualise 3D shapes from 2D drawings | |
make and draw shapes with increasing accuracy, and analyse their geometrical properties |
3. Understanding properties of position and movement
Pupils should:
read and plot coordinates—eventually in all four quadrants; draw, or locate, shapes with given properties in the coordinate plane | |
visualise, predict, and represent the position of a shape following a rotation, reflection, translation, or glide reflection |
4. Understanding measures
Pupils should:
draw and measure lines to the nearest millimetre; combine linear measurements to measure perimeters | |
draw and measure acute and obtuse angles of a given size to the nearest degree; estimate the size of given angles and order them; draw angles reliably as parts of compound shapes | |
read the time to the nearest minute; calculate time intervals from clocks, from timetables, and from calendars | |
use standard units of length, area, volume, mass, and capacity; measure and weigh items; convert between related units | |
find areas of rectangles and of shapes composed of rectangles | |
measure and compare capacities; understand conservation of volume; find volumes of cuboids and of simple shapes composed of cuboids | |
read scales with increasing accuracy; record measurements using decimal notation |
Breadth of Study
1. During the Key Stage pupils should be taught the required Knowledge, Skills, and Understanding through:
extending place value to arbitrary integers and decimals | |
extending their understanding of numbers to include integers (positive and negative), fractions, and decimals | |
extending exact arithmetic to the standard written algorithms for integers and decimals, and the standard procedures for calculating with fractions | |
using structural arithmetic for efficient numerical calculation, and for algebraic simplification of numerical, fractional, and symbolic expressions | |
representing unknowns and variables by letters; using formulae; solving linear equations; representing and interpreting straight lines and linear equations | |
engaging in tasks that develop short chains of deductive reasoning and that bring out the centrality of proof in number, algebra, and geometry | |
drawing and measuring; using ruler and compass constructions; calculating areas and volumes; recording results using diagrams, words, numbers, and symbols; angle-chasing and analysing more complex figures in terms of triangles | |
linking the language of mathematics with spoken and written English; building simple logical expressions such as “… and …”, “… or …”, “if … , then …”, “not only … , but also …”; interpreting carefully crafted “realistic” problems; solving word problems; distinguishing between sensible and misleading uses of mathematics | |
routinely tackling familiar and unfamiliar problems, including multi-step and inverse problems; recognising that mathematical operations often come in ‘direct-inverse’ pairs, and that the inverse operation depends on robust fluency in the direct operation | |
practical work in which they draw inferences from a mathematical analysis of data, and consider how statistics can be used to inform decisions |
Knowledge, Skills, and Understanding
Teaching should ensure that appropriate connections are made between the section on Number and algebra and the section on Geometry and measures.
Ma1 Number and algebra
1. Using and applying “Number and algebra”
Pupils should:
Solving problems
use numerical, geometrical, and logical information in analysing data and in solving simple problems | |
make connections; use the arithmetic of integers, decimals, and fractions when solving problems | |
regularly solve multi-step problems and inverse problems | |
solve problems involving measures, rates and compound measures, ratio and proportion; make and justify estimates |
Communicating
use spoken and written language, notation, diagrams, terminology, and symbols correctly | |
recognise when information is presented in a misleading way | |
present results and solutions to problems clearly, declare unknowns explicitly, and lay out solutions logically line-by-line | |
interpret tables, lists, and information presented graphically; construct and interpret frequency tables; use precise measures of “centre” and “spread” |
Reasoning
understand that some statements can be clearly proved, and that other statements can be shown to be false | |
use place value and structural arithmetic to simplify calculations and expressions; recognise and use the fact that mathematical operations often come in “direct-inverse” pairs | |
use basic results and step-by-step deduction to draw conclusions; investigate apparent patterns and test the validity of statements—proving or disproving these statements conclusively where possible |
2. Numbers, the number system, structural arithmetic, simplification, and algebra
Pupils should:
Counting and numbers
count reliably forwards and backwards across hundreds and thousands boundaries | |
solve problems involving counting [e.g. How many pages from page 171 to 263?—inclusive and exclusive; How many dots are in a 5 by 7 rectangular array? How many chords are there joining 10 points on a circle?] | |
use place value in representing integers to 1 000 000, and decimals with up to four decimal digits; express position as a “power of 10”; choose the power of 10 to transform a given decimal to an integer (by multiplying) |
Sequences; powers and roots
recognise multiples of 2, 4, 5, 10, 20, 25, 50, 100; factorise instantly any output from multiplication tables to 10 × 10; recognise (or test quickly) prime numbers to 100 and test possible primes up to 500; recognise square numbers to 20 × 20; find all the factors of a given integer | |
recognise powers of 2, powers of 3, and powers of 5; recognise square and cube roots of familiar squares and cubes; understand and find, or estimate, the square root of any positive number; use index notation for small positive integer powers | |
find specified terms of a sequence given a term-to-term or a position-to-term rule; guess the simplest position-to-term rule for the nth term given the first few terms of a sequence |
Integers and decimals
read, write (in figures and words), and order whole numbers and decimals with up to six digits; understand, use, and calculate freely with (positive and negative) integers; use correctly the symbols =, ≠, <, ⩽, >, ⩾ and the associated language; order a set of positive and negative integers and decimals, or measurements | |
use correctly the terms factor, multiple, common factor, common multiple; find and use the HCF and LCM of two given integers; test for divisibility by 2, by 3, by 4, by 5, by 9, by 10 | |
multiply, and divide, any integer or decimal by 10, 100, 1000, or 10 000; know the multiplicative complements for 10 (2 × 5), for 100, and for 1000, and the corresponding decimals [e.g. | |
express any given large number as a number less than 10 times a power of 10, and a small number as a number greater than or equal to 1 times a power of 10 | |
compare measurements (in various contexts); round integers and decimals |
Fractions, percentages and ratio
understand general fractions in terms of unit fractions; switch freely between mixed numbers (with fractional part < 1) and standard fractional form | |
find fractional parts of shapes and quantities, and recognise the fractional part represented; solve simple ratio problems | |
understand equivalent fractions; express two given fractions with a common denominator; simplify a given fraction; order a list of integers and fractions | |
understand “percentage” as a fractional operator with denominator 100; find fractions and percentages of given quantities; express one quantity as a fraction of another; use the multiplicative character of percentage as an operator in calculations involving percentage increase and decrease; distinguish between absolute and relative increase and decrease | |
reduce a ratio to its simplest form, and establish the connection with “fractional parts”; divide a given quantity into two parts in a given ratio; solve problems involving ratio and proportion |
3. Calculation
Pupils should:
Number operations and mental methods
extend existing mental calculation to include negative numbers, decimals and fractions | |
calculate effectively in solving problems |
Structural arithmetic
use multiplication tables freely to simplify fractional expressions; convert fractions to decimals and terminating decimals to their simplified fraction equivalents | |
obtain the prime-power factorisation of a given integer by successive division | |
understand and use place value, inverse operations [e.g. cancellation], and structural arithmetic to simplify calculations; represent numbers and roots as powers, including fractional powers; work with powers of 10 | |
understand why (−1) × (−1) = 1 and why a −(−b) = a + b; use these to simplify and to evaluate numerical expressions | |
use the idea of choosing a suitable (common) denominator to add, subtract, multiply and divide fractions | |
solve word problems involving rates and ratios, including the unitary method | |
give both roots of simple quadratic equations; simplify numerical expressions involving simple surds [e.g. |
Algebraic simplification
substitute numerical values into formulae and expressions and evaluate; multiply out brackets, collect like terms, identify and take out common factors to simplify expressions; recognise that different-looking expressions may be identical; prove simple algebraic identities, and explain why two given expressions are not identical |
Written methods
relate decimal arithmetic to integer arithmetic; use standard written methods in column format for addition and subtraction, short and long multiplication, short (and long) division of integers and decimals |
Inequalities
solve simple linear inequalities in one variable and represent solutions on a number line |
Measures
calculate and work with perimeters, areas, volumes, durations, capacities, and simple compound measures; use standard units of length, area, volume, mass, and capacity; read scales with appropriate rounding; record and order measurements using decimal notation; convert between related units | |
estimate the size of any given angle; draw and measure angles reliably to the nearest degree | |
calculate reliably with measures; extract and use information from tables and charts; solve word problems involving money, time, length, and compound measures (speed, rates) |
4. Algebra: equations, formulae, identities, and functions
Pupils should:
set up and solve linear equations in complete generality [e.g.
reduce a linear equation in two variables to standard form (ax + by = c, or y = mx + c); eliminate a variable from two simultaneous linear equations in two unknowns; solve linear inequalities in one unknown | |
change the subject of a formula; draw the graph of a linear function, identifying its gradient, and interpreting its position; construct linear functions arising from real problems, sketch and interpret their graphs; establish the link to ratio and proportion | |
use letters in general expressions; use index notation for small positive integer powers; simplify given expressions | |
use algebra to find the exact solution of two simultaneous linear equations in two unknowns by eliminating a variable | |
sketch the graphs of simple quadratic functions; solve simple quadratic equations |
5. Solving numerical problems
Pupils should:
solve arithmetical problems, word problems, and geometry problems involving numbers and measures; check that their results are reasonable | |
solve multi-step and inverse problems with confidence | |
use the unitary method to solve proportion problems and problems involving ratios and rates | |
use algebraic formulae; set up and solve equations |
6. Processing, representing, and interpreting data
Pupils should:
solve problems involving lists, tables, charts, and graphs; sort, classify, and organise information; discuss the methods they use and explain what they find | |
find the average (i.e. mean) and other measures of “centre”, and measures of spread for small datasets; identify the modal class for grouped data; interpret frequency diagrams and histograms; use cumulative frequency | |
use counting where each outcome is “equally likely” to calculate probabilities |
Ma2: Geometry
1. Using and applying “Geometry”
Pupils should:
Solving problems
solve geometrical problems involving standard geometrical figures in 2D and 3D, and angles, length, area, and volume | |
measure and calculate accurately to construct and analyse 2D and 3D figures; use standard units in geometry |
Communicating
use geometrical language, notation, terminology, and symbols correctly | |
work in all four quadrants of the coordinate plane | |
lay out calculations, constructions, and proofs line-by-line |
use basic geometrical principles to justify each step in a calculation or deduction | |
analyse 2D and 3D configurations in terms of triangles |
2. Constructing and analysing geometrical configurations
Pupils should:
Know and analyse
recognise right angles, perpendicular and parallel lines, and use the associated language precisely; know that angles at a point total 360°, and that angles at a point on a straight line total 180° | |
know that two lines are parallel precisely when alternate angles are equal (or, equivalently, when corresponding angles are equal); prove and use the usual consequences (including the angle-sum in any triangle) | |
use known angles and angle properties to find unknown angles in given configurations (i.e. angle-chasing) | |
motivate the formula for the circumference of the circle and estimate π; solve related problems | |
talk about and work with common 2D and 3D shapes (including triangles [e.g. right angled, isosceles, and equilateral], quadrilaterals [e.g. parallelograms, rhombuses, rectangles, squares, and trapezia], cuboids, and prisms); correctly copy drawings from the board; make and draw shapes with increasing accuracy, and analyse their geometrical properties |
Constructions and congruence
use ruler and protractor to draw triangles with given data; extract and apply the basic congruence criteria (SAS, SSS, ASA; RHS) to prove standard results (including that the base angles in any isosceles triangle are equal, and the converse) | |
draw specified figures using “ruler” (i.e. straightedge) and compasses only; use the basic ruler and compass constructions to complete other constructions |
Area and Pythagoras
find the area of rectangles and shapes made from rectangles; find the area of right angled triangles and of general triangles; find the area of a general parallelogram | |
relate the formula for the area of a circle to the formula for the circumference; use the formula to solve related problems | |
state, prove, and use Pythagoras’ Theorem |
Circles
understand and use the terms centre, radius, chord, diameter, circumference, tangent, arc, sector, segment | |
prove the basic properties of a circle [e.g. centre and any chord form an isosceles triangle; angle in a semicircle is a right angle; tangent is perpendicular to radius; tangents form an external point are equal]; apply these results to solve problems |
Volume and 3D
calculate volumes of cuboids and shapes made of cuboids; calculate volumes of a “wedge” (half a cuboid), polygonal right prisms, and cylinders | |
find lengths and angles in simple 3D figures by considering 2D cross-sections |
Scaling and enlargement
draw figures to scale; interpret distances, angles, and areas on maps and other scale drawings |
interpret a circle as a locus; interpret the perpendicular bisector of a given line segment as a locus |
3. Coordinates and graphs
Pupils should:
read and plot coordinates in all four quadrants | |
use Pythagoras’ Theorem to calculate the distance between two given points (simple cases); find the coordinates of the midpoint of a line segment (simple cases) | |
establish the link between straight lines in the coordinate plane and linear equations in x and y; understand that parallel lines have the same gradient; find the intersection of two given straight lines | |
sketch the graphs of simple quadratic functions | |
explore and use coordinates in 3D |
Breadth of Study
1. During the Key Stage pupils should be taught the required Knowledge, Skills, and Understanding through:
activities that revisit and extend material from Key Stage 3, moving on to achieve fluency and automaticity in using a wide range of procedures | |
using language, terminology, and logic precisely and correctly; linking the language of mathematics with spoken and written English | |
learning basic facts and techniques by heart; using them to tackle two-step and multi-step exercises and problems in different contexts, and in solving unfamiliar problems (including word problems) | |
exploiting connections between superficially different topics; compressing ideas and techniques | |
recognising that operations often come in “direct-inverse” pairs, that the inverse operation is often the more demanding one, and that its mastery depends on robust fluency in the direct operation | |
using calculators intelligently where needed, whilst avoiding inappropriate dependence | |
extending exact arithmetic (without calculators) to fractions, surds, and numerical and algebraic expressions involving powers; routinely using algebraic structure to simplify numerical, fractional, and symbolic expressions | |
making intelligent estimates and approximations and handling the associated calculations reliably | |
combining congruence and ruler and compass constructions, parallels, and similarity to establish a formal basis for elementary Euclidean geometry | |
working with tables and information presented graphically; drawing inferences from a mathematical analysis of data drawn from a population with inherent variability; considering how statistics can be used to inform decisions |
Knowledge, Skills, and Understanding
Teaching should ensure that appropriate connections are made between the section on Number and algebra and the section on Geometry.
Ma1 Number and algebra
1. Using and applying “Number and algebra”
Pupils should:
Solving problems
use numerical, algebraic, geometrical, and logical information in tackling problems in Number and algebra, in solving word problems, and in analysing data | |
use the structure of arithmetic and the laws of algebra when working with integers, decimals, fractions, surds, and algebraic expressions in solving problems | |
regularly solve multi-step problems and inverse problems | |
make use of relevant connections between topics | |
solve problems involving measures, rates and compound measures, ratio and proportion | |
make and justify estimates |
Communicating
use spoken and written language, notation, diagrams, terminology, and symbols correctly | |
recognise when information is presented in a misleading way | |
present results and solutions to problems clearly, declare unknowns explicitly, and lay out solutions and proofs logically line-by-line | |
interpret tables, lists, and charts; present information graphically | |
construct and interpret frequency tables; use precise measures of “centre” and of spread |
Reasoning
investigate apparent patterns; generate, interpret, test, and prove (or disprove) simple conjectures | |
use place value, index laws, and structural arithmetic to simplify calculations and expressions, and to justify the extension of known conventions (including (−1) × (−1) = 1, 20 = 1, cos 120° = − | |
use known results and step-by-step deduction to draw conclusions |
2. From numbers to algebra (including calculation)
Pupils should:
Numbers and arithmetic
Measures
compare measurements; round integers and decimals appropriately | |
calculate and work with perimeters, areas, volumes, durations, capacities; use standard units of length, area, volume, mass, capacity, and simple compound measures (speed, density, and other “rates”); read scales with appropriate rounding; record and order measurements using decimal notation; change between related units—in numerical and algebraic contexts; solve word problems involving money, time, length, and compound measures |
Bounds and estimation
understand the limits of accuracy implied by a given measurement in decimal form and interpret the result of an arithmetical calculation | |
establish bounds on the accuracy of an estimate and understand how this affects a calculation |
Integer factorisation, fractions, and surds
use the terms factor, multiple, common factor, common multiple; find the HCF and LCM of given integers | |
recognise (or test quickly) prime numbers to 120; use the “square root test” to identify primes to 1000 | |
obtain the prime power factorisation of a given integer; list all factors of a given integer | |
move freely between “mixed” fractions and fractions in standard fractional form | |
use factorisation to simplify surd expressions [e.g.
|
Fractions
understand the unit fraction | |
add and subtract fractions; multiply and divide fractions; simplify, and hence evaluate, compound expressions involving fractions |
Fractions and decimals
move freely between terminating decimals and decimal fractions | |
know the equivalence of the exact (unevaluated) fraction notation | |
change any terminating decimal into a fraction in its lowest terms; change any recurring decimal into a fraction |
recognise
use surds (and π) to calculate exactly in geometric contexts; give lengths arising from applications of Pythagoras’ Theorem and solutions to quadratic equations in exact (mixed surd) form | |
use the standard notation for, and calculate with, cube roots; |
Powers, roots, and the index laws
factorise instantly any output from multiplication tables to 10 × 10; recognise square numbers to 25 × 25; recognise cubes to 63. | |
recognise powers of 2, 3, 4, 5; recognise square and cube roots of familiar squares and cubes; extend powers and roots to simple fractions and decimals; find, or estimate, the square root or cube root of any positive number | |
know, understand, and use the index laws; use index notation to present expressions in simplified power form; calculate freely with numerical and algebraic expressions involving powers | |
write any given number in standard form and translate a given standard form into the (approximate) number it represents; calculate with numbers given in standard form “as though they are exact” |
Fractions, decimals, and percentages
Sequences
work with standard integer sequences; generate terms given a term-to-term rule, or a position-to-term rule; guess the simplest position-to-term rule for the nth term given the first few terms of a sequence | |
use a given term-to-term rule to find a closed formula for the position-to-term rule | |
find the term-to-term rule and the position-to-term rule for sequences defined intrinsically | |
understand that when x < 1 (or |x| < 1) the sequence of powers (xn) tends rapidly to 0, and when x > 1 (or |x| > 1) the sequence of powers (xn) grows rapidly without bound; link to compound interest, to population growth, to doubling times and to radioactive half-life |
Ratio and proportion
divide a given quantity into two parts in a given part-to-part, or part-to-whole ratio; express the division of a quantity into two parts as a ratio; work with separate quantities in a given (external) ratio; reduce a ratio to its simplest form | |
calculate the result of a change of units; draw and use scale diagrams and maps; understand the effect of scaling and enlargement on different quantities (including angles, lengths, areas, and volumes) | |
solve proportion problems (where three of the four variables are given, determine the fourth); use the unitary method, and then the general method, to solve proportion problems | |
understand and use “X is inversely proportional to Y” as meaning “X is proportional to |
3. Coordinates, graphs, and functions
Pupils should:
read and plot coordinates in all four quadrants; move freely between straight lines in the coordinate plane and linear equations in x and y; derive the equation of a line through two given points, and the equation of a line through a given point with a given gradient | |
find the coordinates of the midpoint of a line segment; calculate the distance between two points in 2D or 3D | |
interpret straight line graphs arising in real situations | |
know and use the general form y = mx + c (or x = a) for a straight line; use gradient and intercept; find the point of intersection of two given straight lines | |
know that parallel lines have the same gradient; prove and use the fact that two lines with gradients m and m′ are perpendicular precisely when m · m′ = −1 | |
for particular values of m and c interpret the standard form y = mx + c as ‘Y = mX’ relative to an origin at (0, c) or at (− | |
sketch the graph of any given quadratic function by completing the square | |
sketch other graphs—including simple cubic functions, the reciprocal function y = | |
use coordinates to solve simple problems in 3D |
4. Processing, representing, and interpreting data
Pupils should:
engage in practical and theoretical work to construct and interpret tables, lists, and information presented graphically; use precise measures of “centre” and spread; sort, classify, and organise information | |
discuss variability; distinguish between data representing a single idealised measure and informal “random variables” sampled from a population or distribution | |
calculate the mean of a set of numbers or measures; use mode or median as appropriate to summarise the “centre”; identify the modal class for grouped data; refine measures of spread and “central tendency” | |
introduce ideas of probability via standard examples of discrete sample spaces in which each outcome is equally likely; explore the general notion of an “event” | |
understand why prob(A ∪ B) = prob(A) + prob(B) for disjoint events A, B; use simple counting to calculate probabilities in discrete sample spaces; understand and use the inclusion/exclusion formula prob(A ∪ B) = prob(A) + prob(B) − prob(A ∩ B) |
Ma2: Geometry
1. Using and applying “Geometry”
Pupils should:
Solving problems
know and understand basic ruler and compass constructions; use these to devise simple constructions | |
use standard units in geometry; solve geometrical problems in 2D and 3D involving calculation, construction, and deduction | |
measure and calculate accurately to construct and analyse 2D and 3D figures in terms of triangles; use known results to construct simple proofs |
Communicating
use geometrical language, notation, terminology, and symbols correctly | |
work in all four quadrants of the coordinate plane; interpret a given equation as the graph of a function or a circle | |
lay out calculations, constructions, and proofs line-by-line |
Reasoning
use the basic principles of Euclidean geometry and results derived from them to justify each step in a calculation, construction, or deduction | |
analyse 2D and 3D configurations [e.g. by singling out, and using known properties of triangles] |
2. From naïve construction to Euclidean geometry
Pupils should:
Ruler and compass constructions revisited and organised
know that two points A, B determine a line AB, a line segment | |
know and use the conventional notation for labelling the angles and sides of ΔABC | |
accept and use the SAS, SSS, ASA (and later RHS) congruence criteria; prove the basic properties of isosceles triangles; justify the basic ruler and compass constructions and use them to devise other constructions | |
prove that the perpendicular bisector of a given line segment | |
recognise the “perpendicular distance” from a point X to a line as the (shortest) distance to the line; prove the angle bisector of ∠BAC is the (part-) locus of points equidistant from the lines AB and AC; construct the incentre of ΔABC | |
prove that the three altitudes of a triangle are concurrent |
Parallel lines and angles in a triangle
know that angles at a point total 360°, and that angles at a point on a straight line total 180°; conclude that “vertically opposite angles are equal” | |
recognise that “two lines are parallel precisely when alternate angles (or equivalently, when corresponding angles) created by any transversal are equal”; derive the basic properties of a parallelogram and of a rhombus; where possible prove the converse results; prove and use the Midpoint Theorem | |
prove that the angles in any triangle add to 180° and that the exterior angle at any vertex is equal to the sum of the two interior opposite angles; deduce that the angles in any quadrilateral add to 360°; calculate the angle-sum in an n-gon, and the angle size in a regular n-gon | |
combine known results about angles to find unknown angles, and to show that certain pairs of lines are parallel | |
know and use the fact that the tangent and radius at a point on a circle are perpendicular; conclude that tangents from an external point are equal; prove that the angle subtended by a chord on the major arc is half the angle subtended at the centre O; conclude that angles subtended in the same segment are equal, and that opposite angles of a cyclic quadrilateral add to 180°; prove and use the Alternate Segment Theorem | |
prove that the area of a parallelogram is equal to that of a rectangle on the same base and between the same parallels and deduce the formula for the area of a triangle; use this to prove Pythagoras’ Theorem |
Similarity
establish and use the AAA similarity criterion and the SAS similarity criterion for general triangles; prove basic results using similarity | |
extend the Midpoint Theorem to divide a given segment into any number of equal parts; prove and use the Intercept Theorem |
3. Geometric calculation
Pupils should:
Trigonometry
2D and 3D figures
work freely with standard 2D figures | |
draw figures to scale; interpret maps and other scale drawings; apply similarity in analysing problems; understand how enlargement and scaling (or similarity) affects angles, lengths, areas, and volumes | |
find lengths and angles in 3D figures by considering 2D cross-sections; calculate the angle between two planes | |
calculate surface areas and volumes of standard figures |
Circles
understand and use the terms centre, radius, chord, diameter, circumference, tangent, arc, sector, segment | |
understand and use the formula for the circumference of a circle; calculate the length of circular arcs | |
relate the formula for the area of a circle to the formula for the circumference; calculate the area of a sector | |
calculate the circumradius and inradius of a triangle | |
use Pythagoras’ Theorem to find the equation of a circle of radius r centred at the origin and at the point (c, d); complete the square to identify easy quadratic equations as circles and find their centre and radius | |
find the equation of the tangent to a given circle at a specified point |
22http://education.lms.ac.uk/wp-content/uploads/2012/02/KS_1-4_DMJ.pdf






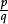 to p ÷ q
to p ÷ q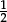 = 0.5,
= 0.5, 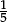 = 0.2,
= 0.2, 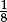 = 0.125]; recognise as alternative representations the decimal and fraction forms of simple fractions
= 0.125]; recognise as alternative representations the decimal and fraction forms of simple fractions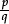
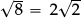 because both are positive and have the same square]
because both are positive and have the same square]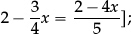
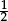 )
)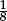 = 0.125]; recognise the decimal forms of simple fractions
= 0.125]; recognise the decimal forms of simple fractions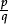 ; reduce a given fraction to lowest terms; rewrite two given fractions with a common denominator; order a list of fractions
; reduce a given fraction to lowest terms; rewrite two given fractions with a common denominator; order a list of fractions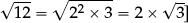
 as “that part, of which q identical copies make 1”; understand a general fraction
as “that part, of which q identical copies make 1”; understand a general fraction 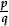 as a multiple
as a multiple 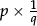 of a unit fraction; move freely from a given fraction to a suitable equivalent fraction
of a unit fraction; move freely from a given fraction to a suitable equivalent fraction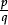 and the result of evaluating p ÷ q; find the decimal of any given fraction; understand why the decimal form of
and the result of evaluating p ÷ q; find the decimal of any given fraction; understand why the decimal form of 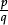 must terminate, or recur
must terminate, or recur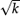 (for k > 0) as the exact positive real number whose square is equal to k; given k > 0 find the exact or approximate value of
(for k > 0) as the exact positive real number whose square is equal to k; given k > 0 find the exact or approximate value of 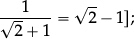
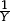 ”
”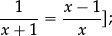
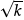 ); interpret this as a statement about the graph of y = x2 − k
); interpret this as a statement about the graph of y = x2 − k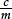 ,0)
,0)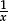 , the exponential function y = kx for easy (positive) values of k, the circular functions y = sin x, y = cos x, and y = tan x
, the exponential function y = kx for easy (positive) values of k, the circular functions y = sin x, y = cos x, and y = tan x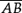 , and a circle with centre A and radius
, and a circle with centre A and radius 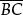 is the locus of points X equidistant from B and C; construct the circumcentre of any triangle
is the locus of points X equidistant from B and C; construct the circumcentre of any triangle