Problem 20

Problem 20: Cosmological models ( $✓$ $✓$ ) 2001 Paper I

In a cosmological model, the radius $R$ of the universe is a function of the age $t$ of the universe. The function $R$ satisﬁes the three conditions:

R (0) = 0, R^{'} (t) > 0 for t > 0, R^{″} (t) < 0 for t > 0,

(

*

)

where $R^{″}$ denotes the second derivative of $R$ . The function $H$ is deﬁned by

H (t) = \frac{R^{'} (t)}{R (t)} .

(i): Sketch a graph of $R (t)$ . By considering a tangent to the graph, show that $t < \frac{1}{H (t)}$ .
(ii): Observations reveal that $H (t) = \frac{a}{t}$ , where $a$ is constant. Derive an expression for $R (t)$ .
What range of values of $a$ is consistent with the three conditions $(*)$ ?
(iii): Suppose, instead, that observations reveal that $H (t) = b t^{- 2}$ , where $b$ is constant. Show that this is not consistent with conditions $(*)$ for any value of $b$ .
Note: $x^{α} e^{- x} \to 0$ as $x \to \infty$ for any constant $α$ .

Comments

The sketch just means any graph starting at the origin and increasing, but with decreasing gradient. The second part of (i) needs a bit of thought (where does the tangent intersect the $x$ -axis?) so don’t despair if you don’t see it immediately. Parts (ii) and (iii) are perhaps easier than part (i).

Solution to problem 20

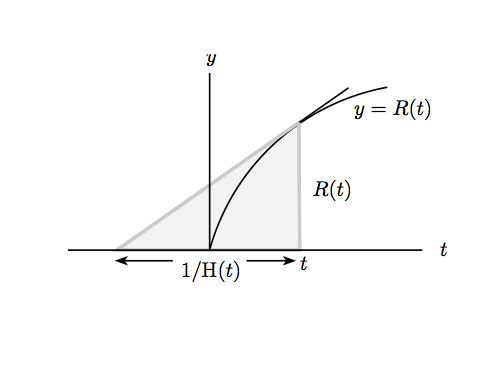
(i) The ﬁgure shows the curve $y = R (t)$ and the tangent to the curve, which meets the $t$ axis.

The height of the right-angled triangle in the ﬁgure is $R (t)$ and the slope of the hypotenuse is $R^{'} (t)$ . The length of the base is therefore $R (t) ∕ R^{'} (t)$ , i.e. $1 ∕ H (t)$ .

The ﬁgure shows that the tangent to the graph for $t > 0$ intersects the negative $t$ –axis, so $1 ∕ H (t) > t$ .

(ii) One way to proceed is to integrate the differential equation:

H (t) = \frac{a}{t} \Rightarrow \frac{R^{'} (t)}{R (t)} = \frac{a}{t} \Rightarrow \int \frac{R^{'} (t)}{R (t)} d t = \int \frac{a}{t} d t \Rightarrow ln R (t) = a ln t + c o n s t a n t \Rightarrow R (t) = A t^{a} .

The ﬁrst two conditions $(*)$ are satisﬁed if $a > 0$ and $A > 0$ . For the third condition, we have $R^{″} (t) = a (a - 1) A t^{a - 1}$ which is negative provided $a < 1$ . The range of $a$ is therefore $0 < a < 1$ .

(iii) The obvious way to do this just follows part (ii). This time, we have

H (t) = \frac{b}{t^{2}} \Rightarrow \frac{R^{'} (t)}{R (t)} = \frac{b}{t^{2}} \Rightarrow \int \frac{R^{'} (t)}{R (t)} d t = \int \frac{b}{t^{2}} d t \Rightarrow ln R (t) = - \frac{b}{t} + c o n s t a n t \Rightarrow R (t) = A e^{- b ∕ t} .

Thus $R^{'} (t) = H (t) R (t) = A b t^{- 2} e^{- b ∕ t}$ . Clearly $A > 0$ since $R (t) > 0$ for $t > 0$ so $R^{'} (t) > 0$ provided $b > 0$ . Furthermore $R (0) = 0$ (think about this!), so only the condition $R^{″} (t) < 0$ remains to be checked. Differentiating $R^{'} (t)$ gives

R^{″} (t) = A b (- 2 t^{- 3}) e^{- b ∕ t} + A b t^{- 2} e^{- b ∕ t} (b t^{- 2}) = A b t^{- 4} e^{- b ∕ t} (- 2 t + b)

This is positive when $t < \frac{1}{2} b$ , which contradicts the condition $R^{″} < 0$ .

Instead of solving the differential equation, we could proceed as follows. We have

\frac{R^{'}}{R} = b t^{- 2} \Rightarrow R^{'} = b R t^{- 2} \Rightarrow R^{″} = b R^{'} t^{- 2} - 2 b R t^{- 3} = b^{2} t^{- 4} R - 2 b R t^{- 3} = b (b - 2 t) t^{- 4} R .

This is positive when $t < \frac{1}{2} b$ , which contradicts the condition $R^{″} < 0$ .

Post-mortem

The interpretation of the conditions in $(*)$ of the question is as follows. The ﬁrst condition $R (0) = 0$ says that the universe started from zero radius — in fact, from the ‘big bang’.

The second condition says that the universe is expanding. This was one of the key discoveries in cosmology in the last century. The quantity $H (t)$ is called Hubble’s constant (though it varies with time). It measures the rate of expansion of the universe. Its reciprocal is the Hubble time. The present-day value of the Hubble time has been a matter of great debate but it seems to be about 14.4 billion years, greater than the age of the universe (as calculated using cosmological models of this sort) by about 0.5 billion years.

The last condition says that the expansion of the universe is slowing down. This is expected on physical grounds because of the gravitational attraction of galaxies on one another. However, current observations indicate that the expansion of the universe is speeding up, and this is thought to be due to the presence of dark energy.