Problem 36:  Root counting ($✓$ $✓$ $✓$) 1999 Paper III

(i)

Let $\mathrm{f}\left(x\right)=\left(1+x^2\right)e^x-k$, where $k$ is a given constant. Show that ${\mathrm{f}}^{\prime }\left(x\right)\ge 0$ and sketch the graph of $\mathrm{f}\left(x\right)$ in the three cases $k<0$,   $0<k<1$ and $k>1$.

Hence, or otherwise, show that the equation

$$\left(1+x^2\right){\mathrm{e}}^x-k=0$$

has exactly one real root if $k>0$ and no real roots if $k\le 0$.

(ii)

Determine the number of real roots of the equation $$\left({\mathrm{e}}^x-1\right)-k{tan}^{-1}x=0$$

in the different cases that arise according to the value of the constant $k$.

Note: If $y={tan}^{-1}x$,  then $\frac{\mathrm{d}y}{\mathrm{d}x}=\frac{1}{1+x^2}$.

Comments

In good STEP style, this question has two related parts. In this case, the first part not only gives you guidance for the second part, but also provides a result that is useful for the second part.

In part (ii) of the original question you were asked to determine the number of real roots in the cases $0<k\le 2∕\pi$  and  $2∕\pi <k<1$. I thought that you would like to work out all the different cases for yourself — but it makes the question considerably harder, especially if you think about the special values of $k$ as well as the ranges of $k$.

For part (i) you need to know that $x{\mathrm{e}}^x\to 0$ as $x\to -\infty$. This is just a special case of the result that exponentials go to zero faster than any power of $x$.

For part (ii), it is not really necessary to do all the sketches, but I think you should (though you perhaps wouldn’t under examination conditions) because it gives you a complete understanding of the way the function depends on the parameter $k$. For the graphs, you may want to consider the sign of ${\mathrm{f}}^{\prime }\left(0\right)$; this will give you an important clue. Remember that, by definition, $-\frac{1}{2}\pi <{tan}^{-1}x<\frac{1}{2}\pi$.

Solution to problem 36

(i) Differentiating gives ${\mathrm{f}}^{\prime }\left(x\right)=2x{\mathrm{e}}^x+\left(1+x^2\right)e^x={\left(1+x\right)}^2{\mathrm{e}}^x$ which is non-negative because the square is non-negative and the exponential is positive.

There is one stationary point, at $x=-1$, which is a point of inflection, since the gradient on either side is positive.

Also, $\mathrm{f}\left(x\right)\to -k$ as $x\to -\infty$, $\mathrm{f}\left(0\right)=1-k$ and $\mathrm{f}\left(x\right)\to \infty$ as $x\to +\infty$. The graph is essentially exponential, with a hiccup at $x=-1$. The differences between the three cases are the positions of the horizontal asymptote ($x\to -\infty$) and the place where the graph cuts the $y$ axis (above or below the $x$ axis?).

Since the graph is increasing and $0<\mathrm{f}\left(x\right)<\infty$, the given equation has one real root if $k>0$ and no real roots if $k\le 0$.

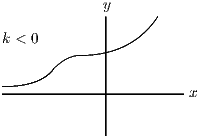
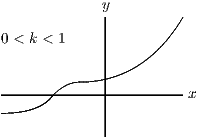
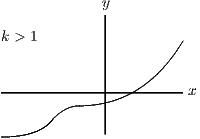
(ii) First we collect up information required to sketch the graph, as in part (i). We have

$\mathrm{f}\left(0\right)=0$,    $\mathrm{f}\left(x\right)\to \frac{1}{2}k\pi -1$ as $x\to -\infty$,    $\mathrm{f}\left(x\right)\to \infty$ as $x\to \infty$,    ${\mathrm{f}}^{\prime }\left(x\right)=e^x-k{\left(1+x^2\right)}^{-1}$ (which we know from the first part can only be zero only if $k>0$),    ${\mathrm{f}}^{\prime }\left(0\right)=1-k$.

The important values of $k$ seem to be $0$, $2∕\pi$ and $1$ so we will have to consider four cases.

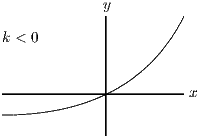
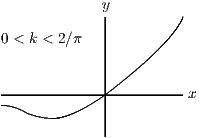
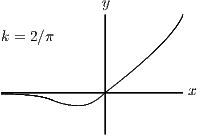
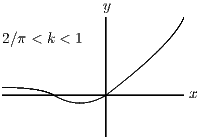
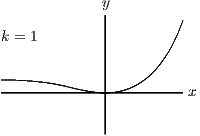
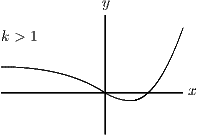
As you see, the equation $\left({\mathrm{e}}^x-1\right)-k{tan}^{-1}x=0$ has one root if $k\le \frac{1}{2}\pi$ and two roots otherwise. The case $k=1$ can be thought of as having one root at $x=0$ or as having two roots, both at $x=0$ (it is a double root).

Post-mortem

I think I made a bit of a meal of this; got carried away with the sketches. But it was reassuring (compulsive, I found) to consider every case. My explanation is pretty compact, so I think you’ll have to work it through on your own to convince yourself of the details.