Problem 38

Problem 38: Discontinuous integrands ( $✓$ $✓$ )

For any number $x$ , the largest integer less than or equal to $x$ is denoted by $[x]$ . For example, $[3.7] = 3$ and $[4] = 4$ .

(i)

Sketch the graph of

y = [x]

for

0 \leq x < 5

and evaluate

\int_{0}^{5} [x] d x .

(ii)

Sketch the graph of

y = [e^{x}]

for

0 \leq x < ln n

, where

n

is an integer, and show that

\int_{0}^{ln n} [e^{x}] d x = n ln n - ln (n!) .

Hence show that $n! \geq n^{n} e^{1 - n}$ .

Comments

I had to add a bit to the original question because it was all dressed up with nowhere to go. The question is clearly about estimating $n!$ so I added in the last line, which makes the question a bit longer but not much more difficult. I could have added another part, but I thought that you would probably add it yourself: you will easily spot, once you have drawn the graphs, that a similar result for $n!$ with the inequality reversed can be obtained by considering rectangles the tops of which are above the graph of $e^{x}$ instead of below it. You therefore end up with a nice sandwich inequality for $n!$ .

Stirling (1692 – 1770) proved in 1730 that $n! \approx \sqrt{2 π} n^{n + \frac{1}{2}} e^{- n}$ for large $n$ . This was a brilliant result — even reading his book, it is hard to see where he got $\sqrt{2 π}$ from (especially as he wrote in Latin). Then he went on to obtain the approximation in terms of an inﬁnite series; the expression above is just the ﬁrst term.

Solution to problem 38

(i)

PICT

The graph of

[x]

consists of the horizontal parts of an ascending staircase with 5 stairs, the lowest at height 0, each of width 1 unit and rising 1 unit.

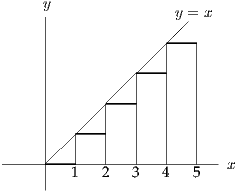
The integral is the sum of the areas of the rectangles shown in the ﬁgure:

area = 0 + 1 + 2 + 3 + 4 = 10 .

(ii)

PICT

The graph of

[e^{x}]

is also a staircase: the height of each stair is 1 unit and the width decreases as

x

increases because the gradient of

e^{x}

increases. It starts at height 1 and ends at height

(n - 1)

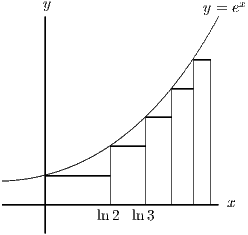
The value of $[e^{x}]$ changes from $k - 1$ to $k$ when $e^{x} = k$ i.e. when $x = ln k$ . Thus $[e^{x}] = k$ when $ln k \leq x < ln (k + 1)$ and the area of the corresponding rectangle is $k (ln (k + 1) - ln k)$ .

The total area under the curve is therefore

1 (ln 2 - ln 1) + 2 (ln 3 - ln 2) + \dots + (n - 1) (ln n - ln (n - 1))

which you can rearrange to obtain $n ln n - ln (n!)$ as required.

For the last part, note that $[e^{x}] \leq e^{x}$ (this is clear from the deﬁnition) so

\int_{0}^{ln n} [e^{x}] d x \leq \int_{0}^{ln n} e^{x} d x = n - 1 i.e. n ln n - ln (n!) \leq n - 1 .

Taking exponentials gives the required result.

Post-mortem

Usually when you draw a graph of a discontinuous function, you should specify at the jump whether the function takes the upper or lower value. For example $[x]$ takes the value 1 at $x = 1$ , which is the upper value. This can be achieved by putting (say) a circle round the upper or lower point, as appropriate. I didn’t bother on the above graphs, because it doesn’t affect the value of the integral and I didn’t want to clutter up the graphs.

Considering $[e^{x} + 1]$ instead of $[e^{x}]$ gives rectangles above the graph of $y = e^{x}$ rather than below. The calculations are roughly the same, so you should easily arrive at $n! \leq n^{n + 1} e^{1 - n}$ . We have therefore proved that

n^{n} e^{1 - n} \leq n! \leq n^{n + 1} e^{1 - n} .

This gives a pretty good (given the rather elementary method at our disposal) approximation for $n!$ for large $n$ .