Problem 42:  Geometry ($✓$ $✓$) 2015 Paper II

In the triangle $ABC$, angle $BAC=\alpha$ and angle $CBA=2\alpha$, where $2\alpha$ is acute, and $BC=x$. Show that $AB=\left(3-4{sin}^2\alpha \right)x$.

The point $D$ is the midpoint of $AB$ and the point $E$ is the foot of the perpendicular from $C$ to $AB$. Find an expression for $DE$ in terms of $x$.

The point $F$ lies on the perpendicular bisector of $AB$ and is a distance $x$ from $C$. The points $F$ and $B$ lie on the same side of the line through $A$ and $C$. Show that the line $FC$ trisects the angle $ACB$.

Comments

I thought it would be good to include at least one plane geometry question in this collection, so here it is. As always with geometry, the first thing to do is draw a BIG diagram. You will probably need to have quite a few tries at it.

Then you have the usual tools at your disposal: similar triangles, congruent triangles, angle-chasing, and — moving away from classical Euclidean geometry — Pythagoras, and sine and cosine rules. I leave it to you to decide what will be useful here.

Solution to problem 42

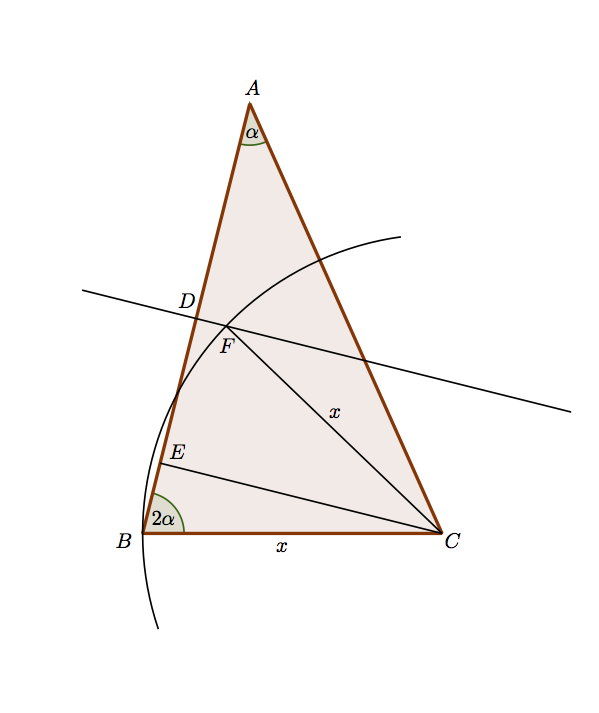
Here is a careful diagram, with a construction arc left in to show that $CB=CF=x$. It took me ages. But it is pretty much plain sailing now.

By the sine rule in $△ABC$ (and calculating an expression for $sin3\alpha$ using double angle formulae)

as required.

Then, since $D$ is the mid-point of $AB$ and $\angle BEC=90^{\circ }$,

rather surprisingly.

For the last part, since $\angle BCA=180^{\circ }-3\alpha$, we need to show that $\angle FCA=60^{\circ }-\alpha$ or, equivalently, $\angle FCB=120^{\circ }-2\alpha$. Now $\angle BCE=90^{\circ }-2\alpha$ so we are done if we can show that $\angle ECF=30^{\circ }$. But that follows almost immediately from the $DE=\frac{1}{2}x$ and $FC=x$: draw the perpendicular from $F$ to $CE$, which has length $\frac{1}{2}x$, and consider the right-angled triangle thus formed.

Post-mortem

I liked the mixture here of angle-chasing and use of the sine rule. Geometry purists, though, would be appalled; using the sine rule in a geometry problem is like using metal screws instead of wooden dowels on an antique wooden cabinet. As it happens, there is a beautiful proof of this result by pure geometry. You have to reflect the whole diagram about the perpendicular bisector of $AB$. For the details, see Ross Honsberger’s excellent Mathematical Chestnuts from around the World (Cambridge University Press, 2001), section 20.