Problem 53:  Tortoise and hare ($✓$ $✓$)

A tortoise and a hare have a race to the vegetable patch, a distance $X$ kilometres from the starting post, and back. The tortoise sets off immediately, at a steady $v$ kilometres per hour. The hare goes to sleep for half an hour and then sets off at a steady speed $V$ kilometres per hour. The hare overtakes the tortoise half a kilometre from the starting post, and continues on to the vegetable patch, where she has another half an hour’s sleep before setting off for the return journey at her previous pace. One and quarter kilometres from the vegetable patch, she passes the tortoise, still plodding gallantly and steadily towards the vegetable patch. Show that

and find $v$ in terms of $X$.

Find $X$ if the hare arrives back at the starting post one and a half hours after the start of the race.

How long does it take the tortoise to reach the vegetable patch?

Comments

The first thing to do is draw a distance–time diagram. You might also find it useful to let the times at which the two animals meet be $T_1$ and $T_2$.

Solution to problem 53

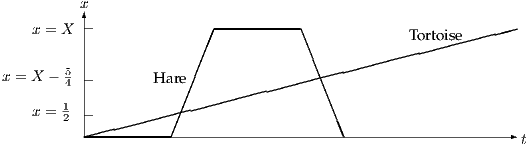
Let the times of the first and second meetings be $T_1$ and $T_2$. Then

The first pair and the second pair of equations give, respectively,

and hence (first eliminating $v$):

The total distance travelled by the hare in $\frac{1}{2}$ hour is $2X$, so

Factorising the quadratic gives two roots $-\frac{1}{4}$ and $\frac{5}{2}$, and we obviously need the positive root.

The speed of the tortoise is given by

so the time taken to travel $\frac{5}{2}$ kilometres is $\frac{11}{4}$ hours.

Post-mortem

It is interesting to see how quickly a mechanics question can change from mechanics to something else: algebra, calculus or, as in this case, coordinate geometry. As soon as the picture is drawn, the equations of the lines can be written down and everything follows as if it were a geometry problem.

Sometimes the change happens even more quickly. There is a well-known problem about a monk ascending a hill one day and descending the next day starting at the same time on each day. The problem is to show that there is a time at which the monk was at the same height on both days. You are not even given the speed at which the monk climbs. But if you draw (or just imagine drawing) height-time graphs of the ascent and descent, and superimpose them, you are done.