Problem 59

Problem 59: Equilibrium of rod of non-uniform density ( $✓$ $✓$ ) 2002 Paper II

A rigid straight rod $A B$ has length $l$ and weight $W$ . Its weight per unit length at a distance $x$ from $B$ is

α W l^{- 1} (\frac{x}{l})^{α - 1},

where $α$ is a constant greater than 1. Show that the centre of mass of the rod is at a distance $\frac{α l}{α + 1}$ from $B$ .

The rod is placed with the end $A$ on a rough horizontal ﬂoor and the end $B$ resting against a rough vertical wall. The rod is in a vertical plane at right angles to the plane of the wall and makes an angle of $𝜃$ with the ﬂoor. The coefficient of friction between the ﬂoor and the rod is $μ$ and the coefficient of friction between the wall and the rod is also $μ$ . Show that, if the equilibrium is limiting at both $A$ and $B$ , then

tan 𝜃 = \frac{1 - α μ^{2}}{(1 + α) μ} .

Given that $α = \frac{3}{2}$ and given also that the rod slides for any $𝜃 < \frac{1}{4} π$ ﬁnd the greatest possible value of $μ$ .

Comments

This is a pretty standard situation: a rod leaning against a wall, prevented from slipping by friction at both ends. The only slight variation is that the rod is not uniform; the only effect of this is to alter the position of the centre of gravity through which the weight of the rod acts.

The question is not general, since the coefficient of friction is the same at both ends of the rod. I think that it is a good idea (at least, if you are not working under examination conditions) to set out the general equations (with coefficients of friction $μ_{A}$ and $μ_{B}$ and frictional forces $F_{A}$ and $F_{B}$ ) without at ﬁrst assuming limiting friction. This will help understand the structure of the equations and highlight the symmetry between the ends of the rod.

You might wonder why the weight per unit length is given in such a complicated way; why not simply $k x^{α}$ ? The reason is to keep the dimensions honest. The factor of $W ∕ l$ appears so that the dimension is clearly weight divided by length. Then $x$ appears only divided by $l$ to make a dimensionless ratio. Finally, the factor of $α$ is required for the total weight of the rod to be $W$ .

Solution to problem 59

The distance, $\bar{x}$ , of the centre of mass from the end $B$ of the rod is given by

\bar{x} = \frac{\int_{0}^{l} α W l^{- α} x^{α} d x}{\int_{0}^{l} α W l^{- α} x^{α - 1} d x} = \frac{\int_{0}^{l} x^{α} d x}{\int_{0}^{l} x^{α - 1} d x} = \frac{{(α + 1)}^{- 1} l^{α + 1}}{{(α)}^{- 1} l^{α}} = \frac{α l}{α + 1} .

The response to the rest of this question should be preceded by an annotated diagram showing all relevant forces on the rod and with $G$ nearer to $A$ than $B$ . This will help to clarify ideas.

PICT

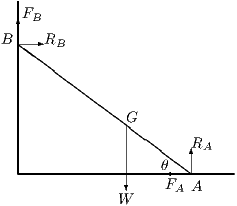
The equations that determine the equilibrium are

\begin{align} F_{B} + R_{A} & = W & (vertical forces) \\ F_{A} - R_{B} & = 0 & (horizontal forces) \\ R_{B} \bar{x} sin 𝜃 + F_{B} \bar{x} cos 𝜃 & = R_{A} (l - \bar{x}) cos 𝜃 - F_{A} (l - \bar{x}) sin 𝜃 . & (clockwise moments about G) \end{align}

If the rod is about to slip then the frictional and normal forces at $A$ can be speciﬁed as $F_{A} = μ R_{A}$ and $F_{B} = μ R_{B}$ . Substituting in ﬁrst two of the above equations gives

R_{A} = \frac{W}{μ^{2} + 1}, R_{B} = \frac{μ W}{μ^{2} + 1}, F_{A} = \frac{μ W}{μ^{2} + 1}, F_{B} = \frac{μ^{2} W}{μ^{2} + 1} .

Substituting into the third equation gives the required result.

For the ﬁnal part, setting $α = \frac{3}{2}$ gives

tan 𝜃 = \frac{2 - 3 μ^{2}}{5 μ}

If the rod slips for any angle less than $𝜃 = \frac{1}{4} π$ , then the angle at which limiting friction occurs at both ends must be at least $\frac{1}{4} π$ . Therefore

\frac{2 - 3 μ^{2}}{5 μ} \geq 1

i.e. $3 μ^{2} + 5 μ - 2 \leq 0$ , or $(3 μ - 1) (μ + 2) \leq 0$ . The greatest possible value of $μ$ is $\frac{1}{3}$ .

Post-mortem

In the original version, the question spoke about limiting friction without saying that it was limiting at both ends. We then wondered whether the friction could be limiting at one end only. The answer is yes. The three equations that govern the system do not determine uniquely the four unknown forces (normal reaction and frictional forces at each end of the rod); extra information is required. If the angle is also to be determined, two extra pieces of information are required; in this case the information is that the friction is limiting at both ends.