Problem 6

Problem 6: The regular Reuleaux heptagon ( $✓$ ) 1987 Specimen Paper I

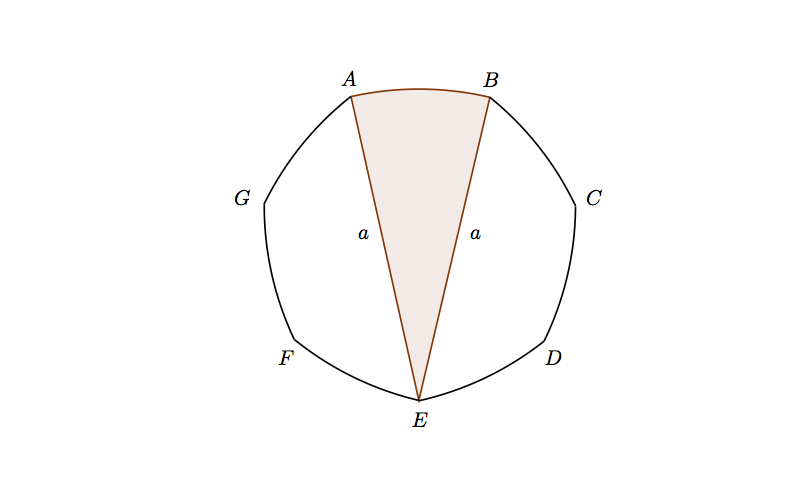
The diagram shows a British 50 pence coin. The seven arcs $A B$ , $B C$ , $\dots$ , $F G$ , $G A$ are of equal length and each arc is formed from the circle of radius $a$ having its centre at the vertex diametrically opposite the mid-point of the arc. Show that the area of the face of the coin is

\frac{a^{2}}{2} (π - 7 tan \frac{π}{14}) .

Comments

The ﬁrst difficulty with this elegant problem is drawing the diagram. However, you can simplify both the drawing and the solution by restricting your attention to just one sector of a circle of radius $a$ .

The ﬁgure sketched above has constant diameter; it can roll between two parallel lines without losing contact with either. (This looks plausible and you can verify it by sellotaping some 50 pence coins together, but a solid proof is not very easy.) The distance between these lines is the diameter of the ﬁgure. Like a circle, the 50 pence piece has circumference equal to $π$ times the diameter, which is in fact always true for a ﬁgure with constant diameter.

Reuleaux polygons are general polygons of constant diameter, and a heptagon has seven sides like, for example, British 50 and 20 pence pieces, Botswanan 50 thebe coins and Jordanian half dinars. The shield on Lancia cars is a Reuleaux triangle.

Solution to problem 6

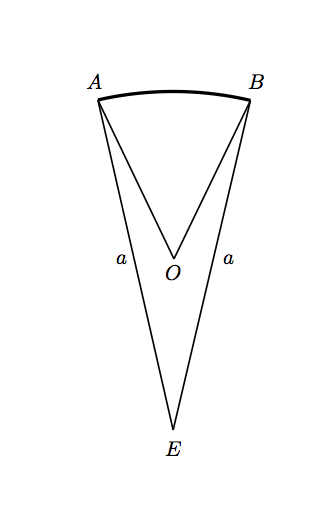
In the ﬁgure, the point $O$ is equidistant from each of three vertices $A$ , $B$ and $E$ . The plan is to ﬁnd the area of the sector $A O B$ by calculating the area of $A E B$ and subtracting the areas of the two congruent isosceles triangles $O B E$ and $O A E$ . The required area is 7 times this.

First we need angle $∠ A E B$ . We know that $∠ A O B = \frac{2}{7} π$ and hence $∠ B O E = \frac{1}{2} (2 π - \frac{2}{7} π) = \frac{6}{7} π$ (using the sum of angles round the point $O$ ). Finally,

∠ A E B = 2 ∠ O E B = 2 \times \frac{1}{2} (π - \frac{6}{7} π) = \frac{1}{7} π,

using the sum of angles of an isosceles triangle.¹⁶

Now $A B E$ is a sector of a circle of radius $a$ , so its area is

π a^{2} \times \frac{\frac{1}{7} π}{2 π} = \frac{π a^{2}}{14} .

The area of triangle $O B E$ is $\frac{1}{2} B E \times$ height, i.e.

\frac{1}{2} a \times \frac{a}{2} tan ∠ O B E = \frac{a^{2}}{4} tan \frac{π}{14} .

The area of the coin is therefore

7 \times (\frac{π a^{2}}{14} - 2 \times \frac{a^{2}}{4} tan \frac{π}{14}),

which reduces to the given answer.

Post-mortem

It is simple now to calculate the area of a regular $n$ -sided Reuleaux polygon. You should of course ﬁnd that the area tends to that of a circle of the same diameter as $n \to \infty$ .

¹⁶After the ﬁrst edition, a correspondent pointed out that the following argument gives angle $E A B$ more quickly: clearly $A$ , $B$ and $E$ all lie on a circle with centre $O$ ; the angle at $O$ subtended by the chord $A B$ is $\frac{2}{7} π$ , so the angle at the circumference is $\frac{1}{7} π$ . Obvious, really — can’t think why I didn’t see it.