Problem 66:  Harry the calculating horse ($✓$ $✓$) 1997 Paper II

Harry the Calculating Horse will do any mathematical problem I set him, providing the answer is 1, 2, 3 or 4. When I set him a problem, he places a hoof on a large grid consisting of unit squares and his answer is the number of squares partly covered by his hoof. Harry has circular hoofs, of radius $\frac{1}{4}$ unit.

After many years of collaboration, I suspect that Harry no longer bothers to do the calculations, instead merely placing his hoof on the grid completely at random. I often ask him to divide 4 by 4, but only about $\frac{1}{4}$ of his answers are right; I often ask him to add 2 and 2, but disappointingly only about $\frac{1}{16}\pi$ of his answers are right. Is this consistent with my suspicions?

I decide to investigate further by setting Harry many problems, the answers to which are 1, 2, 3, or 4 with equal frequency. If Harry is placing his hoof at random, find the expected value of his answers. The average of Harry’s answers turns out to be 2. Should I get a new horse?

Comments

Hans von Osten, a horse, lived in Berlin around the turn of the last century. He was known far and wide for his ability to solve complex arithmetical problems. Distinguished scientists travelled to Berlin to examine Hans and test his marvellous ability. They would write an equation on a chalkboard and Hans would respond by pawing the ground with his hoof. When Hans reached the answer he would stop. Though he sometimes made errors, his success rate was far higher than would be expected if his answers were random. The accepted verdict was that Hans could do arithmetic.

Hans’s reputation as a calculating horse nosedived when an astute scientist simply made sure that neither the person asking the questions nor the audience knew the answers. Hans became an instant failure. His success was based on his ability to sense any change in the audience: a lifted eyebrow, a sigh, a nodding head or the tensing of muscles was enough to stop him from pawing the ground. Anyone who knew the answer was likely to give almost imperceptible clues to the horse. But we shouldn’t overlook Hans’s talents: at least he had terrific examination technique.

We are investigating the situation when Harry places his hoof at random, so that the probability of the centre of his hoof lands in any given region is proportional to the area of the region. We therefore move swiftly from a question about probability to a question about areas. You just have to divide a given square into regions, each determined by the number of squares that will be partially covered by Harry’s hoof if its centre lands in the region under consideration. Remember that the areas must add to one, so the most difficult area calculation can be left until last and deduced from the others.

To answer the last part properly, you really need to set out a hypothesis testing argument: you will accept the null hypothesis (random hoof placing) if, using the distribution implied by the null hypothesis, the probability of obtaining the given result is greater than some pre-decided figure. Obviously, nothing so elaborate was intended here, since it is the last demand of an already long question: just one line would do.

Solution to problem 66

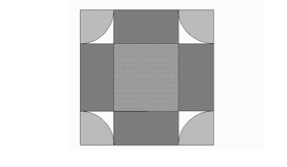
The diagram shows one square of the grid.

Harry’s hoof will land completely within exactly one square if he places the centre of his hoof in a square of side $\frac{1}{2}$ centred on the centre of any square, shown with horizontal and vertical lines in the diagram. The area of any such square is $\frac{1}{4}$ square units.

His hoof will partially cover exactly four squares if he places the centre in a circle of radius $\frac{1}{4}$ centred on any intersection of grid lines. The total area of any one such circle is $\frac{1}{16}\pi$ square units, which may be thought of as four quarter circles, one in each corner of any given square, shown lightly shaded in the diagram.

His hoof will partially cover exactly two squares if he places the centre in any one of four $\frac{1}{2}$ by $\frac{1}{4}$ rectangles, of total area $4\times \frac{1}{8}$ in any given square, shown darkly shaded in the diagram.

Otherwise, his hoof will partially cover three squares; the area of this remaining region, shown with no shading in the diagram, is

If Harry placed his hoof at random, the probabilities of the different outcomes would be equal to the corresponding area calculated above (divided by the total area of the square, which is 1). Thus the data given in the question are exactly consistent with random placement.

The expected value given random placements is

The expected value (given that Harry gets all questions right) is $\left(1+2+3+4\right)∕4=5∕2$. Harry has a less accurate expected value even than the random expected value. He is clearly hopeless and should go.

Post-mortem

The explanations in the first paragraph of the solution are very concise. To understand them, you should draw yourself lots of diagrams.

The proportion of Harry’s answers that are correct, in the case of the $2+2$ calculation is given as ‘about $\frac{1}{16}\pi$. That should have given you pause for thought. Why not $\frac{1}{5}$? Clearly, it was supposed to be helpful, so it should have been no surprise that the probability of getting the answer 4 under the random assumption turned out to be exactly $\frac{1}{16}\pi$. Of course, these questions shouldn’t turn into a game of spotting hidden clues, but it is always worth looking for unusual features of a question — or of any mathematical problem.