8. Computation Theories of Consciousness

Useful computation is in the eye of the beholder. […] It requires an underlying system of whose autonomous dynamics we have a predictive model. […] To solve a problem computational we need to map the problem to be solved onto the underlying behavior of the system and hence produce a starting state from which the autonomous dynamics of the system will produce a solution.

Robert Kentridge, Symbols, Neurons, Soap-Bubbles and the Computation Underlying Cognition1

8.1 Calculators, Special-Purpose Computers and General-Purpose Computers

We can solve many problems in our heads. But it is often easier to use the physical world to solve problems. Suppose you want to calculate 10+4+18+2. Put ten stones in a box, then four, and so on. Count the number of stones in the box to get the result. This is a simple calculator. The abacus, slide rule and Pascaline are more sophisticated calculators. When you enter a problem into a calculator the solution is immediately displayed. As each stone is put in the box you can immediately read off the total number of stones—there is no waiting while the system ‘computes’.

Special-purpose computers take time to solve problems. We enter the problem by modifying the system’s state (turning knobs, pressing keys, etc.). We set the special-purpose computer running and it transforms the starting state into the final state. We read off the result from the final state.

Special-purpose computers can only solve a limited number of closely related problems. A special-purpose computer that uses water to model an economy2 cannot process words or simulate an aircraft wing. Turing machines are special-purpose computers.

Soap bubble computers can find a short path between multiple points (see Figure 8.1). Other special-purpose computers are Turing’s Bombe, which was used to crack German encryption during the Second World War, and Babbage’s difference engine—a mechanical system that uses gears, cams, rods, levers and springs to compute polynomial functions.

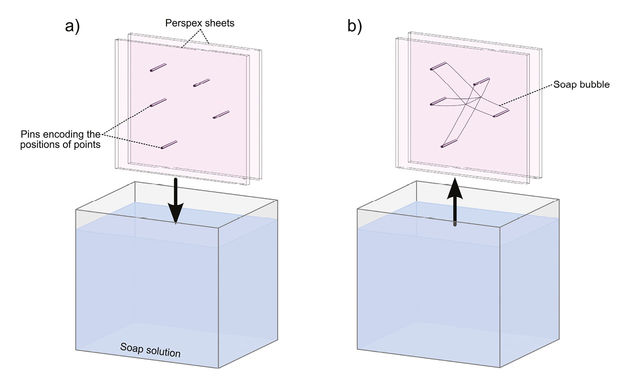
Figure 8.1. Soap bubble computer. a) Pins are placed between two Perspex sheets to indicate the positions of some points. b) The sheets are dipped in soap solution and the resulting bubble contracts to minimize its surface tension, producing a short path between the points. Image © David Gamez, CC BY 4.0.3

General-purpose computers run programs. Programs turn a general-purpose computer into a special-purpose computer for a limited period of time. The operator specifies the program by connecting wires, punching cards, typing code into a terminal, and so on. The program puts the computer into a starting state. Then the computer’s components interact according to the laws of physics, and the result is read off from the computer’s finishing state. Universal Turing machines are general-purpose computers.

Babbage’s Analytical Engine is a design for a general-purpose computer that uses gears, cams, rods, levers and springs to run programs. The ENIAC was the first general-purpose computer to be built. By manipulating switches and cables it could be rewired into a special-purpose computer that corresponded to a desired program. The innovation of the ENIAC was that it was designed to be rewired easily—previous computers could only run a limited range of programs without being heavily modified (by adding components, re-soldering circuits, etc.). The Manchester Baby was the first general-purpose computer that could ‘rewire’ itself electronically from a program stored in a cathode ray tube.

Modern digital computers are general-purpose computers. Their programs are typically written in a high level language, such as C++. Another program, called a compiler, converts this human-readable list of instructions into binary machine code, which is stored as a set of voltages in the computer’s memory. When the program runs, the voltages in the computer’s memory interact with the CPU and other components. This causes the computer to change states in a sequence determined by the program. When the program finishes the result is read back from the computer’s memory.

Special-purpose computers can execute the same computations as general-purpose computers (the same computations can be executed by Turing machines and universal Turing machines). The key difference is that general-purpose computers can be dynamically reconfigured to run different programs. Special-purpose computers have to be custom-built to run a particular program.

When a general-purpose computer runs a program it is executing the computations that are specified in the program—its potential ability to execute other programs does not affect its current computations. General-purpose computers operate as special-purpose computers when they are running a program.4

The brain can operate as a general-purpose computer. I can manually execute a program, using pen and paper to keep track of the variables.5 When a brain is not manually executing programs, it is not operating as a general-purpose computer. In ordinary life the brain works as a special-purpose computer: its state transitions are determined by complex biological structures that are mostly hardwired.

8.2 Computation C-Theories

Computers are artificially intelligent—they can chit-chat, fly planes and play games. A computer that was simulating your brain might behave just like you. In a few short years computers will conquer the world and grind our weak human flesh into fertilizer.

Computation c-theories are defined as follows:

D14. A computation c-theory links consciousness to the execution of computations. Computation CC sets only contain computations, which can be executed by many different types of computer.6

Computation c-theories are motivated by the observation that computers can do the same things as brains. So it is hypothesized that brains work in a similar way to computers. Computation c-theories are encouraged by the fact that a program can run on many different types of machine. This suggests that computations could be objectively present in many different materials.

Computation c-theories claim that computation CC sets are linked to consciousness independently of the system that is executing them. So a computation CC set would be linked to consciousness if it was executed manually, if it ran on the cogs of Babbage’s Analytical Engine or if it was executed on the voltages of a modern digital computer.

The brain is conscious when it is operating as a special-purpose computer. So any computations that might be linked to consciousness can be executed on special-purpose computers. The convenient features of general-purpose computers are irrelevant to computation c-theories.7

8.3 The Subjectivity of Computing

My mate Crystal has asked me to father her children. She wants to be impregnated when the planets are aligned. That way, her children will inherit my good looks and become great warriors. To calculate the date I need a model of the solar system.

The solar system can be simulated on a digital computer. I write a program that uses Newton’s equations to manipulate numerical representations of the masses, positions and velocities of the sun and planets. A compiler converts the program into machine code. When I load the compiled program it becomes a pattern of voltages in the computer’s memory. When I run the program the components in the computer interact according to the laws of physics. After a few seconds the program terminates and I interpret the pattern of output voltages as the date of planetary alignment.

The solar system can be modelled by an orrery, which uses a clockwork mechanism to move metal balls representing the planets around a ball representing the sun. To calculate the date of planetary alignment, I put the spheres into the planets’ current positions, set the mechanism running and read off the date when they align.8

I can increase the accuracy of my orrery by discarding its clockwork mechanism and replacing its balls with metal spheres that have the same masses as the sun and planets. To set up this gravity-powered orrery I put the spheres into positions that correspond to the sun and planets and give them the same velocity. I allow them to rotate under the influence of gravity and note when they align.

It makes no difference to my model if it uses metal spheres or the actual sun and planets. The latter approach requires less effort. The planets are already in their starting state and moving under the influence of gravity. I allow them to rotate and read off the date when they align.

All of these systems are computing the same global function: the date when the planets align. If any of these systems have computational properties (that are potentially linked to consciousness), then all of these systems have computational properties (that are potentially linked to consciousness). Computers can be made from silicon, metal or planets—it does not matter if they are powered by clockwork or gravity.

Prior to my intervention the solar system was not a special-purpose computer: it was not calculating the paths of the planets. It was just a group of massy bodies whose state changes were dictated by the laws of physics. The solar system became a computer when I used it to calculate the paths of the planets. But its new status did not affect its material properties or behaviour—it continued to follow the laws of physics in exactly the same way as before. This suggests that computers are subjective interpretations of the physical world—part of the physical world becomes a computer when I use it to solve problems.

When I use my iPad to bang in a nail it can be useful to describe it as a hammer. Some of its properties can be understood by comparing it with other hammers. But my iPad does not contain ‘hammutations’—I do not need to invoke ‘hammutations’ to explain how I can bang in a nail with my iPad.

When we use part of the physical world to add numbers, it can be useful to describe it as a calculator. Some of its properties can be understood by comparing it with other calculators. But the physical world does not contain calculations. Stones and a box do not contain calculations—I use them to add numbers.

When we use the state changes of physical objects to solve problems it can be useful to describe them as computers. Some of their properties can be understood by comparing them with other computers (a digital computer is faster and more flexible than an orrery). But I do not need to invoke the objective presence of computations in the physical world to explain how I can use digital computers, orreries and solar systems to compute the dates of planetary alignment.

The key difference between digital computers, orreries and solar systems is the extent to which they have been engineered to facilitate our use of them as computers. The solar system has not been engineered at all—it is difficult to set up in a desired starting state and it works on the same time scale as the system it is modelling. Clockwork orreries can be set up easily and work faster, but they can only model one type of system. Digital computers can run many different programs and they typically operate much faster than the systems they are modelling.

If computing is a use that we make of physical objects, then computations cannot be members of CC sets (C1). My consciousness does not appear when someone uses my brain as a computer.

8.4 Information Processing in Computers

Computers are often described as information processing technology. Chapter 7 explained how we use interfaces to extract information from the physical world. Interfaces can also be used to store information in the physical world.9 I can write and read the same number, the same information, to and from many different physical systems.

Information that is stored in the physical world can be altered by changes in the physical world. I write Felicity’s number on a piece of paper and store it as a sequence of pits on a compact disc. A tea stain blurs ‘7’ into ‘8’. A scratch on the disc scrambles Felicity’s number.

We use changes in the physical world to process information. We construct a system that changes in a systematic way. Then we modify part of the system to encode the information that we want to transform (this modification is determined by the interface). We allow the system to change state (to compute). When it has finished we use the same interface to read back the processed information from the system.10

We know that soap bubbles contract to minimize their surface area, but we do not know exactly how they will contract between a given set of pins—if we knew this, there would be no point in using a soap bubble computer to identify a short path. The encoding of positions using pins, the dipping in soap solution and the examination of the resulting bubble are worthwhile because they enable us to read back a short path solution that would be more complicated to obtain in other ways.

Digital computers are engineered to carry out fast and flexible information processing. We initialize a computer by creating voltage patterns in its DRAM that correspond to a program and initial data. The computer then moves through the sequence of physical states that is determined by the data and the program. Digital computers also include a physically implemented interface that uses carefully designed interactions between components in the screen, circuitry and chips to convert the DRAM voltages into graphical shapes painted in light, which we interpret as letters, numbers, etc.

The information processing that is carried out by a physical system depends on the interface that is used to read and write the information. The soap bubble computer can be interpreted as processing information about the shortest roads between cities or about the optimal wiring of electronic components.

Suppose a computer’s memory changes from 011100100110010
101100100 to 011100110111010101101110.11 The information extracted through one interface (8-bit numbers, standard ASCII codes, 114=’r’, 101=’e’, 100=’d’, 115=’s’, 117=’u’, 110=’n’) changes from ‘red’ to ‘sun’. Through a different interface (6-bit numbers, 28=’r’, 38=’u’, 21=’i’, 36=’n’, 55=’a’, 46=’d’), the information changes from ‘ruin’ to ‘raid’. There is no single correct or objective answer about the information processing that is being carried out by this computer. At most we can say that at least one interface exists that leads to the processing of ‘red’ into ‘sun’.12

Information processing is not a unique attribute of computers or brains. Any system can be interpreted as an information processor. A digital computer does not process any more information than a tub of worms. But we can carry out more useful information processing with a digital computer.

Any system that is interpreted as an information processor inherits all of the problems with information that were highlighted in the previous chapter. Information is subjective (C1), it is not likely to be intrinsic (C2) and it does not have e-causal powers (C4). Most or all information sets can be read from the conscious and unconscious brain (C3). If computation is information processing, it cannot be a member of a CC set.

8.5 Digital Physics and Theories of Implementation

Keith is taking time out from his IT support work. He flops into a chair, pushes back his lank long hair, sparks up a joint and relaxes. Suddenly he has a vision of the universe as a giant computer.

Digital physicists claim that digital computation is a fundamental property of the universe.13 Computation cannot be subjective if everything is computing all the time, regardless of whether we are using it to process information. This claim needs to be supported with a definition of what it means to implement a computation. Digital physicists cannot claim that everything is X without specifying the nature of X. When we have a theory of implementation, we can look for computational structures in the universe. If they are ubiquitous and play a fundamental physical role, then it can be claimed that the universe is a giant computer.

A theory of implementation is also required to test computation c-theories. Suppose we want to carry out a pilot study that looks for the computation CC set that is linked to a conscious state. We will need a theory of implementation that maps the brain’s physical states onto computations. This will enable us to identify the computations that are executed in the conscious brain and not executed in the unconscious brain.14

Many theories of implementation have been put forward. None of them are convincing. Theories based on finite state automata lead to panpsychism.15 Combinatorial state automata don’t work.16 Some theories of implementation are based on features of modern digital computers, such as string processing, which do not generalize easily to biological systems.17 Many digital physicists favour cellular automata, but it is far from obvious whether cellular automata can provide a plausible interpretation of the physical world or the systems we call computers.18

Digital physics cannot rescue computation c-theories from subjectivity without a plausible theory of implementation. Computation c-theories cannot get off the ground without a theory of implementation that would enable them to be experimentally tested. We do not have a workable theory of implementation.

8.6 Summary

Computation c-theories claim that computations are sole members of CC sets—the architecture and material of the systems that are executing the computations are irrelevant. The convenient features of general-purpose computers are not necessary to computation c-theories. Any computation that is potentially linked to consciousness can be executed on a special-purpose computer.

If computation is a subjective use we make of the world, then computations cannot be members of CC sets (C1). If computers are information processors, computation c-theories will have the same problems as information c-theories (C1-C4). Digital physicists claim that digital computation is a fundamental property of the universe. But no one has developed a theory of implementation that convincingly supports digital physics or would enable us to identify computational correlates of consciousness in the brain. Until these problems have been resolved, computation c-theories should be set aside or interpreted as physical c-theories.19