9. Predictions and Deductions about Consciousness

9.1 Predictions about Consciousness

I shall certainly admit a system as empirical or scientific only if it is capable of being tested by experience. These considerations suggest that not the verifiability but the falsifiability of a system is to be taken as a criterion of demarcation. In other words: I shall not require of a scientific system that it shall be capable of being singled out, once and for all, in a positive sense; but I shall require that its logical form shall be such that it can be singled out, by means of empirical tests, in a negative sense: it must be possible for an empirical system to be refuted by experience.

Karl Popper, The Logic of Scientific Discovery1

Information and computation c-theories do not conform to constraints C1-C4. The rest of this book will focus on physical c-theories, which are based on the idea that patterns in one or more materials are linked to conscious states (D12).

Physical c-theories convert descriptions of physical states into descriptions of conscious states. This enables them to be tested in the following way:

1. Measure aspect of the physical world that is specified by the c-theory.
2. Convert measurement into p-description, pd1.
3. Use mathematical c-theory to convert p-description into c-description, cd1.
4. Obtain c-report from test subject.
5. Convert c-report into c-description, cd2.
6. Compare cd1 and cd2. If they match, the c-theory passes the test for this physical state and this conscious state.

For example, we could measure the state of a person’s brain and use a c-theory to generate a prediction about their consciousness. This is illustrated in Figure 9.1.

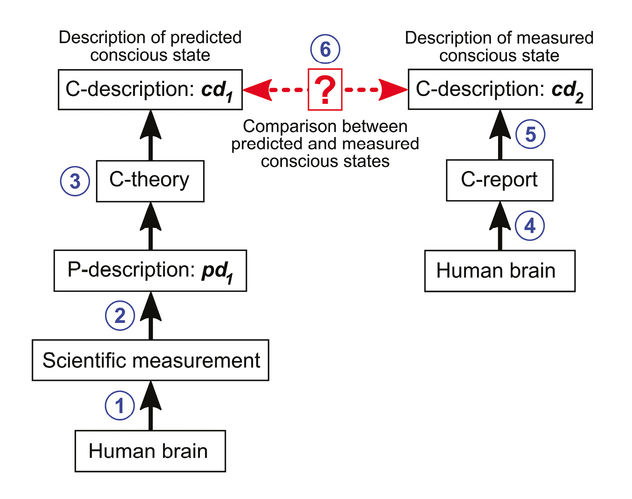
Figure 9.1. Testing a c-theory’s prediction about a conscious state. 1) Scientific instruments measure the physical state of the brain. 2) Scientific measurements are converted into a formal p-description of the brain’s physical state, pd1. 3) C-theory converts p-description, pd1, into a formal c-description of the brain’s predicted conscious state, cd1. 4) The human brain generates a c-report about its conscious state. 5) The c-report is converted into a formal description of the measured conscious state, cd2. 6) The measured and predicted conscious states are compared. If they do not match, the c-theory should be revised or discarded. Image © David Gamez, CC BY 4.0.

The validation of the predicted consciousness (stages 4–6) could be carried out by the subject. First the predicted conscious state could be induced in the subject. Then the subject would compare the induced state of consciousness with their memory of their earlier conscious state (the state they had when their physical state was measured).2

Virtual reality could be used to induce predicted states of consciousness in the subject. The c-description of the predicted consciousness would be converted into a virtual reality file.3 This would be loaded into a virtual reality system and the user would decide whether their consciousness in the virtual reality system was similar to their earlier conscious state.4 We could also develop algorithms that convert c-descriptions of predicted conscious states into natural language. The subject could decide whether the natural language description corresponded to their memory of their earlier conscious state.

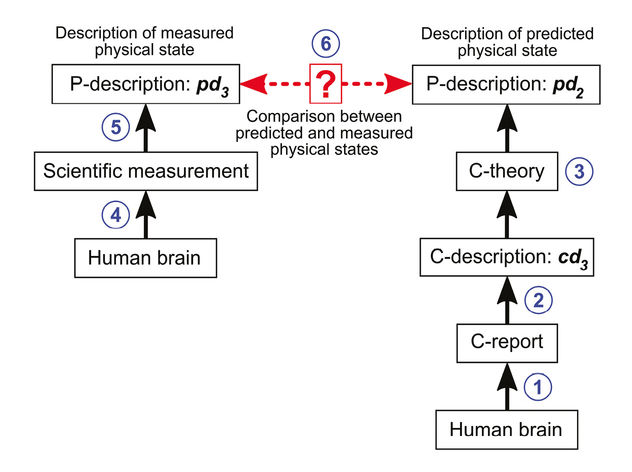
Figure 9.2. Testing a c-theory’s prediction about a physical state. 1) The human brain generates a c-report about its conscious state. 2) The c-report is converted into a formal description of the measured conscious state, cd3. 3) C-theory converts the c-description, cd3, into a formal p-description of the brain’s predicted physical state, pd2. 4) Scientific instruments measure the physical state of the human brain. 5) Scientific measurements are converted into a formal p-description of the brain’s physical state, pd3. 6) The measured and predicted physical states are compared. If they do not match, the c-theory should be revised or discarded. Image © David Gamez, CC BY 4.0.

C-theories can convert descriptions of conscious states into descriptions of physical states. So they can also be tested in the following way (see Figure 9.2):5

1. Obtain c-report from test subject.
2. Convert c-report into c-description, cd3.
3. Use mathematical c-theory to convert c-description into p-description, pd2.
4. Measure aspect of the physical world that is specified by the c-theory.
5. Convert measurement into p-description, pd3.
6. Compare pd2 and pd3. If they match, the c-theory passes the test for this physical state and this conscious state.

For example, a c-theory might predict that a conscious experience of a red rectangle is associated with a particular neuron activity pattern. We can measure the brain of a person who c-reports a red rectangle to see if the predicted neuron activity pattern is present.

C-theories can only be tested on platinum standard systems. On a platinum standard system we can compare a c-theory’s prediction with a measurement of consciousness. Or we can generate a prediction about a physical state from a measurement of consciousness. This type of testable prediction is formally defined as follows:

D15. A testable prediction is a c-description that is generated from a p-description or a p-description that is generated from a c-description. Predictions can be checked by measuring consciousness or they are generated from measurements of consciousness. Predictions can only be generated or confirmed on platinum standard systems during experiments on consciousness. It is only under these conditions that consciousness can be measured using assumptions A1-A6.

Good c-theories generate many testable predictions. We believe c-theories to the extent that their predictions have been successfully tested. Different c-theories can make different testable predictions—we use this to experimentally discriminate between them.

The tests described in this section only check that a c-theory maps between conscious states and particular aspects of the physical world. They do not check that a c-theory is based on minimal and complete sets of spatiotemporal structures (D5). Suppose we have shown that a c-theory maps between neuron activity patterns and consciousness in normally functioning adult human brains. To test the theory fully we have to check that this mapping exists independently of the presence of other materials in the brain, such as electromagnetic waves, glia, haemoglobin and cerebrospinal fluid.

To prove that a c-theory is based on minimal and complete sets of spatiotemporal structures we need to vary the physical world systematically in the manner described in Section 5.3. Many variations of the physical world cannot be achieved with natural experiments. So it is extremely unlikely that the predictions of a c-theory can be fully tested.

9.2 Deductions about Consciousness

I put your head into a guillotine and chop it off. It falls into a basket. I watch your face. Your eyes move; your mouth opens and closes; your tongue twitches. These movements cease. I connect an EEG monitor to your brain. It is silent. After a couple of minutes a wave of activity occurs that fades away after twenty seconds.6

Your decapitated head might be associated with a bubble of experience long after it has been cut off. I cannot measure its consciousness because it is not a platinum standard system. But I can use a theory of consciousness that has been tested on platinum standard systems to make inferences about the consciousness of your decapitated head.

How does consciousness change during death? Which coma patients are conscious? When does consciousness emerge in the embryo or infant? How will my consciousness be affected by a brain operation? Can I copy my consciousness by simulating my brain on a computer? What are the bubbles of experience of bats, cephalopods and plants? Are robots conscious?

Suppose we converge on a c-theory that is commonly agreed to be true. Some of its predictions have been successfully tested. We are confident that it accurately maps between conscious states and physical states on platinum standard systems during consciousness experiments. We can use this reliable c-theory to make inferences about the consciousness of decapitated heads, bats and robots.

In an experiment on a platinum standard system a c-theory’s predictions can be checked because assumptions A1-A6 hold and we can measure consciousness. These assumptions do not apply to decapitated heads, bats and robots. We cannot obtain a believable c-report from these systems, so we cannot compare a c-description generated by a c-theory with a c-description generated from a c-report. Inferences about the consciousness of these systems cannot be confirmed or refuted. This type of untestable prediction will be referred to as a deduction, which is defined as follows:

D16. A deduction is a c-description that is generated from a p-description when consciousness cannot be measured. Deductions are blind logical consequences of a c-theory. They cannot be tested because assumptions A1-A6 do not apply. The plausibility of a deduction is closely tied to the reliability of the c-theory that was used to make it.

Predictions are testable. Deductions are not. However much data I gather about a physical system I cannot ever test the deductions that I make about its consciousness. The assumptions that enable us to measure consciousness do not apply to the systems that we make deductions about.

I grab a bat, measure its physical state, and use a mathematical c-theory to convert a p-description of its physical state into a c-description of its consciousness (see Figure 9.3). If the bat’s consciousness is radically different from my own, then it will be difficult for me to understand this c-description. I might find it impossible to imagine what it is like to be this bat. (How could I imaginatively transform my bubble of experience into the bat’s bubble of experience?)7 While solutions to this problem have been put forward,8 at some point we will have to accept that we have a limited ability to imaginatively transform our bubbles of experience. This failure of imagination does not affect our ability to make scientific deductions about a bat’s consciousness. A reliable c-theory should be able to generate a complete and accurate c-description of a bat’s conscious state from a p-description of its physical state.9

There are strong ethical motivations for making deductions about the consciousness of brain-damaged people, embryos and infants. Deductions have implications for abortion, organ donation and the treatment of the dead and dying. We could use deductions to reduce the suffering of animals that are raised and slaughtered for meat.10 Deductions could satisfy our curiosity about the consciousness of artificial systems.

Deductions will be based on c-theories that have not been fully tested. Poor access to the brain and limited time and money hamper our ability to test c-theories. We cannot check that a c-theory holds across all conscious and physical states. Multiple competing c-theories might be consistent with the evidence and exhibit different trade-offs between simplicity and generality. These problems are common to all scientific theories.

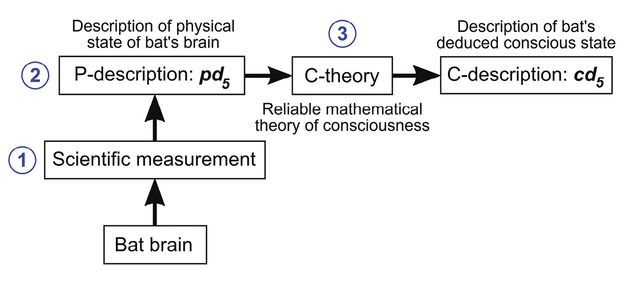
Figure 9.3. Deduction of the conscious state of a bat. 1) Scientific instruments measure the physical state of the bat’s brain. 2) The measurements are converted into a formal p-description of the physical state of the bat’s brain, pd5. 3) A reliable well-tested c-theory converts the p-description into a formal c-description, cd5, of the bat’s deduced conscious state. Image © David Gamez, CC BY 4.0.

Deductions will be based on c-theories that are impossible to fully test. C-theories can only be tested in natural experiments on platinum standard systems. Under these conditions it will be difficult or impossible to prove that a c-theory is based on minimal sets of spatiotemporal structures. So there are likely to be residual ambiguities about CC sets that cannot be experimentally resolved. This is illustrated in Table 9.1.

Spatiotemporal structures				Results of experiments on platinum standard systems	Deductions about c7 in a non-platinum standard system
A	B	C	D	Conscious state c7	Deductions of t1 based on {B,C}	Deduction of t2 based on {B,C,D}
0	0	0	0	?	0	0
0	0	0	1	0	0	0
0	0	1	0	?	0	0
0	0	1	1	0	0	0
0	1	0	0	?	0	0
0	1	0	1	0	0	0
0	1	1	0	?	1	0
0	1	1	1	1	1	1
1	0	0	0	?	0	0
1	0	0	1	0	0	0
1	0	1	0	?	0	0
1	0	1	1	0	0	0
1	1	0	0	?	0	0
1	1	0	1	0	0	0
1	1	1	0	?	1	0
1	1	1	1	1	1	1

Table 9.1. Deductions about consciousness based on limited experimental evidence. A, B and C are spatiotemporal structures in the physical world, such as neuron firing patterns or electromagnetic waves. D is a passive material, such as cerebrospinal fluid.11 ‘1’ indicates that a feature is present; ‘0’ indicates that it is absent. The second column presents the results of experiments on platinum standard systems in which different combinations of A, B, C and D are tested and conscious state c7 is measured. ‘1’ indicates that c7 is present; ‘0’ indicates that c7 is absent. The shaded rows are physical states in which D is absent. In this example D cannot be removed from a platinum standard system in a natural experiment, so the link between D and consciousness is unknown. A question mark in these rows indicates that it is not known whether c7 is present when D is absent. On the basis of this data we can develop two c-theories, t1 and t2. t1 links B and C to c7; t2 links B, C and D to c7. Both of these theories are compatible with the experimental data. They make the same deductions about c7 in the white rows and different deductions about c7 in the shaded rows.

Many biological systems are similar to normally functioning adult human brains. With these systems we do not have to worry about whether a c-theory includes all of the spatiotemporal structures that might be linked to consciousness, because the normally functioning adult human brain and the target system contain similar patterns in similar materials. This will be expressed using the notion of a physical context:

D17. A physical context is everything in a system that is not part of a CC set that is used to make a deduction. Two physical systems have the same physical context if they contain approximately the same materials and if the constant and partially correlated patterns in these materials are approximately the same.12

When two systems share the same physical context we can make deductions about their consciousness that are as strong and believable as the original theory. These will be referred to as conservative deductions, which are defined as follows:

D18. In a conservative deduction a c-theory generates a c-description from a p-description in the same physical context as the one in which the theory was tested.

Suppose a c-theory links some electromagnetic patterns to consciousness. In this case the physical context is everything in the brain apart from these electromagnetic patterns, such as neurons, haemoglobin, cerebrospinal fluid, glia, other electromagnetic patterns, and so on. If these patterns and materials are approximately the same in another system, then they provide the same physical context for the electromagnetic patterns that the c-theory uses to make its deductions about consciousness.13

Other systems, such as cephalopods and robots, lack some of the spatiotemporal structures that are present in normally functioning adult human brains. The link between these spatiotemporal structures and consciousness cannot be tested in natural experiments. We can still make deductions about the consciousness of these systems, but they are likely to be less accurate than conservative deductions. These will be referred to as liberal deductions, which are defined as follows:

D19. In a liberal deduction a c-theory generates a c-description from a p-description in a different physical context from the one in which the theory was tested.14,15

Suppose we have identified a mathematical relationship between neuron firing patterns and conscious states in the normally functioning adult human brain, and none of the brain’s other materials need to be included to make accurate predictions about consciousness. We could use this mathematical relationship to make conservative deductions about the consciousness of a damaged brain, an infant’s brain and possibly a bat’s brain. In these brains, most of the same patterns and materials are present, so we would not have to prove that the c-theory is based on minimal sets of spatiotemporal structures. We could also use this relationship to make liberal deductions about the consciousness of neurons in a Petri dish or about a snail’s consciousness. We would have less confidence in these deductions because these physical contexts lack some of the materials that are potential members of CC sets.

In the system described in Table 9.1, t1 and t2 make conservative deductions about consciousness in the physical states that are coloured white. These deductions are made in the same physical context as the one in which the theories were tested (D is always present), and both theories make identical deductions. t1 and t2 make liberal deductions about the physical states in the shaded rows. The theories have not been tested in this physical context, which lacks D, and they make different deductions. These liberal deductions cannot be confirmed or refuted—all that can be confirmed or refuted is the c-theory on which the deductions are based. For example, we might give preference to the liberal deductions of t2 if it has performed better in experiments on platinum standard systems.

All well-tested c-theories should make the same conservative deductions. If two c-theories make different conservative deductions, then it should be possible to devise an experiment that can discriminate between them.

There can be contradictions between the liberal deductions that are made by equally reliable c-theories (see Table 9.1). Our reaction to this will depend on our motivation for making the deductions. If they are made out of interest, then we can say that the system is conscious according to t1 and not conscious according to t2. If they are made for ethical reasons, then we could base our treatment of the system on whether it has been deduced to be conscious according to any reliable c-theory. An artificial intelligence should not be switched off if it has been deduced to be conscious according to t1, even if t2 claims that it is unconscious.

The distinction between conservative and liberal deductions can be dropped if assumptions A7-A9 are made and a c-theory is considered to be true given these assumptions. In this case, the presence or absence of a physical context does not matter because passive materials, constant patterns and partially correlated patterns have been assumed to be irrelevant to consciousness. All deductions would then be equally valid.

9.3 Summary

A c-theory can generate testable predictions about consciousness or the physical world. Testable predictions can only be made about platinum standard systems during consciousness experiments. It is only under these conditions that we can use measurements of consciousness to generate or confirm the predictions.

When a c-theory has been rigorously tested, we might judge that it can reliably map between c-descriptions and p-descriptions. We can then use it to make deductions about the consciousness of non-platinum standard systems, such as coma patients and bats. These deductions cannot be checked because we cannot measure consciousness in these systems. We make deductions for a variety of ethical, practical and intellectual reasons.

Conservative deductions are made in the same physical context as the one in which the c-theory was tested. They are as reliable as the c-theory and all c-theories should make the same conservative deductions. Liberal deductions are made about systems that are substantially different from the platinum standard systems on which the c-theory was tested. They are less reliable than conservative deductions and different c-theories are likely to make different liberal deductions.