I. Mental Skills

Even a superficial glance at history shows … great innovators … did vast amounts of computation and gained much of their insight in this way. I deplore the fact that contemporary mathematical education tends to give students the idea that computation is demeaning drudgery to be avoided at all costs.

Harold M. Edwards (1936– )

Fermat’s Last Theorem

We start our journey in a way that should be accessible to everyone – with a quick romp through important ideas from secondary school mathematics. The content is at times very elementary; but the problems often hint at something more challenging. The items included in this first chapter also highlight selected facts, techniques and ideas. Some of this early material is included to introduce certain ideas and techniques that later chapters will assume to be “known”. A few problems appeal to more advanced ideas (such as complex numbers), and are included here to indicate that “mental skills” are not restricted to elementary material.

Pencil and paper will be needed, but the items tend to focus on things which a student of mathematics should know by heart, or should learn to see at a glance, or should be able to calculate inside the head. In later problems (e.g. from Problem 18 onwards) the emphasis on mental skills should be interpreted as “ways of thinking”, rather than being taken to mean that everything should be done in your head. This is especially true where extended calculations or proofs are required.

Some of the items in this chapter (such as Problems 1 and 2) should be thoroughly familiar, and are included to underline this fact, rather than because we anticipate that they will need much active attention. Most of the early items in this first chapter are either core or auxiliary. However, there are also some real gems, which may even warrant a place in the the standard core.

The chapter is largely devoted to underlining the need for mastery of a repertoire of instantly available techniques, that can be used mentally, quickly, and flexibly to analyse less familiar problems at sight. But it also seeks to emphasise connections. Hence readers should be prepared to challenge their previous experience, in case it may have led to methods and results being perceived too narrowly.

We repeat the comment made in the section About this book. The “essence of mathematics”, which is referred to in the title, is largely implicit in the problems, and is there for the reader to extract. There is some discussion of this essence in the text interspersed between the problems. But, to avoid spilling the beans prematurely, and hence spoiling the problems, many important observations are buried away in the solutions, or in the Notes which follow many of the solutions.

1.1. Mental arithmetic and algebra

1.1.1 Times tables.

Problem 1 Using only mental arithmetic:

(a) Compute for yourself, and learn by heart, the times tables up to 9 × 9.

(b) Calculate instantly:

(i) 0.004 × 0.02

(ii) 0.0008 × 0.07

(iii) 0.007 × 0.12

(iv) 1.08 ÷ 1.2

(v) (0.08)²

Multiplication tables are important for many reasons. They allow us to appreciate directly, at first hand, the efficiency of our miraculous place value system – in which representing any number, and implementing any operation, are reduced to a combined mastery of

(i) the arithmetical behaviour of the ten digits 0–9, and

(ii) the index laws for powers of 10.

Fluency in mental and written arithmetic then leaves the mind free to notice, and to appreciate, the deeper patterns and structures which may be lurking just beneath the surface.

1.1.2 Squares, cubes, and powers of 2.

Algebra begins in earnest when we start to calculate with expressions involving powers. As one sees in the language we use for squares and cubes (i.e. 2^nd and 3^rd powers), these powers were interpreted geometrically for hundreds and thousands of years – so that higher powers, beyond the third power, were seen as being somehow unreal (like the 4^th dimension). Our uniform algebraic notation covering all powers emerged in the 17^th century (with Descartes (1596–1650)). But before one begins to work with algebraic powers, one should first aim to achieve complete fluency in working with numerical powers.

Problem 2

(a) Compute by mental arithmetic (using pencil only to record results), then learn by heart:

(i) the squares of positive integers: first up to 12²; then to 31²

(ii) the cubes of positive integers up to 11³

(iii) the powers of 2 up to 2¹⁰ .

(b) How many squares are there: (i) < 1000? (ii) < 10 000? (iii) < 100 000?

(c) How many cubes are there: (i) < 1000? (ii) < 10 000? (iii) < 1 000 000?

(d) (i) Which powers of 2 are squares? (ii) Which powers of 2 are cubes?

(e) Find the smallest square greater than 1 that is also a cube. Find the next smallest.

Evaluating powers, and the associated index laws, constitute an example of a direct operation. For each direct operation, we need to think carefully about the corresponding inverse operation – here “extracting roots”. In particular, we need to be clear about the distinction between the fact that the equation x² = 4 has two different solutions, while $\sqrt{4}$ has just one value (namely 2).

Problem 3

(a) The operation of “squaring” is a function: it takes a single real number x as input, and delivers a definite real number x² as output.

– Every positive number arises as an output (“is the square of something”).

– Since x² = (−x)², each output (other than 0) arises from at least two different inputs.

– If a² = b², then 0 = a² − b² = (a−b)(a+b), so either a = b, or a = −b. Hence no two positive inputs have the same square, so each output (other than 0) arises from exactly two inputs (one positive and one negative).

Hence each positive output y corresponds to just one positive input, called $\sqrt{\mathit{y}}$.

Find:

(i) $\sqrt{49}$ (ii) $\sqrt{144}$ (iii) $\sqrt{441}$ (iv) $\sqrt{169}$

(v) $\sqrt{196}$ (vi) $\sqrt{961}$ (vii) $\sqrt{\mathrm{96\; 100}}$

(b) Let a > 0 and b > 0. Then $\sqrt{\mathit{ab}}>0$, and $\sqrt{\mathit{a}}\times \sqrt{\mathit{b}}>0$, so both expressions are positive.

Moreover, they have the same square, since

$$(\sqrt{\mathit{ab}}{)}^2=\mathit{ab}=(\sqrt{\mathit{a}}{)}^2·(\sqrt{\mathit{b}}{)}^2=(\sqrt{\mathit{a}}\times \sqrt{\mathit{b}}{)}^2.$$

$\therefore \sqrt{\mathit{a}\times \mathit{b}}=\sqrt{\mathit{a}}\times \sqrt{\mathit{b}}.$

Use this fact to simplify the following:

(i) $\sqrt{8}$ (ii) $\sqrt{12}$ (iii) $\sqrt{50}$

(iv) $\sqrt{147}$ (v) $\sqrt{288}$ (vi) $\sqrt{882}$

(c) [This part requires some written calculation.] Exact expressions involving square roots occur in many parts of elementary mathematics. We focus here on just one example – namely the regular pentagon.

Suppose that a regular pentagon ABCDE has sides of length 1.

(i) Prove that the diagonal AC is parallel to the side ED.

(ii) If AC and BD meet at X, explain why AXDE is a rhombus.

(iii) Prove that triangles ADX and CBX are similar.

(iv) If AC has length x, set up an equation and find the exact value of x.

(v) Find the exact length of BX.

(vi) Prove that triangles ABD and BXA are similar.

(vii) Find the exact values of cos 36°, cos 72°.

(viii) Find the exact values of sin 36°, sin 72°.

Every calculation with square roots depends on the fact that “ $\sqrt{}$ is a function”. That is: given y > 0,

$\sqrt{\mathit{y}}$ denotes a single value – the positive number whose square is y.

The equation x² = y has two roots, namely $\mathit{x}=\pm \sqrt{\mathit{y}}$; however, $\sqrt{\mathit{y}}$ has just one value (which is positive).

The mathematics of the regular pentagon is important – and generally neglected. It is included here to underline the way exact expressions involving square roots arise naturally.

In Problem 3(c), parts (iii) and (vi) require one to identify similar triangles using angles. The fact that “corresponding sides are then proportional” leads to a quadratic equation – and hence to square roots.

Parts (vii) and (viii) illustrate the fact that basic tools, such as

• the trigonometric identity cos² θ + sin² θ =1,
• the Cosine Rule, and
• the Sine Rule

should be part of one’s stock-in-trade. Notice that the exact values for

cos 36°, cos 72°, sin 36°, and sin 72°

also determine the exact values of

sin54° = cos36°, sin 18° = cos72°, cos54° = sin36°, and cos 18° = sin72°.

1.1.3 Primes

Problem 4

(a) Factorise 12 345 as a product of primes.

(b) Using only mental arithmetic, make a list of all prime numbers up to 100.

(c)(i) Find a prime number which is one less than a square.

(ii) Find another such prime.

There are 4 prime numbers less than 10; 25 prime numbers less than 100; and 168 prime numbers less than 1000.

Problem 4(c) is included to emphasise a frequently neglected message:

Words and images are part of the way we communicate.

But most of us cannot calculate with words and images.

To make use of mathematics, we must routinely translate words into symbols. For example, unknown numbers need to be represented by symbols, and points in a geometric diagram need to be properly labelled, before we can begin to calculate, and to reason, effectively.

1.1.4 Common factors and common multiples

To add two fractions we need to find a common multiple, or the LCM, of the two given denominators. To cancel fractions, or to simplify ratios, we need to be able to spot common factors and to find HCFs. Two positive integers a, b which have no (positive) common factors other than 1 (that is, with HCF (a,b) = 1) are said to be relatively prime, or coprime.

Problem 5 [This problem requires a mixture of serious thought and written proof.]

(a) I choose six integers between 10 and 19 (inclusive).

(i) Prove that some pair of integers among my chosen six must be relatively prime.

(ii) Is it also true that some pair must have a common factor?

(b) I choose six integers in the nineties (from 90–99 inclusive).

(i) Prove that some pair among my chosen integers must be relatively prime.

(ii) Is it also true that some pair must have a common factor?

(c) I choose n + 1 integers from a run of 2n consecutive integers.

(i) Prove that some pair among the chosen integers must be relatively prime.

(ii) Is it also true that some pair must have a common factor?

1.1.5 The Euclidean algorithm

School mathematics gives the impression that to find the HCF of two integers m and n, one must first obtain the prime power factorisations of m and of n, and can then extract the HCF from these two expressions. This is fine for beginners. But arithmetic involves unexpected subtleties. It turns out that, as the numbers get larger, factorising integers quickly becomes extremely difficult - a difficulty that is exploited in modern encryption systems. (The limitations of any method that depends on first finding the prime power factorisation of an integer should have become clear in Problem 4(b), where it is all too easy to imagine that 91 is prime, and in Problem 4(c)(ii), where students regularly think that 143, or that 323 are prime.)

Hence we would like to have a simple way of finding the HCF of two integers without having to factorise each of them first. That is what the Euclidean algorithm provides. We will look at this in more detail later. Meanwhile here is a first taste.

Problem 6

(a) (i) Explain why any integer that is a factor (or a divisor) of both m and n must also be a factor of their difference m − n, and of their sum m + n.

(ii) Prove that

$$\begin{array}{c}HCF(m,n)=HCF(m-n,n).\hfill \end{array}$$

(iii) Use this to calculate in your head HCF (1001, 91) without factorising either number.

(b) (i) Prove that: $HCF(m,m+1)=1$.

(ii) Find $HCF(m,2m+1)$.

(iii) Find $HCF(m^2+1,m-1)$.

1.1.6 Fractions and ratio

Problem 7 Which is bigger: 17% of nineteen million, or 19% of seventeen million?

Problem 8

(a) Evaluate

$$\begin{array}{c}(1+\genfrac{}{}{0.1ex}{}{1}{2})(1+\genfrac{}{}{0.1ex}{}{1}{3})(1+\genfrac{}{}{0.1ex}{}{1}{4})(1+\genfrac{}{}{0.1ex}{}{1}{5}).\hfill \end{array}$$

(b) Evaluate

$$\begin{array}{c}\sqrt{1+\genfrac{}{}{0.1ex}{}{1}{2}}\times \sqrt{1+\genfrac{}{}{0.1ex}{}{1}{3}}\times \sqrt{1+\genfrac{}{}{0.1ex}{}{1}{4}}\times \sqrt{1+\genfrac{}{}{0.1ex}{}{1}{5}}\times \sqrt{1+\genfrac{}{}{0.1ex}{}{1}{6}}\times \sqrt{1+\genfrac{}{}{0.1ex}{}{1}{7}}.\hfill \end{array}$$

(c) We write the product “$4\times 3\times 2\times 1$ ” as “4!” (and we read this as “4 factorial”). Using only pencil and paper, how quickly can you work out the number of weeks in 10! seconds?

Problem 9 The “DIN A” series of paper sizes is determined by two conditions. The basic requirement is that all the DIN A rectangles are similar ; the second condition is that when we fold a given size exactly in half, we get the next smaller size. Hence

• a sheet of paper of size A3 folds in half to give a sheet of size A4 - which is similar to A3; and
• a sheet of size A4 folds in half to give a sheet of size A5; etc..

(a) Find the constant ratio

r = “(longer side length) : (shorter side length)”

for all DIN A paper sizes.

(b) (i) To enlarge A4 size to A3 size (e.g. on a photocopier), each length is enlarged by a factor of r. What is the “enlargement factor” to get from A3 size back to A4 size?

(ii) To “enlarge” A4 size to A5 size (e.g. on a photocopier), each length is “enlarged” by a factor of $\frac{1}{r}$. What is the enlargement factor to get from A5 size back to A4 size?

Problem 10

(a) In a sale which offers “15% discount on all marked prices” I buy three articles: a pair of trainers priced at £ 57.74, a T-shirt priced at £ 17.28, and a yo-yo priced at £ 4.98. Using only mental arithmetic, work out how much I should expect to pay altogether.

(b) Some retailers display prices without adding VAT — or “sales tax” — at 20% (because their main customers need to know the pre-VAT price). Suppose the prices in part (a) are the prices before adding VAT. Each price then needs to be adjusted in two ways — adding VAT and subtracting the discount. Should I add the VAT first and then work out the discount? Or should I apply the discount first and then add the VAT?

(c) Suppose the discount in part (b) is no longer 15%. What level of discount would exactly cancel out the addition of VAT at 20%?

Problem 11

(a) Using only mental arithmetic:

(i) Determine which is bigger:

$$\frac{1}{2}+\frac{1}{5}\text{or}\frac{1}{3}+\frac{1}{4}?$$

(ii) How is this question related to the observation that 10 < 12?

(b) [This part will require some written calculation and analysis.]

(i) For positive real numbers x, compare

$$\frac{1}{x+2}+\frac{1}{x+5}\text{and}\frac{1}{x+3}+\frac{1}{x+4}.$$

(ii) What happens in part (i) if x is negative?

1.1.7 Surds

Problem 12

(a) Expand and simplify in your head:

(i) ${(\sqrt{2}+1)}^2$                      (ii) ${(\sqrt{2}+1)}^2$               (iii) ${(1+\sqrt{2})}^3$

(b) Simplify:

(i) $\sqrt{10+4\sqrt{6}}$

(ii) $\sqrt{5+2\sqrt{6}}$

(iii) $\sqrt{\frac{3+\sqrt{5}}{2}}$

(iv) $\sqrt{10-2\sqrt{5}}$

The expressions which occur in exercises to develop fluency in working with surds often appear arbitrary. But they may not be. The arithmetic of surd arises naturally: for example, some of the expressions in the previous problem have already featured in Problem 3(c). In particular, surds will feature whenever Pythagoras’ Theorem is used to calculate lengths in geometry, or when a proportion arising from similar triangles requires us to solve a quadratic equation. So surd arithmetic is important. For example:

• A regular octagon with side length 1 can be surrounded by a square of side $\sqrt{2}+1$ (which is also the diameter of its incircle); so the area of the regular octagon equals ${(\sqrt{2}+1)}^2-1$ (the square minus the four corners).

• $\sqrt{2}-1$ features repeatedly in the attempt to apply the Euclidean algorithm, or anthyphairesis, to express $\sqrt{2}$ as a “continued fraction”.

• $\sqrt{10-2\sqrt{5}}$ may look like an arbitrary, uninteresting repeated surd, but is in fact very interesting, and has already featured as 4 sin 36° in Problem 3(c).

• One of the simplest ruler and compasses constructions for a regular pentagon ABCDE (see Problem 185) starts with a circle of radius 2, centre O, and a point A on the circle, and in three steps constructs the next point B on the circle, where AB is an edge of the inscribed regular pentagon, and

$$\underset{¯}{AB}=\sqrt{10-2\sqrt{5}}.$$

1.2. Direct and inverse procedures

We all learn to calculate — with numbers, with symbols, with functions, etc. But we may not notice that most calculating procedures come in pairs.

• First we learn a direct, deterministic, handle-turning technique, where answers are easy to churn out (as with addition, or multiplication, or working out powers, or multiplying brackets in algebra, or differentiating).
• Then we try to work backwards, or to “undo” this direct operation (as with subtraction, or division, or finding roots, or factorising, or integrating). This inverse procedure requires one to be completely fluent in the corresponding direct procedure; but it is much more demanding, in that one has to juggle possibilities as one goes, in order to home in on the required answer.

To master inverse procedures requires a surprising amount of time and effort. And because they are harder to master, they can easily get neglected. Even where they receive a lot of time, there are aspects of inverse procedures which tend to go unnoticed.

Problem 13 In how many different ways can the missing digits in this short multiplication be completed?

$$\frac{\begin{array}{c}\square 6\hfill \\ \times \square \hfill \end{array}}{\underset{}{\square 28}}$$

One would like students not only to master the direct operation of multiplying digits effectively, but also to notice that the inverse procedure of

“identifying the multiples of a given integer that give rise to a specified output”

depends on

the HCF of the multiplier and the base (10) of the numeral system.

• Multiplying by 1, 3, 7, or 9 induces a one-to-one mapping on the set of ten digits 0—9; so an inverse problem such as “7 × □ ends in 6” has just one digit-solution.
• Multiplying by 2, 4, 6, or 8 induces a two-to-one mapping onto the set of even digits (multiples of 2); so an inverse problem such as “6 × □ ends in 4” has two digit-solutions, and an inverse problem such as “6 × □ ends in 3” has no digit-solutions.
• Multiplying by 5 induces a five-to-one mapping onto the multiples (0 and 5) of 5, so an inverse problem such as “5 × □ ends in 0” has five digit-solutions and an inverse problem such as “5 × □ ends in 3” has no digit-solutions at all.
• Multiplying by 0 induces a ten-to-one mapping onto the multiples of 0(namely 0); so an inverse problem such as “0 × □ ends in 0” has ten digit-solutions and an inverse problem such as “0 × □ ends in 3 (or any digit other than 0)” has no digit-solutions at all.

The next problem shows — in a very simple setting — how elusive inverse problems can be. Here, instead of being asked to perform a direct calculation, the rules and the answer are given, and we are simply asked to invent a calculation that gives the specified output.

Problem 14

(a) In the “24 game” you are given four numbers. Your job is to use each number once, and to combine the four numbers using any three of the four basic arithmetical operations — using the same operation more than once if you wish, and as many brackets as you like (but never concatenating different numbers, such as “3” and “4” to make “34”). If the given numbers are 3, 3, 4, 4, then one immediately sees $3\times 4+3\times 4=24$. With 3, 3, 5, 5 it may take a little longer, but is still fairly straightforward. However, you may find it more challenging to make 24 in this way:

(i) using the four numbers 3, 3, 6, 6

(ii) using the four numbers 3, 3, 7, 7

(iii) using the four numbers 3, 3, 8, 8.

(b) Suppose we restrict the numbers to be used each time to “four 4s” (4, 4, 4, 4), and change the goal from “make 24”, to “make each answer from 0—10 using exactly four 4s”.

(i) Which of the numbers 0—10 cannot be made?

(ii) What if one is allowed to use squaring and square roots as well as the four basic operations? What is the first inaccessible integer?

Calculating by turning the handle deterministically (as with addition, or multiplication, or multiplying out brackets, or differentiating) is a valuable skill. But such direct procedures are usually only the beginning. Using mathematics and solving problems generally depend on the corresponding inverse procedures — where a certain amount of juggling and insight is needed in order to work backwards (as with subtraction, or division, or factorisation, or integration). For example, in applications of calculus, the main challenge is to solve differential equations (an inverse problem) rather than to differentiate known functions.

Problem 14 captures the spirit of this idea in the simplest possible context of arithmetic: the required answer is given, and we have to find how (or whether) that answer can be generated. We will meet more interesting examples of this kind throughout the rest of the collection.

1.2.1. Factorisation

Problem 15

(a) (i) Expand ($a+b{)}^2$ and ${(a+b)}^3$.

(ii) Without doing any more work, write out the expanded forms of ${(a-b)}^2$ and ${(a-b)}^3$.

(b) Factorise (i) $x^2+2x+1$        (ii) $x^4-2x^2+1$       (iii) $x^6-3x^4+3x^2-1$.

(c)(i) Expand (a - b)(a + b).

(ii) Use (c)(i) and (a)(i) to write down (with no extra work) the expanded form of

$$(a-b-c)(a+b+c)$$

and of

$$(a-b+c)(a+b-c).$$

(d) Factorise $3x^2+2x-1$.

1.3. Structural arithmetic

Whenever the answer to a question turns out to be unexpectedly nice, one should ask oneself whether this is an accident, or whether there is some explanation which should perhaps have led one to expect such a result. For example:

• Exactly 25 of the integers up to 100 are prime numbers — and 25 is exactly one quarter of 100. This is certainly a beautifully memorable fact. But it is a numerical fluke, with no hidden mathematical explanation.
• 11 and 101 are prime numbers. Is this perhaps a way of generating lots of prime numbers:

  $$11,101,1001,10001,100001,\dots ?$$

  It may at first be tempting to think so — until, that is, you remember what you found in Problem 6(a)(iii).

Problem 16 Write out the first 12 or so powers of 4:

$$4,16,64,256,1024,4096,16384,65536,\dots$$

Now create two sequences:

the sequence of final digits:              4, 6, 4, 6, 4, 6, …

the sequence of leading digits:          4, 1, 6, 2, 1, 4, 1, 6, …

Both sequences seem to consist of a single “block”, which repeats over and over for ever.

(a) How long is the apparent repeating block for the first sequence? How long is the apparent repeating block for the second sequence?

(b) It may not be immediately clear whether either of these sequences really repeats forever. Nor may it be clear whether the two sequences are alike, or whether one is quite different from the other. Can you give a simple proof that one of these sequences recurs, that is, repeats forever?

(c) Can you explain why the other sequence seems to recur, and decide whether it really does recur forever?

Problem 17 The 4 by 4 “multiplication table” below is completely familiar.

$$\begin{array}{rrrr}\hfill 1& \hfill 2& \hfill 3& \hfill 4\\ \hfill 2& \hfill 4& \hfill 6& \hfill 8\\ \hfill 3& \hfill 6& \hfill 9& \hfill 12\\ \hfill 4& \hfill 8& \hfill 12& \hfill 16\end{array}$$

What is the total of all the numbers in the 4 by 4 square? How should one write this answer in a way that makes the total obvious?

1.4. Pythagoras’ Theorem

From here on the idea of “mental skills” tends to refer to ways of thinking rather than to doing everything in your head.

Pythagoras’ Theorem is one of the first truly surprising results in school mathematics: it is hard to see why anyone would think of “adding the squares of the two shorter sides”. Despite the apparent attribution to a named person (Pythagoras), the origin of the theorem, and its proof, are unclear. There certainly was someone called Pythagoras (around 500 BC). But the main ancient references to him were written many hundreds of years after he died, and are not very reliable. The truth is that we know very little about him, or his theorem. The proof in Problem 18 below appeared in Book I of Euclid's thirteen books of Elements (written around 300 BC — two hundred years after Pythagoras). Much that is said (wrongly) to stem from Pythagoras is attributed in some sources to the Pythagoreans — a loose term which refers to any philosopher in what is seen as a tradition going back to Pythagoras. (This is a bit like interpreting anything called Christian in the last 2000 years as stemming directly from Christ himself.)

Clay tablets from around 1700 BC suggest that some Babylonians must have known “Pythagoras’ Theorem”; and it is hard to see how one could know the result without having some kind of justification. But we have no evidence of either a clear statement, or a proof, at that time. There are also Chinese texts that refer to Pythagoras’ Theorem (or as they call it, “Gougu”), which are thought to have originated BC — though the earliest surviving edition is from the 13^th century AD. There is even an interesting little book by Frank Swetz, with the tongue-in-cheek title Was Pythagoras Chinese?.

The history may be confused, but the result — and its Euclidean proof — embodies something of the surprise and elegance of the very best mathematics. The Euclidean proof is included here partly because it is one that can, and should, be remembered (or rather, reconstructed — once one realises that there is really only one possible way to split the “square on the hypotenuse” in the required way). But, as we shall see, the result also links to exact mental calculation with surds, to trigonometry, to the familiar mnemonic “CAST”, to the idea of a “converse”, to sums of two squares, and to Pythagorean triples.

1.4.1 Pythagoras’ Theorem, trig for special angles, and CAST

Problem 18 (Pythagoras’ Theorem) Let ΔABC be a right angled triangle, with a right angle at C. Draw the squares ACQP, CBSR, and BAUT on the three sides, external to ΔABC. Use the resulting diagram to prove in your head that the square BAUT on BA is equal to the sum of the other two squares by:

• drawing the line through C perpendicular to AB, to meet AB at X and UT at Y
• observing that PA is parallel to QCB, so that ΔACP (half of the square ACQP, with base AP and perpendicular height AC) is equal in area to ΔABP (with base AP and the same perpendicular height)
• noting that ΔABP is SAS-congruent to ΔAUC, and that ΔAUC is equal in area to ΔAUX (half of rectangle AUYX, with base AU and height AX).
• whence ACQP is equal in area to rectangle AUYX
• similarly BCRS is equal in area to BTYX.

The proof in Problem 18 is the proof to be found in Euclid's Elements Book 1, Proposition 47. Unlike many proofs,

• it is clear what the proof depends on (namely SAS triangle congruence, and the area of a triangle), and
• it reveals exactly how the square on the hypotenuse AB divides into two summands — one equal to the square on AC and one equal to the square on BC.

Problem 19

(a) Use Pythagoras’ Theorem in a square ABCD of side 1 to show that the diagonal AC has length $\sqrt{2}$. Use this to work out in your head the exact values of sin 45°, cos 45°, tan 45°.

(b) In an equilateral triangle ΔABC with sides of length 2, join A to the midpoint M of the base BC. Apply Pythagoras’ Theorem to find AM. Hence work out in your head the exact values of sin 30°, cos 30°, tan 30°, sin 60°, cos 60°, tan 60°.

(c)(i) On the unit circle with centre at the origin O:(0, 0), mark the point P so that P lies in the first quadrant, and so that OP makes an angle θ with the positive x-axis (measured anticlockwise from the positive x-axis). Explain why P has coordinates (cos θ, sin θ).

(ii) Extend the definitions of cos θ and sin θ to apply to angles beyond the first quadrant, so that for any point P on the unit circle, where OP makes an angle θ measured anticlockwise from the positive x-axis, the coordinates of P are (cos θ, sin θ). Check that the resulting functions sin and cos satisfy:

* and cos are both positive in the first quadrant,

* is positive and cos is negative in the second quadrant,

* and cos are both negative in the third quadrant, and

* is negative and cos is positive in the fourth quadrant.

(iii) Use (a), (b) to calculate the exact values of cos 315°, sin 225°, tan 210°, cos 120°, sin 960°, tan (-135°).

(d) Given a circle of radius 1, work out the exact area of a regular n-gon inscribed in the circle:

(i) when n = 3

(ii) when n = 4

(iii) when n = 6

(iv) when n = 8

(v) when n = 12.

(e) Given a circle of radius 1, work out the area of a regular n-gon circumscribed around the circle:

(i) when n = 3

(ii) when n = 4

(iii) when n = 6

(iv) when n = 8

(v) when n = 12.

Knowing the exact values of sin, cos and tan for the special angles 0°, 30°, 45°, 60°, 90° is like knowing one's tables. In particular, it allows one to evaluate trigonometric functions mentally for related angles in all four quadrants (using the CAST mnemonic — C being in the SE of the unit circle, A in the NE quadrant, S in the NW quadrant, and T in the SW quadrant — to remind us which functions are positive in each quadrant). These special angles arise over and over again in connection with equilateral triangles, squares, regular hexagons, regular octagons, regular dodecagons, etc., where one can use what one knows to calculate exactly in geometry.

Problem 20

(a) Use Pythagoras’ Theorem to calculate the exact length of the diagonal AC in a square ABCD of side length 2.

(b) Let X be the centre of the square ABCD in part (a). Draw lines through X parallel to the sides of ABCD and so divide the large square into four smaller squares, each of side 1. Find the length of the diagonals AX and XC.

(c) Compare your answers to parts (a) and (b) and your answer to Problem 3(b)(i).

Pythagoras’ Theorem holds the key to calculating exact distances in the plane. To calculate distances on the Earth's surface one needs a version of Pythagoras for “right angled triangles” on the sphere. We address this in Chapter 5.

1.4.2 Converses and Pythagoras’ Theorem

Each mathematical statement of the form

“if … (Hypothesis H),
then … (Consequence C)”

has a converse statement — namely

“if C,
then H”.

If the first statement is true, there is no a priori reason to expect its converse to be true. For example, part (c) of Problem 25 below proves that

“if an integer has the form 4k + 3,
then it cannot be written as the sum of two squares”.

However, the converse of this statement

“if an integer cannot be written as a sum of two squares,
then it has the form 4k + 3”

is false — since 6 cannot be written as the sum of two squares.

Despite this counterexample, whenever we prove a standard result, it makes sense to ask whether the converse is also true. For example,

“if PQRS is a parallelogram, then opposite angles are equal:
∠P = ∠R, and ∠Q = ∠S” (see Problem 157(ii)).

However you may not have considered the truth (or otherwise) of the converse statement:

If ABCD is a quadrilateral in which opposite angles are equal (∠A = ∠C and ∠B = ∠D), is it true that ABCD has to be a parallelogram?

The next problem invites you to prove the converse of Pythagoras’ Theorem. You should not use the Cosine Rule, since this is a generalisation of both Pythagoras’ Theorem and its converse.

Problem 21 Let ABC be a triangle. We use the standard labelling convention, whereby the side BC opposite A has length a, the side CA opposite B has length b, and the side AB opposite C has length c. Prove that, if c² = a² + b², then ∠BCA is a right angle.

1.4.3 Pythagorean triples

The simplest example of a right angled triangle with integer length sides is given by the familiar triple 3, 4, 5:

$$3^2+4^2=5^2.$$

Any such integer triple is called a Pythagorean triple.

The classification of all Pythagorean triples is a delightful piece of elementary number theory, which is included in this chapter both because the result deserves to be memorised, and because (like Pythagoras’ Theorem itself) the proof only requires one to juggle a few simple ideas that should be part of one's armoury.

Pythagorean triples arise in many contexts (e.g. see the text after Problem 180). The classification given here shows that Pythagorean triples form a family depending on three parameters p, q, s (in which s is simply a “scaling” parameter, so the most important parameters are p, q). As a warm-up we consider two “one-parameter subfamilies” related to the triple 3, 4, 5.

Problem 22 Suppose a² + b² = c² and that b, c are consecutive integers.

(a) Prove that a must be odd — so we can write it as a = 2m + 1 for some integer m.

(b) Prove that c must be odd — so we can write it as c = 2n + 1 for some integer n. Find an expression for n in terms of m.

Problem 22 reveals the triple (3, 4, 5) as the first instance (m = 1) of a one-parameter infinite family of triples, which continues

$$(5,12,13)(m=2),(7,24,25)(m=3),(9,40,41)(m=4),\dots ,$$

whose general term is

$$(2m+1,2m(m+1),2m(m+1)+1).$$

The triple (3, 4, 5) is also the first member of a quite different “one-parameter infinite family” of triples, which continues

$$(6,8,10),(9,12,15),\dots .$$

Here the triples are scaled-up versions of the first triple (3, 4, 5).

In general, common factors simply get in the way:

If a² + b² = c² and HCF(a, b) = s, then s² divides a² + b², and a² + b² = c²; so s divides c.
And if a² + b² = c² and HCF(b, c) = s, then s² divides c² - b² = a², so s divides a.

Hence a typical Pythagorean triple has the form (sa, sb, sc) for some scale factor s, where (a, b, c) is a triple of integers, no two of which have a common factor: any such triple is said to be primitive (that is, basic — like prime numbers). Every Pythagorean triple is an integer multiple of some primitive Pythagorean triple. The next problem invites you to find a simple formula for all primitive Pythagorean triples.

Problem 23 Let (a, b, c) be a primitive Pythagorean triple.

(a) Show that a and b have opposite parity (i.e. one is odd, the other even) — so we may assume that a is odd and b is even.

(b) Show that

$${\left(\frac{b}{2}\right)}^2=\left(\frac{c-a}{2}\right)\left(\frac{c+a}{2}\right),$$

where

$$HCF\text{}\left(\frac{c-a}{2},\frac{c+a}{2}\right)=1$$

and $\frac{c-a}{2},\frac{c+a}{2}$ have opposite parity.

(c) Conclude that

$$\frac{c+a}{2}=p^2\text{and}\frac{c-a}{2}=q^2,$$

where HCF(p, q) = 1 and p and q have opposite parity, so that c = p² + q², a = p² - q², b = 2pq.

(d) Check that any pair p, q having opposite parity and with HCF(p, q) = 1 gives rise to a primitive Pythagorean triple

$$c=p^2+q^2,a=p^2-q^2,b=2pq$$

satisfying a² + b² = c².

Problem 24 The three integers a = 3, b = 4, c = 5 in the Pythagorean triple (3, 4, 5) form an arithmetic progression: that is, c - b = b - a. Find all Pythagorean triples (a, b, c) which form an arithmetic progression — that is, for which c - b = b - a.

1.4.4 Sums of two squares

The classification of Pythagorean triples tells us precisely which squares can be written as the sum of two squares. We now turn to the wider question: “Which integers are equal to the sum of two squares?”

Problem 25

(a) Which of the prime numbers < 100 can be written as the sum of two squares?

(b) Find an easy way to immediately write (a² + b²)(c² + d²) in the form (x² + y²). (This shows that the set of integers which can be written as the sum of two squares is “closed” under multiplication.)

(c) Prove that no integer (and hence no prime number) of the form 4k + 3 can be written as the sum of two squares.

(d) The only even prime number can clearly be written as a sum of two squares: 2 = 1² + 1². Euler (1707—1783) proved that every odd prime number of the form 4k + 1 can be written as the sum of two squares in exactly one way. Find all integers < 100 that can be written as a sum of two squares.

(e) For which integers N < 100 is it possible to construct a square of area N, with vertices having integer coordinates?

In Problem 25 parts (a) and (d) you had to decide which integers < 100 can be written as a sum of two squares as an exercise in mental arithmetic. In part (b) the fact that this set of integers is closed under multiplication turned out to be an application of the arithmetic of norms for complex numbers. Part (e) then interpreted sums of two squares geometrically by using Pythagoras’ Theorem on the square lattice. These exercises are worth engaging in for their own sake. But it may also be of interest to know that writing an integer as a sum of two squares is a serious mathematical question — and in more than one sense.

Gauss (1777—1855), in his book Disquisitiones arithmeticae (1801) gave a complete analysis of when an integer can be represented by a ‘quadratic form’, such as x² + y² (as in Problem 25) or x² - 2y² (as in Problem 54(c) in Chapter 2).

A completely separate question (often attributed to Edward Waring (1736—1798)) concerns which integers can be expressed as a k^th power, or as a sum of n such powers. If we restrict to the case k = 2 (i.e. squares), then:

• When n = 2, Euler (1707—1783) proved that the integers that can be written as a sum of two squares are precisely those of the form

  $$m^2\times p_0\times p_1\times p_2\times \dots \times p_s,$$

  where p₀ = 1 or 2, and p₁ < p₂< … < p_s are odd primes of the form 4l + 1.

• When n = 3, Legendre (1752—1833) and Gauss proved between them that the integers which can be written as a sum of three squares are precisely those that are not of the form 4^m × (8l + 7).
• When n = 4, Lagrange (1736—1813) had previously proved that every positive integer can be written as a sum of four squares.

1.5. Visualisation

Problem 26 (Pages of a newspaper) I found a (double) sheet from an old newspaper, with pages 14 and 27 next to each other. How many pages were there in the original newspaper?

Problem 27 (Overlapping squares) A square ABCD of side 2 sits on top of a square PQRS of side 1, with vertex A at the centre O of the small square, side AB cutting the side PQ at the point X, and ∠AXQ = θ.

(a) Calculate the area of the overlapping region.

(b) Replace the two squares in part (a) with two equilateral triangles. Can you find the area of overlap in that case? What if we replace the squares (i.e. regular 4-gons) in part (a) with regular 2n-gons?

Problem 28 (A folded triangle) The equilateral triangle ΔABC has sides of length 1cm. D and E are points on the sides AB and AC respectively, such that folding ΔADE along DE folds the point A onto A' which lies outside ΔABC.

What is the total perimeter of the region formed by the three single layered parts of the folded triangle (i.e. excluding the quadrilateral with a folded layer on top)?

Problem 29 (A + B = C) The 3 by 1 rectangle ADEH consists of three adjacent unit squares: ABGH, BCFG, CDEF left to right, with A in the top left corner. Prove that

$$\angle DAE+\angle DBE=\angle DCE.$$

Problem 30 (Dissections)

(a) Joining the midpoints of the edges of an equilateral triangle ABC cuts the triangle into four identical smaller equilateral triangles. Removing one of the three outer small triangles (say AMN, with M on AC) leaves three-quarters of the original shape in the form of an isosceles trapezium MNBC. Show how to cut this isosceles trapezium into four congruent pieces.

(b) Joining the midpoints of opposite sides of a square cuts the square into four congruent smaller squares. If we remove one of these squares, we are left with three-quarters of the original square in the form of an L-shape. Show how to cut this L-shape into four congruent pieces.

Problem 31 (Yin and Yang) The shaded region in Figure 1, shaped like a large comma, is bounded by three semicircles — two of radius 1 and one of radius 2.

Cut each region (the shaded region and the unshaded one) into two ‘halves’, so that all four parts are congruent (i.e. of identical size and shape, but with possibly different orientations).

Figure 1: Yin and Yang

In Problem 31 your first thought may have been that this is impossible. However, since the wording indicated that you are expected to succeed, it was clear that you must be missing something — so you tried again. The problem then tests both flexibility of thinking, and powers of visualisation.

1.6. Trigonometry and radians

1.6.1. Sine Rule

School textbooks tend to state the Sine Rule for a triangle ABC without worrying why it is true. So they often fail to give the result in its full form:

Theorem If R is the radius of the circumcircle of the triangle ABC, then

$$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R.$$

This full form explains that the three ratios

$$\frac{a}{\sin A},\frac{b}{\sin B},\frac{c}{\sin C}$$

are all equal because they are all equal to the diameter 2R of the circumcircle of ΔABC — an additional observation which may well suggest how to prove the result (see Problem 32).

Problem 32 Given any triangle ABC, construct the perpendicular bisectors of the two sides AB and BC. Let these two perpendicular bisectors meet at O.

(a) Explain why OA = OB = OC.

(b) Draw the circle with centre O and with radius OA. There are three possibilities:

(i) The centre O lies on one of the sides of triangle ABC.

(ii) The centre O lies inside triangle ABC.

(iii) The centre O lies outside triangle ABC.

Case (i) leads directly to the Sine Rule for a right angled triangle ABC (remembering that sin 90° = 1). We address case (ii), and leave case (iii) to the reader.

(ii) Extend the line BO to meet the circle again at the point A'. Explain why ∠BA'C = ∠BAC = ∠A, and why ∠A'CB is a right angle. Conclude that

$$\sin A=\frac{BC}{A^{\prime }B}=\frac{a}{2R},$$

and hence that

$$\frac{a}{\sin A}=2R\left(=\frac{b}{\sin B}=\frac{c}{\sin C}\right).$$

Problem 33 Let Δ = area(ΔABC).

(a) Prove that

$$\Delta =\frac{1}{2}\cdot ab\cdot \sin C.$$

(b) Prove that $4R\Delta =abc$.

1.6.2 Radians and spherical triangles

There is no God-given unit for measuring distance; different choices of unit give rise to answers that are related by scaling. However the situation is different for angles. In primary and secondary school we measure turn in degrees — where a half turn is 180°, a right angle is 90°, and a complete turn is 360°. This angle unit dates from the ancient Babylonians (~ 2000 BC). We are not sure why they chose 360 units in a full turn, but it seems to be related to the approximate number of days in a year (the time required for the heavens to make a complete rotation in the night sky), and to the fact that they wrote their numbers in “base 60”. However the choice is no more objectively mathematical than measuring distance in inches or in centimetres.

After growing up with the idea that angles are measured in degrees, we discover towards the end of secondary school that:

there is another unit of measure for angles — namely radians.

It may not at first be clear that this is an entirely natural, God-given unit. The size of, or amount of turn in, an angle at the point A can be captured in an absolute way by drawing a circle of radius r centred at the point A, and measuring the arc length which the angle cuts off on this circle. The angle size (in radians) of the angle at A is then defined to be the ratio

$$\frac{\text{arc length}}{\text{radius}}.$$

That is,

size of angle at the point A = arc length cut off on a circle of radius 1, centred at the apex A.

Hence a right angle is of size $\frac{\pi }{2}$ radians; a half turn is equal to $\pi$ (radians); a full turn is equal to $2\pi$ (radians); each angle in an equilateral triangle is equal to $\frac{\pi }{3}$ (radians); the three angles of a triangle have sum $\pi$; and the angles of a polygon with n sides have sum $(n-2)\pi$ (see Problem 230 in Chapter 6).

For a while after the introduction of radians we continue to emphasise the word radians each time we give the measure of an angle in order to stress that we are no longer using degrees. But this is not really a switch to a new unit: this new way of measuring angles is in some sense objective — so we soon drop all mention of the word “radians” and simply refer to the size of an angle (in radians) as if it were a pure number.

This switch affects the meaning of the familiar trigonometric functions. And though we continue to use the same names (sin, cos, tan, etc.), they become slightly different as functions, since the inputs are now always assumed to be in radians.

The real payoff for making this change stems from the way it recognizes the connection between angles and circles. This certainly makes calculating circular arc lengths and areas of sectors easy (an arc with angle θ on a circle of radius r now has length θ r; and a circular sector with angle 2θ now has area θr²). But the main benefit — which one hopes all students appreciate eventually — is that this change of perspective highlights the fundamental link between sin x, cos x, and e^x:

• “cos x” becomes the derivative of sin x
• “-sin x” becomes the derivative of cos x, and
• the three functions are related by the totally unexpected identity

$$\begin{array}{c}{e}^{i\theta }=\cos \theta +i\sin \theta .\hfill \end{array}$$

The next problem draws attention to a beautiful result which reveals, in a pre-calculus, pre-complex number setting, a beautiful consequence of thinking about angles in terms of radians. The goal is to discover a formula for the area of a spherical triangle in terms of its angles and $\pi$, which links the formula for the circumference of a circle with that for the surface area of a sphere.

Suppose we wish to do geometry on the sphere. There is no problem deciding how to make sense of points. But it is less clear what we mean by (straight) lines, or line segments.

Before making due allowance for the winds and the tides, an airline pilot and a ship's Captain both need to know how to find the shortest path joining two given points A, B on a sphere. If the two points both lie on the equator, it is plausible (and correct) that the shortest route is to travel from A to Balong the equator. If we think of the equator as being in a horizontal plane through the centre O of the sphere, then we may notice that we can change the equator into a circle of longitude by rotating the sphere so that the “horizontal” plane (through O) becomes a “vertical” plane (through O). So we may view two points A and B which both lie on the same circle of longitude as lying on a “vertical equator” passing through A, B and the North and South poles: the shortest distance from A to B must therefore lie along that circle of longitude.

If we now rotate the sphere through some other angle, we get a “tilted equator” passing through the images of the (suitably tilted) points A and B: these “tilted equators” are called great circles. Each great circle is the intersection of the sphere with a plane through the centre O of the sphere. So

to find the shortest path from A to B:

• take the plane determined by the points A, B and the centre of the sphere O;
• find the great circle where this plane cuts the sphere;
• then follow the arc from A to B along this great circle.

Once we have points and line segments (i.e. arcs of great circles) on the sphere, we can think about triangles, and about the angles in such a triangle. In a triangle ABC on the sphere, the sides AB and AC are arcs of great circles meeting at A. By rotating the sphere we can imagine A as being at the North pole; so the two sides AB and AC behave just like arcs of two circles of longitude emanating from the North pole. In particular, we can measure the angle between them (this is exactly how we measure longitude): the two arcs AB, AC of circles of longitude set off from the North pole A in different horizontal directions before curving southwards, and the angle between them is the angle between these two initial horizontal directions (that is, the angle between the plane determined by O, A, B and the plane determined by O, A, C).

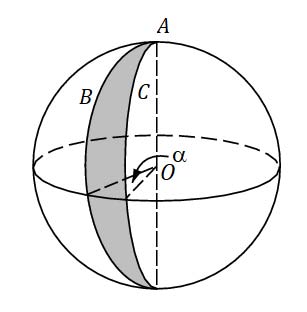
Figure 2: Angles on a sphere

Problem 34 Imagine a triangle ABC on the unit sphere (with radius r = 1), with angle α between AB and AC, angle β between BC and BA, and angle γ between CA and CB. You are now in a position to derive the remarkable formula for the area of such a spherical triangle.

(a) Let the two great circles containing the sides AB and AC meet again at A'. If we imagine A as being at the North pole, then A' will be at the South pole, and the angle between the two great circles at A' will also be α. The slice contained between these two great circles is called a lune with angle α.

(i) What fraction of the surface area of the whole sphere is contained in this lune of angle α? Write an expression for the actual area of this lune.

(ii) If the sides AB and AC are extended backwards through A, these backward extensions define another lune with the same angle α, and the same surface area. Write down the total area of these two lunes with angle α.

(b)(i) Repeat part (a) for the two sides BA, BC meeting at the vertex B, to find the total area of the two lunes meeting at B and B' with angle β.

(ii) Do the same for the two sides CA, CB meeting at the vertex C, to find the total area of the two lunes meeting at C and C' with angle γ.

(c)(i) Add up the areas of these six lunes (two with angle α, two with angle β, and two with angle γ). Check that this total includes every part of the sphere at least once.

(ii) Which parts of the sphere have been covered more than once? How many times have you covered the area of the original triangle ABC? And how many times have you covered the area of its sister triangle A'B'C'?

(iii) Hence find a formula for the area of the triangle ABC in terms of its angles — α at A, β at B, and γ at C.

1.6.3. Polar form and sin(A+B)

The next problem is less elementary than most of Chapter 1, but is included here to draw attention to the ease with which the addition formulae in trigonometry can be reconstructed once one knows about the polar form representation of a complex number. Those who are as yet unfamiliar with this material may skip the problem — but should perhaps remember the underlying message (namely that, once one is familiar with this material, there is no need ever again to get confused about the trig addition formulae).

Problem 35

(a) You may know that any complex number z = cosθ + isinθ of modulus 1 (that is, which lies on the unit circle centred at the origin) can be written in the modulus form z = e^iθ. Use this fact to reconstruct in your head the trigonometric identities for sin(A + B) and for cos(A + B). Use these to derive the identity for tan(A + B).

(b) By choosing X, Y so that $A=\frac{X+Y}{2}$, and $B=\frac{X-Y}{2}$, use part (a) to reconstruct the standard trigonometric identities for

$$\sin X+\sin Y,\sin X-\sin Y,\cos X+\cos Y,\cos X-\cos Y.$$

(c) (i) Check your answer to (a) for sin(A + B) by substituting A = 30°, and B = 60°.

(ii) Check your answer to (b) for cos X - cos Y by substituting X = 60°, and Y = 0°.

(d) (i) If $A+B+C+D=\pi$, prove that

$$\sin A\sin B+\sin C\sin D=\sin (B+C)\sin (B+D).$$

(ii) Given a cyclic quadrilateral WXYZ, with ∠XWY = A, ∠WXZ = B, ∠YXZ = C, ∠WYX = D, deduce Ptolemy's Theorem:

$$WX\times YZ+WZ\times XY=WY\times XZ.$$

1.7. Regular polygons and regular polyhedra

Regular polygons have already featured rather often (e.g. in Problems 3, 12, 19, 27, 28, 29). This is a general feature of elementary mathematics; so the neglect of the geometry of regular polygons, and their 3D companions, the regular polyhedra, is all the more unfortunate. We end this first chapter with a first brief look at polygons and polyhedra.

1.7.1. Regular polygons are cyclic

Problem 36 A polygon ABCDE… consists of n vertices A, B, C, D, E, …, and n sides AB, BC, CD, DE… which are disjoint except that successive pairs meet at their common endpoint (as when AB, BC meet at B). A polygon is regular if any two sides are congruent (or equal), and any two angles are congruent (or equal). Can a regular n-gon ABCDE… always be inscribed in a circle? In other words, does a regular polygon automatically have a “centre”, which is equidistant from all n vertices?

1.7.2. Regular polyhedra

Problem 37 (Wrapping)

(a) You are given a regular tetrahedron with edges of length 2. Is it possible to choose positive real numbers a and b so that an a by b rectangular sheet of paper can be used to “wrap”, or cover, the regular tetrahedron without leaving any gaps or overlaps?

(b) Given a cube with edges of length 2, what is the smallest sized rectangle that can be used to wrap the cube in the same way without cutting the paper? (In other words, if we want to completely cover the cube, what is the smallest area of overlap needed? How small a fraction of the paper do we have to waste?)

Problem 38 (Cross-sections) Can a cross-section of a cube be:

(i) an equilateral triangle?

(ii) a square?

(iii) a polygon with more than six sides?

(iv) a regular hexagon?

(v) a regular pentagon?

Problem 39 (Shadows) Can one use the Sun's rays to produce a plane shadow of a cube:

(i) in the form of an equilateral triangle?

(ii) in the form of a square?

(iii) in the form of a pentagon?

(iv) in the form of a regular hexagon?

(v) in the form of a polygon with more than six sides?

The imparting of factual knowledge is for us a secondary consideration. Above all we aim to promote in the reader a correct attitude, a certain discipline of thought, which would appear to be of even more essential importance in mathematics than in other scientific disciplines. …

General rules which could prescribe in detail the most useful discipline of thought are not known to us. Even if such rules could be formulated, they would not be very useful. Rather than knowing the correct rules of thought theoretically, one must have assimilated them into one's flesh and blood ready for instant and instinctive use. Therefore for the schooling of one's powers of thought only the practice of thinking is really useful.

G. Pólya (1887–1985) and G. Szegö (1895–1985)

1.8. Chapter 1: Comments and solutions

1.

(a) Assuming that the 2×, 3×, 4×, and 5× tables are known, and that one has understood that the order of the factors does not matter, all that remains to be learned is 6× 6, 6× 7, 6× 8, 6× 9; 7× 7, 7× 8, 7× 9; 8× 8, 8× 9; and 9× 9.

(b) (i) $(4\times {10}^{-3})\times (2\times {10}^{-2})=8\times {10}^{-5}=0.00008$

(ii) $(8\times {10}^{-4})\times (7\times {10}^{-2})=56\times {10}^{-6}=0.000056$

(iii) $(7\times {10}^{-3})\times (12\times {10}^{-2})=84\times {10}^{-5}=0.00084$

(iv) $1.08÷1.2=10.8÷12=108÷(12\times 10)=0.9$

(v) ${(8\times {10}^{-2})}^2=64\times {10}^{-4}=0.0064$

2.

(a) (i) 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144; 169, 196, 225, 256, 289, 324, 361, 400, 441, 484, 529, 576, 625, 676, 729, 784, 841, 900, 961

(ii) 1, 8, 27, 64, 125, 216, 343, 512, 729, 1000, 1331

(iii) $1=2^0$, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024

(b) (i) 31 (${31}^2=961$, ${32}^2=2^{10}=1024$)

(ii) 99 (${100}^2={10}^4=10000$)

(iii) 316 (${310}^2=96100<100000<{320}^2$; so look more carefully between 310 and 320)

(c) (i) 9 ($9^3=729<{10}^3=1000$)

(ii) 21 (${20}^3=8000$, ${22}^3=10648$)

(iii) 99 (${100}^3={10}^6=1000000$)

(d) (i) Those powers $2^e$ of the form $2^{2n}$ for which the exponent e is a multiple of 2: i.e. $e\equiv 0\left(\mathrm{mod}2\right)$.

(ii) Those powers 2^e of the form $2^{3n}$ for which the exponent e is a multiple of 3: i.e. $e\equiv 0\left(\mathrm{mod}3\right)$.

(e) $64=2^6=4^3=8^2$. $729=3^6=9^3={27}^2$.

3.

(a) (i) 7; (ii) 12; (iii) 21; (iv) 13; (v) 14; (vi) 31; (vii) $10\times 31=310$

(b) (i) $2\sqrt{2}$; (ii) $2\sqrt{3}$; (iii) $5\sqrt{2}$; (iv) $7\sqrt{3}$; (v) $12\sqrt{2}$; (vi) $21\sqrt{2}$

(c) (i) ∠ABC = 108°. ΔBAC is isosceles ($BA=BC$), so ∠BAC = ∠BCA = 36°.

$\therefore \angle CAE=\angle BAE-\angle BAC={72}^{°}={180}^{°}-\angle AE\mathrm{D.}$

So AC is parallel to ED (since corresponding angles add to 180°).

(ii) AX is parallel to ED; similarly DX is parallel to EA. Hence AXDE is a parallelogram, with EA = ED.

(iii) The two triangles are both isosceles and ∠AXD = ∠CXB = 108° (vertically opposite angles). Hence ∠XAD = ∠XCB = 36°, and ∠XDA = ∠XBC = 36°.

(iv) AD: CB = DX: BX, so x: 1 = 1: (x - 1); hence x² - x - 1 = 0 and $x=\frac{1+\sqrt{5}}{2}$ — the Golden Ratio, usually denoted by the Greek letter $\tau$ (tau), with approximate value $1.6180339887\dots$.

(v) $BX=x-1=\frac{\sqrt{5}-1}{2}$ ($=\frac{1}{\tau }=\tau -1$), with approximate value $0.6180339887\dots$.

(vi) We may either check that corresponding angles are equal in pairs (36°, 72°, 72°), or that corresponding sides are in the same ratio $x:1=1:(x-1$).

(vii) $\cos {36}^{°}=\frac{\sqrt{5}+1}{4}$; $\cos {72}^{°}=\frac{\sqrt{5}-1}{4}$ (drop perpendiculars from D to AB and from X to BC; or use the Cosine Rule).

(viii) Use ${\sin }^2{36}^{°}+{\cos }^2{36}^{°}=1$: $\sin {36}^{°}=\frac{\sqrt{10-2\sqrt{5}}}{4}$; $\sin {72}^{°}=\frac{\sqrt{10+2\sqrt{5}}}{4}$.

Note: The Golden Ratio crops up in many unexpected places (including the regular pentagon, and the Fibonacci numbers). Unfortunately much that is written about its ubiquity is pure invention. One of the better popular treatments, that highlights the number's significance, while taking a sober view of spurious claims, is the book The Golden Ratio by Mario Livio.

4.

(a) $12345=5\times 2469=3\times 5\times 823$. But is 823 a prime number?

It is easy to check that 823 is not divisible by 2, or 3, or 5, or 7, or 11. The Square Root Test (displayed below) tells us that it is only necessary to check four more potential prime factors.

Square Root Test: If $N=a\times b$ with $a\le b$, then $a\times a\le a\times b=N$, so the smaller factor $a\le \sqrt{N}$.

Hence, if N ($=823$ say) is not prime, its smallest factor > 1 is at most equal to $\sqrt{N}$ ($=\sqrt{823}<29$). Checking a = 13, 17, 19, 23 shows that the required prime factorisation is $12345=3\times 5\times 823$.

(b) There are 25 (2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97).

Notes:

(i) For small primes, mental arithmetic should suffice. But one should also be aware of the general Sieve of Eratosthenes (a Greek polymath from the $3^{\text{rd}}$ century BC). Start with the integers 1—100 arranged in ten columns, and proceed as follows:

$$\begin{array}{c}\begin{array}{cccccccccc}\hfill 1& \hfill 2& \hfill 3& \hfill 4& \hfill 5& \hfill 6& \hfill 7& \hfill 8& \hfill 9& \hfill 10\\ \hfill 11& \hfill 12& \hfill 13& \hfill 14& \hfill 15& \hfill 16& \hfill 17& \hfill 18& \hfill 19& \hfill 20\\ \hfill 21& \hfill 22& \hfill 23& \hfill 24& \hfill 25& \hfill 26& \hfill 27& \hfill 28& \hfill 29& \hfill 30\\ \hfill 31& \hfill 32& \hfill 33& \hfill 34& \hfill 35& \hfill 36& \hfill 37& \hfill 38& \hfill 39& \hfill 40\\ \hfill 41& \hfill 42& \hfill 43& \hfill 44& \hfill 45& \hfill 46& \hfill 47& \hfill 48& \hfill 49& \hfill 50\\ \hfill 61& \hfill 62& \hfill 63& \hfill 64& \hfill 65& \hfill 66& \hfill 67& \hfill 68& \hfill 69& \hfill 70\\ \hfill 71& \hfill 72& \hfill 73& \hfill 74& \hfill 75& \hfill 76& \hfill 77& \hfill 78& \hfill 79& \hfill 80\\ \hfill 81& \hfill 82& \hfill 83& \hfill 84& \hfill 85& \hfill 86& \hfill 87& \hfill 88& \hfill 89& \hfill 90\\ \hfill 91& \hfill 92& \hfill 93& \hfill 94& \hfill 95& \hfill 96& \hfill 97& \hfill 98& \hfill 99& \hfill 100\end{array}\hfill \end{array}$$

Delete 1 (which is not a prime: see (ii) below).

Circle the first undeleted integer; remove all other multiples of 2.

Circle the first undeleted integer; remove all other multiples of 3.

Circle the first undeleted integer; remove all other multiples of 5.

Circle the first undeleted integer; remove all other multiples of 7.

All remaining undeleted integers < 100 must be prime (by the Square Root Test (see part (a)).

(ii) The multiplicative structure of integers is surprisingly subtle. The first thing to notice is that 1 has a special role, in that it is the multiplicative identity: for each integer n, we have $1\times n=n$. Hence 1 is “multiplicatively neutral” — it has no effect.

The “multiplicative building blocks” for integers are the prime numbers: every integer > 1 can be broken down, or factorised as a product of prime numbers, in exactly one way. The integer 1 has no proper factors, and has no role to play in breaking down larger integers by factorisation. So 1 is not a prime. (If we made the mistake of counting 1 as a prime number, then we would have to make all sorts of silly exceptions — for example, to allow for the fact that $2=2\times 1=2\times 1\times 1=\dots$, so 2 could then be factorised in infinitely many ways.)

(iii) Notice that 91 = 7 × 13 is not a prime; so there is exactly one prime in the 90s — namely 97.

How many primes are there in the next run of 10 (from 100—109)?

How many primes are there from 190—199? How many from 200—210?

(c)(i) $3=2^2-1$.

(ii) Many students struggle with this, and may suggest 143, or 323, or even 63. The problem conceals a (very thinly) disguised message:

One cannot calculate with words.

To make use of mathematics, we must routinely translate words into symbols.

As soon as “one less than a square” is translated into symbols, bells should begin to ring. For you know that $x^2-1=(x-1)(x+1)$, so $x^2-1$ can only be prime if the smaller factor ($x-1$) is equal to 1.

5.

(a) (i) If we try to avoid such a “relatively prime pair”, then we must not choose any of 11, 13, 17, 19 (since they are prime, and have no multiples in the given range). So we are forced to choose the other six integers: 10, 12, 14, 15, 16, 18 — and there are then exactly two pairs which are relatively prime, namely 14, 15 and 15, 16.

(ii) If we try to avoid such a pair, then we can choose at most one even integer. So we are then forced to choose all five available odd integers, and our list will be: “unknown even, 11, 13, 15, 17, 19”. If the even integer is chosen to be 14, or 16, then every pair in my list has LCM = 1. So the answer is “No”.

(b) (i) If we try to avoid such a pair, then we must not choose 97 (the only prime number in the nineties). And we must not choose $95=5\times 19$ (which is relatively prime to all other integers in the given range — except for 90); and we must not choose $91=7\times 13$ (which is relatively prime to all other integers in the given range — except for 98). So we are forced to choose six integers from 90, 92, 93, 94, 96, 98, 99. Whichever integer we then omit leaves a pair which is relatively prime.

(ii) If we try to avoid such a pair, then we can choose at most one even integer. So we are then forced to choose all five available odd integers, and our list will be: “unknown even, 91, 93, 95, 97, 99”, and so must include the pair 93, 99 — with common factor 3. So the answer is “Yes”.

(c) In parts (a) and (b), the possible integers are limited (in (a) to the “teens”, and in (b) to the “nineties”); so it is natural to reach for ad hoc arguments as we did above. But in part (c) you know nothing about the numbers chosen.

Note: The question says that “I choose”, and asks whether “you” can be sure. So you have to find either a general argument that works for any n, or a counterexample. And the theme of this chapter indicates that it should not require any extended calculation.

The relevant “general idea” is the Pigeon Hole Principle which we may meet in the second part of this collection. So this problem may be viewed as a gentle introduction.

(i) Group the 2n consecutive integers

$$a+1,a+2,\dots ,a+2n$$

into n pairs of consecutive integers

$$\{a+1,a+2\},\{a+3,a+4\},\dots ,\{a+(2n-1),a+2n\}.$$

– If we choose at most one integer from each pair, then we never get more than n integers.

– So as soon as we choose n+1 integers from 2n consecutive integers, we are forced to choose both integers in some pair k, k+1, and this pair of consecutive integers is always relatively prime (see Problem 6(b)(i)).

(ii) We saw in part (a)(ii) that, if n = 5 and the 2n integers start at 10, then we can choose six integers (either 11, 13, 14, 15, 17, 19, or 11, 13, 15, 16, 17, 19), and in each case every pair has LCM = 1. So for n = 5 the answer is “No” (because there is at least one case where one cannot be sure).

However, as soon as n is at least 6, we show that the argument in part (a)(ii) breaks down. As before, if we try to choose a subset in which no pair has a common factor, then we can choose at most one even integer. So we are forced to choose all the odd integers. But any run of at least six consecutive odd integers includes two multiples of 3. So for $n\ge 6$, the answer is “Yes”.

6.

(a)(i) Suppose k is a factor of m and n. Then we can write m = kp and n = kq for some integers p, q. Hence m - n = k(p - q), so k is a factor of m - n. Also m + n = k(p + q), so k is a factor of m + n.

(ii) Any factor of m and n is also a factor of their difference m - n; so the set of common factors of m and n is a subset of the set of common factors of m - n and n.

And any factor of m - n and n is also a factor of their sum m; so the set of common factors of m - n and n is a subset of the set of common factors of m and n.

Hence the two sets of common factors are identical. In particular, the two “highest common factors” are equal.

(iii) Subtract 91 from 1001 ten times to see that

$$HCF(1001,91)=HCF(1001-910,91)=91.$$

(b) (i) Subtract m from m + 1 once to see that

$$HCF(m+1,m)=HCF(1,m)=1.$$

(ii) Subtract m from 2m + 1 twice to see that

$$HCF(2m+1,m)=HCF(m+1,m)=HCF(1,m)=1.$$

(iii) Subtract m - 1 from m² + 1 “m + 1 times” to see that

$$HCF(m^2+1,m-1)=HCF((m^2+1)-(m^2-1),m-1)=HCF(2,m-1).$$

Hence, if m is odd, the HCF = 2; if m is even, the HCF = 1.

7. They are equal. (The first is

$$\frac{17}{100}\times 19000000,$$

the second is

$$\frac{19}{100}\times 17000000,$$

which are equal since multiplication is commutative and associative.)

8.

(a)

$$\frac{3}{2}\times \frac{4}{3}\times \frac{5}{4}\times \frac{6}{5}=\frac{6}{2}=3$$

(b)

$$\sqrt{\frac{3}{2}\times \frac{4}{3}\times \frac{5}{4}\times \frac{6}{5}\times \frac{7}{6}\times \frac{8}{7}}=\sqrt{\frac{8}{2}}=2$$

(c)

$$\begin{array}{ccc}\hfill & \hfill & 10\times 9\times 8\times 7\times \times 5\times 4\times 3\times 2\times 1\text{seconds}\hfill \\ \hfill & \hfill & =\genfrac{}{}{0.1ex}{}{10\times 9\times 8\times 7\times 6\times 5\times 4\times 3\times 2\times 1}{60}\text{minutes}\hfill \\ \hfill & \hfill & =\genfrac{}{}{0.1ex}{}{10\times 9\times 8\times 7\times 6\times 5\times 4\times 3\times 2\times 1}{60\times 60}\text{hours}\hfill \\ \hfill & \hfill & =\genfrac{}{}{0.1ex}{}{10\times 9\times 8\times 7\times 6\times 5\times 4\times 3\times 2\times 1}{60\times 60\times 24}\text{days}\hfill \\ \hfill & \hfill & =\genfrac{}{}{0.1ex}{}{10\times 9\times 8\times 7\times 6\times 5\times 4\times 3\times 2\times 1}{60\times 60\times 24\times 7}\text{weeks}\hfill \\ \hfill & \hfill & =6\text{weeks (after cancelling)}.\hfill \end{array}$$

Note: These three questions underline what we mean by structural arithmetic. Fractions should never be handled by evaluating numerators and denominators. Instead one should always be on the lookout for structural features which simplify calculation — such as cancellation.

9. (a) Suppose a rectangle in the “DIN A” series has dimensions a by b, with a < b. Folding in half produces a rectangle of size $\frac{b}{2}$ by a. Hence $b:a=a:\frac{b}{2}$, so $b^2=2a^2$, and $b:a=\sqrt{2}:1$.

(b) (i) $\frac{1}{r}$. (ii) r.

10.

(a) “15% discount” means the price actually charged is “85% of the marked price”. Hence each marked price needs to be multiplied by 0.85.

The distributive law says we may add the marked prices first and then multiply the total (exactly £ 80) by 0.85 to get

$$\pounds \left(\frac{85}{100}\times 80\right)=\pounds (17\times 4)=\pounds 68.$$

Note: The context (shopping, sales tax, and discount) is mathematically uninteresting. What matters here is the underlying multiplicative structure of the solution, which arises in many different contexts.

(b) “Add 20% VAT” means multiplying the discounted pre-VAT total (£68) by 1.2, or $\frac{6}{5}$. Hence the final price, with VAT added, is £ (1.2 × 0.85 × 80).

If the VAT were added first, the price before discount would be £ (1.2 × 80), and the final price after allowing for the discount would be £ (0.85 × 1.2 × 80).

Since multiplication is commutative, the two calculations have the same result, so the order does not matter (just as the final result in Problem 9 is the same whether one first enlarges A4 to A3 and then reduces A3 to A4, or first reduces A4 to A5 and then enlarges A5 to A4).

Note: Notice that we did not evaluate the two answers to see that they gave the same output £81.60. If we had, then the equality might have been a fluke due to the particular numbers chosen. Instead we left the answer unevaluated, in structured form, which showed that the equality would hold for any input.

(c) To cancel out multiplying by $\frac{6}{5}$ we need to multiply by $\frac{5}{6}$ — a discount of $\frac{1}{6}$, or $16\frac{2}{3}\%$.

Note: This question has nothing to do with financial applications. It is included to underline the fact that although percentage change questions use the language of addition and subtraction (“increase”, or “decrease”), the mathematics suggests they should be handled multiplicatively.

11.

(a) (i) $2\times 5<3\times 4$, so

$$\frac{7}{2\times 5}>\frac{7}{3\times 4}.$$

Hence

$$\frac{1}{2}+\frac{1}{5}>\frac{1}{3}+\frac{1}{4}.$$

(ii) At first sight, “$10\le 12$” may not seem related to “$\frac{1}{2}+\frac{1}{5}>\frac{1}{3}+\frac{1}{4}$”. Yet the crucial fact we started from in part (i) was “$2\times 5=10\le 12=3\times 4$”.

(b) 10 < 12, so

$$(x+2)(x+5)=x^2+7x+10<x^2+7x+12=(x+3)(x+4).$$

(i) If all four brackets are positive (i.e. if x > − 2), then we also have 2x + 7 > 0, and it follows that

$$\begin{array}{ccc}\genfrac{}{}{0.1ex}{}{1}{x+2}+\genfrac{}{}{0.1ex}{}{1}{x+5}\hfill & =\hfill & \genfrac{}{}{0.1ex}{}{2x+7}{(x+2)(x+5)}\hfill \\ \hfill & >\hfill & \genfrac{}{}{0.1ex}{}{2x+7}{(x+3)(x+4)}\hfill \\ \hfill & =\hfill & \genfrac{}{}{0.1ex}{}{1}{x+3}+\genfrac{}{}{0.1ex}{}{1}{x+4}.\hfill \end{array}$$

(ii) When calculating with the given algebraic expression, the values

$$x=-2,-3,-4,-5$$

are “forbidden values”.

If x > − 2, then (as in part (i)) we have

$$\begin{array}{ccc}\genfrac{}{}{0.1ex}{}{1}{x+2}+\genfrac{}{}{0.1ex}{}{1}{x+5}\hfill & =\hfill & \genfrac{}{}{0.1ex}{}{2x+7}{(x+2)(x+5)}\hfill \\ \hfill & >\hfill & \genfrac{}{}{0.1ex}{}{2x+7}{(x+3)(x+4)}\hfill \\ \hfill & =\hfill & \genfrac{}{}{0.1ex}{}{1}{x+3}+\genfrac{}{}{0.1ex}{}{1}{x+4}.\hfill \end{array}$$

For permitted values of x < -2, one or more of the brackets (x + 2), (x + 5), (x + 3), (x + 4) will be negative. However, one can still carry out the algebra to simplify

$$\frac{1}{x+2}+\frac{1}{x+5}=\frac{2x+7}{(x+2)(x+5)}\text{and}$$ $$\frac{1}{x+3}+\frac{1}{x+4}=\frac{2x+7}{(x+3)(x+4)}$$

When $x=-\frac{7}{2}$ both expressions are equal, and equal to 0. The simplified numerators are both positive if $x>-\frac{7}{2}$, and both negative if $x<-\frac{7}{2}$; and the sign of the denominators changes as one moves through the four intervals −3 > x > −2, −4 > x > −3, −5 > x > −4, x > −5, with the inequality switching

$$\begin{array}{c}\hfill \mathrm{from}“>”(\mathrm{for}x>-2)\mathrm{to}“<”(\mathrm{for}-3<x<-2),\\ \hfill \mathrm{to}“>”(\mathrm{for}-3.5<x<-3),\\ \hfill \mathrm{to}“<”(\mathrm{for}-4<x<-3.5),\\ \hfill \mathrm{to}“>”(\mathrm{for}-5<x<-4),\\ \hfill \mathrm{to}“<”(\mathrm{for}x<-5).\end{array}$$

12.

(a) (i) $3+2\sqrt{2}$; (ii) $3-2\sqrt{2}$; (iii) $7+5\sqrt{2}$.

Note: Notice that you can write down the answer to (ii) as soon as you have finished (i), without doing any further calculation.

(b) (i) $2+\sqrt{6}$; (ii) $\sqrt{2}+\sqrt{3}$; (iii) $\frac{1+\sqrt{5}}{2}$ (the Golden Ratio $\frac{1+\sqrt{5}}{2}=\tau$ is the larger root of the quadratic equation $x^2-x-1=0$. Hence $\frac{3+\sqrt{5}}{2}=\tau +1={\tau }^2$); (iv) $\sqrt{10-2\sqrt{5}}$: this does not simplify further.

Note: Some readers may think an apology is in order for part (iv). The lesson here is that, while one should always try to simplify, there is no way of knowing in advance whether a simplification is possible. And there is no way out of this dilemma. So one is reduced to thinking: any simplification would involve $\sqrt{5}$, and if one tries to solve ${(a+b\sqrt{5})}^2=10-2\sqrt{5}$, then the solutions for a and b do not lead to anything “simpler”. (This repeated surd should perhaps have rung bells, as it was equal to the exact expression for 4sin 36° in Problem 3(c). It was included here partly because the question of its simplification should already have arisen when it featured in that context.)

13. In reconstructing the missing digits the number of possible solutions is determined by the highest common factor of the multiplier and 10. At the first step (in the units column):

because HCF(6, 10) = 2, $\square \times 6=8\left(\mathrm{mod}10\right)$ has two solutions which differ by 5 — namely 3 and 8.

The first possibility then requires us to solve $(\square \times 3)+1=2\left(\mathrm{mod}10\right)$: because $HCF(3,10)=1$, this has just one solution — namely 7. This gives rise to the solution $76\times 3=228$.

The second possibility requires us to solve $(\square \times 8)+4=2\left(\mathrm{mod}10\right)$: because HCF(8, 10) = 2, this has two solutions which differ by 5 — namely 1 and 6. This gives rise to two further solutions: $16\times 8=128$, and $66\times 8=528$.

14.

(a) The solutions are entirely elementary, with no trickery. But they can be surprisingly elusive. And since this elusiveness is the only reason for including the problem, we hesitate to relieve any frustration by giving the solution.

The whole thrust of the “24 game” is to underline the scope for “getting to know” the many faces of a number like 24: for example, as 24=12 + 12 ($=3\times 4+3\times 4$ for 3, 3, 4, 4); as 24=25 −1 ($=5\times 5-3÷3$ for 3, 3, 5, 5); and as 24=27 - 3 ($=3\times 3\times 3-3$ for 3, 3, 3, 3). So one should be looking for ways of exploiting other important arithmetical aspects of 24— in particular, as $4\times 6$ and as $3\times 8$.

(b) (i) 0 = (4 − 4) + (4 − 4); $1=(4÷4)\times (4÷4)$; $2=(4÷4)+(4÷4)$; $3=(4+4+4)÷4$; $4=((4-4)\times 4)+4$; $5=((4\times 4)+4)÷4$; $6=4+((4+4)÷4)$; $7=4+4-(4÷4)$; 8 = $(4+4)\times (4÷4)$; . The output 10 seems to be impossible with the given restrictions.

(ii) With squaring and $\sqrt{}$ allowed we can manage $10=4+4+4-\sqrt{4}$. Indeed, one can make everything up to 40 except (perhaps) 39.

15.

(a) (i) a² + 2ab + b²; $a^3+3a^{2}b+3a{b}^2+b^3$

(ii) Replace b by (−b): $a^2-2ab+b^2$; $a^3-3a^{2}b+3a{b}^2-b^3$

(b) (i) ${(x+1)}^2$; (ii) ${(x^2-1)}^2$; (iii) ${(x^2-1)}^3$

(c) (i) $a^2-b^2$

(ii) Replace “b” by “b + c”: $a^2-{(b+c)}^2=a^2-b^2-c^2-2bc$

Replace “b” by “b − c”: $a^2-{(b-c)}^2=a^2-b^2-c^2+2bc$

(d) One way is to rewrite this expression as a difference of two squares:

$$\begin{array}{ccc}{\left(2x\right)}^2-(x^2-2x+1)\hfill & =\hfill & {\left(2x\right)}^2-{(x-1)}^2\hfill \\ \hfill & =\hfill & (2x-(x-1\left)\right)(2x+(x-1\left)\right)\hfill \\ \hfill & =\hfill & (x+1)(3x-1)\hfill \end{array}$$

Note: As so often, the messages here are largely implicit. In part (a)(ii) we\linebreak explicitly highlight the intention to use what you already know (by simply substituting “-b” in place of “b”. In part (b), you are expected to recognise (i), and then to see (ii) and (iii) as mild variations on the expansions of ${(a-b)}^2$ and ${(a-b)}^3$ in part (a). Part (c) repeats (in silence) the message of (a)(ii): think — don't slog it out. And part (d) encourages you to keep an eye out for thinly disguised instances of “a difference of two squares”.

16.

(a) Final digits: ‘block’ 4, 6 of length 2;

leading digits: “block” 4, 1, 6, 2, 1 of length 5.

(b) Claim The sequence of “units digits” really does recur.

Proof Given a power of 4 that has units digit 4, the usual multiplication algorithm for multiplying by 4 produces a number with units digit 6.

Given this new power of 4 with units digit 6, the usual multiplication algorithm for multiplying by 4 produces a number with units digit 4.

At this stage the sequence of units digits begins a new cycle.

[Alternatively: The units digit is simply equal to the relevant power of $4\left(\mathrm{mod}10\right)$. Multiplying by 4 changes 4 to $6\left(\mathrm{mod}10\right)$; multiplying by 4 changes 6 to $4\left(\mathrm{mod}10\right)$; — and the cycle repeats.]

(c) The sequence of leading digits seems to recur every 5 terms, because $4^5=2^{10}=1024$ is almost exactly equal to 1000. Each time we move on 5 steps in the sequence, we multiply by $4^5=1024$. As far as the leading digit is concerned, this has the same effect as multiplying the initial term (4) by slightly more than 1.024 (then adding any ‘carries'), which is very like multiplying by 1— and so does not change the leading digit (yet).

However, each time we move on 10 steps in the sequence, we multiply by $4^{10}={1024}^2=1048576$. As far as the leading digit is concerned, this has the same effect as multiplying by slightly more than 1.048576.

When we move on 25 steps, we multiply by $4^{25}=1125899906842624$. And as far as the leading digit is concerned, this has the same effect as multiplying by slightly more than 1.12599906842624. And so on.

Eventually, the multiplier becomes large enough to change one of the leading digits.

17. The total is 100.

Having found this by direct calculation, we should think indirectly and notice that $100={10}^2$.

And we should then ask: “Why 10? What has 10 got to do with the $4\times$ multiplication table?”

A quick check of the $1\times$ multiplication table (total = 1), the $2\times$ multiplication table (total = 9), etc. may suggest what we should have seen immediately.

The first row has sum: $(1+2+3+4)$.

The second row has total $2\times (1+2+3+4)$.

The third row has total $3\times (1+2+3+4)$.

The fourth row has total $4\times (1+2+3+4)$.

$\therefore$ The total is $(1+2+3+4)\times (1+2+3+4)={(1+2+3+4)}^2$.

19.

(a) $\sin {45}^{°}=\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2}=\cos {45}^{°}$; $\tan {45}^{°}=1$

(b) $AM=\sqrt{3}$; $\sin {30}^{°}=\frac{1}{2}$, $\cos {30}^{°}=\frac{\sqrt{3}}{2}$, $\tan {30}^{°}=\frac{1}{\sqrt{3}}=\frac{\sqrt{3}}{3}$; $\sin {60}^{°}=\frac{\sqrt{3}}{2}$, $\cos {60}^{°}=\frac{1}{2}$, $\tan {60}^{°}=\sqrt{3}$.

(c) (iii) $\cos {315}^{°}=\cos {45}^{°}=\frac{\sqrt{2}}{2}$; $\sin {225}^{°}=-\sin {45}^{°}=-\frac{\sqrt{2}}{2}$; $\tan {210}^{°}=\tan {30}^{°}=\frac{\sqrt{3}}{3}$; $\cos {120}^{°}=-\cos {60}^{°}=-\frac{1}{2}$; $\sin {960}^{°}=\sin {240}^{°}=-\sin {60}^{°}=-\frac{\sqrt{3}}{2}$; $\tan (-{135}^{°})=\tan {45}^{°}=1$.

(d) Cut the n-gon into n“cake slices”, and use the formula “$\frac{1}{2}ab\sin C$” for each slice.

(i) $\frac{3\sqrt{3}}{4}$; (ii) 2; (iii) $\frac{3\sqrt{3}}{2}$; (iv) $2\sqrt{2}$; (v) 3

(e) Work out the side length of the n-gon, then cut the n-gon into n“slices”, and use the formula “$\frac{1}{2}(\text{base}\times \text{height}$)” for each slice.

(i) $3\sqrt{3}$; (ii) 4; (iii) $2\sqrt{3}$; (iv) $8(\sqrt{2}-1)$; (v) $12(2-\sqrt{3})$

Note: There is no hidden trig here: all you need is Pythagoras’ Theorem. For example, in part (e)(iv) we can extend alternate sides of the regular octagon to form the circumscribed 2 by 2 square. The four corner triangles are isosceles right angled triangles with hypotenuse of length s (the side of the octagon). Hence each side of the square is equal to $s+2\cdot \frac{s}{\sqrt{2}}=2$, whence $s=2(\sqrt{2}-1)$.

20. (a) $\sqrt{8}$; (b) $\sqrt{2}$, $\sqrt{2}$; (c) $\sqrt{8}=\sqrt{4\times 2}=2\sqrt{2}$

21. Construct the perpendicular from A to BC (possibly extended); let this meet the line BC at X. There are four possibilities:

(i) either X = C, in which case ∠BCA is a right angle as required; or X = B, in which case $b^2=a^2+c^2$, contradicting $a^2+b^2=c^2$;

(ii) $X\ne B,C$, and C lies between B and X;

(iii) $X\ne B,C$, and X lies between B and C;

(iv) $X\ne B,C$, and B lies between X and C.

We analyse case (ii) and leave cases (iii) and (iv) to the reader.

(ii) ΔAXC and ΔAXB are both right angled triangles; so by Pythagoras’ Theorem we know that

$$\begin{array}{ccc}A{C}^2\hfill & =\hfill & A{X}^2+X{C}^2,\text{and}\hfill \\ A{B}^2\hfill & =\hfill & A{X}^2+X{B}^2\hfill \\ \hfill & =\hfill & A{X}^2+{(XC+CB)}^2\hfill \\ \hfill & =\hfill & A{X}^2+X{C}^2+C{B}^2+2XC\cdot CB\hfill \\ \hfill & =\hfill & A{C}^2+C{B}^2+2XC\cdot CB.\hfill \end{array}$$

Since we are told that $A{C}^2+C{B}^2=A{B}^2$, it follows that $2XC\cdot CB=0$, contrary to $X\ne C$.

Note: Notice that the proof of the converse of Pythagoras’ Theorem makes use of Pythagoras’ Theorem itself.

22.

(a) c = b + 1, so $a^2=c^2-b^2=2b+1$. Hence a is odd, and we can write $a=2m+1$.

(b) Suppose $b=2n-1$ is also odd. Then $c^2=4n^2$ is divisible by 4— which contradicts the fact that $b^2=4(n^2-n)+1$, and $a^2=4(m^2+m)+1$, so $a^2+b^2$ leaves remainder 2 on division by 4.

Hence b = 2n is even and c = 2n + 1 is odd. But then

$${(2m+1)}^2+{(2n)}^2=a^2+b^2=c^2={(2n+1)}^2,$$

so $4(m^2+m)=4n$, and $n=m(m+1)$.

23. (a) If a and b are both even, then $HCF(a,b)\ne 1$, so the triple would not be primitive.

If a and b are both odd, we use the idea from Problem 22(b). Suppose a = 2m + 1, b = 2n + 1; then $a^2=4(m^2+m)+1$, and $b^2=4(n^2+n)+1$, so $a^2+b^2=2\times (2(m^2+m+n^2+n)+1)$. But this is “twice an odd number”, so cannot be equal to $c^2$ (since c would have to be even, and any even square must be a multiple of 4).

Hence we may assume that a is odd and b is even: so c is is odd.

(b) Then $a^2+b^2=c^2$ yields $b^2=c^2-a^2=(c-a)(c+a)$, so

$${\left(\frac{b}{2}\right)}^2=\left(\frac{c-a}{2}\right)\left(\frac{c+a}{2}\right).$$

Any common factor of $\frac{c+a}{2}$ and $\frac{c-a}{2}$ divides their sum c and their difference a, so $HCF(\frac{c-a}{2},\frac{c+a}{2})=1$. Since the difference of these two factors is a, which is odd, they have opposite parity.

(c) If two integers are relatively prime, and their product is a square, then each of the factors has to be a square (consider their prime factorisations). Hence $\frac{c+a}{2}=p^2$ and $\frac{c-a}{2}=q^2$, where $HCF(p,q)=1$ and p and q have opposite parity. Therefore

$$c=p^2+q^2,a=p^2-q^2,b=2pq.$$

(d) It is easy to check that any triple of the given form is (i) primitive, and (ii) satisfies $a^2+b^2=c^2$.

24. Claim The only such triples are those of the form (3s, 4s, 5s).

Proof We show that the only primitive Pythagorean triple which forms an arithmetic progression is the familiar triple (3, 4, 5).

By Problem 23, one of the numbers in any primitive Pythagorean triple is even (namely 2pq) and two are odd (p and q are of opposite parity, so $p^2-q^2$ and $p^2+q^2$ are both odd).

∴ 2pq is the “middle term”, and the smallest and largest terms differ by $2q^2$.

∴ the common difference d = c - b = b - a is equal to $q^2$.

∴ $2pq=p^2$, so p = 2q.

Finally, since p and q are relatively prime, we must have q = 1, p = 2. QED

Note: Alternatively, let (a, b, c) be any Pythagorean triple (not necessarily primitive), which forms an arithmetic progression. Then

$$a^2=c^2-b^2=(c-b)(c+b)=(b-a)(c+b).$$

So b(c + b) = a(a + b + c). Hence $a\cdot 3b=a(a+b+c)=b(c+b)$. It then follows that $3b^2=b(a+b+c)=4ba$, so 3b = 4a and a: b = 3: 4.

25.

(a) $2=1^2+1^2$, $5=2^2+1^2$, $13=3^2+2^2$, $17=4^2+1^2$, $29=5^2+2^2$, $37=6^2+1^2$, $41=5^2+4^2$, $53=7^2+2^2$, $61=6^2+5^2$, $73=8^2+3^2$, $89=8^2+5^2$, $97=9^2+4^2$.

(b) $(a^2+b^2)(c^2+d^2)={(ac-bd)}^2+{(ad+bc)}^2$.

Note: It is easy to check this identity once it is given, but most of us are not so fluent in algebra as to spot this handy identity without help! However, Chapter 1 is about “Mental skills”, and one such technique (once you have mastered it) arises from the arithmetic of complex numbers. If you have met complex numbers, then this identity can be written down immediately. Let us explain briefly how.

Every complex number $w=a+bi$ (where $i^2=-1$) can be represented as a point in the complex plane with coordinates (a, b). The “size”, or modulus, of w is its length $\left|w\right|$ (the distance of (a, b) from the origin (0, 0)); and the square of this length $a^2+b^2$ is referred to as the norm of the complex number w=a+bi. The required identity is an immediate consequence of the two facts:

• the modulus of a product is equal to the product of the two moduli: $\left|wz\right|=\left|w\right|\cdot \left|z\right|$, and
• the norm $a^2+b^2$ can be expressed algebraically as $a^2+b^2=(a+bi)(a-bi)$.

Once we know these facts:

• $a^2+b^2$ can be interpreted as the norm of w=a+bi, and
• $c^2+d^2$ as the norm of z = c + di;

the product of the two norms $(a^2+b^2)(c^2+d^2)$ is then equal to the norm of the product $w\cdot z=(ac-bd)+(ad+bc)i$.

Note: If we choose z = c − di, then wz = (ac +bd) + (bc - ad)i, and we get a second identity: $(a^2+b^2)(c^2+d^2)={(ac+bd)}^2+{(bc-ad)}^2$.

(c) The square ${(2n)}^2$ of any even number 2n is a multiple of $2^2=4$.

Any odd number has the form 2n + 1; its square ${(2n+1)}^2=4n^2+4n+1$ is 1 more than a multiple of 4. So in the sum of two squares, we have

(i) both squares are even and their sum is a multiple of 4, or

(ii) one square is even and one is odd and their sum is of the form 4k + 1, or

(iii) both squares are odd and their sum is of the form 4k + 2.

Hence no number of the form 4k + 3 can be written as a sum of two squares.

(d) We are told that $2=1^2+1^2$, and that Euler showed every prime of the form 4k + 1 can be written as the sum of two squares. Part (b) then shows that any product of such primes can be written as the sum of two squares. And if we multiply a sum of two squares by a square, the result can again be written as the sum of two squares. This allows us to construct the list of forty six integers N < 100 which can be so written. These are precisely the integers of the form

“(a square) × (a product of distinct primes p, where p = 2 or p = 4k + 1)”:
0, 1, 2, 4, 5, 8, 9, 10, 13, 16, 17, 18, 20, 25, 26, 29, 32, 34, 36, 37, 40, 41, 45, 49,
50, 52, 53, 58, 60, 61, 64, 65, 68, 72, 73, 74, 80, 81, 82, 83, 85, 87, 89, 90, 97, 98.

(e) The side of such a square is the hypotenuse of a right angled triangle whose legs run in the x- and y- directions, and have integer lengths (because their vertices are at points with integer coordinates). Hence the answer is exactly the same as for part (d) (provided one does not quibble about the idea of a square with side 0 and area 0).

26. Most sheets in a newspaper are double sheets with four pages. If we assume that all sheets are double sheets, then the 13 pages before page 14 match up with the 13 pages after page 27, so there are 27 + 13 = 40 pages in all. (If the paper included inserted ‘single sheets’ — with just two pages, then there is no solution.)

27.

(a) If θ = 90°, then the overlap is clearly one quarter of the small square. In general, the continuations of the sides BA and DA cut the small square into four congruent quadrilaterals, one of which is the area of overlap. So the overlap is always one quarter of the lower square.

(b) The area of overlap for “a large equilateral ΔABC on top of a small equilateral ΔPQR” is not constant, but depends on the angle of orientation of the large triangle. However, if viewed in the right way, something similar works for a large regular 2n-gon on top of a small regular 2n-gon with one corner of the large polygon at the centre of the small one.

The key is to realise how the fraction “one quarter” arises for a regular 4-gon. There 2n = 4, so n = 2, and each vertex angle is equal to $\left(\frac{{360}^{°}}{2n}\right)(n-1)={90}^{°}$, which is exactly $\frac{n-1}{2n}=\frac{1}{4}$ of ${360}^{°}$. For a regular 2n-gon, the large polygon always covers a fraction equal to exactly $\frac{n-1}{2n}$ of the small polygon.

28. 3 cm, the same as the perimeter of triangle ABC.²

What if A were folded to some point A'' on BC?

29. In extremis one may reach for trigonometry: if we denote the three angles by α (at A), β (at B), and γ (at C), then the arrangement of squares implies that $\tan \alpha =\frac{1}{3}$, $\tan \beta =\frac{1}{2}$, and $\tan \gamma =1$, so we can use the standard identity

$$\tan (\alpha +\beta )=\frac{\tan \alpha +\tan \beta }{1-\tan \alpha \tan \beta }$$

to see that $\tan (\alpha +\beta )=1=\tan \gamma$.

² From: Y. Wu, The examination system in China: the case of zhongkao mathematics. 12th International Congress on Mathematical Education. 8 July – 15 July, 2012, COEX, Seoul, Korea

However, it is worth looking for a more elementary explanation than ‘brute force calculation'. If we embed the horizontal 3 by 1 rectangle ADEH in the top right hand corner of a 4 by 4 square ZDXY, (with Z labelling the top left hand corner), then we can complete the square AEPQ, which has AE as one side, with P on side XY and Q on side YZ.

Then ∠AEH = ∠DAE, and ∠AEQ = ∠DCE. So all we need to explain is why ∠HEQ = ∠DBE — and this follows from the fact that EQ passes through the centre of the 4 by 4 square ZDXY.

30.

(a) Construct points P and Q inside the trapezium so that MNPQ is similar to BCMN. If the line through P parallel to AB meets BC at X, and the line through Q parallel to AC meets BC at Y, then MNPQ, NBXP, XYQP, MCYQ are the required pieces.

(b) Each of the four pieces must be three-quarters of one of the small squares. So we have to lose one quarter of each small square. There are various ways to do this, but most create non-congruent parts. Cut each of the smaller squares into quarters as for the original square. If O is the centre of the original square, lump together the three mini-squares which have O as a vertex to form an L-shape. Each of the three remaining small squares has lost a quarter and forms an identical L-shape.

31. To divide the shaded region in 2 congruent parts, rotate the lower small semicircle through the angle $\frac{\pi }{2}$ anticlockwise about the centre of the large circle.

Note: The same idea allows one to divide the shaded region into n congruent parts: rotate the lower small semicircle successively through the angle $\frac{\pi }{n}$ anticlockwise about the centre of the large circle.³

32.

(a) The point O lies on the perpendicular bisector of AB, and so is equidistant from the two endpoints A and B, so OA = OB. The point O also lies on the perpendicular bisector of BC, and so is equidistant from the two endpoints B and C, so OB = OC.

(b) (ii) ∠BA'C and ∠BAC are angles subtended in the same segment of the circle by the same chord BC, so are equal (“angles in the same segment”).

∠A'CB is the angle subtended on the circumference (at C) by the diameter A'B, and so must be a right angle. In ΔA'BC we then see that

$$sinA=\sin A^{\prime }=\frac{a}{2R}.$$

If we now switch attention from the angle at A to the angle at B, and then to the angle at C, we can show that $\sin B=\frac{b}{2R}$, and that $\sin C=\frac{c}{2R}$.

³ From: Introductory Assignment, Gelfand Correspondence Program in Mathematics.

33.

(a) Drop a perpendicular from A to meet the line BC at X. Then $AX=b\cdot \sin C$, so

$$\Delta =\frac{1}{2}\cdot (a\times b\sin C).$$

(b) Substitute “$\sin C=\frac{c}{2R}$” (from the Sine Rule) into the formula in part (a).

34.

(a) (i) $\frac{\alpha }{2\pi }$; $\frac{\alpha }{2\pi }\times (\text{surface area of unit sphere}=4\pi )=2\alpha$.

(ii) $4\alpha$

(b) (i) $4\beta$; (ii) $4\gamma$

(c)(i) $4(\alpha +\beta +\gamma )$

(ii) Triangle ABC and its sister triangle $A^{\prime }{B}^{\prime }{C}^{\prime }$ are congruent, and each is covered 3 times.

(iii)

$$\begin{array}{ccc}4(\alpha +\beta +\gamma )\hfill & =\hfill & \left(\text{total surface area of the unit sphere}\right)\hfill \\ \hfill & \hfill & +(4\times (\text{area of the spherical triangle\hspace{0.22em}\hspace{0.05em}}ABC\left)\right)\hfill \\ \therefore area(△ABC)\hfill & =\hfill & (\alpha +\beta +\gamma )-\pi .\hfill \end{array}$$

Note: In particular, the formula for the area of a spherical triangle implies:

• the angle sum $\alpha +\beta +\gamma$ in any spherical triangle is always greater than $\pi$, and
• the larger the triangle ABC, the more its angle sum must exceed $\pi$.

35.

(a)

$$\begin{array}{ccc}\cos (A+B)+i\sin (A+B)\hfill & =\hfill & e^{i(A+B)}\hfill \\ \hfill & =\hfill & e^{iA}\cdot e^{iB}\hfill \\ \hfill & =\hfill & (\cos A+i\sin A)(\cos B+i\sin B).\hfill \end{array}$$

Hence

$$\sin (A+B)=\sin A\cos B+\cos A\sin B,$$

and

$$\cos (A+B)=\cos A\cos B-\sin A\sin B.$$

To reconstruct tan(A + B), divide these two expressions, and then divide numerator and denominator by “cos A cos B” to get

$$\tan (A+B)=\frac{\sin (A+B)}{\cos (A+B)}=\frac{\tan A+\tan B}{1-\tan A\tan B}.$$

(b)

$$\begin{array}{ccc}\sin X\hfill & =\hfill & \sin (A+B)\hfill \\ \hfill & =\hfill & \sin A\cos B+\cos A\sin B\hfill \\ \hfill & =\hfill & \sin \left(\genfrac{}{}{0.1ex}{}{X+Y}{2}\right)\cos \left(\genfrac{}{}{0.1ex}{}{X-Y}{2}\right)+\cos \left(\genfrac{}{}{0.1ex}{}{X+Y}{2}\right)\sin \left(\genfrac{}{}{0.1ex}{}{X-Y}{2}\right),\hfill \end{array}$$

and

$$\begin{array}{ccc}\sin Y\hfill & =\hfill & \sin (A-B)\hfill \\ \hfill & =\hfill & \sin A\cos B-\cos A\sin B\hfill \\ \hfill & =\hfill & \sin \left(\genfrac{}{}{0.1ex}{}{X+Y}{2}\right)\cos \left(\genfrac{}{}{0.1ex}{}{X-Y}{2}\right)-\cos \left(\genfrac{}{}{0.1ex}{}{X+Y}{2}\right)\sin \left(\genfrac{}{}{0.1ex}{}{X-Y}{2}\right),\hfill \end{array}$$ $$\therefore \sin X+\sin Y=2\sin \left(\frac{X+Y}{2}\right)\cos \left(\frac{X-Y}{2}\right).$$

For sin X - sin Y, substitute “-Y” in place of Y to get:

$$\sin X-\sin Y=2\sin \left(\frac{X-Y}{2}\right)\cos \left(\frac{X+Y}{2}\right).$$

Similarly

$$\begin{array}{ccc}\cos X+\cos Y\hfill & =\hfill & \cos (A+B)+\cos (A-B)\hfill \\ \hfill & =\hfill & (\cos A\cos B-\sin A\sin B)+(\cos A\cos B+\sin A\sin B)\hfill \\ \hfill & =\hfill & 2\cos A\cos B\hfill \\ \hfill & =\hfill & 2\cos \left(\genfrac{}{}{0.1ex}{}{X+Y}{2}\right)\cos \left(\genfrac{}{}{0.1ex}{}{X-Y}{2}\right)\hfill \end{array}$$ $$\begin{array}{ccc}\cos X-\cos Y\hfill & =\hfill & \cos (A+B)-\cos (A-B)\hfill \\ \hfill & =\hfill & (\cos A\cos B-\sin A\sin B)-(\cos A\cos B+\sin A\sin B)\hfill \\ \hfill & =\hfill & -2\sin A\sin B\hfill \\ \hfill & =\hfill & -2\sin \left(\genfrac{}{}{0.1ex}{}{X+Y}{2}\right)\sin \left(\genfrac{}{}{0.1ex}{}{X-Y}{2}\right).\hfill \end{array}$$

(c)

(i) $\sin (A+B)=\sin {90}^{°}=1$;

$$\sin A\cos B+\cos A\sin B={\left(\frac{1}{2}\right)}^2+{\left(\frac{\sqrt{3}}{2}\right)}^2=1.$$

(ii) $\cos X-\cos Y=\frac{1}{2}-1=-\frac{1}{2}$;

$$-2\sin \left(\frac{X+Y}{2}\right)\sin \left(\frac{X-Y}{2}\right)=-2{\sin }^2{30}^{°}=-\frac{1}{2}.$$

(d) (i) $2\sin A\sin B=\cos (A-B)-\cos (A+B)$.

$$\begin{array}{cc}\hfill & \therefore 2\sin A\sin B+2\sin C\sin D\hfill \\ \hfill & =[\cos (A-B)-\cos (A+B)]\hfill \\ \hfill & +[\cos (C-D)-\cos (C+D)]\hfill \\ \hfill & =\cos (A-B)+\cos (C-D)\hfill \\ \hfill & (\text{since}C+D=\pi -(A+B\left)\right)\hfill \\ \hfill & =2\cos \left(\genfrac{}{}{0.1ex}{}{A+C-(B+D)}{2}\right)\cos \left(\genfrac{}{}{0.1ex}{}{A+D-(B+C)}{2}\right)\hfill \\ \hfill & =2\cos (\genfrac{}{}{0.1ex}{}{\pi }{2}-(B+D\left)\right)\cos (\genfrac{}{}{0.1ex}{}{\pi }{2}-(B+C\left)\right)\hfill \\ \hfill & =2\sin (B+D)\sin (B+C).\hfill \end{array}$$

Note: We can swap A and B without changing the expression “$\sin A\sin B+\sin C\sin D$”. Hence the same should be true of the RHS “sin(B + C)sin(B + D)”. Fortunately, since $A+B+C+D=\pi$, we know that sin(A + C) = sin(B + D), and sin(A + D) = sin(B + C).

(ii) In triangle WXY we see that $A+B+C+D=\pi$. Hence

$$\sin A\sin B+\sin C\sin D=\sin (A+D)\sin (B+D).$$

Now let R be the radius of the circle. Use “equality of angles in the same segment” and the Sine Rule (in its full form: see Problem 32) to write:

2Rsin A = XY, 2Rsin B = WZ, 2Rsin C = YZ, 2Rsin D = WX,

2Rsin(A+D) = WY, 2Rsin(B+D) = XZ.

$\therefore WX\times YZ+WZ\times XY=WY\times XZ.$

36. Yes.

Let the perpendicular bisectors of AB and BC meet at the point O.

Then OA = OB and OB = OC, so the circle with centre O passing through A also goes through B and C.

We have to prove that this circle also passes through D, E, etc..

To do this we prove that ΔOBC ≡ ΔOCD.

We know that ΔOAB ≡ ΔOBC (by SSS-congruence: OA = OB and OB = OC by the construction of O; and AB = BC since both are sides of a regular n-gon). Moreover

$$\begin{array}{ccc}\angle OAB\hfill & =\hfill & \angle OBA\text{(base angles of the isosceles triangle}△OAB)\hfill \\ \hfill & =\hfill & \angle OCB\text{(since}△OAB\equiv △OBC)\hfill \\ \hfill & =\hfill & \angle OBC\text{(base angles of the isosceles triangle}△OBC).\hfill \end{array}$$

And ∠ABC = ∠BCD (angles of the same regular n-gon).

$\therefore$ ∠OCD = ∠BCD - ∠OCB = ∠ABC – ∠OBA = ∠OBC.

$\therefore$ ΔOBC ≡ △ OCD (by the SAS-congruence criterion).

Hence OC = OD.

Continuing in this way we can prove that OA = OD = OE, etc..

37.

(a) Yes. There are two nets for a regular tetrahedron. One of these consists of four equilateral triangles in a row (alternately right side up and right side down). In making the tetrahedron, the two sloping ends are glued together. So if we cut half a triangle from one end and stick it on the other end, we get a 4 by $\sqrt{3}$ rectangle which folds round the tetrahedron exactly without any gaps or overlaps.

(b) The usual way to wrap a cube with edges of length 2 is to take a 4 by 8 rectangular piece of wrapping paper, to position the cube centrally on an edge of length 4(1 unit from each edge), and to wrap the paper to cover a circuit of four faces. The overlapping residue can then be folded down to cover each side face, with overlaps. Hence the ratio

“area of paper” : “surface area of cube” = 8 : 6.

The same ‘wastage rate’ can be achieved with a square $4\sqrt{2}$ by $4\sqrt{2}$ piece of paper. Position the cube centrally on the paper, but turned through an angle of 45°. Then fold the four corners of the paper up each of the four side faces (with folds to tuck in four ‘wasted’ isosceles right angled triangles — one in the middle of each edge of the paper, with total wasted area 8). Finally, the four isosceles right angled triangles at the four corners of the paper can be folded in to exactly cover the top face without further overlaps.

However, one can do significantly better if the paper can be folded back on itself. Take a 2 by 14 rectangle, and think of this as being marked into seven 2 by 2 squares. Place the cube to cover the central 2 by 2 square — leaving three 2 by 2 squares sticking out each side. Fold one 2 by 6 strip up to cover the top square, before folding back along a diagonal of the top square to reveal the inside of the paper and to cover half of the top square twice before folding down to cover one side square. Do the same with the other 2 by 6 strip, with the reverse fold along the diagonal of the top square resulting in the other half of the top square being covered twice, with the tail folding down to cover the other side square. Hence the ratio

“area of paper” : “surface area of cube” = 7 : 6.

(This lovely solution was provided by Julia Gog. We do not know whether one can do better.)

38.

(i) Yes. (Cut off a corner A say with a plane passing through the three neighbours of A.)

(ii) Yes. (Cut the cube parallel to a face.)

(iii) No. (Any cross-section of the cube is a polygon. Each edge of this polygonal cross-section is the line segment formed by the intersection of the cutting plane with one of the faces of the cube. Since the cube has just six faces, the cross-section can have at most six sides.)

(iv) Yes. (Let A and G be two opposite corners — so that AG passes through the centre O of the cube. Then the plane through O which is perpendicular to AG cuts the surface of the cube in a regular hexagon.)

(v) No. (It may not be clear how to prove this easily. It is perfectly possible to obtain a pentagonal cross-section by cutting with a plane that misses exactly one face. But if the cutting plane misses exactly one face, we can be sure that it must cut both faces belonging to some “opposite pair”; and these two faces are parallel, so the resulting edges of the cross-sectional pentagon are parallel. Hence the pentagon can never be regular.)

39.

(i) No; (ii) Yes; (iii) No; (iv) Yes; (v) No.

The 12 edges of the cube come in three groups of four — namely the four parallel edges in each of three directions.

Consider the four edges in one of these parallel groups. If the Sun's rays are parallel to these four edges, then each of these edges projects to a single vertex of the outline of the shadow — which is a projection of a square.

In all other cases two of the four parallel edges in the group give rise to shadows that form part of the boundary of the shadow polygon, while the other two edges project to the inside of the shadow (and so do not feature in the boundary of the shadow). Hence each of the three groups provides two edges to the boundary of the shadow polygon, and we obtain a hexagon.

To obtain a regular hexagon, align the Sun's rays parallel to the line AG joining two opposite corners A and G of the cube, and position the shadow plane perpendicular to this direction. The three edges at these two corners A and G then project to the inside of the shadow, while the six remaining edges project to a regular hexagon. (Since there are four body diagonals like AG, there are four ways to make such a projection. In each case, the six edges of the cube that project to the regular hexagon form a non-planar hexagon on the surface of the cube, that zig-zags its way round the polyhedron like a ‘wobbly equator’, turning alternately left and right each time it reaches a vertex. Such a closed circuit on a regular polyhedron is called a Petrie polygon — named after John Flinders Petrie (1907—1972), son of the famous Egyptologist Flinders Petrie).