III. Word Problems

All the evidence suggests that the shapes of reality are mathematical.

George Steiner (1929– )

The previous chapter focused on aspects of the arithmetic of pure numbers - mostly without any surrounding context. However, our mathematical experience does not begin with pure numbers. At school level, mathematical concepts, and the reasoning we bring to understanding and using them, have their roots in language. And in real life, every application of mathematics starts out with a situation which is described in words, and which has to be reformulated mathematically before we can begin to calculate, and to draw meaningful mathematical conclusions. Word problems play an important, if limited, role in helping students to appreciate, and to handle the subtleties involved in

the art of using the mathematics we know
to solve problems given in words.

This art of using mathematics involves two distinct - but interacting - processes, which we refer to here as “simplifying” and “recognising structure”.

• To identify the mathematical heart of a problem arising in the real world, one may first have to simplify - that is, to side-line details that seem unimportant or irrelevant, and then simplify as much as possible without changing the underlying problem (e.g. by replacing some awkward feature by a different quantity which is easier to measure, or by an approximation which is easier to work with).

This “simplifying” stage is well-illustrated by the tongue-in-cheek title of the classic textbook Consider a spherical cow ... by John Harte (1985):

Milk production at a dairy farm was low, so [... ] a multidisciplinary team of professors was assembled. [... After] two weeks of intensive on-site investigation [... ] the farmer received the write up, and opened it to read [... ] “Consider a spherical cow . . . ”.

The point to emphasise here is that the judgements needed when “simplifying” are subtle, depend on an understanding of the particular situation being modelled, and may lead to a model which at first sight seems to be counterintuitive, but which may not be as silly as it seems - and which therefore needs to be explained sensitively to non-mathematicians.

In contrast word problems by-pass the “simplifying” stage, and focus instead on “recognising structure”: they present the solver with a problem which is already essentially mathematical, but where the inner structure is contextualised, and is described in words. All the solver has to do is to interpret the verbal description in a way that extracts the structure just beneath the surface, and to translate it into a familiar mathematical form. That is, word problems are designed to develop facility with the process of “recognising structure”, while avoiding the complication of expecting students to make modelling judgements of the kind required by the subtler “simplifying” process.

Because word problems focus on the second process of “recognising structure”, they tend to incorporate the relevant mathematical structure isomorphically. The underlying structure still needs to be identified and interpreted, but the interpretations are likely to be standard, with no need for imaginative assumptions and simplifications before the structure can be discerned. For example, if a problem in primary school refers to an unknown number of “sweets” to be “shared” between six children, then the collection of “sweets” is isomorphic to a pure number (the number of sweets); and the act of “sharing” is a thinly veiled reference to numerical division.

The story in a word problem may be a purely mathematical problem in disguise. But the art of identifying the correspondence between

the data given in the story line, and

the mathematical entities to which they correspond and

and between

the actions in the story line, and

the corresponding mathematical operations on those mathematical entities

is non-trivial, and has to be learned the hard way. The first problem below illustrates the remarkable variety of instances of even the simplest subtraction, or difference.

As in Chapters 1 and 2 the “essence of mathematics” is to be found in the problems themselves. Some discussion of this “essence” is presented in the text between the problems; but most of the relevant observations are either to be found in the solutions (or in the Notes which follow many of the solutions), or are left for readers to extract for themselves.

3.1. Twenty problems which embody “3 — 1 = 2”

The answer to every one of the questions in Problem 78 is the same - at least, as a ‘pure number’. The goal is therefore not to “solve” each problem, but to distinguish between, and to reflect upon, the different ways in which the very simple mathematical structure “3 — 1 = 2” turns out to be the relevant “model” in each case.

Problem 78

(a) I was given three apples, and then ate two of them. How many were left?

(b) A barge-pole three metres long stands upright on the bottom of the canal, with one metre protruding above the surface. How deep is the water in the canal?

(c) Tanya said: “I have three more brothers than sisters”. How many more boys are there in Tanya’s family than girls?

(d) How many cuts do you have to make to saw a log into three pieces?

(e) A train was due to arrive one hour ago. We are told that it is three hours late. When can we expect it to arrive?

(f) A brick and a spade weigh the same as three bricks. What is the weight of the spade?

(g) The distance between each successive pair of milestones is 1 mile. I walk from the first milestone to the third one. How far do I walk?

(h) The arithmetic mean (or average) of two numbers is 3. If half their difference is 1, what is the smaller number?

(i) The distance from our house to the train station is 3 km. The distance from our house to Mihnukhin’s house along the same road is 1 km. What is the distance from the station to Mihnukhin’s house?

(j) In one hundred years’ time we will celebrate the tercentenary of our university. How many centuries ago was it founded?

(k) In still water I can swim 3 km in three hours. In the same time a log drifts 1 km downstream in the river. How many kilometres would I be able to swim in the same time travelling upstream in the same river?

(l) December 2^nd fell on a Sunday. How many working days preceded the first Tuesday of that month?⁴

⁴ This question is historically correct. In 1946, in the Soviet Union, when these problems were formulated, Saturday was a working day.

(m) I walk with a speed of 3 km per hour. My friend is some distance ahead of me, and is walking in the same direction pushing his broken down motorbike at 1 km per hour. At what rate is the distance between us diminishing?

(n) A trench 3 km long was dug in a week by three crews of diggers, all working at the same rate as each other. How many such crews would be needed to dig a trench 1 km shorter in the same time?

(o) Moscow and Gorky are cities in adjacent time zones. What is the time in Moscow when it is 3 pm in Gorky?⁵

(p) An old ‘rule-of-thumb’ for anti-aircraft gunners stated that: To hit a plane from a stationary anti-aircraft gun, one should aim at a point exactly three plane’s lengths ahead of the moving plane. Now suppose that the gun was actually moving in the same direction as the plane with one third of the plane’s speed. At what point should the gunner aim his fire?

(q) My brother is three times as old as I am. How many times my present age was his age when I was born?

(r) I add 1 to a number and the result is a multiple of 3. What would the remainder be if I were to divide the original number by 3?

(s) It takes 1 minute for a train 1 km long to completely pass a telegraph pole by the track side. At the same speed the train passes right through a tunnel in 3 minutes. What is the length of the tunnel?

(t) Three trams operate on a two-track route, with trams travelling in one direction on one track and returning on the other track. Each tram remains a fixed distance of 3 km behind the tram in front. At a particular moment one tram is exactly 1 km away from the tram on the opposite track. How far is the third tram from its nearest neighbour?

3.2. Some classical examples

Problem 79 Katya and her friends stand in a circle in such a way that the two neighbours of each child are of the same gender. If there are five boys in the circle, how many girls are there?

Problem 80 How much pure water must be added to a vat containing 10 litres of 60% solution of acid to dilute it into a 20% solution of acid?

⁵ Gorky (now the city of Nizhny Novgorod) lies to the east of Moscow.

Problem 81 A mother is $2\genfrac{}{}{0.1ex}{}{1}{2}$ times as old as her daughter. Six years ago the mother was 4 times as old as her daughter. How old are mother and daughter?

Problem 82

(a) Tom takes 2 hours to complete a job. Dick takes 3 hours to complete the same job. Harry takes 4 hours to complete the same job. How long would they take to complete the job, all working together (at their own rates)?

(b) Tom and Dick take 2 hours to complete a job working together. Dick and Harry take 3 hours to complete the same job. Harry and Tom take 4 hours to complete the same job. How long would they take to complete the same job, all working together?

Problem 83 A team of mowers had to mow two fields, one twice as large as the other. The team spent half-a-day mowing the larger field. After that the team split: one half continued working on the big field and finished it by evening; the other half worked on the smaller field, and did not finish it that day - but the remaining part was mowed by one mower in one day. How many mowers were there?

3.3. Speed and acceleration

Problem 84 Jack and Jill went up the hill, and averaged 2 mph on the way up. They then turned round and went straight back down by the same route, this time averaging 4 mph. What was their average speed for the round trip (up and down)?

Problem 85

(a) (i) A cycling road race requires one to complete 3 laps of a long road circuit. On the first lap I average 40 km/h; on the second lap I average 30 km/h; and on the third lap I only average 20 km/h. What is my average speed for the whole race?

(ii) I cycle for 3 hours round the track of a velodrome, averaging 40 km/h for the first hour, 30 km/h for the second hour, and 20 km/h for the final hour. What is my average speed over the whole 3 hours?

(b) Two cyclists compete in an endurance event.

(i) The first cyclist pedals at 60 km/h for half the time and then at 40 km/h for the other half. The second cyclist pedals at 60 km/h for half of the total distance and then at 40 km/h for the remaining half. Who wins?

(ii) In a two hour event, the first cyclist pedals at u km/h for the first hour and then at v km/h for the second hour. The second cyclist pedals at u km/h for half of the total distance and then at v km/h for the remaining half. Who wins?

(c) (i)Apply your argument in (b)(ii) to prove an inequality between

* the arithmetic mean

$$\begin{array}{c}\genfrac{}{}{0.1ex}{}{u+v}{2}\hfill \end{array}$$

of two positive quantities u, v, and

* the harmonic mean

$$\begin{array}{c}\genfrac{}{}{0.1ex}{}{2}{\genfrac{}{}{0.1ex}{}{1}{u}+\genfrac{}{}{0.1ex}{}{1}{v}}.\hfill \end{array}$$

(ii) Give a purely algebraic proof of your inequality in (i).

Problem 86 A train started from a station and, moving with a constant acceleration, covered a distance of 4 km, finally reaching a speed of 72 km/hour. Find the acceleration of the train, and the time taken for the 4 km.

Problem 87 (Average speed of an accelerating car) A typical car (and maybe also a typical train!) does not move with constant acceleration. Starting from a standstill, a car moves through the gears and “accelerates more quickly” in lower gears, when travelling at lower speeds, than it does in higher gears, when travelling at higher speeds. Use this empirical fact to prove that the average speed of a car accelerating from rest is more than half of its final measured speed after the acceleration.

3.4. Hidden connections

Problem 88 Two old women set out at sunrise and each walked with a constant speed. One went from A to B, and the other went from B to A. They met at noon, and continuing without a stop, they arrived respectively at B at 4 pm and at A at 9 pm. At what time was sunrise on that day?

Problem 89 A paddle-steamer takes five days to travel from St Louis to New Orleans, and takes seven days for the return journey. Assuming that the rate of flow of the current is constant, calculate how long it takes for a raft to drift from St Louis to New Orleans.

Problem 90 [From Paolo dell’Abbaco’s Trattato d’aritmetica] “From here to Florence is 60 miles, and there is one who walks it in 8 days [in one direction], another in five days [in the opposite direction]. It is asked: Departing at the same time, in how many days will they meet?”

Problem 91 Notice that in Problem 88 sunrise occurs $t=\sqrt{4\times 9}$ hours before noon, and that $\sqrt{4\times 9}$ is the geometric mean of 4 and 9. Once this is pointed out, can you reformulate your solution to Problem 88 to solve a more general problem?

3.5. Chapter 3: Comments and solutions

78.

(a) This is the simplest form of all: 3 are given; 2 are removed; so what remains is “3 - 2”.

(b) Length is a continuous quantity (rather than discrete quantity - like apples, or sweets). So we have to perceive a line segment (partially hidden beneath the water) rather than a quantity. We know the total length of the pole, and the length of the protruding portion. We can then infer the hidden length by subtraction.

Note: This kind of “geometrical subtraction” is needed in many contexts (such as: proving the general formula

$$\begin{array}{c}\genfrac{}{}{0.1ex}{}{1}{2}(\text{base}\times \text{height})\hfill \end{array}$$

for the area of a triangle, or showing that the area of the parallelogram spanned by the origin and vectors (a,b), (c,d) is |ad — bc|, or in Euclid’s Elements, Book I, Proposition 2). The idea can be strangely elusive

(c) The situation here is significantly different. We start with Tanya’s brothers and sisters, and finish with the related, but different, notion of “boys and girls in Tanya’s family”. The “3” does not represent anything specific: it is a numerical excess (of Tanya’s brothers over her sisters). In contrast, the “1” seems to represent Tanya herself, who needs to be taken into account when we switch from the initial scenario (Tanya’s brothers and sisters) to the final question about “boys and girls in Tanya’s family”.

(d) No doubt this can be solved by drawing a picture in which the underlying structure is only appreciated superficially. But beneath the surface, it seems to be a much more abstract representation of “3 — 1 = 2”. The “3” certainly stands for the “three pieces”. But the operation “—1” is not obviously subtracting anything.

The relevant observation is simply that, starting from one end, pieces and cuts alternate. So if we ignore the starting end, there must be the same number of pieces and cuts - except that if we start with a log (rather than a long tape from which we are cutting off pieces), the “last cut” is “the other end of the log”, which has already been cut - so does not need to be cut again, and this obliges us to subtract 1 from the number of pieces to get the number of additional cuts.

Note: This idea arises in many settings, and is sometimes referred to as “Posts and gaps”. Sometimes one has to “subtract 1” as here; at other times one has to “add 1” (e.g. when counting the number of “posts”, if we are given the number of “gaps”, or “fence panels”).

(e) Once again we are dealing with a continuous quantity - time. On this occasion the problem invites us to construct a (horizontal?) diagram very like the pole and the water in (b). But this time, the origin is likely to be perceived as “now”, with a time-line stretching back 1 hour (to the left?) to mark the time when the train was due, and then moving on 3 hours (to the right), passing through the origin to a point 2 hours from now.

(f) It is unclear how young children might tackle this with “bare hands”. However, at some stage one would like them to see the words as evoking the powerful (and rather different) underlying image of “scales”, or an imagined “equation”. Once one ‘sees’ the two pans of a balance, with a “brick and a spade” on one side being balanced by “three bricks” on the other, one can imagine removing “1 brick” from each pan to be left with the spade on its own balanced by “3 — 1 = 2” bricks.

(g) This is in some ways a simpler version of “Posts and gaps”. However, there is an additional step - since we are no longer merely counting the gaps, but translating this counting number into a distance. In this instance, if one does not pay too much attention to the extra step, both give an answer “2”.

Note: The impact of the extra step (switching from discrete counting number to continuous distance) can be seen more clearly in the number of errors made when students are faced with such variations as:

“There are ten lamp posts in my street, and they are 70 metres apart.
How far is it from the first to the last?”

(h) One suspects that this superficially simple problem would prove inaccessible unless pupils have learned to represent word problems diagrammatically, or have already mastered simple algebra. The “3” and the “1” do not represent real-world entities; so one has to be prepared to mark a “3” on a number line, and to interpret “average” as indicating that the two unknown quantities lie equally spaced either side of it. “Half their difference” is then staring one in the face, and the smaller number (to the left) is clearly “3 — 1”.

Note: This may look rather like the overdue train in part (e). We suggest that it is significantly different.

(i) The story line clearly adds layers of difficulty which we tend to overlook. Learning to “recognise structure” and to translate words into a form that allows one to calculate is clearly a non-trivial (and neglected) art. Distances in kilometres may convey something more active than the given “length of a barge pole” in part (b), or the reported times in part (e), even if the diagram - once constructed - is very similar (provided of course that “along the same road” is interpreted as meaning “in the same direction”).

Note: Consider the following item from an authoritative international study TIMSS 2011⁶ for pupils aged around 14:

“Points A, B, and C lie in a line and B is between A and C. If AB = 10 cm and BC = 5.2 cm, what is the distance between the midpoints of AB and BC?

A 2.4 cm B 2.6 cm C 5.0 cm D 7.6 cm”

The question is a multiple choice question, and the options represent different ways of failing to translate the words into a suitable diagram, or to interpret them correctly. The sampling (in around 50 countries) was done very carefully. So the different success rates in different countries (of which 5 are given below) suggest that some systems give far too little attention to helping pupils to learn the relevant underlying art:

Russia 60%, Hungary 41%, Australia 40%, England 38%, USA 29%

(j) The story line here has a different flavour. The time-line is the reverse of the overdue train in part (e), yet the measuring in centuries may make the question less immediately accessible. It may be harder to “feel” a natural interpretation, and so success may be more dependent on a willingness to represent the given information abstractly.

(k) Up to now, all problems were either static, or involved motion in a directly accessible form. Here we meet for the first time the need to interpret the words in terms of “relative motion”. I may get as far as picturing myself swimming upstream in the river (against the current); but neither the “3” nor the “1” have any direct relevance to me at that time: they have to be imagined (as “me swimming in still water”, and “the effect of the river in slowing me down”), and then interpreted in a way that allows a simple calculation.

(l) The words need to be interpreted from a very different kind of story line: if the 2^nd is on a Sunday, then the “first Tuesday” must be the 4^th. There are therefore “3” days preceding the first Tuesday - of which just “1” (Sunday) is not a working day. All that is needed is “counting”; but the wording requires a different kind of interpretation.

⁶ Trends in International Mathematics and Science Study, https://timssandpirls.bc.edu/timss2011/index.html

(m) This is another example of “relative velocities” - but the need for subtraction no longer arises because of travel in opposite directions. In some ways it is simpler than (k); yet the final question relates to something less tangible - namely the “rate at which the distance between us is diminishing”. Before one understands relative velocities, one has to choose to focus on “what happens during each hour”, where I cover 3 km and my friend covers only 1 km, with the difference “3 — 1” measuring nothing tangible, but being the amount by which our separation decreases during that hour.

(n) Here it is even more important to translate the given information about “rates” into concrete form. “In the same time” should trigger the questions: “How many crews would be needed for (3 — 1) km?”, which may then trigger the question: “How long a ditch could 1 crew dig in the same time?”. Whatever approach is taken, it is worth asking “If the answer is “3 — 1”, what exactly is the “3”? And what is the “1”?”

(o) This does presume a degree of fluency in “modelling” the given information (e.g. knowing that “adjacent time zones” almost always differ by 1 hour, and that the Earth’s rotation is from West to East, so that the Sun “rises” first in the East). On the surface, if the “3” is interpreted as the “3” in 3 pm, then the calculation “3 — 1” is an adjustment, rather than a strict subtraction (the 3 pm and the “1 hour time difference” are not really comparable quantities with which one can do arithmetic). At a deeper level one can turn both the “3” and the “1” into comparable quantities, and so justify the arithmetic.

(p) Here we face full-on what has been lurking just below the surface of certain earlier problems (such as (n)) - namely that we are dealing with (approximate) proportion. We ignore marginal differences in the distance to a distant object at slightly different angles, and compare on the one hand

distances along the plane’s path (measured in “plane’s lengths”), and

and on the other hand

the time taken by the anti-aircraft fire to reach the plane.

This comparison has to be made because of the added complication of the change in the relative velocity of the gun and the plane.

The given rule of thumb specifies the direction in which a stationary gunner should aim; and the reported (unrealistically fast, yet presumed to be steady) motion of the gun introduces a 2-dimensional (vector) version of “swimming upstream” - which suggests the expected answer “two thirds of 3 plane lengths”, so that “1” of the “3 plane’s lengths” is compensated by the gun’s motion.

(q) A solution is again dependent on representing the given information in some form. Whether or not one uses symbols, the wording invites the solver to use “my present age (in years)” as a preferred unit, and to represent “my brother’s present age” as “3” of these basic units. The “3 — 1” then represents how much older he is than I am - and hence how old he was when I was born, or “how many times my present age he was when I was born”.

Note: The choice of unit may conceal the fact that the question and solution are rooted in ratio and proportion.

(r) The subtraction “3 — 1” here only makes sense in arithmetic (mod 3), where “remainder 0 (on division by 3)” and “remainder 3” are in some sense equivalent. Although the “1” in “3 — 1” may be taken to be the “1” that is added to the original number in the question, the “3” is an invented remainder - which is interchangeable with “0” when working (mod 3).

(s) In the usual answer “3 — 1”, one could argue that the “1” does appear in the question, but that the “3” does not. Again we are dealing with proportion, where the times taken (at constant speed) are proportional to lengths, or to distances travelled. First the given length (1 km) of the train and the given time (1 minute) in relation to the “pole by the track side” gives a simple constant of proportion (= 1), which allows us to translate the time taken into the distance travelled (and hence to calculate speed). If we re-interpret the “endpoint of the tunnel” as being just like another “pole by the track side”, then it takes 1 minute for the train to emerge from the tunnel, and hence “3 — 1 minutes” for the front buffers of the train to cover the full length of the tunnel, which is therefore “(3 — 1) km” long (given that the constant of proportionality = 1).

(t) It is not clear how to interpret the “3” and the “1” in “3 — 1” without getting one’s hands dirty with the configuration described. In particular, somewhere along the line one has to interpret the “3 km” separation between trams as revealing that the total length of the track is 9 km, and hence that each of the two parallel stretches of track is 4.5 km.

The “tram on the opposite track” is travelling in the opposite direction, is 1 km away, and is “3 km ahead” (or ”3 km behind”); so one of these trams is 1 km from the end of the track, and the other is on the other track and 2 km from one end (travelling in the opposite direction). There are exactly two possible configurations - each arising from the other if we reverse the direction of travel. By choosing the direction of travel (or by allowing “negative speed”) we may assume that tram A is 2 km from the same end of the track and that tram B in front of it is 1 km beyond the end of the track on the opposite side. Tram C is 3 km ahead of B, and hence 4 km down that 4.5 km stretch of track (so has not yet “turned the corner”). Hence it is 1 km closer to its nearest neighbour (A) than it is to B.

79. If we ignore the first sentence, then there could be zero girls (and five boys). But the first sentence guarantees that there is at least one girl (“Katya and her friends”). So boys and girls must alternate, giving rise to 5 girls.

80. The problem requires a degree of “modelling” in that “60% solution of acid” suggests that the initial ratio

$$\begin{array}{c}\text{“acid}:\text{water”}=60:40.\hfill \end{array}$$

Hence the initial 10 litres is made up of 4 litres of water and 6 litres of acid. Adding water does not change the amount of acid; so we want 6 litres to be 20% of the final mix - which must therefore be 30 litres. Hence we should add 20 litres.

81. The difference in ages is $\genfrac{}{}{0.1ex}{}{3}{2}\times d$, where d is the daughter’s age in years. Six years ago the difference was three times the daughter’s age, which was then d — 6 years. Hence

$$\begin{array}{c}3(d-6)=\genfrac{}{}{0.1ex}{}{3}{2}\times d,\hfill \end{array}$$

so d = 12.

82.

Note: Underpinning all such problems is the “unitary method”, which here comes into its own. It is an essential tool, which is scarcely taught, and not sufficiently practised. (As a result many students mindlessly translate “Tom takes 2 hours” as “T = 2”, etc..)

(a) When they all work together we need to know not how long each takes to do the job, but at what rate each contributor works.

Tom does the job in 2 hours, so works at the rate of “$\genfrac{}{}{0.1ex}{}{1}{2}$ of a job in 1 hour”. Dick works at a rate of “$\genfrac{}{}{0.1ex}{}{1}{3}$ of a job in 1 hour”, and Harry works at the rate of “$\genfrac{}{}{0.1ex}{}{1}{4}$ of a job in 1 hour”.

So working together, they can manage

$$\begin{array}{c}\genfrac{}{}{0.1ex}{}{1}{2}+\genfrac{}{}{0.1ex}{}{1}{3}+\genfrac{}{}{0.1ex}{}{1}{4}=\genfrac{}{}{0.1ex}{}{13}{12}\hfill \end{array}$$

of a job in 1 hour.

Hence, to complete 1 job they require $\genfrac{}{}{0.1ex}{}{12}{13}$ of an hour.

(b) As in part (a), we need to know the rate at which each man works.

Suppose that Tom completes the fraction t of a job in 1 hour, that Dick completes the fraction d of a job in 1 hour, and that Harry completes the fraction h of a job in 1 hour.

Then in 1 hour, working together, they complete (t + d + h) jobs; so to complete 1 job takes them

$$\begin{array}{c}\genfrac{}{}{0.1ex}{}{1}{t+d+h}\text{hours.}\hfill \end{array}$$

We therefore need to find “t + d + h”.

In 1 hour, Tom and Dick together complete t + d jobs. And we are told that in 2 hours they complete 1 job, so $t+d=\genfrac{}{}{0.1ex}{}{1}{2}$. Similarly $d+h=\genfrac{}{}{0.1ex}{}{1}{3}$, and $h+t=\genfrac{}{}{0.1ex}{}{1}{4}$.

Adding yields

$$\begin{array}{c}2(t+d+h)=\genfrac{}{}{0.1ex}{}{1}{2}+\genfrac{}{}{0.1ex}{}{1}{3}+\genfrac{}{}{0.1ex}{}{1}{4},\hfill \end{array}$$

so

$$\begin{array}{c}t+d+h=\genfrac{}{}{0.1ex}{}{13}{24}.\hfill \end{array}$$

Hence the time required for Tom, Dick and Harry to finish 1 job working together is

$$\begin{array}{c}\genfrac{}{}{0.1ex}{}{1}{t+d+h}=\genfrac{}{}{0.1ex}{}{24}{13}\hfill \end{array}$$

hours.

Note: Alternatively, one might let Tom take T hours to complete 1 job, Dick take D hours to complete 1 job, and Harry take H hours to complete 1 job. Then

$$\begin{array}{c}t=\genfrac{}{}{0.1ex}{}{1}{T},d=\genfrac{}{}{0.1ex}{}{1}{D},h=\genfrac{}{}{0.1ex}{}{1}{H}.\hfill \end{array}$$

83. Imagine the two fields as strips of equal width - with the larger field twice as long as the smaller one.

The large strip was completely mowed in two parts:

(i) by the whole team working for the first half day, and

(ii) by half the team working for the second half of the day.

Hence the whole team mowed two thirds of the large field and the half team mowed the remaining one third.

So the half team, who worked on the smaller field, mowed the equivalent of one third of the larger field - that is, two thirds of the (half-size) smaller field. Therefore the remaining one third of the smaller field was mowed by a single man on the second day.

The previous two thirds of the smaller field (twice as much) was mowed in half a day (half the time), so must have required 4 (= four times as many) men. So the whole team contained 8 mowers.

Alternatively, we may suppose that there are 2n mowers (since the team is said to split into two halves), and that each mower mows at the rate of “r large fields per day”.

The total work done in completing the larger field is then

(i) $(2n\times r)\times \genfrac{}{}{0.1ex}{}{1}{2}$ in the morning and

(ii) $(n\times r)\times \genfrac{}{}{0.1ex}{}{1}{2}$ in the afternoon

where each part is equal to

$$\begin{array}{c}(\text{number of men}\times \text{rate of working})\times \left(\text{length of time worked}\right).\hfill \end{array}$$

That is $\genfrac{}{}{0.1ex}{}{3}{2}nr$. So $\genfrac{}{}{0.1ex}{}{3}{2}nr=1$.

The total work done on the smaller field is

(i) $(n\times \mathit{r})\times \genfrac{}{}{0.1ex}{}{1}{2}$ in the afternoon of the first day, and

(ii) (1 × r) on the second day.

That is $\genfrac{}{}{0.1ex}{}{n+2}{2}\times r$. So $\genfrac{}{}{0.1ex}{}{n+2}{2}\times r=\genfrac{}{}{0.1ex}{}{1}{2}$ (since the smaller field is half the larger field). Hence $\genfrac{}{}{0.1ex}{}{3}{2}n=n+2$.

84. The words “average speed” often provoke an unthinking assumption that one is simply being asked to find the average of the “speed numbers” given in the problem. A moment’s thought should remind us that the “average speed” for a journey is not equal to the “average of the various speeds taken as pure numbers”; it is equal to

$$\begin{array}{c}\left(\mathrm{the\; total\; distance\; travelled}\right)÷\left(\mathrm{the\; total\; time\; taken}\right).\hfill \end{array}$$

If the distance up the hill is m miles, then the climb takes $\genfrac{}{}{0.1ex}{}{m}{2}$ hours, and the descent takes $\genfrac{}{}{0.1ex}{}{m}{4}$ hours. The total distance for the round trip is 2m miles, so Jack and Jill’s average speed is

$$\begin{array}{c}\genfrac{}{}{0.1ex}{}{2m}{\genfrac{}{}{0.1ex}{}{3m}{4}}=\genfrac{}{}{0.1ex}{}{8}{3}\text{mph}.\hfill \end{array}$$

Note: We first meet averages for discrete quantities, or whole numbers, where the goal is to replace a collection of quantities, or numbers, by a single representative statistic. If n quantities contribute equally, then each contributes exactly ${\left(\genfrac{}{}{0.1ex}{}{1}{n}\right)}^{\mathrm{th}}$ to the average.

One way of looking at this is to represent each of the quantities being averaged in a bar chart - as rectangles of width 1, and with height corresponding to the quantity represented. “Adding all the quantities and dividing by n” is then the same as “calculating the total area under the graph and then dividing by the total length of the interval”. In other words, we have replaced the complicated bar chart by a constant function (or a single rectangle), which has the same domain as the bar chart, and which has the same area under it (or integral) as the more complicated bar chart.

More generally, given a function y = f(x) defined for values of x in the interval [a,b], its average f_[a,b] (over the interval [a,b]) is defined to be

$$\begin{array}{c}{f}_{[a,b]}=\genfrac{}{}{0.1ex}{}{{\displaystyle \underset{a}{\overset{b}{\int }}}f\left(x\right)dx}{|b-a|}.\hfill \end{array}$$

When we talk about “average speed”, we are thinking of speed changing as a function of time; and the total distance covered in any given time interval [a, b] is equal to the area under the graph. We want a single “average speed” v_[a,b] (a constant function) that would cover the same distance in the same time as the more complicated reality of varying speed. That is,

• we consider the speed v(t) as a function of time t,
• then we integrate with respect to t over the specified time interval [a,b], and
• finally we divide the result by the total length $|b-a|$ of the time interval:

$$\begin{array}{c}{v}_{[a,b]}=\genfrac{}{}{0.1ex}{}{{\displaystyle \underset{a}{\overset{b}{\int }}}v\left(t\right)dt}{|b-a|}.\hfill \end{array}$$

In Problem 84 the walking speed is misleadingly given in terms of “up” and “down” - which represent the first half distance travelled, and the second half distance travelled. The careful solver knows that s/he has to find “total distance travelled” and divide by “total time taken”; but s/he may not notice that s/he has in fact reinterpreted the given information so that speed is seen as a function of time (rather than of distance).

85.

Let the distance covered on each lap be m km. Then the first lap takes me $\genfrac{}{}{0.1ex}{}{m}{40}$ hours; the second lap takes me $\genfrac{}{}{0.1ex}{}{m}{30}$ hours; the third lap takes me $\genfrac{}{}{0.1ex}{}{m}{20}$ hours. So the total time taken for the three laps is

$$\begin{array}{c}\genfrac{}{}{0.1ex}{}{m}{40}+\genfrac{}{}{0.1ex}{}{m}{30}+\genfrac{}{}{0.1ex}{}{m}{20}=\genfrac{}{}{0.1ex}{}{13m}{120}\text{hours}.\hfill \end{array}$$

Hence my average speed for the race covering 3m km is

$$\begin{array}{c}\genfrac{}{}{0.1ex}{}{3m}{\left(\genfrac{}{}{0.1ex}{}{13m}{120}\right)}=\genfrac{}{}{0.1ex}{}{360}{13}\text{km/h}.\hfill \end{array}$$

Note: Alternatively, because the two factors of m in the numerator and the denominator cancel each other, this answer may be formulated as the harmonic mean of the given speeds:

$$\begin{array}{c}\genfrac{}{}{0.1ex}{}{3}{[\genfrac{}{}{0.1ex}{}{1}{40}+\genfrac{}{}{0.1ex}{}{1}{30}+\genfrac{}{}{0.1ex}{}{1}{20}]}.\hfill \end{array}$$

(ii) In the first hour I cycle 40 km; in the second hour I cycle 30 km; in the third hour I cycle 20 km. So in the three hours I cycle 40 + 30 + 20 = 90 km. So my average speed is 30 km/h.

Note: Alternatively, as long as the three time intervals t are equal, we land up with t as a factor in both the numerator and the denominator, so these common factors cancel out, and the answer is simply the arithmetic mean of the given speeds:

$$\begin{array}{c}\genfrac{}{}{0.1ex}{}{20+30+40}{3}.\hfill \end{array}$$

(b) (i) The second cyclist spends more time cycling at 40 km/h than at 60 km/h, so the first cyclist spends more time cycling at the higher speed. Hence the first cyclist wins

(ii) Again (unless u = v), the first cyclist spends more time cycling at the higher speed. Hence the first cyclist wins.

(c) (i) As in part (a)(ii), the first cyclist finishes with average speed $\genfrac{}{}{0.1ex}{}{u+v}{2}$ km/h; and as in part (a)(i) the second cyclist finishes with average speed

$$\begin{array}{c}\genfrac{}{}{0.1ex}{}{2}{[\genfrac{}{}{0.1ex}{}{1}{u}+\genfrac{}{}{0.1ex}{}{1}{v}]}\text{km/h}.\hfill \end{array}$$

Hence, part (b)(ii) shows that

$$\begin{array}{c}\genfrac{}{}{0.1ex}{}{u+v}{2}\ge \genfrac{}{}{0.1ex}{}{2}{[\genfrac{}{}{0.1ex}{}{1}{u}+\genfrac{}{}{0.1ex}{}{1}{v}]}=\genfrac{}{}{0.1ex}{}{2uv}{u+v}.\hfill \end{array}$$

(ii) If we rearrange the required inequality

$$\begin{array}{c}\genfrac{}{}{0.1ex}{}{u+v}{2}\ge \genfrac{}{}{0.1ex}{}{2uv}{u+v},\hfill \end{array}$$

then we see that it is equivalent to proving that ${(u+v)}^2\ge 4uv$. This suggests that we should start with the universally true statement:

$$\begin{array}{c}{(u-v)}^2\ge 0\text{for all}u,v\ge 0.\hfill \end{array}$$

Adding 4uv to both sides yields ${(u+v)}^2\ge 4uv$.

Multiplying both sides by the non-negative quantity $\genfrac{}{}{0.1ex}{}{1}{2(u+v)}$ then gives the required inequality.

86. The only “modelling” required here is to translate the problem using the standard equations of kinematics. For motion from rest we have

(i) v = at, where t is the time, a is the uniform acceleration, and v the final speed, and

(ii) $s=\genfrac{}{}{0.1ex}{}{1}{2}a{t}^2$ where s is the distance travelled.

There is a question as to what units we should use. For the moment we stick to measuring v in km/h as given, s in km, t in hours, and a in the (unfamiliar) units of km/h²: so 72 = at and $4=\genfrac{}{}{0.1ex}{}{1}{2}a{t}^2$.

Dividing the second equation by the first gives $\genfrac{}{}{0.1ex}{}{1}{18}=\genfrac{}{}{0.1ex}{}{1}{2}t$, so $t=\genfrac{}{}{0.1ex}{}{1}{9}$ hours (= 400 seconds).

Substituting in the first equation gives a = 72 x 9 km/h² ( $=\genfrac{}{}{0.1ex}{}{1}{20}$ m/sec²).

Note: Equations (i) and (ii) can be summarised as saying that, under uniform acceleration a, the distance travelled is $s=\left(\genfrac{}{}{0.1ex}{}{1}{2}at\right)\times t$. Hence the average speed for the complete journey is equal to exactly half of the final speed v = at.

In general, those tackling the problem may agree that the familiar units of speed and distance do not give us a very good gut feeling for the scale of acceleration. If we measure acceleration in km/h², then we get huge numbers for acceleration which one cannot easily relate to. And if we switch to m (metres), m/sec, and m/sec², then we get rather small numbers for the acceleration, which again convey relatively little.

[The original (Russian) version of this problem had the train travelling 2.1 km and reaching a speed of 54 km/h. This produces a nice answer for the time taken, but a relatively inscrutable answer for the acceleration. So we have changed the parameters.]

87.

“We explain why, when a vehicle accelerates from 0 to 20 mph, its average speed is more than 10 mph. In general, the average speed of an accelerating vehicle is more than half the final speed after the acceleration.

Consider first the case when the acceleration is constant: this means that the graph which represents the speed of the vehicle as a function of time is a straight line:

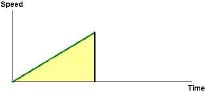
In that case, the distance travelled is equal to the area under the graph. But from the formula for the area of a triangle we know that this area equals the area of the rectangle with the same base and half the height of the triangle:

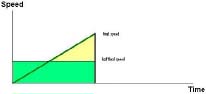
This means that the average speed in that case is exactly half of the final (maximum) speed.

But a car has higher acceleration in lower gears, that is, at smaller speeds. Therefore the graph of speed as a function of time is concave, and the area under the graph is greater than in the case of constant acceleration. Hence, while reaching the same speed, the car travels further and its average speed is higher:

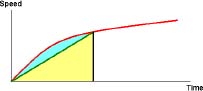
We come to the conclusion that the average speed of an accelerating car is greater than half its speed at the end of acceleration.”

Note: The text of this solution is reproduced from the appendix to a document prepared for, and submitted to, the Crown Prosecution Service in England. This may partly explain why it contains not a single formula. It was written by a student studying economics, and the mixture of language and graphs used illustrates the typical economist’s way of thinking. Economists rarely have complete data, so they tend to rely on a combination of common sense and the basic patterns of economic variables - such as the “convexity” or “concavity” of functions. Indeed some chapters of mathematical economics could be described as outlining “the kinematics of money”, and have surprising similarities to mechanics.

88. Suppose sunrise was t hours before noon - so that the first woman covers the total distance in t + 4 hours, while the second covers the same distance in t + 9 hours.

We know nothing about the distance from A to B, so it makes sense to choose this distance as our unit.

Then the first woman’s speed is $\genfrac{}{}{0.1ex}{}{1}{t+4}$, while the second woman’s speed is $\genfrac{}{}{0.1ex}{}{1}{t+9}$ units per hour.

The relative speed of A and B (the speed with which the distance between them changes) is $\genfrac{}{}{0.1ex}{}{1}{t+4}+\genfrac{}{}{0.1ex}{}{1}{t+9}$

They meet at noon, so in t hours, the distance between them reduces from 1 unit to 0.

Hence

$$\begin{array}{c}1=t\times (\genfrac{}{}{0.1ex}{}{1}{t+4}+\genfrac{}{}{0.1ex}{}{1}{t+9});\hfill \end{array}$$

that is, t² = 36, so t = 6, and sunrise was at (12 — 6) = 6 am.

89. Let us introduce a new measure of distance - which we call a league. (Readers may know from old documents or from poetry that this was an old measure of distance for journeys, without knowing exactly how far it was; so we feel free to use it as an abstract unit of unknown size.)

To mesh distance and time, the journey from St Louis to New Orleans needs to be some multiple of 7, and the journey from New Orleans to St Louis needs to be some multiple of 5. Hence we choose the distance to be equal to 5 × 7 = 35 “leagues”.

Then the speed of the paddle-steamer upstream is:

$$\begin{array}{c}\genfrac{}{}{0.1ex}{}{35}{7}=5\text{“leagues per day”}\hfill \end{array}$$

and the speed downstream is:

$$\begin{array}{c}\genfrac{}{}{0.1ex}{}{35}{5}=7\text{“leagues per day”}.\hfill \end{array}$$

The speed of the current gets subtracted from the speed of the paddle-steamer going upstream, and gets added to the speed of the paddle-steamer going downstream; so the speed of the current is:

$$\begin{array}{c}\genfrac{}{}{0.1ex}{}{7-5}{2}=1\text{“league per day”}.\hfill \end{array}$$

Hence a raft will drift from St Louis to New Orleans in $\genfrac{}{}{0.1ex}{}{35}{1}=35$ days.

Note: This elegant solution involves the introduction of a hidden intermediate parameter, an unknown quantity which helps us reason about the problem. The parameter is apparently the distance (from St Louis to New Orleans); but it is in fact a measure of distance chosen so as to be compatible with the time taken.

The art of identifying, and choosing, relevant “hidden parameters”, and the analysis of their relation to the data, and their mutual relations, constitute an important and challenging part of the mathematical modelling process.

Notice that if we reformulate the problem in more general terms, with the paddle-steamer taking “a days” downstream and “b days” upstream, then the answer “d days” (for the time to drift downstream) happens to be the harmonic mean of the quantities “a” and “—b”:

$$\begin{array}{c}d=\genfrac{}{}{0.1ex}{}{2}{\genfrac{}{}{0.1ex}{}{1}{a}+\genfrac{}{}{0.1ex}{}{1}{-b}}.\hfill \end{array}$$

90. [This is “Problem 108” in Paolo dell’Abbaco’s Trattato d’aritmetica (c.1370), with a rough translation of the solution procedure given there courtesy of Roy Wagner.]

“Do the following: multiply 5 by 8, which makes 40. Then say thus: in 40 days one will make the trip 8 times, and the other 5 times, so both together will make the trip 13 times.

Now say: if 40 days equals 13 trips, how many days are needed [on average] for one trip? And so multiply 1 times 40, which makes 40; then divide this by 13, which makes 3 days and, $\genfrac{}{}{0.1ex}{}{1}{13}$ of a day.

And so I say that in 3 days and $\genfrac{}{}{0.1ex}{}{1}{13}$ of a day the two will come together.

And as this is done, so all similar problems are done.”

Note: The problem as stated conveys an air of reality by giving the distance “from here to Florence” in miles; but this fact is not mentioned in the solution! Instead, the solution starts by introducing a hidden parameter, measured by a dimensionless unit: a trip.

This move (to invent a natural unit of measurement) also featured in Problem 89 above and has deep mathematical reasons. Problem 89 was borrowed from an interview with Vladimir Arnold (Notices of the AMS, vol. 44, no. 4), where we read:

Interviewer: Please tell us a little bit about your early education. Were you already interested in mathematics as a child?

Arnold: [...] The first real mathematical experience I had was when our schoolteacher I.V. Morotzkin gave us the following problem [VA then formulated Problem 89].

I spent a whole day thinking on this oldie, and, the solution (based on what are now called scaling arguments, dimensional analysis, or toric variety theory, depending on your taste) came as a revelation.

The feeling of discovery that I had then (1949) was exactly the same as in all the subsequent much more serious problems - be it the discovery of the relation between algebraic geometry of real plane curves and four-dimensional topology (1970), or between singularities of caustics and of wave fronts and, simple Lie algebras and Coxeter groups (1972). It is the greed to experience such a wonderful feeling more and more times that was, and still is, my main motivation in mathematics.

Arnold refers here to scaling arguments or dimensional analysis: that is, the mathematical art of choosing and analysing the use of units of measurement. This has its origins in, and includes as an integral part, Euclid’s classical theory of proportion.

91. Suppose as before that the sun rises t hours before noon; but replace 4 pm (the time the woman starting at A arrived at B) by a pm, and replace 9 pm (the time the woman starting at B arrived at A) by b pm. Let C be the point where they meet (at noon).

Then, since each woman walks at a constant speed, we have

$$\begin{array}{c}\genfrac{}{}{0.1ex}{}{t}{a}=\genfrac{}{}{0.1ex}{}{\left|AC\right|}{\left|CB\right|}\text{(for the woman starting from}A),\hfill \end{array}$$

and

$$\begin{array}{c}\genfrac{}{}{0.1ex}{}{t}{b}=\genfrac{}{}{0.1ex}{}{\left|BC\right|}{\left|CA\right|}\text{(for the woman starting from}B).\hfill \end{array}$$

Hence

$$\genfrac{}{}{0.1ex}{}{t}{a}=\genfrac{}{}{0.1ex}{}{\left|AC\right|}{\left|CB\right|}=\genfrac{}{}{0.1ex}{}{b}{t},$$

so t² = ab.

Note: This totally unexpected result validates the choice of the unknown t as the time in hours from sunrise to noon. Not knowing its significance in advance, this choice was motivated by the observation that “noon” occurs in the problem as the only common “origin”, or reference point for time data.