V. Geometry

Those who fear to experiment with their hands will never know anything.

George Sarton (1884-1956)

Mathematical truth is not determined arbitrarily by the rules of some ‘man-made’ formal system, but has an absolute nature and lies beyond any such system of specifiable rules.

Roger Penrose (1930– )

Geometry is in many ways the most natural branch of elementary mathematics through which to convey “the essence” of the discipline.

• The underlying subject matter is rooted in seeing, moving, doing, drawing, making, etc., and so is accessible to everyone.
• At secondary level this practical experience leads fairly naturally to a semi-formal treatment of “geometry as a mental universe”
  • — a universe that is bursting with surprising facts, whose statements can be easily understood; and
  • — which has a clear logical structure, in terms of which the proofs of these facts are accessible, if sometimes tantalisingly elusive.

This combination of elusive problems to be solved and the steady accumulation of proven results has provided generations of students with their first glimpse of serious mathematics. All readers can imagine the kind of experiences which lie behind the first bullet point above: many of the problems we have already met (such as Problems 4, 19, 20, 26, 27, 28, 29, 30, 31, 37, 38, 39) do not depend on the “semi-formal treatment” referred to in the second bullet point, so can be tackled by anyone who is interested - provided they accept the importance of learning to construct their own diagrams (in the spirit of the George Sarton quotation).

The hand is the cutting edge of the mind.

Jacob Bronowski (1908-1974)

But there is a catch - which explains why the present chapter appears so late in the collection. For many problems to successfully convey “the essence of mathematics” there has to be some shared understanding of what constitutes a solution. And in geometry, many solutions require the construction of a proof. Yet many readers will never have experienced a coherent “semi-formal treatment” of elementary geometry in the spirit of the second bullet point. Hence in Problems 3(c), 18, 21, 32, 34, 36 we committed the cardinal sin of leading the reader by the nose - breaking each problem into steps in order to impose a logical structure. This may have been excusable in Chapter 1; but in a chapter explicitly devoted to geometry, the underlying challenge has to be faced head on: that is, the raw experience of the hand has to be refined to provide a deductive structure for the mind.

As in Chapter 1, some of the problems listed from Section 5.3 onwards can be tackled without worrying too much about the logical structure of elementary geometry. But in many instances, the “essence” that is captured by a problem requires that the problem be seen within an agreed logical hierarchy - a sequencing of properties, results, and methods, which establishes what is a consequence of what - and hence, what can be used as part of a solution. In particular, we need to construct proofs that avoid circular reasoning.

If B is a consequence of A, or if B is equivalent to A, then a ‘proof’ of A which makes use of B is at best dubious, and may well be a delusion.

The need to avoid such circular reasoning arose already in Problem 21 (the converse of Pythagoras’ Theorem), where we felt the need to state explicitly that it would be inappropriate to use the Cosine Rule: (see Problem 192 below).

Such concerns may explain why this chapter on geometry is the last of the chapters relating to elementary ‘school mathematics’, and why we begin the chapter with

• an apparent digression (Section 5.1), and
• an outline of elementary Euclidean geometry (Section 5.2).

Those with a strong background in geometry may choose to skip these sections on a first reading, and move straight on to the problems which start in Section 5.3. But they may then fail to see how the cumulative architecture of Section 5.2 conveys a rather different aspect of the “essence of mathematics”, deriving not just from the individual problems, but from the way a carefully crafted, systematic arrangement of simple “bricks” can create a much more significant mathematical structure.

5.1. Comparing geometry and arithmetic

The opening quotations remind us that the mental universe of formal mathematics draws much of its initial inspiration from human perception and activity - activity which starts with infants observing, moving around, and operating with objects in time and in space. Many of our earliest pre-mathematical experiences are quintessentially proto-geometrical. We make sense of visual inputs; we learn to recognise faces and objects; we crawl around; we learn to look ‘behind’ and ‘underneath’ obstructions in search of hidden toys; we sort and we build; we draw and we make; etc.. However, for this experience to develop into mathematics, we then need to

• identify certain semi-formal “objects” (points, lines, angles, triangles),
• pinpoint the key relations between them (bisectors, congruence, parallels, similarity), and then
• develop the associated language that allows us to encapsulate insights from prior experience into a coherent framework for calculation and deduction.

Too little attention has been given to achieving a consensus as to how this transition (from informal experience, to formal reasoning) can best be established for beginners in elementary geometry. In contrast, number and arithmetic move much more naturally

• from our early experience of time and quantity
• to the notation, the operations, the calculational procedures, and the rules of formal arithmetic and algebra.

Counting is rooted in the idea of a repeated unit - a notion that may stem from the ever-present, regular heartbeat that envelops every embryo (where the beat is presumably felt long before it is heard). Later we encounter repeated units with longer time scales (such as the cycles of day and night, and the routines of feeding and sleeping). The first months and years of life are peppered with instances of numerosity, of continuous quantity, of systematic ordering, of sequences, of combinations and partitions, of grouping and replicating, and of relations between quantities and operations - experiences which provide the raw material for the mathematics of number, of place value, of arithmetic, and later of ‘internal structure’ (or algebra).

The need for political communities to construct a formal school curriculum linking early infant experience and elementary formal mathematics is a recent development. Nevertheless, in the domain of number, quantity, and arithmetic (and later algebra), there is a surprising level of agreement about the steps that need to be incorporated - even though the details may differ in different educational systems and in different classrooms. For example:

• One must somehow establish the idea of a unit, which can be replicated to produce larger numbers, or multiples.
• One must then group units relative to a chosen base (e.g. 10), iterate this grouping procedure (by taking “ten tens”, and then “ten hundreds”), and use position to create place value notation.
• One must introduce “0” - both as a number in its own right, and as a placeholder for expressing numbers using place value.
• One can then use combinations and differences, multiples and sharing (and partitions), to develop arithmetic.
• At some stage one introduces subunits (i.e. unit fractions) and submultiples (i.e. multiples of these subunits) to produce general fractions; one can then use equivalence and common submultiples to extend arithmetic to fractions.
• If we restrict to decimal fractions, then our ideas of place value for integers can be extended to the right of the decimal point to produce decimals.
• At every stage we need to

  — relate these ideas to quantities,

  — require pupils to interpret and solve word problems, and

  — cultivate both mental arithmetic and standard written algorithms

  .
• Towards the end of primary school, attention begins to move beyond bare hands computation, to consciously exploit internal structure in preparation for algebra.

Our early geometrical experience is just as natural as that relating to number; but it is more subtle. And there is as yet no comparable consensus about the path that needs to be followed if our primitive geometrical experience is to be formalised in a useable way.

The 1960s saw a drive to modernise school mathematics, and at the same time to make it accessible to all. Elementary geometry certainly needed a re-think. But the reformers in most countries simply dismissed the traditional mix (e.g. in England, where one found a blend of technical drawing, Euclidean, and coordinate geometry in different proportions for different groups of students) in favour of more modern-sounding alternatives. Some countries favoured a more abstract, deductive framework; some tried to exploit motion and transformations; some used matrices and groups; some used vectors and linear algebra; some even toyed with topology. More recently we have heard similarly ambitious claims on behalf of dynamic geometry software. And although each approach has its attractions,

none of the alternatives has succeeded in helping more students to visualise, to reason, and to calculate effectively in geometrical settings.

At a much more advanced level, geometry combines

• with abstract algebra (where the approach proposed by Felix Klein (1849-1925) shows how to identify each geometry with a group of transformations), and
• with analysis and linear algebra (where, following Gauss (1777-1855), Riemann (1826-1866) and Grassmann (1809-1877), calculus, vector spaces, and later topology can be used to analyse the geometry of surfaces and other spaces).

However, these subtle formalisms are totally irrelevant for beginners, who need an approach

• based on concepts which are relatively familiar (points, lines, triangles etc.), and
• whose basic properties can be formulated relatively simply.

The subtlety and flexibility of dynamic geometry software may be hugely impressive; but if students are to harness this power, they need prior mastery of some simple, semi-formal framework, together with the associated language and modes of reasoning. Despite the lack of an accepted consensus, the experience of the last 50 years would seem to suggest that the most relevant framework for beginners at secondary level involves some combination of:

• static, relatively traditional Euclidean geometry, and
• Cartesian, or coordinate (analytic) geometry.

5.2. Euclidean geometry: a brief summary

Philosophy is written in this grand book - I mean the universe - which stands continually open to our gaze, but it cannot be understood unless one first learns to comprehend the language and to interpret the characters in which it is written. It is written in the language of mathematics, and its characters are triangles, circles, and other geometrical figures, without which it is humanly impossible to understand a single word of it; without these, one is wandering about in a dark labyrinth.

Galileo Galilei (1564-1642)

This section provides a detailed, but compressed, outline of an initial formalisation of school geometry - of a kind that one would like good students and all teachers to appreciate. It is unashamedly a semi-formal approach for beginners, not a strictly formal treatment (such as that provided by David Hilbert (1862-1943) in his 1899 book Foundations of Geometry, or in the more detailed exposition by Edwin Moise (1918-1998) Elementary Geometry from an Advanced Standpoint, published in 1963). In particular:

• we work with relatively informal notions of points, lines, and angles in the plane;
• we focus attention on certain simple issues which really matter at school level (such as how points, lines, line segments, and angles are referred to; the notion of a triangle as an ordered triple of vertices; the fact that the vertices of a quadrilateral must be labelled cyclically; etc.);
• we limit the formal deductive structure to just three central criteria, namely the criteria for congruence, for parallels, and for similarity, and show how they allow one to develop results and methods in a logical sequence.

We begin with the intuitive idea of points and lines in the plane. Two points A, B determine

• the line segment AB (with endpoints A and B), and
• the line AB (which extends the line segment AB in both directions - beyond A, and beyond B).

Three points A, B, C determine an angle ∠ABC (between the two line segments BA and BC).

We can then begin to build more complicated figures, such as

• a triangle ABC (with three vertices A, B, C; three sides AB, BC, CA; and three angles ∠ABC at the vertex B, ∠BCA at C, and ∠CAB at A),
• a quadrilateral ABCD (with four vertices A, B, C, D; and four sides AB, BC, CD, DA which meet only at their endpoints).

And so on. Two given points A, B also allow us to construct the circle with centre A, and passing through B (that is, with radius AB).

This very limited beginning already opens up the world of ruler and compasses constructions. In particular, given a line segment AB one can draw:

• the circle with centre A, and passing through B, and
• the circle with centre B, and passing through A.

If the two circles meet at C,

• then AB = AC (radii of the first circle), and BA = BC (radii of the second circle).

Hence we have constructed the equilateral triangle ΔABC on the given segment AB. This construction is the very first proposition in Book 1 of the Elements of Euclid (flourished c. 300 BC). Euclid’s second proposition is presented next as a problem.

Problem 137 Given three points A, B, C, show how to construct - without measuring - a point D such that the segments AB and CD are equal (in length).

Problem 137 looks like a simple starter (where the only available construction is to produce the third vertex of an equilateral triangle on a given line segment). However, to produce a valid solution requires a clear head and a degree of ingenuity.

Given two points A, B, the process of constructing an equilateral triangle ΔABC illustrates how we are allowed to construct new points from old.

• Whenever we construct two lines or circles that cross, the points where they cross (such as the point C in the above construction of the equilateral triangle ΔABC) become available for further constructions. So, if points A and B are given, then once C has been constructed, we may proceed to draw the lines AC and BC.

However, the fact that we can construct a line segment AB does not allow us to ‘measure’ the segment with a ruler, and then to use the resulting measurement to ‘copy’ the segment AB to the point C in order to construct the required point D such that AB = CD. The “ruler” in ruler and compasses constructions is used only to draw the line through two known points - not to measure. (Measuring is an approximate physical action, rather than an exact “mental construction”, and so is not really part of mathematics.) Hence in Problem 137 we have to find another way to produce a copy CD of the segment AB starting at the point C. Similarly, we can construct the circle with centre A and passing through B, but this does not allow us to use the pair of compasses to transfer distances physically (e.g. by picking up the compasses from AB and placing the compass point at C, like using the old geometrical drawing instrument that was called a pair of dividers). In seeking the construction required in Problem 137, we are restricted to “exact mental constructions” which may be described in terms of:

• drawing (or constructing) the line joining any two known points,
• constructing the circle with centre at a known point and passing through a known point, and
• obtaining a new point D as the intersection of two constructed lines or circles (or of a line and a circle).

If on the line AB, the point X lies between A and B, then we obtain a straight angle ∠AXB at X (or rather two straight angles at X - one on each side of the line AB). If we assume that all straight angles are equal, then it follows easily that “vertically opposite angles are always equal”.

Problem 138 Two lines AB and CD cross at X, where X lies between A and B and between C and D. Prove that ∠AXC=∠BXD.

Define a right angle to be ‘half a straight angle’. Then we say that two lines which cross at a point X are perpendicular if an angle at X is a right angle (or equivalently, if all four angles at X are equal). The next step requires us to notice two things - partly motivated by experience when coordinating hand, eye and brain to construct, and to think about, physical structures.

• First we need to recognise that triangles hold the key to the analysis of more complicated shapes.
• Then we need to realise that triangles in different positions can still be “equal”, or congruent - which then focuses attention on the minimal conditions under which two triangles can be guaranteed to be congruent.

The first of these two bullet points has an important consequence - namely that solving any problem in 2- or in 3-dimensions generally reduces to working with triangles. In particular, solving problems in 3-dimensions reduces to working in some 2-dimensional cross-section of the given figure (since three points not only determine a triangle, but also determine the plane in which that triangle lies). It follows that 2-dimensional geometry holds the key to solving problems in 3-dimensions, and that working with triangles is central in all geometry.

The second bullet point forces us to think carefully about:

• what we mean by a triangle (and in particular, to understand why ΔABC and ΔBCA are in some sense different triangles, even though they use the same three vertices and sides), and
• what it means for two triangles to be “the same”.

A triangle ΔABC incorporates six pieces of data, or information: the three sides AB, BC, CA and the three angles ∠ABC, ∠BCA, ∠CAB. We say that two (ordered) triangles ΔABC and ΔAʹBʹCʹ are congruent (which we write as

$$\Delta ABC\equiv \Delta A^{\prime }{B}^{\prime }{C}^{\prime },$$

where the order in which the vertices are listed matters) if their sides and angles “match up” in pairs, so that

$$\begin{array}{l}\underset{\_}{AB}=\underset{\_}{A^{\prime }{B}^{\prime }},\underset{\_}{BC}={\underset{\_}{B^{\prime }{C}^{\prime }}}^{\prime },\underset{\_}{CA}=\underset{\_}{C^{\prime }{A}^{\prime }},\\ \angle ABC=\angle A^{\prime }{B}^{\prime }{C}^{\prime },\angle BCA=\angle B^{\prime }{C}^{\prime }{A}^{\prime },\angle CAB=\angle C^{\prime }{A}^{\prime }{B}^{\prime }.\end{array}$$

As a result of drawing and experimenting with our hands, our minds may realise that certain subsets of these six conditions suffice to imply the others. In particular:

SAS-congruence criterion: if

$$\underset{\_}{AB}=\underset{\_}{A^{\prime }{B}^{\prime }},\angle ABC=\angle A^{\prime }{B}^{\prime }{C}^{\prime },\underset{\_}{BC}=\underset{\_}{B^{\prime }{C}^{\prime }},$$

then

$$\Delta ABC\equiv \Delta A^{\prime }{B}^{\prime }{C}^{\prime }$$

(where the name “SAS” indicates that the three listed match-ups occur in the specified order S (side), A (angle), S (side) as one goes round each triangle).

SSS-congruence criterion: if

$$\underset{\_}{AB}=\underset{\_}{A^{\prime }{B}^{\prime }},\underset{\_}{BC}=\underset{\_}{B^{\prime }{C}^{\prime }},\underset{\_}{CA}=\underset{\_}{C^{\prime }{A}^{\prime }},$$

then

$$\Delta ABC\equiv \Delta A^{\prime }{B}^{\prime }{C}^{\prime }.$$

ASA-congruence criterion: if

$$\angle ABC=\angle A^{\prime }{B}^{\prime }{C}^{\prime },\underset{\_}{BC}=\underset{\_}{B^{\prime }{C}^{\prime }},\angle BCA=\angle B^{\prime }{C}^{\prime }{A}^{\prime },$$

then

$$\Delta ABC\equiv \Delta A^{\prime }{B}^{\prime }{C}^{\prime }.$$

If in a given triangle ΔABC we have AB = AC, then we say that ΔABC is isosceles with apex A, and base BC (iso = same, or equal; sceles = legs).

Problem 139 Let ΔABC be an isosceles triangle with apex A. Let M be the midpoint of the base BC. Prove that ΔAMB = ΔAMC and conclude that AM is perpendicular to the base BC.

Problem 140 Construct two non-congruent triangles, ΔABC and ΔAʹBʹCʹ, where $\angle BCA=\angle B^{\prime }{C}^{\prime }{A}^{\prime }={30}^{°},\left|\underset{\_}{CA}\right|=\left|\underset{\_}{C^{\prime }}\right|=\sqrt{3},\left|\underset{\_}{AB}\right|=\left|\underset{\_}{A^{\prime }{B}^{\prime }}\right|=1.$

Conclude that there is in general no “ASS-congruence criterion”.

The congruence criteria allow one to prove basic results such as:

Claim In any isosceles triangle ΔABC with apex A (i.e. with AB = AC), the two base angles ∠B and ∠C are equal.

Proof 1 Let M be the midpoint of BC.

Then ΔAMB = ΔAMC (by the SSS-congruence criterion, since

AM = AM,

MB = MC (by construction of M as the midpoint)

BA = CA (given)).

$\therefore \angle B=\angle ABM=\angle ACM=\angle C.$              QED

Proof 2 ΔBAC = ΔCAB (by the SAS-congruence criterion, since BA

BA = CA (given),

∠BAC = ∠CAB (same angle),

AC = AB (given),

$\therefore \angle B=\angle ABC=\angle ACB=\angle C.$              QED

We also have the converse result:

Claim In any triangle ΔABC, if the base angles ∠B and ∠C are equal, then the triangle is isosceles with apex A (i.e. AB = AC).

Proof ΔABC = ΔACB (by the ASA-congruence criterion, since

∠ABC = ∠ACB (given),

BC = CB, and

∠BAC = ∠CAB (given)).

$\therefore \underset{\_}{AB}=\underset{\_}{AC}.$              QED

Problem 141

(i) A circle with centre O passes through the point A. The line AO meets the circle again at B. If C is a third point on the circle, prove that ∠ACB is equal to ∠CAB + ∠CAB.

(ii) Conclude that, if the angles in ΔABC add to a straight angle, then ∠ACB is a right angle.

Once we introduce the parallel criterion, and hence can prove that the three angles in any triangle add to a straight angle, Problem 141 will guarantee that “the angle subtended on the circumference by a diameter is always a right angle”.

Problem 142 Show how to implement the basic ruler and compasses constructions:

(i) to construct the midpoint M of a given line segment AB;

(ii) to bisect a given angle ∠ABC;

(iii) to drop a perpendicular from P to a line AB (that is, to locate X on the line AB, so that the two angles that PX makes with the line AB on either side of PX are equal).

Prove that your constructions do what you claim.

Problem 143 Given two points A and B.

(a) Prove that each point X on the perpendicular bisector of AB is equidistant from A and from B (that is, that XA = XB).

(b) Prove that, if X is equidistant from A and from B, then X lies on the perpendicular bisector of AB.

Problem 143 shows that, given a line segment AB, the perpendicular bisector of AB is the locus of all points X which are equidistant from A and from B. This observation is what lay behind the construction of the circumcentre of a triangle (back in Chapter 1, Problem 32(a)):

Given any ΔABC.

Let O be the point where the perpendicular bisectors of AB and BC meet.

Then OA = OB

and OB = OC.

$\therefore \underset{\_}{OA}=\underset{\_}{OB}=\underset{\_}{OC}.$

Hence O is the centre of a circle passing through all three vertices A, B, C.

Moreover O also lies on the perpendicular bisector of CA.

This circle is called the circumcircle of ΔABC, and O is called the circumcentre of ΔABC. As indicated back in Problem 32, the radius of the circumcircle of ΔABC (called the circumradius of the triangle) is generally denoted by R. Later we will meet other circles and “centres” associated with a given triangle ΔABC.

Before moving on it is worth extending Problem 143 to three dimensions

Problem 144 Given any two points N, S in 3D space, prove that the locus of all points X which are equidistant from N and from S form the plane perpendicular to the line NS and passing through the midpoint M of NS.

The next two fundamental results are often neglected.

Problem 145 Given any ΔABC, if we extend the side BC beyond C to a point X, then the “exterior angle” ∠ACX at C is greater than each of the “two interior opposite angles” ∠A and ∠B.

Problem 146

(a) If in ΔABC we have AB > AC, then ∠ACB > ∠ABC. (“In any triangle, the larger angle lies opposite the longer side.”)

(b) If in ΔABC we have ∠ACB > ∠ABC, then AB > AC. (“In any triangle, the longer side lies opposite the larger angle.”)

(c) (The triangle inequality) Prove that in any triangle ΔABC,

$$\underset{\_}{AB}+\underset{\_}{BC}>\underset{\_}{AC}.$$

The results in Problems 145 and 146 have surprisingly many consequences. For example, they allow one to prove the converse of the result in Problem 141

Problem 147 Suppose that in ΔABC, ∠C = ∠A + ∠B. Prove that C lies on the circle with diameter AB.

(In particular, if the angles of ΔABC add to a straight angle, and ∠ACB is a right angle, then C lies on the circle with diameter AB.

We come next to a result whose justification is often fudged. At first sight it is unclear how to begin: there seems to be so little information to work with - just two points and a line through one of the points.

Problem 148 A circle with centre O passes through the point P. Prove that the tangent to the circle at P is perpendicular to the radius OP.

Problem 148 is an example of a result which implies its own converse - though in a backhanded way. Suppose a circle with centre O passes through the point P. If OP is perpendicular to a line m passing through P, then m must be tangent to the circle (because we know that the tangent at P is perpendicular to OP, so the angle between m and the tangent is “zero”, which forces m to be equal to the tangent). This converse will be needed later, when we meet the incircle.

Problem 149 Let P be a point and m a line not passing through P. Prove that, among all possible line segments PX with X on the line m, a perpendicular from P to the line m is the shortest.

The result in Problem 149 allows us to define the “distance” from P to the line m to be the length of any perpendicular from P to m. (As far as we know at this stage of the development, there could be more than one perpendicular from P to m.)

Note that all the results mentioned so far have avoided using the Euclidean “parallel criterion” (or - equivalently - the fact that the three angles in any triangle add to a straight angle). So results proved up to this point should still be “true” in any geometry where we have points, lines, triangles, and circles satisfying the congruence criteria - whether or not the geometry satisfies the Euclidean “parallel criterion”.

The idea that there is only one “shortest” distance from a point to a line may seem “obvious”; but it is patently false on the sphere, where every line (i.e. ‘great circle’) from the North pole P to the equator is perpendicular to the equator (and all these lines have the same “length”). The proof that there is just one such perpendicular from P to m depends on the parallel criterion (see below) - a criterion which fails to hold for geometry on the sphere.

Euclid’s Elements started with a few basic axioms that formalised the idea of ruler and compasses constructions. He then added a simple axiom that allowed one to compare angles in different locations. He made the forgivable mistake of omitting an axiom for congruence of triangles - imagining that it can be proved. (It can’t.) However he then stated, and carefully developed the consequences of, a much more subtle axiom about parallel lines (two lines m, n in the plane are said to be parallel if they never meet, no matter how far they are extended). For reasons that remain unclear, instead of appreciating that Euclid's “parallel postulate” constituted a profound insight into the foundations of geometry, mathematicians in later ages saw the complexity of Euclid’s postulate as some kind of flaw, and so tried to show that it could be derived from the other, simpler postulates. The attempt to “correct” this perceived flaw became a kind of Holy Grail.

The story is instructive, but too complicated to summarise accurately here. The situation was eventually clarified by two nineteenth century mathematicians (more-or-less at the same time, but working independently). In the revolutionary, romantic spirit of the nineteenth century, János Bolyai (Hungarian: 1802-1860) and Nikolai Lobachevski (Russian: 1792-1856) each allowed himself to consider what would happen if one adopted a different assumption about how “parallel lines” behave. Both discovered that one can then derive an apparently coherent theory of a completely novel kind, with its own beautiful results: that is, a geometry which seemed to be internally “consistent” - but different from Euclidean geometry. Lobachevski published brief notes of his work in 1829-30 (in Kazan); Bolyai knew nothing of this and published incomplete notes of his researches in 1832. Lobachevski published a more detailed booklet in 1840.

Neither mathematician got the recognition he might have anticipated, and it was only much later (largely after their deaths) that others realised how to show that the fantasy world they had each dreamt up was just as “internally consistent” as traditional Euclidean geometry. The story is further complicated by the fact that the dominant mathematician of the time - namely Gauss (1777-1855) - claimed to have proved something similar (and he may well have done so, but exactly what he knew has to be inferred from cryptic remarks in occasional letters, since he published nothing on the subject). If there is a moral to the story, it could be that success in mathematics may not be recognised, or may only be recognised after one’s death: so those who spend their lives exploring the mathematical universe had better appreciate the delights of the mathematical journey, rather than being primarily motivated by a desire for immediate recognition and acclaim!

Two lines m, n in the plane are said to be parallel if they never meet - no matter how far they are extended. We sometimes write this as “m||n”.

Given two lines m, n in the plane, a third line p which crosses both m and n is called a transversal of m and n.

Parallel criterion: Given two lines m and n, if some transversal p is such that the two “internal” angles on one side of the line p (that is the two angles that p makes with m and with n, and which lie between the two lines m and n) add to less than a straight angle, then the lines m and n must meet on that side of the line p.

If the internal angles on one side of p add to more than a straight angle, then internal angles on the other side of p add to less than a straight angle, so the lines m and n must meet on the other side of p. It follows.

• that two lines m and n are parallel precisely when the two internal angles on one side of a transversal add to exactly a straight angle.

Parallel lines can be thought of as “all having the same direction”; so it is convenient to insist that “every line is parallel to itself” (even though it has lots of points in common with itself). It then follows

• that, given three lines k, m, n, if k is parallel to m and m is parallel to n, then k is parallel to n; and
• that given a line m and a point P, there is a unique line n through P which is parallel to m.

All this then allows one

• to conclude that, if m and n are any two lines, and p is a transversal, then m and n are parallel if and only if alternate angles are equal (or equivalently, if and only if corresponding angles are equal); and
• to extend the basic ruler and compasses constructions to include the construction:

  “given a line AB and a point P, construct the line through P which is parallel to AB”

  (namely, by first constructing the line PX through P, perpendicular to AB, and then the line through P, perpendicular to PX).

One can then prove the standard result about the angles in any triangle.

Claim The angles in any triangle ΔABC add to a straight angle.

Proof Construct the line m through A that is parallel to BC. Then AB and AC are transversals, which cross both the line m and the line BC, and which make three angles at the point A on m:

• one being just the angle ∠A in the triangle ΔABC,
• one being equal to ∠B (alternate angles relative to the transversal AB) and
• one being equal to ∠C (alternate angles relative to the transversal AC).

The three angles at A clearly add to a straight angle, so the three angles ∠A, ∠B, ∠C also add to a straight angle.                QED

Once we know that the angles in any triangle add to a straight angle, we can prove all sorts of other useful facts. One is a simple reformulation of the above Claim.

Problem 150 Given any triangle ΔABC, extend BC beyond C to a point X. Then the exterior angle

$$\angle XCA=\angle A+\angle B.$$

(“In any triangle, each exterior angle is equal to the sum of the two interior opposite angles.”)

Another important consequence is the result which underpins the sequence of “circle theorems”.

Problem 151 Let O be the circumcentre of ΔABC. Prove that

$$\angle AOB=2·\angle ACB.$$

Problem 151 implies that

“the angles subtended by any chord AB on a given arc of the circle are all equal”,

and are equal to exactly one half of the angle subtended by AB at the centre O of the circle. This leads naturally to the familiar property of cyclic quadrilaterals.

Problem 152 Let ABCD be a quadrilateral inscribed in a circle (such a quadrilateral is said to be cyclic, and the four vertices are said to be concyclic - that is, they lie together on the same circle). Prove that opposite angles (e.g. ∠B and ∠D) must add to a straight angle. (Two angles which add to a straight angle are said to be supplementary.)

These results have lots of lovely consequences: we shall see one especially striking example in Problem 164. Meantime we round up our summary of the "circle theorems".

Problem 153 Suppose that the line XAY is tangent to the circumcircle of ΔABC at the point A, and that X and C lie on opposite sides of the line AB. Prove that ∠XAB = ∠ACB.

Problem 154

(a) Suppose C, D lie on the same side of the line AB.

(i) If D lies inside the circumcircle of ΔABC, then ∠ADB > ∠ACB.

(ii) If D lies outside the circumcircle of ΔABC, then ∠ADB < ∠ACB.

(b) Suppose C, D lie on the same side of the line AB, and that ∠ACB = ∠ADB. Then D lies on the circumcircle of ΔABC.

(c) Suppose that ABCD is a quadrilateral, in which angles ∠B and ∠D are supplementary. Then ABCD is a cyclic quadrilateral.

Another result which follows now that we know that the angles of a triangle add to a straight angle is a useful additional congruence criterion - namely the RHS-congruence criterion. This is a ‘limiting case’ of the failed ASS-congruence criterion (see the example in Problem 140). In the failed ASS criterion the given data correspond to two different triangles - one in which the angle opposite the first specified side (the first “S” in “ASS”) is acute, and one in which the angle opposite the first specified side is obtuse. In the RHS-congruence criterion, the angle opposite the first specified side is a right angle, and the two possible triangles are in fact congruent.

RHS-congruence criterion: If ∠ABC and ∠AʹBʹCʹ are both right angles, and BC = BʹCʹ, CA = CʹAʹ, then

$$\Delta ABC\equiv \Delta A^{\prime }{B}^{\prime }{C}^{\prime }.$$

Proof Suppose that AB = AʹBʹ. Then

AB = AʹBʹ

∠ABC = ∠AʹBʹCʹ,

BC = BʹCʹ

Hence we may apply the SAS-congruence criterion to conclude that ΔABC = ΔAʹBʹCʹ.

If on the other hand $AB\ne \underset{\_}{A^{\prime }{B}^{\prime }}$ , we may suppose that BA > BʹAʹ. Now construct Aʹʹ on BA such that BAʹʹ = BʹAʹ. Then

AʹʹB = AʹBʹ,

∠AʹʹBC = ∠AʹBʹCʹ,

BC = BʹCʹ,

$\therefore \Delta A^{\prime \prime }BC\equiv \Delta A^{\prime }{B}^{\prime }{C}^{\prime }$ (by SAS-congruence).

Hence AʹʹC = AʹCʹ = AC, so ΔCAAʹʹ is isosceles.

$$\therefore \angle C{A}^{\prime \prime }A=\angle CA{A}^{\prime \prime }.$$

However, ∠CAʹʹA > ∠CBA (since the exterior angle ∠CAʹʹA in ΔCBAʹʹ must be greater than the interior opposite angle ∠CBA, by Problem 145).

But then the two base angles in the isosceles triangle ΔCAAʹʹ are each greater than a right angle - so the angle sum of ΔCAAʹʹ is greater than a straight angle, which is impossible. Hence this case cannot occur.                 QED

RHS-congruence seems to be needed to prove the basic result (Problem 161 below) about the area of parallelograms, and this is then needed in the proof of Pythagoras’ Theorem (Problem 18). In one sense RHS-congruence looks like a special case of SSS-congruence (as soon as two pairs of sides in two right angled triangles are equal, Pythagoras’ Theorem guarantees that the third pair of sides are also equal). However this observation cannot be used to justify RHS-congruence if RHS-congruence is needed to justify Pythagoras’ Theorem.

Problem 155 Given a circle with centre O, let Q be a point outside the circle, and let QP, QP' be the two tangents from Q, touching the circle at P and at P'. Prove that QP = QPʹ, and that the line OQ bisects the angle ∠PQPʹ.

Problem 156 You are given two lines m and n crossing at the point B.

(a) If A lies on m and C lies on n, prove that each point X on the bisector of angle ∠ABC is equidistant from m and from n.

(b) If X is equidistant from m and from n, prove that X must lie on one of the bisectors of the two angles at B.

Problem 156 shows that, given two lines m and n that cross at B, the bisectors of the two pairs of vertically opposite angles formed at B form the locus of all points X which are equidistant from the two lines m and n. This allows us to mimic the comments following Problem 143 and so to construct the incentre of a triangle.

Given any ΔABC, let I be the point where the angle bisectors of ∠ABC and ∠BCA meet.

Let the perpendiculars from I to the three sides AB, BC, CA meet the sides at P, Q, R respectively. Then

IP = IQ (since I lies on the bisector of ∠ABC) and

IQ = IR (since I lies on the bisector or ∠BCA).

Hence the circle which has centre I and which passes through P also passes through Q and R.

Moreover, I also lies on the bisector of ∠CAB; and since the radii IP, IQ, IR are perpendicular to the sides of the triangle, the circle is tangent to the three sides of the triangle (by the comments following Problem 148)

This circle is called the incircle of ΔABC, and I is called the incentre of ΔABC. The radius of the incircle of ΔABC is called the inradius, and is generally denoted by r.

A quadrilateral ABCD in which AB ∥ DC and BC ∥ AD is called a parallelogram. A parallelogram ABCD with a right angle is a rectangle. A parallelogram ABCD with AB = AD is called a rhombus. A rectangle which is also a rhombus is called a square.

Problem 157 Let ABCD be a parallelogram.

(i) Prove that ΔABC = ΔCDA, so that each triangle has area exactly half of area(ABCD).

(ii) Conclude that opposite sides of ABCD are equal in pairs and that opposite angles are equal in pairs.

(iii) Let AC and BD meet at X. Prove that X is the midpoint of both AC and BD.

Problem 158 Let ABCD be a parallelogram with centre X (where the two main diagonals AC and BD meet), and let m be any straight line passing through the centre. Prove that m divides the parallelogram into two parts of equal area.

We defined a parallelogram to be “a quadrilateral ABCD in which AB ∥ DC and BC ∥ AD however, in practice, we need to be able to recognise a parallelogram even if it is not presented in this form. The next result hints at the variety of other conditions which allow us to recognise a given quadrilateral as being a parallelogram “in mild disguise”.

Problem 159

(a) Let ABCD be a quadrilateral in which AB ∥ DC, and AB = DC. Prove that BC ∥ AD, and hence that ABCD is a parallelogram.

(b) Let ABCD be a quadrilateral in which AB = DC and BC = AD. Prove that AB ∥ DC, and hence that ABCD is a parallelogram.

(c) Let ABCD be a quadrilateral in which ∠A = ∠C and ∠B = ∠D. Prove that AB ∥ DC and that BC ∥ AD, and hence that ABCD is a parallelogram.

The next problem presents a single illustrative example of the kinds of things which we know in our bones must be true, but where the reason, or proof, may need a little thought.

Problem 160 Let ABCD be a parallelogram. Let M be the midpoint of AD and N be the midpoint of BC. Prove that MN || AB, and that MN passes through the centre of the parallelogram (where the two diagonals meet).

Problem 161 Prove that any parallelogram ABCD has the same area as the rectangle on the same base DC and “with the same height” (i.e. lying between the same two parallel lines AB and DC).

The ideas and results we have summarised up to this point provide exactly what is needed in the proof of Pythagoras’ Theorem outlined back in Chapter 1, Problem 18. They also allow us to identify two more “centres” of a given triangle ΔABC.

Problem 162 Given any triangle ΔABC, draw the line through A which is parallel to BC, the line through B which is parallel to AC, and the line through Cʹ which is parallel to AB. Let the first two constructed lines meet at C, the second and third lines meet at Aʹ, and the first and third lines meet at Bʹ.

(a) Prove that A is the midpoint of BʹCʹ, that B is the midpoint of CʹAʹ and that C is the midpoint of AʹBʹ.

(b) Conclude that the perpendicular from A to BC, the perpendicular from B to CA, and the perpendicular from C to AB all meet in a single point H. (H is called the orthocentre of ΔABC.)

Let the foot of the perpendicular from A to BC be P, the foot of the perpendicular from B to CA be Q, and the foot of the perpendicular from C to AB be R. Then ΔPQR is called the orthic triangle of ΔABC. The “circle theorems” (especially Problems 151 and 154(c)) lead us to discover that this triangle has two quite unexpected properties. As a partial preparation for one of the properties we digress slightly to introduce a classic problem.

Problem 163 My horse is tethered at H some distance away from my village V. Both H and V are on the same side of a straight river. How should I choose the shortest route to lead the horse from H to V, if I want to water the horse at the river en route?

Problem 164 Let ΔABC be an acute angled triangle.

(a) Prove that, among all possible triangles ΔPQR inscribed in ΔABC, with P on BC, Q on CA, R on AB, the orthic triangle is the one with the shortest perimeter.

(b) Suppose that the sides of ΔABC act like mirrors. A ray of light is shone along one side of the orthic triangle PQ, reflects off CA, and the reflected beam then reflects in turn off AB. Where does the ray of light next hit the side BC? (Alternatively, imagine the sides of the triangle as billiard table cushions, and explain the path followed by a ball which is projected, without spin, along PQ.)

We come next to the fourth among the standard “centres of a triangle”.

Problem 165 Given ΔABC, let L be the midpoint of the side BC. The line AL is called a median of ΔABC. (It is not at all obvious, but if we imagine the triangle as a lamina, having a uniform thickness, then ΔABC would exactly balance if placed on a knife-edge running along the line AL.) Let M be the midpoint of the side CA, so that BM is another median of ΔABC. Let G be the point where AL and BM meet.

(a) (i) Prove that ΔABL and ΔACL have equal area. Conclude that ΔABG and ΔACG have equal area.

(ii) Prove that ΔBCM and ΔBAM have equal area. Conclude that ΔBCG and ΔBAG have equal area.

(b) Let N be the midpoint of AB. Prove that CG and GN are the same straight line (i.e. that ∠CGN is a straight angle). Hence conclude that the three medians of any triangle always meet in a point G.

The point where all three medians meet is called the centroid of the triangle. For the geometry of the triangle, this is all you need to know. However, it is worth noting that the centroid is the point that would be the ‘centre of gravity’ of the triangle if the triangle is thought of as a thin lamina with a uniform distribution of mass.

Next we revisit, and reprove in the Euclidean spirit, a result that you proved in Problem 95 using coordinates - namely the Midpoint Theorem.

Problem 166 (The Midpoint Theorem) Given any triangle ΔABC, let M be the midpoint of the side AC, and let N be the midpoint of the side AB. Draw in MN and extend it beyond N to a point Mʹ such that MN = NMʹ.

(a) Prove that ΔANM = ΔBNMʹ.

(b) Conclude that BMʹ = CM and that BMʹ || CM.

(c) Conclude that MMʹBC is a parallelogram, so that CB = MMʹ. Hence MN is parallel to CB and half its length.

The Midpoint Theorem can be reworded as follows:

Given ΔAMN.

Extend AM to C such that AM = MC and extend AN to B such

that AN = NB.

Then CB || MN and CB = 2. MN.

This rewording generalizes SAS-congruence in a highly suggestive way, and points us in the direction of “SAS-similarity”.

SAS-similarity (x2): if AʹBʹ = 2 . AB, ∠BAC = ∠BʹAʹCʹ, and

AʹCʹ = 2 . AC, then

BʹCʹ = 2 . BC, ∠ABC = ∠AʹBʹCʹ, and ∠BAC = ∠BʹAʹCʹ.

Proof Extend AB to the point Bʹʹ such that ABʹʹ = AʹBʹ, and extend AC to the point Cʹʹ such that ACʹʹ = AʹCʹ. Then ΔBʹʹACʹʹ = ΔBʹAʹCʹ (by SAS-congruence), so BʹʹCʹʹ = BʹCʹ, ∠BʹʹCʹʹA = ∠BʹCʹAʹ, ∠CʹʹBʹʹA = ∠CʹBʹAʹ. By construction we have ABʹʹ = 2 . AB and ACʹʹ = 2 . AC. Hence (by the Midpoint Theorem): BʹʹCʹʹ = 2 . BC (so BʹCʹ = 2 . BC), and BC || BʹʹCʹʹ (so ∠BCA = ∠BʹʹCʹʹA and ∠CBA = ∠CʹʹBʹʹA).

∴ ∠BʹʹCʹʹA = ∠BʹCʹAʹ = ∠BCA,

and ∠CʹʹBʹʹA = ∠CʹBʹAʹ = ∠CBA.           QED

The SAS-similarity ($\times 2$) interpretation of the Midpoint Theorem is like the SAS-congruence criterion in that one pair of corresponding angles in ΔBAC and ΔBʹAʹCʹ are equal, while the sides on either side of this angle in the two triangles are related; but instead of the two pairs of corresponding sides being equal, the sides of ΔBʹAʹCʹ are double the corresponding sides of ΔBAC.

In general we say that

ΔABC is similar to ΔAʹBʹCʹ (written as ΔABC ~ ΔAʹBʹCʹ) with scale-factor m if each angle of ΔAʹBʹCʹ is equal to the corresponding angle of ΔABC, and if corresponding sides are all in the same ratio:

$$\underset{\_}{A^{\prime }{B}^{\prime }}:\underset{\_}{AB}=\underset{\_}{B^{\prime }{C}^{\prime }}:\underset{\_}{BC}=\underset{\_}{C^{\prime }{A}^{\prime }}:\underset{\_}{CA}=m:1.$$

If two triangles ΔAʹBʹCʹ and ΔABC are similar, with (linear) scale factor ΔAʹBʹCʹ, then the ratio between their areas is

$$area\left(\Delta A^{\prime }{B}^{\prime }{C}^{\prime }\right):area(\Delta ABC)=m^2:1.$$

Two similar triangles Δ ABC and Δ A'B'C' give rise to six matching pairs:

• the three pairs of corresponding angles (which are equal in pairs), and
• the three pairs of corresponding sides (which are in the same ratio).

In the case of congruence, the congruence criteria tell us that we do not need to check all six pairs to guarantee that two triangles are congruent: these criteria guarantee that certain triples suffice. The similarity criteria guarantee much the same for similarity.

Suppose we are given triangles ΔABC, ΔAʹBʹCʹ.

AAA-similarity: If

$$\angle ABC=\angle A^{\prime }{B}^{\prime }{C}^{\prime },\angle BCA=\angle B^{\prime }{C}^{\prime }{A}^{\prime },\angle CAB=\angle C^{\prime }{A}^{\prime }{B}^{\prime },$$

then

$$\underset{\_}{A^{\prime }{B}^{\prime }}:\underset{\_}{AB}=\underset{\_}{B^{\prime }{C}^{\prime }}:\underset{\_}{BC}=\underset{\_}{C^{\prime }{A}^{\prime }}:\underset{\_}{CA},$$

so the two triangles are similar.

SSS-similarity: If

$$\underset{\_}{A^{\prime }{B}^{\prime }}:\underset{\_}{AB}=\underset{\_}{B^{\prime }{C}^{\prime }}:\underset{\_}{BC}=\underset{\_}{C^{\prime }{A}^{\prime }}:\underset{\_}{CA},$$

then

$$\angle ABC=\angle A^{\prime }{B}^{\prime }{C}^{\prime },\angle BCA=\angle B^{\prime }{C}^{\prime }{A}^{\prime },\angle CAB=\angle C^{\prime }{A}^{\prime }{B}^{\prime },$$

so the two triangles are similar.

SAS-similarity: If

$$\underset{\_}{A^{\prime }{B}^{\prime }}:\underset{\_}{AB}=\underset{\_}{A^{\prime }{C}^{\prime }}:\underset{\_}{AC}=m:1$$

and

$$\angle B^{\prime }{A}^{\prime }{C}^{\prime }=\angle BAC,$$

then

$$\underset{\_}{B^{\prime }{C}^{\prime }}:\underset{\_}{BC}=\underset{\_}{A^{\prime }{B}^{\prime }}:\underset{\_}{AB}={\underset{\_}{A}}^{\prime }{C}^{\prime }:\underset{\_}{AC}$$

and

$$\angle A^{\prime }{B}^{\prime }{C}^{\prime }=\angle ABC,\angle B^{\prime }{C}^{\prime }{A}^{\prime }=\angle BCA,$$

so the two triangles are similar.

Our rewording of the Midpoint Theorem gave rise to a version of the third of these criteria, with m = 2.

AAA-similarity in right angled triangles is what makes trigonometry possible. Suppose that two triangles ΔABC,ΔAʹBʹCʹ have right angles at A and at Aʹ. If ∠ABC,∠AʹBʹCʹ, then (since the angles in each triangle add to two right angles) we also have ∠BCA,∠BʹCʹAʹ. It then follows (from AAA-similarity) that

$$\underset{\_}{A^{\prime }{B}^{\prime }}:\underset{\_}{AB}=\underset{\_}{B^{\prime }{C}^{\prime }}:\underset{\_}{BC}=\underset{\_}{C^{\prime }{A}^{\prime }}:\underset{\_}{CA},$$

so the trig ratio in ΔABC

$$\sin B=\frac{\underset{\_}{AC}}{\underset{\_}{BC}}$$

has the same value as the corresponding ratio in ΔAʹBʹCʹ

$$\sin B^{\prime }=\frac{\underset{\_}{A^{\prime }{C}^{\prime }}}{\underset{\_}{B^{\prime }{C}^{\prime }}}.$$

Hence this ratio depends only on the angle B, and not on the triangle in which it occurs. The same holds for cos ∠B and for tan ∠B.

The art of solving geometry problems often depends on looking for, and identifying, similar triangles hidden in a complicated configuration. As an introduction to this, we focus on three classic properties involving circles, where the figures are sufficiently simple that similar triangles should be fairly easy to find.

Problem 167 The point P lies outside a circle. The tangent from P touches the circle at T, and a secant from P cuts the circle at A and at B. Prove that $\underset{\_}{PA}\times \underset{\_}{PB}={\underset{\_}{PT}}^2$ .

Problem 168 The point P lies outside a circle. Two secants from P meet the circle at A, B and at C, D respectively. Prove in two different ways that

$$\underset{\_}{PA}\times \underset{\_}{PB}=\underset{\_}{PC}\times \underset{\_}{PD}.$$

Problem 169 The point P lies inside a circle. Two secants from P meet the circle at A, B and at C, D respectively. Prove in two different ways that

$$\underset{\_}{PA}\times \underset{\_}{PB}=\underset{\_}{PC}\times \underset{\_}{PD}.$$

We end our summary of the foundations of Euclidean geometry by deriving the familiar formula for the area of a trapezium and its 3-dimensional analogue, and a formulation of the similarity criteria which is often attributed to Thales (Greek 6^th century BC).

Problem 170 Let ABCD be a trapezium with AB || DC, in which AB has length a and DC has length b.

(a) Let M be the midpoint of AD and let N be the midpoint of BC. Prove that MN || AB and find the length of MN.

(b) If the perpendicular distance between AB and DC is d, find the area of the trapezium ABCD.

Problem 171 A pyramid ABCDE, with apex A and square base BCDE of side length b, is cut parallel to the base at height d above the base, leaving a frustum of a pyramid, with square upper face of side length a. Find a formula for the volume of the resulting solid (in terms of a, b, and d).

The following general result allows us to use “equality of ratios of line segments” whenever we have three parallel lines (without first having to conjure up similar triangles).

Problem 172 (Thales’ Theorem) The lines AA' and BB' are parallel. The point C lies on the line AB, and C' lies on the line A'B' such that CCʹ || BBʹ. Prove that AB : BC = AʹBʹ : BʹCʹ.

Under certain conditions, the similarity criteria guarantee the equality of ratios of sides of two triangles. Thales’ Theorem extends this “equality of ratios” to line segments which arise whenever two lines cross three parallel lines. One of the simplest, but most far-reaching, applications of this result is the tie-up between geometry and algebra which lies behind ruler and compasses constructions, and which underpins Descartes’ (1596-1650) re-formulation of geometry in terms of coordinates (see Problem 173).

Thales (c. 620-c. 546 BC) was part of the flowering of Greek thought having its roots in Milesia (in the south west of Asia Minor, or modern Turkey). Thales seems to have been interested in almost everything - philosophy, astronomy, politics, and also geometry. In Britain his name is usually attached to the fact that the angle subtended by a diameter is a right angle. On the continent, his name is more strongly attached to the result in Problem 172. His precise contribution to geometry is unclear - but he seems to have played a significant role in kick-starting what became (300 years later) the polished version of Greek mathematics that we know today.

Thales’ contributions in other spheres were perhaps even more significant than in geometry. He seems to have been among the first to try to “explain” phenomena in reductionist terms - identifying “water” as the single “element”, or first principle, from which all substances are derived. Anaximenes (c. 586-c. 526 BC) later argued in favour of “air” as the first principle. These two elements, together with “fire” and “earth”, were generally accepted as the four Greek “elements” - each of which was supposed to contribute to the construction of observed matter and change in different ways.

Problem 173 To define “length”, we must first decide which line segment is deemed to have unit length. So suppose we are given line segments XY of length 1, AB of length a, (i.e. AB : XY = a : 1), and CD of length b.

(a) Use Problem 137 to construct a segment of length a + b, and if $a⩾b$, a segment of length a — b.

(b) Show how to construct a line segment of length ab and a segment of length $\frac{a}{b}$ .

(c) Show how to construct a line segment of length $\sqrt{a}$ .

5.3. Areas, lengths and angles

Problem 174 A rectangular piece of fruitcake has a layer of icing on top and down one side to form a larger rectangular slab of cake (as shown in Figure 3).

Figure 3: Icing on the cake

Describe how to make a single straight cut so as to divide both the fruitcake and the icing exactly in half. (The thickness of the icing on top is not necessarily the same as the thickness down the side.)

Problem 175

(a) What is the angle between the two hands of a clock at 1:35? Can you find another time when the angle between the two hands is the same as this?

(b) How many times each day do the two hands of a clock ‘coincide’? And at what times do they coincide?

(c) If we add a second hand, how many times each day do the three hands coincide?

Problem 176 The twelve hour marks for a clock are marked on the circumference of a unit circle to form the vertices of a regular dodecagon ABCDEFGHIJKL. Calculate exactly (i.e. using Pythagoras’ Theorem rather than trigonometry) the lengths of all the possible line segments joining two vertices of the dodecagon.

Problem 177 Consider the lattice of all points (k,m,n) in 3-dimensions with integer coordinates k, m, n. Which of the following distances can be realised between lattice points?

$$\sqrt{1},\sqrt{2},\sqrt{3},\sqrt{4},\sqrt{5},\sqrt{6},\sqrt{7},\sqrt{8},\sqrt{9},\sqrt{10},\sqrt{11},\sqrt{13},\sqrt{13},\sqrt{15},\sqrt{16},\sqrt{16},\sqrt{17}$$

Problem 178

(a) Five vertices A, B, C, D, E are arranged in cyclic order. However instead of joining each vertex to its two immediate neighbours to form a convex pentagon, we join each vertex to the next but one vertex to form a pentagonal star, or pentagram ACEBD. Calculate the sum of the five “angles” in any such pentagonal star.

(b) There are two types of 7-gonal stars. Calculate the sum of the angles at the seven vertices for each type.

(c) Try to extend the previous two results (and the proofs) to arbitrary n-gonal stars.

Problem 179

(a) A regular pentagon ABCDE with edges of length 1 is surrounded in the plane by five new regular pentagons - ABLMN joined to AB, BCOPQ joined to BC, and so on.

(i) Prove that M, N, X, Y lie on a line.

(ii) Prove that MPSVY is a regular pentagon.

(iii) Find the edge length of this larger surrounding regular pentagon.

(b) Given a regular pentagon MPSVY, with edge length 1, draw the five diagonals to form the pentagram MSYPV. Let PY meet MV at A, and MS at B; let PV meet MS at C and SY at D; and let SY meet VM at E.

(i) Prove that ABCDE is a regular pentagon.

(ii) Prove that A, B, and M are three vertices of a regular pentagon ABLMN, where L lies on MP and N lies on MY.

(iii) Find the edge length of the regular pentagon ABCDE.

5.4. Regular and semi-regular tilings in the plane

In Problem 36 we saw that a regular n-gon has a circumcentre O. If we join each vertex to the point O, we get n triangles, each with angle sum π. Hence the total angle sum in all n triangles is πn. Since the n angles around the point O add to 2π, the angles of the regular n-gon itself have sum (n-2)π. Hence each angle of the regular n-gon has size $\left(1-\frac{2}{n}\right)\pi$ .(In the next chapter you will prove the general result that the sum of the angles in any n-gon is equal to (n-2)π radians.)

Problem 180 A regular tiling of the plane is an arrangement of identical regular polygons, which fit together edge-to-edge so as to cover the plane with no overlaps.

(a) Prove that if a regular tiling of the plane with p-gons is possible, then p = 3,4, or 6.

(b) Prove that a regular tiling of the plane exists for each of the values in (a).

We refer to the arrangement of tiles around a vertex as the vertex figure. In a regular tiling all vertex figures are automatically identical, so it is natural to refer to the tiling in terms of its vertex figure. When p = 3, exactly q = 6 tiles fit together at each vertex, and we abbreviate “six equilateral triangles” as 3⁶. In the same way we denote the tiling whose vertex figure consists of “four squares” as 4⁴, and the tiling whose vertex figure consists of “three regular hexagons” as 6³.

The natural approach in part (a) of Problem 180 is first to identify which vertex figures have no gaps or overlaps - giving a necessary condition for a regular tiling to exist. It is tempting to stop there, and to assume that this obvious necessary condition is also sufficient. The temptation arises in part because 2-dimensional regular tilings are so familiar. But it is important to recognize the distinction between a necessary and a sufficient condition; so the temptation should be resisted, and a construction given.

The procedure hidden in the solution to Problem 180 illustrates a key strategy, which dates back to the ancient Greeks, and which is called the method of analysis.

• First, we imagine that we have a typical solution to the problem - perhaps by giving it a name (even though we do not yet know anything about such a solution).
• We then use the given conditions to deduce features which any such solution must necessarily have.
• And we continue deriving more and more necessary conditions until we believe our list of derived conditions may also be sufficient.
• Finally we show that any configuration which satisfies our final derived list of necessary conditions is in fact a solution to the original problem, so that the list of necessary conditions is in fact sufficient, and we have effectively pinned down all possible solutions.

This is what we did in a very simple way in the solution to Problem 180: the condition on vertex figures gave an evident necessary condition, which turned out to be sufficient to guarantee that such a tiling exists. The same general strategy guided our classification of primitive Pythagorean triples back in Problem 23.

In the seventeenth century, this ancient Greek strategy was further developed by Fermat (1601-1665), and by Descartes (1596-1650). For example, Fermat left very few proofs; but his proof that the equation

$$x^4+y^4=z^4$$

has no solutions in positive integers x, y, z illustrated the method:

• Fermat started by supposing that a solution exists, and concluded that (x², y², z²) would then be a Pythagorean triple.
• The known formula for such Pythagorean triples then allowed him to derive even stronger necessary conditions on x, y, z.
• These conditions were so strong they could never be satisfied!

Descartes developed a “method”, whereby hard geometry problems could be solved by translating them into algebra - essentially using the method of analysis.

• Faced with a hard problem, Descartes first imagined that he had a point, or a locus, or a curve of the kind required for a solution.
• Then he introduced coordinates “x” and “y” to denote unknowns that were linked in the problem to be solved, and interpreted the given conditions as equations which the unknowns x and y would have to satisfy (i.e. as necessary constraints).
• The solutions to these equations then corresponded to possible solutions of the original problem.
• Sometimes the algebra did not quite generate a sufficient condition, giving rise to “pseudo-solutions” (values of x that satisfy the necessary conditions, but which did not correspond to actual solutions). So it was important to check each apparent solution - exactly as we did in Problem 180(b), where we checked that we can construct tilings for each of the vertex figures that arise in part (a).

The importance of the final step in this process (checking that the list of necessary constraints is also sufficient) is underlined in the next problem where we try to classify certain “almost regular” tilings.

Problem 181 A semi-regular tiling of the plane is an arrangement of regular polygons (not necessarily all identical), which fit together edge-to-edge so as to cover the plane without overlaps, and such that the arrangements of tiles around any two vertices are congruent.

(a) (i) Refine your argument in Problem 180(a) to list all possible vertex figures in a semi-regular tiling.

(ii) Try to find additional necessary conditions to eliminate vertex figures which cannot be realized, until your list of necessary conditions seems likely to be sufficient.

(b) The necessary conditions in part (a) give rise to a finite list of possible vertex figures. Construct all possible tilings corresponding to this list of possible vertex figures.

Semi-regular tilings are often called Archimedean tilings. The reason for this name remains unclear. Pappus (c. 290-c. 350 AD), writing more than 500 years after the death of Archimedes (d. 212 BC), stated that Archimedes classified the semi-regular polyhedra. Now the classification of semi-regular polyhedra (Problem 190) uses a similar approach to the classification of planar tilings, except that the sum of the angles at each vertex has sum less than (rather than exactly equal to) 360°. So it may be that the semi-regular tilings are named after Archimedes simply because he did something similar for polyhedra; or it may be that, since inequalities are harder to control than equalities, someone inferred (perhaps dodgily) that Archimedes must have known about semi-regular tilings as well as about semi-regular polyhedra. Whatever the reason, tilings and polyhedra have fascinated mathematicians, artists and craftsmen for all sorts of unexpected reasons - as indicated by:

• the fact that the classification and construction of the five regular polyhedra appear as the culmination of the thirteen books of Elements by Euclid (flourished c. 300 BC);
• the ancient Greek attempt to link the five regular polyhedra with the four elements (earth, air, fire, and water) and the cosmos;
• the ceramic tilings to be found in Islamic art - for example, on the walls of the Alhambra in Grenada;
• the book De Divina Proportions by Luca Pacioli (c. 1445-1509), and the continuing fascination with the Golden Ratio;
• the geometric sketches of Leonardo da Vinci (1452-1519);
• the work of Kepler (1571-1630) who used the regular polyhedra to explain his bold theoretical cosmology in the Astronomia Nova (1609).

5.5. Ruler and compasses constructions for regular polygons

Euclid’s Elements include methods for constructing the regular polygons that are required for the construction of the regular polyhedra (see Section 5.6). In one sense, Euclid is thoroughly modern: he is reluctant to work with entities that cannot be constructed. And for him, geometrical construction means construction “using ruler and compasses” only.

For each regular polygon, there are two related (and sometimes very different) construction problems:

• given two points A and B, construct the regular n-gon with AB as an edge of the regular polygon;
• given two points O and A, construct the regular n-gon ABCD. . . inscribed in the circle with centre O and passing through A, that is with circumradius OA.

Before Problem 137 we saw how to construct an equilateral triangle ABC given the points A, B. And in Problem 36 we saw that every regular polygon has a circumcentre O.

Problem 182 Given points O, A, show how to construct the regular 3-gon ABC with circumcentre O.

Problem 183

(a) Given two points O, A, show how to construct a regular 4-gon ABCD with circumcentre O.

(b) Given points A, B, show how to construct a regular 4-gon ABCD.

Problem 184

(a)(i) Given two points O, A, show how to construct a regular 6-gon ABCDEF with circumcentre O.

(ii) Given two points O, A, show how to construct a regular 8-gon ABCDEFGH with circumcentre O.

(b)(i) Given points A, B, show how to construct a regular 6-gon ABCDEF.

(ii) Given points A, B, show how to construct a regular 8-gon ABCDEFGH.

Problem 185

(a) (i) Given two points O, A, show how to construct a regular 5-gon ABCDE with circumcentre O.

(ii) Given points O, A, show how to construct a regular 10-gon ABCDEFGHIJ with circumcentre O.

(b) (i) Given points A, B, show how to construct a regular 5-gon ABCDE.

(ii) Given points A, B, show how to construct a regular 10-gon ABCDEFGHIJ.

We shall not prove it here, but it is impossible to construct a regular 7-gon, or a regular 9-gon, or a regular 11-gon using ruler and compasses. All constructions with ruler and compasses come down to two moves:

• if a is a known length, then $\sqrt{a}$ can be constructed (see Problem 173(c));
• if an n-gon can be constructed, then the sides can be bisected to produce a 2n-gon.

Put slightly differently, all ruler and compasses constructions involve solving linear or quadratic equations, so the only new points, or lengths we can construct are those which involve iterated square roots of expressions or lengths which were previously known.

This iterated extraction of square roots is linked to a fact first proved by Gauss (1777-1855), namely that the only regular p-gons (where p is a prime) that can be constructed are those where p is a Fermat prime - that is, a prime of the form p = 2^k + 1 (in which case k has to be a power of 2: see Problem 118). Gauss proved (as a teenager, though it was first published in his book Disquisitiones arithmeticae in 1801):

a regular n-gon can be constructed with ruler and compasses if and only if n has the form

$$2^m·p_1·p_2·p_3\cdots p_k,$$

where p₁,p₂,p₃,... ,p_k are distinct Fermat primes.

As we noted in Chapter 2, the only known Fermat primes are the five discovered by Fermat himself, namely 3, 5, 17, 257, and 65 537.

5.6. Regular and semi-regular polyhedra

We have seen how regular polygons sometimes fit together edge-to-edge in the plane to create tilings of the whole plane. When tiling the plane, the angles of polygons meeting edge-to-edge around each vertex must add to 360°, or two straight angles. If the angles at a vertex add to less than 360°, then we are left with an empty gap and two free edges; and when these two free edges are joined, or glued together, the vertex figure rises out of the plane and becomes a 3-dimensional corner, or solid angle.

To form such a corner we need at least three polygons, or faces - and hence at least three edges and three faces meet around each vertex. For example, three squares fit nicely together in the plane, but leave a 90° gap. When the two spare edges are glued together, the result is to form a corner of a cube, where we have a vertex figure consisting of three regular 4-gons: so we refer to this vertex figure as 4³.

Given a 3-dimensional corner, it may be possible to extend the construction, repeating the same vertex figure at every vertex. The resulting shape may then ‘close up’ to form a convex polyhedron. The assumption that in each vertex figure, the angles meeting at that vertex add to less than 360°, means that all the corners then project outwards - which is roughly what we mean when we say that the polyhedron is “convex”.

A regular polygon is an arrangement of finitely many congruent line segments, with two line segments meeting at each vertex (and never crossing, or meeting internally), and with all vertices alike; a regular polygon can be inscribed in a circle (Problem 36), and so encloses a convex subset of the plane. In the same spirit, a regular polyhedron is an arrangement of finitely many congruent regular polygons, with two polygons meeting at each edge, and with the same number of polygons in a single cycle around every vertex, enclosing a convex subset of 3-dimensional space (i.e. the polyhedron separates the remaining points of 3D into those that lie ‘inside’ and those that lie ‘outside’, and the line segment joining any two points of the polyhedral surface contains no points lying outside the polyhedron).

The important constraints here are the assumptions: that the polygons meet edge-to-edge with exactly two polygons meeting at each edge; that the same number of polygons meet around every vertex; and that the overall number of polygons, or faces, is finite. The assumption that the figure is convex should be seen as a temporary additional constraint, which means that the angles in polygons meeting at each vertex have sum less than 360°.

Problem 186 A vertex figure is to be formed by fitting regular p-gons together, edge-to-edge, for a fixed p. If there are q of these p-gons at a vertex, we denote the vertex figure by p^q. If the angles at each vertex add to less than 360°, prove that the only possible vertex figures are 3³, 3⁴, 3⁵, 4³, 5³.

The vertex figure 4³ is realized by the way the positive axes meet at the vertex (0,0,0), where

• the unit square (0, 0,0), (1, 0,0), (1,1,0), (0,1,0) in the xy-plane (with equation z = 0) meets
• the unit square (0,0,0), (1,0,0), (1,0,1), (0,0,1) in the xz-plane (with equation y = 0), and
• the unit square (0, 0, 0), (0,1,0), (0,1,1), (0, 0,1) in the yz-plane (with equation x = 0).

If we include an eighth vertex (1, 1, 1), and

• the unit square (0, 0, 1), (1, 0, 1), (1, 1, 1), (0, 1, 1) in the plane with equation z = 1,
• the unit square (0,1,0), (1,1,0), (1,1,1), (0,1,1) in the plane with equation y = 1,
• the unit square (1,0,0), (1,1,0), (1,1,1), (1,0,1) in the plane with equation x = 1,

we see that all eight vertices have the same vertex figure 4³. Hence the possible vertex figure 4³ in Problem 186 arises as the vertex figure of a regular polyhedron - namely the cube.

If we select the four vertices whose coordinates have odd sum A = (1, 0, 0), B = (0,1, 0), C = (0, 0,1), D = (1,1,1), then the distance between any two of these vertices is equal to $\sqrt{2}$, so each triple of vertices (such as (1, 0, 0), (0,1,0), (0, 0,1)) defines a regular 3-gon ABC, with three such 3-gons meeting at each vertex of ABCD. Hence the possible vertex figure 3³ in Problem 186 arises as the vertex figure of a regular polyhedron - namely the regular tetrahedron (tetra = four; hedra = faces).

Problem 187 With A = (1,0,0) etc. as above, write down the coordinates of the six midpoints of the edges of the regular tetrahedron ABCD (or equivalently, the six centres of the faces of the original cube). Each edge of the regular tetrahedron meets four other edges of the regular tetrahedron (e.g. AB meets AC and AD at one end, and BC and BD at the other end). Choose an edge AB and its midpoint P. Calculate the distance from P to the midpoints Q, R, S, T of the four edges which AB meets (namely the midpoints of AB, AD, BD, BC respectively). Confirm that the triangles ΔPQR, ΔPRS, ΔPST, ΔPTQ are all regular 3-gons, and that the vertex figure at P is of type 3⁴ . Conclude that the possible vertex figure 3⁴ in Problem 186 arises as the vertex figure of a regular polyhedron PQRSTU - namely the regular octahedron (octa = eight; hedra = faces).

Problem 188

(a) A regular tetrahedron ABCD has edges of length 2, and sits with its base BCD on the table. Find the height of A above the base.

(b) A regular octahedron ABCDEF has four triangles meeting at each vertex.

(i) Let the four triangles which meet at A be ABC, ACD, ADE, AEB. Prove that BCDE must be a square.

(ii) Suppose that all the triangles have edges of length 2, and that the octahedron sits with one face BCF on the table - next to the regular tetrahedron from part (a). Which of these two solids is the taller?

Problem 189 Let O = (0, 0, 0), A = (1,0,0), B = (0,1,0), C = (0,0,1) be four vertices of the cube as described after Problem 186 above. Draw equal and parallel line segments (initially of unknown length 1 — 2a) through the centres of each pair of opposite faces - running in the three directions parallel to OA, or to OB, or to OC

• from $N=\left(a,\frac{1}{2},0\right)$ to $P=\left(1-a,\frac{1}{2},0\right)$ and from $Q=\left(a,\frac{1}{2},1\right)$ to $R=\left(1-a,\frac{1}{2},1\right)$
• from $S=\left(\frac{1}{2},0,a\right)$ to $T=\left(\frac{1}{2},0,1-a\right)$ and from $U=\left(\frac{1}{2},1,a\right)$ to $V=\left(\frac{1}{2},1,1-a\right)$
• from $W=\left(0,a,\frac{1}{2}\right)$ to $X=\left(0,1-a,\frac{1}{2}\right)$ and from $Y=\left(1,a,\frac{1}{2}\right)$ to $Z=\left(1,1-a,\frac{1}{2}\right)$ .

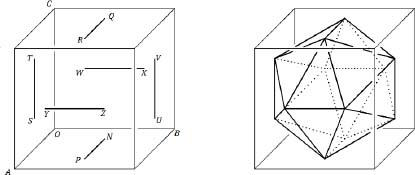
Figure 4: Construction of the regular icosahedron.

These are to form all 12 vertices and six of the 30 edges (of length 1 — 2a) of a polyhedron, see Figure 4. The other 24 edges join each of these 12 vertices to its four natural neighbours on adjacent faces of the cube - to form the 20 triangular faces of the polyhedron: for example,

N joins: to S; to W; to X; and to U.

(i) Prove that NS = NW = NX = NU and calculate the length of NS.

(ii) Choose the value of the parameter a to guarantee that NP = NS, so that the five triangular faces meeting at the vertex N are all equilateral triangles, and each vertex figure of the resulting polyhedron then has vertex figure 3⁵.

The polyhedron is called the regular icosahedron (icosa = twenty, hedra = faces).

In the paragraph before Problem 187 we constructed the dual of the cube by marking the circumcentre of each of the six square faces of the cube, and then joining each circumcentre to its four natural neighbours. We now construct the dual of the regular icosahedron in exactly the same way. Each of the 20 circumcentres of the 20 triangular faces of a regular icosahedron has three natural neighbours (namely the circumcentres of the three neighbouring triangular faces). If we construct the 30 edges joining these 20 circumcentres, the five circumcentres of the five triangles in each vertex figure of the regular icosahedron form a regular pentagon, which becomes a face of the dual polyhedron - so we get 12 regular pentagons (one for each vertex of the regular icosahedron), with three pentagons meeting at each vertex of the dual polyhedron to give a vertex figure 5³ at each of the 20 vertices, which form a regular dodecahedron.

Hence each of the five possible vertex figures in Problem 186 can be realised by a regular polyhedron. These are sometimes called the Platonic solids because Plato (c. 428-347 BC) often used them as illustrative examples in his writings on philosophy.

Constructing the five regular polyhedra is part of the essence of mathematics for everyone. In contrast, what comes next (in Problem 190) may be viewed as “optional” at this stage. The ideas are worth noting, but the details may be best postponed for a rainy day.

Just as you classified semi-regular tilings in Section 5.4, so one can look for semi-regular polyhedra. A polyhedron is semi-regular if all of its faces are regular polygons (possibly with differing numbers of edges), fitting together edge-to-edge, with exactly the same ring of polygons around each vertex - the vertex figure of the polyhedron. Problem 190 uses “the method of analysis” - combining simple arithmetic, inequalities, and a little geometric insight - to achieve a remarkable complete classification of semi-regular polyhedra. There are usually said to be thirteen individual semi-regular polyhedra (excluding the five regular polyhedra); but one of these has a vertex figure that extends to a polyhedron in two different ways - each being the reflection of the other. There are in addition two infinite families - namely

• the n-gonal prisms, which consist of two parallel regular n-gons, with the top one positioned exactly above the bottom one, the two being joined by a belt of n squares (so with vertex figure n . 4²); and
• the n-gonal antiprisms, which consist of two parallel regular n-gons, but with the top n-gon turned through an angle of n radians relative to the bottom one, the two being joined by a belt of 2n equilateral triangles (so with a vertex figure n . 3³).

Notice that the cube can also be interpreted as being a “4-gonal prism”, and the regular octahedron can be interpreted as being a “3-gonal antiprism”. Those interested in regular and semi-regular polyhedra are referred to the classic book Mathematical models by H.M. Cundy and A.P. Rollett.

Problem 190 Find possible combinations of three or more regular polygons whose angles add to less than 360°, and hence derive a complete list of possible vertex figures for a (convex) semi-regular polyhedron. Try to eliminate those putative vertex figures that cannot be extended to a semi-regular polyhedron.

5.7. The Sine Rule and the Cosine Rule

Where given information, or a specified geometrical construction, determines an angle or length uniquely, it is sometimes - but not always - possible to find this angle or length using simple-minded angle-chasing and congruence.

Problem 191

(a) In the quadrilateral ABCD the two diagonals AC and BD cross at X. Suppose AB = BC, ∠BAC = 60°, ∠DAC = 40°, ∠BXC = 100°.

(i) Calculate (exactly) ∠ADB and ∠CBD.

(ii) Calculate ∠BDC and ∠ACD.

(b) In the quadrilateral ABCD the two diagonals AC and BD cross at X. Suppose AB = BC, ∠BAC = 70°, ∠DAC = 40°, ∠BXC = 100°.

(i) Calculate (exactly) the size of ∠BDC + ∠ACD.

(ii) Explain how we can be sure that ∠BDC and ∠ACD are uniquely determined, even though we cannot calculate them immediately.

If it turns out that the simplest tools do not allow us to determine angles and lengths, this is usually because we are only using the most basic properties: the congruence criteria, and the parallel criterion. The general art of ‘solving triangles’ depends on the similarity criterion (usually via trigonometry). And the two standard techniques for ‘solving triangles’ that go beyond “angle-chasing” and congruence are the Sine Rule, which was established back in Problem 32 (and its consequences, such as the area formula $\frac{1}{2}ab\sin C$ - see Problem 33), and the Cosine Rule.

The next problem invites you to use Pythagoras’ Theorem to prove the Cosine Rule - an extension of Pythagoras’ Theorem which applies to all triangles ABC (including those where the angle at C may not be a right angle).

Problem 192 (The Cosine Rule) Given ΔABC, let the perpendicular from A to BC meet BC at P. If P = C, then we know (by Pythagoras’ Theorem) that c² = a² + b². Suppose $P\ne C$ .

(i) Suppose first that P lies on the line segment CB, or on CB extended beyond B. Express the lengths of PC and AP in terms of b and ∠C. Then apply Pythagoras’ Theorem to A ΔAPB to conclude that

$$c^2=a^2+b^2-2ab\cos C.$$

(ii) Suppose next that P lies on the line segment BC extended beyond C. Prove once again that

$$c^2=a^2+b^2-2ab\cos C.$$

Problem 193 Go back to the configuration in Problem 191(b). The required angles are unaffected by scaling, so we may choose AB = BC = 1. Devise a strategy using the Sine Rule and the Cosine Rule to calculate ∠BDC and ∠ACD exactly.

It is worth reflecting on what the Cosine Rule really tells us:

(i) if in a triangle, we know any two sides (a and b) and the included angle (C), then we can calculate the third side (c); and

(ii) if we know all three sides (a, b, c), then we can calculate any angle (say C).

Hence if we know three sides, or two sides and the angle between them, we can work out all of the angles. The Sine Rule then complements this by ensuring that:

(iii) if we know any side and two angles (in which case we also know the third angle), then we can calculate the other two sides; and

(iv) if we know any angle A, and two sides - one of which is the side a opposite A, then we can calculate (one and hence) both the other angles (and hence the third side).

The upshot is that once a triangle is uniquely determined by the given data, we can “solve” to find all three sides and all three angles.

Trigonometry has a long and very interesting history (which is not at all easy to unravel). Euclid (flourished c. 300 BC) understood that corresponding sides in similar figures were “proportional”. And he stated and proved the generalization of Pythagoras’ Theorem, which we now call the Cosine Rule; but he did this in a theoretical form, without introducing cosines. Euclid’s versions for acute-angled and obtuse-angled triangles involved correction terms with opposite signs, so he proved them separately (Elements, Book II, Propositions 12 and 13).

However, the development of trigonometry as an effective theoretical and practical tool seems to have been due to Hipparchus (died c. 125 BC), to Menelaus (c. 70-130 AD), and to Ptolemy (died 168 AD). Once trigonometry moved beyond the purely theoretical, the combination of

• the (exact) language of trigonometry, together with the Sine Rule and the Cosine Rule, and
• (approximate) “tables of trigonometric ratios” (nowadays replaced by calculators)

liberated astronomers, and later engineers, to calculate lengths and angles efficiently, and as accurately as they required.

In mathematics we either work with exact values, or we have to control errors precisely. But trigonometry can still be a valuable exact tool, provided we remember the lessons of working with fractions such as $\frac{2}{3}$ or with surds such as , or with constants such as $\sqrt{2}$, and resist the temptation to replace them by some unenlightening approximate decimal. We can replace ${\cos }^{-1}\left(\frac{1}{2}\right)\left(=\frac{\pi }{3}\right)$ and ${\cos }^{-1}\left(-\frac{1}{2}\right)\left(=\frac{2\pi }{3}\right)$ by their exact values; but in general we need to be willing to work with, and to think about, exact forms such as “${\cos }^{-1}\left(\frac{1}{3}\right)$” and “${\cos }^{-1}\left(-\frac{1}{3}\right)$” , without switching to some approximate evaluation.

Problem 194

(a) Let ABCD be a regular tetrahedron with edges of length 2. Calculate the (exact) angle between the two faces ABC and DBC.

(b) We know that in 2D five equilateral triangles fit together at a point leaving just enough of an angle to allow a sixth triangle to fit. How many identical regular tetrahedra can one fit together, without overlaps around an edge, so that they all share the edge BC (say)?

Problem 195

(a) Let ABCDEF be a regular octahedron with vertices B, C, D, E adjacent to A forming a square BCDE, and with edges of length 2. Calculate the (exact) angle between the two faces ABC and FBC.

(b) How many identical regular octahedra can one fit together around an edge, without overlaps, so that they all share the edge BC (say)?

Problem 196 Go back to the scenario of Problem 188, with a regular tetrahedron and a regular octahedron both having edges of length 2, and both having one face flat on the table. Suppose we slide the tetrahedron across the table towards the octahedron. What unexpected phenomenon is guaranteed by Problems 194(a) and 195(a)?

Problem 197 Consider the cube with edges of length 2 running parallel to the coordinate axes, with its centre at the origin (0,0,0), and with opposite corners at (1,1,1) and (—1, —1, —1). The x-, y-, and z-axes, and the xy-, yz-, and zx-planes cut this cube into eight unit cubes - one sitting in each octant.

(i) Let A = (0,0,1), B = (1, 0, 0), C = (0,1,0), W = (1,1,1). Describe the solid ABCW.

(ii) Let D = (—1, 0, 0), X = (—1,1,1). Describe the solid ACDX.

(iii) Let E = (0, —1,0), Y = (—1, —1,1). Describe the solid ADEY.

(iv) Let Z = (1, —1,1). Describe the solid AEBZ.

(v) Let F = (0,0, —1) and repeat steps (i)-(iv) to obtain the four mirror image solids which lie beneath the xy-plane.

(vi) Describe the solid ABCDEF which is surrounded by the eight identical solids in (i)-(v).

Problem 198 Consider a single face ABCDE of the regular dodecahedron, with edges of length 1, together with the five pentagons adjacent to it - so that each of the vertices A, B, C, D, E has vertex figure 5³. Each vertex figure is rigid, so the whole arrangement of six regular pentagons is also rigid. Let V, W, X, Y, Z be the five vertices adjacent to A, B, C, D, E respectively. Calculate the dihedral angle between the two pentagonal faces that meet at the edge AB.

Problem 199 Suppose a regular icosahedron (Problem 189) has edges of length 2. Position vertex A at the ‘North pole’, and let BCDEF be the regular pentagon formed by its five neighbours.

(a)(i) Calculate the exact angle between the two faces ABC and ACD.

(ii) How many identical regular icosahedra can one fit together, without overlaps, around a single edge?

(b) Let C be the circumcircle of BCDEF, and let O be the circumcentre of this regular pentagon.

(i) Prove that the three edge lengths of the right-angled triangle ΔBOA are the edge lengths of the regular hexagon inscribed in the circle C, of the regular 10-gon inscribed in the circle C, and of the regular 5-gon inscribed in the circle C.

(ii) Calculate the distance separating the plane of the regular pentagon BCDEF, and the plane of the corresponding regular pentagon joined to the ‘South pole’.

Notice that Problem 199(b) shows that the regular icosahedron can be ‘constructed’ in the Euclidean spirit: part (b)(i) is essentially Proposition 10 of Book XIII of Euclid’s Elements, and part (b)(ii) is implicit in Proposition 16 of the Book XIII. Once we are given the radius OB, we can:

• construct the regular pentagon BCDEF in the circle C;
• bisect the sides of the regular pentagon and hence construct the regular 10-gon BVC . . . in the same circle;
• construct the vertical perpendicular at O, and transfer the length BV to the point O to determine the vertex A directly above O;
• transfer the radius OB to the vertical perpendicular at O to determine the plane directly below O, and hence construct the lower regular pentagon; etc..

It may be worth commenting on a common confusion concerning the regular icosahedron. Each regular polyhedron has a circumcentre, with all vertices lying on a corresponding sphere. If we join any triangular face of the regular icosahedron to the circumcentre O, we get a tetrahedron. These 20 tetrahedra are all congruent and fit together exactly at the point O “without gaps or overlaps”. But they are not regular tetrahedra: the circumradius is less than the edge length of the regular icosahedron.

Problem 200 Prove that the only regular polyhedron that tiles 3D (without gaps or overlaps) is the cube.

In one sense the result in Problem 200 is disappointing. However, since we know that there are all sorts of interesting 3-dimensional arrangements related to crystals and the way atoms fit together, the message is really that we need to look beyond regular tilings. For example, the construction in Problem 197 shows how the familiar regular tiling of space with cubes incorporates a semi-regular tiling of space with eight regular tetrahedra and two regular octahedra at each vertex.

5.8. Circular arcs and circular sectors

Length is defined for straight line segments, and area is defined in terms of rectangles; neither measure is defined for shapes with curved boundaries - unless, that is, they can be cunningly dissected and the pieces rearranged to make a straight line, or a rectangle.

Figure 5: Dumbbell.

Problem 201 Four identical semicircles of radius 1 fit together to make the dumbbell shape shown in Figure 5. Find the exact area enclosed without using the formula for the area of a circle.

In general, making sense of length and area for shapes with curved boundaries requires us to combine a little imagination with what we know about straight line segments and polygons. Our goal here is to lead up to the familiar results for the length of circular arcs and the area of circular sectors. But first we need to explore the perimeter and area of regular polygons, and the surface area of prisms and pyramids.

As so often in mathematics, to make sense of the perimeter and area of regular polygons we need to look beyond their actual values (which will vary according to the size of the polygon), and instead interpret these values as a function of some normalizing parameter - such as the radius. The calculations will be simpler if you first prove a general result.

Problem 202

(a) A regular n-gon and a regular 2n-gon are inscribed in a circle of radius 1. The regular n-gon has edges of length s_n = s, while the regular 2 n-gon has edges of length s_2n = t. Prove that

$$t^2=2-\sqrt{4-s^2}.$$

(b) A regular “2-gon” inscribed in the unit circle is just a diameter (repeated twice), so has two identical edges of length s₂ = 2. Use the result in part (a) to calculate the edge length s₄ of a regular 4-gon, and the edge length s₈ of a regular 8-gon inscribed in the same circle.

(c) A regular 6-gon inscribed in the unit circle has edge length s₆ equal to the radius 1. Use the result in part (a) to calculate the edge length s₃ of a regular 3-gon inscribed in the unit circle, and the edge length s₁₂ of a regular 12-gon inscribed in the unit circle.

(d) In Problem 185 we saw that a regular 5-gon inscribed in the unit circle has edge length

$$s_5=\frac{\sqrt{10-2\sqrt{5}}}{2}.$$

Use the result in part (a) to calculate the edge length s₁₀ of a regular 10-gon inscribed in the same circle.

Problem 203

(a) A regular n-gon is inscribed in a circle of radius r.

(i) Find the exact perimeter p_n (in surd form): when n = 3; when n = 4; when n = 5; when n = 6; when n = 8; when n = 10; when n = 12.

(ii) Check that, for each n:

$$p_n=c_n\times r$$

for some constant c_n, where

$$c_3<c_4<c_5<c_6<c_8<c_{10}<c_{12}\cdots$$

(b) A regular n-gon is circumscribed about a circle of radius r.

(i) Find the exact perimeter P_n (in surd form): when n = 3; when n = 4; when n = 5; when n = 6; when n = 8; when n = 10; when n = 12.

(ii) Check that, for each n:

$$p_n=c_n\times r$$

for some constant C_n, where

$$c_3<c_4<c_5<c_6<c_8<c_{10}<c_{12}\cdots$$

(c) Explain why c₁₂ < C₁₂.

It follows from Problem 203 that

• the perimeters p_n and P_n of regular n-gons inscribed in, or circumscribed about, a circle of radius r all have the same form:

  $$(inscribed)p_n=c_n\times r;(circumscribed)P_n=C_n\times r.$$

• The perimeters of inscribed regular n-gons all increase with n, but remain less than the perimeter of the circle, while
• the perimeters of the circumscribed regular n-gons all decrease with n, but remain greater than the perimeter of the circle.

Hence

• the perimeter P of the circle appears to have the form P = K × r, where the ratio

  $$K=\frac{\text{ perimeter }}{\text{ radius }}$$

  satisfies

  $$c_3<c_4<c_5<c_6<c_8<c_{10}<\cdots <K<\cdots <C_{10}<C_8<C_6<C_5<C_4<C_3.$$

  In particular, the value of the constant K lies somewhere between c₄₂ = 6.21 . . . and C12 = 6.43 . . . . If we now define the quotient K to be equal to “2π”, we see that

  $$(perimeterofcircleofradiusr)=2\pi r,$$

  where π denotes some constant lying between 3.1 and 3.22

  In this spirit one might reinterpret the first two bullet points as defining two sequences of constants "π_n" and "Π_n" for $n⩾3$, such that

• (perimeter of a regular n-gon with circumradius r) = 2π_nr, where

  $${\pi }_3=\frac{3\sqrt{3}}{2}=2.59\cdots ,{\pi }_4=2\sqrt{2}=2.82\cdots ,{\pi }_5=\frac{5\sqrt{10-2\sqrt{5}}}{4}=2.93\cdots ,{\pi }_6=3,$$

  etc.,

  and

• (perimeter of a regular n-gon with inradius r)= 2Π_nr, where

  $${\Pi }_3=3\sqrt{3}=5.19\cdots ,{\Pi }_4=4,{\Pi }_5=5\sqrt{5-2\sqrt{5}}=3.63\cdots ,{\Pi }_6=2\sqrt{3}=3.46\cdots ,$$

  etc.,

  Moreover

  $${\pi }_3<{\pi }_4<{\pi }_5<{\pi }_6<{\pi }_8<\cdots <\pi <\cdots <{\Pi }_8<{\Pi }_6<{\Pi }_5<{\Pi }_4<{\Pi }_3.$$

Problem 204 Find the exact length (in terms of π)

(i) of a semicircle of radius r;

(ii) of a quarter circle of radius r;

(iii) of the length of an arc of a circle of radius r that subtends an angle θ radians at the centre.

In the next problem we follow a similar sequence of steps to conclude that the quotient

$$L=\frac{\text{ area of circle of radius }r}{r^2}$$

is also constant. The surprise lies in the fact that this different constant is so closely related to the previous constant K.

Problem 205

(a) A regular n-gon is inscribed in a circle of radius r.

(i) Find the exact area a_n (in surd form): when n = 3; when n = 4; when n = 5; when n = 6; when n = 8; when n = 10; when n = 12.

(ii) Check that, for each n:

$$a_n=d_n\times r^2$$

for some constant d_n, where

$$d_3<d_4<d_5<d_6<d_8<d_{10}<d_{12}\cdots$$

(b) A regular n-gon is circumscribed about a circle of radius r.

(i) Find the exact area A_n (in surd form): when n = 3; when n = 4; when n = 5; when n = 6; when n = 8; when n = 10; when n = 12.

(ii) Check that, for each n:

$$A_n=D_n\times r^2$$

for some constant D_n, where

$$D_3>D_4>D_5>D_6>D_8>D_{10}>D_{12}\cdots$$

(c) Explain why d₁₂ < D₁₂.

It follows from Problem 205 that

the areas a_n and A_n of regular n-gons inscribed in, or circumscribed about, a circle of radius r all have the same form:

$$(inscribed)a_n=d_n\times r^2;(circumscribed)A_n=D_n\times r^2.$$

• The areas of inscribed regular n-gons all increase with n, but remain less than the area of the circle, while
• the areas of the circumscribed regular n-gons all decrease with n, but remain greater than the area of the circle, whence
• the area A of the circle appears to have the form A = L × r², where the ratio

  $$L=\frac{\text{ area of circle of radius }r}{\text{ radius squared }}$$

  satisfies

  $$d_3<d_4<d_5<d_6<d_8<d_{10}\cdots <L<\cdots <D_{10}<D_8<D_6<D_4<D_3.$$

  In particular, the value of L lies somewhere between d₁₂ = 3 and $D_{12}=12(2-\sqrt{3})=3.21\cdots$ . The surprise lies in the fact that the constant L is exactly half of the constant K - that is, L = π, so

  $$(areaofcircleofradiusr)=\pi r^2.$$

The next problem offers a heuristic explanation for this surprise.

Figure 6: Circle cut into 8 slices.

Problem 206 A regular 2n-gon ABCDE . . . is inscribed in a circle of radius r. The 2n radii OA, OB,... joining the centre O to the 2n vertices cut the circle into 2n sectors, each with angle $\frac{\pi }{n}$ (Figure 6).

These 2n sectors can be re-arranged to form an “almost rectangle”, by orienting them alternately to point “up” and “down”. In what sense does this “almost rectangle” have “height = r” and πr?

Problem 207

(a) Find a formula for the surface area of a right cylinder with height h and with circular base of radius r.

(b) Find a similar formula for the surface area of a right prism with height h, whose base is a regular n-gon with inradius r.

Problem 208

(a) Find the exact area (in terms of π)

(i) of a semicircle of radius r;

(ii) of a quarter circle of radius r;

(iii) of a sector of a circle of radius r that subtends an angle θ radians at the centre.

(b) Find the area of a sector of a circle of radius 1, whose total perimeter (including the two radii) is exactly half that of the circle itself.

Problem 209

(a) Find a formula for the surface area of a right circular cone with base of radius r and slant height l.

(b) Find a similar formula for the surface area of a right pyramid with apex A whose base BCDE. . . is a regular n-gon with inradius r.

Problem 210

(a) Find an expression involving “$\sin \frac{\pi }{n}$ ” for the ratio

$$\frac{\text{ perimeter of inscribed regular }n\text{ -gon }}{\text{ perimeter of circumscribed circle }}.$$

(b) Find an expression involving “$\tan \frac{\pi }{n}$ ” for the ratio

$$\frac{\text{ perimeter of circumscribed regular }n\text{ -gon }}{\text{ perimeter of inscribed circle }}.$$

Problem 211

(a) Find an expression involving “$\sin \frac{2\pi }{n}$ ” for the ratio

$$\frac{\text{ area of inscribed regular }n-\text{gon}}{\text{ area of circumscribed circle }}.$$

(b) Find an expression involving “$\tan \frac{\pi }{n}$ ” for the ratio

$$\frac{areaofcircumscribedregularn-\text{gon}}{areaofinscribedcircle}.$$

5.9. Convexity

This short section presents a simple result which to some extent justifies the assumptions made in the previous section - namely that the perimeter (or area) of a regular n-gon inscribed in a circle is less than the perimeter (or area) of the circle, and of the circumscribed regular n-gon.

Problem 212 A convex polygon P₁ is drawn in the interior of another convex polygon P₂.

(a) Explain why the area of P₁ must be less than the area of P₂.

(b) Prove that the perimeter of P₁ must be less than the perimeter of P₂.

5.10. Pythagoras’ Theorem in three dimensions

Pythagoras’ Theorem belongs in 2-dimensions. But does it generalise to 3-dimensions? The usual answer is to interpret the result in terms of coordinates.

Problem 213

(a) Construct a right angled triangle that explains the standard formula for the distance from P = (a, b) to Q = (d, e).

(b) Use part (a) to derive the standard formula for the distance from P =(a, b, c) to Q = (d, e, f).

This extension of Pythagoras’ Theorem to 3-dimensions is extremely useful, but not very profound. In contrast, the next result is more intriguing, but seems to be a complete uke of limited relevance. In 2D, a right angled triangle is obtained by

• taking one corner A of a rectangle ABCD, together with its two neighbours B and D;
• then “cutting off the corner” to get the triangle ABD.

This suggests that a corresponding figure in 3D might be obtained by

taking one corner A of a cuboid, together with its three neighbours B, C, D;

then cutting off the corner to get a pyramid ABCD, with the right angled triangle ΔABC as base, and with apex D.

The obvious candidate for the “3D-hypotenuse” is then the sloping face BCD, and the three right angled triangles ΔABC, ΔACD, ΔADB presumably correspond to the ‘legs’ (the shorter sides) of the right triangle in 2D.

Problem 214 You are given a pyramid ABCD with all three faces meeting at A being right angled triangles with right angles at A. Suppose AB = b, AC = c, AD = d.

(a) Calculate the areas of ΔABC, ΔACD, ΔADB in terms of b, c, d.

(b) Calculate the area of ΔBCD in terms of b, c, d.

(c) Compare your answer in part (b) with the sum of the squares of the three areas you found in part (a).

More significant (e.g. for navigation on the surface of the Earth) and more interesting than Problem 214 is to ask what form Pythagoras’ Theorem takes for “lines on a sphere”.

For simplicity we work on a unit sphere. We discovered in the run-up to Problem 34 that lines, or shortest paths, on a sphere are arcs of great circles. So, if the triangle ΔABC on the unit sphere is right angled at A, we may rotate the sphere so that the arc AB lies along the equator and the arc AC runs up a circle of longitude. It is then clear that, once the lengths c, b of AB and AC are known, the locations of B and C are essentially determined, and hence the length of the arc BC on the sphere is determined. So we would like to have a simple formula that would allow us to calculate the length of the arc BC directly in terms of c and b.

Problem 215 Given a spherical triangle ΔABC on the unit sphere with centre O, such that ∠BAC is a right angle, and such that AB has length c, and AC has length b.

(a) We have (rightly) referred to b and c as ‘lengths’. But what are they really?

(b) We want to know how the inputs b and c determine the value of the length a of the arc BC; that is, we are looking for a function with inputs b and c, which will allow us to determine the value of the "output" a. Think about the answer to part (a). What kind of standard functions do we already know that could have inputs b and c?

(c) Suppose $c=0\ne b$ . What should the output a be equal to? (Similarly if $b=0\ne c$.) Which standard function of b and of c does this suggest is involved?

(d) (i) Suppose $\angle B=\angle C=\frac{\pi }{2}$ , what should the output a be equal to?

(ii) Suppose $\angle B=\frac{\pi }{2}$ , but ∠C (and hence c) is unconstrained. The output a is then determined - but the formula must give this fixed output for different values of c. What does this suggest as the “simplest possible” formula for a?

The answers to Problem 215 give a pretty good idea what form Pythagoras’ Theorem must take on the unit sphere. The next problem proves this result as a simple application of the familiar 2D Cosine Rule.

Problem 216 Given any triangle ΔABC on the unit sphere with a right angle at the point A, we may position the sphere so that A lies on the equator, with AB along the equator and AC up a circle of longitude. Let O be the centre of the sphere and let T be the tangent plane to the sphere at the point A. Extend the radii OB and OC to meet the plane T at Bʹ and Cʹ respectively.

(a) Calculate the lengths of the line segments ABʹ and ACʹ, and hence of BʹCʹ.

(b) Calculate the lengths of OBʹ and OCʹ, and then apply the Cosine Rule to ΔBʹOCʹ to find an equation linking b and c with ∠BʹOCʹ(=a).

When “solving triangles” on the sphere the same principles apply as in the plane: right angled triangles hold the key - but Pythagoras’ Theorem and trig in right angled triangles must be extended to obtain variations of the Sine Rule and the Cosine Rule for spherical triangles. The corresponding results on the sphere are both similar to, and intriguingly different from, those we are used to in the plane. For example, there are two forms of the Cosine Rule extending the result in Problem 216.

Problem 217 Given a (not necessarily right angled) triangle ΔABC on the unit sphere, apply the same proof as in Problem 216 to show (with the usual labelling) that:

$$\cos a=\cos b·\cos c+\sin b·\sin c·\cos A$$

The other form of the Cosine Rule is “dual” to that in Problem 217 (with arcs and angles interchanged, and with an unexpected change of sign) - namely:

$$\cos A=-\cos B·\cos C+\sin B·\sin C·\cos a$$

The next two problems derive a version of the Sine Rule for spherical triangles.

Problem 218 Let ΔABC be a triangle on the unit sphere with a right angle at A. Let Aʹ lie on the arc BA produced, and Cʹ lie on the arc BC produced so that ΔAʹBCʹ is right angled at Aʹ. With the usual labelling (so that x denotes the length of the side of a triangle opposite vertex X, with arc AC = b, arc BC = a, arc BCʹ = aʹ, and arc AʹCʹ = bʹ, prove that:

$$\frac{\sin b}{\sin a}=\frac{\sin b^{\prime }}{\sin a^{\prime }}$$

Problem 219 Let ΔABC be a general triangle on the unit sphere with the usual labelling (so that x denotes the length of the side of a triangle opposite vertex X, and X is used both to label the vertex and to denote the size of the angle at X). Prove that:

$$\frac{\sin a}{\sin A}=\frac{\sin b}{\sin B}=\frac{\sin c}{\sin C}.$$

It is natural to ask (cf Problem 32):

“If the three ratios in Problem 219 are all equal, what is it that they are all equal to?”

The answer may not at first seem quite as nice as in the Euclidean 2-dimensional case: one answer is that they are all equal to

$$\frac{\sin a·\sin b·\sin c}{\text{ volume of the tetrahedron }OABC}.$$

Notice that this echoes the result in the Euclidean plane, where the three ratios in the Sine Rule are all equal to 2R, and

$$2R=\frac{abc}{2(\text{ area of }\Delta ABC)}.$$

5.11. Loci and conic sections

This section offers a brief introduction to certain classically important loci in the plane. The word locus here refers to the set of all points satisfying some simple geometrical condition; and all the examples in this section are based on the notion of distance from a point and from a line.

Given a point O and a positive real r, the locus of points at distance r from O is precisely the circle of radius r with centre O. If r < 0, then the locus is empty; while if r = 0, the locus consists of the point O alone.

Given a line m and a positive real r, the locus of all points at distance r from the line m consists of a pair of parallel lines - one either side of the line m. Given a circle of radius r, and a positive real number d < r; the locus of points at distance d from the circle consists of two circles, each concentric with the given circle (one inside the given circle and one outside). If d > r, the locus consists of a single circle outside the given circle.

Given two points A and B, the locus of points which are equidistant from A and from B is precisely the perpendicular bisector of the line segment AB. And given two lines m, n the locus of points which are equidistant from m and from n takes different forms according as m and n are, or are not, parallel.

• If m and n are parallel, then the locus consists of a single line parallel to m and n and half way between them.
• If m and n meet at X (say), then the locus consists of the pair of perpendicular lines through X, that bisect the four angles at X.

Problem 220 Given a point F and a line m, choose m as the x-axis and the line through F perpendicular to m as the y-axis. Let F have coordinates (0, 2a).

(i) Find the equation that defines the locus of points which are equidistant from F and from m.

(ii) Does the equation suggest a more natural choice of axes - and hence a simpler equation for the locus?

The locus, or curve, in Problem 220 is called a parabola; the point F is called the focus of the parabola, and the line m is called the directrix. In general, the ratio

"the distance from X to F” : “the distance from X to m"

is called the eccentricity of the curve. Hence the parabola has eccentricity e = 1.

The parabola has many wonderful properties: for example, it is the path followed by a projectile under the force of gravity; if viewed as the surface of a mirror, a parabola reflects the sun's rays (or any parallel beam) to a single point - the focus F. Since the only variable in the construction of the parabola is the distance “2a” between the focus and the directrix, we can scale distances to see that any two different-looking parabolas must in fact be similar to one another - just as with any two circles. (It is hard not to infer from the graphs that y = 10x² is a “thin” parabola, and that $y=\left(\frac{1}{10}\right)x^2$ is a “fat” parabola. But the first can be rewritten in the form 10y=(10x)², and the second can be rewritten in the form $\left(\frac{y}{10}\right)={\left(\frac{x}{10}\right)}^2$ , so each is a re-scaled version of Y = X².)

So far we have considered loci defined by some pair of distances being equal, or in the ratio 1 : 1. More interesting things begin to happen when we consider conditions in which two distances are in a fixed ratio other than 1 : 1.

Problem 221

(a) Given two points A, B, with AB = 6. Find the locus of all points X such that AX : BX = 2:1.

(b) Given points A, B, with AB = 2b and a positive real number f. Find the locus of all points X such that AX : BX = f : 1.

Problem 222

(a) Given points A, B, with AB = 2c and a real number a > c. Find the locus of all points X such that AX + BX = 2a.

(b) Given a point F and a line m, find the locus of all points X such that the ratio

distance from X to the point F : distance from X to the line m

is a positive constant e < 1.

(c) Prove that parts (a) and (b) give different ways of specifying the same curve, or locus.

Problem 223

(a) Given points A, B, with AB = 2c, and a positive real number a. Find the locus of all points X such that |AX - BX| = 2a.

(b) Given a point F and a line m, find the locus of all points X such that the ratio

distance from X to the point F : distance from X to the line m

is a constant e > 1.

(c) Prove that parts (a) and (b) give different ways of specifying the same curve, or locus.

Problem 221 is sometimes presented in the form of a mild joke.

Two dragons are sleeping, one at A and one at B. Dragon A can run twice as fast as dragon B. A specimen of homo sapiens is positioned on the line segment AB, twice as far from A as from B, and cunningly decides to crawl quietly away, while maintaining the ratio of his distances from A and from B (so as to make it equally difficult for either dragon to catch him should they wake).

The locus that emerges generally comes as a surprise: if the man sticks to his imposed restriction, by moving so that his position X satisfies XA = 2 . XB, then he follows a circle and lands back where he started! The circle is called the circle of Apollonius, and the points A and B are sometimes referred to as its foci.

The locus in Problem 222 is an ellipse - with foci A (or F = (-ae, 0)) and B (= (ae, 0)), and with directrix m (the line $y=-\frac{a}{e}$ ; the line y = a is the second directrix of the ellipse). The “focus-focus” description in part (a) is symmetrical under reflection in both the line AB and the perpendicular bisector of AB. The “focus-directrix” description in (b) is clearly symmetrical in the line through F perpendicular to m; but it is a surprise to find that the equation

$$\frac{x^2}{a^2}+\frac{y^2}{a^2\left(1-e^2\right)}=1$$

is also symmetrical under reflection in the y-axis. If we set b² = a²(1 - e²), the equation takes the form

$$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1,$$

which crosses the x-axis when x = ±a, and crosses the y-axis when y = +b. In its standard form, we usually choose coordinates so that b < a: the line segment from (-a, 0) to (a, 0) is then called the major axis, and half of it (say from (0,0) to (a, 0)) - of length a - is called the semi-major axis; the line segment from (0, -b) to (0, b) is called the minor axis, and half of it (say from (0, 0) to (0, b)) - of length b - is called the semi-minor axis.

The form of the equation shows that an ellipse is obtained from a unit circle by stretching by a factor “a” in the x-direction, and by a factor “b” in the y-direction. This implies that the area of an ellipse is equal to πab (since each small s by s square that arises in the definition of the “area” of the unit circle gets stretched into an “as by bs rectangle”). However, the equation tells us nothing about the perimeter of an ellipse. Attempts to pin down the perimeter of an ellipse gave rise in the 18^th century to the subject of “elliptic integrals”.

Like parabolas, ellipses arise naturally in many important settings. For example, Kepler (1571-1630) discovered that the planetary orbits are not circular (as had previously been believed), but are ellipses - with the Sun at one focus (a conjecture which was later explained by Isaac Newton (1642-1727)). Moreover, the tangent to an ellipse at any point X is equally inclined to the two lines XA and XB, so that a beam emerging from one focus is reflected at every point of the ellipse so that all the reflected rays pass through the other focus.

The curve in Problem 223 is a hyperbola - with foci A (or F = (-ae, 0)) and B (= (ae, 0)), and with directrix m (the line $y=-\genfrac{}{}{0.1ex}{}{a}{e}$; the line $y=\genfrac{}{}{0.1ex}{}{a}{e}$ is the second directrix of the hyperbola). The “focus-focus” description in part (a) is symmetrical under reflection in both the line AB and the perpendicular bisector of AB. The “focus-directrix” description in (b) is clearly symmetrical in the line through F perpendicular to m; but it is a surprise to find that the equation

$$\frac{x^2}{a^2}-\frac{y^2}{a^2\left(e^2-1\right)}=1$$

is also symmetrical under reflection in the y-axis. Like parabolas and ellipses, hyperbolas arise naturally in many important settings - in mathematics and in the natural sciences.

All these loci were introduced and studied by the ancient Greeks without the benefit of coordinate geometry and equations. They were introduced as planar cross-sections of a cone - that is, as natural extensions of straight lines and circles (since the doubly infinite cone is the surface traced out when one rotates a line about an axis through a point on that line). The equivalence of the focus-directrix definition in Problems 220, 222, and 223 and cross sections of a cone follows from the next problem. All five constructions in Problem 224 work with the doubly-infinite cone, which we may represent as x² +y² = (rz)² - although this representation is not strictly needed for the derivations. The surface of the double cone extends to infinity in both directions, and is obtained by taking the line y = rz in the yz-plane (where r > 0 is constant), and rotating it about the z-axis. Images of this rotated line are called generators of the cone; and the point they all pass through (i.e. the origin) is called the apex of the cone.

Problem 224 (Dandelinʹs spheres: Dandelin (1794-1847))

(a) Describe the cross-sections obtained by cutting such a double cone by a horizontal plane (i.e. a plane perpendicular to the z-axis). What if the cutting plane is the xy-plane?

Figure 7: Conic sections.

(b) (i) Describe the cross-section obtained by cutting such a cone by a vertical plane through the origin, or apex.

(ii) What cross-section is obtained if the cutting plane passes through the apex, but is not vertical?

(c) Give a qualitative description of the curve obtained as a cross-section of the cone if we cut the cone by a plane which is parallel to a generator: e.g. the plane y - rz = c.

(i) What happens if c = 0?

(ii) Now assume the cutting plane is parallel to a generator, but does not pass through the apex of the cone - so we may assume that the plane cuts only the bottom half of the cone. Insert a small sphere inside the bottom half of the cone and above the cutting plane, and inflate the sphere as much as possible - until it touches the cone around a horizontal circle (the “contact circle with the cone”), and touches the plane at a single point F. Let the horizontal plane of the “contact circle with the cone” meet the cutting plane in the line m. Prove that each point of the cross-sectional curve is equidistant from the point F and from the line m - and so is a parabola.

(d) (i) Give a qualitative description of the curve obtained as a cross-section of the cone if we cut the cone by a plane which is less steep than a generator, but does not pass through the apex - and so cuts right across the cone.

(ii) We may assume that the plane cuts only the bottom half of the cone. Insert a small sphere inside the bottom half of the cone and above the cutting plane (i.e. on the same side of the cutting plane as the apex of the cone), and inflate the sphere as much as possible - until it touches the cone around a horizontal circle, and touches the plane at a single point F. Let the horizontal plane of the contact circle meet the cutting plane in the line m. Prove that, for each point X on the cross-sectional curve, the ratio

"distance from X to F” : “distance from X to m” = e : 1

is constant, with e < 1, and so is an ellipse.

Figure 8: The conic section arising in Problem 224(d).

(e) (i) Give a qualitative description of the curve obtained as a cross-section if we cut the cone by a plane which is steeper than a generator, but does not pass through the apex (and hence cuts both halves of the cone)?

(ii) We can be sure that the plane cuts the bottom half of the cone (as well as the top half). Insert a small sphere inside the bottom half of the cone and on the same side of the cutting plane as the apex, and inflate the sphere as much as possible - until it touches the cone around a horizontal circle, and touches the plane at a single point F. Let the horizontal plane of the contact circle meet the cutting plane in the line m. Prove that, for each point X on the cross-sectional curve, the ratio

“distance from X to F” : “distance from X to m” = e : 1

is constant, with e > 1, and so is a hyperbola.

Problem 224 reveals a remarkable correspondence. It is not hard to show algebraically that any quadratic equation in two variables x, y represents either a point, or a pair of crossing (possibly identical) straight lines, or a parabola, or an ellipse, or a hyperbola: that is, by changing coordinates, the quadratic equation can be transformed to one of the standard forms obtained in this section. Hence, the possible quadratic curves are precisely the same as the possible cross-sections of a cone. This remarkable equivalence is further reinforced by the many natural contexts in which these conic sections arise.

5.12. Cubes in higher dimensions

This final section on elementary geometry seeks to explore fresh territory by going beyond three dimensions. Whenever we try to jump up to a new level, it can help to first take a step back and 'take a longer run up'. So please be patient if we initially take a step or two backwards.

We all know what a unit 3D-cube is. And - going backwards - it is not hard to guess what is meant by a unit “2D-cube": a unit 2D-cube is just another name for a unit square. It is then not hard to notice that a unit 3D-cube can be constructed from two unit 2D-cubes as follows:

• first position two unit 2D-cubes 1 unit apart in 3D space, with one directly above the other;
• make sure that each vertex of the lower 2D-cube is directly beneath a vertex of the upper 2D-cube;
• then join each vertex of the upper 2D-cube to the corresponding vertex below it.

Perhaps a unit 2D-cube can be constructed in a similar way from “unit lD-cubes"! This idea suggests that a unit “1D-cube” is just another name for a unit line segment.

Take the unit lD-cube to be the line segment from 0 to 1:

• position two such 1D-cubes in 2D (e.g. one joining (0,0) to (1, 0), and the other joining (0,1) to (1,1));
• check that each vertex of the lower 1D-cube is directly beneath a vertex of the upper 1D-cube;
• then join corresponding pairs of vertices - one from the upper 1D-cube and one from the lower 1D-cube ((0, 0) to (0,1), and (1,0) to (1,1)) - to obtain a unit 2D-cube.

Having taken a step back, we repeat (and reformulate) the previous construction of a 3D-cube: ^o

• position two such unit 2D-cubes in 3D: with one 2D-cube joining (0, 0, 0) to (1,0,0), then to (1,1, 0), then to (0,1, 0) and back to (0, 0, 0), and the other 2D-cube joining (0,0,1) to (1, 0,1), then to (1,1,1), then to (0,1,1), and back to (1,0, 0);
• with one 2D-cube directly above the other,
• then join corresponding pairs of vertices - one from the upper 2D-cube and one from the lower 2D-cube ((0,0,0) to (0,0,1), and (1, 0,0) to (1, 0,1), and (1,1, 0) to (1,1,1), and (0,1, 0) to (0,1,1)) - to obtain a unit 3D-cube.

To sum up: a unit cube in 1D, or in 2D, or in 3D:

• has as “vertices” all points whose coordinates are all “0s or 1s” (in 1D, or 2D, or 3D)
• has as “edges” all the unit segments (or unit 1D-cubes) joining vertices whose coordinates differ in exactly one place
• and a unit 3D-cube has as “faces” all the unit 2D-cubes spanned by vertices with a constant value (0 or 1) in one of the three coordinate places (that is, for the unit 3D-cube: the four vertices with x = 0, or the four vertices with x = 1; or the four vertices with y = 0, or the four vertices with y = 1; or the four vertices with z = 0, or the four vertices with z = 1).

A 3D-cube is surrounded by six 2D-cubes (or faces), and a 2D-cube is surrounded by four 1D-cubes (or faces). So it is natural to interpret the two end vertices of a 1D-cube as being '0D-cubes'. We can then see that a cube in any dimension is made up from cubes of smaller dimensions. We can also begin to make a reasonable guess as to what we might expect to find in a '4D-cuhe'.

Problem 225

(a) (i) How many vertices (i.e. 0D-cubes) are there in a 1D-cube?

(ii) How many edges (i.e. 1D-cubes) are there in a 1D-cube?

(b) (i) How many vertices (or 0D-cubes) are there in a 2D-cube?

(ii) How many “faces” (i.e. 2D-cubes) are there in a 2D-cube?

(iii) How many edges (i.e. 1D-cubes) are there in a 2D-cube?

(c) (i) How many vertices (or 0D-cubes) are there in a 3D-cube?

(ii) How many 3D-cubes are there in a 3D-cube?

(iii) How many edges (i.e. 1D-cubes) are there in a 3D-cube?

(iv) How many “faces” (i.e. 2D-cubes) are there in a 3D-cube?

(d) (i) How many vertices (or 0D-cubes) do you expect to find in a 4D-cube?

(ii) How many 4D-cubes do you expect to find in a 4D-cube?

(iii) How many edges (i.e. lD-cubes) do you expect to find in a 4D-cube?

(iv) How many “faces” (i.e. 2D-cubes) do you expect to find in a 4D-cube?

(v) How many 3D-cubes do you expect to find in a 4D-cube?

Problem 226

(a) (i) Sketch a unit 2D-cube as follows. Starting with two unit lD-cubes - one directly above the other. Then join up each vertex in the upper lD-cube to the vertex it corresponds to in the lower lD-cube (directly beneath it).

(ii) Label each vertex of your sketch with coordinates (x, y) (x,y = 0 or 1) so that the lower 2D-cube has the equation “y = 0” and the upper 2D-cube has the equation “y = 1”.

(b) (i) Sketch a unit 3D-cube, starting with two unit 2D-cubes - one directly above the other. Then join up each vertex in the upper 2D-cube to the vertex it corresponds to in the lower 2D-cube (directly beneath it).

(ii) Label each vertex of your sketch with coordinates (x, y, z) (where each x,y,z = 0 or 1) so that the lower 2D-cube has the equation “z = 0” and the upper 2D-cube has the equation “z = 1”.

(c) (i) Now sketch a unit 4D-cube in the same way - starting with two unit 3D-cubes, one “directly above” the other.

[Hint: In part (b) your sketch was a projection of a 3D-cube onto 2D paper, and this forced you to represent the lower and upper 2D-cubes as rhombuses rather than genuine 2D-cubes (unit squares). In part (c) you face the even more difficult task of representing a 4D-cube on 2D paper; so you must be prepared for other “distortions”. In particular, it is almost impossible to see what is going on if you try to physically position one 3D-cube “directly above” the other on 2D paper. So start with the “upper” unit 3D-cube towards the top right of your paper, and then position the “lower” unit 3D-cube not directly below it on the paper, but below and slightly to the left, before pairing off and joining up each vertex of the upper 3D-cube with the corresponding vertex in the lower 3D-cube.]

(ii) Label each vertex of your sketch with coordinates (w, x, y, z) (where each w,x,y, z = 0 or 1) so that the lower 3D-cube has the equation “z = 0” and the upper 3D-cube has the equation “z = 1”.

Problem 227 The only possible path along the edges of a 2D-cube uses each vertex once and returns to the start after visiting all four vertices.

(a) (i) Draw a path along the edges of a 3D-cube that visits each vertex exactly once and returns to the start.

(ii) Look at the sequence of coordinate triples as you follow your path. What do you notice?

(b) (i) Draw a path along the edges of a 4D-cube that visits each vertex exactly once and returns to the start.

(ii) Look at the sequence of coordinate 4-tuples as you follow your path. What do you notice?

5.13. Chapter 5: Comments and solutions

137. Note: The spirit of constructions restricts us to:

• drawing the line joining two known points
• drawing the circle with centre a known point and passing through a known point.

The whole thrust of this first problem is to find some way to “jump” from A (or B) to C. So the problem leaves us with very little choice; AB is given, and A and B are more-or-less indistinguishable, so there are only two possible 'first moves’ - both of which work with the line segment AC (or BC).

Join AC.

Then construct the point X such that ΔACX is equilateral (i.e. use Euclid's Elements, Book I, Proposition 1). Construct the circle with centre A which passes through B; let this circle meet the line AX at the point Y, where either

(i) Y lies on the segment AX (if $\underset{\_}{AB}⩽\underset{\_}{AC}$ ), or

(ii) Y lies on AX produced (i.e. beyond X, if AB > AC).

In each case, AY = AB. Finally construct the circle with centre X which passes through Y. In case (i), let the circle meet the line segment XC at D; in case (ii), let the circle meet CX produced (beyond X) at D.

In case (i), CX = CD + DX; therefore

$$\begin{array}{l}\underset{\_}{CD}=\underset{\_}{CX}-\underset{\_}{DX}\\ =\underset{\_}{AX}-\underset{\_}{YX}\\ =\underset{\_}{AY}=\underset{\_}{AB}.\end{array}$$

In case (ii),

$$\begin{array}{l}\underset{\_}{CD}=\underset{\_}{CX}+\underset{\_}{XD}\\ =\underset{\_}{AX}+\underset{\_}{XY}\\ =\underset{\_}{AY}=\underset{\_}{AB}.\end{array}$$          QED

138.

$$\begin{array}{l}\angle AXC=\angle AXB-\angle CXB\\ =\angle CXD-\angle CXB(\text{ since the two straight angles }\angle AXBand\angle CXDareequal)\\ =\angle BXD.\end{array}$$           QED

139.

AM = AM

MB = MC (by construction of the midpoint M)

BA = CA (given).

$\therefore \Delta AMB\equiv \mathrm{\Delta }AMC$ (by SSS-congruence)

$\therefore \angle AMB=\angle AMC$, so each angle is exactly half the straight angle =BMC. Hence AM is perpendicular to BC.          QED

140. Let ABCDEF be a regular hexagon with sides of length 1. Then ΔABC (formed by the first three vertices) satisfies the given constraints, with ∠ABC = 120°.

Let ∠B'C'D be an equilateral triangle with sides of length 2, and with A' the midpoint of B'D. Then ∠A'B'C' satisfies the given constraints with angle ∠A'B'C' = 60°.

141.

(i) Join CO. Then ΔACO is isosceles (since OA = OC) and ΔBCO is isosceles (since OB = OC).

Hence ∠OAC = ∠OCA = x (say), and ∠OBC = ∠OCB = y (say).

So ∠C = x + y (and ∠A +∠B+∠C= x +(x+y)+y = 2(x + y)).          QED

(ii) If ∠A+∠B+∠C =2(x+y) is equal to a straight angle, then ∠C= x + y is half a straight angle, and hence a right angle.          QED

142.

(i) Draw the circle with centre A and passing through B, and the circle with centre B passing through A. Let these two circles meet at C and D.

Wherever the midpoint M of AB may be, we know from Euclid Book I, Proposition 1 and Problem 139:

that ΔABC is equilateral, and that CM is perpendicular to AB, and that ΔABD is equilateral, and that DM is perpendicular to AB.

Hence CMD is a straight line.

So if we join CD, then this line cuts AB at its midpoint M.          QED

(ii) We may suppose that BA ≤ BC.

Then the circle with centre B, passing through A meets BC internally at Aʹ (say).

Let the circle with centre A and passing through B meet the circle with centre Aʹ and passing through B at the point D.

Claim BD bisects ∠ABC.

Proof

BA = BAʹ(radii of the same circle with centre B)

AD = AB (radii of the same circle with centre A)

      = AʹB= AʹD (radii of same circle with centre Aʹ)

BD = BD

Hence Δ BAD ≡ Δ BAʹD (by SSS-congruence).

∴ ∠ABD =∠AʹBD.          QED

(iii) Suppose first that PA = PB. Then the circle with centre P and passing through A meets the line AB again at B. If we construct the midpoint M of AB as in part (i), then PM will be perpendicular to AB.

Now suppose that one of PA and PB is longer than the other. We may suppose that PA>PB, so B lies inside the circle with centre P and passing through A. Hence this circle meets the line AB again at Aʹ where B lies between A and Aʹ. If we now construct the midpoint M of AAʹ as in part (i), then PM will be perpendicular to AAʹ, and hence to AB. QED

143. Let M be the midpoint of AB.

(a) Let X lie on the perpendicular bisector of AB.

∴ Δ XMA ≡ Δ XMB (by SAS congruence, since XM = XM, ∠XMA =∠XMB, MA = MB)

∴ XA = XB.

(b) If X is equidistant from A and from B, then Δ XMA ≡ Δ XMB (by SSS-congruence, since XM = XM, MA = MB, AX = BX).

∴ ∠XMA =∠XMB, so each must be exactly half a straight angle.

∴ X lies on the perpendicular bisector of AB.          QED

144. Let X lie on the plane perpendicular to NS, through the midpoint M.

∴ Δ XMN ≡ Δ XMS (by SAS congruence, since XM = XM, ∠XMN =∠XMS, MN = MS)

∴ XN = XS.

Let X be equidistant from N and from S, then Δ XMN ≡ Δ XMS (by SSS-congruence, since XM = XM, MN = MS, NX = SX).

∴ ∠XMN =∠XMS, so each must be exactly half a straight angle.

∴ X lies on the perpendicular bisector of NS.          QED

145. Let M be the midpoint of AC. Join BM and extend the line beyond M to the point D such that MB = MD. Join CD. Then Δ AMB ≡ Δ CMD (by SAS-congruence, since

AM = CM (by construction of the midpoint M)

∠AMB =∠CMD (vertically opposite angles)

MB = MD (by construction)).

∴ ∠DCM =∠BAM.

Now

$$\begin{array}{l}\angle ACX=\angle DCM+\angle DCX\\ >DCM\\ =\angle BAM\\ =\angle A.\end{array}$$

Hence∠ACX >∠A.

Similarly, we can extend AC beyond C to a point Y. Let N be the midpoint of BC. Join AN and extend the line beyond N to the point E such that NA = NE.

Join CE.

Then Δ BNA ≡ Δ CNE (again by SAS-congruence).

∴ ∠BCY >∠BCE =∠CBA =∠B.          QED

146.

(a) Suppose that AB > AC.

Let the circle with centre A, passing through C, meet AB (internally) at X.

Then Δ ACX is isosceles, so∠ACX =∠AXC.

By Problem 145, ∠AXC >∠ABC.

∴ ∠ACB; (>∠ACX =∠AXC) >∠ABC.          QED

(b) Suppose the conclusion does not hold. Then either

(i) AB = AC, or

(ii) AC > AB.

(i) If AB = AC, then Δ ABC is isosceles, so∠ACB =∠ABC – contrary to assumption.

(ii) If AC > AB, then∠ABC >∠ACB (by part (a)) – again contrary to assumption.

Hence, if∠ACB >∠ABC, it follows that AB > AC.          QED

(c) Extend AB beyond B to the point D, such that BD = BC.

Then Δ BDC is isosceles with apex B, so∠BDC =∠BCD.

Now

∠ACD =∠ACB +∠BCD >∠BCD =∠BDC.

Hence, by part (b), AD > AC.

By construction,

AD = AB + BD = AB +BC,

so AB +BC > AC.          QED

147. Suppose∠C =∠A +∠B, but that C does not lie on the circle with diameter AB. Then C lies either inside, or outside the circle. Let O be the midpoint of AB.

(i) If C lies outside the circle, then OC > OA = OB.

∴ ∠OAC >∠OCA and∠OBC >∠OCB (by Problem 146(a)).

∴ ∠C =∠OCA +∠OCB <∠A +∠B – contrary to assumption.

Hence C does not lie outside the circle.

(ii) If C lies inside the circle, then OC < OA = OB.

∴ ∠OAC < ∠OCA and∠OBC < ∠OCB (by Problem 146(a)).

∴ ∠C =∠OCA +∠OCB >∠A +∠B – contrary to assumption.

Hence C does not lie inside the circle.

Hence C lies on the circle with diameter AB.          QED

148. Suppose, to the contrary, that OP is not perpendicular to the tangent at P.

Drop a perpendicular from O to the tangent at P to meet the tangent at Q. Extend PQ beyond Q to some point X. Then ∠OQP and ∠OQX are both right angles. Since Q (≠ P) lies on the tangent, Q lies outside the circle, so OQ > OP. Hence (by Problem 146(a))∠OPQ >∠OQP = ∠OQX – contrary to the fact that∠OQX >∠OPQ (by Problem 145).          QED

149. Let Q lie on the line m such that PQ is perpendicular to m.

Let X be any other point on the line m, and let Y be a point on m such that Q lies between X and Y.

Then ∠PQX and ∠PQY are both right angles.

Suppose that PX < PQ.

Then∠PQY =∠PQX < ∠PXQ (by Problem 146(a)), which contradicts Problem 145 (since ∠PQY is an exterior angle of Δ PQX).

Hence PX ≥ PQ as required.          QED

150.∠A +∠B +∠C, and∠XCA +∠C are both equal to a straight angle. So∠A +∠B =∠XCA.

151. Join OA, OB, OC. Since these radii are all equal, this produces three isosceles triangles. There are five cases to consider.

(i) Suppose first that O lies on AB. Then AB is a diameter, so ∠ACB is a right angle (by Problem 141), ∠AOB is a straight angle, and the result holds.

(ii) Suppose O lies on AC, or on BC. These are similar, so we may assume that O lies on AC.

Then Δ OBC is isosceles, so∠OBC =∠OCB.

∠AOB is the exterior angle of Δ OBC, so

∠AOB =∠OBC +∠OCB = 2· ∠ACB

(by Problem 150).

(iii) Suppose O lies inside Δ ABC.

Δ OAB, Δ OBC, Δ OBC are isosceles, so let ∠OAB =∠OBA = x, ∠OBC =∠OCB = y, ∠OBC =∠OAC = z.

Then∠ACB = y + z, ∠ABC = x + y, ∠BAC = x + z.

The three angles of Δ ABC add to a straight angle, so 2(x + y + z) equals a straight angle.

Hence, in Δ OBA,

∠AOB = 2(x + y + z) - (∠OAB +∠OBA) = 2(y + z)= 2· ∠ACB.

(iv) Suppose O lies outside Δ ABC with O and B on opposite sides of AC.

Δ OAB, Δ OBC, Δ OBC are isosceles, so let ∠OAB =∠OBA = x, ∠OBC =∠OCB = y, ∠OBC =∠OAC = z.

Then∠ACB = y - z, ∠ABC = x + y, ∠BAC = x - z.

The three angles of Δ ABC add to a straight angle, so 2x + 2y - 2z equals a straight angle.

Hence

2x + 2y - 2z =∠AOB +∠OAB +∠OBA =∠AOB + 2x,

so∠AOB = 2y - 2z = 2· ∠ACB.

(v) Suppose O lies outside Δ ABC with O and B on the same side of AC.

Δ OAB, Δ OBC, Δ OBC are isosceles, so let ∠OAB =∠OBA = x, ∠OBC =∠OCB = y, ∠OBC =∠OAC = z.

Then∠ACB = y + z, ∠ABC = y - x, ∠BAC = z - x.

The three angles of ABC add to a straight angle, so 2y + 2z - 2x equals a straight angle.

Since C lies on the minor arc relative to the chord AB, we need to interpret “the angle subtended by the chord AB at the centre O” as the reflex angle outside the triangle Δ AOB – which is equal to “2x more than a straight angle” , so ∠AOB = 2y + 2z = 2· ∠ACB.          QED

152. The chord AB subtends angles at C and at D on the same arc. Similarly BC subtends angles at A and at D on the same arc. Hence (by Problem 151)

∠ACB =∠ADB, and∠BAC =∠BDC.

Hence

∠ADC =∠ADB +∠BDC =∠ACB +∠BAC, so ∠ADC +∠ABC equals the sum of the three angles in Δ ABC.          QED

153. Let O be the circumcentre of Δ ABC, and let∠XAB = x.

Then ∠XAO is a right angle, and Δ OAB is isosceles. There are two cases.

(i) If X and O lie on opposite sides of AB, then∠OBA =∠OAB = 90° - x.

∴ ∠AOB = 2x.

∴ ∠ACB = X =∠XAB.

(ii) If X and O lie on the same side of AB, then Y and O lie on opposite sides of AB and of AC. Hence we can apply case (i) (with Y in place of X, AC in place of AB, ∠YAC in place of ∠XAB, and ∠ABC in place of ∠ACB) to conclude that∠YAC =∠ABC. Hence

∠XAB +∠BAC +∠YAC =∠XAB + ∠BAC +∠ABC

are both straight angles, so ∠XAB =∠ACB (since the three angles of Δ ABC also add to a straight angle).          QED

154.

(a) (i) Extend AD to meet the circumcircle at X. Then (applying Problem 145 to Δ DXB), the exterior angle∠ADB > ∠DXB = ∠AXB = ∠ACB.

(ii) We are told that the points C, D lie “on the same side of the line AB”. This “side” of the line AB (or “half-plane” ) is split into three parts by the half-lines “AC produced beyond C” and “BC produced beyond C” . There are two very different possibilities.

Suppose first that D lies in one of the two overlapping wedge-shaped regions “between AB produced and AC produced” or “between BA produced and BC produced”. Then either DA or DB cuts the arc AB at a point X (say), and ∠ACB = ∠AXB > ∠ADB (by Problem 145 applied to Δ AXD or to Δ BXD).

The only alternative is that D lies in the wedge shaped region outside the circle at the point C, lying “between AC produced and BC produced”. Then C lies inside Δ ADB, so C lies inside the circumcircle of Δ ADB. Hence part (i) implies that ∠ACB < ∠ADB as required.           QED

(b) If D does not lie on the circumcircle of Δ ABC, then it lies either inside, or outside the circle – in which case ∠ADB ≠ ∠ACB (by part (a)).

(c) ∠D is less than a straight angle, so D must lie outside Δ ABC. Moreover, B, D lie on opposite sides of the line AC (since the edges BC, DA do not cross internally, and neither do the edges CD, AB). Consider the circumcircle of Δ ABC, and let X be any point on the circle such that X and D lie on the same side of the line AC. Then ABCX is a cyclic quadrilateral, so ∠ABC and ∠CXA are supplementary. Hence∠CXA =∠CDA =∠D. But then D lies on the circle (by part (b)).

155. Δ OPQ ≡ Δ OPʹQ (by RHS-congruence: ∠OPQ =∠OPʹQ are both right angles, OP = OPʹ, OQ = OQ)

∴ QP = QPʹ, and∠QOP =∠QOPʹ.          QED

156.

(a) Let X be any point on the bisector of ∠ABC. Drop the perpendiculars XY from X to AB and XZ from X to CB. Then:∠XYB =∠XZB are both right angles by construction; and∠XBY =∠XBZ since X lies on the bisector of ∠YBZ; hence∠BXY =∠BXZ (since the three angles in each triangle have the same sum; so as soon as two of the angles are equal in pairs, the third pair must also be equal). Hence Δ BXY ≡ Δ BXZ (by ASA-congruence:∠YBX =∠ZBX, BX = BX, ∠BXY =∠BXZ.)

∴ XY= XZ.          QED

(b) Suppose X is equidistant from m and from n. Drop the perpendiculars XY from X to m, and XZ from X to n.

Then Δ BXY ≡ Δ BXZ (by RHS-congruence:

∠BYX =∠BZX are both right angles XY = XZ, since we are assuming X is equidistant from m and from n BX = BX).

Hence∠XBY =∠XBZ, so X lies on the bisector of ∠YBZ.          QED

157.

(i) Join AC. Then Δ ABC ≡ Δ CDA by ASA-congruence:

∠BAC =∠DCA (alternate angles, since AB || DC)

AC = CA

∠ACB =∠CAD (alternate angles, since CB || DA).

In particular, Δ ABC and Δ CDA must have equal area, and so each is exactly half of ABCD.          QED

Note: Once we prove (Problem 161 below) that a parallelogram has the same area as the rectangle on the same base and lying between the same pair of parallels (whose area is equal to “base × height” ), the result in part (i) will immediately translate into the familiar formula for the area of the triangle

$$\begin{array}{cc}& \genfrac{}{}{0.1ex}{}{1}{2}(\text{base}\times \text{height}).\hfill \end{array}$$

(ii) Δ ABC ≡ Δ CDA by part (i). Hence AB = CD, BC = DA; and∠B =∠ABC =∠CDA =∠D.

To show that∠A =∠C, we can either copy part (i) after joining BD to prove that Δ BCD ≡ Δ DAB, or we can use part (i) directly to note that∠A =∠BAC +∠DAC =∠DCA +∠BCA =∠C.          QED

(iii) Δ AXB ≡ Δ CXD by ASA-congruence:

∠XAB =∠XCD (alternate angles, since AB || DC)

AB = CD (by part (ii))

∠XBA =∠XDC (alternate angles, since AB || DC).

Hence XA (in Δ AXB) = XC (in Δ CXD), and XB (in Δ AXB) = XD (in Δ CXD).          QED

158. We may assume that m cuts the opposite sides AB at Y and DC at Z.

Δ XYB ≡ Δ XZD by ASA-congruence:

∠YXB =∠ZXD (vertically opposite angles)

XB = XD (by Problem 157(iii))

∠XBY =∠XDZ (alternate angles).

Therefore

area(YZCB) = area(Δ BCD) - area(Δ XZD) + area(Δ XYB)

      = area(Δ BCD)

      $=\frac{1}{2}area(ABCD)$.

QED

159.

(a) Join AC. Then Δ ABC ≡ Δ CDA by SAS-congruence:

BA = DC (given)

∠BAC =∠DCA (alternate angles, since AB || DC)

AC = CA.

Hence∠BCA =∠DAC, so AD || BC as required.          QED

(b) Join AC. Then Δ ABC≡ Δ CDA by SSS-congruence:

AB = CD (given)

BC = DA (given)

CA = AC.

Hence∠BAC =∠DCA, so AB || DC; and∠BCA =∠DAC, so BC || AD.

QED

(c)∠A +∠B +∠C +∠D = 2 ∠A + 2 ∠B = 2 ∠A + 2 ∠D are each equal to two straight angles.

∴ ∠A +∠B is equal to a straight angle, so AD || BC; and∠A +∠D is equal to a straight angle, so AB || DC.          QED

Note: The fact that the angles in a quadrilateral add to two straight angles is proved in the next chapter. However, if preferred, it can be proved here directly. If we imagine pins lOBCted at A, B, C, D, then a string tied around the four points defines their “convex hull” – which is either a 4-gon (if the string touches all four pins), or a 3-gon (if one vertex is inside the triangle formed by the other three). In the first case, either diagonal (AC or BD) will split the quadrilateral internally into two triangles; in the second case, one of the three ‘edges’ joining vertices of the convex hull to the internal vertex cannot be an edge of the quadrilateral, and so must be a diagonal, which splits the quadrilateral internally into two triangles.

160. AM = MD (by construction of M as the midpoint), and BN = NC.

∴AM = BN (since AD = BC by Problem 157(ii)).

∴ ABNM is a parallelogram (by Problem 159(a)), so MN || AB.

Let AC cross MN at Y.

Then Δ AYM ≡ Δ CYN (by ASA-congruence, since

∠YAM =∠YCN (alternate angles, since AD || BC)

AM = CN

∠AMY =∠CNY (alternate angles, since AD || BC).

Hence AY = CY, so Y is the midpoint of AC –the centre of the parallelogram (where the two diagonals meet (by Problem 157(iii))).          QED

161.

Note: In the easy case, where the perpendicular from A to the line DC meets the side DC internally at X, it is natural to see the parallelogram ABCD as the “sum” of a trapezium ABCX and a right angled triangle Δ AXD. If the perpendicular from B to DC meets DC at Y, then Δ AXD ≡ Δ BYC. Hence we can rearrange the two parts of the parallelogram DCBA to form a rectangle XYBA.

However, a general proof cannot assume that the perpendicular from A (or from B) to DC meets DC internally. Hence we are obliged to think of the parallelogram in terms of differences. This is a strategy that is often useful, but which can be surprisingly elusive.

Draw the perpendiculars from A and B to the line CD, and from C and D to the line AB. Choose the two perpendiculars which, together with the lines AB and CD define a rectangle that completely contains the parallelogram ABCD (that is, if AB runs from left to right, take the left-most, and the right-most perpendiculars). These will be either the perpendiculars from B and from D, or the perpendiculars from A and from C (depending on which way the sides AC and BD slope).

Suppose the chosen perpendiculars are the one from B – meeting the line DC at P, and the one from D – meeting the line AB at Q.

Then BP || QD (by Problem 159(c)), so BQDP is a parallelogram with a right angle – and hence a rectangle. Hence BQ = PD, and BP = QD (by Problem 157(ii)).

Δ QAD ≡ Δ PCB (by RHS-congruence), so each is equal to half the rectangle on base PC and height PB. Hence

area(ABCD) = area(rectangle; BQDP)

- area(rectangle on base PC with height PB)

= area(rectangle on base CD with height DQ).

QED

162.

(a) ABCBʹ is a parallelogram, so ABʹ|| CB and ABʹ = BC.

Similarly, BCACʹ is a parallelogram, so ACʹ|| CB and ACʹ= CB.

Hence BʹA = ACʹ, so A is the midpoint of BʹCʹ.

Similarly B is the midpoint of CʹAʹ, and C is the midpoint of AʹBʹ.

(b) Let H be the circumcentre of Δ AʹBʹCʹ – that is, the common point of the perpendicular bisectors of AʹBʹ, BʹCʹ, and CʹAʹ. Then H is a common point of the three perpendiculars from A to BC, from B to CA, and from C to AB.

163. Consider any path from H to V. Suppose this reaches the river at X. The shortest route from H to X is a straight line segment; and the shortest route from X to V is a straight line segment.

If we reflect the point H in the line of the river, we get a point Hʹ, where HHʹ is perpendicular to the river and meets the river at Y (say).

Then Δ HXY ≡ Δ HʹXY (by SAS-congruence, since HY = HʹY, ∠HYX =∠HʹYX, and YX = YX).

Hence HX = HʹX, so the distance from H to V via X is equal to HX + XV = HʹX + XV, and this is shortest when Hʹ, X, and V are collinear.(So to find the shortest route, reflect H in the line of the river to Hʹ, then draw HʹV to cross the line of the river at X, and travel from H to V via X.)

164.

(a) Let Δ PQR be any triangle inscribed in Δ ABC, with P on BC, Q on CA, R on AB (not necessarily the orthic triangle). Let Pʹ be the reflection of P in the side AC, and let Pʹʹ be the reflection of P in the side AB. Then PQ = PʹQ, and PR = PʹʹR (as in Problem 163).

∴ PQ + QR + RP = PʹQ + QR + RPʹʹ.

Each choice of the point P on AB determines the positions of Pʹ and Pʹʹ. Hence the shortest possible perimeter of Δ PQR arises when PʹQRPʹʹ is a straight line. That is, given a choice of the point P, choose Q and R by:

– constructing the reflections Pʹ of P in AC, and Pʹʹ of P in AB;

– join PʹPʹʹand let Q, R be the points where this line segment crosses AC, AB respectively.

It remains to decide how to choose P on BC so that PʹPʹʹ is as short as possible.

The key here is to notice that A lies on both AC and on AB.

∴ AP = APʹ, and AP = APʹʹ, so Δ APʹPʹʹis isosceles.

Also∠PAC =∠PʹAC, and∠PAB =∠PʹʹAB.

∴ ∠PʹAPʹʹ= 2· ∠A.

Hence, for each position of the point P, Δ APʹPʹʹ is isosceles with apex angle equal to 2· ∠A. Any two such triangles are similar (by SAS-similarity).

Hence the triangle Δ APʹPʹʹ with the shortest “base” PʹPʹʹoccurs when the legs APʹ and APʹʹare as short as possible. But AP = APʹ = APʹʹ, so this occurs whenAP is as short as possible – namely when AP is perpendicular to BC.

Since the same reasoning applies to Q and to R, it follows that the required triangle Δ PQR must be the orthic triangle of Δ ABC. QED

(b) Let Δ PQR be the orthic triangle of Δ ABC, with P on BC, Q on CA, R on AB. Let H be the orthocenter of Δ ABC.

∠BPH and ∠BRH are both right angles, so add to a straight angle. Hence (by Problem 154(c)), BPHR is a cyclic quadrilateral. Similarly CPHQ and AQHR are cyclic quadrilaterals.

In the circumcircle of CPHQ, we see that the initial “angle of incidence” ∠CQP =∠CHP. Also∠CHP =∠AHR (vertically opposite angles); and in the circumcircle of AQHR, ∠AHR =∠AQR.

Hence∠CQP =∠AQR, so a ray of light which traverses PQ will reflect at Q along the line QR. Similarly one can show that∠ARQ =∠BRP, so that the ray will then reflect at R along RP; and∠BPR =∠CPQ, so the ray will then reflect at P along PQ.          QED

165.

(a) (i) Triangles Δ ABL and Δ ACL have equal bases BL = CL, and the same apex A – so lie between the same parallels. Hence they have equal area (by Problems 157 and 161).

Similarly, Δ GBL and Δ GCL have equal bases BL = CL, and the same apex G – so have equal area.

Hence the differences Δ ABG = Δ ABL - Δ GBL and Δ ACG = Δ ACL - Δ GCL have equal area.

(ii) [Repeat the solution for part (i) replacing A, B, C, L, G by B, C, A, M, G.]

(b) Δ ABL and Δ ACL have equal area (as in (a)(i)). Similarly Δ GBL and Δ GCL have the same area – say x (since BL = CL). Hence Δ ABG and Δ ACG have equal area.

In the same way Δ BCM and Δ BAM have equal area; and Δ GCM and Δ GAM have the same area – say y (since CM = AM). Hence Δ BCG and

Δ BAG have equal area.

But then Δ ABG = Δ ACG = Δ BCG and Δ ACG = Δ AMG + Δ CMG = 2y, Δ BCG = Δ BLG + Δ CLG = 2x. Hence X = y, so Δ AMG, Δ CMG, Δ CLG, Δ BLG all have the same area x, and Δ ABG has area 2x.

The segment GN divides Δ ABG into two equal parts (Δ ANG andΔ BNG), so each part has area x.

Hence Δ CAG + Δ ANG has the same area (3x) as Δ CAN. Hence ∠CGN is a straight angle, and the three medians AL, BM, CN all pass through the point G.

Note: At first sight, the ‘proof’ of the result in (b) using vectors seems considerably easier.(If A, B, C have position vectors a, b, c respectively, then L has the position vector $\frac{1}{2}$(b + c), and M has position vector $\frac{1}{2}$(c + a), and it is easy to see that AL and BM meet at G with position vector $\frac{1}{3}$(a + b + c). One can then check directly that G lies on CN, or notice that the symmetry of the expression $\frac{1}{3}$(a + b + c) guarantees that G is also the point where BM and CN meet.

The inscrutable aspect of this ‘proof’ lies in the fact that all the geometry has been silently hidden in the algebraic assumptions which underpin the unstated axioms of the 2-dimensional vector space, and the underlying field of real numbers. Hence, although the vector ‘proof’ may seem simpler, the two different apprOAChes cannot really be compared.

166.

(a) AN = BN (by construction of N as the midpoint of AB)

∠ANM =∠BNMʹ (vertically opposite angles)

NM = NMʹ (by construction).

∴ Δ ANM ≡ Δ BNMʹ (by SAS-congruence).          QED

(b) BMʹ = AM = CM.

∠NAM =∠NBMʹ (since Δ ANM ≡ Δ BNMʹ)

∴ BMʹ || MA (i.e. BMʹ || CM).          QED

(c) BMʹMC is a quadrilateral with opposite sides CM, BMʹ equal and parallel.

∴ BMʹMC is a (by Problem 158(a)).          QED

167. Since A and B are interchangeable in the result to be proved, we may assume that A is the point on the secant that lies between P and B.

In order to make deductions, we have to create triangles – so join AT and BT. This creates two triangles: Δ PAT and Δ PTB, in which we see that:

∠TPA =∠BPT,

∠PTA =∠PBT (by Problem 153),

∴ ∠PAT = ∠PTB (since the three angles in each triangle add to a straight angle).

Hence Δ PAT ~ Δ PTB (by AAA-similarity).

∴ PT: PB= PA: PT, orPA × PB= PT².          QED

168. Since A, B are interchangeable in the result to be proved, and C, D are interchangeable, we may assume that A lies between P and B, and that C lies between P and D.

(i) Let the tangent from P to the circle touch the circle at T.

Then Problem 167 guarantees that PA × PB= PT².

Replacing the secant PAB by PCD shows similarly that PC × PD= PT².

Hence PA ×PB = PC × PD.          QED

(ii) Note: The first proof is so easy, one may wonder why anyone would ask for a second proof. The reason lies in Problem 169 – which looks very much like Problem 168, but with P inside the circle. Hence, when we come to the next problem, the easy apprOACh in (i) will not be available, so it is worth looking for another proof of 168 which has a chance of generalizing.

Notice that AC is a chord which links the two secants PAB and PCD. So join AD and CB.

Then Δ PAD ~ Δ PCB (by AAA-similarity: since∠APD =∠CPB, and∠PDA =∠PBC).

∴ PA: PC = PD: PB, orPA × PB= PC × PD.          QED

169. Join AD and CB.

Then Δ PAD ~ Δ PCB (by AAA-similarity: since

∠APD =∠CPB (vertically opposite angles)

∠PDA =∠PBC (angles subtended by chord AC on the same arc)

∠PAD =∠PCB (angles subtended by a chord BD on the same arc)).

∴ PA: PC= PD: PB, orPA × PB= PC × PD.          QED

170.

(a) If a = b, then ABCD is a parallelogram (by Problem 159(a)).

∴ AD = BC (by Problem 157(ii)).

∴ AM = BN, so ABNM is a parallelogram (by Problem 159(a)).

∴ MN = AB has length a, and MN || AB (by Problem 160).

If a ≠ B, then a < B, or B < a. We may assume that a < b.

Construct the line through b parallel to AD, and let this line meet DC at Q.

Then ABQD is a parallelogram, so DQ = AB, and AD = BQ. Hence QC has length B - a.

Construct the line through M parallel to QC (and hence parallel to BA), and let this meet BQ at P, and BC at Nʹ.

Then ABPM and MPQD are both parallelograms.

∴ MP = AB has length a, and

BP = AM = MD = PQ.

Now Δ BPNʹ ~ Δ BQC (by AAA-similarity, since PNʹ || QC); so

BP: BQ = BNʹ: BC = 1: 2.

Hence Nʹ = n is the midpoint of BC, MN || BC, and MN has length

$\begin{array}{cc}& a+\genfrac{}{}{0.1ex}{}{b-a}{2}=\genfrac{}{}{0.1ex}{}{a+b}{2}.\hfill \end{array}$

(b) Suppose first that a = b. Then ABCD is a parallelogram (by Problem 159(a)), so the area of ABCD is given by a × d ( “(length of base) × height” ). (by Problem 161). Hence we may suppose that a < b.

Solution 1: Extend AB beyond B to a point X such that BX = DC (so AX has length a + b).

Extend DC beyond C to a point Y such that CY = AB (so DY has length a + b).

Clearly ABCD and YCBX are congruent, so each has area one half of area(AXYD).

Now AX || DY, and AX = DY, so AXYD is a parallelogram (by Problem 159(a)).

Hence AXYD has area “(length of base)× height” (by Problem 161), so ABCD has area $\frac{a+b}{2}$ × d.

Solution 2: [We give a second solution as preparation for Problem 171.]

Now a < B implies that∠BAD +∠ABC is greater than a straight angle.

[Proof. The line through B parallel to AD meets DC at Q, and ABQD is a parallelogram.

Hence DQ = AB, so Q lies between D and C, and

∠ABC =∠ABQ +∠QBC >∠ABQ.

∴ ∠BAD +∠ABC >∠BAD +∠ABQ, which is equal to a straight angle.]

So if we extend DA beyond A, and CB beyond B, the lines meet at X, where X, D are on opposite sides of AB. Then Δ XAB ~ Δ XDC (by AAA-similarity), whence corresponding lengths in the two triangles are in the ratio AB: DC = a: b. In particular, if the perpendicular from X to AB has length h, then $\frac{h}{h+d}=\frac{a}{b}$, so h(b - a) = ad.

Now

area(ABCD) = area(Δ XDC) - area(Δ XAB)

= $\frac{1}{2}b(h+d)-\frac{1}{2}ah$

= $\frac{1}{2}bd+\frac{1}{2}h(b-a)$

= $\frac{1}{2}bd+\frac{1}{2}ad$

= $\left(\frac{a+b}{2}\right)d$.

171. Note: The volume of a pyramid or cone is equal to

$\frac{1}{3}$ × (area of base) ×height.

There is no elementary general proof of this fact. The initial coefficient of $\frac{1}{3}$ arises because we are “adding up” , or integrating, cross-sections parallel to the base, whose area involves a square x², where x is the distance from the apex (just as the coefficient $\frac{1}{2}$ in the formula for the area of a triangle arises because we are integrating linear cross-sections whose size is a multiple of x – the distance from the apex). Special cases of this formula can be checked – for example, by noticing that a cube ABCDEFGH of side s, with base ABCD, and upper surface EFGH, with E above D, F above A, and so on, can be dissected into three identical pyramids – all with apex E: one with base ABCD, one with base BCHG, and one with base ABGF. Hence each pyramid has volume $\frac{1}{3}$s³, which may be interpreted as

$\frac{1}{3}\times (areaofbase=s^2)\times (height=s)$.

To obtain the frustum of height d, a pyramid with height h (say) is cut off a pyramid with height h + d.

∴ volume(frustum) = $\left[\frac{1}{3}\times b^2\times (h+d)\right]-\left[\frac{1}{3}\times a^2\times h\right]$

$=\left[\frac{1}{3}\times b^2\times d\right]+\left[\frac{1}{3}\times (b^2-a^2)\times h\right]$.

Let N be the midpoint of BC, and let the line AN meet the upper square face of the frustum at M.

Let the perpendicular from the apex A to the base BCDE meet the upper face of the frustum at Y and the base BCDE at Z.

ThenΔ AYM ~ Δ AZN (by AAA-similarity), so AY: AZ = YM: ZN.

∴$\frac{h}{h+d}=\frac{a}{b},soh(b-a)=ad$.

∴ $volume(frustum)=\frac{1}{3}{b}^{2}d+\frac{1}{3}\left(b^2-a^2\right)h$

$=\frac{1}{3}{b}^{2}d+\frac{1}{3}(b+a)ad$

$=\frac{1}{3}\left(b^2+ab+a^2\right)d$.

172. Construct the line through A which is parallel to AʹBʹ, and let it meet the line BBʹ at P. Similarly, construct the line through B which is parallel to BʹCʹ and let it meet the line CCʹ at Q.

Then Δ ABP ~ Δ BCQ (by AAA-similarity), so AB: BC = AP: BQ.

Now AAʹBʹP is a parallelogram, so AP = AʹBʹ, and BBʹCʹQ is a parallelogram, so BQ = BʹCʹ.

∴ AB: BC = AʹBʹ: BʹCʹ.          QED

173.

(a) Suppose AB has length a and CD has length b. Problem 137 allows us to construct a point X such that AX = CD, so AX has length b. Now construct the point Y where the circle with centre A and radius AX meets BA produced (beyond A). Then YB has length a + b.

If a > B, let Z be the point where the circle with centre A and passing through X meets the segment AB internallyThen ZB has length a - b.

(b) Use Problem 137 to construct a point U (not on the line CD) such that DU = XY, and a point V on DU (possibly extended beyond U) such that DV = AB. Hence DU has length 1 and DV has length a.

Construct the line through V parallel to UC and let it meet the line DC at W. Then Δ DVW ~ Δ DUC, with scale factor DW: DC = DV: DU = a: 1. Hence DW has length ab.

To construct a line segment of length $\frac{a}{b}$ construct U, V as above. Then let the circle with centre D and radius DU meet CD at Uʹ. Let the line through Uʹ parallel to CV meet DV at X. The Δ DUʹX ~ Δ DCV, with scale factor DX: DV = DUʹ: DC = 1: B, so DX has length $\frac{a}{b}$.

(c) Use Problem 137 to construct a point G so that AG = XY = 1. Then draw the circle with centre A passing through G to meet BA extended at H. Hence HA = 1, AB = a.

Construct the midpoint M of HB; draw the circle with centre M and passing through H and B.

Construct the perpendicular to HB at the point A to meet the circle at K.

Then Δ HAK ~ Δ KAB, so AB: AK = AK: AH. Hence AK = $\sqrt{a}$.

174. The key to this problem is to use Problem 158: a parallelogram(and hence any rectangle) is divided into two congruent pieces by any straight cut through the centre. If A is the centre of the rectangular piece of fruitcake, and B is the centre of the combined rectangle consisting of “fruitcake plus icing” , then the line AB gives a straight cut that divides both the fruitcake and the icing exactly in two.

175.

(a) The minute hand is pointing exactly at “7” , but the hour hand has moved $\frac{7}{12}$ of the way from “1” to “2” : that is, $\frac{7}{12}$ of 30°, or 17$\frac{1}{2}$°. Hence the angle between the hands is 162$\frac{1}{2}$°.

The same angle arises whenever the hands are trying to point in opposite directions, but are off-set by $\frac{7}{12}$ of 30°, or 17$\frac{1}{2}$°. This suggests that instead of “35 minutes after 1” we should consider “35 minutes before 11” , or 10:25.

(b) The two hands coincide at midnight. The minute hand then races ahead, and the hands do not coincide again until shortly after 1:00 – and indeed after 1:05.

More precisely, in 60 minutes, the minute hand turns through 360°, so in x minutes, it turns through 6x°. In 60 minutes the hour hand turns through 30°, so in x minutes, the hour hand turns through $\frac{1}{2}$x°.

The hands overlap when

$$\frac{1}{2}x\equiv 6x\left(\mathrm{mod}360\right),$$

or when $\frac{11}{2}$x is a multiple of 360.

This occurs when X = 0 (i.e. at midnight); then not until

X = $\frac{720}{11}=65\frac{5}{11}$,

and the time is 5$\frac{5}{11}$ minutes past 1: that is, after 1$\frac{1}{11}$ hours.

It occurs again 1$\frac{1}{11}$ hours, or 65$\frac{5}{11}$ minutes, later – namely at 10$\frac{10}{11}$ minutes past 2, and so on.

Hence the phenomenon occurs at midnight, and then 11 more times until noon (with noon as the 12th time; and then 11 more times until midnight – and hence 23 times in all (including both midnight occurrences).

(c) If we add a third hand (the ‘second hand'), all three hands coincide at midnight. In x minutes, the second hand turns through 360x°.

We now know exactly when the hour hand and minute hand coincide, so we can check where the second hand is at these times. For example, at 5$\frac{5}{11}$ minutes past 1, the second hand has turned through (360 × 65$\frac{5}{11}$)°, and

360 × 65$\frac{5}{11}$ ≡ 360 × $\frac{5}{11}\left(\mathrm{mod}360\right)$,

so the second hand is nowhere near the other two hands.

The k^th occasion when the hour hand and minute hands coincide occurs at k × 1$\frac{1}{11}$ hours after midnight, when the two hands point in a direction $\left(\frac{360k}{11}\right)$° clockwise beyond “12” . At the same time, the second hand has turned through (360 × 65$\frac{5}{11}$ × k)°, and

$360\times 65\frac{5}{11}\times k\equiv 360\times \frac{5}{11}\times k\left(\mathrm{mod}360\right)$,

or five times as far round, and these two are never equal $\left(\mathrm{mod}360\right)$.

176.

Note: One of the things that makes it possible to calculate distances exactly here is that the angles are all known exactly, and give rise to lots ofright angled triangles.

The rotational symmetry of the clockface means we only have to consider segments with one endpoint at 12 o'clock (say A). The reflectional symmetry in the line AG means that we only have to find AB, AC, AD, AE, AF, and AG.

Clearly AG = 2. If O denotes the centre of the clockface, then AD is the hypotenuse of an isosceles triangle Δ OAD with legs of length 1, so AD = $\sqrt{2}$.

Δ ACO is isosceles (OA = OC = 1) with apex angle∠AOC = 60°, so the triangle is equilateral. Hence AC = OA = 1.

It follows that ACEGIK is a regular hexagon, so AE = $\sqrt{3}$ (if OC meets AE at X, then Δ ACX is a 30-60-90 triangle, and so is half of an equilateral triangle, whence AX = $\frac{\sqrt{3}}{2})$.

It remains to find AB and AF.

Let OB meet AC at Y. Then OY = $\frac{\sqrt{3}}{2}$ (since Δ OYA is a 30-60-90 triangle).

∴ BY= 1 - $\frac{\sqrt{3}}{2}$, AY = $\frac{1}{2}$, so AB = $\sqrt{2-\sqrt{3}}$.

Finally, AB subtends∠AOB = 30° at the centre, whence∠OAB =∠OBA = 75° and∠AGB = 15°.

∴ ∠ABG = 90° so we may apply Pythagoras’ Theorem to Δ ABG to find BG =AF = $\sqrt{2+\sqrt{3}}$.

177.

$\sqrt{1}$ is the distance from (0, 0, 0) to (1, 0, 0).

$\sqrt{2}$ is the distance from (0, 0, 0) to (1, 1, 0).

$\sqrt{3}$ is the distance from (0, 0, 0) to (1, 1, 1).

$\sqrt{4}$ is the distance from (0, 0, 0) to (2, 0, 0).

$\sqrt{5}$ is the distance from (0, 0, 0) to (2, 1, 0).

$\sqrt{6}$ is the distance from (0, 0, 0) to (2, 1, 1).

$\sqrt{7}$ cannot be realized as a distance between integer lattice points in 3D.

$\sqrt{8}$ is the distance from (0, 0, 0) to (2, 2, 0).

$\sqrt{9}$ is the distance from (0, 0, 0) to (3, 0, 0).

$\sqrt{10}$ is the distance from (0, 0, 0) to (3, 1, 0).

$\sqrt{11}$ is the distance from (0, 0, 0) to (3, 1, 1).

$\sqrt{12}$ is the distance from (0, 0, 0) to (2, 2, 2).

$\sqrt{13}$ is the distance from (0, 0, 0) to (3, 2, 0).

$\sqrt{14}$ is the distance from (0, 0, 0) to (3, 2, 1).

$\sqrt{15}$ cannot be realized as a distance between integer lattice points in 3D.

$\sqrt{16}$ is the distance from (0, 0, 0) to (4, 0, 0).

$\sqrt{17}$ is the distance from (0, 0, 0) to (4, 1, 0).

Note: The underlying question extends Problem 32:

Which integers can be represented as a sum of three squares?

This question was answered by Legendre (1752–1833):

Theorem. A positive integer can be represented as a sum of three squares if and only if it is not of the form 4^a(8b + 7).

178.

(a) Let AD and CE cross at X. Join DE. Then∠AXC =∠EXD (vertically opposite angles). Hence∠CAD +∠ACE =∠ADE +∠CED, so the five angles of the pentagonal star have the same sum as the angles of Δ BED. Hence the five angles have sum $\pi$ radians.

(b) Start with seven vertices A, B, C, D, E, F, G arranged in cyclic order.

(i) Consider first the 7-gonal star ADGCFBE. Let GD and BE cross at X and let GC and BF cross at Y. Join DE, BG. As in part (a),

∠BGC +∠GBF =∠BFC +∠GCF,

and

∠BGD +∠GBE =∠BED +∠GDE,

so the angles in the 7-gonal star have the same sum as the angles in Δ ADE. Hence the seven angles have sum $\pi$ radians.

(ii) Similar considerations with the 7-gonal star ACEGBDF show that its seven angles have sum 3$\pi$ radians.

Note: Notice that the three possible “stars” (including the polygon ABCDEFG) have angle sums $\pi$ radians, 3$\pi$ radians, and 5$\pi$ radians.

(c) if n = 2k + 1 is prime, we may join A to its immediate neighbour B (1-step), or to its second neighbor C (2-step), … , or to its k^th neighbour (k-step), so there are k different stars, with angle sums

$$\begin{array}{cc}& (n-2)\pi ,(n-4)\pi ,(n-6)\pi ,\dots \mathrm{,3}\pi ,\pi \hfill \end{array}$$

respectively.

If n is not prime, the situation is slightly more complicated, since, for each divisor m of n, the km-step stars break up into separate components.

179.

(a) (i) Let the other three pentagons be CDRST, DEUVW, EAXYZ.

At A we have three angles of 108°, so∠NAX = 36°.

Δ ANX is isosceles (AN = AB = AE = AX), so ∠AXN = 72°.

Hence∠AXY +∠AXN = 180°, so Y, X, N lie in a straight line.

Similarly M, N, X lie in a straight line.

Hence M, N, X, Y lie on a straight line segment MY of length 1 + YN = 2 + NX.

(ii) In the same way it follows that MP passes through L and Q, that PS passes through O and T, etc. so that the figure fits snugly inside the pentagon MPSVY, whose angles are all equal to 108°. Moreover, Δ ANX ≡ Δ BQL (by SAS-congruence), so XN = LQ, whence MP = YM. Similarly MP = PS = SV = VY, so MPSVY is a regular pentagon.

(iii) In the regular pentagon EAXYZ the diagonal EY || AX.

Moreover XAC is a straight line, and ∠ACB +∠NBC = 180°, so AC || NB.

Hence YE || NB, and YE = NB = $(n-2)\pi ,(n-4)\pi ,(n-6)\pi ,\dots ,3\pi ,\pi$ (the Golden Ratio $\tau$), so YEBN is a parallelogram.

Hence YN = EB = $\frac{1+\sqrt{5}}{2}$, so YM = 1 + ${\tau }^2$ .

(b)(i)

Δ MPY ≡ Δ PSM ≡ Δ SVP ≡ Δ VYS ≡ Δ YMV

(by SAS-congruence), so

YP = MS = PV = SY = VM

Also∠PMS =∠MPY = 36°;

∴ Δ BMP has equal base angles, and so is isosceles.

Hence BM =BP, and∠MBP = 108° =∠ABC.

Similarly∠AMY =∠AYM = 36°.

∴ Δ AMY ≡ Δ BPM (by ASA-congruence), so

AY = AM = BM = BP.

Δ MAB ≡ Δ PBC – by ASA-congruence:

∠BPC = 108° -∠BPM -∠CPS = 36° =∠AMB,

MA = PB, and ∠PBC =∠MBA =∠MAB.

Hence AB = BC.

Continuing round the figure we see that

AB = BC = CD = DE = EA

and that

∠A =∠B =∠C =∠D =∠E.

(ii) Extend DB to meet MP at L, and extend DA to meet MY at N. Then 36° =∠DBC =∠LBM (vertically opposite angles). Hence Δ LBM has equal base angles and so is isosceles: LM = LB. Similarly NM = NA. Now Δ LBM ≡Δ NAM (by ASA-congruence, since MA = MB), so LM = LB = NA = NM.

In the regular pentagon ABCDE we know that∠DBC = 36°; and in Δ LBM, ∠LBM =∠DBC (vertically opposite angles), so ∠MLB = 108°. Hence∠ BLP = 72° =∠LBP, so Δ PLB is isosceles: PL = PB. In the regular pentagon MPSVY, Δ PMA is isosceles, so PM = PA. ∴ LM = PM -PL = PA - PB = BA.

Hence ABLMN is a pentagon with five equal sides. It is easy to check that the five angles are all equal.

(iii) We saw in (i) that the five diagonals of MPSVY are equal. We showed in Problem 3 that each has length $\tau ={\tau }^2$, and that MPDY is a rhombus, so DY = PM = 1. Similarly SE = 1.

Hence SD = $\tau$- 1, and DE = SE - SD = 2 - $\tau$ = ${\left({\tau }^2\right)}^{-1}$ .

180.

(a) Since the tiles fit together “edge-to-edge” , all tiles have the same edge length. The number k of tiles meeting at each vertex must be at least 3 (since the angle at each vertex of a regular n-gon =$\left(1-\frac{2}{n}\right)\pi \text{ <}\pi )$, and can be at most 6 (since the smallest possible angle in a regular n-gon occurs when n = 3, and is then $\frac{\pi }{3}$ ).

We consider each possible value of k in turn.

– If k = 6, then n = 3 and we have six equilateral triangles at each vertex.

– If k = 5, then we would have $\left(1-\frac{2}{n}\right)\pi =\frac{2\pi }{5},\mathrm{so}n=\frac{10}{3}$ is not an integer.

– If k = 4, then n = 4 and we have four squares at each vertex.

– If k = 3, then n = 6 and we have three regular hexagons at each vertex.

Hence n = 3, or 4, or 6.

(b)(i) If k = n = 4, it is easy to form the vertex figure. It may seem ‘obvious’ that it continues “to infinity” ; but if we think it is obvious, then we should explain why: (choose the scale so that the common edge length is “1” ; then let the integer lattice points be the vertices of the tiling, with the tiles as translations of the unit square formed by (0, 0), (1, 0), (1, 1), (0, 1)).

(ii) If k = 6, n = 3, let the vertices correspond to the complex numbers p + q$\omega$ , where p, q are integers, and where $\omega$ is a complex cube root of 1

(that is, a solution of the equation $\omega$³ = 1 ≠ $\omega$, or $\omega$² + $\omega$ + 1 = 0), with the edges being the line segments of length 1 joining nearest neighbours (at distance 1).

(iii) If k = 3, n = 6, take the same vertices as in (ii), but eliminate all those for which p + q ≡ 0 (mod 3), then let the edges be the line segments of length 1 joining nearest neighbours.

181.

(a)(i) As before, the number k of tiles at each vertex lies between 3 and 6. However, this time k does not determine the shape of the tiles. Hence we introduce a new parameter: the number of t of triangles at each vertex, which can range from 0 up to 6. The derivations are based on elementary arithmetic, for which it is easier to work with angles in degrees.

* If t = 6, then the vertex figure must be 3⁶.

* If t = 5, the remaining gap of 60° could only take a sixth triangle, so this case cannot occur.

* If t = 4, we are left with angle of 120°, so the only possible vertex figure is 3⁴.6.

* If t = 3, then we are left with an angle of 180°, so the only possible configurations are 3³.4² (with the two squares together), or 3².4.3.4 (with the two squares separated by a triangle).

* If t = 2, we are left with an angle of 240°, which cannot be filled with 3 or more tiles (since the average angle size would then be at most 80°, and no more triangles are allowed), so the only possible vertex figures are 3².4.12, 3.4.3.12, 3².6², 3.6.3.6 (since 3².5.n or 3.5.3.n would require a regular n-gon with an angle of 132°, which is impossible).

Note: The compactness of the argument based on the parameter t is about to end. We continue the same apprOACh, with the focus shifting from the parameter tto a new parameter s– namely the number of squares in each vertex figure.

* Suppose t= 1. We are left with an angle of 300°.

If s = 0, the 300° cannot be filled with 3 or more tiles (since then the average angle size would be at most 100°, and no squares can be used), so there are exactly two additional tiles. Since each tile has angle $\le$ 180°, we cannot use a hexagon, so the smallest tile has at least 7 sides; and since the average of the two remaining angle sizes is 150°, the smallest tile has at most 12 sides. It is now easy to check that the only possible vertex figures are 3.7.42, 3.8.24, 3.9.20, 3.10.15, 3.12².

If s = 1, we would be left with an angle of 210°, which would require two larger tiles with average angle size 105°, which is impossible.

If s = 2, the only possible vertex figures are 3.4².6, or3.4.6.4.

Clearly we cannot have s = 3 (or we would be left with a gap of 30°); and t = 1, s > 3 is also impossible.

* Hence we may assume that t = 0, in which case s is at most 4.

If s = 4, then the vertex figure is 4⁴.

If s = 3, then the remaining gap could only take a fourth square, so this case does not occur.

If s = 2, we are left with an angle of 180°, which cannot be filled.

If s = 1, we are left with an angle of 270°, so there must be exactly two additional tiles and the only possible vertex figures are 4.5.20, 4.6.12, or 4.8² (since a regular 7-gon would leave an angle of 141${\frac{3}{7}}^{\circ }$ ).

* Hence we may assume that t = s = 0, and proceed using the parameter f– namely the number of regular pentagons. Clearly f is at most 3, and cannot equal 3 (or we would leave an angle of 36°).

If F = 2, we are left with an angle of 144°, so the only vertex figure is 5².10.

If F = 1, we are left with an angle of 252°, which requires exactly two further tiles, whose average angle is 126°; but this forces us to use a hexagon – leaving an angle of 132°, which is impossible.

* Hence we may assume that t = s = F = 0. So the smallest possible tile is a hexagon, and since we need at least 3 tiles at each vertex, the only possible vertex figure is 6³.

Hence, the simple minded necessary condition (namely that the vertex figure should have no gaps) gives rise to a list of twenty-one possible vertex figures:

3⁶, 3⁴.6, 3³.4², 3².4.3.4, 3².4.12, 3.4.3.12, 3².6², 3.6.3.6, 3.7.42, 3.8.24, 3.9.20, 3.10.15, 3.12², 3.4².6, 3.4.6.4, 4⁴, 4.5.20, 4.6.12, 4.8², 5².10, 6³.

(ii) Lemma. The vertex figures 3².4.12, 3.4.3.12, 3².6², 3.7.42, 3.8.24, 3.9.20, 3.10.15, 3.4².6, 4.5.20, 5².10 do not extend to semi-regular tilings of the plane.

Proof. Suppose to the contrary that any of these vertex figures could be realized by a semi-regular tiling of the plane. Choose a vertex B and consider the tiles around vertex B.

In the first eight of the listed vertex figures we may choose a triangle T = ABC, which is adjacent to polygons of different sizes on the edges BA (say) and BC.

In the two remaining vertex figures, there is a face T = ABC·swith an odd number of edges, which has the same property – namely that of being adjacent to an a-gon on the edge BA (say) and a b-gon on the edge BC with a ≠ b.(For example, in the vertex figure 3².4.12, T = ABC is a triangle, and the faces on BA and on BC are – in some order – a 3-gon and a 4-gon, or a 3-gon and a 12-gon.)

In each case let the face T be a p-gon.

If the face adjacent to T on the edge BA is an a-gon, and that on edge BC is a b-gon, then the vertex figure symbol must include the sequence “$\dots$ a.p.b$\dots$” .

If we now switch attention from vertex B to the vertex A, then we know that A has the same vertex figure, so must include the sequence “$\dots$ a.p.b$\dots$” , so the face adjacent to the other edge of T at A must be a b-gon. As one traces round the edges of the face T, the faces adjacent to

T are alternately a-gons and b-gons – contradicting the fact that T has an odd number of edges.

Hence none of the listed vertex figures extends to a semi-regular tiling of the plane.          QED

(b) It transpires that the remaining eleven vertex figures

3⁶, 3⁴.6, 3³.4², 3².4.3.4, 3.6.3.6, 3.12², 3.4.6.4, 4⁴, 4.6.12, 4.8², 6³

can all be realized as semi-regular tilings(and one– namely 3⁴.6 – can be realized in two different ways, one being a reflection of the other).

In the spirit of Problem 180(b), one should want to do better than to produce plausible pictures of such tilings, by specifying each one in some canonical way. We leave this challenge to the reader.

182. [We construct a regular hexagon, and take alternate vertices.]

Draw the circle with centre O passing through A. The circle with centre A passing through O meets the circle again at X and Y.

The circle with centre X and passing through A and O meets the circle again at B; and the circle with centre Y and passing through A and O, meets the circle again at C.

Then Δ AOX, Δ AOY, Δ XOB, Δ YOC are equilateral, so∠AXB = 120° =∠AYC, and ∠XAB = 30° =∠YAC.

Hence Δ AXB ≡ Δ AYC, so AB = AC.Δ ABC is isosceles so∠B =∠C, with apex angle∠BAC =∠XAY -∠XAB -∠YAC = 60°; hence Δ ABC is equiangular and so equilateral.

183.

(a) Draw the circle with centre O and passing through A.

Extend AO beyond O to meet the circle again at C.

Construct the perpendicular bisector of AC, and let this meet the circle at B and at D.

Then BA = BC (since the perpendicular bisector of AC is the locus of points equidistant from A and from C); similarly DA = DC.

Δ OAB and Δ OCB are both isosceles right angled triangles, so ∠ABC is a right angle (or appeal to “the anglesubtended on the circle by the diameter AC” ). Similarly ∠A, ∠C, ∠D are right angles, so ABCD is a rectangle with BA = BC, and hence a square.

Note: This construction starts with the regular 2-gon AC inscribed in its circumcircle, and doubles it to get a regular 4-gon, by constructing the perpendicular bisectors of the “two sides” to meet the circumcircle at B and at D.

(b) Erect the perpendiculars to AB at A and at B.

Then draw the circles with centre A and passing through B, and with centre B and passing through A.

Let these circles meet the perpendiculars to AB (on the same side of AB) at D and at C.

Then AD = BC, and AD || BC, so ABCD is a parallelogram (by Problem 159(a)), and hence a (being a parallelogram with a right angle), and so a square (since AB = AD).

184.

(a)(i) First construct the regular 3-gon ACE with circumcentre O. Then construct the perpendicular bisectors of the three sides AC, CE, EA, and let these meet the circumcircle at B, D, F.

Note: Here we emphasise the general step from inscribed regular n-gon to inscribed regular 2n-gon – even though this may seem perverse in the case of a regular 3-gon (since we constructed the inscribed regular 3-gon in Problem 182 by first constructing the regular 6-gon and then taking alternate vertices).

(ii) First construct the regular 4-gon ACEG with circumcentre O. Then construct the perpendicular bisectors of the four sides AC, CE, EG, GA, and let these meet the circumcircle at B, D, F, H.

(b)(i) Construct an equilateral triangle ABO.

Then draw the circle with centre O and passing through A and B. Then proceed as in 182.

(ii) Extend AB beyond B, and let this line meet the circle with centre B and passing through A at X.

Now construct a square BXYZ on the side BX as in 183(a), and let the diagonal BY meet the circle at C.

Construct the circumcentre O of Δ ABC (the point where the perpendicular bisectors of AB, BC meet).

Construct the next vertex D as the point where the circle with centre O and passing through A meets the circle with centre C and passing through B. The remaining points E, F, G, H can be found in a similar way.

185.

(a)(i) There are various ways of doing this – none of a kind that most of us might stumble upon. Draw the circumcircle with centre O and passing through A. Extend the line AO beyond O to meet thecircle again at X.

Construct the perpendicular bisector of AX, and let this meet the circle at Y and at Z. Construct the midpoint M of OZ, and join MA.

Let the circle with centre M and passing through A meet the line segment OY at the point F.

Finally let the circle with centre A and passing through F meet the circumcircle at B. Then AB is a side of the required regular 5-gon.(The vertex C on the circumcircle is then obtained as the second meeting point of the circumcircle with the circle having centre B and passing through A. The points D, E can be found in a similar way.)

The proof that this construction does what is claimed is most easily accomplished by calculating lengths.

Let OA = 2. Then OF = $\sqrt{5}$ - 1, so AF = $\sqrt{10-2\sqrt{5}}$ = AB. It remains to prove that this is the correct length for the side of a regular pentagon inscribed in a circle of radius 2. Fortunately the work has already been done, since Δ OAB is isosceles with apex angle equal to 72°. If we drop a perpendicular from O to AB, then we need to check whether it is true that

$$\begin{array}{cc}& \sin 36°=\genfrac{}{}{0.1ex}{}{\sqrt{10-2\sqrt{5}}}{4}.\hfill \end{array}$$

But this was already shown in Problem 3(c).

(ii) To construct a regular 10-gon ABCDEFGHIJ, first construct a regular 5-gon ACEGI with circumcentre O; then construct the perpendicular bisectors of the five sides, and so find B, D, F, H, J as the points where these bisectors meet the circumcircle.

(b)(i) The first move is to construct a line BX through B such that∠ABX = 108°. Fortunately this can be done using part (a), by temporarily treating B as the circumcentre, drawing the circle with centre B and passing through A, and beginning the construction of a regular 5-gon AP·s inscribed in this circle.

Then∠ABP = 72°; so if we extend the line PB beyond B to X, then ∠ABX = 108°. Let BX meet the circle with centre B through A at the point C. Then BA = BC and ∠ABC = 108°, so we are up and running.

If we let the perpendicular bisectorsof AB and BC meet at O, then the circle with centre O and passing through A also passes through B and C (and the yet to be lOBCted points D and E). The circle with centre C and passing through B meets this circle again at D; and the circle with centre A and passing through B meets the circle again at E.

(ii) To construct the regular 10-gon ABCDEFGHIJ, treat B as the point O in (a)(i) and construct a regular 5-gon AXCYZ inscribed in the circle with centre B and passing through A.

Then∠ABC = 144°, and BA = BC, so C is the next vertex of the required regular 10-gon. We may now proceed as in (a)(ii) to first construct the circumcentre O of the required regular 10-gon as the point where the perpendicular bisectors of AB and BC meet, then draw the circumcircle, and finally step off successive vertices D, E, $$\text{. }\text{. }\text{.}$$ of the 10-gon around the circumcircle.

186. The number k of faces meeting at each vertex can be at most five (since more would produce an angle sum that is too large). And k ≥ 3 (in order to create a genuine corner.

• If k = 5, then the vertex figure must be 3⁵ (or the angle sum would be>360°).
• If k = 4, then the vertex figure must be 3⁴ (or the angle sum would be too large).
• If k = 3, the angle in each of the regular polygons must be<120°, so the only possible vertex figures are 5³, 4³, and 3³.

187. The respective midpoints have coordinates:

of AB: $\left(\frac{1}{2},\frac{1}{2},0\right)$; of AC: $\left(\frac{1}{2},0,\frac{1}{2}\right)$; of AD: $\left(1,\frac{1}{2},\frac{1}{2}\right)$; of BC: $\left(0,\frac{1}{2},\frac{1}{2}\right)$; of BD: $\left(\frac{1}{2},1,\frac{1}{2}\right)$ ; of CD: $\left(\frac{1}{2},\frac{1}{2},1\right)$ .

∴ PQ = $\frac{1}{\sqrt{2}}$ = PR = PS = PT = QR = RS = ST = TQ.

188.

(a) There are infinitely many planes through the apex A and the base vertex B. Among these planes, the one perpendicular to the base BCD is the one that passes through the midpoint M of CD. Let the perpendicular from A to the base, meet the base BCD at the point X, which must lie on BM. Let AX have length h. To find h we calculate the area of Δ ABM in two ways.

First, BM has length $\sqrt{3}$, so area(Δ ABM) = $\frac{1}{2}\left(\sqrt{3}\times h\right)$

Second, Δ ABM is isosceles with base AB and apex M, so has height $\sqrt{2}$.

∴ area(Δ ABM)= $\frac{1}{2}(2\times \sqrt{2})$ = $\sqrt{2}$.

If we now equate the two expressions for area(Δ ABM), we see that h = $\sqrt{\frac{8}{3}}$.

(b)(i) When constructing a regular octahedron (whether using card, or tiles such as Polydron®) one begins by arranging four equilateral triangles around a vertex such as A. This ‘vertex figure’ is not rigid: though we know that BC = CD = DE = EB, there is no a priori reason why the four neighbours B, C, D, E of A should form a square, or a rhombus, or a planar quadrilateral. We show that these four neighbours lie in a single plane:B, C, D, E are all distance 2 from A and distance 2 from F, so (by Problem 144) they must all lie in the plane perpendicular to the line AF and passing through the midpoint X of AF. Moreover, Δ ABX ≡ Δ ACX (by RHS-congruence, since AB = AC = 2, AX = AX, and∠AXB =∠AXC are both right angles). Hence XB = XC, so B, C lie on a circle in this plane with centre X. Similarly Δ ABX ≡ Δ ADX ≡ Δ AEX, so BCDE is a cyclic quadrilateral (and a rhombus), and hence a square – with X as the midpoint of both BD and CE.

(ii) Let M be the midpoint of BC and N the midpoint of DE.

Then NM and AF cross at X and so define a single plane. In this plane, Δ ANM ≡ Δ FMN (by SSS-congruence, since AN= FM = $\sqrt{3}$, NM = MN, MA = NF = $\sqrt{3}$); hence ∠ANM =∠FMN, so AN || MF.

Similarly, if P is the midpoint of AE and Q is the midpoint of FC, then Δ DPQ ≡ Δ BQP, so DP || QB. Hence the top face DEA is parallel to the bottom face BCF, so the height of the octahedron sitting on the table is equal to the height of Δ FMN. But this triangle has sides of lengths 2, $\sqrt{3}$, $\sqrt{3}$, so this height is exactly the same as the height h in part (a).

189.

(i) Let L = $\left(\frac{1}{2},0,0\right)andM=$ $\left(\frac{1}{2},\frac{1}{2},0\right)$. Then L lies on the line ST and M is the midpoint of NP.

Δ LSM is a right angled trianglewith legs of length LS = A, LM = $\frac{1}{2}$, so MS = $\sqrt{a^2+\frac{1}{4}}$.

Δ MNS is a right angled trianglewith legs of length MN = $\frac{1}{2}$ - A, MS = $\sqrt{a^2+\frac{1}{4}}$.

HenceNS = $\sqrt{2a^2-a+\frac{1}{2}}$.

Similarly NU = $\sqrt{2a2-a+\frac{1}{2}}$.

Let Lʹ = $0,\frac{1}{2}$, 0\right) and Mʹ = $\left(0,\frac{1}{2},\frac{1}{2}\right)$. Then Mʹ is the midpoint of WX and Lʹ lies immediately below Mʹ on the line joining (0, 0, 0) to (0, 1, 0). In the right angled triangleΔ LʹNMʹ we find NMʹ = $\sqrt{a^2+\frac{1}{4}}$, and in the right angled triangle Δ MʹWN we then find NW = $\sqrt{2a^2-a+\frac{1}{2}}$. Similarly NX= $\sqrt{2a^2-a+\frac{1}{2}}$.

(ii) NP = NS precisely when 1 - 2a = $\sqrt{2a^2-a+\frac{1}{2}}>0$; that is, whena = $\frac{3-\sqrt{5}}{4}$, so all edges of the polyhedron have length$\frac{\sqrt{5}-1}{2}=\tau -1$.

Note: The rectangle NPRQ is a “1 by $\tau -1$” rectangle, and 1: $\tau$ - 1 = $\tau$: 1. Hence the regular icosahedron can be constructed from three congruent, and pairwise perpendicular, copies of a “Golden rectangle” .

190. We mimic the classification of possible vertex figures for semi-regular tilings.

We are assuming that the angles meeting at each vertex add to<360°, so the number k of faces at each vertex lies between 3 and 5. Because faces are regular, but not necessarily congruent, k does not determine the shape of the faces. Hence we let t denote the number of triangles at each vertex, which can range from 0 up to 5.

• If t = 5, then the vertex figure must be 3⁵.
• If t = 4, the remaining polygons have angle sum<120°, so the possible vertex figures are 3⁴, 3⁴.4, and 3⁴.5.
• If t = 3, then the remaining polygons have angle sum<180°, so the only possible vertex figures are 3³, and 3³.n (for any n >3).
• If t = 2, then the remaining polygons have angle sum< 240°, so there are at most 2 additional faces in the vertex figure (since if there were 3 or more extra faces, the average angle size would then be at most 80°, with no more triangles allowed). If there is just 1 additional face, we get the vertex figure 3².n for any n>3. So we may assume that there are 2 additional faces – the smallest of which must then be a 4-gon or a 5-gon.

If the next smallest face is a 4-gon, then we get the possible vertex figures

3².4² and 3.4.3.4, 3².4.5 and 3.4.3.5, 3².4.6 and 3.4.3.6, 3².4.7 and 3.4.3.7, 3².4.8 and 3.4.3.8, 3².4.9 and 3.4.3.9, 3².4.10 and 3.4.3.10, 3².4.11 and 3.4.3.11.

If the next smallest face is a 5-gon, then we get the possible vertex figures

3².5² and 3.5.3.5, 3².5.6 and 3.5.3.6, 3².5.7 and 3.5.3.7.

Note: Before proceeding further it is worth deciding which among the putative vertex figures identified so far seem to correspond to semi-regular polyhedra – and then to prove that these observations are correct.

• The vertex figure 3⁵ corresponds to the regular icosahedron.
• The vertex figure 3⁴ corresponds to the regular octahedron; 3⁴.4 corresponds to the snubcube; 3⁴.5 corresponds to the snub dodecahedron – which comes in left-handed and right-handed forms.
• The vertex figure 3³ corresponds to the regular tetrahedron, and 3³.n (for any n>3) corresponds to the n-gonal antiprism.
• The vertex figure 3².n for any n > 3 does not seem to arise.
• The vertex figure 3².4² does not seem to arise; 3.4.3.4 corresponds to the cuboctahedron; 3².4.5 and 3.4.3.5, 3².4.6 and 3.4.3.6, 3².4.7 and 3.4.3.7, 3².4.8 and 3.4.3.8, 3².4.9 and 3.4.3.9, 3².4.10 and 3.4.3.10, 3².4.11 and 3.4.3.11 do not seem to arise.
• The vertex figure 3².5² does not seem to arise, whereas 3.5.3.5 corresponds to the icosidodecahedron; 3².5.6 and 3.5.3.6, 3².5.7 and 3.5.3.7 do not seem to arise.

To avoid further proliferation of spurious ‘putative vertex figures’ we inject a version of the Lemma used for tilings somewhat earlier than we did fortilings, and then apply the underlying idea to eliminate other spurious possibilities as they arise.

Lemma. The vertex figures

3².4², 3².n (n>3), 3².4.5, 3.4.3.5, 3².4.6, 3.4.3.6, 3².4.7, 3.4.3.7, 3².4.8, 3.4.3.8, 3².4.9, 3.4.3.9, 3².4.10, 3.4.3.10, 3².4.11, 3.4.3.11, 3².5², 3².5.6, 3.5.3.6, 3².5.7, 3.5.3.7

do not arise as vertex figures of any semi-regular polyhedron.

Proof outline. Each of these requires that the vertex figure of any vertex B includes a tile T = ABC·swith an odd number of edges, for which the edge BA is adjacent to an a-gon, the edge BC is adjacent to a b-gon (where a ≠ b), and where the subsequent faces adjacent to T are forced to alternate –a-gon, b-gon, a-gon, $\dots$ – which is impossible.          QED

For the rest we introduce the additional parameter s to denote the number of 4-gons in the vertex figure.

Suppose t= 1. Then the remaining polygons have angle sum< 300°, so there are at most 3 additional faces in the vertex figure (since if there were 4 or more extra faces, the average angle size would be<75°, with no more triangles allowed).

If there are 3 additional faces, the average angle size is<100°, so s > 0.

• If s > 1, then the possible vertex figures are 3.4³ (which corresponds to the rhombicuboctahedron), 3.4² (which corresponds to the 3-gonal prism), 3.4².5 (which is impossible as in the Lemma) and 3.4.5.4 (which corresponds to the small rhombicosidodecahedron).
• If s = 1, then the remaining faces have angle sum<210°, so there can only be one additional face, and every 3.4.n (n > 4) is impossible as in the Lemma.
• If s = 0, then the remaining faces have angle sum < 300°, so there are exactly two other faces and the smallest face has < 12 edges, so the only possible vertex figures are

  – 3.5.n (4 < n), which is impossible as in the Lemma;

  – 3.6², which corresponds to the truncated tetrahedron;

  – 3.6.n (6 < n), which is impossible as in the Lemma;

  – 3.7.n (6 < n), which is impossible as in the Lemma;

  – 3.8², which corresponds to the truncated cube;

  – 3.8.n (8 < n), which is impossible as in the Lemma;

  – 3.9.n (8 < n), which is impossible as in the Lemma;

  – 3.10², which corresponds to the truncated dodecahedron;

  – 3.10.n (10 < n), which is impossible as in the Lemma;

  – 3.11.n (10 < n), which is impossible as in the Lemma.

Thus we may assume that t = 0 – in which case, s<4.

• If s = 3, then the only possible vertex figure is 4³, which corresponds to the cube.
• If s = 2, then the remaining faces have angle sum<180°, so there is exactly one additional face, and every 4².n (n>4) corresponds to the n-gonal prism.
• If s = 1, then the remaining faces have angle sum<270°, so there are at most 2 other faces with the smallest face having<8 edges, so the only possible vertex figures are 4.5.n (for 4<n<20), 4.6², 4.6.n (for 6<n<12), 4.7², 4.7.n (for 7<n<10). Among these 4.5.n is impossible as in the Lemma; 4.6² corresponds to the truncated octahedron; 4.6.n with n odd is impossible as in the Lemma; 4.6.8 corresponds to the great rhombicuboctahedron; 4.6.10 corresponds to the great rhombicosidodecahedron; 4.7.n is impossible as in the Lemma.
• If s = 0, there must be exactly three faces at each vertex, and the smallest must be a 5-gon, so the only possible vertex figures are 5³, which corresponds to the regular dodecahedron; 5².n (for n>5), which is impossible as in the Lemma; 5.6², which corresponds to the truncated icosahedron; or 5.6.7, which is impossible as in the Lemma.

191.

(a)(i)∠AXD = 100°, so∠ADB = 40°. In Δ ABD we then see that∠ABD = 40°, so Δ ABD is isosceles with AB = AD. Δ ABC is isosceles with a base angle∠BAC = 60°, so Δ ABC is equilateral. Hence∠CBD = 20°.

(ii) Δ ABC is equilateral, so AC = AB = AD. Hence Δ ADC is isosceles, so∠ACD = 70° =∠ADC, whence∠BDC = 70° -∠ADB = 30°.

(b)(i) As before ∠AXD = 100°, so∠ADB = 40°.

In Δ ABD we then see that∠ABD = 30°, so Δ ABD is not isosceles (as it was in (a)).

Δ ABC is isosceles, so∠BCA = 70°, whence∠CBD = 10°.

In Δ XCD, ∠CXD = 80°, so∠BDC +∠ACD = 100°, but there is no obvious way of determining the individual summands: ∠BDC and ∠ACD.

(ii) No lengths are specified, so we may choose the length of AC. The point B then lies on the perpendicular bisector of AC, and∠CAB = 70° determines the lOBCtion of B exactly. The line AD makes an angle of 40° with AC, and BD makes an angle of 80° with AC, so the lOBCtion of D is determined. Hence, despite our failure in part (i), the angles are determined.

192.

(i) If P lies on CB, then PC = b cos C, AP = B sin C, and in the right angled triangle Δ APB we have:

c² = (b sin C)² + (a - B cos C)²

   = a² + b²(sin² C + cos² C) - 2ab cos C

   = a² + b² - 2ab cos C.

If P lies on CB extended beyond B, then PC = B cos C, AP = B sin C as before, and in the right angled triangle Δ APB we have:

c² = (b sin C)² + (b cos C -a)²

   = (bsin C)² + (a - bcos C)²

   = a² + b²(sin² C + cos² C) - 2abcos C

   = a² + b² - 2abcos C.

(ii) If P lies on BC extended beyond C, then PC = bcos ∠ACP= -bcos C, AP = bsin ∠ACP = bsin C, and in the right angled triangle Δ APB we have:

c² = (bsin C)² + (a + PC)²

   = (bsin C)² + (a - bcos C)²

   = a² + b²(sin² C + cos² C) - 2abcos C

   = a² + b² - 2abcos C.

193. There are many ways of doing this – once one knows the Sine Rule and Cosine Rule. If we let ∠BDC = y and ∠ACD = z, then one route leads to the identity cos(z - 10°) = 2 sin 10° · sin z, from which it follows that z = 80°, y = 20°.

194.

(a) The angle between two faces, or two planes, is the angle one sees “end-on” – as one looks along the line of intersection of the two planes. This is equal to the angle between two perpendiculars to the line of intersection – one in each plane. If M is the midpoint of BC, then Δ ABC is isosceles with apex A, so the median AM is perpendicular to BC; similarly Δ DBC is isosceles with apex D, so the median DM is perpendicular to BC.

Δ MAD is isosceles with apex M, MA = MD = $\sqrt{3}$, AD= 2, so we can use the Cosine Rule to conclude that 2² = 3 + 3 - 2· 3· cos(∠AMD), whence cos(∠AMD) = $\frac{1}{3}$.

(b) cos(∠AMD) = $\frac{1}{3}$, and $\frac{1}{3}$ < $\frac{1}{2}$, so∠AMD > 60°; hence we cannot fit six regular tetrahedra together so as to share an edge.

Since ∠AMD is acute, ∠AMD < 90°, so we can certainly fit four regular tetrahedra together with lots of room to spare.

We can now appeal to “trigonometric tables” , or a calculator, to see that

$\arccos \left(\frac{1}{3}\right)\text{<}1.24$,

that is1.24 radians, so five tetrahedra use up less than 6.2 radians – which is less than 2$\pi$. Hence we can fit five regular tetrahedra together around a common edge with room to spare (but not enough to fit a sixth).

195.

(a) The angle between the faces ABC and FBC is equal to the angle between two perpendiculars to the common edge BC. Since the two triangles are isosceles with the common base BC, it suffices to find the angle between the two mediansAM and FM.

In Problem 188 we saw that BCDE is a square, with sides of length 2. If we switch attention from the opposite pair of vertices A, F to the pair C, E, then the same proof shows that ABFD is a square with sides of length 2. Hence the diagonal AF = 2$\sqrt{2}$.

Now apply the Cosine Rule to Δ AMF to conclude that:

$\left(2\sqrt{2}\right)$² = 3 + 3 - 2· 3 · cos(∠AMF),

so it follows that cos(∠AMF) = -$\frac{1}{3}$.

(b) cos(∠AMF) = -$\frac{1}{3}$ < 0, so∠AMF > 90°; hence we cannot fit four regular octahedra together so as to share a common edge. Moreover, -$\frac{1}{2}$ < -$\frac{1}{3}$, so∠ AMD < 120°; hence we can fit three octahedra together to share an edge with room to spare (but not enough room to fit a fourth).

196. The angle ∠AMD = $\arccos \left(\frac{1}{3}\right)$ in Problem 194 is acute, and the angle∠AMF = $\arccos \left(-\frac{1}{3}\right)$ in Problem 195 is obtuse. Hence these angles are supplementary; so the regular tetrahedron fits exactly into the wedge-shaped hole between the face ABC of the regular octahedron and the table.

197.

(i) AB = $\sqrt{2}$ = BC = CA = AW = BW = CW. Hence the four faces ABC, BCW, CWA, WAB are all equilateral triangles, so the solid is a regular tetrahedron (or, more correctly, the surface of the solid is a regular tetrahedron).

(ii) AC = $\sqrt{2}$ = CD = DA = AX = CX = DX. Hence the four faces ACD, CDX, DXA, XAC are equilateral triangles, so the solid is a regular tetrahedron.

(iii) AD = $\sqrt{2}$ = DE = EA = AY = DY = EY. Hence the four faces ADE, DEY, EYA, YAD are equilateral triangles, so the solid is a regular tetrahedron.

(iv) AE = $\sqrt{2}$ = EB = BA = AZ = EZ = BZ. Hence the four faces AEB, EBZ, BZA, ZAE are equilateral triangles, so the solid is a regular tetrahedron.

(v) We get another four regular tetrahedra– such as FBCP, where P = (1, 1, -1).

(vi) ABCDEF is a regular octahedron (or, more correctly, the surface of the solid is a regular octahedron).

Note: The six vertices (± 1, 0, 0), (0, ± 1, 0), (0, 0, ± 1) span a regular octahedron, with a regular tetrahedron fitting exactly on each face. The resulting compound star-shaped figure is called the stellated octahedron. Johannes Kepler (1571–1630) made an extensive study of polyhedra and this figure is sometimes referred to as Kepler's ‘stella octangula'. It is worth making in order to appreciate the way it appears to consist of two interlocking tetrahedra.

198. Let the unlabeled vertex of the pentagonalface ABW-V be P. In the pentagon ABWPV the edge AB is parallel to the diagonal VW. Hence ABWV is an isosceles trapezium. The sides VA and WB (produced)meet at S in the plane of the pentagon ABWPV.

Δ SAB has equal base angles, so SA = SB.

Hence SV = SW.

Similarly BC || WX, and WB and XC meet at some point Sʹ on the line WB.

Now Δ SʹBC ≡ Δ SAB, so SʹB = SA= SB. Hence Sʹ = S, and the lines VA, WB, XC, YD, ZE all meet at S.

Since VW || AB, we know that Δ SAB ~ Δ SVW, with scale factor

$\tau :1$ = VW: AB = SV: SA.

If SA = x, then X + 1: X = $\tau :1$, so X = $\tau$.

Let M be the midpoint of AB and let O denote the circumcentre of the regular pentagon ABCDE.

Δ OAB is isosceles, so OM is perpendicular to AB, and the required dihedral angle between the two pentagonal faces is ∠OMP.

It turns out to be better to find not the dihedral angle ∠OMP, but its supplement: namely the angle ∠SMO.

From Δ OAM we see that

OA= $\frac{1}{2\sin {36}^{°}}$,

and we know that SA = $\tau =2\cos$ 36°. One can then check that OS = $\cot$ 36°.

Similarly, in Δ OAM we have

OM = $\frac{\cot {36}^{°}}{2}$.

Hence in Δ OMS we have

tan(∠SMO) = 2.

Hence the required dihedral angle is equal to $\pi -\arctan 2\approx$ 116.56°.

199.

(a)(i) Let M be the midpoint of AC. The angle between the two faces is equal to ∠BMD.

In Δ BMD, we have BM = DM = $\sqrt{3}$, BD = 2$\tau$ = 1 + $\sqrt{5}$. So the Cosine Rule in Δ BMD gives:

$6+2\sqrt{5}=3+3$ - 2· 3· cos(∠BMD),

so cos(∠BMD) = -$\frac{\sqrt{5}}{3}$,

∠$BMD=\arccos \left(-\frac{\sqrt{5}}{3}\right)=\pi -\arccos \left(\frac{\sqrt{5}}{3}\right)\approx {138.19}^{°}$.

(ii) $\frac{\sqrt{5}}{3}>\frac{1}{2}$; hence∠BMD>$\frac{2\pi }{3}$, so we can fit two copies along a common edge, but not three.

(b)(i) Now let M denote the midpoint of BC, and suppose that OM extended beyond M meets the circumcircle at V. Then BV is an edge of the regular 10-goninscribed in the circumcircle. The circumradius OB of BCDEF (which is equal to the edge length of the inscribed regular hexagon) is

OB= $\frac{1}{\sin {36}^{°}}$;

and ∠MBV = 18°,

so BV= $\frac{1}{\cos {18}^{°}}$.

It is easiest to use the converse of Pythagoras’ Theorem, and to write everything first in terms of cos 36°, then (since $\tau$ $=2\cos 36$°, so $\cos {36}^{°}=\frac{1+\sqrt{5}}{4})$ write everything in terms of $\sqrt{5}$.

If we use sin² 36° = 1 - cos² 36°, and 2cos² 18° - 1 = cos 36° = $\frac{1+\sqrt{5}}{4}$, then

BV² + OB² = ${\left(\frac{1}{\cos {18}^{°}}\right)}^2+\left(\frac{1}{\sin {36}^{°}}\right)$²

= $\frac{8}{5+\sqrt{5}}+\frac{8}{5-\sqrt{5}}$

= $\frac{80}{20}$ = 2²

= AB².

Hence, in the right angled triangle Δ AOB, we must have OA = BV as claimed.

(ii) Miraculously no more work is needed. Let the vertex at the ‘south pole’ be L, and let the pentagon formed by its five neighbours be GHIJK. It helps if we can refer to the circumcircle of BCDEF as the ‘tropic of Cancer', and to the circumcircle of GHIJK as the ‘tropic of Capricorn'.

The pentagon GHIJK is parallel to BCDEF, but the vertices of the southern pentagon have been rotated through $\frac{\pi }{5}$ relative to BCDEF, so that G (say) lies on the circumcircle of the pentagon GHIJK, but sits directly below the midpoint of the minor arc BC. Let X denote the point on the ‘tropic of Capricorn’ which is directly beneath B. Then Δ BXG is a right angled triangle with BG = AB = 2, and XG = BV is equal to the edge length of a regular 10-gon inscribed in the circumcircle of GHIJK. Hence, by the calculation in (i), BX is equal to the edge length of the regular hexagon inscribed in the same circle – which is also equal to the circumradius.

200. A necessary condition for copies of a regular polyhedron to “tile 3D (without gaps or overlaps)” is that an integral number of copies should fit together around an edge. That is, the dihedral angle of the polyhedron should be an exact submultiple of 2$\pi$. Only the cube satisfies this necessary condition.

Moreover, if we take as vertices the points (p, q, r) with integer coordinates p, q, r, and as our regular polyhedra all possible translations of the standard unit cube having opposite corners at (0, 0, 0) and (1, 1, 1), then we see that it is possible to tile 3D using just cubes.

201. The four diameters form the four edges of a square ABCD of edge length 2.

The protruding semicircular segments on the left and right can be cut off and inserted to exactly fill the semicircular indentations above and below.

Hence the composite shape has area exactly equal to 2² = 4 square units.

202.

(a) If the regular n-gon is ACEG·sand the regular 2n-gon is ABCDEFG·s, then AC = s_n = s and AB = s_2n = t. If M is the midpoint of AC, AM= $\frac{s}{2}$ and

MB = $1-\sqrt{(1-\left(\frac{s}{2}\right)=\left(\frac{s}{2}\right)}$².

$$\begin{array}{ccc}\therefore t^2\hfill & ={AB}^2\hfill & \hfill \text{(1)}\\ \hfill & ={\left(\genfrac{}{}{0.1ex}{}{s}{2}\right)}^2+{[1-\sqrt{1-{\left(\genfrac{}{}{0.1ex}{}{s}{2}\right)}^2}]}^2\hfill \\ \hfill & =1+1-2\sqrt{1-{\left(\genfrac{}{}{0.1ex}{}{s}{2}\right)}^2}\hfill \\ \hfill & =2-\sqrt{4-s^2}.\hfill \end{array}$$

(b) Put s = s₂= 2 in (1) to get

t = s₄= $\sqrt{2}$. Then put s = s₄= $\sqrt{2}$ in (1) to get t = s₈= $\sqrt{2-\sqrt{2}}$.

(c) Put t = s₆= 1 in (1) to get s = s₃= $\sqrt{3}$. Then put s = s₆= 1 to get

t = s₁₂= $\sqrt{2-\sqrt{3}}$.

(d) Put s = s₅= $\frac{\sqrt{10-2\sqrt{5}}}{2}$ to get

$t=s_{10}=\sqrt{\frac{3-\sqrt{5}}{2}}$.

203.

(a) (i)

n = 3: p₃ = 3$\sqrt{3}\times r$

n = 4: p₄ = $4\sqrt{2}\times r$

n = 5: p₅ = $\frac{5\sqrt{10-2\sqrt{5}}}{2}\times r$

n = 6: p₆ = 6 $\times r$

n = 8: p₈ = 8$\sqrt{2-\sqrt{2}}\times r$

n = 10: p₁₀ = 5$\sqrt{6-2\sqrt{5}}\times r$

n = 12: p₁₂ = 12$\sqrt{2-\sqrt{3}}\times r$.

(ii)

$$\begin{array}{ccc}{c}_3=5.19\cdots \hfill & <\hfill & c_4=5.65\cdots \hfill \\ \hfill & <\hfill & c_5=5.87\cdots \hfill \\ \hfill & <\hfill & c_6=6\hfill \\ \hfill & <\hfill & c_8=6.12\cdots \hfill \\ \hfill & <\hfill & c_{10}=6.18\cdots \hfill \\ \hfill & <\hfill & c_{12}=6.21\cdots .\hfill \end{array}$$

(b)(i)

n = 3: P₃ = 6$\sqrt{3}\times r$

n = 4: P₄ = 8 $\times r$

n = 5: P₅ = 10$\sqrt{5-2\sqrt{5}}\times r$

n = 6: P₆ = 4$\sqrt{3}\times r$

n = 8: P₈ = 8$\left(2\sqrt{2}-2\right)\times r$

n = 10: P₁₀ = $4\sqrt{25-10\sqrt{5}}\times r$

n = 12: P₁₂ = $12\left(4-2\sqrt{3}\right)\times r$.

(ii)

$$\begin{array}{ccc}{C}_3=10.39\cdots \hfill & >\hfill & C_4=8\hfill \\ \hfill & >\hfill & C_5=7.26\cdots \hfill \\ \hfill & >\hfill & C_6=6.92\cdots \hfill \\ \hfill & >\hfill & C_8=6.62\cdots \hfill \\ \hfill & >\hfill & C_{10}=6.49\cdots \hfill \\ \hfill & >\hfill & C_{12}=6.43\cdots .\hfill \end{array}$$

(c) Let O be the centre of the circle of radius r. Let A, B lie on the circle with∠AOB = 30°.

Let M be the midpoint of AB – so that Δ OAB is isosceles, with apex O and height h = OM.

Let Aʹ lie on OA produced, and let Bʹ lie on OB produced, such that OAʹ = OBʹ and AʹBʹ is tangent to the circle.

Then Δ OAB ~ Δ OAʹBʹ with Δ OAʹBʹ larger than Δ OAB, so the scale factor $\frac{1}{h}=2\sqrt{2-\sqrt{3}}>1$.

Hence $P_{12}=2\sqrt{2-\sqrt{3}}\times p_{12}>p_{12},so{C}_{12}>c_{12}$.

204. (i) $\pi r$ (ii) $\frac{\pi }{2}r$ (iii) $\theta r$

205.

(a) (i) Note: This could be a long slog. However we have done much of the work before: when the radius is 1, the most of the required areas were calculated exactly back in Problem 3 and Problem 19.

Alternatively, the area of each of the n sectors is equal to $\frac{1}{2}\sin \theta$, where $\theta$ is the angle subtended at the centre of the circle, and the exact values of the required trig functions were also calculated back in Chapter 1.

$a_3=\frac{3\sqrt{3}}{4}\times$ r²

$a_4=2\times$ r²

$a_5=\frac{5}{8}\sqrt{10+2\sqrt{5}}\times$ r²

$a_6=\frac{3\sqrt{3}}{2}\times$ r²

$a_8=2\sqrt{2}\times$ r²

$a_{10}=\frac{5}{4}\sqrt{10-2\sqrt{5}}\times$ r²

$a_{12}=3\times$ r²

(ii)

$$\begin{array}{ccc}{d}_3=1.29\cdots \hfill & <\hfill & d_4=2\hfill \\ \hfill & <\hfill & d_5=2.37\cdots \hfill \\ \hfill & <\hfill & d_6=2.59\cdots \hfill \\ \hfill & <\hfill & d_8=2.82\cdots \hfill \\ \hfill & <\hfill & d_{10}=2.93\cdots \hfill \\ \hfill & <\hfill & d_{12}=3.\hfill \end{array}$$

(b)(i) Note: This could also be a long slog. However we have done much of the work before. But notice that, when the radius is 1, the area of each of the n sectors is equal to half the edge length times the height (= 1); so if r=1, then the total area is numerically equal to “half the perimeter P_n” .

$A_3=3\sqrt{3}\times$ r²

$A_4=4\times$ r²

$A_5=5\sqrt{5-2\sqrt{5}}\times$ r²

$A_6=2\sqrt{3}\times$ r²

$A_8=8\left(\sqrt{2}-1\right)\times$ r²

$A_{10}=2\sqrt{25-10\sqrt{5}}\times$ r²

$A_{12}=12\left(2-\sqrt{3}\right)\times$ r²

(ii)

$$\begin{array}{ccc}{D}_3=5.19\cdots \hfill & >\hfill & D_4=4\hfill \\ \hfill & >\hfill & D_5=3.63\cdots \hfill \\ \hfill & >\hfill & D_6=3.46\cdots \hfill \\ \hfill & >\hfill & D_8=3.31\cdots \hfill \\ \hfill & >\hfill & D_{10}=3.24\cdots \hfill \\ \hfill & >\hfill & D_{12}=3.21\cdots .\hfill \end{array}$$

(c) Let O be the centre of the circle of radius r. Let A, B lie on the circle with∠AOB = 30°.

Let M be the midpoint of AB – so that Δ OAB is isosceles, with apex O and height h = OM.

Let Aʹ lie on OA produced, and let Bʹ lie on OB produced, such that OAʹ = OBʹ and AʹBʹ is tangent to the circle.

Then Δ OAB ~ Δ OAʹBʹ with Δ OAB contained in Δ OAʹBʹ, so the scale factor $\frac{1}{h}=2\sqrt{2-\sqrt{3}}>1$.

Hence 4(2 - $\sqrt{3}$)· $a_{12} = A_{12} > a_{12}$,

so $D_{12} > d_{12}$.

206. The rearranged shape (shown in Figure 9 is an “almost rectangle” , where OAforms an “almost height” and OA = r. Half of the 2n circular arcs such as AB form the upper “width” , and the other half form the “lower width” , so each of these “almost widths” is equal to half the perimeter of the circle –namely $\pi$ r.

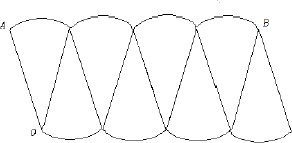
Figure 9: Rectification of a circle.

Hence the area of the rearranged shape is very close to

$r\times \pi r=\pi$ r².

207.

(a) Cut along a generator, open up and lay the surface flat to obtain: a 2$\pi$ r by h rectangle and two circular discs of radius r.

Hence the total surface area is

2$\pi$ r²+ 2$\pi$ rh = $2\pi r(r+h)$.

(b) The lateral surface consists of n rectangles, each with dimensions s_n by h (where s_n is the edge length of the regular n-gon), and hence has area P_nh = 2${\Pi }_{n}rh$.

Adding in the twoend discs (each with area $\frac{1}{2}{P}_{n}r)$ then gives total surface area $2{\Pi }_{n}r(r+h)$.

208.

(a) (i) $\frac{1}{2}\pi$ r²; (ii) $\frac{1}{4}\pi$ r²; (iii) $\frac{\theta }{2}$r².

(b) The sector has two radii of total length 2r. Hence the circular must have length $(\pi -2)r$, and so subtends an angle $\pi$ - 2 at the centre, so has area $\frac{\pi -2}{2}$r².

209.

(a) Focus first on the sloping surface. If we cut along a “generator” (a straight line segment joining the apex to a point on the circumference of the base), the surface opens up and lays flat to form a sector of a circle of radius l. The outside arc of this sector has length 2$\pi$ r, so the sector angle at the centre is equal to $\frac{r}{l}$· 2$\pi$, and hence its area is $\frac{r}{l}$· $\pi$ l² = $\pi$ rl.

Adding the area of the base gives the total surface area of the cone as

$\pi r(r+l)=\frac{1}{2}$· $2\pi r(r+l)$.

(b) Let M be the midpoint of the edge BC and let l denote the ‘slant height’ AM.

Then the area of the n sloping faces is equal to $\frac{1}{2}{P}_n$· l, while the area of the base is equal to $\frac{1}{2}{P}_n$· r.

Hence the surface area is precisely$\frac{1}{2}{P}_n(r+l)$.

210.

(a) If AB is an edge of the inscribed regular n-gon ABCD$\mathrm{...}$, and O is the circumcentre, then∠AOB = $\frac{2\pi }{n}$, so AB = 2r$\sin \frac{\pi }{n}$. Hence the required ratio is equal to $\frac{\sin \frac{\pi }{n}}{\frac{\pi }{n}}$, which tends to 1 as n tends to $\infty$.

(b) If AB is an edge of the circumscribed regular n-gon ABCD$\mathrm{...}$, and O is the circumcentre, then∠AOB = $\frac{2\pi }{n}$, so AB = 2r$\tan \frac{\pi }{n}$. Hence the required ratio is equal to $\frac{\tan \frac{\pi }{n}}{\frac{\pi }{n}}$, which tends to 1 as n tends to $\infty$.

211.

(a) If AB is an edge of the inscribed regular n-gon ABCD$\mathrm{...}$, and O is the circumcentre, then∠AOB = $\frac{2\pi }{n}$, so area(Δ OAB) = $\frac{1}{2}{r}^2\sin \frac{2\pi }{n}$. Hence the required ratio is equal to $\frac{\sin \frac{2\pi }{n}}{\frac{2\pi }{n}}$, which tends to 1 as n tends to $\infty$.

(b) If AB is an edge of the circumscribed regular n-gon ABCD$\mathrm{...}$, and O is the circumcentre, then∠AOB = $\frac{2\pi }{n}$, so area(Δ OAB) = r²$\tan \frac{\pi }{n}$. Hence the required ratio is equal to $\frac{\tan \frac{\pi }{n}}{\frac{\pi }{n}}$, which tends to 1 as n tends to $\infty$.

212.

(a) area(P₂) = area(P₁) + area(P₂ - P₁) > area(P₁).

(b) This general result is clearly related to the considerations of the previous section. But it is not clear whether we can really expect to prove it with the tools available. So it has been included partly in the hope that readers might come to appreciate the difficulties inherent in proving such an “obvious” result.

In the end, any attempt to prove it seems to underline the need to use “proof by induction” – for example, on the number of edges of the inner polygon. This method is not formally treated until Chapter 6, but is needed here.

• Suppose the inner polygon P₁ = ABC has just n= 3 edges, and has perimeter p₁.

Draw the line through A parallel to BC, and let it meet the (boundary of the) polygon P₂ at the points U and V. The triangle inequality (Problem 146(c)) guarantees that the length UV is less than or equal to the length of the compound path from U to V along the perimeter of the polygon P₂ (keeping on the opposite side of the line UV from B and C). So, if we cut off the part of P₂ on the side of the line UV opposite to B and C, we obtain a new outer convex polygon P₃, which contains P₁, and whose perimeter is no larger than that of P₂.

Now draw the line through B parallel to AC, and let it meet the boundary of P₃ at points W, X. If we cut off the part of P₃ on the side of the line WX opposite to A and C, we obtain a new outer convex polygon P₄, which contains P₁, and whose perimeter is no larger than that of P₃.

If we now do the same by drawing a line through C parallel to AB, and cut off the appropriate part of P₄, we obtain a final outer convex polygon P₅, which contains the polygon P₁, and whose perimeter is no larger than that of P₄– and hence no larger than that of the original outer polygon P₂.

All three vertices A, B, C of P₁ now lie on the boundary of the outer polygon P₅, so the triangle inequality guarantees that AB is no larger than the length of the compound path along the boundary of P₅ from A to B (staying on the opposite side of the line AB from C). Similarly BC is no larger than the length of the compound path along the boundary of P₅ from B to C; and CA is no larger than the length of the compound path along the boundary of P₅ from C to A.

Hence the perimeter p₁ of the triangle P₁ is no larger than the perimeter of the outer polygon P₅, whose perimeter was no larger than the perimeter of the original outer polygon P₂. Hence the result holds when the inner polygon is a triangle.

• Now suppose that the result has been proved when the inner polygon is a k-gon, for some k ≥ 3, and suppose we are presented with a pair of polygons P₁, P₂ where the inner polygon P₁ = ABCD·sis a convex (k+1)-gon.

Draw the line m through C parallel to BD. Let this line meet the outer polygon P₂ at U and V. Cut off the part of P₂ on the opposite side of the the line UCV to B and D, leaving a new outer convex polygon P with perimeter no greater than that of P₂. We prove that the perimeter of polygon P₁ is less than that of polygon P – and hence less than that of P₂. Equivalently, we may assume that UCV is an edge of P₂.

Translate the line m parallel to itself, from m to BD and beyond, until it reaches a position of final contact with the polygon P₁, passing through the vertex X (and possibly a whole edge XY)of the inner polygon P₁. Let this final contact line parallel to m be mʹ.

Since P₁ is convex and k ≥qslant 3, we know that X is different from B and from D. As before, we may assume that mʹ is an edge of the outer polygon P₂. Cut both P₂ and P₁ along the line CX to obtain two smaller configurations, each of which consists of an inner convex polygon inside an outer convex polygon, but in which

• each of the inner polygons has at most k edges, and

• in each of the smaller configurations, the inner and outer polygons both share the edge CX.

Then (by induction on the number of edges of the inner polygon) the perimeter of each inner polygon is no larger than the perimeter of the corresponding outer polygon; so for each inner polygon, the partial perimeter running from C to X (omitting the edge CX) is no larger than the partial perimeter of the corresponding outer polygon running from C to X (omitting the edge CX). So when we put the two parts back together again, we see that the perimeter of P₁is no larger than the perimeter of P₂.

Hence the result holds when P₁is a triangle; and if the result holds whenever the inner polygon has k ≥qslant 3 edges, it also holds whenever the inner polygon has (k+ 1) edges.

It follows that the result holds whatever the number of edges of the inner polygon may be.          QED

213.

(a) Join PQ. Then the lines y = B and X = d meet at R to form the right angled triangle PQR.

Pythagoras’ Theorem then implies that (d - a)² + (e - b)² = PQ².

(b) Join PQ. The points P = (a, B, c) and R = (d, e, c) lie in the plane z = c. If we work exclusively in this plane, then part (a) shows that

PR² = (d - a)² + (e - b)².

QR = | F - c|, and Δ PRQ has a right angle at R.

Hence

PQ² = PR² + RQ² = (d - a)² + (e - b)² + (f - c)².

214.

(a) area(Δ ABC) = $\frac{bc}{2}$, area(Δ ACD) = $\frac{cd}{2}$, area(Δ ABD) = $\frac{bd}{2}$.

(b) [This can be a long algebraic slog. And the answer can take very different looking forms depending on how one proceeds. Moreover, most of the resulting expressions are not very pretty, and are likely to incorporate errors.

One way to avoid this slog is to appeal to the fact that the modulus of the vector product DB × DC is equal to the area of the parallelogram spanned by DB

and DC – and so is twice the area of Δ BCD.]

(c) However part (b) is apprOAChed, it is in fact true that area(Δ $BCD{)}^2={\left(\frac{bc}{2}\right)}^2+$ ${\left(\frac{cd}{2}\right)}^2+{\left(\frac{bd}{2}\right)}^2$,

so that

area(Δ ABC)² + area(Δ ACD)² + area(Δ ABD)² = area(Δ BCD)².

215.

(a) b and c are indeed lengths of arcs of great circles on the unit sphere: that is, arcs of circles of radius 1 (centred at the centre of the sphere). However, back in Chapter 1 we used the ‘length’ of such circular arcs to define the angle (in radians) subtended by the arc at the centre. So b and c are also angles (in radians).

(b) The only standard functions of angles are the familiar trig functions (sin, cos).

(c) If c = 0, then the output should specify that a = B, so c should have no effect on the output. This suggests thatwe might expect a formula that involves “adding sin c” or “multiplying by cos c” .

Similarly when B = 0, the output should give a= c, so we might expect a formula that involved “adding sin b” or “multiplying by cos b” .

In general, we should expect a formula in which b and c appear interchangeably (since the input pair(b, c) could equally well be replaced by the input pair (c, b) and should give the same output value of a).

(d)(i) If BC runs along the equator and∠B =∠C = $\frac{\pi }{2}$, then BA and CA run along circles of longitude, so A must be at the North pole. Since A is a right angle, it follows that a = B = c = $\frac{\pi }{2}$.(This tends to rule out the idea that the formula might involve “adding sin B and adding sin c” .)

(ii) Suppose that∠B = $\frac{\pi }{2}$. Since we can imagine AB along the equator, and since there is a right angle at A, it follows that AC and BC both lie along circles of longitude, and so meet at the North pole. Hence C will be at the North pole, so a = B = $\frac{\pi }{2}$.

The inputs to any spherical version of Pythagoras’ Theorem are then B = $\frac{\pi }{2}$, and c. And c is not constrained, so every possible input value of c mustlead to the same output a = $\frac{\pi }{2}$. This tends to suggest that the formula involves some multiple of a product combining “cos b” with some function ofc. And since the inputs “b” and “c” must appear symmetrically, we might reasonably expect some multiple of “cos B · cos c” .

216.

(a) Δ OABʹ has a right angle at A with∠AOBʹ =∠AOB = c. Hence ABʹ = tan c. Similarly ACʹ= tan b.

Hence BʹCʹ²= tan² B + tan² c.

(b) In Δ OABʹ we see that OBʹ = sec c. Similarly OCʹ = sec b. We can now apply the Cosine Rule to Δ OBʹCʹ to obtain:

$$\begin{array}{l}{\tan }^{2}b+{\tan }^{2}c={\sec }^{2}b+{\sec }^{2}c-2\sec b·\sec c·\cos \left(\angle B^{\prime }O{C}^{\prime }\right)\\ ={\sec }^{2}b+{\sec }^{2}c-2\sec b·\sec c·\cos a.\end{array}$$

Hence cos a = cos B · cos c.          QED

217. Construct the plane tangent to the sphere at A. Extend OB to meet this plane at Bʹ, and extend OC to meet the plane at Cʹ.

Δ OABʹ has a right angle at A with∠AOBʹ =∠AOB = c. Hence ABʹ = tan c. Similarly ACʹ = tan b.

Hence BʹCʹ²= tan² B + tan² c - 2· tan B · tan c· cos A.

In Δ OABʹ we see that OBʹ = sec c. Similarly OCʹ = sec b.

We can now apply the Cosine Rule to Δ OBʹCʹ to obtain:

$$\begin{array}{l}{\tan }^{2}b+{\tan }^{2}c-2·\tan b·\tan c·\cos A\\ ={\sec }^{2}b+{\sec }^{2}c-2\sec b·\sec \left(\angle B^{\prime }O{C}^{\prime }\right)\\ ={\sec }^{2}b+{\sec }^{2}c-2\sec b·\sec c·\cos a.\end{array}$$

Hence cos a = cos b· cos c + sin b· sin c · cos A.          QED

218. We show that $\frac{\sin b}{\sin a}=\sin B$ (where B denotes the angle ∠ABC at the vertex B).

Construct the plane T which is tangent to the sphere at B. Let O be the centre of the sphere; let OA

produced meet the plane T at Aʹʹ, and let OC produced meet the plane T at Cʹʹ.

Imagine BA positioned along the equator; then BAʹʹ is horizontal; AC lies on a circle of longitude, so AʹʹCʹʹis vertical. Hence∠Cʹʹ BAʹʹ=∠B, and∠BAʹʹ Cʹʹis a right angle; so sin $B=\frac{A\prime \prime C\prime \prime }{BC\prime \prime }$.

Δ OAʹʹCʹʹ is right angled at Aʹʹ; and∠AʹʹOCʹʹ = b; so sin B = $\frac{A\prime \prime C\prime \prime }{OC\prime \prime }$.

Δ OBCʹʹ is right angled at B; and∠BOCʹʹ = a; so sin a = $\frac{BC\prime \prime }{OC\prime \prime }$.

Hence$\frac{\sin b}{\sin a}$ = sin B depends only on the angle at B, so $\frac{\sin b}{\sin a}=\frac{\sin b^{\prime }}{\sin a^{\prime }}=\sin B$.

219. We show that

$\frac{\sin a}{\sin A}=\frac{\sin b}{\sin B}$.

Position the triangle (or rather “rotate the sphere” ) so that AB runs along the equator, with AC leading into the northern hemisphere.

(i) If ∠A is a right angle, then

$\frac{\sin b}{\sin a}=\sin B=\frac{\sin B}{\sin A}$

by Problem 218. Hence

$\frac{\sin a}{\sin A}=\frac{\sin b}{\sin B}$.

The same is true if ∠B is a right angle.

(ii) If ∠A and ∠B are both less than a right angle, one can draw the circle of longitude from C to some point X on AB. One can then apply Problem 218 to the two triangles Δ CXA and Δ CXB (each with a right angle at X). Let x denote the length of the CX. Then $\frac{\sin x}{\sin b}=\sin A,and\frac{\sin x}{\sin a}=\sin B$.

Hence sin B · sin A = sin X = sin a · sin B, so

$\frac{\sin a}{\sin A}=\frac{\sin b}{\sin B}$.

(iii) If ∠A (say) is greater than a right angle, the circle of longitude from C meets the line BA extended beyond A at a point X (say). If we let CX= x, then one can argue similarly using the triangles Δ CXA and Δ CXB to get $\frac{\sin x}{\sin a}=\sin B,and\frac{\sin x}{\sin b}=\sin A$, whence

$\frac{\sin a}{\sin A}=\frac{\sin b}{\sin B}$.

220. Let X = (x, y) be an arbitrary point of the locus.

(i) Then the distance from X to m is equal to y, so setting this equal to XF gives the equation:

y² = x² + (y - 2a)²,

or

$x^2=4a(y-a)$.

(ii) If we change coordinates and choose the line y = a as a new x-axis, then the equation becomes x² = 4aY. The curve is then tangent to the new x-axis at the (new) origin, and is symmetrical about the y-axis.

221.

(a) Choose the line AB as x-axis, and the perpendicular bisector of AB as the y-axis. Then A = (-3, 0) and B = (3, 0). The point X = (x, y) is a point of the unknown locus precisely when

(x + 3)² + y² = XA² = (2· XB)² = 2²((x - 3)² + y²)

that is, when

(x - 5)² + y² = 4².

This is the equation of a circle with centre (5, 0) and radius r = 4.

(b) Choose the line AB as x-axis, and the perpendicular bisector of AB as the y-axis.

If F = 1, the locus is the perpendicular bisector of AB.

We may assume that F > 1 (since if F < 1, then BX: AX = f^-1: 1 and f^-1 > 1, so we may simplyswap the labelling of A and B).

Now A = (-b, 0) and B = (b, 0), and the point X = (x, y) is a point of the unknown locus precisely when

(x + b)² + y² = XA² = (f· XB)² = f²[(x - b)² + y²]

that is, when

x²(f² - 1) - 2bx(f² + 1) + y²(f² - 1) + b²(f² - 1) = 0

${\left(x-\frac{b(f^2+1)}{f^2-1}\right)}^2+y^2={\left(\frac{2fb}{f^2-1}\right)}^2.$

This is the equation of a circle with centre $\left(\frac{b(f^2+1)}{f^2-1},0\right)$ and radius r = $\frac{2fb}{f^2-1}$.

222.

(a) Choose the line AB as x-axis, and the perpendicular bisector of AB as the y-axis.

Then A = (-c, 0) and B = (c, 0). The point X = (x, y) is a point of the unknown locus precisely when

2a - $2a=AX+BX=\sqrt{{(x+c)}^2+y^2}+\sqrt{{(x-c)}^2+y^2}$,

that is, when

$$2a-\sqrt{{(x+c)}^2+y^2}=\sqrt{{(x-c)}^2+y^2}$$

∴ 4a² - 4a$\sqrt{{(x+c)}^2+y^2}=\sqrt{{(x-c)}^2+y^2}$ $\sqrt{{(x+c)}^2+y^2}+[{(x+c)}^2$

∴ a² + cx = a (x + c)² + y²

∴ (a² - c²)x²+ a²y² = a²(a² - c²)

Setting $\genfrac{}{}{0.1ex}{}{c}{a}$ = e then yields the equation for the locus in the form:

$\frac{x^2}{a^2}+\frac{y^2}{a^2(1-e^2)}=1$.

Note: In the derivation of the equation we squared both sides (twice). This may introduce spurious solutions. So we should check that every solution (x, y) of the final equation satisfies the original condition.

(b) The real number e< 1 is given, so we may set the distance from F to m be $\frac{a}{e}\left(1-e^2\right)$. Choose the line through F and perpendicular to m as x-axis. To start with, we choose the line m as y-axis and adjust later if necessary.

Hence F has coordinates $\left(\frac{a}{e}\left(1-e^2\right),0\right)$, and the point X = (x, y) is a point of the unknown locus precisely when

${\left(x-\frac{a}{e}\left(1-e^2\right)\right)}^2+y^2={(ex)}^2$,

which can be rearranged as

$\left(1-e^2\right)x^2-2\frac{a}{e}(1-e^2)x+{\left(\frac{a}{e}\right)}^2{(1-e^2)}^2+y^2=0$,

and further as

(1 - e²)$\left[x^2-2\frac{a}{e}x+{\left(\frac{a}{e}\right)}^2\right]+y^2={\left(\frac{a}{e}\right)}^2(1-e^2)-{\left(\frac{a}{e}\right)}^2{(1-e^2)}^2$

= $\left(\frac{a}{e}\right)$²(e² - e⁴)

= a²(1 - e²)

∴${\left(x-\frac{a}{e}\right)}^2+\frac{y^2}{1-e^2}=a^2$.

If we now move the y-axis to the line $x=\frac{a}{e}$ the equation takes the simpler form:

$\frac{x^2}{a^2}+\frac{y^2}{a^2(1-e^2)}=1$.

(c) This was done in the derivations in the solutions to parts (a) and (b).

223.

(a) The triangle inequality shows that, if AX > BX, then AB + BX ≥qslant AX; hence the locus is non-empty only when a $⩽$ c. If a = c, then X must lie on the line AB, but not between A and B, so the locus consists of the two half-lines on AB outside AB. Hence we may assume that a < c.

Choose the line AB as x-axis, and the perpendicular bisector of AB as y-axis.

Then A = (-c, 0) and B = (c, 0). The point X = (x, y) is a point of the unknown locus precisely when

$2a=|<i><u>AX</u></i>-<i><u>BX</u></i>|=\left|\sqrt{{(x+c)}^2+y^2}-\sqrt{{(x-c)}^2+y^2}\right|$.

If AX > BX, we can drop the modulus signs and calculate as in Problem 222.

$2a+\sqrt{{(x-c)}^2+y^2}=\sqrt{{(x+c)}^2+y^2}$.

∴ $4a^2+4a\sqrt{{(x-c)}^2+y^2}+{(x-c)}^2+y^2={(x+c)}^2+y^2$

∴ $a^2-cx=-a\sqrt{{(x-c)}^2+y^2}$

∴ $(c^2-a^2)x^2-a^2{y}^2=a^2(c^2-a^2)$

Setting $\genfrac{}{}{0.1ex}{}{c}{a}$ = e (> 1), then yields the equation for the locus in the form:

$\frac{x^2}{a^2}-\frac{y^2}{a^2(e^2-1)}=1$.

Note: In the derivation of the equation we squared both sides (twice). This may introduce spurious solutions. So we should check that every solution (x, y) of the final equation satisfies the original condition. In fact, the squaring process introduces additional solutions in the form of a second branch of the locus, corresponding precisely to points X where AX < BX.

(b) The real number e> 1 is given, so we may set the distance from F to m be $\frac{a}{e}$(e² - 1). Choose the line through F and perpendicular to m as x-axis. To start with, we choose the line m as y-axis and adjust later if necessary.

Hence F has coordinates $\left(\frac{a}{e}(e^2-1),0\right)$$\left(\frac{a}{e}(e^2-1),0\right)$, and the point X = (x, y) is a point of the unknown locus precisely when

${\left(x-\frac{a}{e}(e^2-1)\right)}^2+y^2={(ex)}^2$

∴ (e^{2 - 1})x² + $\frac{2a}{e}(e^2-1)x-y^2={\left(\frac{a}{e}\right)}^2{(e^2-1)}^2$

∴ $(e^2-1)\left[x^2+\frac{2a}{e}x+{\left(\frac{a}{e}\right)}^2\right]-y^2={\left(\frac{a}{e}\right)}^2{(e^2-1)}^2+{\left(\frac{a}{e}\right)}^2(e^2-1)$

= ${\left(\frac{a}{e}\right)}^2(e^4-e^2)$

∴ (e^{2 - 1})$\left[x^2+\frac{2a}{e}x+{\left(\frac{a}{e}\right)}^2\right]-y^2=a^2(e^2-1)$

∴ ${\left(x+\frac{a}{e}\right)}^2-\frac{y^2}{e^2-1}=a^2$

If we now move the y-axis to the line X = -$\frac{a}{e}$ the equation takes the simpler form:

$\frac{x^2}{a^2}-\frac{y^2}{a^2(e^2-1)}=1$.

(c) This was done in derivations in the solutions to parts (a) and (b).

224.

(a) When z = k is a constant, the equation reduces to that of a circle

x² + y² = (rk)² in the plane z = k. When the cutting plane is the

xy-plane “z = 0” , the circle has radius 0, so is a single point.

(b) (i) A vertical plane through the apex cuts the cone in a pair of generators crossing at the apex.

(ii) If the cutting plane through the apex is less steep than a generator, then it cuts the cone only at the apex.

If the cutting plane through the apex is parallel to a generator, then it cuts the cone in a generator – a single line (the next paragraph indicates that this line may be better thought of as a pair of “coincident” lines).

What happens when the cuttingplane through the apex is steeper than a generator may not be intuitively clear. One way to make sense of this is to treat the cross-section as the set of solutions of two simultaneous equations – one for the cone, and the other for the plane (say y = nz, with n < r). This leads to the equation

$x^2=(r^2-n^2)z^2,y=nz$,

with solution set

$x=\pm z\sqrt{r^2-n^2},xy=nz$

which specifies a pair of lines crossing at the apex.

A slightly easier way to visualize the cross-section in this case is to let the apex of the double cone be A, and to let X be any other point of the cross-section. Then the line AX is a generator of the cone, so lies on the cone's surface. But A and X also lie in the cutting plane – so the whole line AX must lie in the cutting plane. Hence the cross-section contains the whole line AX.

(c)(i) If the cutting plane passes through the apex and is parallel to a generator of the cone, then we saw in (b) that the cross-section is simply the generator itself.

(ii) Thus we assume that the cutting plane does not pass through the apex, and may assume that it cuts the bottom half of the cone. If V is the point nearest the apex where the cutting plane meets the cone, then the cross-section curve starts at V and becomes wider as we go down the cone. Because the plane is parallel to a generator, the plane never cuts the “other side” of the bottom half of the cone, so the cross section never “closes up” – but continues to open up wider and wider as we go further and further down the bottom half of the cone.

Let S be the sphere, which is inscribed in the cone above the cutting plane, and which is tangent to the cutting plane at F. Let C be the circle of contact between S and the cone. Let A be the apex of the cone, and let the apex angle of the cone be equal to 2$\theta$. Let X be an arbitrary point of the cross-section. To illustrate the general method, consider first the special case where X = V is the “highest” point of the cross-section. The line segment VA is tangent to the sphere S, so crosses the circle C at some point M. Now VF lies in the cutting plane, so is also tangent to the sphere S at the point F. Any two tangents to a sphere from the same exterior point are equal, so it follows that VM = VF. Moreover, VM is exactly equal to the distance from V to the line m (since

• firstly the line m lies in the horizontal plane through C and so is on the same horizontal level as M, and

• secondly the shortest line VM* from V to m, runs straight up the cutting plane, which is parallel to a generator – so the angle∠MVM*= 2 $\theta$, whence VM* = VM = VF).

Now let X be an arbitrary point of the cross-sectional curve, and use a similar argument. First the line XA is always a generator of the cone, so is tangent to the sphere S, and crosses the circle C at some point Y. Moreover, XF is also tangent to the sphere. Hence XY = XF. It remains to see that XY is equal to the distance XY* from X to the closest point Y* on the line m – since

• firstly the two points Y and Y* both lie on the same horizontal level (namely the horizontal plane through the circle C), and

• secondly both make the same angle $\theta$ with the vertical.

Hence the cross-sectional curve is a parabola with focus F and directrix m.

(d) (i) If the cutting plane is less steep than a generator, the cross-section is a closed curve. If V and W are the highest and lowest points of intersection of the plane with the cone, then the cross-section is clearly symmetrical under reflection in the line VW. Intuitively it is tempting to think that the lower end near W should be ‘fatter’ than the upper part of the curve (giving an egg-shaped cross-section). This turns out to be false, and the correct version was known to the ancient Greeks, though the error was repeated in many careful drawings from the 14th and 15th centuries (e.g. Albrecht Dürer (1471–1528)).

(ii) The derivation is very similar to that in part (c), and we leave the reader to reconstruct it.

An alternative apprOACh is to insert a second sphere S’ below the cutting plane, and inflate it until it makes contact with the cone along a circle C’ while at the same time touching the cutting plane at a point Fʹ. If X is an arbitrary point of the cross-sectional curve, then XA is tangent to both spheres, so meets the circle C at some point Y and meets the circle C’ at some point Yʹ. Then Y, X, Yʹ are collinear. Moreover, XY = XF (since both are tangents to the sphere S from the point X), and XYʹ = XFʹ (since both are tangents to the sphere S’ from the point X), so

XF + XFʹ = XY + XYʹ = YYʹ

But YY’ is equal to the slant height of the cone between the two fixed circles C and C', and so is equal to a constant k. Hence, the focus-focus specification in Problem 222 shows that the cross-section is an ellipse.

(e)(i) If the cutting plane is steeper than a generator, the cross-section cuts both the bottom half and the top half of the cone to give two separate parts of the cross-section. Neither part “closes up” , so each part opens up more and more widely.

If V is the highest point of the cross-section on the lower half of the cone, and W is the lowest point of the cross-section on the upper half of the cone, then it seems clear that the cross-section is symmetrical under reflection in the line VW. But it is quite unclear that the two halves of the cross-section are exactly congruent (though again it was known to the ancient Greeks).

(ii) The formal derivation is very similar to that in part (c), and we leave the reader to reconstruct it.

An alternative apprOACh is to copy the alternative in (d), and to insert a second sphere S'in the upper part of the cone, on the same side of the cutting plane as the apex, inflate it until it makes contact with the cone along a circle C’ while at the same time touching the cutting plane at a point Fʹ. If

X is an arbitrary point of the cross-sectional curve, then XA is tangent to both spheres, so meets the circle C at some point Y and meets the circle C’ at some point Yʹ. Then Y, X, Yʹ are collinear. Moreover, X, F, and Fʹ all lie on the cutting plane. Now XY = XF (since both are tangents to the sphere S from the point X), and XY’ = XFʹ (since both are tangents to the sphere S’ from the point X). If X is on the upper half of the cone, then

XF -XFʹ = XY- XYʹ = YYʹ.

But YYʹ is equal to the slant height of the cone between the two fixed circles C and C', and so is equal to a constant k. Hence, the focus-focus specification in Problem 223 shows that the cross-section is a hyperbola.

225.

(a)(i) 2¹; (ii) 1 = 2⁰

(b) (i) 2²; (ii) 1 = 2⁰; (iii) 4 = 2 \times 2⁰ + 2¹

(c) (i) 2³; (ii) 1 = 2⁰; (iii) 12 = 2 \times 4 + 2²; (iv) 6 = 2 \times 2⁰ + 4

(d) (i) 2⁴; (ii) 1 = 2⁰; (iii) 32 = 2 \times 12 + 2³; (iv) 24 = 2 \times 6 + 12; (v) 8 = 2 \times 2⁰ + 6

226.

(c) (i)If you look carefully at the diagram shown here you should be able to see not only the upper and lower 3D-cubes, but also the four other 3D-cubes formed by joining each 2D-cube in the upper 3D-cube to the corresponding 2D-cube in the lower3D-cube.

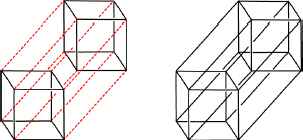
Note: Once we have the 3D-cube expressed in coordinates, we can specify precisely which planes produce which cross-sections in Problem 38. The plane X + y + z = 1 passes through the three neighbours of (0, 0, 0) and creates an equilateral triangular cross-section. Any plane of the form z = c (where c is a constant between 0 and 1) produces a square cross-section. And the plane X + y + z = $\frac{3}{2}$ is the perpendicular bisector of the line joining (0, 0, 0) to (1, 1, 1), and creates a regular hexagon as cross-section.

227.

(a) View the coordinates as (x, y, z). Start at the origin (0, 0, 0) and travel round 3 edges of the lower 2D-cube “z = 0” to the point (0, 1, 0). Copy this path of length 3 on the upper 2D-cube “z = 1” (from (0, 0, 1) to (0, 1, 1). Then join (0, 0, 0) to (0, 0, 1) and join (0, 1, 0) to (0, 1, 1). The result

(0, 0, 0), (1, 0, 0), (1, 1, 0), (0, 1, 0), (0, 1, 1), (1, 1, 1), (1, 0, 1), (0, 0, 1) (and back to (0, 0, 0))

has the property that exactly one coordinate changes when we move from each vertex to the next. This is an example of a Gray code of length 3.

Note: How many such paths/circuits are there in the 3D-cube?We can certainly count those of the kind described here. Each such circuit has a “direction” : the 12 edges of the 3D-cube lie in one of 3 “directions” , and each such circuit contains all four edges in one of these 3 directions. Moreover this set of four edges can be completed to a circuit in exactly 2 ways. So there are 3 × 2 such circuits. In 3D this accounts for all such circuits. But in higher dimensions the numbers begin to explode (in the 4D-cube there are 1344 such circuits).

(b) View the coordinates as (w, x, y, z). Start at the origin (0, 0, 0, 0) and travel round the 8 vertices of the lower 3D-cube “z = 0” to the point (0, 0, 1, 0). Then copy this path on the upper 3D-cube “z = 1” from (0, 0, 0, 1) to (0, 0, 1, 1). Finally join (0, 0, 0, 0) to (0, 0, 0, 1) and join (0, 0, 1, 0) to (0, 0, 1, 1). The result

(0, 0, 0.0), (1, 0, 0, 0), (1, 1, 0, 0), (0, 1, 0, 0), (0, 1, 1, 0), (1, 1, 1, 0),

(1, 0, 1, 0), (0, 0, 1, 0) (0, 0, 1, 1), (1, 0, 1, 1), (1, 1, 1, 1), (0, 1, 1, 1),

(0, 1, 0, 1), (1, 1, 0, 1), (1, 0, 0, 1), (0, 0, 0, 1) (and back to (0, 0, 0, 0))

has the property that exactly one coordinate changes when we move from each vertex to the next. This is an example of a Gray code of length 4.

Note: The general construction in dimension n + 1 depends on the previous construction in dimension n, so makes use of mathematical induction (see Problem 262 in Chapter 6).