VI. Infinity: recursion, induction, infinite descent

Mathematical induction – i.e. proof by recurrence – is... imposed on us, because it is... the affirmation of a property of the mind itself.

Henri Poincaré (1854–1912)

Allez en avant, et la foi vous viendra. (Press on ahead, and understanding will follow.)

Jean le Rond d’Alembert (1717–1783)

Mathematics has been called “the science of infinity”. However, infinity is a slippery notion, and many of the techniques which are characteristic of modern mathematics were developed precisely to tame this slipperiness. This chapter introduces some of the relevant ideas and techniques.

There are aspects of the story of infinity in mathematics which we shall not address. For example, astronomers who study the night sky and the movements of the planets and stars soon note its immensity, and its apparently ‘fractal’ nature – where increasing the detail or magnification reveals more or less the same level of complexity on different scales. And it is hard then to avoid the question of whether the stellar universe is finite or infinite.

In the mental universe of mathematics, once counting, and the process of halving, become routinely iterative processes, questions about infinity and infinitesimals are almost inevitable. However, mathematics recognises the conceptual gulf between the finite and the infinite (or infinitesimal), and rejects the lazy use of “infinity” as a metaphor for what is simply “very large”. Large finite numbers are still numbers; and long finite sums are conceptually quite different from sums that “go on for ever”. Indeed, in the third century BC, Archimedes (c. 287–212 BC) wrote a small booklet called The Sand Reckoner, dedicated to King Gelon, in which he introduced the arithmetic of powers (even though the ancient Greeks had no convenient notation for writing such numbers), in order to demonstrate that – contrary to what some people had claimed – the number of grains of sand in the known universe must be finite (he derived an upper bound of approximately 8×10⁶³ The influence wielded by ideas of infinity on mathematics has been profound, even if we now view some of these ideas as flights of fancy –

• from Zeno of Elea (c. 495 BC – c. 430 BC), who presented his paradoxes to highlight the dangers inherent in reasoning sloppily with infinity,
• through Giordano Bruno (1548–1600), who declared that there were infinitely many inhabited universes, and who was burned at the stake when he refused to retract this and other “heresies”,
• to Georg Cantor (1845–1918) whose groundbreaking work in developing a true “mathematics of infinity” was inextricably linked to his religious beliefs.

In contrast, we focus here on the delights of the mathematics, and in particular on how an initial doorway into “ideas of infinity” can be forged from careful reasoning with finite entities. Readers who would like to explore what we pass over in silence could do worse than to start with the essay on “infinity” in the MacTutor History of Mathematics archive:

http://www-history.mcs.st-and.ac.uk/HistTopics/Infinity.html.

The simplest infinite processes begin with recursion – a process where we repeat exactly the same operation over and over again (in principle, continuing for ever). For example, we may start with 0, and repeat the operation “add 1”, to generate the sequence:

$$\begin{array}{cc}& \mathrm{0,\; 1,\; 2,\; 3,\; 4,\; 5,\; 6,\; 7,\dots .}\hfill \end{array}$$

Or we may start with 2⁰ = 1 and repeat the operation “multiply by 2”, to generate:

$$\begin{array}{cc}& \mathrm{1,\; 2,\; 4,\; 8,\; 16,\; 32,\; 64,\; 128,\dots .}\hfill \end{array}$$

Or we may start with 1.000000 ⋯, and repeat the steps involved in “dividing by 7” to generate the infinite decimal for $\frac{1}{7}$ :

$$\begin{array}{c}\genfrac{}{}{0.1ex}{}{1}{7}=0.1428571428571428571\cdots .\hfill \end{array}$$

We can then vary this idea of “recursion” by allowing each operation to be “essentially” (rather than exactly) the same, as when we define triangular numbers by “adding n” at the n^th stage to generate the sequence:

$$\begin{array}{cc}& \mathrm{0,\; 1,\; 3,\; 6,\; 10,\; 15,\; 21,\; 28,\dots .}\hfill \end{array}$$

In other words, the sequence of triangular numbers is defined by a recurrence relation:

$T_0=\mathrm{0;}$ and

when $n\ge \mathrm{1,}$ $T_n=T_{n-1}+\mathrm{n.}$

We can vary this idea further by allowing more complicated recurrence relations – such as that which defines the Fibonacci numbers:

$F_0=\mathrm{0,}$ $F_1=\mathrm{1;}$ and
when $n\ge 1$ $F_{n+1}=F_n+F_{n-1.}$

All of these “images of infinity” hark back to the familiar counting numbers.

• We know how the counting numbers begin (with 0, or with 1); and
• we know that we can “add 1” over and over again to get ever larger counting numbers.

The intuition that this process is, in principle, never–ending (so is never actually completed), yet somehow manages to count all positive integers, is what Poincaré called a “property of the mind itself”: that is, the idea that we can define an infinite sequence, or process, or chain of deductions (involving digits, or numbers, or objects, or statements, or truths) by

• specifying how it begins, and by then
• specifying in a uniform way “how to construct the next term ”, or “how to perform the next step”.

This idea is what lies behind “proof by mathematical induction”, where we prove that some assertion P(n) holds for all $n\ge 1$ – so demonstrating infinitely many separate statements at a single blow. The validity of this method of proof depends on a fundamental property of the positive integers, or of the counting sequence

$$\begin{array}{cc}& \mathrm{“1,\; 2,\; 3,\; 4,\; 5,\; \dots ”,}\hfill \end{array}$$

namely:

The Principle of Mathematical Induction: If a subset S of the positive integers

• contains the integer “1”,
  and has the property that
• whenever an integer k is in the set S, then the next integer $k+1$ is always in S too,

then S contains all positive integers.

6.1. Proof by mathematical induction I

When students first meet “proof by induction”, it is often explained in a way that leaves them feeling distinctly uneasy, because it appears to break the fundamental taboo:

never assume what you are trying to prove.

This tends to leave the beginner in the position described by d'Alembert's quote at the start of the chapter: they may “press on” in the hope that “understanding will follow”, but a doubt often remains. So we encourage readers who have already met proof by induction to take a step back, and to try to understand afresh how it really works. This may require you to study the solutions (Section 6.10), and to be prepared to learn to write out proofs more carefully than, and rather differently from, what you are used to.

When we wish to prove a general result which involves a parameter n, where n can be any positive integer, we are really trying to prove infinitely many results all at once. If we tried to prove such a collection of results in turn, “one at a time”, not only would we never finish, we would scarcely get started (since completing the first million, or billion, cases leaves just as much undone as at the start). So our only hope is:

• to think of the sequence of assertions in a uniform way, as consisting of infinitely many different, but similar–looking, statements P(n), one for each n separately (with each statement depending on a particular n); and
• to recognise that the overall result to be proved is not just a single statement P(n), but the compound statement that “P(n) is true, for all $n\ge 1$ ”.

Once the result to be proved has been formulated in this way, we can

• use bare hands to check that the very first statement is true (usually P(1)); and
• try to find some way of demonstrating that,

– as soon as we know that “P(k) is true, for some (particular, but unspecified) $k\ge 1$”,

– we can prove in a uniform way that the next result $\mathbf{P}(k+1)$ is then automatically true.

Having implemented the first of the two induction steps, we know that P(1) is true.

The second bullet point above then comes into play and assures us that (since we know that P(1) is true), P(2) must be true.

And once we know that P(2) is true, the second bullet point assures us that P(3) is also true.

And once we know that P(3) is true, the second bullet point assures us that P(4) is also true.

And so on for ever.

We can then conclude that the whole sequence of infinitely many statements are all true – namely that:

“every statement P(n) is true”,

or that

“P(n) is true, for all $n\ge 1$.”

In other words, if we define S to be the set of positive integers n for which the statement P(n) is true, then S contains the element “1”, and whenever k is in S, so is $k+1$; hence, by the Principle of Mathematical Induction we know that S contains all positive integers.

At this stage we should acknowledge an important didactical (rather than mathematical) ploy in our recommended layout here. It is important to underline the distinction between

(i) the individual statements P(n) which are the separate ingredients in the overall statement to be proved, namely:

“P(n) is true, for all $n\ge 1$”,

where infinitely many individual statements have been compressed into a single compound statement, and

(ii) the induction step, where we

– assume some particular P(k) is known to be true, and

– show that the next statement $\mathbf{P}(k+1)$ is then automatically true.

To underline this distinction we consistently use a different “dummy variable” (namely “k”) in the latter case. This distinction is a psychological ploy rather than a logical necessity. However, we recommend that readers should imitate this distinction (at least initially).

6.2. ‘Mathematical induction’ and ‘scientific induction’

The idea of a “list that goes on for ever” arose in the sequence of powers of 4 back in Problem 16, where we asked

Do the two sequences arising from successive powers of 4:

• the leading digits:

$$\begin{array}{cc}& \mathrm{4,\; 2,\; 6,\; 2,\; 1,\; 4,\; 2,\; 6,\; 2,\; 1,\; 4,\dots ,}\hfill \end{array}$$

and

• the units digits:

$$\begin{array}{cc}& \mathrm{4,\; 6,\; 4,\; 6,\; 4,\; 6,\; 4,\; 6,\dots ,}\hfill \end{array}$$

really “repeat for ever” as they seem to?

This example illustrates the most basic misconception that sometimes arises concerning mathematical induction – namely to confuse it with the kind of pattern spotting that is often called ‘scientific induction’.

In science (as in everyday life), we routinely infer that something that is observed to occur repeatedly, apparently without exception (such as the sun rising every morning; or the Pole star seeming to be fixed in the night sky) may be taken as a “fact”. This kind of “scientific induction” makes perfect sense when trying to understand the world around us – even though the inference is not warranted in a strictly logical sense.

Proof by mathematical induction is quite different. Admittedly, it often requires intelligent guesswork at a preliminary stage to make a guess that allows us to formulate precisely what it is that we should be trying to prove. But this initial guess is separate from the proof, which remains a strictly deductive construction. For example,

the fact that “1”, “$1+3$”, “$1+3+5$”, “$1+3+5+7$”, etc. all appear to be successive squares gives us an idea that perhaps the identity

P(n): $1+3+5+\cdots +(2n-1)=n^2$
is true, for all $n\ge 1$.

This guess is needed before we can start the proof by mathematical induction. But the process of guessing is not part of the proof. And until we construct the “proof by induction” (Problem 231), we cannot be sure that our guess is correct.

The danger of confusing ‘mathematical induction’ and ‘scientific induction’ may be highlighted to some extent if we consider the proof in Problem 76 above that “we can always construct ever larger prime numbers”, and contrast it with an observation (see Problem 228 below) that is often used in its place – even by authors who should know better.

In Problem 76 we gave a strict construction by mathematical induction:

• we first showed how to begin (with $p_1=2$ say);
• then we showed how, given any finite list of distinct prime numbers $p_1,p_2,p_3,\dots ,p_k$, it is always possible to construct a new prime $p_{k+1}$ (as the smallest prime number dividing $N_k=p_1\times p_2\times p_3\times \cdots \times p_k+1$).

This construction was very carefully worded, so as to be logically correct.

In contrast, one often finds lessons, books and websites that present the essential idea in the above proof, but “simplify” it into a form that encourages anti–mathematical “pattern–spotting” which is all–too–easily misconstrued. For example, some books present the sequence

$$\begin{array}{cc}& (2;)2+1=\mathbf{3};2\times 3+1=\mathbf{7};2\times 3\times 5+1=\mathbf{31};2\times 3\times 5\times 7+1=\mathbf{211};\dots \hfill \end{array}$$

as a way of generating more and more primes.

Problem 228

(a) Are 3, 7, 31, 211 all prime?

(b) $2\times 3\times 5\times 7\times 11+1$ prime?

(c) Is $2\times 3\times 5\times 7\times 11\times 13+1$ prime? A

We have already met two excellent historical examples of the dangers of plausible pattern–spotting in connection with Problem 118. There you proved that:

“if $2^n-1$ is prime, then n must be prime.”

You then showed that $2^2-1$, $2^3-1$, $2^5-1$, $2^7-1$ are all prime, but that $2^{11}-1=2047=23\times 89$ is not. This underlines the need to avoid jumping to (possibly false) conclusions, and never to confuse a statement with its converse.

In the same problem you showed that:

“if $a^b+1$ is to be prime and $a\ne 1$, then a must be even, and b must be a power of 2.”

You then looked at the simplest family of such candidate primes namely the sequence of Fermat numbers $f_n$:

$$\begin{array}{cc}& f_0=2^1+1=3,f_1=2^2+1=5,f_2=2^4+1=17,f_3=2^8+1=257,f_4=2^{16}+1.\hfill \end{array}$$

It turned out that, although fo, $f_0,f_1,f_2,f_3,f_4$ are all prime, and although Fermat (1601–1665) claimed (in a letter to Marin Mersenne (1588–1648)) that all Fermat numbers $f_n$ are prime, we have yet to discover a sixth Fermat prime!

There are times when a mathematician may appear to guess a general result on the basis of what looks like very modest evidence (such as noticing that it appears to be true in a few small cases). Such “informed guesses” are almost always rooted in other experience, or in some unnoticed feature of the particular situation, or in some striking analogy: that is, an apparent pattern strikes a chord for reasons that go way beyond the mere numbers. However those with less experience need to realise that apparent patterns or trends are often no more than numerical accidents.

Pell’s equation (John Pell (1611–1685)) provides some dramatic examples.

• If we evaluate the expression “$n^2+1$” for $n=\mathrm{1,2}\mathrm{,\; 3},\dots$, we may notice that the outputs $\mathrm{2,5}\mathrm{,\; 10}\mathrm{,\; 17}\mathrm{,\; 26},\dots$ never give a perfect square. And this is to be expected, since the next square after $n^2$ is

$\begin{array}{cc}& {(n+1)}^2=n^2+2n+1,\hfill \end{array}$ ,

and this is always greater than $n^2+1$.

• However, if we evaluate “$991n^2+1$” for $n=\mathrm{1,\; 2,\; 3,\dots ,}$ we may observe that the outputs never seem to include a perfect square. But this time there is no obvious reason why this should be so – so we may anticipate that this is simply an accident of “small” numbers. And we should hesitate to change our view, even though this accident goes on happening for a very, very, very long time: the smallest value of n for which $991n^2+1$ gives rise to a perfect square is apparently

$\begin{array}{cc}& n=12055735790331359447442538767.\hfill \end{array}$

6.3. Proof by mathematical induction II

Even where there is no confusion between mathematical induction and ‘scientific induction', students often fail to appreciate the essence of “proof by induction”. Before illustrating this, we repeat the basic structure of such a proof.

A mathematical result, or formula, often involves a parameter n, where n can be any positive integer. In such cases, what is presented as a single result, or formula, is a short way of writing an infinite family of results. The proof that such a result is correct therefore requires us to prove infinitely many results at once. We repeat that our only hope of achieving such a mind–boggling feat is

• to formulate the stated result for each value of n separately: that is, as a statement P(n) which depends on n;
• then to use bare hands to check the “beginning” – namely that the simplest case (usually P(1)) is true;
• finally to find some way of demonstrating that,

– as soon as we know that P(k) is true, for some (unknown) $k\ge 1$,

– we can prove that the next result $\mathbf{P}(k+1)$ is then automatically true.

We can then conclude that

“every statement P(n) is true”,

or that

“P(n) is true, for all $n\ge 1$”.

Problem 229 Prove the statement:

“5²ⁿ⁺² – 24n – 25 is divisible by 576, for all $\mathit{n}⩾1$”.

When trying to construct proofs in private, one is free to write anything that helps as ‘rough work'. But the intended thrust of Problem 229 is two–fold:

• to introduce the habit of distinguishing clearly between

  (i) the statement P(n) for a particular n, and

  (ii) the statement to be proved – namely “P(n) is true, for all $n\ge 1$”; and

• to draw attention to the “induction step” (i.e. the third bullet point above), where

  (i) we assume that some unspecified P(k) is known to be true, and

  (ii) seek to prove that the next statement $\mathbf{P}(k+1)$ must then be true.

The central lesson in completing the “induction step” is to recognize that:

to prove that $\mathbf{P}(k+1)$ is true, one has to start by looking at what $\mathbf{P}(k+1)$ says.

In Problem 229 $\mathbf{P}(k+1)$ says that

“$5^{2(k+1)+2}-24(k+1)-25$ is divisible by 576”.

Hence one has to start the induction step with the relevant expression

$$\begin{array}{cc}& 5^{2(k+1)+2}-24(k+1)-25,\hfill \end{array}$$

and look for some way to rearrange this into a form where one can use P(k) (which we assume is already known to be true, and so are free to use).

It is in general a false strategy to work the other way round – by “starting with P(k), and then fiddling with it to try to get $\mathbf{P}(k+1)$”. (This strategy can be made to work in the simplest cases; but it does not work in general, and so is a bad habit to get into.) So the induction step should always start with the hypothesis of $\mathbf{P}(k+1)$.

The next problem invites you to prove the formula for the sum of the angles in any polygon. The result is well–known; yet we are fairly sure that the reader will never have seen a correct proof. So the intention here is for you to recognise the basic character of the result, to identify the flaws in what you may until now have accepted as a proof, and to try to find some way of producing a general proof.

Problem 230 Prove by induction the statement:

“for each $n\ge 3$, the angles of any n–gon in the plane have sum equal to $(n-2)\pi$ radians.”

The formulation certainly involves a parameter $n\ge 3$; so you clearly need to begin by formulating the statement P(n). For the proof to have a chance of working, finding the right formulation involves a modest twist! So if you get stuck, it may be worth checking the first couple of lines of the solution.

No matter how P(n) is formulated, you should certainly know how to prove the statement P(3) (essentially the formula for the sum of the angles in a triangle). But it is far from obvious how to prove the “induction step”:

“if we know that P(k) is true for some particular $k\ge 1$, then $\mathbf{P}(k+1)$ must also be true”.

When tackling the induction step, we certainly cannot start with P(k)! The statement $\mathbf{P}(k+1)$ says something about polygons with $k+1$ sides: and there is no way to obtain a typical $(k+1)$–gon by fiddling with some statement about polygons with k sides. (If you start with a k–gon, you can of course draw a triangle on one side to get a $(k+1)$–gon; but this is a very special construction, and there is no easy way of knowing whether all $(k+1)$–gons can be obtained in this way from some k–gon.) The whole thrust of mathematical induction is that we must always start the induction step by thinking about the hypothesis of $\mathbf{P}(k+1)$ – that is in this case, by considering an arbitrary $(k+1)$–gon and then finding some guaranteed way of “reducing” it in order to make use of P(k).

The next two problems invite you to prove some classical algebraic identities. Most of these may be familiar. The challenge here is to think carefully about the way you lay out your induction proof, to learn from the examples above, and (later) to learn from the detailed solutions provided.

Problem 231 Prove by induction the statement:

“$1+3+5+\cdots +(2\mathit{n}-1)={\mathit{n}}^2$ holds, for all $\mathit{n}⩾1$”

The summation in Problem 231 was known to the ancient Greeks. The mystical Pythagorean tradition (which flourished in the centuries after Pythagoras) explored the character of integers through the ‘spatial figures’ which they formed. For example, if we arrange each successive integer as a new line of dots in the plane, then the sum “$1+2+3+\cdots +\mathit{n}$” can be seen to represent a triangular number. Similarly, if we arrange each odd number $2\mathit{k}-1$ in the sum “$1+2+3+\cdots +\mathit{n}$” as a “k-by-k reverse L-shape”, or gnomon (a word which we still use to refer to the L-shaped piece that casts the shadow on a sundial), then the accumulated L-shapes build up an n by n square of dots - the “1” being the dot in the top left hand corner, the “3” being the reverse L-shape of 3 dots which make this initial “1” into a 2 by 2 square, the “5” being the reverse L-shape of 5 dots which makes this 2 by 2 square into a 3 by 3 square, and so on. Hence the sum “$1+3+5+...+(2\mathit{n}-1)$” can be seen to represent a square number.

There is much to be said for such geometrical illustrations; but there is no escape from the fact that they hide behind an ellipsis (the three dots which we inserted in the sum between “5” and “$2\mathit{n}-1$”, which were then summarised when arranging the reverse L-shapes by ending with the words “and so on”). Proof by mathematical induction, and its application in Problem 231, constitute a formal way of avoiding both the appeal to pictures, and the hidden ellipsis.

Problem 232 The sequence

$2,5,13,35,\dots$

is defined by its first two terms ${\mathit{u}}_0=2,{\mathit{u}}_1=5$, and by the recurrence relation:

${\mathit{u}}_{\mathit{n}+2}=5{\mathit{u}}_{\mathit{n}+1}-6{\mathit{u}}_{\mathit{n}}$.

(a) Guess a closed formula for the n^th term u_n.

(b) Prove by induction that your guess in (a) is correct for all $\mathit{n}⩾0$.

Problem 233 The sequence of Fibonacci numbers

$0,1,1,2,3,5,8,13,\dots$

is defined by its first two terms ${\mathit{F}}_0=0,{\mathit{F}}_1=1$, and by the recurrence relation:

${\mathit{F}}_{\mathit{n}+2}={\mathit{F}}_{\mathit{n}+1}+{\mathit{F}}_{\mathit{n}}$ when $\mathit{n}⩾0$.

Prove by induction that, for all $\mathit{n}⩾0$,

${\mathit{F}}_{\mathit{n}}=\frac{{\alpha }^{\mathit{n}}-{\beta }^{\mathit{n}}}{\sqrt{5}},\mathrm{where}\alpha =\frac{1+\sqrt{5}}{2}\mathrm{and}\beta =\frac{1-\sqrt{5}}{2}$

Problem 234 Prove by induction that

$5^{2\mathit{n}+1}·2^{\mathit{n}+2}+3^{\mathit{n}+2}·2^{2\mathit{n}+1}$

is divisible by 19, for all $\mathit{n}⩾0$.

Problem 235 Use mathematical induction to prove that each of these identities holds, for all $\mathit{n}⩾1$:

(a) $1+2+3+\cdots +\mathit{n}=\frac{\mathit{n}(\mathit{n}+1)}{2}$

(b) $\frac{1}{1·2}+\frac{1}{2·3}+\frac{1}{3·4}+\cdots +\frac{1}{\mathit{n}(\mathit{n}+1)}=1-\frac{1}{\mathit{n}+1}$

(c) $1+\mathit{q}+{\mathit{q}}^2+{\mathit{q}}^3+\cdots +{\mathit{q}}^{\mathit{n}-1}=\frac{1}{1-\mathit{q}}-\frac{{\mathit{q}}^{\mathit{n}}}{1-\mathit{q}}$

(d) $0·0!+1·1!+2·2!+\cdots +(\mathit{n}-1)·(\mathit{n}-1)!=\mathit{n}!-1$

(e) $(\cos \theta +\mathit{i}\sin \theta {)}^{\mathit{n}}=\cos \mathit{n}\theta +\mathit{i}\sin \mathit{n}\theta$.

Problem 236 Prove by induction the statement:

“$(1+2+3+\cdots +\mathit{n}{)}^2=1^3+2^3+3^3+\cdots +{\mathit{n}}^3$, for all $\mathit{n}⩾1$”.

We now know that, for all $\mathit{n}⩾1$:

$1+1+1+\cdots +1(\mathit{n}\mathrm{terms})=\mathit{n}$.

And if we sum these “outputs” (that is, the first n natural numbers), we get the n^th triangular number:

$1+2+3+\cdots +\mathit{n}=\frac{\mathit{n}(\mathit{n}+1)}{2}={\mathit{T}}_{\mathit{n}}$.

The next problem invites you to find the sum of these “outputs”: that is, to find the sum of the first n triangular numbers.

Problem 237

(a) Experiment and guess a formula for the sum of the first n triangular numbers:

${\mathit{T}}_1+{\mathit{T}}_2+{\mathit{T}}_3+\cdots +{\mathit{T}}_{\mathit{n}}=1+3+6+\cdots +\frac{\mathit{n}(\mathit{n}+1)}{2}.$

(b) Prove by induction that your guessed formula is correct for all $\mathit{n}⩾1$.

A We now know closed formulae for

“$1+2+3+\cdots +\mathit{n}$”

and for

“$1·2+2·3+3·4+\cdots +(\mathit{n}-1)\mathit{n}$”.

The next problem hints firstly that these identities are part of something more general, and secondly that these results allow us to find identities for the sum of the first n squares:

$1^2+2^2+3^2+\cdots +{\mathit{n}}^2$

for the first n cubes:

$1^3+2^3+3^3+\cdots +{\mathit{n}}^3$

and so on.

Problem 238

(a) Note that

$1·2+2·3+3·4+\cdots +\mathit{n}(\mathit{n}+1)=1·(1+1)+2·(2+1)+3·(3+1)+\cdots +\mathit{n}·(\mathit{n}+1)$.

Use this and the result of Problem 237 to derive a formula for the sum:

$1^2+2^2+3^2+\cdots +{\mathit{n}}^2$.

(b) Guess and prove a formula for the sum

$1·2·3+2·3·4+3·4·5+\cdots +(\mathit{n}-2)(\mathit{n}-1)\mathit{n}$.

Use this to derive a closed formula for the sum:

$1^3+2^3+3^3+\cdots +{\mathit{n}}^3$.

It may take a bit of effort to digest the statement in the next problem. It extends the idea behind the “method of undetermined coefficients” that is discussed in Note 2 to the solution of Problem 237(a).

Problem 239

(a) Given $\mathit{n}+1$ distinct real numbers

${\mathit{a}}_0,{\mathit{a}}_1,{\mathit{a}}_2\mathrm{,...,}{\mathit{a}}_{\mathit{n}}$

find all possible polynomials of degree n which satisfy

$\mathit{f}\left({\mathit{a}}_0\right)=\mathit{f}\left({\mathit{a}}_1\right)=\mathit{f}\left({\mathit{a}}_2\right)=\cdots =\mathit{f}\left({\mathit{a}}_{\mathit{n}-1}\right)=0,\mathit{f}\left({\mathit{a}}_{\mathit{n}}\right)=\mathit{b}$

for some specified number b.

(b) For each $\mathit{n}⩾1$, prove the following statement:

Given two labelled sets of $\mathit{n}+1$ real numbers

${\mathit{a}}_0,{\mathit{a}}_1,{\mathit{a}}_2\mathrm{,...},{\mathit{a}}_{\mathit{n}}$,

and

${\mathit{b}}_0,{\mathit{b}}_1,{\mathit{b}}_2,\dots ,{\mathit{b}}_{\mathit{n}}$,

where the a_i are all distinct (but the b need not be), there exists a polynomial f_n of degree n, such that

${\mathit{f}}_{\mathit{n}}\left({\mathit{a}}_0\right)={\mathit{b}}_0,{\mathit{f}}_{\mathit{n}}\left({\mathit{a}}_1\right)={\mathit{b}}_1,{\mathit{f}}_{\mathit{n}}\left({\mathit{a}}_2\right)={\mathit{b}}_2,\dots ,{\mathit{f}}_{\mathit{n}}\left({\mathit{a}}_{\mathit{n}}\right)={\mathit{b}}_{\mathit{n}}.$

We end this subsection with a mixed bag of three rather different induction problems. In the first problem the induction step involves a simple construction of a kind we will meet later.

Problem 240 A country has only 3 cent and 4 cent coins.

(a) Experiment to decide what seems to be the largest amount, N cents, that cannot be paid directly (without receiving change).

(b) Prove by induction that “n cents can be paid directly for each $\mathit{n}>\mathit{N}$”.

Problem 241

(a) Solve the equation $\mathit{z}+\frac{1}{\mathit{z}}=1$. Calculate ${\mathit{z}}^2$, and check that ${\mathit{z}}^2+\frac{1}{{\mathit{z}}^2}$ is also an integer.

(b) Solve the equation $\mathit{z}+\frac{1}{\mathit{z}}=2$. Calculate ${\mathit{z}}^2+\frac{1}{{\mathit{z}}^2}$, and check that ${\mathit{z}}^2+\frac{1}{{\mathit{z}}^2}$ is also an integer.

(c) Solve the equation $\mathit{z}+\frac{1}{\mathit{z}}=3$. Calculate ${\mathit{z}}^2+\frac{1}{{\mathit{z}}^2}$, and check that ${\mathit{z}}^2+\frac{1}{{\mathit{z}}^2}$ is also an integer.

(d) Solve the equation $\mathit{z}+\frac{1}{\mathit{z}}=\mathit{k}$, where k is an integer. Calculate z², and check that ${\mathit{z}}^2+\frac{1}{{\mathit{z}}^2}$ is also an integer.

(e) Prove that if a number z has the property that $z+\frac{1}{z}$ is an integer, then ${\mathit{z}}^{\mathit{n}}+\frac{1}{{\mathit{z}}^{\mathit{n}}}$ is also an integer for each $\mathit{n}⩾1$.

Problem 242 Let p be any prime number. Use induction to prove:

“${\mathit{n}}^{\mathit{p}}-\mathit{n}$ is divisible by p for all $\mathit{n}⩾1$”.

6.4. Infinite geometric series

Elementary mathematics is predominantly about equations and identities. But it is often impossible to capture important mathematical relations in the form of exact equations. This is one reason why inequalities become more central as we progress; another reason is because inequalities allow us to make precise statements about certain infinite processes.

One of the simplest infinite process arises in the formula for the “sum” of an infinite geometric series:

$1+\mathit{r}+{\mathit{r}}^2+{\mathit{r}}^3+\cdots +{\mathit{r}}^{\mathit{n}}+\cdots$ (for ever).

Despite the use of the familiar-looking “+” signs, this can be no ordinary addition. Ordinary addition is defined for two summands; and by repeating the process, we can add three summands (thanks in part to the associative law of addition). We can then add four, or any finite number of summands. But this does not allow us to “add” infinitely many terms as in the above sum. To get round this we combine ordinary addition (of finitely many terms) and simple inequalities to find a new way of giving a meaning to the above “endless sum”. In Problem 116 you used the factorisation

${\mathit{r}}^{\mathit{n}+1}-1=(\mathit{r}-1)\left(1+\mathit{r}+{\mathit{r}}^2+{\mathit{r}}^3+\cdots +{\mathit{r}}^{\mathit{n}}\right)$

to derive the closed formula:

$1+\mathit{r}+{\mathit{r}}^2+{\mathit{r}}^3+\cdots +{\mathit{r}}^{\mathit{n}}=\frac{1-{\mathit{r}}^{\mathit{n}+1}}{1-\mathit{r}}$.

This formula for the sum of a finite geometric series can be rewritten in the form

$$1+\mathit{r}+{\mathit{r}}^2+{\mathit{r}}^3+\cdots +{\mathit{r}}^{\mathit{n}}=\frac{1}{1-\mathit{r}}-\frac{{\mathit{r}}^{\mathit{n}+1}}{1-\mathit{r}}$$.

At first sight, this may not look like a clever move! However, it separates the part that is independent of n from the part on the RHS that depends on n; and it allows us to see how the second part behaves as n gets large:

when $|\mathit{r}|<1$, successive powers of r get smaller and smaller and converge rapidly towards 0,

so the above form of the identity may be interpreted as having the form:

$1+\mathit{r}+{\mathit{r}}^2+{\mathit{r}}^3+\cdots +{\mathit{r}}^{\mathit{n}}=\frac{1}{1-\mathit{r}}$ — (an “error term”).

Moreover if $|\mathit{r}|<1$, then the “error term” converges towards 0 as $\mathit{n}\to \infty$. In particular, if $1>\mathit{r}>0$, the error term is always positive, so we have proved, for all $\mathit{n}⩾1$:

$1+\mathit{r}+{\mathit{r}}^2+{\mathit{r}}^3+\cdots +{\mathit{r}}^{\mathit{n}}<\frac{1}{1-\mathit{r}}$

and

the difference between the two sides tends rapidly to 0 as $\mathit{n}\to \infty$.

We then make the natural (but bold) step to interpret this, when $|\mathit{r}|<1$, as offering a new definition which explains precisely what is meant by the endless sum

$1+\mathit{r}+{\mathit{r}}^2+{\mathit{r}}^3+\cdots$ (for ever),

declaring that, when $|\mathit{r}|<1$,

$1+\mathit{r}+{\mathit{r}}^2+{\mathit{r}}^3+\cdots$ (for ever) = $\frac{1}{1-\mathit{r}}$.

More generally, if we multiply every term by a, we see that

$\mathit{a}+\mathit{ar}+{\mathit{ar}}^2+{\mathit{ar}}^3+\cdots$ (for ever) = $\frac{\mathit{a}}{1-\mathit{r}}$.

Problem 243 Interpret the recurring decimal 0.037037037 ··· (for ever) as an infinite geometric series, and hence find its value as a fraction.

Problem 244 Interpret the following endless processes as infinite geometric series.

(a) A square cake is cut into four quarters, with two perpendicular cuts through the centre, parallel to the sides. Three people receive one quarter each - leaving a smaller square piece of cake. This smaller piece is then cut in the same way into four quarters, and each person receives one (even smaller) piece - leaving an even smaller residual square piece, which is then cut in the same way. And so on for ever. What fraction of the original cake does each person receive as a result of this endless process?

(b) I give you a whole cake. Half a minute later, you give me half the cake back. One quarter of a minute later, I return one quarter of the cake to you. One eighth of a minute later you return one eighth of the cake to me. And so on. Adding the successive time intervals, we see that

$\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\cdots$ (for ever) = 1,

so the whole process is completed in exactly 1 minute. How much of the cake do I have at the end, and how much do you have?

Problem 245 When John von Neumann (1903-1957) was seriously ill in hospital, a visitor tried (rather insensitively) to distract him with the following elementary mathematics problem.

Have you heard the one about the two trains and the fly? Two trains are on a collision course on the same track, each travelling at 30 km/h. A super-fly starts on Train A when the trains are 120 km apart, and flies at a constant speed of 50 km/h - from Train A to Train B, then back to Train A, and so on. Eventually the two trains collide and the fly is squashed. How far did the fly travel before this sad outcome?

6.5. Some classical inequalities

The fact that our formula for the sum of a geometric series gives us an exact sum is very unusual - and hence very precious. For almost all other infinite series - no matter how natural, or beautiful, they may seem - you can be fairly sure that there is no obvious exact formula for the value of the sum. Hence in those cases where we happen to know the exact value, you may infer that it took the best efforts of some of the finest mathematical minds to discover what we know.

One way in which we can make a little progress in estimating the value of an infinite series is to obtain an inequality by comparing the given sum with a geometric series.

Problem 246

(a)(i) Explain why

$\frac{1}{3^2}<\frac{1}{2^2}$,

so

$\frac{1}{2^2}+\frac{1}{3^2}<\frac{2}{2^2}=\frac{1}{2}$.

(ii) Explain why $\frac{1}{5^2},\frac{1}{6^2},\frac{1}{7^2}$ are all $<\frac{1}{4^2}$, so

$\frac{1}{4^2}+\frac{1}{5^2}+\frac{1}{6^2}+\frac{1}{7^2}<\frac{4}{4^2}=\frac{1}{4}.$

(b) Use part (a) to prove that

$$\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+\cdots +\frac{1}{n^2}<2$$, for all $\mathit{n}⩾1$.

(c) Conclude that the endless sum

$$\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+\cdots +\frac{1}{{\mathit{n}}^2}+\cdots$$ (for ever)

has a definite value, and that this value lies somewhere between $\frac{17}{12}$ and 2.

The next problem presents a rather different way of deriving a similar equality. Once the relevant inequality has been guessed, or given (see Problem 247(a) and (b)), the proof by mathematical induction is often relatively straightforward. And after a little thought about Problem 246, it should be clear that much of the inaccuracy in the general inequality arises from the rather poor approximations made for the first few terms (when n = 1, when n = 2, when n = 3, etc.); hence by keeping the first few terms as they are, and only approximating for $\mathit{n}⩾2$, or $\mathit{n}⩾3$, or $\mathit{n}⩾4$, we can often prove a sharper result.

Problem 247

(a) Prove by induction that

$\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+\cdots +\frac{1}{{\mathit{n}}^2}⩽2-\frac{1}{\mathit{n}}$, for all $\mathit{n}⩾1$.

(b) Prove by induction that

$\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+\cdots +\frac{1}{{\mathit{n}}^2}<1.68-\frac{1}{\mathit{n}}$ for all $\mathit{n}⩾4$.

The infinite sum

$\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+\cdots +\frac{1}{{\mathit{n}}^2}+\cdots$ (for ever)

is a historical classic, and has many instructive stories to tell. Recall that, in Problems 54, 62, 63, 236, 237, 238 you found closed formulae for the sums

$1+2+3+\cdots +\mathit{n}$

$1^2+2^2+3^2+\cdots +{\mathit{n}}^2$

$1^3+2^3+3^3+\cdots +{\mathit{n}}^3$

and for the sums

$1\times 2+2\times 3+3\times 4+\cdots +(\mathit{n}-1)\mathit{n}$

$1\times 2\times 3+2\times 3\times 4+3\times 4\times 5+\cdots +(\mathit{n}-2)(\mathit{n}-1)\mathit{n}$.

Each of these expressions has a “natural” feel to it, and invites us to believe that there must be an equally natural compact answer representing the sum. In Problem 235 you took this idea one step further by finding a beautiful closed expression for the sum

$\frac{1}{1·2}+\frac{1}{2·3}+\frac{1}{3·4}+\cdots +\frac{1}{\mathit{n}(\mathit{n}+1)}=1-\frac{1}{\mathit{n}+1}$

When we began to consider infinite series, we found the elegant closed formula

$1+\mathit{r}+{\mathit{r}}^2+{\mathit{r}}^3+\cdots +{\mathit{r}}^{\mathit{n}}=\frac{1}{1-\mathit{r}}-\frac{{\mathit{r}}^{\mathit{n}+1}}{1-\mathit{r}}$.

We then observed that the final term on the RHS could be viewed as an “error term”, indicating the amount by which the LHS differs from $\frac{1}{1-\mathit{r}}$, and noticed that, for any given value of r between −1 and +1, this error term “tends towards 0 as the power n increases”. We interpreted this as indicating that one could assign a value to the endless sum

$1+\mathit{r}+{\mathit{r}}^2+{\mathit{r}}^3+\cdots$ (for ever) = $\frac{1}{1-\mathit{r}}$.

In the same way, in the elegant closed formula

$\frac{1}{1·2}+\frac{1}{2·3}+\frac{1}{3·4}+\cdots +\frac{1}{\mathit{n}(\mathit{n}+1)}=1-\frac{1}{\mathit{n}+1}$

the final term on the RHS indicates the amount by which the finite sum on the LHS differs from 1; and since this “error term” tends towards 0 as n increases, we may assign a value to the endless sum

$\frac{1}{1·2}+\frac{1}{2·3}+\frac{1}{3·4}+\cdots$ (for ever) = 1.

It is therefore natural to ask whether other infinite series, such as

$\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+\cdots +\frac{1}{{\mathit{n}}^2}+\cdots$ (for ever)

may also be assigned some natural finite value. And since the series is purely numerical (without any variable parameters, such as the “r” in the geometric series formula), this answer should be a strictly numerical answer. And it should be exact - though all we have managed to prove so far (in Problems 246 and 247) is that this numerical answer lies somewhere between $\frac{17}{12}$ and 1.68.

This question arose naturally in the middle of the seventeenth century, when mathematicians were beginning to explore all sorts of infinite series (or “sums that go on for ever”). With a little more work in the spirit of Problems 246 and 247 one could find a much more accurate approximate value. But what is wanted is an exact expression, not an unenlightening decimal approximation. This aspiration has a serious mathematical basis, and is not just some purist preference for elegance. The actual decimal value is very close to

$1.649934\cdots$.

But this conveys no structural information. One is left with no hint as to why the sum has this value. In contrast, the eventual form of the exact expression suggests connections whose significance remains of interest to this day.

The greatest minds of the seventeenth and early eighteenth century tried to find an exact value for the infinite sum - and failed. The problem became known as the Basel problem (after Jakob Bernoulli (1654-1705) who popularised the problem in 1689 - one of several members of the Bernoulli family who were all associated with the University in Basel). The problem was finally solved in 1735 - in truly breathtaking style - by the young Leonhard Euler (1707-1783) (who was at the time also in Basel). The answer

$\frac{{\pi }^2}{6}$

illustrates the final sentence of the preceding paragraph in unexpected ways, which we are still trying to understand.

In the next problem you are invited to apply similar ideas to an even more important series. Part (a) provides a relatively crude first analysis. Part (b) attacks the same question; but it does so using algebra and induction (rather than the formula for the sum of a geometric series) in a way that is then further refined in part (c).

Problem 248

(a)(i) Choose a suitable r and prove that

$\frac{1}{1!}+\frac{1}{2!}+\cdots +\frac{1}{\mathit{n}!}<1+\mathit{r}+{\mathit{r}}^2+\cdots +{\mathit{r}}^{\mathit{n}-1}<2$.

(ii) Conclude that

$\frac{1}{0!}+\frac{1}{1!}+\frac{1}{2!}+\cdots +\frac{1}{\mathit{n}!}<3$ for every $\mathit{n}⩾0$,

and hence that the endless sum

$\frac{1}{0!}+\frac{1}{1!}+\frac{1}{2!}+\cdots +\frac{1}{\mathit{n}!}+\cdots$ (forever)

can be assigned a value “e” satisfying $2<\mathit{e}⩽3$.

(b) (i) Prove by induction that

$\frac{1}{0!}+\frac{1}{1!}+\frac{1}{2!}+\cdots +\frac{1}{\mathit{n}!}⩽3-\frac{1}{\mathit{n}.\mathit{n}!}$, for all $\mathit{n}⩾1$.

(ii) Use part (i) to conclude that the endless sum

$\frac{1}{0!}+\frac{1}{1!}+\frac{1}{2!}+\cdots +\frac{1}{\mathit{n}!}+\cdots$ (forever)

can be assigned a definite value “e”, and that this value lies somewhere between 2.5 and 3.

(c) (It may help to read the Note at the start of the solution to part (c) before attempting parts (c), (d).)

(i) Prove by induction that

$\frac{1}{0!}+\frac{1}{1!}+\frac{1}{2!}+\cdots +\frac{1}{\mathit{n}!}⩽2.75-\frac{1}{\mathit{n}.\mathit{n}!}$ for all $\mathit{n}⩾2$.

(ii) Use part (i) to conclude that the endless sum

$\frac{1}{0!}+\frac{1}{1!}+\frac{1}{2!}+\cdots +\frac{1}{\mathit{n}!}+\cdots$ (for ever)

can be assigned a definite value “e”, and that this value lies somewhere between 2.6 and 2.75.

(d) (i) Prove by induction that

$\frac{1}{0!}+\frac{1}{1!}+\frac{1}{2!}+\cdots +\frac{1}{\mathit{n}!}⩽2.722\cdots (\mathrm{forever})-\frac{1}{\mathit{n}.\mathit{n}!},\mathit{foral}\ln ⩾3$.

(ii) Use part (i) to conclude that the endless sum

$\frac{1}{0!}+\frac{1}{1!}+\frac{1}{2!}+\cdots +\frac{1}{\mathit{n}!}+\cdots$ (for ever)

can be assigned a definite value “e”, and that this value lies somewhere between 2.708 and 2.7222... (forever).

We end this section with one more inequality in the spirit of this section, and two rather different inequalities whose significance will become clear later.

Problem 249 Prove by induction that

$\frac{1}{\sqrt{1}}+\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{3}}+\cdots +\frac{1}{\sqrt{\mathit{n}}}⩾\sqrt{\mathit{n}}$, forall $\mathit{n}⩾1$.

Problem 250 Let a, b be real numbers such that $\mathit{a}\ne \mathit{b}$, and $\mathit{a}+\mathit{b}>0$. Prove by induction that

$2^{\mathit{n}-1}\left({\mathit{a}}^{\mathit{n}}+{\mathit{b}}^{\mathit{n}}\right)⩾(\mathit{a}+\mathit{b}{)}^{\mathit{n}}$, for all $\mathit{n}⩾1$.

Problem 251 Let x be any real number $⩾-1$. Prove by induction that

$(1+\mathit{x}{)}^{\mathit{n}}⩾1+\mathit{nx}$, for all $\mathit{n}⩾1$

6.6. The harmonic series

The great foundation of mathematics is the principle of contradiction, or of identity, that is to say that a statement cannot be true and false at the same time, and that thus A is A, and cannot be not A. And this single principle is enough to prove the whole of arithmetic and the whole of geometry, that is to say all mathematical principles.

Gottfried W. Leibniz (1646-1716)

We have seen how some infinite series, or sums that go on for ever, can be assigned a finite value for their sum:

$$1+r+r^2+r^3+\cdots (\text{for ever})=\frac{1}{1-r}$$ $$\frac{1}{1\cdot 2}+\frac{1}{2\cdot 3}+\frac{1}{3\cdot 4}+\cdots +\frac{1}{n(n+1)}+\cdots (\text{for ever})=1$$ $$\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+\cdots +\frac{1}{n^2}+\cdots (\text{for ever})=\frac{{\pi }^2}{6}$$ $$\frac{1}{0!}+\frac{1}{1!}+\frac{1}{2!}+\cdots +\frac{1}{n!}+\cdots (\text{for ever})=e.$$

We say that these series converge (meaning that they can be assigned a finite value).

This section is concerned with another very natural series, the so-called harmonic series

$$\frac{1}{1}+\frac{1}{2}+\frac{1}{3}+\cdots +\frac{1}{n}+\cdots (\text{for ever}).$$

It is not entirely clear why this is called the harmonic series. The natural overtones that arise in connection with plucking a stretched string (as with a guitar or a harp) have wavelengths that are $\genfrac{}{}{0.1ex}{}{1}{2}$ the basic wavelength, or $\genfrac{}{}{0.1ex}{}{1}{3}$ of the basic wavelength, and so on. It is also true that, just as each term of an arithmetic series is the arithmetic mean of its two neighbours, and each term of a geometric series is the geometric mean of its two neighbours, so each term of the harmonic series after the first is equal to the harmonic mean (see Problems 85., 89.) of its two neighbours:

$$\frac{1}{k}=\frac{2}{{\left(\frac{1}{k-1}\right)}^{-1}+{\left(\frac{1}{k+1}\right)}^{-1}}.$$

Unlike the first two series above, there is no obvious closed formula for the finite sum

$$s_n=\frac{1}{1}+\frac{1}{2}+\frac{1}{3}+\cdots +\frac{1}{n}.$$

Certainly the sequence of successive sums

$$s_1=1,s_2=\frac{3}{2},s_3=\frac{11}{6},s_4=\frac{25}{12},s_5=\frac{137}{60},\dots$$

does not suggest any general pattern.

Problem 252 Suppose we denote by S the “value” of the endless sum

$$\frac{1}{1}+\frac{1}{2}+\frac{1}{3}+\cdots +\frac{1}{n}+\cdots \text{(for ever)}$$

(i) Write out the endless sum corresponding to “$\frac{1}{2}S$”.

(ii) Remove the terms of this endless sum from the endless sum S, to obtain another endless sum corresponding to “$S-\frac{1}{2}S$” $=\frac{1}{2}S$.

(iii) Compare the first term of the series in (i) (namely $\genfrac{}{}{0.1ex}{}{1}{2}$) with the first term in the series in (ii) (namely 1); compare the second term in the series in (i) with the second term in the series in (ii); and so on. What do you notice?

The Leibniz quotation above emphasizes that the reliability of mathematics stems from a single principle – namely the refusal to tolerate a contradiction. We have already made explicit use of this principle from time to time (see, for example, the solution to Problem 125.). The message is simple: whenever we hit a contradiction, we know that we have “gone wrong” – either by making an error in calculation or logic, or by beginning with a false assumption. In Problem 252. the observations you were expected to make are paradoxical: you obtained two different series, which both correspond to “$\frac{1}{2}S$”, but every term in one series is larger than the corresponding term in the other! What one can conclude may not be entirely clear. But it is certainly clear that something is wrong: we have somehow created a contradiction. The three steps ((i), (ii), (iii)) appear to be relatively sensible. But the final observation “$\frac{1}{2}S<\frac{1}{2}S$” (since $\frac{1}{2}<1$, $\frac{1}{4}<\frac{1}{3}$, etc.) makes no sense. And the only obvious assumption we have made is to assume that the endless sum

$$\frac{1}{1}+\frac{1}{2}+\frac{1}{3}+\cdots +\frac{1}{n}+\cdots \text{(for ever)}$$

can be assigned a value “S”, which can then be manipulated as though it were a number.

The conclusion would seem to be that, whether or not the endless sum has a meaning, it cannot be assigned a value in this way. We say that the series diverges. Each finite sum

$$\frac{1}{1}+\frac{1}{2}+\frac{1}{3}+\cdots +\frac{1}{n}$$

has a value, and these values “grow more and more slowly” as n increases:

• the first term immediately makes the sum = 1
• it takes 4 terms to obtain a sum > 2;
• it takes 11 terms to obtain a sum > 3; and
• it takes $12367$ terms before the series reaches a sum > 10.

However, this slow growth is not enough to guarantee that the corresponding endless sum corresponds to a finite numerical value.

The danger signals should already have been apparent in Problem 249., where you proved that

$$\frac{1}{\sqrt{1}}+\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{3}}+\cdots +\frac{1}{\sqrt{n}}\ge \sqrt{n}$$

The $n^{\mathrm{th}}$ term $\frac{1}{\sqrt{n}}$ tends to 0 as n increases; so the finite sums grow ever more slowly as n increases. However, the LHS can be made larger than any integer K simply by taking K² terms. Hence there is no way to assign a finite value to the endless sum

$$\frac{1}{\sqrt{1}}+\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{3}}+\cdots +\frac{1}{\sqrt{n}}+\cdots (\text{for ever}).$$

Problem 253.

(a)(i) Explain why

$$\frac{1}{2}+\frac{1}{3}<1.$$

(ii) Explain why

$$\frac{1}{4}+\frac{1}{5}+\frac{1}{6}+\frac{1}{7}<1.$$

(iii) Extend parts (i) and (ii) to prove that

$$\frac{1}{1}+\frac{1}{2}+\frac{1}{3}+\cdots +\frac{1}{2^n-1}<n,\text{ for all }n\ge 2.$$

(iv) Finally use the fact that, when $n\ge 3$,

$$\frac{1}{2^n}<\frac{1}{2}-\frac{1}{3}$$

to modify the proof in (iii) slightly, and hence show that

$$\frac{1}{1}+\frac{1}{2}+\frac{1}{3}+\cdots +\frac{1}{2^n}<n,\text{ for all }n\ge 3.$$

(b)(i) Explain why

$$\frac{1}{3}+\frac{1}{4}>\frac{1}{2}.$$

(ii) Explain why

$$\frac{1}{5}+\frac{1}{6}+\frac{1}{7}+\frac{1}{8}>\frac{1}{2}.$$

(iii) Extend parts (i) and (ii) to prove that

$$\frac{1}{1}+\frac{1}{2}+\frac{1}{3}+\cdots +\frac{1}{2^n}>1+\frac{n}{2},\text{ for all }n\ge 2.$$

(c) Combine parts (a) and (b) to show that, for all $n\ge 2$, we have the two inequalities

$$1+\frac{n}{2}<\frac{1}{1}+\frac{1}{2}+\frac{1}{3}+\cdots +\frac{1}{2^n}<n.$$

Conclude that the endless sum

$$\frac{1}{1}+\frac{1}{2}+\frac{1}{3}+\cdots +\frac{1}{n}+\cdots \text{ (for ever)}$$

cannot be assigned a finite value.

The result in Problem 253.(c) has an unexpected consequence.

Problem 254 Imagine that you have an unlimited supply of identical rectangular strips of length 2. (Identical empty plastic CD cases can serve as a useful illustration, provided one focuses on their rectangular side profile, rather than the almost square frontal cross-section.) The goal is to construct a ‘stack’ in such a way as to stick out as far as possible beyond a table edge. One strip balances exactly at its midpoint, so can protrude a total distance of 1 without tipping over.

(a) Arrange a stack of n strips of length 2, one on top of the other, with the bottom strip protruding distance $\frac{1}{n}$ beyond the edge of the table, the second strip from the bottom protruding $\frac{1}{n-1}$ beyond the leading edge of the bottom strip, the third strip from the bottom protruding $\frac{1}{n-2}$ beyond the leading edge of the strip below it, and so on until the ${(n-1)}^{\text{th}}$ strip from the bottom protrudes distance $\genfrac{}{}{0.1ex}{}{1}{2}$ beyond the leading edge of the strip below it, and the top strip protrudes distance 1 beyond the leading edge of the strip below it (see Figure 10). Prove that a stack of n identical strips arranged in this way will just avoid tipping over the table edge.

(b) Conclude that we can choose n so that an arrangement of n strips can (in theory) protrude as far beyond the edge of the table as we wish – without tipping.

The next problem illustrates, in the context of the harmonic series, what is in fact a completely general phenomenon: an endless sum of steadily decreasing positive terms may converge or diverge; but provided the terms themselves converge to 0, then the the corresponding “alternating sum” – where the same terms are combined but with alternately positive and negative signs – always converges.

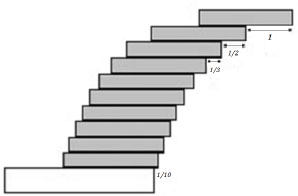
Figure 10: Overhanging strips, n = 10.

Problem 255

(a) Let

$$s_n=\frac{1}{1}-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5}-\cdots \pm \frac{1}{n}$$

(where the final operation is “+” if n is odd and “-” if n is even).

(i) Prove that

$$s_{2n-2}<s_{2n}<s_{2m+1}<s_{2m-1},$$ for all $m,n\ge 1$ .

(ii) Conclude that the endless alternating sum

$$\frac{1}{1}-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5}-\cdots \text{ (for ever)}$$

can be assigned a value s that lies somewhere between $s_6=\frac{37}{60}$ and $s_5=\frac{47}{60}$.

(b) Let

$$a_1,a_2,a_3,\dots$$

be an endless, decreasing sequence of positive terms (that is, $a_{n+1}<a_n$ for all $n\ge 1$). Suppose that the sequence of terms $a_n$ converges to 0 as $n\to \infty$.

(i) Let

$$s_n=a_1-a_2+a_3-a_4+a_5-\cdots \pm a_n$$

(where the final operation is “+” if n is odd and “−” if n is even). Prove that

$$s_{2n-2}<s_{2n}<s_{2m+1}<s_{2m-1},\text{ for all }m,n\ge 1.$$

(ii) Conclude that the endless alternating sum

$$a_1-a_2+a_3-a_4+a_5-\cdots \text{ (for ever)}$$

can be assigned a value s that lies somewhere between $s_2=a_1-a_2$ and $s_3=a_1-a_2+a_3$.

Just as with the series

$$\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+\cdots +\frac{1}{n^2}+\cdots (\text{for ever})$$ $$\frac{1}{0!}+\frac{1}{1!}+\frac{1}{2!}+\cdots +\frac{1}{n!}+\cdots (\text{for ever}),$$

we can show relatively easily that

$$\frac{1}{1}-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5}-\cdots (\text{for ever})$$

can be assigned a value s. It is far less clear whether this value has a familiar name! (It is in fact equal to the natural logarithm of 2: “${\log }_{e}2$”.) A similarly intriguing series is the alternating series of odd terms from the harmonic series:

$$\frac{1}{1}-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\frac{1}{9}-\cdots (\text{for ever})$$

You should be able to show that this endless series can be assigned a value somewhere between $s_2=\frac{2}{3}$ and $s_3=\frac{13}{15}$; but you are most unlikely to guess that its value is equal to $\frac{\pi }{4}$. This was first discovered in 1674 by Leibniz (1646-1716). One way to obtain the result is using the integral of ${(1+x^2)}^{-1}$ from 0 to 1: on the one hand the integral is equal to $\arctan x$ evaluated when $x=1$ (that is, $\frac{\pi }{4}$); on the other hand, we can expand the integrand as a power series $1-x^2+x^4-x^6+\cdots$, integrate term by term, and prove that the resulting series converges when $x=1$. (It does indeed converge, though it does so very, very slowly.)

The fact that the alternating harmonic series has the value ${\log }_{e}2$ seems to have been first shown by Euler (1707-1783), using the power series expansion for $\log (1+x)$.

6.7. Induction in geometry, combinatorics and number theory

We turn next to a mixed collection of problems designed to highlight a range of applications.

Problem 256 Let $f_1=2$, $f_{k+1}=f_k(f_k+1)$. Prove by induction that $f_k$ has at least k distinct prime factors.

Problem 257

(a) Prove by induction that n points on a straight line divide the line into $n+1$ parts.

(b)(i) By experimenting with small values of n, guess a formula $R_n$ for the maximum number of regions which can be created in the plane by an array of n straight lines.

(ii) Prove by induction that n straight lines in the plane divide the plane into at most $R_n$ regions.

(c)(i) By experimenting with small values of n, guess a formula $S_n$ for the maximum number of regions which can be created in 3-dimensions by an array of n planes.

(ii) Prove by induction that n planes in 3-dimensions divide space into at most $S_n$ regions.

Problem 258 Given a square, prove that, for each $n\ge 6$, the initial square can be cut into n squares (of possibly different sizes).

Problem 259 A tree is a connected graph, or network, consisting of vertices and edges, but with no cycles (or circuits). Prove that a tree with n vertices has exactly $n-1$ edges.

The next problem concerns spherical polyhedra. A spherical polyhedron is a polyhedral surface in 3-dimensions, which can be inflated to form a sphere (where we assume that the faces and edges can stretch as required). For example, a cube is a spherical polyhedron; but the surface of a picture frame is not. A spherical polyhedron has

• faces (flat 2-dimensional polygons, which can be stretched to take the form of a disc),
• edges (1-dimensional line segments, where exactly two faces meet), and
• vertices (0-dimensional points, where several faces and edges meet, in such a way that they form a single cycle around the vertex).

Each face must clearly have at least 3 edges; and there must be at least three edges and three faces meeting at each vertex.

If a spherical polyhedron has V vertices, E edges, and F faces, then the numbers V, E, F satisfy Euler's formula

$$V-E+F=2.$$

For example, a cube has $V=8$ vertices, $E=12$ edges, and $F=6$ faces, and $8-12+6=2$.

Problem 260

(a) (i) Describe a spherical polyhedron with exactly 6 edges.

(ii) Describe a spherical polyhedron with exactly 8 edges.

(b) Prove that no spherical polyhedron can have exactly 7 edges.

(c) Prove that for every $n\ge 8$, there exists a spherical polyhedron with n edges.

Problem 261 A map is a (finite) collection of regions in the plane, each with a boundary, or border, that is `polygonal' in the sense that it consists of a single sequence of distinct vertices and – possibly curved – edges, that separates the plane into two parts, one of which is the polygonal region itself. A map can be properly coloured if each region can be assigned a colour so that each pair of neighbouring regions (sharing an edge) always receive different colours. Prove that the regions of such a map can be properly coloured with just two colours if and only if an even number of edges meet at each vertex.

Problem 262 (Gray codes) There are $2^n$ sequences of length n consisting of 0s and 1s. Prove that, for each $n\ge 2$, these sequences can be arranged in a cyclic list such that any two neighbouring sequences (including the last and the first) differ in exactly one coordinate position.

Problem 263 (Calkin-Wilf tree) The binary tree in the plane has a distinguished vertex as `root', and is constructed inductively. The root is joined to two new vertices; and each new vertex is then joined to two further new vertices – with the construction process continuing for ever (Figure 11). Label the vertices of the binary tree with positive fractions as follows:

• the root is given the label $\genfrac{}{}{0.1ex}{}{1}{1}$
• whenever we know the label $\frac{i}{j}$ of a ‘parent’ vertex, we label its `left descendant' as $\frac{i}{i+j}$, and its `right descendant' $\frac{i+j}{j}$.

(a) Prove that every positive rational $\frac{r}{s}$ occurs once and only once as a label, and that it occurs in its lowest terms.

(b) Prove that the labels are left-right symmetric in the sense that labels in corresponding left and right positions are reciprocals of each other.

Problem 264 A collection of n intervals on the x-axis is such that every pair of intervals have a point in common. Prove that all n intervals must then have at least one point in common.

6.8. Two problems

Problem 265 Several identical tanks of water sit on a horizontal base. Each pair of tanks is connected with a pipe at ground level controlled by a valve, or tap. When a valve is opened, the water level in the two connected tanks becomes equal (to the average, or mean, of the initial levels). Suppose we start with tank T which contains the least amount of water. The aim is to open and close valves in a sequence that will lead to the final water level in tank T being as high as possible. In what order should we make these connections?

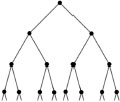
Figure 11: A (rooted) binary tree.

Problem 266 I have two flasks. One is ‘empty’, but still contains a residue of a dangerous chemical; the other contains a fixed amount of solvent that can be used to wash away the remaining traces of the dangerous chemical. What is the best way to use the fixed quantity of solvent? Should I use it all at once to wash out the first flask? Or should I first wash out the flask using just half of the solvent, and then repeat with the other half? Or is there a better way of using the available solvent to remove as much as possible of the dangerous chemical?

6.8. Infinite descent

In this final section we touch upon an important variation on mathematical induction. This variation is well-illustrated by the next (probably familiar) problem.

Problem 267 Write out for yourself the following standard proof that $\sqrt{2}$ is irrational.

(i) Suppose to the contrary that $\sqrt{2}$ is rational. Then $\sqrt{2}=\frac{m}{n}$ for some positive integers m, n. Prove first that m must be even.

(ii) Write $m=2m^{\prime }$, where $m^{\prime }$ is also an integer. Show that n must also be even.

(iii) How does this lead to a contradiction?

Problem 267. has the classic form of a proof which reaches a contradiction by infinite descent.

1. We start with a claim which we wish to prove is true. Often when we do not know how to begin, it makes sense to ask what would happen if the claim were false. This then guarantees that there must be some counterexample, which satisfies the given hypothesis, but which fails to satisfy the asserted conclusion.
2. Infinite descent becomes an option whenever each such counterexample gives rise to some positive integer parameter n (such as the denominator in Problem 267.(i)).
3. Infinite descent becomes a reality, if one can prove that the existence of the initial counterexample leads to a construction that produces a counterexample with a smaller value $n^{\prime }$ of the parameter n, since repeating this step then gives rise to an endlessly decreasing sequence $$n>n^{\prime }>n\text{'}\text{'}>\dots >0$$ of positive integers, which is impossible (since such a chain can have length at most n).
4. Hence the initial assumption that the claim was false must itself be false – so the claim must be true (as required).

Proof by “infinite descent” is an invaluable tool. But it is important to realise that the method is essentially a variation on proof by mathematical induction. As a first step in this direction it is worth reinterpreting Problem 267. as an induction proof.

Problem 268 Let $P(n)$ be the statement:

“$\sqrt{2}$ cannot be written as a fraction with positive denominator $\le n$”.

(i) Explain why $P(1)$ is true.

(ii) Suppose that $P(k)$ is true for some $k\ge 1$. Use the proof in Problem 267. to show that $P(k+1)$ must then be true as well.

(iii) Conclude that $P(n)$ is true for all $n\ge 1$, whence $\sqrt{2}$ must be irrational.

Problem 268. shows that, in the particular case of Problem 267. one can translate the standard proof that “$\sqrt{2}$ is irrational” into a proof by induction. But much more is true. The contradiction arising in step 3. above is an application of an important principle, namely

The Least Element Principle: Every non-empty set S of positive integers has a smallest element.

The Least Element Principle is equivalent to The Principle of Mathematical Induction which we stated at the beginning of the chapter:

The Principle of Mathematical Induction: If a subset S of the positive integers

• contains the integer “1”, and has the property that
• whenever an integer k is in the set S, then the next integer $k+1$ is always in S too,

then S contains all positive integers.

Problem 269

(a) Assume the Least Element Principle. Suppose a subset T of the positive integers contains the integer “1”, and that whenever k is in the set T, then $k+1$ is also in the set T. Let S be the set of all positive integers which are not in the set T. Conclude that S must be empty, and hence that T contains all positive integers.

(b) Assume the Principle of Mathematical Induction. Let T be a non-empty set of positive integers, and suppose that T does not have a smallest element. Let S be the set of all positive integers which do not belong to the set T. Prove that “1” must belong to S, and that whenever the positive integer k belongs to S, then so does $k+1$. Derive the contradiction that T must be empty, contrary to assumption. Conclude that T must in fact have a smallest element.

To round off this final chapter you are invited to devise a rather different proof of the irrationality of $\sqrt{2}$.

Problem 270 This sequence of constructions presumes that we know – for example, by Pythagoras' Theorem – that, in any square $OPQR$, the ratio

“diagonal: side” $=OQ:OP=\sqrt{2}:1$.

Let $OPQR$ be a square. Let the circle with centre Q and passing through P meet $\underset{¯}{OQ}$ at $P^{\prime }$. Construct the perpendicular to $\underset{¯}{OQ}$ at $P^{\prime }$, and let this meet $\underset{¯}{OR}$ at $Q^{\prime }$.

(i) Explain why $\underset{¯}{O{P}^{\prime }}=\underset{¯}{P^{\prime }{Q}^{\prime }}$. Construct the point $R^{\prime }$ to complete the square $O{P}^{\prime }{Q}^{\prime }{R}^{\prime }$.

(ii) Join $\underset{¯}{Q{Q}^{\prime }}$. Explain why $\underset{¯}{P^{\prime }{Q}^{\prime }}=\underset{¯}{R{Q}^{\prime }}$.

(iii) Suppose $\underset{¯}{OQ}:\underset{¯}{OP}=m:n$. Conclude that $\underset{¯}{O{Q}^{\prime }}:\underset{¯}{O{P}^{\prime }}=2n-m:m-n$.

(iv) Prove that $n<m<2n$, and hence that $0<m-n<n$, $0<2n-m$.

(v) Explain how, if m, n can be chosen to be positive integers, the above sequence of steps sets up an “infinite descent” – which is impossible.

6.10. Chapter 6: Comments and solutions

Note: It is important to separate the underlying idea of “induction” from the formal way we have chosen to present proofs. As ever in mathematics, the ideas are what matter most. But the process of struggling with (and slowly coming to understand why we need) the formal structure behind the written proofs is part of the way the ideas are tamed and organised.

Readers should not be intimidated by the physical extent of the solutions to this chapter. As explained in the main text it is important for all readers to review the way they approach induction proofs: so we have erred in favour of completeness – knowing that as each reader becomes more confident, s/he will increasingly compress, or abbreviate, some of the steps.

228.

(a) Yes.

(b) Yes.

$$2\times 3\times 5\times 7\times 11+1=2311,$$ and $\sqrt{2311}=48.07\dots$ , so we only need to check prime factors up to $47$ .

(c) No.

$$2\times 3\times 5\times 7\times 11\times 13+1=30031,$$

and $\sqrt{30031}=173.29\dots$ so we might have to check all $40$ possible prime factors up to $173$. However, we only have to start at $17$ [Why?], and checking with a calculator is very quick. In fact $30031$ factorises rather prettily as $59\times 509$.

229. Note: The statement in the problem includes the quantifier “for all $n\ge 1$”.

What is to be proved is the compound statement

“$P(n)$ is true for all $n\ge 1$”.

In contrast, each individual statement $P(n)$ refers to a single value of n.

It is essential to be clear when you are dealing with the compound statement, and when you are referring to some particular statement $P(1)$, or $P(n)$, or $P(k)$.

Let $P(n)$ be the statement:

“$5^{2n+2}-24n-25$ is divisible by $576$”.

• $P(1)$ is the statement:

“$5^4-24\times 1-25$ is divisible by $576$”.

That is:

“$625-49=576$ is divisible by $576$”,

which is evidently true.

• Now suppose that we know $P(k)$ is true for some $k\ge 1$. We must show that $P(k+1)$ is then also true.

To prove that $P(k+1)$ is true, we have to consider the statement $P(k+1)$. It is no use starting with $P(k)$. However, since we know that $P(k)$) is true, we are free to use it at any stage if it turns out to be useful.

To prove that $P(k+1)$ is true, we have to show that

“$5^{2(k+1)+2}-24(k+1)-25$ is divisible by $576$”.

So we must start with $5^{2(k+1)+2}-24(k+1)-25$ and try to “simplify” it (knowing that “simplify” in this case means “rewrite it in a way that involves $5^{2k+2}-24k-25$”).

$\begin{array}{c}{5}^{2(k+1)+2}-24(k+1)-25\hfill \\ \hfill & =\left[5^{2k+4}\right]-24k-24-25\hfill \\ \hfill & =[5^2(5^{2k+2}-24k-25)+5^2\cdot \left(24k\right)+5^2\cdot 25]\hfill \\ \hfill & -24k-(24+25)\hfill \\ \hfill & =5^2(5^{2k+2}-24k-25)+[(5^2-1)\times \left(24k\right)]\hfill \\ \hfill & +[5^2\times 25-24-25]\hfill \\ \hfill & =5^2(5^{2k+2}-24k-25)+24^{2}k+[5^2\times 25-24-25]\hfill \\ \hfill & =5^2(5^{2k+2}-24k-25)+24^{2}k+[5^4-24-25].\hfill \end{array}$

The first term on the RHS is a multiple of $(5^{2k+2}-24k-25)$, so is divisible by $576$ (since we know that P(k) is true); the second term on the RHS is a multiple of 24² = 576; and the third term on the RHS is the expression arising in P(1), which we saw is equal to 576.

$\therefore$ the whole RHS is divisible by $576$

$\therefore$ the LHS is divisible by $576$, so $P(k+1)$ is true.

Hence

• $P(1)$ is true; and
• whenever $P(k)$ is true for some $k\ge 1$, we have proved that $P(k+1)$ must be true.

$\therefore$ $P(n)$ is true for all $n\ge 1$.

230. Let $P(n)$ be the statement:

“the angles of any p-gon, for any value of p with $3\le p\le n$, have sum exactly $(p-2)\pi$ radians”.

1. $P(3)$ is the statement:

   “the angles of any triangle have sum $\pi$ radians”.

   This is a known fact: given triangle ΔABC, draw the line $XAY$ through A parallel to $BC$, with X on the same side of $AC$ as B and Y on the same side of $AB$ as C. Then $\angle XAB=\angle CBA$ and $\angle YAC=\angle BCA$ (alternate angles), so

   $$\angle B+\angle A+\angle C=\angle XAB+\angle A+\angle YAC=\angle XAY=\pi .$$
2. Now we suppose that $P(k)$ is known to be true for some $k\ge 3$. We must show that $P(k+1)$ is then necessarily true.

To prove that $P(k+1)$ is true, we have to consider the statement $P(k+1)$: that is,

“the angles of a p-gon, for any value of p with $3\le p\le k+1$, have sum exactly $(p-2)\pi$ radians”.

This can be reworded by splitting it into two parts:

“the angles of any p-gon for $3\le p\le k$ have sum exactly $(p-2)\pi$ radians;”

and

“the angles of any (k + 1)-gon have sum exactly $((k+1)-2)\pi$ radians”.

The first part of this revised version is precisely the statement $P(k)$, which we suppose is known to be true. So the crux of the matter is to prove the second part – namely that the angles of any (k + 1)-gon have sum $(k-1)\pi$.

Let $A_0{A}_1{A}_2\cdots A_k$ be any (k + 1)-gon.

[Note: The usual move at this point is to say “draw the chord $A_k{A}_1$ to cut the polygon into the triangle $A_k{A}_1{A}_0$ (with angle sum $\pi$ (by $P(3)$), and the k-gon $A_1{A}_2\cdots A_k$ (with angle sum $(k-2)\pi$ (by $P(k)$), whence we can add to see that $A_0{A}_1{A}_2\cdots A_k$ has angle sum $((k+1)-2)\pi$. However, this only works

• if the triangle $A_k{A}_1{A}_0$ “sticks out” rather than in, and
• if no other vertices or edges of the (k+ 1)-gon encroach into the part that is cut off – which can only be guaranteed if the polygon is “convex”.

So what is usually presented as a “proof” does not work in general.

If we want to prove the general result – for polygons of all shapes – we have to get round this unwarranted assumption. Experiment may persuade you that “there is always some vertex that sticks out and which can be safely “cut off”; but it is not at all clear how to prove this fact (we know of no simple proof). So we have to find another way.]

Consider the vertex $A_1$, and its two neighbours $A_0$ and $A_2$.

Imagine each half-line, which starts at $A_1$, and which sets off into the interior of the polygon. Because the polygon is finite, each such half-line defines a line segment $\underset{¯}{A_{1}X}$, where X is the next point of the polygon which the half line hits (that is, X is one of the vertices $A_m$, or a point on one of the sides $\underset{¯}{A_m{A}_{m+1}}$).

Consider the locus of all such points X as the half line swings from $\underset{¯}{A_1{A}_0}$ (produced) to $\underset{¯}{A_1{A}_2}$ (produced). There are two possibilities: either

(a) these points X all belong to a single side of the polygon; or

(b) they don't.

(a) In the first case none of the vertices or sides of the polygon $A_0{A}_1{A}_2\cdots A_k$ intrude into the interior of the triangle $A_0{A}_1{A}_2$, so the chord $\underset{¯}{A_0{A}_2}$ separates the (k + 1)-gon $A_0{A}_1{A}_2\cdots A_k$ into a triangle $A_0{A}_1{A}_2$ and a k-gon $A_0{A}_2{A}_3\cdots A_k$. The angle sum of $A_0{A}_1{A}_2\cdots A_k$ is then equal to the sum of (i) the angle sum of the triangle $A_0{A}_1{A}_2$ and (ii) the angle sum of $A_0{A}_2{A}_3\cdots A_k$ – which are equal to $\pi$ and $(k-2)\pi$ respectively (by $P(k)$). So the angle sum of the (k + 1)-gon $A_0{A}_2{A}_3\cdots A_k$ is equal to $((k+1)-2)\pi$ as required.

(b) In the second case, as the half-line $A_{1}X$ rotates from $A_1{A}_0$ to $A_1{A}_2$, the point X must at some instant switch from lying on one side of the polygon to lying on another side; at the very instant where X switches sides, $X=A_m$ must be a vertex of the polygon.

Because of the way the point X was chosen, the chord $\underset{¯}{A_{1}X}=\underset{¯}{A_1{A}_m}$ does not meet any other point of the (k + 1)-gon $A_0{A}_1{A}_2\cdots A_k$, and so splits the (k + 1)-gon into an m-gon $A_1{A}_2{A}_3\cdots A_m$ (with angle sum $(m-2)\pi$ by $P(k)$) and a (k - m + 3)-gon $A_m{A}_{m+1}{A}_{m+2}\cdots A_k{A}_0{A}_1$ (with angle sum $(k-m+1)\pi$ by $P(k)$). So the (k + 1)-gon $A_0{A}_1{A}_2\cdots A_k$ has angle sum $((k+1)-2)\pi$ as required.

Hence $P(k+1)$ is true.

$\therefore$ $P(n)$ is true for all $n\ge 3$.

231. Let $P(n)$ be the statement

$$1+3+5+\cdots +(2n-1)=n^2$$.

• LHS of $P(1)=1$; RHS of $P(1)=1^2$. Since these two are equal, $P(1)$ is true.

• Suppose that $P(k)$ is true for some particular (unspecified) $k\ge 1$; that is, we know that, for this particular k,

  $$1+3+5+\cdots +(2k-1)=k^2$$.

  We wish to prove that $P(k+1)$ must then be true.

  Now $P(k+1)$ is an equation, so we start with the LHS of $P(k+1)$ and try to simplify it in an appropriate way to get the RHS of $P(k+1)$:

  $\begin{array}{ccc}\text{LHS of}\mathbf{P}(k+1)\hfill & =\hfill & 1+3+5+\dots +\left(2\right(k+1)-1)\hfill \\ \hfill & =\hfill & (1+3+5+\dots +(2k-1\left)\right)+(2k+1).\hfill \end{array}$

  If we now use $P(k)$, which we are supposing to be true, then the first bracket is equal to k², so this sum is equal to:

  $\begin{array}{ccc}\hfill & =\hfill & k^2+(2k+1)\hfill \\ \hfill & =\hfill & {(k+1)}^2\hfill \\ \hfill & =\hfill & \text{RHS of}\mathbf{P}(k+1).\hfill \end{array}$

  Hence $P(k+1)$ holds.

Combining these two bullet points then shows that “$P(n)$ holds, for all $n\ge 1$”.

232.

(a) The only way to learn is by trying and failing; then trying again and failing slightly better! So don't give up too quickly. It is natural to try to relate each term to the one before. You may then notice that each term is slightly less than 3 times the previous term.

(b) Note: The recurrence relation for $u_n$ involves the two previous terms. So when we assume that $P(k)$ is known to be true and try to prove $P(k+1)$, the recurrence relation for $u_{k+1}$ will involve $u_k$ and $u_{k-1}$, so $P(n)$ needs to be formulated to ensure that we can use closed expressions for both these terms. For the same reason, the induction proof has to start by showing that both $P(0)$ and $P(1)$ are true.

Let $P(n)$ be the statement:

“$u_m=2^m+3^m$ for all m, $0\le m\le n$”.

• LHS of $P(0)=u_0=2$; RHS of $P(0)=2^0+3^0=1+1$. Since these two are equal, $P(0)$ is true.

  $P(1)$ combines $P(0)$, and the equality of $u_1=5$ and $2^1+3^1$; since these two are equal, $P(1)$ is true.

• Suppose that $P(k)$ is true for some particular (unspecified) $k\ge 1$; that is, we know that, for this particular k,

  “$u_m=2^m+3^m$ for all m, $0\le m\le k$.”

  We wish to prove that $P(k+1)$ must then be true.

  Now $P(k+1)$ requires us to prove that

  “$u_m=2^m+3^m$ for all m, $0\le m\le k+1$.”

  Most of this is guaranteed by $P(k)$, which we assume to be true. It remains for us to check that the equality holds for $u_{k+1}$. We know that

  $$u_{k+1}=5u_k-6u_{k-1}.$$

  And we may use $P(k)$), which we are supposing to be true, to conclude that:

  $\begin{array}{ccc}{u}_{k+1}\hfill & =\hfill & 5(2^k+3^k)-6(2^{k-1}+3^{k-1})\hfill \\ \hfill & =\hfill & (10-6)2^{k-1}+(15-6)3^{k-1}\hfill \\ \hfill & =\hfill & 2^{k+1}+3^{k+1}.\hfill \end{array}$

  Hence $P(k+1)$ holds.

Combining these two bullet points then shows that “$P(n)$ holds, for all $n\ge 0$”.

233. Let $P(n)$ be the statement:

“$F_m=\frac{{\alpha }^m-{\beta }^m}{\sqrt{5}}$ for all m, $0\le m\le n$”,

where $\alpha =\frac{1+\sqrt{5}}{2}$ and $\beta =\frac{1-\sqrt{5}}{2}$.

• LHS of $P(0)=F_0=0$; RHS of $P(0)=\frac{1-1}{\sqrt{5}}=0$. Since these two are equal, $P(0)$ is true.

  LHS of $P(1)=F_1=1$; RHS of $P(1)=\frac{\alpha -\beta }{\sqrt{5}}=1$. Since these two are equal, $P(1)$ is true.

• Suppose that $P(k)$ is true for some particular (unspecified) $k\ge 1$; that is, we know that, for this particular k,

  “$F_m=\frac{{\alpha }^m-{\beta }^m}{\sqrt{5}}$ for all m, $0\le m\le k$.”

  We wish to prove that $P(k+1)$ must then be true.

  Now $P(k+1)$ requires us to prove that

  “$F_m=\frac{{\alpha }^m-{\beta }^m}{\sqrt{5}}$ for all m, $0\le m\le k+1$.”

  Most of this is guaranteed by $P(k)$, which we assume to be true. It remains to check this for $F_{k+1}$. We know that

  $$F_{k+1}=F_k+F_{k-1}.$$

  And we may use $P(k)$, which we are supposing to be true to conclude that:

  $\begin{array}{ccc}{F}_{k+1}\hfill & =\hfill & \genfrac{}{}{0.1ex}{}{{\alpha }^k-{\beta }^k}{\sqrt{5}}+\genfrac{}{}{0.1ex}{}{{\alpha }^{k-1}-{\beta }^{k-1}}{\sqrt{5}}\hfill \\ \hfill & =\hfill & \genfrac{}{}{0.1ex}{}{{\alpha }^k+{\alpha }^{k-1}}{\sqrt{5}}-\genfrac{}{}{0.1ex}{}{{\beta }^k+{\beta }^{k-1}}{\sqrt{5}}\hfill \\ \hfill & =\hfill & \genfrac{}{}{0.1ex}{}{{\alpha }^{k+1}-{\beta }^{k+1}}{\sqrt{5}}\hfill \end{array}$

  (since $\alpha$ and $\beta$ are roots of the equation $x^2-x-1=0$) Hence $P(k+1)$ holds.

Combining these two bullet points then shows that “$P(n)$ holds, for all $n\ge 1$”.

Note: You may understand the above solution and yet wonder how such a formula could be discovered. The answer is fairly simple. There is a general theory about linear recurrence relations which guarantees that the set of all solutions of a second order recurrence (that is, a recurrence in which each term depends on the two previous terms) is “two dimensional” (that is, it is just like the familiar 2D plane, where every vector (p, q) is a combination of the two “base vectors” (1, 0) and (0, 1):

$$(p,q)=p(1,0)+q(0,1)).$$

Once we know this, it remains:

• to find two special solutions (like the vectors (1, 0) and (0, 1) in the plane), which we do here by looking for sequences of the form “$1,x,x^2,x^3,\dots$” that satisfy the recurrence, which implies that $1+x=x^2$, so $x=\alpha$, or $x=\beta$;
• then to choose a linear combination $F_m=p{\alpha }^m+q{\beta }^m$ of these two power solutions to give the correct first two terms: $0=F_0=p+q$, $1=F_1=p\alpha +q\beta$, so $p=\frac{1}{\sqrt{5}}$, $q=-\frac{1}{\sqrt{5}}$.

234. Let $P(n)$ be the statement:

“$5^{2n+1}·2^{n+2}+3^{n+2}·2^{2n+1}$ is divisible by $19$”.

• $P(0)$ is the statement: “$5\times 4+9\times 2$ is divisible by 19”, which is true.
• Now suppose that we know that $P(k)$ is true for some $k\ge 0$. We must show that $P(k+1)$ is then also true.
• To prove that $P(k+1)$ is true, we have to show that

  “$5^{2k+3}·2^{k+3}+3^{k+3}·2^{2k+3}$ is divisible by $19$”.

  $\begin{array}{ccc}{5}^{2k+3}\cdot 2^{k+3}+3^{k+3}\cdot 2^{2k+3}\hfill & =\hfill & 5^2\cdot 2(5^{2k+1}\cdot 2^{k+2}+3^{k+2}\cdot 2^{2k+1})\hfill \\ \hfill & \hfill & -5^2\cdot 2\cdot 3^{k+2}\cdot 2^{2k+1}+3^{k+3}\cdot 2^{2k+3}\hfill \\ \hfill & =\hfill & 5^2\cdot 2\cdot (5^{2k+1}\cdot 2^{k+2}+3^{k+2}\cdot 2^{2k+1})\hfill \\ \hfill & \hfill & -(5^2-3\cdot 2)3^{k+2}\cdot 2^{2k+2}.\hfill \end{array}$

  The bracket in the first term on the RHS is divisible by 19 (by $P(k)$), and the bracket in the second term is equal to 19. Hence both terms on the RHS are divisible by 19, so the RHS is divisible by 19. Therefore the LHS is also divisible by 19, so $P(k+1)$ is true.

$\therefore$ $P(n)$ is true for all $n\ge 0$.

235.

Note: The proofs of identities such as those in Problem 235., which are given in many introductory texts, ignore the lessons of the previous two problems. In particular,

• they often fail to distinguish between

– the single statement $P(n)$ for a particular n, and

– the “quantified” result to be proved (“for all $n\ge 1$”),

and

• they proceed in the `wrong' direction (e.g. starting with the identity $P(n)$ and “adding the same to both sides”).

This latter strategy is psychologically and didactically misleading – even though it can be justified logically when proving very simple identities. In these very simple cases, each statement $P(n)$ to be proved is unusual in that it refers to exactly one configuration, or equation, for each $n$. And since there is exactly one configuration for each n, the configuration or identity for $k+1$ can often be obtained by fiddling with the configuration for k. In contrast, in Problem 230., for each value of n, there is a bewildering variety of possible polygons with n vertices, ranging from regular polygons to the most convoluted, re-entrant shapes: the statement $P(n)$ makes an assertion about all such configurations, and there is no way of knowing whether we can obtain all such configurations for $k+1$ in a uniform way by fiddling with some configuration for k.

Readers should try to write each proof in the intended spirit, and to learn from the solutions – since this style has been chosen to highlight what mathematical induction is really about, and it is this approach that is needed in serious applications.

(a) Let $P(n)$ be the statement:

“$1+2+3+\cdots +n=\frac{n(n+1)}{2}$”.

• LHS of $P(1)=1$; RHS of $P(1)=\frac{1·(1+1)}{2}=1$. Since these two are equal, $P(1)$ is true.
• Suppose that $P(k)$ is true for some particular (unspecified) $k\ge 1$; that is, we know that, for this particular k,

  “$1+2+3+\cdots +k=\frac{k(k+1)}{2}$ ”.

  We wish to prove that $P(k+1)$ must then be true.

  Now $P(k+1)$ is an equation, so we start with the LHS of $P(k+1)$ and try to simplify it in an appropriate way to get the RHS of $P(k+1)$):

  $\begin{array}{ccc}\text{LHS of}\mathbf{P}(k+1)\hfill & =\hfill & 1+2+3+\cdots +k+(k+1)\hfill \\ \hfill & =\hfill & (1+2+3+\cdots +k)+(k+1).\hfill \end{array}$

  If we now use $P(k)$, which we are supposing to be true, then the first bracket is equal to $\frac{k(k+1)}{2}$, so the complete sum is equal to:

  $\begin{array}{ccc}\hfill & =\hfill & \genfrac{}{}{0.1ex}{}{k(k+1)}{2}+(k+1)\hfill \\ \hfill & =\hfill & \genfrac{}{}{0.1ex}{}{(k+1)(k+2)}{2}\hfill \\ \hfill & =\hfill & \text{RHS of}\mathbf{P}(k+1).\hfill \end{array}$

  Hence $P(k+1)$ holds.

  If we combine these two bullet points, then we have proved that “$P(n)$ holds for all $n\ge 1$”.

(b) Let $P(n)$ be the statement:

“$\frac{1}{1·2}+\frac{1}{2·3}+\frac{1}{3·4}+\cdots +\frac{1}{n·(n+1)}=1-\frac{1}{n+1}$”.

• LHS of $P(1)=\frac{1}{1·2}=\frac{1}{2}$; RHS of $P(1)=1-\frac{1}{2}=\frac{1}{2}$. Since these two are equal, $P(1)$ is true.
• Suppose that $P(k)$ is true for some particular (unspecified) $k\ge 1$; that is, we know that, for this particular k,

  “$\frac{1}{1·2}+\frac{1}{2·3}+\frac{1}{3·4}+\cdots +\frac{1}{k·(k+1)}=1-\frac{1}{k+1}$”.

  We wish to prove that $P(k+1)$ must then be true.

  Now $P(k+1)$ is an equation, so we start with the LHS of $P(k+1)$ and try to simplify it in an appropriate way to get the RHS of $P(k+1)$:

  $\begin{array}{ccc}\text{LHS of}\mathbf{P}(k+1)\hfill & =\hfill & \genfrac{}{}{0.1ex}{}{1}{1\cdot 2}+\genfrac{}{}{0.1ex}{}{1}{2\cdot 3}+\genfrac{}{}{0.1ex}{}{1}{3\cdot 4}+\cdots +\genfrac{}{}{0.1ex}{}{1}{(k+1)(k+2)}\hfill \\ \hfill & =\hfill & [\genfrac{}{}{0.1ex}{}{1}{1\cdot 2}+\genfrac{}{}{0.1ex}{}{1}{2\cdot 3}+\genfrac{}{}{0.1ex}{}{1}{3\cdot 4}+\genfrac{}{}{0.1ex}{}{1}{k(k+1)}]\hfill \\ \hfill & \hfill & +\genfrac{}{}{0.1ex}{}{1}{(k+1)(k+2)}.\hfill \end{array}$

  If we now use $P(k)$, which we assume is true, then the first bracket is equal to $1-\frac{1}{k+1}$, so the complete sum is equal to:

  $\begin{array}{ccc}\hfill & =\hfill & [1-\genfrac{}{}{0.1ex}{}{1}{k+1}]+\genfrac{}{}{0.1ex}{}{1}{(k+1)(k+2)}\hfill \\ \hfill & =\hfill & 1-[\genfrac{}{}{0.1ex}{}{1}{k+1}-\genfrac{}{}{0.1ex}{}{1}{(k+1)(k+2)}]\hfill \\ \hfill & =\hfill & 1-\genfrac{}{}{0.1ex}{}{1}{k+2}\hfill \\ \hfill & =\hfill & \text{RHS of}\mathbf{P}(k+1).\hfill \end{array}$

  Hence $P(k+1)$ holds.

  If we combine these two bullet points, we have proved that “$P(n)$ holds for all $n\ge 1$”.

(c) Note: If $q=1$, then the LHS is equal to n, but the RHS makes no sense. So we assume $q\ne 1$.

Let $P(n)$ be the statement:

“$1+q+q^2+q^3+\cdots +q^{n-1}=\frac{1}{1-q}-\frac{q^n}{1-q}$ ”.

• LHS of $P(1)=1$; RHS of $P(1)=\frac{1}{1-q}-\frac{q}{1-q}=1$. Since these two are equal, $P(1)$ is true.
• Suppose that $P(k)$ is true for some particular (unspecified) $k\ge 1$; that is, we know that, for this particular k,

  “$1+q+q^2+q^3+\cdots +q^{k-1}=\frac{1}{1-q}-\frac{q^k}{1-q}$”.

  We wish to prove that $P(k+1)$ must then be true.

Now $P(k+1)$ is an equation, so we start with the LHS of $P(k+1)$ and try to simplify it in an appropriate way to get the RHS of $P(k+1)$:

$\begin{array}{ccc}\text{LHS of}\mathbf{P}(k+1)\hfill & =\hfill & 1+q+q^2+q^3+\cdots +q^k\hfill \\ \hfill & =\hfill & (1+q+q^2+q^3+\cdots +q^{k-1})+q^k.\hfill \end{array}$

If we now use $P(k)$, which we assume is true, then the first bracket is equal to

$$\frac{1}{1-q}-\frac{q^k}{1-q}$$

so the complete sum is equal to:

$\begin{array}{ccc}\hfill & =\hfill & \genfrac{}{}{0.1ex}{}{1}{1-q}-[\genfrac{}{}{0.1ex}{}{q^k}{1-q}-q^k]\hfill \\ \hfill & =\hfill & \genfrac{}{}{0.1ex}{}{1}{1-q}-\genfrac{}{}{0.1ex}{}{q^{k+1}}{1-q}\hfill \\ \hfill & =\hfill & \text{RHS of}\mathbf{P}(k+1).\hfill \end{array}$

Hence $P(k+1)$ holds.

If we combine these two bullet points, we have proved that “$P(n)$ holds for all $n\ge 1$”.

(d) Note: The statement to be proved starts with a term involving “0!”. The definition

$$n!=1\times 2\times 3\times \cdots \times n$$

does not immediately tell us how to interpret “$0!$”. The correct interpretation emerges from the fact that several different thoughts all point in the same direction.

(i) When $n>0$, then to get from $n!$ to $(n+1)!$ we multiply by (n + 1). If we extend this to $n=0$, then “to get from $0!$ to $1!$, we have to multiply by 1” – which suggests that $0!=1$.

(ii) When $n>0$, $n!$ counts the number of permutations of n symbols, or the number of different linear orders of n objects (i.e. how many different ways they can be arranged in a line). If we extend this to $n=0$, we see that there is just one way to arrange 0 objects (namely, sit tight and do nothing).

(iii) The definition of $n!$ as a product suggests that $0!$ involves a “product with no terms” at all. Now when we “add no terms together” it makes sense to interpret the result as “= 0” (perhaps because if this “sum of no terms” were added to some other sum, it would make no difference). In the same spirit, the product of no terms should be taken to be “= 1” (since if this empty product were included at the end of some other product, it would make no difference to the result).

Let $P(n)$ be the statement:

“$0·0!+1·1!+2·2!+\cdots +(n-1)·(n-1)!=n!-1$”.

• LHS of $P(1)=0·0!=0$; RHS of $P(1)=1!-1=0$. Since these two are equal, $P(1)$ is true.

• Suppose that $P(k)$ is true for some particular (unspecified) $k\ge 1$; that is, we know that, for this particular k,

“$0·0!+1·1!+2·2!+\cdots +(k-1)·(k-1)!=k!-1$”.

We wish to prove that $P(k+1)$ must then be true.

Now $P(k+1)$ is an equation, so we start with the LHS of $P(k+1)$ and try to simplify it in an appropriate way to get the RHS of $P(k+1)$):

$\begin{array}{ccc}\text{LHS of}\mathbf{P}(k+1)\hfill & =\hfill & 0\cdot 0!+1\cdot 1!+2\cdot 2!+\cdots +k\cdot k!\hfill \\ \hfill & =\hfill & [0\cdot 0!+1\cdot 1!+2\cdot 2!+\cdots +(k-1)\cdot (k-1)!]+k.k!.\hfill \end{array}$

If we now use $P(k)$, which we assume is true, then the first bracket is equal to $k!-1$, so the complete sum is equal to:

$\begin{array}{ccc}\hfill & =\hfill & (k!-1)+k\cdot k!\hfill \\ \hfill & =\hfill & (k+1)\cdot k!-1\hfill \\ \hfill & =\hfill & (k+1)!-1=\text{RHS of}\mathbf{P}(k+1).\hfill \end{array}$

Hence $P(k+1)$ holds.

If we combine these two bullet points, we have proved that “$P(n)$ holds for all $n\ge 1$”.

(e) Let $P(n)$ be the statement:

“${\left(\cos \theta +i\sin \theta \right)}^n=\cos n\theta +i\sin n\theta$ ”

• LHS of $P(1)={\left(\cos \theta +i\sin \theta \right)}^1$; RHS of $P(1)=\cos \theta +i\sin \theta$. Since these two are equal, $P(1)$ is true.

• Suppose that $P(k)$ is true for some particular (unspecified) $k\ge 1$; that is, we know that, for this particular k,

“${(\cos \theta +i\sin \theta )}^k=\cos k\theta +i\sin k\theta$ ”.

We wish to prove that $P(k+1)$ must then be true.

Now $P(k+1)$ is an equation, so we start with the LHS of $P(k+1)$ and try to simplify it in an appropriate way to get the RHS of $P(k+1)$:

$\begin{array}{ccc}\text{LHS of}\mathbf{P}(k+1)\hfill & =\hfill & {(\cos \theta +i\sin \theta )}^{k+1}\hfill \\ \hfill & =\hfill & {(\cos \theta +i\sin \theta )}^k(\cos \theta +i\sin \theta ).\hfill \end{array}$

If we now use $P(k)$, which we assume is true, then the first bracket is equal to $(\cos k\theta +i\sin k\theta )$, so the complete expression is equal to:

$\begin{array}{cc}=\hfill & (\cos k\theta +i\sin k\theta )(\cos \theta +i\sin \theta )\hfill \\ =\hfill & [\cos k\theta \cdot \cos \theta -\sin k\theta \cdot \sin \theta ]+i[\cos k\theta \cdot \sin \theta +\sin k\theta \cdot \cos \theta ]\hfill \\ =\hfill & \cos (k+1)\theta +i\sin (k+1)\theta =\text{RHS of}\mathbf{P}(k+1).\hfill \end{array}$

Hence $P(k+1)$ holds.

If we combine these two bullet points, we have proved that “$P(n)$ holds for all $n\ge 1$”.

236. Let $P(n)$ be the statement:

“${(1+2+3+\cdots +n)}^2=1^3+2^3+3^3+\cdots +n^3$ ”.

• LHS of $P(1)=1^2$; RHS of $P(1)=1^3$. Since these two are equal, $P(1)$ is true.

• Suppose that $P(k)$ is true for some particular (unspecified) $k\ge 1$; that is, we know that, for this particular k,

“${(1+2+3+\cdots +k)}^2=1^3+2^3+3^3+\cdots +k^3$ ”.

We wish to prove that $P(k+1)$ must then be true.

Now $P(k+1)$ is an equation, so we start with one side of $P(k+1)$ and try to simplify it in an appropriate way to get the other side of $P(k+1)$. In this instance, the RHS of $P(k+1)$ is the most promising starting point (because we know a formula for the $k^{\mathrm{th}}$ triangular number, and so can see how to simplify it):

$\begin{array}{ccc}\text{RHS of}\mathbf{P}(k+1)\hfill & =\hfill & 1^3+2^3+3^3+\cdots +k^3+{(k+1)}^3\hfill \\ \hfill & =\hfill & [1^3+2^3+3^3+\cdots +k^3]+{(k+1)}^3.\hfill \end{array}$

If we now use $P(k)$, which we assume is true, then the first bracket is equal to

$${(1+2+3+\cdots +k)}^2,$$

so the complete RHS is:

$\begin{array}{cc}=\hfill & {(1+2+3+\cdots +k)}^2+{(k+1)}^3\hfill \\ =\hfill & {\left[\genfrac{}{}{0.1ex}{}{k(k+1)}{2}\right]}^2+{(k+1)}^3\hfill \\ =\hfill & \genfrac{}{}{0.1ex}{}{1}{4}{(k+1)}^2[k^2+4k+4]\hfill \\ =\hfill & {\left[\genfrac{}{}{0.1ex}{}{(k+1)(k+2)}{2}\right]}^2\hfill \\ =\hfill & {(1+2+3+\cdots +(k+1\left)\right)}^2\hfill \\ =\hfill & \text{LHS of}\mathbf{P}(k+1).\hfill \end{array}$

Hence $P(k+1)$ holds.

If we combine these two bullet points, we have proved that “$P(n)$ holds for all $n\ge 1$”.

Note: A slightly different way of organizing the proof can sometimes be useful. Denote the two sides of the equation in the statement $P(n)$ by $f(n)$ and $g(n)$ respectively. Then

• $f(1)=1^2=1^3=g(1)$; and

• simple algebra allows one to check that, for each $k\ge 1$,

$$f(k+1)-f(k)={(k+1)}^3=g(k+1)-g(k).$$

It then follows (by induction) that $f(n)=g(n)$ for all $n\ge 1$.

237.

(a) $T_1=1$, $T_1+T_2=1+3=4$, $T_1+T_2+T_3=1+3+6=10$. These may not be very suggestive. But

$$T_1+T_2+T_3+T_4=20=5\times 4,$$ $$T_1+T_2+T_3+T_4+T_5=35=5\times 7,$$

and

$$T_1+T_2+T_3+T_4+T_5+T_6=56=7\times 8$$

may eventually lead one to guess that

$$T_1+T_2+T_3+\cdots +T_n=\frac{n(n+1)(n+2)}{6}.$$

Note 1: This will certainly be easier to guess if you remember what you found in Problem 17. and Problem 63.

Note 2: There is another way to help in such guessing. Suppose you notice that

– adding values for $k=1$ up to $k=n$ of a polynomial of degree 0 (such as $p(x)=1$) gives an answer that is a “polynomial of degree 1”,

$$1+1+\cdots +1=n,$$

and

– adding values for $k=1$ up to $k=n$ of a polynomial of degree 1 (such as $p(x)=x$) gives an answer that is a “polynomial of degree 2”,

$$1+2+3+\cdots +n=\frac{n(n+1)}{2}.$$

Then you might guess that the sum

$$T_1+T_2+T_3+\cdots +T_n$$

will give an answer that is a polynomial of degree 3 in n. Suppose that

$$T_1+T_2+T_3+\cdots +T_n=A{n}^3+B{n}^2+Cn+D.$$

We can then use small values of n to set up equations which must be satisfied by A, B, C, D and solve them to find A, B, C, D:

– when $n=0$, we get $D=0$;

– when $n=1$, we get $A+B+C=1$;

– when $n=2$, we get $8A+4B+2C=4$;

– when $n=3$, we get $27A+9B+3C=10$.

This method assumes that we know that the answer is a polynomial and that we know its degree: it is called “the method of undetermined coefficients”.

There are various ways of improving the basic method (such as writing the polynomial $A{n}^3+B{n}^2+Cn+D$ in the form

$$Pn(n-1)(n-2)+Qn(n-1)+Rn+S,$$

which tailors it to the values $n=0,1,2,3$ that one intends to substitute).

(b) Let $P(n)$ be the statement:

“$T_1+T_2+T_3+\cdots +T_n=\frac{n(n+1)(n+2)}{6}$”.

• LHS of $P(1)=T_1=1$; RHS of $P(1)=\frac{1\times 2\times 3}{6}=1$. Since these two are equal, $P(1)$ is true.

• Suppose that $P(k)$ is true for some particular (unspecified) $k\ge 1$; that is, we know that, for this particular k,

$$T_1+T_2+T_3+\cdots +T_k=\frac{k(k+1)(k+2)}{6}.$$

We wish to prove that $P(k+1)$ must then be true.

Now $P(k+1)$ is an equation, so we start with the LHS of $P(k+1)$ and try to simplify it in an appropriate way to get the RHS of $P(k+1)$:

$\begin{array}{ccc}\text{LHS of}\mathbf{P}(k+1)\hfill & =\hfill & T_1+T_2+T_3+\cdots +T_k+T_{k+1}\hfill \\ \hfill & =\hfill & [T_1+T_2+T_3+\cdots +T_k]+T_{k+1}.\hfill \end{array}$

If we now use $P(k)$, which we assume is true, then the first bracket is equal to

$$\frac{k(k+1)(k+2)}{6}.$$

so the complete sum is equal to:

$\begin{array}{cc}=\hfill & \genfrac{}{}{0.1ex}{}{k(k+1)(k+2)}{6}+\genfrac{}{}{0.1ex}{}{(k+1)(k+2)}{2}\hfill \\ =\hfill & \genfrac{}{}{0.1ex}{}{(k+1)(k+2)(k+3)}{6}\hfill \\ =\hfill & \text{RHS of}\mathbf{P}(k+1).\hfill \end{array}$

Hence $P(k+1)$ holds.

If we combine these two bullet points, we have proved that “$P(n)$ holds for all $n\ge 1$”.

Note: The triangular numbers $T_1,T_2,T_3,\dots ,T_k,\dots T_n$ are also equal to the binomial coefficients $k+1choose2$. And the sum of these binomial coefficients is another binomial coefficient $n+2choose3$, so the result in Problem 237. can be written as:

$$\left(\begin{array}{c}2\\ 2\end{array}\right)+\left(\begin{array}{c}3\\ 2\end{array}\right)+\left(\begin{array}{c}4\\ 2\end{array}\right)+\cdots +\left(\begin{array}{c}n+1\\ 2\end{array}\right)=\left(\begin{array}{c}n+2\\ 3\end{array}\right).$$

You might like to interpret Problem 237. in the language of binomial coefficients, and prove it by repeated use of the basic Pascal triangle relation (Pascal (1623--1662)):

$$\left(\begin{array}{c}k\\ r\end{array}\right)+\left(\begin{array}{c}k\\ r+1\end{array}\right)=\left(\begin{array}{c}k+1\\ r+1\end{array}\right).$$

Start by rewriting

$$\left(\begin{array}{c}n+2\\ 3\end{array}\right)=\left(\begin{array}{c}n+1\\ 2\end{array}\right)+\left(\begin{array}{c}n+1\\ 3\end{array}\right).$$

238.

(a) We know from Problem 237.(b) that

$$1\cdot 2+2\cdot 3+3\cdot 4+\cdots +n(n+1)=\frac{n(n+1)(n+2)}{3}.$$

Also

$\begin{array}{ccc}1\cdot 2+2\cdot 3+3\cdot 4+\cdots +n(n+1)\hfill & =\hfill & 1\cdot (1+1)+2\cdot (2+1)+3\cdot (3+1)\hfill \\ \hfill & \hfill & +\cdots +n\cdot (n+1)\hfill \\ \hfill & =\hfill & (1^2+1)+(2^2+2)+(3^2+3)\hfill \\ \hfill & \hfill & +\cdots +(n^2+n)\hfill \\ \hfill & =\hfill & (1^2+2^2+3^2+\cdots +n^2)\hfill \\ \hfill & \hfill & +(1+2+3+\cdots +n).\hfill \end{array}$

Therefore

$\begin{array}{ccc}{1}^2+2^2+3^2+\cdots +n^2\hfill & =\hfill & \genfrac{}{}{0.1ex}{}{n(n+1)(n+2)}{3}-\genfrac{}{}{0.1ex}{}{n(n+1)}{2}\hfill \\ \hfill & =\hfill & \genfrac{}{}{0.1ex}{}{n(n+1)(2n+1)}{6}.\hfill \end{array}$

(b) Guess:

$$1\cdot 2\cdot 3+2\cdot 3\cdot 4+3\cdot 4\cdot 5+\cdots +n(n+1)(n+2)=\frac{n(n+1)(n+2)(n+3)}{4}.$$

The proof by induction is entirely routine, and is left for the reader.

$\begin{array}{ccc}1\cdot 2\cdot 3+2\cdot 3\cdot 4+\cdots +n(n+1)(n+2)\hfill & =\hfill & 1\cdot (1+1)(1+2)+2\cdot (2+1)(2+2)\hfill \\ \hfill & \hfill & +\cdots +n\cdot (n+1)(n+2)\hfill \\ \hfill & =\hfill & (1^3+3\cdot 1^2+2\cdot 1)\hfill \\ \hfill & \hfill & +(2^3+3\cdot 2^2+2\cdot 2)\hfill \\ \hfill & \hfill & +\cdots +(n^3+3n^2+2n)\hfill \\ \hfill & =\hfill & (1^3+2^3+\cdots +n^3)\hfill \\ \hfill & \hfill & +3(1^2+2^2+\cdots +n^2)\hfill \\ \hfill & \hfill & +2(1+2+\cdots +n).\hfill \end{array}$

Therefore

$\begin{array}{ccc}{1}^3+2^3+3^3+\cdots +n^3\hfill & =\hfill & \genfrac{}{}{0.1ex}{}{n(n+1)(n+2)(n+3)}{4}\hfill \\ \hfill & \hfill & -3\left[\genfrac{}{}{0.1ex}{}{n(n+1)(2n+1)}{6}\right]\hfill \\ \hfill & \hfill & -n(n+1)\hfill \\ \hfill & =\hfill & {\left[\genfrac{}{}{0.1ex}{}{n(n+1)}{2}\right]}^2.\hfill \end{array}$

239.

(a) Let $f(x)$ be any such polynomial. If $f(a_k)=0$, then we know (by the Remainder Theorem) that $f(x)$ has $(x-a_k)$ as a factor. Since the $a_k$ are all distinct, and $f(a_k)=0$ for each k, $0\le k\le n-1$, we have

$$f(x)=(x-a_0)(x-a_1)(x-a_2)\cdots (x-a_{n-1})\cdot g(x)$$

for some polynomial $g(x)$. And since we are told that $f(x)$ has degree n, $g(x)$ has degree 0, so is a constant. Hence every such polynomial of degree n has the form

$$C\cdot (x-a_0)(x-a_1)(x-a_2)\cdots (x-a_{n-1}).$$

Since $f(a_n)=b$, we can substitute to find C:

$$C=\frac{b}{(a_n-a_0)(a_n-a_1)(a_n-a_2)\cdots (a_n-a_{n-1})}.$$

(b) Let $P(n)$ be the statement:

“Given any two labelled sets of $n+1$ real numbers $a_0,a_1,a_2,\dots ,a_n$, and $b_0,b_1,b_2,\dots ,b_n$, where the $a_i$ are all distinct (but the $b_i$ need not be), there exists a polynomial $f_n$ of degree n, such that $f_n(a_0)=b_0$, $f_n(a_1)=b_1$, $f_n(a_2)=b_2$, …, $f_n(a_n)=b_n$.”

• When $n=0$, we may choose $f_0(x)=b_0$ to be the constant polynomial. Hence $P(0)$ is true.

• Suppose that $P(k)$ is true for some particular (unspecified) $k\ge 0$; that is, we know that, for this particular k:

“Given any two labelled sets of $k+1$ real numbers $a_0,a_1,a_2,\dots ,a_k$, and $b_0,b_1,b_2,\dots ,b_k$, where the $a_i$ are all distinct (but the $b_i$ need not be), there exists a polynomial $f_k$ of degree k, such that $f_k(a_0)=b_0$, $f_k(a_1)=b_1$, $f_k(a_2)=b_2,\dots ,f_k(a_k)=b_k$.”

We wish to prove that $P(k+1)$ must then be true.

Now $P(k+1)$ is the statement:

“Given any two labelled sets of $(k+1)+1$ real numbers $a_0,a_1,\dots ,a_{k+1}$, and $b_0,b_1,b_2,\dots ,b_{k+1}$, where the $a_i$ are all distinct (but the $b_i$ need not be), there exists a polynomial $f_{k+1}$ of degree $k+1$, such that $f_{k+1}(a_0)=b_0$, $f_{k+1}(a_1)=b_1$, $f_{k+1}(a_2)=b_2$, …, $f_{k+1}(a_{k+1})=b_{k+1}$.”

So to prove that $P(k+1)$ holds, we must start by considering

any two labelled sets of $(k+1)+1$ real numbers $$a_0,a_1,a_2,\dots ,a_{k+1},\text{ and }{b}_0,b_1,b_2,\dots ,b_{k+1},$$ where the $a_i$ are all distinct (but the $b_i$ need not be).

We must then somehow construct a polynomial function $f_{k+1}$ of degree $k+1$ with the required property.

Because we are supposing that $P(k)$ is known to be true, we can focus on the first $k+1$ numbers in each of the two lists – $a_0,a_1,a_2,\dots ,a_k$, and $b_0,b_1,b_2,\dots ,b_k$ – and we can then be sure that there is a polynomial $f_k$ of degree k such that

$$f_k(a_0)=b_0,f_k(a_1)=b_1,f_k(a_2)=b_2,\dots ,f_k(a_k)=b_k.$$

The next step is slightly indirect: we make use of the polynomial $f_{k+1}$ which we are still trying to construct, and focus on the polynomial

$$f(x)=f_{k+1}(x)-f_k(x)$$

satisfying

$$f(a_0)=f(a_1)=\dots =f(a_k)=0,f(a_{k+1})=b_{k+1}-f_k(a_{k+1})=b(\text{say}).$$

Part (a) guarantees the existence of such a polynomial $f(x)$ of degree $k+1$ and tells us exactly what this polynomial function $f(x)$ is equal to. Hence we can construct the required polynomial $f_{k+1}(x)$) by setting it equal to $f(x)+f_k(x)$, which proves that $P(k+1)$ is true.

If we combine these two bullet points, we have proved that “$P(n)$ holds for all $n\ge 1$”.

240.

(a) 5 cents cannot be made; $6=3+3$; $7=3+4$; $8=4+4$; $9=3+3+3$; etc.

Guess: Every amount > N = 5 can be paid directly (without receiving change).

(b) Let $P(n)$ be the statement:

“n cents can be paid directly (without change) using 3 cent and 4 cent coins”.

– $P(6)$ is the statement: “6 cents can be paid directly”. And $6=3+3$, so $P(6)$ is true.

– Now suppose that we know $P(k)$ is true for some $k\ge 6$. We must show that $P(k+1)$ must then be true.

To prove $P(k+1)$ we consider the statement $P(k+1)$:

“$k+1$ cents can be paid directly”.

We know that $P(k)$ is true, so we know that “k cents can be paid directly”.

– If a direct method of paying k cents involves at least one 3 cent coin, then we can replace one 3 cent coin by a 4 cent coin to produce a way of paying $k+1$ cents.

Hence we only need to worry about a situation in which the only way to pay k cents directly involves no 3 cent coins at all – that is, paying k cents uses only 4 cent coins. But then there must be at least two 4 cent coins (since $k\ge 6$), and we can replace two 4 cent coins by three 3 cent coins to produce a way of paying $k+1$ cents directly.

Hence

• $P(6)$ is true; and

• whenever $P(k)$ is true for some $k\ge 6$, we know that $P(k+1)$ is also true.

$\therefore$ $P(n)$ is true for all $n\ge 6$.

241.

(a) $z^2-z+1=0$, so $z=\frac{1\pm \sqrt{-3}}{2}$ (these are the two primitive sixth roots of unity).

$\therefore$ $z^2=\frac{-1\pm \sqrt{-3}}{2}$ (the two primitive cube toots of unity), and

$$z^2+\frac{1}{z^2}=-1.$$

(b) $z^2-2z+1=0$, so $z=1$ (repeated root). $\therefore$ $z^2=1$ and $z^2+\frac{1}{z^2}=2$.

(c) (d) $z^2-3z+1=0$, so $z=\frac{3\pm \sqrt{5}}{2}$.

As soon as one starts calculating z² and $\frac{1}{z^2}$, it becomes clear that it is time to p-a-u-s-e and think.

$${\left(z+\frac{1}{z}\right)}^2=\left(z^2+\frac{1}{z^2}\right)+2,$$

so whenever $z+\frac{1}{z}=k$ is an integer,

$$z^2+{\left(\frac{1}{z}\right)}^2=k^2-2$$

is also an integer.

(e) Let $P(n)$ be the statement:

“if z has the property that $z+\frac{1}{z}$ is an integer, then $z^m+\frac{1}{z^m}$ is also an integer for all m, $0\le m\le n$”.

• $P(0)$ and $P(1)$ are clearly both true; and $P(2)$ was proved in part (d) above.

• Suppose that $P(k)$ is true for some particular (unspecified) $k\ge 2$; that is, we know that, for this particular k:

“if z has the property that $z+\frac{1}{z}$ is an integer, then $z^m+\frac{1}{z^m}$ is also an integer for all m, $0\le m\le k$”.

We wish to prove that $P(k+1)$ must then be true.

If $z+\frac{1}{z}$ is an integer, then, by $P(k)$,

“$z^m+\frac{1}{z^m}$ is also an integer for all m, $0\le m\le k$”.

So to prove that $P(k+1)$ holds, we only need to show that

“$z^{k+1}+\frac{1}{z^{k+1}}$ is an integer”.

By the Binomial Theorem:

$\begin{array}{ccc}{(z+\genfrac{}{}{0.1ex}{}{1}{z})}^{k+1}\hfill & =\hfill & (z^{k+1}+\genfrac{}{}{0.1ex}{}{1}{z^{k+1}})+\left(\genfrac{}{}{0ex}{}{k+1}{1}\right)(z^{k-1}+\genfrac{}{}{0.1ex}{}{1}{z^{k-1}})\hfill \\ \hfill & \hfill & +\left(\genfrac{}{}{0ex}{}{k+1}{2}\right)(z^{k-3}+\genfrac{}{}{0.1ex}{}{1}{z^{k-3}})+\cdots \hfill \end{array}$

The LHS is an integer (since $z+\frac{1}{z}$ is an integer), and (by $P(k)$) every term on the RHS is an integer except possibly the first. Hence the first term is the difference of two integers, so must also be an integer.

Hence $P(k+1)$ is true.

If we combine these two bullet points, we have proved that “$P(n)$ holds for all $n\ge 1$”. QED

Note: If $k+1=2m$ is even, the expansion of ${\left(z+\frac{1}{z}\right)}^{k+1}$ has an odd number of terms, so the RHS of the above re-grouped expansion ends with the term $\left(\begin{array}{c}2m\\ m\end{array}\right)·z^m·{\left(\frac{1}{z}\right)}^m$, which is also an integer.

242.

Note: In the solution to Problem 241. we included the condition on z as part of the statement $P(n)$.

In Problem 242. the result to be proved has a similar background hypothesis – “Let p be a prime number”. It may make the induction clearer if, as in the statement of the Problem, this hypothesis is stated before starting the induction proof.

Let p be any prime number. We let $P(n)$ be the statement:

“$n^p-n$ is divisible by p ”.

• $P(1)$ is true (since $1^p-1=0=0\times p$, which is divisible by p).

• Suppose that $P(k)$ is true for some particular (unspecified) $k\ge 1$; that is, we know that, for this particular k:

“$k^p-k$ is divisible by p”.

We wish to prove $P(k+1)$ – that is,

“${(k+1)}^p-(k+1)$ is divisible by p”

must then be true. Using the Binomial Theorem again we see that

$$\begin{array}{lll}{(k+1)}^p-(k+1)\hfill & =\hfill & \left[k^p+\left(\begin{array}{c}p\\ p-1\end{array}\right)k^{p-1}+\left(\begin{array}{c}p\\ p-2\end{array}\right)k^{p-2}+\cdots +\left(\begin{array}{c}p\\ 1\end{array}\right)k+1\right]\hfill \\ \hfill & \hfill & -(k+1)\hfill \\ \hfill & =\hfill & (k^p-k)+\left[\left(\begin{array}{c}p\\ p-1\end{array}\right)k^{p-1}+\left(\begin{array}{c}p\\ p-2\end{array}\right)k^{p-2}+\cdots +\left(\begin{array}{c}p\\ 1\end{array}\right)k\right].\hfill \end{array}$$

By $P(k)$, the first bracket on the RHS is divisible by p; and in each of the other terms each of the binomial coefficients $\left(\begin{array}{c}p\\ r\end{array}\right)$ , $0<r<p$,

• is an integer, and

• has a factor “p” in the numerator and no such factor in the denominator.

Hence each term in the second bracket is a multiple of p. So the RHS (and hence the LHS) is divisible by p.

Hence $P(k+1)$ is true.

If we combine these two bullet points, we have proved that “$P(n)$ holds for all $n\ge 1$”. QED

243.

$$0.037037037\dots \text{ (for ever) }=\frac{37}{1000}+\frac{37}{1000000}+\frac{37}{1000000000}+\cdots \text{ (for ever)}.$$

This is a geometric series with first term $a=\frac{37}{1000}$ and common ratio $r=\frac{1}{1000}$, and so has sum

$$\frac{a}{1-r}=\frac{37}{999}=\frac{1}{27}.$$

244.

(a) Each person receives in total:

$$\frac{1}{4}+{\left(\frac{1}{4}\right)}^2+{\left(\frac{1}{4}\right)}^3+{\left(\frac{1}{4}\right)}^4+\cdots \text{ (for ever) }=\frac{1}{3}$$

(here $a=\frac{1}{4}=r$).

(b) You have

$$1-\frac{1}{2}+\frac{1}{4}-\frac{1}{8}+\cdots \text{ (for ever) }=\frac{2}{3}$$

(here $a=1$, $r=-\frac{1}{2}$); I have

$$\frac{1}{2}-\frac{1}{4}+\frac{1}{8}-\cdots \text{ (for ever) }=\frac{1}{3}$$

(here $a=\frac{1}{2}$, $r=-\frac{1}{2}$).

245. The trains are 120 km apart, and the fly travels at 50 km/h towards Train B, which is initially 120 km away and travelling at 30 km/h.

The relative speed of the fly and Train B is 80 km/h, so it takes $\genfrac{}{}{0.1ex}{}{3}{2}$ hours before they meet. In this time Train A and Train B have each travelled 45 km, so they are now 30 km apart. The fly then turns right round and flies back to Train A.

The relative speed of the fly and Train A is then also 80 km/h, so it takes just $\genfrac{}{}{0.1ex}{}{3}{8}$ hours (or 22.5 minutes) for the fly to return to Train A. Train A and Train B have each travelled $\genfrac{}{}{0.1ex}{}{45}{4}$ km in this time, so they are now $\genfrac{}{}{0.1ex}{}{30}{4}$ km apart. The fly then turns round and flies straight back to Train B.

Train B is $\genfrac{}{}{0.1ex}{}{30}{4}$ km away and the relative speed of the fly and Train B is again 80 km/h, so the journey takes $\genfrac{}{}{0.1ex}{}{3}{32}$ hours (or 5.625 minutes).

Continuing in this way, we see that the fly takes

$$\frac{3}{2}+\frac{3}{8}+\frac{3}{32}+\frac{3}{128}+\cdots \text{ (for ever) }=2\text{ hours}.$$ Hence the fly travels 100 km before being squashed.

Note: The two trains are approaching each other at 60 km/h, so they crash in exactly 2 hours – during which time the fly travels 100 km.

246.

(a) (i) $3^2>2^2$; therefore

$$\frac{1}{3^2}<\frac{1}{2^2},$$

so

$$\frac{1}{2^2}+\frac{1}{3^2}<\frac{2}{2^2}=\frac{1}{2}.$$

(ii) $7^2>6^2>5^2>4^2$; therefore

$$\frac{1}{7^2}<\frac{1}{6^2}<\frac{1}{5^2}<\frac{1}{4^2},$$

so

$$\frac{1}{4^2}+\frac{1}{5^2}+\frac{1}{6^2}+\frac{1}{7^2}<\frac{4}{4^2}=\frac{1}{4}.$$

(b) The argument in part (a) gives an upper bound for each bracketed expression in the sum

$$\left(\frac{1}{1^2}\right)+\left(\frac{1}{2^2}+\frac{1}{3^2}\right)+\left(\frac{1}{4^2}+\frac{1}{5^2}+\frac{1}{6^2}+\frac{1}{7^2}\right)+\left(\frac{1}{8^2}+\cdots +\frac{1}{{15}^2}\right)+\cdots$$

Replacing each bracket by its upper bound, we see that the sum is

$\begin{array}{ccc}\hfill & <\hfill & \genfrac{}{}{0.1ex}{}{1}{1^2}+\genfrac{}{}{0.1ex}{}{2}{2^2}+\genfrac{}{}{0.1ex}{}{4}{4^2}+\genfrac{}{}{0.1ex}{}{8}{8^2}+\cdots \hfill \\ \hfill & =\hfill & 1+\genfrac{}{}{0.1ex}{}{1}{2}+\genfrac{}{}{0.1ex}{}{1}{4}+\genfrac{}{}{0.1ex}{}{1}{8}+\cdots \text{(for ever)}\hfill \\ \hfill & =\hfill & 2.\hfill \end{array}$

(c) The finite partial sums

$$S_n=\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+\cdots +\frac{1}{n^2}$$

• increase steadily as we take more and more terms, and

• every partial sum $S_n$ is less than $2$. It is clear that these partial sums form a sequence

$$1=S_1<S_2<S_3<\dots <S_n<S_{n+1}<\dots <2.$$

It follows that there is some (unknown) number $S\le 2$ to which the partial sums converge as $n\to \infty$, and we take this (unknown) exact value S to be the exact value of the endless sum

$$\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+\cdots +\frac{1}{n^2}+\cdots \text{ (for ever)}$$

To see, for example, that $S>\frac{17}{12}$, notice that

$\begin{array}{ccc}S\hfill & >\hfill & S_4\hfill \\ \hfill & =\hfill & \genfrac{}{}{0.1ex}{}{1}{1^2}+\genfrac{}{}{0.1ex}{}{1}{2^2}+\genfrac{}{}{0.1ex}{}{1}{3^2}+\genfrac{}{}{0.1ex}{}{1}{4^2}\hfill \\ \hfill & =\hfill & 1+\genfrac{}{}{0.1ex}{}{1}{4}+\genfrac{}{}{0.1ex}{}{1}{9}+\genfrac{}{}{0.1ex}{}{1}{16}\hfill \\ \hfill & >\hfill & \genfrac{}{}{0.1ex}{}{17}{12}.\hfill \end{array}$

Note 1: The claim that

“an increasing sequence of partial sums $S_n$, all less than 2, must converge to some number $S\le 2$”

is a fundamental property of the real numbers – called completeness.

Note 2: Just as one can obtain better and better lower bounds for S – like “$\frac{17}{12}<S$”, so one can improve the upper bound “$S<2$”. For example, if in part (b) we avoid replacing the third term $\genfrac{}{}{0.1ex}{}{1}{9}$ by $\genfrac{}{}{0.1ex}{}{1}{4}$, we get a better upper bound “$S<\frac{67}{36}$”, which is $\genfrac{}{}{0.1ex}{}{5}{36}$ less than 2.

247.

(a) Let $P(n)$ be the statement:

“$\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+\cdots +\frac{1}{n^2}\le 2-\frac{1}{n}$”.

• Then LHS of $P(1)=\frac{1}{1^2}=1$, and RHS of $P(1)=2-1=1$. Hence $P(1)$ is true.

• Suppose we know that $P(k)$ is true for some $k\ge 1$. We want to prove that $P(k+1)$ holds.

$\begin{array}{ccc}\text{LHS of}\mathbf{P}(k+1)\hfill & =\hfill & \genfrac{}{}{0.1ex}{}{1}{1^2}+\genfrac{}{}{0.1ex}{}{1}{2^2}+\genfrac{}{}{0.1ex}{}{1}{3^2}+\cdots +\genfrac{}{}{0.1ex}{}{1}{k^2}+\genfrac{}{}{0.1ex}{}{1}{{(k+1)}^2}\hfill \\ \hfill & =\hfill & [\genfrac{}{}{0.1ex}{}{1}{1^2}+\genfrac{}{}{0.1ex}{}{1}{2^2}+\genfrac{}{}{0.1ex}{}{1}{3^2}+\cdots +\genfrac{}{}{0.1ex}{}{1}{k^2}]+\genfrac{}{}{0.1ex}{}{1}{{(k+1)}^2}\hfill \\ \hfill & \le \hfill & [2-\genfrac{}{}{0.1ex}{}{1}{k}]+\genfrac{}{}{0.1ex}{}{1}{{(k+1)}^2}\hfill \\ \hfill & =\hfill & 2-[\genfrac{}{}{0.1ex}{}{1}{k}-\genfrac{}{}{0.1ex}{}{1}{{(k+1)}^2}]\hfill \\ \hfill & <\hfill & 2-\genfrac{}{}{0.1ex}{}{1}{k+1}.\hfill \end{array}$

Hence $P(k+1)$ holds.

$\therefore$ $P(1)$ holds; and whenever $P(k)$ is known to be true, $P(k+1)$ is also true.

$\therefore$ $P(n)$ is true, for all $n\ge 1$. QED

(b) Let $P(n)$ be the statement:

“$\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+\cdots +\frac{1}{n^2}<1.68-\frac{1}{n}$”.

• Then

$$\text{LHS of }P(4)=\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}=1.423611111\cdots ,$$

and RHS of $P(4)=1.43$. Hence $P(4)$ is true.

• Suppose we know that $P(k)$ is true for some $k\ge 4$. We want to prove that $P(k+1)$ holds.

$\begin{array}{ccc}\text{LHS of}\mathbf{P}(k+1)\hfill & =\hfill & \genfrac{}{}{0.1ex}{}{1}{1^2}+\genfrac{}{}{0.1ex}{}{1}{2^2}+\genfrac{}{}{0.1ex}{}{1}{3^2}+\cdots +\genfrac{}{}{0.1ex}{}{1}{k^2}+\genfrac{}{}{0.1ex}{}{1}{{(k+1)}^2}\hfill \\ \hfill & =\hfill & (\genfrac{}{}{0.1ex}{}{1}{1^2}+\genfrac{}{}{0.1ex}{}{1}{2^2}+\genfrac{}{}{0.1ex}{}{1}{3^2}+\cdots +\genfrac{}{}{0.1ex}{}{1}{k^2})+\genfrac{}{}{0.1ex}{}{1}{{(k+1)}^2}\hfill \\ \hfill & <\hfill & [1.68-\genfrac{}{}{0.1ex}{}{1}{k}]+\genfrac{}{}{0.1ex}{}{1}{{(k+1)}^2}\hfill \\ \hfill & =\hfill & 1.68-[\genfrac{}{}{0.1ex}{}{1}{k}-\genfrac{}{}{0.1ex}{}{1}{{(k+1)}^2}]\hfill \\ \hfill & <\hfill & 1.68-\genfrac{}{}{0.1ex}{}{1}{k+1}.\hfill \end{array}$

Hence $P(k+1)$ holds.

$\therefore$ $P(1)$ holds; and whenever $P(k)$ is known to be true, $P(k+1)$ is also true.

$\therefore$ $P(n)$ is true, for all $n\ge 1$.

248.

(a) (i) $n!=n\times (n-1)\times (n-2)\times \cdots \times 3\times 2\times 1\ge 2\times 2\times 2\times \cdots \times 2\times 1=2^{n-1}$ whenever $n\ge 1$.

$\therefore$ $\frac{1}{n!}\le {\left(\frac{1}{2}\right)}^{n-1}$ for all $n\ge 1$.

$\therefore$ $\frac{1}{0!}+\frac{1}{1!}+\frac{1}{2!}+\cdots +\frac{1}{n!}\le 1+\left[1+\frac{1}{2}+{\left(\frac{1}{2}\right)}^2+\cdots +{\left(\frac{1}{2}\right)}^{n-1}\right]<3$ for all $n\ge 0$.

(ii) As we go on adding more and more terms, each finite sum

$$\frac{1}{0!}+\frac{1}{1!}+\frac{1}{2!}+\cdots +\frac{1}{n!}$$

is bigger than the previous sum. Since every finite sum

$$\frac{1}{0!}+\frac{1}{1!}+\frac{1}{2!}+\cdots +\frac{1}{n!}<3,$$

the sums increase, but never reach 3, so they accumulate closer and closer to a value “e” $\le 3$. Moreover, this value “e” is certainly larger than the sum of the first two terms $\frac{1}{0!}+\frac{1}{1!}=2$, so $2<e\le 3$.

(b) (i) Let $P(n)$ be the statement:

“$\frac{1}{0!}+\frac{1}{1!}+\frac{1}{2!}+\cdots +\frac{1}{n!}\le 3-\frac{1}{n\cdot n!}$”.

• $\text{LHS of }P(1)=2=\text{RHS of }P(1)$. Hence $P(1)$ is true.

• Suppose we know that $P(k)$ is true for some $k\ge 1$. We want to prove that $P(k+1)$ holds.

$\begin{array}{ccc}\text{LHS of}\mathbf{P}(k+1)\hfill & =\hfill & \genfrac{}{}{0.1ex}{}{1}{0!}+\genfrac{}{}{0.1ex}{}{1}{1!}+\genfrac{}{}{0.1ex}{}{1}{2!}+\cdots +\genfrac{}{}{0.1ex}{}{1}{(k+1)!}\hfill \\ \hfill & =\hfill & [\genfrac{}{}{0.1ex}{}{1}{0!}+\genfrac{}{}{0.1ex}{}{1}{1!}+\genfrac{}{}{0.1ex}{}{1}{2!}+\cdots +\genfrac{}{}{0.1ex}{}{1}{k!}]+\genfrac{}{}{0.1ex}{}{1}{(k+1)!}\hfill \\ \hfill & \le \hfill & 3-\genfrac{}{}{0.1ex}{}{1}{k\cdot k!}+\genfrac{}{}{0.1ex}{}{1}{(k+1)!}\hfill \\ \hfill & =\hfill & 3-\genfrac{}{}{0.1ex}{}{1}{k(k+1)!}\hfill \\ \hfill & <\hfill & 3-\genfrac{}{}{0.1ex}{}{1}{(k+1)\cdot (k+1)!}\hfill \end{array}$

Hence $P(k+1)$ holds.

$\therefore$ $P(1)$ holds; and whenever $P(k)$ is known to be true, $P(k+1)$ is also true.

$\therefore$ $P(n)$ is true, for all $n\ge 1$.

(ii) [The reasoning here uses the constant “3” while ignoring the refinement “$3-\frac{1}{n.n!}$”, and so sounds exactly like part (a)(ii).] As we add more terms, each finite sum

$$\frac{1}{0!}+\frac{1}{1!}+\frac{1}{2!}+\cdots +\frac{1}{n!}$$

is bigger than the previous sum. Since every finite sum

$$\frac{1}{0!}+\frac{1}{1!}+\frac{1}{2!}+\cdots +\frac{1}{n!}<3,$$

the partial sums increase, but never reach 3; so they accumulate closer and closer to a value “e” $\le 3$. Moreover, this value “e” is certainly larger than the sum of the first three terms $\frac{1}{0!}+\frac{1}{1!}+\frac{1}{2!}=2.5$, so $2.5<e\le 3$.

(c) Note: Examine carefully the role played by the number “3” in the above induction proof in (b)(ii). It is needed precisely to validate the statement $P(1)$: since $\frac{1}{0!}+\frac{1}{1!}=3-\frac{1}{1\times 1!}$”. But the number “3” plays no active part in the second induction step, and could be replaced by any other number we choose.

The exact value “e” of the infinite series is not really affected by what happens when $n=1$. Suppose we ask: “What number $C_2$ should replace “3” if we only want to prove that

$$\frac{1}{0!}+\frac{1}{1!}+\frac{1}{2!}+\cdots +\frac{1}{n!}\le C_2-\frac{1}{n\cdot n!},\text{ for all }n\ge 2?$$

The only part of the induction proof where $C_2$ then matters is when we try to check that $P(2)$ holds; so we must choose the smallest possible $C_2$ to satisfy

$\frac{1}{0!}+\frac{1}{1!}+\frac{1}{2!}\le C_2-\frac{1}{2.2!}:$

that is, $C_2=2.75$.

(i) Let $P(n)$ be the statement:

“$\frac{1}{0!}+\frac{1}{1!}+\frac{1}{2!}+\cdots +\frac{1}{n!}\le 2.75-\frac{1}{n\cdot n!}$”.

• LHS of $P(2)=2.5$; RHS of $P(2)=2.75-\frac{1}{4}$. Hence $P(2)$ is true.

• Suppose we know that $P(k)$ is true for some $k\le 2$. We want to prove that $P(k+1)$ holds.

$\begin{array}{ccc}\text{LHS of}\mathbf{P}(k+1)\hfill & =\hfill & \genfrac{}{}{0.1ex}{}{1}{0!}+\genfrac{}{}{0.1ex}{}{1}{1!}+\genfrac{}{}{0.1ex}{}{1}{2!}+\cdots +\genfrac{}{}{0.1ex}{}{1}{(k+1)!}\hfill \\ \hfill & =\hfill & [\genfrac{}{}{0.1ex}{}{1}{0!}+\genfrac{}{}{0.1ex}{}{1}{1!}+\genfrac{}{}{0.1ex}{}{1}{2!}+\cdots +\genfrac{}{}{0.1ex}{}{1}{k!}]+\genfrac{}{}{0.1ex}{}{1}{(k+1)!}\hfill \\ \hfill & \le \hfill & 2.75-\genfrac{}{}{0.1ex}{}{1}{k\cdot k!}+\genfrac{}{}{0.1ex}{}{1}{(k+1)!}\hfill \\ \hfill & =\hfill & 2.75-\genfrac{}{}{0.1ex}{}{1}{k(k+1)!}\hfill \\ \hfill & <\hfill & 2.75-\genfrac{}{}{0.1ex}{}{1}{(k+1)(k+1)!}\hfill \end{array}$

Hence $P(k+1)$ holds.

$\therefore$ $P(2)$ holds; and whenever $P(k)$ is known to be true, $P(k+1)$ is also true.

$\therefore$ $P(n)$ is true, for all $n\ge 2$. QED

(ii) As we add more terms, each finite sum

$$\frac{1}{0!}+\frac{1}{1!}+\frac{1}{2!}+\cdots +\frac{1}{n!}$$

is bigger than the previous sum.

Since every finite sum

$$\frac{1}{0!}+\frac{1}{1!}+\frac{1}{2!}+\cdots +\frac{1}{n!}<2.75,$$

the finite sums increase, but never reach 2.75, so they accumulate closer and closer to a value “e” $\le 2.75$. Moreover, this value “e” is certainly larger than the sum of the first four terms

$$\frac{1}{0!}+\frac{1}{1!}+\frac{1}{2!}+\frac{1}{3!}>2.66,$$

so $2.66<e\le 2.75$.

(d) (i) Let $P(n)$ be the statement:

“$\frac{1}{0!}+\frac{1}{1!}+\frac{1}{2!}+\cdots +\frac{1}{n!}\le 2.7222\cdots (\text{for ever)}-\frac{1}{n.n!}$”.

• $\text{LHS of }P(3)=\frac{1}{0!}+\frac{1}{1!}+\frac{1}{2!}+\frac{1}{3!}=2.666\cdots \text{(for ever)}$; $\text{RHS of }P(3)=2.7222\cdots \text{(for ever) }-\frac{1}{18}=2.666\cdots \text{(for ever)}$. Hence $P(3)$ is true.

• Suppose we know that $P(k)$ is true for some $k\ge 3$. We want to prove that $P(k+1)$ holds.

$\begin{array}{ccc}\text{LHS of}\mathbf{P}(k+1)\hfill & =\hfill & \genfrac{}{}{0.1ex}{}{1}{0!}+\genfrac{}{}{0.1ex}{}{1}{1!}+\genfrac{}{}{0.1ex}{}{1}{2!}+\cdots +\genfrac{}{}{0.1ex}{}{1}{(k+1)!}\hfill \\ \hfill & =\hfill & [\genfrac{}{}{0.1ex}{}{1}{0!}+\genfrac{}{}{0.1ex}{}{1}{1!}+\genfrac{}{}{0.1ex}{}{1}{2!}+\cdots +\genfrac{}{}{0.1ex}{}{1}{k!}]+\genfrac{}{}{0.1ex}{}{1}{(k+1)!}\hfill \\ \hfill & \le \hfill & 2.7222\cdots \left(\text{for ever}\right)-\genfrac{}{}{0.1ex}{}{1}{k\cdot k!}+\genfrac{}{}{0.1ex}{}{1}{(k+1)!}\hfill \\ \hfill & =\hfill & 2.7222\cdots \left(\text{for ever}\right)-\genfrac{}{}{0.1ex}{}{1}{k(k+1)!}\hfill \\ \hfill & <\hfill & 2.7222\cdots \left(\text{for ever}\right)-\genfrac{}{}{0.1ex}{}{1}{(k+1)(k+1)!}\hfill \end{array}$

Hence $P(k+1)$ holds.

$\therefore$ $P(3)$ holds; and whenever $P(k)$ is known to be true, $P(k+1)$ is also true.

$\therefore$ $P(n)$ is true, for all $n\ge 3$.

(ii) As we add more terms, each finite sum

$$\frac{1}{0!}+\frac{1}{1!}+\frac{1}{2!}+\cdots +\frac{1}{n!}$$

is bigger than the previous sum.

Since every finite sum

$$\frac{1}{0!}+\frac{1}{1!}+\frac{1}{2!}+\cdots +\frac{1}{n!}<2.7222\cdots \text{ (for ever)},$$

the finite sums increase, but never reach $2.7222\cdots$ (for ever), so they accumulate closer and closer to a value “e” $\le 2.7222\cdots$ (for ever). Moreover, this value “e” is certainly larger than the sum of the first five terms

$$\frac{1}{0!}+\frac{1}{1!}+\frac{1}{2!}+\frac{1}{3!}+\frac{1}{4!}>2.708,$$

so $2.708<e\le 2.7222\cdots \text{ (for ever)}$.

Note: This process of refinement can continue indefinitely. But we only have to go one further step to pin down the value of “e” with surprising accuracy.

The next step uses the same proof to show that

“$\frac{1}{0!}+\frac{1}{1!}+\frac{1}{2!}+\cdots +\frac{1}{n!}\le 2.7185-\frac{1}{n\cdot n!}$, for all $n\ge 4$”,

and to conclude that the endless sum

$$\frac{1}{0!}+\frac{1}{1!}+\frac{1}{2!}+\cdots +\frac{1}{n!}+\cdots (\text{for ever})$$

has a definite value “e” that lies somewhere between $2.716$ and $2.71875$.

We could then repeat the same proof to show that

$$\frac{1}{0!}+\frac{1}{1!}+\frac{1}{2!}+\cdots +\frac{1}{n!}\le 2.718333\cdots (\text{for ever})-\frac{1}{n\cdot n!},\text{ for all }n\ge 5,$$

and use the lower bound $2.7177\dots$ from the first seven terms to conclude that the endless sum

$$\frac{1}{0!}+\frac{1}{1!}+\frac{1}{2!}+\cdots +\frac{1}{n!}+\cdots \text{ (for ever)}$$

has a definite value “e” that lies somewhere between $2.7177$ and $2.718333\cdots$ (for ever). And so on.

249. Let $P(n)$ be the statement:

“$\frac{1}{\sqrt{1}}+\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{3}}+\cdots +\frac{1}{\sqrt{n}}\ge \sqrt{n}$”.

• LHS of $P(1)=1=$ RHS of $P(1)$. Hence $P(1)$ is true.

• Suppose we know that $P(k)$ is true for some $k\ge 1$. We want to prove that $P(k+1)$ holds.

$\begin{array}{ccc}\text{LHS of}\mathbf{P}(k+1)\hfill & =\hfill & \genfrac{}{}{0.1ex}{}{1}{\sqrt{1}}+\genfrac{}{}{0.1ex}{}{1}{\sqrt{2}}+\genfrac{}{}{0.1ex}{}{1}{\sqrt{3}}+\cdots +\genfrac{}{}{0.1ex}{}{1}{\sqrt{k+1}}\hfill \\ \hfill & =\hfill & (\genfrac{}{}{0.1ex}{}{1}{\sqrt{1}}+\genfrac{}{}{0.1ex}{}{1}{\sqrt{2}}+\genfrac{}{}{0.1ex}{}{1}{\sqrt{3}}+\cdots +\genfrac{}{}{0.1ex}{}{1}{\sqrt{k}})+\genfrac{}{}{0.1ex}{}{1}{\sqrt{(k+1)}}\hfill \\ \hfill & \ge \hfill & \sqrt{k}+\genfrac{}{}{0.1ex}{}{1}{\sqrt{k+1}}\hfill \\ \hfill & \ge \hfill & \sqrt{k+1}(\text{since}\genfrac{}{}{0.1ex}{}{1}{\sqrt{k+1}}\ge \genfrac{}{}{0.1ex}{}{1}{\sqrt{k+1}+\sqrt{k}}).\hfill \end{array}$

Hence $P(k+1)$ holds.

$\therefore$ $P(1)$ holds; and whenever $P(k)$ is known to be true, $P(k+1)$ is also true.

$\therefore$ $P(n)$ is true, for all $n\ge 1$. QED

250. Let a, b be real numbers such that $a\ne b$, and $a+b>0$.

One of a, b is then the greater, and we may suppose this is a – so that $a>b$. If $a>b>0$, then $a^n>b^n>0$ for all n; if $b<0$, then $a+b>0$ implies that $a=\left|a\right|>\left|b\right|$, so $a^n>b^n$ for all n.

Let $P(n)$ be the statement:

“$\frac{a^n+b^n}{2}\ge {\left(\frac{a+b}{2}\right)}^n$”.

• LHS of $P(1)=\frac{a+b}{2}=\text{RHS of }P(1)$. Hence $P(1)$ is true.

• Suppose we know that $P(k)$ is true for some $k\ge 1$. We want to prove that $P(k+1)$ holds.

$\begin{array}{ccc}\text{RHS of}\mathbf{P}(k+1)\hfill & =\hfill & {\left(\genfrac{}{}{0.1ex}{}{a+b}{2}\right)}^{k+1}\hfill \\ \hfill & =\hfill & \genfrac{}{}{0.1ex}{}{a+b}{2}\cdot {\left(\genfrac{}{}{0.1ex}{}{a+b}{2}\right)}^k\hfill \\ \hfill & \le \hfill & \genfrac{}{}{0.1ex}{}{a+b}{2}\cdot \genfrac{}{}{0.1ex}{}{a^k+b^k}{2}\left(\text{by}\mathbf{P}\right(k\left)\right)\hfill \\ \hfill & =\hfill & \genfrac{}{}{0.1ex}{}{a^{k+1}+b^{k+1}}{4}+\genfrac{}{}{0.1ex}{}{a{b}^k+b{a}^k}{4}\hfill \\ \hfill & <\hfill & \genfrac{}{}{0.1ex}{}{a^{k+1}+b^{k+1}}{2}\left(\text{since}\right(a^k-b^k\left)\right(a-b)>0).\hfill \end{array}$

Hence $P(k+1)$ holds.

$\therefore$ $P(1)$ holds; and whenever $P(k)$ is known to be true, $P(k+1)$ is also true.

$\therefore$ $P(n)$ is true, for all $n\ge 1$.

251. Let x be any real number $\ge -1$.

If $x=-1$, then ${(1+x)}^n=0\ge 1-n=1+nx$ , for all $n\ge 1$.

Thus we may assume that $x>-1$, so $1+x>0$.

Let $P(n)$ be the statement: “${(1+x)}^n\ge 1+nx$ ”.

• LHS of $P(1)=1+x=\text{RHS of }P(1)$. Hence $P(1)$ is true.

• Suppose we know that $P(k)$ is true for some $k\ge 1$. We want to prove that $P(k+1)$ holds.

$\begin{array}{ccc}\text{LHS of}\mathbf{P}(k+1)\hfill & =\hfill & {(1+x)}^{k+1}\hfill \\ \hfill & =\hfill & (1+x)\cdot {(1+x)}^k\hfill \\ \hfill & \ge \hfill & (1+x)\cdot (1+kx)\left(\text{by}\mathbf{P}\right(k),\text{since}1+x>0)\hfill \\ \hfill & =\hfill & 1+(k+1)x+k{x}^2\hfill \\ \hfill & \ge \hfill & 1+(k+1)x\hfill \end{array}$

Hence $P(k+1)$ holds.

$\therefore$ $P(1)$ holds; and whenever $P(k)$ is known to be true, $P(k+1)$ is also true.

$\therefore$ $P(n)$ is true, for all $n\ge 1$.

252. The problem is discussed after the statement of Problem 252. in the main text.

253.

(a) (i) $3>2$, so $\frac{1}{3}<\frac{1}{2}$. $\therefore$ $\frac{1}{2}+\frac{1}{3}<\frac{1}{2}+\frac{1}{2}=1$.

(ii) $5,6,7>4$; hence $\frac{1}{5},\frac{1}{6},\frac{1}{7}$ are all $<\frac{1}{4}$. $\therefore$ $\frac{1}{4}+\frac{1}{5}+\frac{1}{6}+\frac{1}{7}<\frac{1}{4}+\frac{1}{4}+\frac{1}{4}+\frac{1}{4}=1$.

(iii) Let $P(n)$ be the statement:

“$\frac{1}{1}+\frac{1}{2}+\frac{1}{3}+\cdots +\frac{1}{2^n-1}<n$ ”.

Then

• $P(2)$ is true by (i), since

$$\frac{1}{1}+\frac{1}{2}+\frac{1}{3}<1+\left(\frac{1}{2}+\frac{1}{2}\right)=2.$$

• Suppose that $P(k)$ is true for some $k\ge 2$.

$$\begin{array}{lll}\text{LHS of }P(k+1)\hfill & =\hfill & \left[\frac{1}{1}+\frac{1}{2}+\frac{1}{3}+\cdots +\frac{1}{2^k-1}\right]\hfill \\ \hfill & \hfill & +\left[\frac{1}{2^k}+\cdots +\frac{1}{2^{k+1}-1}\right].\hfill \end{array}$$

The first bracket is $<k$ (by $P(k)$); and each of the $2^k$ terms in the second bracket is $\le \frac{1}{2^k}$, so the whole bracket is $\le 1$.

Hence the LHS of $P(k+1)<k+1$, so $P(k+1)$ is true.

Hence $P(n)$ is true for all $n\ge 2$.

(iv) At the very first stage (part (i)) we replaced $\frac{1}{2}+\frac{1}{3}$ by $\frac{1}{2}+\frac{1}{2}=1$. Hence when $n\ge 2$, we know that the two sides of $P(n)$ differ by at least $\frac{1}{2}-\frac{1}{3}$. This difference is greater than $\frac{1}{2^n}$ when $n\ge 3$, so (iv) follows.

(b)

(i) $3<4$, so $\frac{1}{3}>\frac{1}{4}$.

$\therefore$ $\frac{1}{3}+\frac{1}{4}>\frac{1}{4}+\frac{1}{4}=\frac{1}{2}$.

(ii) $5,6,7<8$; hence $\frac{1}{5},\frac{1}{6},\frac{1}{7}$ are all $>\frac{1}{8}$.

$\therefore$ $\frac{1}{5}+\frac{1}{6}+\frac{1}{7}+\frac{1}{8}>\frac{1}{8}+\frac{1}{8}+\frac{1}{8}+\frac{1}{8}=\frac{1}{2}$.

(iii) Let $P(n)$ be the statement:

“$\frac{1}{1}+\frac{1}{2}+\frac{1}{3}+\cdots +\frac{1}{2^n}>1+\frac{n}{2}$”.

Then

• $P(2)$ is true by (i), since

$\begin{array}{ccc}\genfrac{}{}{0.1ex}{}{1}{1}+\genfrac{}{}{0.1ex}{}{1}{2}+\genfrac{}{}{0.1ex}{}{1}{3}+\genfrac{}{}{0.1ex}{}{1}{4}\hfill & =\hfill & 1+\genfrac{}{}{0.1ex}{}{1}{2}+(\genfrac{}{}{0.1ex}{}{1}{3}+\genfrac{}{}{0.1ex}{}{1}{4})\hfill \\ \hfill & >\hfill & 1+\genfrac{}{}{0.1ex}{}{1}{2}+(\genfrac{}{}{0.1ex}{}{1}{4}+\genfrac{}{}{0.1ex}{}{1}{4})\hfill \\ \hfill & =\hfill & 1+2\times \genfrac{}{}{0.1ex}{}{1}{2}.\hfill \end{array}$

• Suppose that $P(k)$ is true for some $k\ge 2$.

LHS of $P(k+1)=\left[\frac{1}{1}+\frac{1}{2}+\frac{1}{3}+\cdots +\frac{1}{2^k}\right]+\left[\frac{1}{2^k+1}+\cdots +\frac{1}{2^{k+1}}\right]$.

The first bracket is $>1+\frac{k}{2}$ (by $P(k)$); and each of the $2^k$ terms in the second bracket is $\ge \frac{1}{2^{k+1}}$, so the whole bracket is $\ge \frac{1}{2}$. Hence the LHS of $P(k+1)>1+\frac{k+1}{2}$, so $P(k+1)$ is true.

Hence $P(n)$ is true for all $n\ge 2$.

254.

(a) We use induction. Let $P(n)$ be the statement:

“n identical rectangular strips of length 2 balance exactly on the edge of a table if the successive protrusion distances (first beyond the edge of the table, then beyond the leading edge of the strip immediately below, and so on) are the terms $\frac{1}{n},\frac{1}{n-1},\frac{1}{n-2},\dots ,\frac{1}{3},\frac{1}{2},\frac{1}{1}$ of the finite harmonic series in reverse order.”

• When $n=1$, a single strip which protrudes distance 1 beyond the edge of the table has its centre of gravity exactly over the edge of the table. Hence $P(1)$ is true.

• Suppose that we know that $P(k)$ is true for some $k\ge 1$.

Let $k+1$ identical strips be arranged as described in the statement $P(k+1)$.

The statement $P(k)$ guarantees that the top k strips would exactly balance if the leading edge of the bottom strip were in fact the edge of the table; hence the combined centre of gravity of the top k strips is positioned exactly over the leading edge of the bottom strip.

Let M be the mass of each strip; since the leading edge of the bottom strip is distance $\frac{1}{k+1}$ beyond the edge of the table, the top k strips produce a combined moment about the edge of the table equal to $kM\times \frac{1}{k+1}$.

The centre of gravity of the bottom strip is distance $1-\frac{1}{k+1}=\frac{k}{k+1}$ from the edge of the table in the opposite direction; hence it contributes a moment about the edge of the table equal to $M\times \left(-\frac{k}{k+1}\right)$.

$\therefore$ the total moment of the whole stack about the edge of the table is equal to zero, so the centre of gravity of the combined stack of $k+1$ strips lies exactly over the edge of the table. Hence $P(k+1)$ is true.

Hence $P(n)$ is true for all $n\ge 1$.

(b) Problem 253.(b)(iii) now guarantees that a stack of $2^n$ strips can protrude a distance $>1+\frac{n}{2}$ beyond the edge of the table.

Note: Ivars Petersen's Mathematical Tourist blog contains an entry in 2009

http://mathtourist.blogspot.com/2009/01/overhang.html

which explores how one can obtain large overhangs with fewer strips if one is allowed to use strips to counterbalance those that protrude beyond the edge of the table.

255.

(a) (i) Let $P(n)$ be the statement:

“$s_{2p-2}<s_{2p}<s_{2q+1}<s_{2q-1}$ for all $p,q$ such that $1\le p,q\le n$”.

• $P(1)$ is true (since $s_0$ is the empty sum, so

$$0=s_0<s_2=\frac{1}{2}<s_3=\frac{5}{6}<s_1=1.$$

• Suppose that $P(k)$ is true for some $k\ge 1$. Then most of the inequalities in the statement $P(k+1)$ are part of the statement $P(k)$; the only outstanding inequalities which remain to be proved are:

$$s_{2k}<s_{2k+2}<s_{2k+3}<s_{2k+1}.$$

which are true, since

$$s_{2k+3}=s_{2k+2}+\frac{1}{2k+3}=s_{2k+1}-\frac{1}{2k+2}+\frac{1}{2k+3}$$

and

$$s_{2k+2}=s_{2k}+\frac{1}{2k+1}-\frac{1}{2k+2}.$$

Hence $P(k+1)$ is true.

Hence $P(n)$ is true for all $n\ge 2$.

(ii) The “even sums” $s_0,s_2,s_4,\dots$ are increasing, but all are less than $s_1=1$, so they approach some value $s_{even}\le 1$.

The “odd sums” $s_1,s_3,s_5,\dots$ are decreasing, but all are greater than $s_2=\frac{1}{2}$, so they approach some value $s_{odd}\ge \frac{1}{2}$.

The “even sums” $s_0,s_2,s_4,\dots$ are increasing, but all are less than $s_5=\frac{47}{60}$, so they approach some value $s_{even}\le \frac{47}{60}$.

The “odd sums” $s_1,s_3,s_5,\dots$ are decreasing, but all are greater than $s_6=\frac{37}{60}$, so they approach some value $s_{odd}\ge \frac{37}{60}$.

Moreover, the difference between successive sums is $\frac{1}{n}$, and this tends towards zero, so the difference between each “odd sum” and the next “even sum” tends to zero, so $s_{even}=s_{odd}$.

(b) The proof from part (a) carries over word for word, with “$\frac{1}{k}$” replaced at each stage by “$a_k$”.

256. Let $P(n)$ be the statement:

“$f_k$ has at least k distinct prime factors”.

• $f_1=2$ has exactly 1 prime factor, so $P(1)$ is true.

• Suppose that $P(k)$ is true for some $k\ge 1$.

Then $f_{k+1}=f_k(f_k+1)$. The first factor $f_k$ has at least k distinct prime factors.

And the second factor $f_k+1>f_k>1$, so has at least one prime factor.

Moreover $HCF(f_k,f_k+1)=1$, so the second bracket has no factor in common with $f_k$.

Hence $f_{k+1}$ has at least $k+1$ distinct prime factors, so $P(k+1)$ is true.

Hence $P(n)$ is true for all $n\ge 1$.

Note: This problem [suggested by Serkan Dogan] gives a different proof of the result (Problem 76.(d)) that the list of prime numbers goes on for ever.

257.

(a) Let $P(n)$ be the statement: “n distinct points on a straight line divide the line into $n+1$ intervals”.

• 0 points leave the line in pristine condition – namely a single interval – so $P(0)$ is true.

• Suppose that $P(k)$ is true for some $k\ge 0$.

Consider an arbitrary straight line divided by $k+1$ points $A_0,A_1,\dots ,A_k$.

Then the k points $A_1,\dots ,A_k$ divide the line into $k+1$ intervals (by $P(k)$).

The additional point $A_0$ is distinct from $A_1$, …, $A_k$ and so must lie inside one of these $k+1$ intervals, and divides it in two – giving $(k+1)+1=k+2$ intervals altogether.

Hence $P(k+1)$ is true.

Hence $P(n)$ is true for all $n\ge 0$.

(b) (i) We want a function R satisfying

$R_0=1,R_1=2,R_2=4,R_3=7.$

If we notice that in part (a) $n+1=1+\left(\begin{array}{c}n\\ 1\end{array}\right),$ then we might guess that

$$R_n=1+\left(\begin{array}{c}n\\ 1\end{array}\right)+\left(\begin{array}{c}n\\ 2\end{array}\right).$$

(ii) Let $P(n)$ be the statement:

“n distinct straight lines in the plane divide the plane into at most $f(n)=1+\left(\begin{array}{c}n\\ 1\end{array}\right)+\left(\begin{array}{c}n\\ 2\end{array}\right)$ regions”.

• 0 lines leave the plane in pristine condition – namely a single region – so $P(0)$ is true, provided that

$$1+\left(\begin{array}{c}0\\ 1\end{array}\right)+\left(\begin{array}{c}0\\ 2\end{array}\right)=1.$$

• Suppose that $P(k)$ is true for some $k\ge 0$.

Consider the plane divided by $k+1$ straight lines $m_0,m_1,\dots ,m_k$.

Then the k lines $m_1,\dots ,m_k$ divide the plane into at most

$$R_k=1+\left(\begin{array}{c}k\\ 1\end{array}\right)+\left(\begin{array}{c}k\\ 2\end{array}\right)$$

regions (by $P(k)$).

The additional line $m_0$ is distinct from $m_1,\dots ,m_k$ and so meets each of these lines in at most a single point – giving at most k points on the line $m_0$. These points divide $m_0$ into at most $k+1$ intervals, and each of these intervals corresponds to a cut-line, where the line $m_0$ cuts one of the regions created by the lines $m_1,m_2,\dots ,m_k$ into two pieces – giving at most

$\begin{array}{ccc}{R}_k+(k+1)\hfill & =\hfill & 1+\left(\genfrac{}{}{0ex}{}{k}{1}\right)+\left(\genfrac{}{}{0ex}{}{k}{2}\right)+k+1\hfill \\ \hfill & =\hfill & 1+\left(\genfrac{}{}{0ex}{}{k+1}{1}\right)+\left(\genfrac{}{}{0ex}{}{k+1}{2}\right)\hfill \\ \hfill & =\hfill & R_{k+1}\hfill \end{array}$

regions altogether.

Hence $P(k+1)$ is true.

Hence $P(n)$ is true for all $n\ge 0$.

(c) (i) We want a function S satisfying

$$S_0=1,S_1=2,S_2=4,S_3=8,S_4=15,\dots$$

After thinking about the differences between successive terms in part (b), we might guess that

$$S_n=\left(\begin{array}{c}n\\ 0\end{array}\right)+\left(\begin{array}{c}n\\ 1\end{array}\right)+\left(\begin{array}{c}n\\ 2\end{array}\right)+\left(\begin{array}{c}n\\ 3\end{array}\right).$$

(ii) Let $P(n)$ be the statement:

“n distinct planes in 3-space divide space into at most

$S_n=\left(\begin{array}{c}n\\ 0\end{array}\right)+\left(\begin{array}{c}n\\ 1\end{array}\right)+\left(\begin{array}{c}n\\ 2\end{array}\right)+\left(\begin{array}{c}n\\ 3\end{array}\right)$

regions”.

• 0 planes leave our 3D space in pristine condition – namely a single region – so $P(0)$ is true – provided that

$$\left(\begin{array}{c}0\\ 0\end{array}\right)+\left(\begin{array}{c}0\\ 1\end{array}\right)+\left(\begin{array}{c}0\\ 2\end{array}\right)+\left(\begin{array}{c}0\\ 3\end{array}\right)=1.$$

• Suppose that $P(k)$ is true for some $k\ge 0$.

Consider 3D divided by $k+1$ planes $m_0,m_1,\dots ,m_k$.

Then the k planes $m_1,\dots ,m_k$ divide 3D into at most

$$S_k=\left(\begin{array}{c}k\\ 0\end{array}\right)+\left(\begin{array}{c}k\\ 1\end{array}\right)+\left(\begin{array}{c}k\\ 2\end{array}\right)+\left(\begin{array}{c}k\\ 3\end{array}\right)$$

regions (by $P(k)$).

The additional plane $m_0$ is distinct from $m_1,\dots ,m_k$ and so meets each of these planes in (at most) a line – giving rise to at most k lines on the plane $m_0$. This arrangement of lines on the plane $m_0$ divides $m_0$ into at most

$R_k=1+\left(\begin{array}{c}k\\ 1\end{array}\right)+\left(\begin{array}{c}k\\ 2\end{array}\right)$

regions, and each of these regions on the plane $m_0$ is the “cut” where the plane $m_0$ cuts an existing region into two pieces – giving rise to at most

$\begin{array}{ccc}{S}_k+R_k\hfill & =\hfill & [\left(\genfrac{}{}{0ex}{}{k}{0}\right)+\left(\genfrac{}{}{0ex}{}{k}{1}\right)+\left(\genfrac{}{}{0ex}{}{k}{2}\right)+\left(\genfrac{}{}{0ex}{}{k}{3}\right)]+[1+\left(\genfrac{}{}{0ex}{}{k}{1}\right)+\left(\genfrac{}{}{0ex}{}{k}{2}\right)]\hfill \\ \hfill & =\hfill & \left(\genfrac{}{}{0ex}{}{k+1}{0}\right)+\left(\genfrac{}{}{0ex}{}{k+1}{1}\right)+\left(\genfrac{}{}{0ex}{}{k+1}{2}\right)+\left(\genfrac{}{}{0ex}{}{k+1}{3}\right)\hfill \\ \hfill & =\hfill & S_{k+1}\hfill \end{array}$

regions altogether. (There is no need for any algebra here: one only needs to use the Pascal triangle condition.)

Hence $P(k+1)$ is true whenever $P(k)$ is true.

Hence $P(n)$ is true for all $n\ge 0$.

258. Notice that, given a dissection of a square into k squares, we can always cut one square into four quarters (by lines through the centre, and parallel to the sides), and so create a dissection with $k+3$ squares.

Let $P(n)$ be the statement:

“Any given square can be cut into m (not necessarily congruent) smaller squares, for each m, $6\le m\le n$”.

• Let $n=6$. Given any square of side s (say). We may cut a square of side $\frac{2s}{3}$ from one corner, leaving an L-shaped strip of width $\frac{s}{3}$, which we can then cut into 5 smaller squares, each of side $\frac{s}{3}$. Hence $P(6)$ is true.

Let $n=7$. Given any square, we can divide the square first into four quarters; then divide one of these smaller squares into four quarters to obtain a dissection into 7 smaller squares. Hence $P(7)$ is true.

Let $n=8$. Given a square of side s (say). We may cut a square of side $\frac{3s}{4}$ from one corner, leaving an L-shaped strip of width $\frac{s}{4}$, which we can then cut into 7 smaller squares, each of side $\frac{s}{4}$. Hence $P(8)$ is true.

• Suppose that $P(k)$ is true for some $k\ge 8$.

Then $k-2\ge 6$, so any given square can be dissected into $k-2$ smaller squares (by $P(k)$). Taking this dissection and dividing one of the smaller squares into four quarters gives a dissection of the initial square into $k-2+3$ squares. Hence $P(k+1)$ is true.

Hence $P(n)$ is true for all $n\ge 6$.

259. Let $P(n)$ be the statement:

“Any tree with n vertices has exactly $n-1$ edges”.

• A tree with 1 vertex is simply a vertex with 0 edges (since any edge would have to be a loop, and would then create a cycle). Hence $P(1)$ is true.

• Suppose that $P(k)$ is true for some $k\ge 1$.

Consider an arbitrary tree T with $k+1$ vertices.

[Idea: We need to find some way of reducing T to a tree $T^{\prime }$ with k vertices. This suggests “removing an end vertex”. So we must first prove that “any tree T has an end vertex”.]

Definition The number of edges incident with a given vertex v is called the valency of v.

Lemma Let S be a finite tree with $s>1$ vertices. Then S has a vertex of valency 1 – that is an “end vertex”.

Proof Choose any vertex $v_0$. Then $v_0$ must be connected to the rest of the tree, so $v_0$ has valency at least 1.

If $v_0$ is an “end vertex”, then stop; if not, then choose a vertex $v_1$ which is adjacent to $v_0$.

If $v_1$ is an “end vertex”, then stop; if not, choose a vertex $v_2\ne v_0$ which is adjacent to $v_1$.

If $v_2$ is an “end vertex”, then stop; if not, choose a vertex $v_3\ne v_1$ which is adjacent to $v_2$.

Continue in this way.

All of the vertices $v_0,v_1,v_2,v_3,\dots$ must be different (since any repeat $v_m=v_n$ with $m<n$ would define a cycle

$$v_m,v_{m+1},v_{m+2},\dots ,v_{n-1},v_n=v_m$$

in the tree S). Since we know that the tree is finite (having precisely s vertices), the process must terminate at some stage. The final vertex $v_e$ is then an “end vertex”, of valency 1.

If we apply the Lemma to our arbitrary tree T with $k+1$ vertices, we can choose an “end vertex” v and remove both it and the edge e incident with it to obtain a tree $T^{\prime }$ having k vertices. By $P(k)$ we know that $T^{\prime }$ has exactly $k-1$ edges, so when we reinstate the edge e, we see that T has exactly $(k-1)+1$ edges, so $P(k+1)$ is true.

Hence $P(n)$ is true for all $n\ge 1$.

260.

Note: All the polyhedra described in this solution are “spherical” by virtue of having their vertices located on the unit sphere.

(a) (i) A regular tetrahedron.

(ii) A square based pyramid with its apex at the North pole.

(b) If a spherical polyhedron has V vertices, E edges, and F faces, then

$$V-E+F=2.$$

Now each edge has exactly two end vertices, so $2E$ counts the exact number of ordered pairs (v, e), where e is an edge, and v is a vertex “incident with e”.

On the other hand, in a spherical polyhedron, each vertex v has valency at least 3; so each vertex v occurs in at least 3 pairs (v, e) of this kind. Hence $2E\ge 3V$.

In the same way, each edge e lies on the boundary of exactly 2 faces, so $2E$ counts the exact number of ordered pairs (f, e), where e is an edge of the face f.

On the other hand, in a spherical polyhedron, each face f has at least 3 edges; so each face f occurs in at least 3 pairs (f, e) of this kind. Hence $2E\ge 3F$.

If $E=7$, then $14\ge 3V$, and $14\ge 3F$; now V and F are integers, so $V\le 4$ and $F\le 4$. Hence $V+F\le 8$. However $V+F=E+2=9$. This contradiction shows that no such polyhedron exists.

(c) We show by induction how to construct certain “spherical” polyhedra, with at most one non-triangular face. Let $P(n)$ be the statement:

“There exists a spherical polyhedron with at most one non-triangular face, and with e edges for each $e,$ $8\le e\le n$”.

• We know that there exists a such a spherical polyhedron with $n=6$ edges – namely the regular tetrahedron (with four faces, which are all equilateral triangles).

We know there is no such polyhedron with $n=7$ edges (by part (b)).

When $n=8$, there is no spherical polyhedron with $n=8$ edges and all faces triangular (since we would then have $16=2E=3F$, as in part (b)). However, there exists a spherical polyhedron with $n=8$ edges and just one non-triangular face – namely the square based pyramid with its apex at the North pole.

When $n=9$, we can join three points on the equator to the North and South poles to produce a triangular bi-pyramid (the dual of a triangular prism), with all faces triangular, and with $n=9$ edges.

When $n=10$, there is no spherical polyhedron with $n=10$ edges and with all faces triangles (since we would then have to have $20=2E=3F$, as in part (b)); but there exists a spherical polyhedron with $n=10$ edges and just one face which is not an equilateral triangle – namely the pentagonal based pyramid with its apex at the North pole.

This provides us with a starting point for the inductive construction. In particular $P(8)$, $P(9)$, and $P(10)$ are all true.

• Suppose that $P(k)$ is true for some $k\ge 10$. The only part of the statement $P(k+1)$ that remains to be demonstrated is the existence of a suitable polyhedron with $k+1$ edges.

Since $k\ge 10$, we know that $k-2\ge 8$, so (by $P(k)$) there exists a polyhedron with all its vertices on the unit sphere, with at most one non-triangular face, and with $e=k-2$ edges. Take this polyhedron and remove a triangular face $ABC$. Now add a new vertex X on the sphere, internal to the spherical triangle $ABC$, and add the edges $XA$, $XB$, $XC$ and the three triangular faces $XAB$, $XBC$, $XCA$, to produce a spherical polyhedron with $e=(k-2)+3=k+1$ edges, and with at most one non-triangular face. Hence $P(k+1)$ is true.

Hence $P(n)$ is true for all $n\ge 8$.

261. To prove a result that is given in the form of an “if and only if” statement, we have to prove two things: “if”, and “only if”.

We begin by proving the “only if” part:

“a map can be properly coloured with two colours only if every vertex has even valency”.

Let M be a map that can be properly coloured with two colours. Let v be any vertex of the map M.

The edges $e_1,e_2,e_3,\dots$ incident with v form parts of the boundaries of the sequence of regions around the vertex v (with $e_1$, $e_2$ bordering one region; $e_2$, $e_3$ bordering the next; and so on). Since we are assuming that the regions of the map M can be “properly coloured” with two colours, the succession of regions around the vertex v can be properly coloured with just two colours. Hence the colours of the regions around the vertex v must alternate (say black-white-black- …). And since the map is finite, this sequence must return to the start – so the number of such regions at the vertex v (and hence the number of edges incident with v – that is, the valency of v) must be even.

We now prove the “if” part:

“a map can be properly coloured with two colours if every vertex has even valency”.

Suppose that we have a map M in which each vertex has even valency. We must prove that any such map M can be properly coloured using just two colours.

Let $P(n)$ be the statement:

“any map with m edges, in which each vertex has even valency, can be properly coloured with two colours whenever m satisfies $1\le m\le n$,”.

• If $n=1$, a map in which every vertex has even valency, and which has just one edge $e$, must consist of a single vertex v, with $e$ as a loop from $v$ to $v$ (so $v$ has valency 2, since the edge $e$ is incident with $v$ twice). This creates a map with two regions – the “island” inside the loop, and the “sea” outside; so we can colour the “island” black and the “sea” white. Hence $P(1)$ is true.

• Suppose that $P(k)$ is true for some $k\ge 1.$

Most of the contents of the statement $P(k+1)$ are already guaranteed by $P(k)$. To prove that $P(k+1)$ is true, all that remains to be proved is that

any map with exactly $k+1$ edges, in which every vertex has even valency, can be properly coloured using just two colours.

Consider an arbitrary map M with $k+1$ edges, in which each vertex has even valency.

[Idea: We need to find some way of reducing the map M to a map $M^{\prime }$ with $\le k$ edges, in which every vertex still has even valency.]

Since $k\ge 1$, the map M has at least 2 edges. Choose any edge e of M, with (say) vertices $u_1$, $u_2$ as its endpoints, and with regions R, S on either side of e.

Suppose first that $u_1=u_2$, so the boundary of the region R (say) consists only of the edge e. Hence e is a loop, and S is the only region neighbouring R. The edge e contributes 2 to the valency of $u_1$; so if we delete the edge e, we obtain a map $M^{\prime }$ in which every vertex again has even valency, in which the regions R and S have been amalgamated into a region $S^{\prime }$. Since $M^{\prime }$ has just k edges, $M^{\prime }$ can be properly coloured with just two colours. If we now reinstate the edge e and the region R, we can give S the same colour as $S^{\prime }$ (in the proper colouring of $M^{\prime }$) and give R the opposite colour to $S^{\prime }$ to obtain a proper colouring of the map M with just two colours.

Hence we may assume that $u_1\ne u_2$, so that e is not the complete boundary of R. We may then slowly shrink the edge e to a point – eventually fusing the old vertices $u_1$, $u_2$ together to form a new vertex $u^{\prime }$, where two new regions $R^{\prime }$, $S^{\prime }$ meet. The result is then a new map $M^{\prime }$, in which all other vertices are unchanged (and so have even valency), and in which

$$\text{valency}(u^{\prime })=(\text{valency}(u_1)-1)+(\text{valency}(u_2)-1)$$

which is also even.

Hence every vertex of the new map $M^{\prime }$ has even valency. Moreover, $M^{\prime }$ has at most k edges, so (by $P(k)$) we know that the map $M^{\prime }$ can be properly coloured with just two colours. And in this colouring of $M^{\prime }$, there are an odd number of colour changes as one goes from $R^{\prime }$ to $S^{\prime }$ through the other regions that meet around the old vertex $u_1$ of M, so $S^{\prime }$ receives the opposite colour to $R^{\prime }$. The guaranteed proper two-colouring of $M^{\prime }$ therefore extends back to give a proper two-colouring of the original map M. Hence $P(k+1)$ is true.

Hence $P(n)$ is true for all $n\ge 1$.

262. Let $P(n)$ be the statement:

“The $2^n$ sequences of length n consisting of 0s and 1s can be arranged in a cyclic list such that any two neighbouring sequences (including the last and the first) differ in exactly one coordinate position.”

• When $n=2$ , the required cycle is obvious:

$$00\to 10\to 11\to 01(\to 00).$$ So $P(2)$ is true.

• The general construction is perhaps best illustrated by first showing how $P(2)$ leads to $P(3)$.

The above cycle for sequences of length 2 gives rise to two disjoint cycles for sequences of length 3:

– first by adding a third coordinate “0”:

$$000\to 100\to 110\to 010(\to 000)$$

– then by adding a third coordinate “1”:

$$001\to 101\to 111\to 011(\to 001).$$

Now eliminate the final join in each cycle ($010\to 000$ and $011\to 001$) and instead link the two cycles together by first reversing the order of the first cycle, and then inserting the joins $000\to 001$ and $011\to 010$ to form a single cycle.

In general, suppose that $P(k)$ is true for some $k\ge 1$. Then we construct a single cycle for the $2^{k+1}$ sequences of length $k+1$ as follows:

Take the cycle of the $2^k$ sequences of length k guaranteed by $P(k)$, and form two disjoint cycles of length $2^k$

• first by adding a final coordinate “0“

• then by adding a final coordinate “1”.

Then link the two cycles into a single cycle of length $2^{k+1}$, by eliminating the final step

$$v_1{v}_2\cdots v_{k}0\to 00\cdots 00$$ in the first cycle, and $v_1{v}_2\cdots v_{k}1\to 00\cdots 01$

in the second cycle, reversing the first cycle, and inserting the joins

$$00\cdots 00\to 00\cdots 01\text{ and }{v}_1{v}_2\cdots v_{k}1\to v_1{v}_2\cdots v_{k}0$$

to produce a single cycle of the required kind joining all $2^{k+1}$ sequences of length $k+1$. Hence $P(k+1)$ is true.

Hence $P(n)$ is true for all $n\ge 2$.

Note: The significance of what we call Gray codes was highlighted in a 1953 patent by the engineer Frank Gray (1887-1969) – where they were called reflected binary codes (since the crucial step in their construction above involves taking two copies of the previous cycles, reversing one of the cycles, and then producing half of the required cycle by traversing the first copy before returning backwards along the second copy). Their most basic use is to re-encode the usual binary counting sequence

$$1\to 10\to 11\to 100\to 101\to 110\to 111\to 1000\to 1001\to 1010\to \cdots ,$$

where a single step can lead to the need to change arbitrarily many binary digits (e.g. the step from $3=\text{''}11$” to $4=\text{''}100$” changes 3 digits, and the step from $7=\text{''}111$” to $8=$“1000” changes 4 digits, etc.) – a requirement that is inefficient in terms of electronic “switching”, and which increases the probability of errors. In contrast, the Gray code sequence changes a single binary digit at each step. However, the physical energy which is saved through reducing the amount of “switching” in the circuitry corresponds to an increase in the need for unfamiliar mathematical formulae, which re-interpret each vector in the Gray code as the ordinary integer in the counting sequence to which it corresponds.

263.

(a) The whole construction is inductive (each label derives from an earlier label). So let $P(n)$ be the statement:

“if $HCF(r,s)=1$ and $2\le r+s\le n$, then the positive rational $\frac{r}{s}$ occurs once and only once as a label, and it occurs in its lowest terms”.

• By construction the root is given the label $\genfrac{}{}{0.1ex}{}{1}{1}$, so $\genfrac{}{}{0.1ex}{}{1}{1}$ occurs. And it cannot occur again, since the numerator and denominator of each parent vertex are both positive, neither i nor j can ever be 0. Hence $P(2)$ is true.

Notice that the basic construction:

“if $\frac{i}{j}$ is a `parent' vertex, then we label its `left descendant' as $\frac{i}{i+j}$, and its `right descendant' $\frac{i+j}{j}$”

guarantees that, since we start by labelling the root with the positive rational $\genfrac{}{}{0.1ex}{}{1}{1}$, all subsequent `descendants' are positive.

Moreover, if any `descendant' were suddenly to appear not “in lowest terms”, then either

– $HCF(i,i+j)>1$, in which case $HCF(i,i+j)=HCF(i,j)$, so $HCF(i,j)>1$ at the previous stage; or

– $HCF(i+j,j)>1$, in which case $HCF(i+j,j)=HCF(i,j)$, so $HCF(i,j)>1$ at the previous stage.

Since we begin by labelling the root $\genfrac{}{}{0.1ex}{}{1}{1}$, where $HCF(1,1)=1$, it follows that all subsequent labels are positive rationals in lowest terms.

• Suppose that $P(k)$ is true from some $k\ge 2$.

Most parts of the statement $P(k+1)$ are guaranteed by $P(k)$. To show that $P(k+1)$ is true, it remains to consider cases where $HCF(r,s)=1$ and $r+s=k+1$ ($\ge 3$). Either (i) $r>s$, or (ii) $s>r$.

(i) Suppose that $r>s$. Then $\frac{r}{s}$ arises in this (fully cancelled) form only as a direct (right) descendant of $\frac{r-s}{s}$. So $\frac{r}{s}$ occurs. Moreover, every label occurs in its lowest terms, so $\frac{r}{s}$ cannot occur again.

(ii) Suppose that $s>r$. Then $\frac{r}{s}$ arises in this (fully cancelled) form only as a direct (left) descendant of $\frac{r}{s-r}$. So $\frac{r}{s}$ occurs. Moreover, every label occurs in its lowest terms, so $\frac{r}{s}$ cannot occur again.

Hence $P(k+1)$ is true.

Hence $P(n)$ is true for all $n\ge 2$.

(b) The fact that the labels are left-right symmetric is also an inductive phenomenon. We note that the one fully “left-right symmetric” label, namely $\genfrac{}{}{0.1ex}{}{1}{1}$, occurs in the only fully “left-right symmetric” position – namely at the root.

All other labels occur in reciprocal pairs: $\frac{r}{s}$ and $\frac{s}{r}$, where we may assume that $r>s$. The fact that these occur as labels of “left-right symmetric” vertices derives from the fact that

$\frac{r}{s}$ is the `right descendant' of $\frac{r-s}{s}$ and

$\frac{s}{r}$ is the `left descendant' of $\frac{s}{r-s}$.

So if we know that the earlier reciprocal pair reciprocal pair $\frac{r-s}{s}$ and $\frac{s}{r-s}$ occur as labels of symmetrically positioned vertices, then it follows that the same is true of the descendant reciprocal pair $\frac{r}{s}$ and $\frac{s}{r}$. We leave the reader to write out the proof by induction – for example, using the statement

“$P(n)$: if $r,s>0$, and $2\le r+s\le n$, then the reciprocal pair $\frac{r}{s}$, $\frac{s}{r}$ occur as labels of vertices at the same level below the root, with the two labelled vertices being mirror images of each other about the vertical mirror through the root vertex.”

264. The intervals in this problem may be of any kind (including finite or infinite). Each interval has two “endpoints”, which are either ordinary real numbers, or $\pm \infty$ (signifying that the interval goes off to infinity in one or both directions).

Let $P(n)$ be the statement:

“if a collection of n intervals on the x-axis has the property that any two intervals overlap in an interval (of possibly zero length – i.e. a point), then the intersection of all intervals in the collection is a non-empty interval”.

When $n=2$, the hypothesis of $P(2)$ is the same as the conclusion. So $P(2)$ is true.

Suppose that $P(k)$ is true for some $k\ge 2$. We seek to prove that $P(k+1)$ is true.

So consider a collection of $k+1$ intervals with the property that any two intervals in the collection intersect in a non-empty interval. If this collection includes one interval that is listed more than once, then the required conclusion follows from $P(k)$. So we may assume that the intervals in our collection are all different.

Among the $k+1$ intervals, consider first those with the largest right hand endpoint. If there is only one such interval, denote it by $I_0$; if there is more than one interval with the same largest right hand endpoint, let $I_0$ be the interval among those with the largest right hand endpoint that has the largest left hand endpoint. In either case, put $I_0$ aside for the moment, leaving a collection S of k intervals with the required property.

By $P(k)$ we know that the intervals in the collection S intersect in a non-empty interval I, with left hand endpoint a and right hand endpoint b (say).

We have to show that the intersection $I\cap I_0$ is non-empty.

The proof that follows works if the endpoint b is included in the interval I. The slight adjustment needed if b is not included in the interval I is left to the reader.

Since the right hand endpoint of $I_0$ is the largest possible, and since points between a and b belong to all the intervals of S, we can be sure that the right hand endpoint of $I_0$ is $\ge b$.

Moreover, for each point $x>b$, we know that there must be some interval $I_x$ in the collection S which does not stretch as far to the right as x. Since, by hypothesis, the intersection $I_0\cap I_x$ is non-empty, the left hand endpoint of $I_0$ lies to the left of every such point x, so $I_0$ must overlap the interval I, whence it follows that $I\cap I_0$ is a non-empty interval as required.

Hence $P(k+1)$ is true.

Hence $P(n)$ is true for all $n\ge 2$.

265. If one experiments a little, it should become clear

• that if tank $T_2$ contains more than tank $T_1$, then linking tank T to $T_2$ leads to a better immediate outcome (i.e. a larger amount in tank T) than linking T to $T_1$;

• that if, at some stage in the linking sequence, tank T contains an interim amount of a litres, and is about to link successively to a tank containing b litres, and then to the tank containing c litres, this ordered pair of changes alters the amount in the tank T to $\frac{a+b+2c}{4}$ litres; so for a better final outcome we should always choose the sequence so that $b<c$;

• once the tap linking tank T to another tank has been opened, so that the two levels become equal, there is no benefit from opening the tap linking these two tanks ever again, so tank T should be linked with each other tank at most once.

These three observations essentially determine the answer – namely that tank T should be joined to the other tanks in increasing order of their initial contents.

For a proof by induction, let $P(n)$ be the statement:

“given n tanks containing $a_1,a_2,a_3,\dots ,a_n$ litres respectively, where

$a_1<a_2<a_3<\dots <a_n,$

if T is the tank containing the smallest amount $a_1$ litres, then the optimal sequence for linking the other $n-1$ tanks to tank T (optimal in the sense that it transfers the maximum amount of water to tank T) is the sequence that links T successively to the other tanks in increasing order of their initial contents”.

• When $n=2$, there is only one possible sequence, which is the one described, so $P(2)$ is true.

• Suppose that $P(k)$ is true for some $k\ge 2$, and consider an unknown collection of $k+1$ tanks containing $a_1,a_2,a_3,\dots ,a_{k+1}$ litres respectively, where

$$a_1<a_2<a_3<\dots <a_{k+1},$$

and where T is the tank which initially contains $a_1$ litres.

Suppose that in the optimal sequence of k successive joins to the other k tanks (that is, that transfers the largest possible amount of water to tank T), the succession of joins is to join T first to tank $T_2$, then to tank $T_3$, and so on up to tank $T_{k+1}$ (where tank $T_m$ is not necessarily the tank containing $a_m$ litres). There are now two possibilities: either

(i) $T_{k+1}$ is the tank containing $a_{k+1}$ litres, or

(ii) $T_{k+1}$ contains less than $a_{k+1}$ litres.

(i) Suppose tank $T_{k+1}$ is the tank containing $a_{k+1}$ litres. Then the first $k-1$ joins involve the k tanks containing $a_1,a_2,a_3,\dots ,a_k$ litres. And we know (by the very first bullet point above) that, in order to maximize the final amount in tank T, the amount in tank T after linking it to tank $T_k$ must be “as large as it could possibly be”. Hence, by $P(k)$, the first $k-1$ joins link T successively to the other tanks in increasing order of their contents – before finally linking to the tank containing $a_{k+1}$ litres. Hence the conclusion of $P(k+1)$ holds.

(ii) Now suppose that tank $T_{k+1}$ contains $a_m<a_{k+1}$ litres.

By the very first bullet point, in order to guarantee the optimal overall outcome of the final linking with tank $T_{k+1}$ the amount in tank T after it has been linked to tank $T_k$ must be “as large as it can possibly be” (given the amounts in the tanks $T,T_2,T_3,\dots ,T_k$). Hence statement $P(k)$ applies to the initial sequence of $k-1$ joins (of T to $T_2$, then to $T_3$, and so on up to $T_k$), and guarantees that these tanks must be in increasing order of their initial contents. In particular, the last tank in this sequence, $T_k$, must be the one containing $a_{k+1}$ litres. But if we denote by a litres the amount in tank T just before it links with tank $T_k$ (containing $a_{k+1}$ litres), then the last two linkings, with $b=a_{k+1}$ and $c=a_m$ contradict the second bullet point at the start of this solution. Hence case (ii) cannot occur.

Hence $P(k+1)$ is true.

Hence $P(n)$ is true for all $n\ge 2$.

266.

Note: Like all practical problems, this one requires an element of initial “modelling” in order to make the situation amenable to mathematical analysis.

`Residue' clings to surfaces; so the total amount of `residue' will depend on

(a) the viscosity of the chemical (how `thick', or `sticky' it is), and

(b) the total surface area of the inside of the flask.

Since we are given no information about quantities, we may fix the amount of residue remaining in the `empty' flask at “1 unit”, and the amount of solvent in the other flask as “s units”.

If we add the solvent, we get a combined amount of $1+s$ units of solution – which we may assume (after suitable shaking) to be homogeneous, with the chemical concentration reduced to “1 part in $1+s$”.

The first modelling challenge arises when we try to make mathematical sense of what remains at each stage after we empty the flask. The internal surface area of the flask, to which any diluted residue may adhere, is fixed. If we make the mistake of thinking of the original chemical as “thick and sticky” and the solvent as “thin”, then the viscosity of the diluted residue will change relative to the original, and will do so in ways that we cannot possibly know. Hence the only reasonable assumption (which may or may not be valid in a particular instance) is to assume that the viscosity of the original chemical is roughly the same as the viscosity of the chemical-solvent mixture. This then suggests that, on emptying the diluted mixture, roughly the same amount (1 unit) of diluted mixture will remain adhering to the walls of the flask. So we will be left with 1 unit of residue, with a concentration of $\frac{1}{1+s}$. In particular, if $s=1$, using all the solvent at once reduces the amount of toxic chemical residue to $\genfrac{}{}{0.1ex}{}{1}{2}$ unit (with the other $\genfrac{}{}{0.1ex}{}{1}{2}$ unit consisting of solvent).

But what if we use only half of the solvent first, empty the flask, and then use the other half? Adding $\frac{s}{2}$ units of solvent (and shaking thoroughly) produces $1+\frac{s}{2}$ units of homogeneous mixture, with a concentration of 1 part per $1+\frac{s}{2}$. When we empty the flask, we expect roughly 1 unit of residue with this concentration – so just $\frac{2}{2+s}$ units of the chemical, with $\frac{s}{2+s}$ units of solvent.

If we then add the other $\frac{s}{2}$ units of solvent, this produces $1+\frac{s}{2}$ units of mixture with a concentration of 1 part per ${\left(1+\frac{s}{2}\right)}^2$. When we empty the flask, we expect roughly 1 unit of residue with concentration 1 part per ${\left(1+\frac{s}{2}\right)}^2$. In particular, if $s=1$, this strategy reduces the amount of toxic chemical in the 1 unit of residue to $\genfrac{}{}{0.1ex}{}{4}{9}$ units. Since $\frac{4}{9}<\frac{1}{2}$ this two-stage strategy seems more effective than the previous “all at once” strategy.

Suppose that we use a four-stage strategy – using first one quarter of the solvent, then another quarter, and so on. We then land up with roughly 1 unit of residue with concentration 1 part per ${\left(1+\frac{s}{4}\right)}^4$. In particular, if $s=1$, we land up with the amount of toxic chemical in the 1 unit of residue equal to $\genfrac{}{}{0.1ex}{}{256}{625}$ units, and $\frac{256}{625}<\frac{4}{9}$. More generally, if we use $\left(\frac{1}{n}\right)$th of the solvent, n times, the final amount of toxic chemical in the 1 unit of residue is equal to ${\left(1+\frac{s}{n}\right)}^{-n}$. And as n gets larger and larger, this expression gets closer and closer to $e^{-s}$. In particular, when $s=1$, this strategy leaves a final amount of chemical in the 1 unit of residue approximately equal to $\frac{1}{e}=0.367879\cdots$.

Note: The situation here is similar to that faced by a washing machine designer, who wishes to remove traces of detergent from items that have been washed, without using unlimited amounts of water. The idea of having a “fixed amount of solvent” corresponds to the goal of “water efficient” rinsing. However, the washing machine cycle, or programme, clearly cannot repeat the rinsing indefinitely (as would be required in the limiting case above).

267.

(i) If $\sqrt{2}=\frac{m}{n}$, then

$$2n^2=m^2$$

Hence m² is even.

It follows that m must be even.

Note: It is a fact that, if $m=2k$ is even, then $m^2=4k^2$ is also even. But this is completely irrelevant here. In order to conclude that “m must be even”, we have to prove:

Claim m cannot be odd.

Proof Suppose m is odd.

$\therefore$ $m=2k+1$ for some integer k.

But then

$$m^2={(2k+1)}^2=4k^2+4k+1$$

would be odd, contrary to “m² must be even”.

Hence m cannot be odd.

(ii) Since m is even, we may write $m=2m^{\prime }$ for some integer $m^{\prime }$. Equation (*) in (i) above then becomes $n^2=2{(m^{\prime })}^2$ , so n² is even. Hence, as in the Note above, n must be even, so we can write $n=2n^{\prime }$ for some integer $n^{\prime }$.

(iii) If $\sqrt{2}=\frac{m}{n}$, then $m=2m^{\prime }$, and $n=2n^{\prime }$ are both even.

$\therefore$ $\sqrt{2}=\frac{m}{n}=\frac{2m^{\prime }}{2n^{\prime }}=\frac{m^{\prime }}{n^{\prime }}$.

In the same way, it follows that $m^{\prime }$ and $n^{\prime }$ are both even, so we may write $m^{\prime }=2m\text{'}\text{'}$, $n^{\prime }=2n\text{'}\text{'}$ for some integers $m\text{'}\text{'}$, $n\text{'}\text{'}$.

Continuing in this way then produces an endless decreasing sequence of positive denominators

$$n>n^{\prime }>n\text{'}\text{'}>\dots >0.$$

contrary to the fact that such a sequence can have length at most $n-1$ (or in fact, at most $1+{\log }_{2}n$).

268.

(i) If $a<b$ and $c>0$, then $ac<bc$.

If $0<\sqrt{2}\le 1$, then (multiplying by $\sqrt{2}$) it follows that $2\le \sqrt{2}\le 1$, which is false. Hence $\sqrt{2}>1$.

We now know that $1<\sqrt{2}$, so multiplying by $\sqrt{2}$ gives $\sqrt{2}<2$. Hence $1<\sqrt{2}<2$. In particular, $\sqrt{2}$ cannot be written as a fraction with denominator 1, so $P(1)$ is true.

(ii) Suppose $P(k)$ is true for some $k\ge 1$. Most of the statement $P(k+1)$ is implied by $P(k)$: all that remains to be proved is that $\sqrt{2}$ cannot be written as a fraction with denominator $n=k+1$.

Suppose $\sqrt{2}=\frac{m}{n}$, where $n=k+1$ and m are positive integers.

Then $m=2m^{\prime }$ and $n=2n^{\prime }$ are both even (as in Problem 267).

So $\sqrt{2}=\frac{m^{\prime }}{n^{\prime }}$ with $n^{\prime }\le k$, contrary to $P(k)$. Hence $P(k+1)$ holds.

$\therefore$ $P(n)$ is true for all $n\ge 1$.

269.

(a) Suppose that S is not empty. Then by the Least Element Principle the set S must contain a least element k: that is, a smallest integer k which is not in the set T. Then $k\ne 1$ (since we are told that T contains the integer 1). Hence $k>1$.

Therefore $k-1$ is a positive integer which is smaller than k. So $k-1$ is not an element of S, and hence must be an element of T. But if $k-1$ is an element of T, then we are told that $(k-1)+1$ must also be a member of T. This contradiction shows that S must be empty, so T contains all positive integers.

(b) Suppose that T does not have a smallest element. Clearly 1 does not belong to the set T (or it would be the smallest element of T). Hence 1 must be an element of the set S.

Now suppose that, for some $k\ge 1$, all positive integers $1,2,3,\dots ,k$ are elements of S, but $k+1$ is not an element of S. Then $k+1$ would be an element of T, and would be the smallest element of T, which is not possible. Hence S has the property that

“whenever $k\ge 1$ is an element of S, we can be sure that $k+1$ is also an element of S.”

The Principle of Mathematical Induction then guarantees that these two observations (that 1 is an element of S, and that whenever k is an element of S, so is $k+1$) imply that S contains all the positive integers, so that the set T must be empty – contrary to assumption.

Hence T must have a smallest element.

270.

(i) Triangle $O{P}^{\prime }{Q}^{\prime }$ is a right angled triangle with $\angle P^{\prime }O{Q}^{\prime }={45}^{°}$. Hence the two base angles (at O and at $Q^{\prime }$) are equal, so the triangle is isosceles: $\underset{\_}{P^{\prime }{Q}^{\prime }}=\underset{\_}{P^{\prime }O}$.

(ii) Triangles $Q{Q}^{\prime }{P}^{\prime }$ and $Q{Q}^{\prime }R$ are congruent by RHS (since they share the hypotenuse $\underset{\_}{Q{Q}^{\prime }}$, and have equal sides ($\underset{\_}{Q{P}^{\prime }}=\underset{\_}{QP}=\underset{\_}{QR}$). Hence $\underset{\_}{Q^{\prime }{P}^{\prime }}=\underset{\_}{Q^{\prime }R}$.

(iii) If $\underset{\_}{OQ}:\underset{\_}{OP}=m:n$, we may choose a unit so that $\underset{\_}{OQ}$ has length m units and $\underset{\_}{OP}$ has length n units. Then

$$\underset{\_}{O{P}^{\prime }}=\underset{\_}{OQ}-\underset{\_}{Q{P}^{\prime }}=\underset{\_}{OQ}-\underset{\_}{QP}=m-n,$$

and

$$\underset{\_}{O{Q}^{\prime }}=\underset{\_}{OR}-\underset{\_}{Q^{\prime }R}=\underset{\_}{OR}-\underset{\_}{Q^{\prime }{P}^{\prime }}=\underset{\_}{OR}-\underset{\_}{O{P}^{\prime }}=n-(m-n).$$

(iv) $\underset{\_}{OP}<\underset{\_}{OQ}<\underset{\_}{OP}+\underset{\_}{PQ}$, so $n<m<n+n$. Hence $0<m-n<n$, and $0<2n-m$.

(v) In the square $O{P}^{\prime }{Q}^{\prime }{R}^{\prime }$, the ratio “diagonal: side” $=\underset{\_}{O{Q}^{\prime }}:\underset{\_}{O{P}^{\prime }}=\sqrt{2}:1$. If the ratio $\underset{\_}{OQ}:\underset{\_}{OP}=m:n$, with m, n positive integers, then the construction here replaces the positive integers m, n by smaller positive integers $2n-m$ and $m-n$, with $m-n<n$. And the process can be repeated indefinitely to generate an endless sequence of decreasing positive integers

$$n>m-n>(2n-m)-(m-n)=3n-2m>\dots >0.$$

Zarathustra's last, most vital lesson: “Now do without me.”

George Steiner (1929-)