4. Values and Prices

After part 1, in which Marx develops a philosophy of “labour value”, he uses this notion as a measure of surplus value and the rate of exploitation throughout the remainder of Capital, volume 1. Abstract labour is the substance of value, according to the labour theory of value. However, the expression “abstract labour” almost disappears outside part 1 or, rather, it appears mainly in the notion of “labour time”, as it must when the labour hour is used as a unit of measurement.1 The real scientific problem addressed by Marx in Capital is bringing to light the social relations of production through which surplus value is extracted. The theory of value serves to provide a measurement tool capable of highlighting those relations, and Marx believes that embodied labour has this property.

In section 1 of the present chapter, I illustrate the labour theory of value in the simplest way possible.2 I describe an economy in which perfect competition and constant returns to scale prevail, and in which there are no scarce resources, no fixed capital, no joint production, no luxury goods, no complex labour and no growth. These simplifying hypotheses are assumed not just to make the text accessible to a broad readership, but also because my goal is to disclose the basic limitation of the labour theory of value. If this limitation is evident in the simplest model, there is no need to complicate the analysis. I argue that, since labour values are determined in a model of “commodity production in general”, they only express the technical conditions of production. This is true even if surplus value and the value of labour power are introduced into the equations that determine labour values. In fact, changes in the distribution of value added between wages and profits do not have any consequence on the value of commodities, as long as the latter is determined by the amount of labour contained in them.

In section 2, I elucidate the determination of production prices, and argue that they provide a correct expression of the technical and social conditions of production. Moreover, they provide a transparent account of exploitation when they are reduced to quantities of labour commanded. I then propose a comparison between the labour embodied in and the labour commanded by a commodity, and show that the latter expresses any change in the degree of exploitation in a way the former is unable to.

In section 3, I tackle the transformation problem: given a double system approach, with a labour value system and a production price system, is it possible to transform the former into the latter whilst keeping the profit and exploitation rates invariant? I show that, even when some aggregate invariance postulates are validated with opportune normalization, the basic problem remains unsolved, i.e. the inability of labour values to correctly express the social relations of production in a capitalist economy. In fact, no reasonable normalization can achieve the invariance of the rate of exploitation and the rate of profit.3

4.1. Labour Values

A use value, or useful article, […] has value only because human labour in the abstract has been embodied or materialized in it. How, then, is the magnitude of this value to be measured? Plainly, by the quantity of the value-creating substance, the labour, contained in the article (Marx 1996, 48).

Not only living labour, living labour employed during the current year, enters into the exchangeable value of the total annual product, but also past labour, product of the labour of past years. Not only labour in living form, but labour in objectified form. The exchangeable value of the product = the total labour time which it contains, a part of which consists of living labour and a part of objectified labour (Marx 1989a, 153).

In other words:

v = l + v A(1)

where v is the labour value of the “useful article”, l the quantity of living labour contained in it, A the quantity of means of production used to produce it, and vA the labour objectified in it. The solution of equation (1) is:

v = l(I − A)−1 = l(I + A +  … At + …)(2)

Now value has been decomposed into quantities of labour used directly, l, and indirectly, l(A + … At + …). The two equations may refer to an economy that produces a single good, in which case all symbols represent scalars and I=1. They can also be interpreted as referring to an economy producing n commodities. Just define v as a vector of labour values, I as the identity matrix, l as a vector of labour coefficients and A as an indecomposable and productive matrix of technical coefficients.

Equation (1) applies to a system of “production in general”, or “simple commodity production”. There are no profits and no wages. The producers earn the entire value added they produce. Moreover, this economy is in a state of reproduction equilibrium,4 i.e. markets clear and market prices coincide with the exchange values determined by the structure of production.

Marx uses labour values to measure exploitation. He often provides examples based on a single commodity, and defines value both in terms of embodied labour and in terms of Pounds, for instance: £590=£410+£90+£90=C+V+S, where the commodity value has been decomposed into constant capital, variable capital and surplus value. He then defines the rate of exploitation as £90/£90=(surplus labour)/(necessary labour) (1996, 221). He is convinced that money valuation is not a problem because, at least in his most abstract theorizations, he maintains that money is a real commodity (gold), so its value is determined by its labour content (Mohun and Veneziani 2017, 8). Nor does he consider problematic the fact that his examples refer to a single commodity rather than an array of them. At the highest level of abstraction, he assumes that all commodities exchange at money prices that are proportional to labour values. What is strange is that he measures exploitation in a capitalist economy using values prevailing in a non-capitalist economy.

Equation (1) can be converted into the following: C+V+S=vAq+wvL+(1–wv)L=vq, where q is a vector of gross outputs, L=lq is the labour force employed, or aggregate living labour, and wv is the unit value of labour power, or the labour embodied in a worker’s consumption. Notice that, since V+S=wvL+(1–wv)L=L, the distribution of output between the capitalists and the workers does not affect value determination. Moreover, the relation between surplus value and necessary labour is linear, S=(1–wv)L. Marx reasons precisely in this way, even in microeconomic analysis. When, in a working day of 12 hours, necessary labour is reduced from 6 to 5 hours, surplus value rises from 6 to 7.

One may ask: how can abstract labour be “embodied or materialised” in the value of a commodity? As I observed in chapter 1, some metaphors used by Marx convey the idea that abstract labour is the flow of a natural substance that “congeals” or “crystallises” into a value form. These metaphors seem to justify an interpretation according to which abstract labour consists of a productive activity entailing an expenditure of human energy. So, what is “materialised” in the value of a commodity seems to be the energy used in its production, or something akin to that.

However, such an interpretation is pointless, as “the value of commodities is the very opposite of the coarse materiality of their substance […] the value of commodities has a purely social reality” (Marx 1996, 57). Thus, what gives rise to value is a social substance. And this might be true in two different senses.

First, the market process brings about a “law of value” that determines the exchange values prevailing in a reproduction equilibrium. The value relations among commodities are the fetishistic appearances of the social relations among their producers. Since such relations consist of the efficient employment of certain quantities of labour time, value could be considered an expression of the labour costs incurred in production. This makes sense. If “commodity production in general” is considered, as in equations (1) and (2), the higher-valued commodities are those whose production has required, directly and indirectly, the expenditure of a higher quantity of labour time.

The second sense in which value may be considered a social substance emerges as soon as we consider a capitalist economy. In this case, the social relations reflected in the value of commodities are those involving the social classes who participate in production, workers and capitalists. Value could still be considered an expression of direct and indirect labour costs. Since they pertain to a capitalist economy, the former are calculated as wage costs, the latter are reckoned by taking into account a capitalization factor. Therefore, this second sense in which value is the expression of a social substance cannot be represented by equations (1) and (2), where no wages and no capitalization appear.

4.2. Production Prices

It is competition of capitals in different spheres, which first brings out the price of production equalizing the rates of profit (Marx 1998, 179).

The fundamental law of capitalist competition […], the law which regulates the general rate of profit and the so-called prices of production determined by it, rests, as we shall later see, on this difference between the value and the cost price of commodities (42).

In volumes 1 and 2 of Capital, Marx is already well aware that in a reproduction equilibrium, commodities exchange at production prices which differ from labour values, but only in volume 3 does he try to clarify this problem.

Whilst labour values have a natural standard, the labour hour, production prices depend on an arbitrary choice of numeraire. Therefore, to make them comparable to labour values, it might be useful to normalise them with the price of labour time. This is the approach I shall take in some of the following equations. In this way, production prices are expressed as labour commanded, a measure proposed by Adam Smith. Marx appreciates Smith’s notion of “labour commanded”, but he does not fully grasp his motivation for preferring it to embodied labour as a measure of value (Marx 1989a, 153), i.e. that value determination based on embodied labour is only valid in a non-capitalist economy. In fact, he also appreciates Ricardo’s rejection of the notion of labour commanded.5

The prices of production, p, are determined as

p = l + (1 + r) pA(3)

where r is the rate of profit. Prices are expressed in labour commanded by posing the nominal wage wp=1. The technical structure of production is the same as that in the economy represented by equation (1).

Equation (3) implies that wages are paid post factum, i.e. at the end of the working day or week or month. Marx is very clear about the fact that ‘the labourer is not paid until after he has expended his labour power’ (1996, 567), although, to comply with “the jargon of political economy”, he “provisionally” adopts a formula, r=S/(C+V), implying an advanced payment of wages.6

The solution of equation (3) is

p = l(I − (1 + r) A)−1 = l(I + (1 + r) A + … (1 + r)t At + …)(4)

Exchange values have been decomposed into direct labour inputs, l, and indirect labour inputs, l((1+r)A+…(1+r)tAt+…). The former are the current wage costs, the latter are the capitalised wage costs incurred in past investments.

It is evident that there are differences between production prices and labour values. Marx knows that, but does not understand the fundamental reason why this is so. He believes that the rate of surplus value is uniform in the labour value system and that the value/price differences arise because the profit rate is uniform in the production price system.

Now, assume the above equations refer to a one-commodity model. Thus, there is no problem of profit rate uniformity. Yet equations (2) and (4) reveal that, with 0<r<rmax, it holds p(r)>v. As shown in figure 1, the labour commanded by one unit of commodity is greater than the labour embodied in it, and the higher the profit rate. Labour commanded is a correct expression of value in an economy in which capitalists exploit wageworkers, since it rises when exploitation rises. Instead, given the technique, the embodied labour does not change when the profit rate changes because it does not depend on the distribution of value added. In other words, a price-value divergence arises whenever production is production for profits, i.e. capitalist production. The fundamental reason why labour values and production prices are different is not so much because the profit rate is uniform, but rather because it exists.

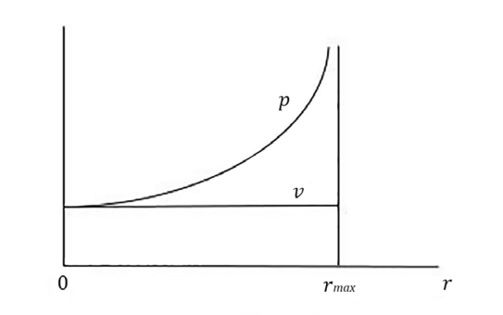
Figure 1

Let us now interpret (1)-(4) as matrix equations. They represent an economy made up of n industries and n goods. It remains true that, with 0<r<rmax, it holds p(r)>v.7 In any case, whatever the numeraire, p(r)≠v holds generically.8 The question arises: which of the two is a significant theory of value, i.e. a theory that expresses the social relations of production in a capitalist economy? The answer is immediate: only prices yield a correct valuation, for they change when the social relations of exploitation change.

Among all the possible price vectors, those normalised as labour commanded have a peculiar property: they are increasing functions of r even in the n-commodity case.9 They are a transparent measure of value–transparent with respect to social relations–as the labours commanded by all commodities rise with exploitation, given the technique.

The rate of exploitation, measured in labour commanded, ec, is:

$e_c=\frac{p\left(I-A\right)q-L}{L}=\frac{l{\left(I-\left(1+r\right)A\right)}^{-1}\left(I-A\right)q-L}{L}=\frac{L^{*}}{L}$ (5)

where L*=p(I–A)q–L is the quantity of labour that can be bought by surplus value.

Equation (5) measures the rate of exploitation as a ratio between two quantities of labour: that commanded by surplus value, and that commanded by the wage. Capitalists have bought power over L workers, then they have exerted power over them in the production process so as to make them produce a surplus value, which may buy power over a further amount of labour, L*. Given the magnitude of living labour, the higher the rate of exploitation, the greater is L*.

Rather interesting is the factor of exploitation, 1+ec=(L+L*)/L, which is equal to the inverse of the wage share in net output. It is a ratio between the labour commanded by the net output and that used to produce it (Screpanti, 2003). In the presence of exploitation, this factor is greater than 1 as “the value of the total product can […] buy more living labour than is contained in it” (Marx 1997, 153).

4.3. The Transformation Problem

As already observed, Marx knows very well that relative prices are different from relative labour values. Yet he maintains there is no problem in the aggregate. He thinks that abstract labour is the substance of value, whilst production prices only express the surface appearance of market exchanges in reproduction equilibrium, and the appearance should not alter the substance.

He seems to believe in a sort of a law of value conservation. He is confident that exchanges at production prices only redistribute value and surplus value among the different industries without altering their overall amount. He postulates that the aggregate value of capital and surplus value are not modified by exchanges at production prices: “The sum total of [the] cost prices of all the commodities taken together will be equal to their value [and] the total profit will be = to the total surplus value” (1989a, 415). Thus, the general rate of profit is assumed not to change when labour values are transformed into production prices. Aggregate variable capital is also supposed to be invariant (Marx 1998, 160), and this implies that not even the general rate of exploitation should change.

The aggregate invariance assumptions are expressed in various ways in different parts of Capital. In volume 2, they take an even stronger form. In that volume, Marx presents a two-sector model and investigates reproduction conditions in terms of the ability of the industrial system to produce the capital and consumption commodities demanded by the system itself. To define the demands and supplies of the various sectors, Marx uses both labour values and monetary prices, convinced that “the fact that prices diverge from values cannot, however, exert any influence on the movement of the social capital. On the whole, there is the same exchange of the same quantities of products, although the individual capitalists are involved in value relations no longer proportional to their respective advances and to the quantities of surplus value produced singly by every one of them” (1997, 392). When defining reproduction conditions, Marx assumes the equality of aggregate labour values and production prices, not only for the whole economy, but also for the sectorial components.10

Awkwardly, the aggregate invariance postulates do not hold true in the way Marx supposes, as I shall show. And this is a decisive limitation. In fact, only if the law of value conservation were correct would it be possible to use the general rates of profit and exploitation, as determined in the labour value system, even when dealing with the price system.

Now, let ev and ep represent the rates of exploitation in labour values and production prices respectively; rv and rp the rates of profit in labour values and production prices respectively; p̂ the price vector with a new normalization; wv and wp the unit value of labour power and the wage. And consider the following:

a) Fundamental invariance postulates

1. ev = ep

2. rv = rp

b) Subordinate invariance postulates

1. v(I − A)q = p̂(I − A)q

2. wvL = wpL

3. vAq = p̂Aq

Other invariance postulates can be deduced from these three. The invariance of gross output results from (b.1) and (b.3). The invariance of surplus value, from (b.1) and (b.2). I consider them subordinate in that they are expedient to ensuring postulates (a.1) and (a.2). These are the fundamental ones because they define the conditions that make ev a correct measure of exploitation and rv a correct measure of profitability, in other words, the conditions that justify Marx’s practice of using ev and rv when dealing with the price system.

The transformation problem11 boils down to finding a diagonal matrix D such as vD=p̂. In general, prices are determined up to a proportionality factor. Therefore, there are many D, one for each possible numeraire, and the standard can be chosen to obtain one of the subordinate invariance postulates.

The labour value system is made up of n equations with n unknowns. Once labour values have been determined, it is sufficient to fix a bundle of wage goods, g, to determine variable capital, V=wvL=vgL, and the surplus value, S=L–vgL. There are no degrees of freedom, because labour values are determined without knowing the distributive variables. The case of the price system, in which prices depend on labour costs and the rate of profit, is different. Since social and political forces exogenously determine either wp or rp, the system is made up of n equations with n+1 unknown. There is one degree of freedom, and the possibility of introducing a normalization equation to validate one subordinate invariance postulate, but only one (Mohun and Veneziani 2017, 15).12

Validation of a subordinate invariance postulate does not imply validation of the fundamental ones. The rates of exploitation in the two systems are:

$e_v=\frac{v\left(I-A\right)q-w_{v}L}{w_{v}L}$ (6)

$e_p=\frac{\hat{p}\left(I-A\right)q-w_{p}L}{w_{p}L}$ (7)

The rates of profits are:

$r_v=\frac{v\left(I-A\right)q-w_{v}L}{v\mathrm{Aq}}$ (8)

$r_p=\frac{\hat{p}\left(I-A\right)q-w_{p}L}{\hat{p}Aq}$ (9)

It is easy to see that ev = ep and rv = rp if and only if (b.1), (b.2) and (b.3) hold, which is not the case.

Summing up, if value is a social relation, as claimed by Marx, then production prices are meaningful measures of value. This is because they convey information about both the technical and the distribution conditions of production, and change when exploitation changes. Labour values, instead, respond only to changes in technical conditions. This is the reason why the rate of exploitation and the profit rate are not invariant in the transformation procedure. Now, equation 5 shows that the actual rate of profit, rp, is associated with the actual rate of exploitation, ep, not with ev. Thus, the latter is an improper measure of exploitation.

---