7 Picture and sound
© Stephen Robertson, CC BY 4.0 https://doi.org/10.11647/OBP.0225.07
For this chapter and the following two, we leave aside for the moment the world of writing and characters, alphabets and numerical digits, to consider pictures and sound.
As we saw in Chapter 1, pictures played an early role in the development of writing systems. However, at that point the paths split apart. When it comes to recording information in a form other than conventional language, such as diagrams or images or pictures, moving images, and sound, we have (broadly speaking) bypassed the language-writing-alphabet-digital code sequence. But pictures, in particular, have their own sequence that leads from the development of photography in the first half of the nineteenth century, to the almost universal digitisation of everything today.
Most people today are aware that pictures are usually made up of dots (pixels), in a rectangular array—cameras are typically sold on the number of pixels they have. If you look through a magnifying glass at a picture printed in a magazine, you can see the pixels. Below, I will describe the sequence of development from the first photographs to today’s pixel-based images. However, first it is worth exploring a couple of byways of image-making.
Art
A very early art form, visible for example in the cities of Pompeii and Herculaneum, which were buried in volcanic ash in the first century CE, uses the method of mosaic. In mosaic, a picture is built up out of small tiles; each tile is a single colour. The subtlety that can be expressed by such means is astonishing. However, there is a significant difference between the layout of a mosaic and the modern notion of digitised images. In the modern version, the picture is built on a rectangular grid—the colour at each intersection of the grid is recorded. In mosaic, typically the tiles (even if they are often square individually) are usually laid following the shape of the design, so that a curved boundary in the picture is usually made of two curved lines of tiles (see for example Figure 3).

Very much later, in the late nineteenth century, a small group of artists (Georges Seurat and others) developed a technique of painting relying on small dots of colour. Rather than creating a particular desired colour by mixing a small number of basic or primary colours on a palette, they would use the same basic colours individually, close to each other in small dots, so that to the eye they would appear to mix into the desired colour. The method was known as pointillism. One of its effects is supposed to be to brighten the colour sense of the viewer (see Figure 4).

Weaving
A simple form of weaving involves a set of parallel warp threads stretched over a frame, a mechanism to lift alternate threads away from the others, and a shuttle to pass the weft thread from one side to the other, in between the lifted warp threads and those left flat. Before the next pass, the lifted threads are returned to level and the remaining threads lifted instead.
If you want to weave a coloured pattern of any kind, the warp and/or weft threads can be of different colours. But to weave a complex pattern, even a picture, requires more complex control. One way to do this is as follows. The weft thread is a single neutral colour, but the warp threads are set as a sequence of colours, as it might be yellow / green / red / blue, repeated over the width of the fabric. Then the colour of a particular location in the woven fabric, on the front or top face, is determined by which warp threads have been lifted (and are visible) and which have been left flat. As in pointillist painting, if the threads are close enough together, the eye perceives the mixture of the selected basic colours as a new colour.
A method like this gave rise to a fascinating invention at the start of the nineteenth century, due to Joseph-Marie Jacquard. He devised a system for controlling a loom, using a sequence of punched pasteboard cards, one for each pass of the shuttle. The positions of the punched holes in each card controlled which of the warp threads were to be lifted for the next pass. A sequence of cards could be punched, potentially of any degree of complexity, to produce a complex design in the fabric. The cards with punched holes can be seen now as a digitised representation of the finished design (see Figure 5).

Each punched card determines the pattern of lifted warp threads for a single pass of the shuttle.
Jacquard’s loom was a major development in weaving technology. Predating photography, it continued in use for almost two centuries, in parallel with but independently of the developments in photographic imaging described below. Today’s computer-controlled looms are direct descendants of Jacquard’s invention, but finally now integrated into the rest of the digital world. However, Jacquard’s use of punched cards was to inspire two quite different developments, as we shall see in later chapters. James Essinger, in Jacquard’s Web, argues convincingly for Jacquard’s seminal position in the development of information technologies.
Photography
The idea of photography, using light-sensitive chemicals, was developed in the first half of the nineteenth century. The best-known name from that time, Louis Daguerre, invented a form of photograph called the daguerreotype in 1839, but a much more successful and long-lived method was the calotype of William Henry Fox Talbot (1841). This was the forerunner of the negative process that was the norm for photography right up until the development of the digital camera at the end of the twentieth century.
As an aside, Talbot’s name is a great example of the kind of issue with names that I discussed in the previous chapter. He is usually referred to as ‘Fox Talbot’, on the assumption that this was a double-barrelled but unhyphenated surname—he was referred to thus even in his lifetime. Actually, he did not regard Fox, a family name of his mother’s, as part of his surname. In addition, he normally used the ‘first’ name Henry, not William.
Photography in this form can be described an analogue process. We make a distinction between analogue and digital: in an analogue representation of something, a continuous or smooth variable in the outside world is represented by a continuous or smooth variable in the system. In the case of chemically-based photography, light causes a chemical change on the plate—more light causes more change, in a more-or-less smoothly varying way.
At this point, someone familiar with traditional chemical photography might well object ‘What about grain and graininess?’. It’s true that at a fine level, the chemical process is not smooth. But this is not a matter of design: it’s rather an accident of the process. It’s when we start designing in granularity that we call something ‘digital’.
When we deliberately slice up the world, or some smoothly varying part of the world, into discrete parts, in order to measure or represent or process it, we are beginning the process of digitisation. As we will see below, some processes are mixed, in that they include some continous elements that have been divided into discrete parts and some that have not—this is particularly so in the development from simple monochrome chemical photography to today’s digital images.
However, in order to make this process a little clearer, we start with a simpler example: sound.
Sound
As with so many things, digitised sound predates the computer era, though not by very much. The standard form of digitised sound, pulse code modulation, was invented by Alec Reeves in 1937 and is still in use today.
Sound is waves of pressure moving through the air or other medium. A pure musical note is a simple sinusoidal wave of fixed frequency (middle C is about 260 Hertz, or cycles per second); all other sounds are more complex patterns of pressure change. One can draw a graph of how pressure varies over time—it looks like an undulating line (see Figure 6). A microphone (invented in the nineteenth century) turns the pressure waves into electrical waves, in an analogue fashion, so that the pattern of varying electrical current looks like the pattern of varying pressure in the air.
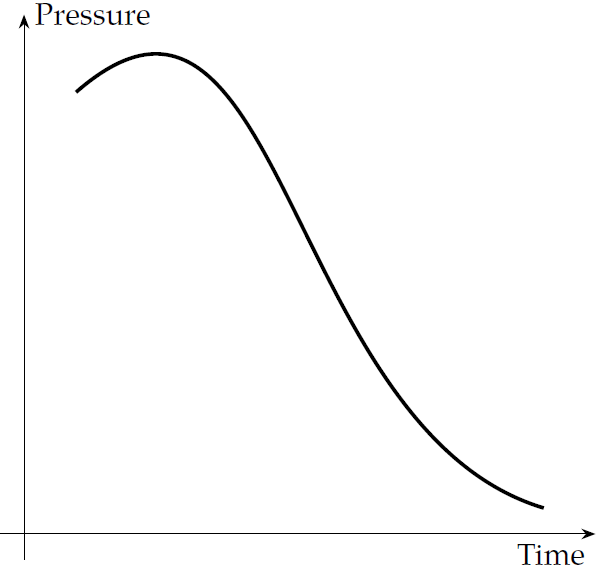
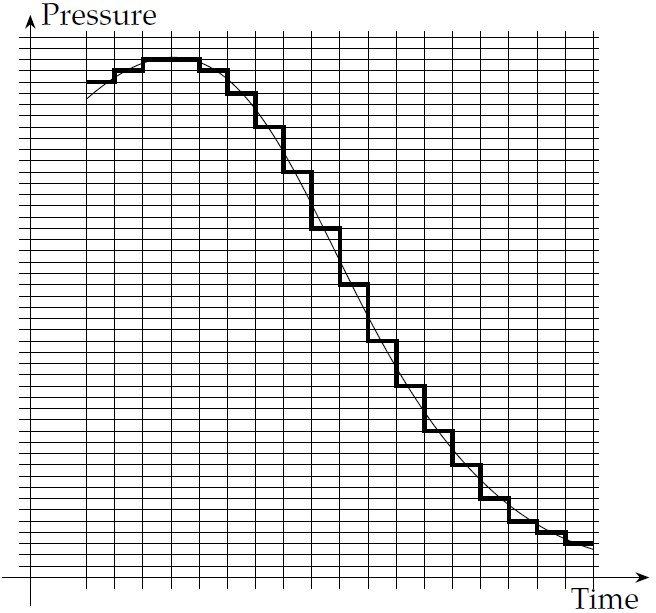
Fig. 6. Sound. Diagram: the author.
In order to digitise a continuous curve like this, we need to make two separate quantities, which are naturally continuous, into discrete lumps. The two quantities are time and pressure. So first we divide up time: we choose discrete time intervals—in the case of CD audio, 44,000 times a second. Then we measure and discretise the pressure at each of those times. Again, in CD audio, the discrete pressure levels are defined with 16 bits—that is, there are (which is about 65,000) pressure ranges. The result is a representation that can be thought of as turning the smooth pressure curve into a stepped line, with very tiny steps—again, the diagram shows a rough picture. On playback, the player has to recreate (to a close approximation) the smooth curve from this digitised step curve.
This is pulse-code modulation, and is all we need to digitise a single sound channel. For stereo sound (again as on CDs), we need two separate channels like this (more on stereo sound in the next chapter). The invention of the CD as a digital recording medium in the late 1970s allowed the recorded music industry to make a relatively smooth transition into the digital era—though the relationship between music more generally and the digital world is more complex than this, as discussed further in Chapter 9.
Now let us turn back to photography and its developments.
Moving images
A photograph shows a static image, a snapshot in time. How do we turn this into a moving image?
Probably you already know the answer to this question—and in any case, it is very like part of what I described above for sound. Although time is, in principle, a continuous variable, we can treat it as discrete by taking very small steps in time, and at each of these time steps, we take a photograph. Actually the steps do not need to be nearly as small as for sound—film typically works at just 24 frames a second. If you see an image changing in small steps 24 times a second, it looks pretty much as if it is moving smoothly. Mostly, you probably aren’t aware of the step-changes.
This principle, on which film is based, was understood in Victorian times—in museums you will sometimes see Victorian toys using the same idea, for example a spinning drum with slits. If you look at it from the side, each slit gives you a momentary view of a drawing; the next, which appears a moment later, is like its predecessor but with small changes. The impression is of movement. Actually making a film camera was somewhat tricky, but in the 1870s Eadweard Muybridge demonstrated the idea with a series of photographs of a galloping horse. The photographs were taken by separate still cameras, on the side of the course, but the effect is of a single film camera tracking the horse. Muybridge developed a device to show the moving image, the Zoopraxiscope, very like the toy described above.
The first patent for a cine camera was due to Louis Le Prince in 1888, and the process became practical in the 1890s. Notice that it is only the time variable that we are treating discretely. Ordinary old-fashioned celluloid film retains the ordinary analogue process for each individual frame.
Colour
In parallel with the challenge of recording moving images, Victorian inventors concerned themselves with that of developing colour photography.
The basic principle is based on the idea of primary colours. This idea had been around from at least the seventeenth century, and a specific theory concerning human perception was put forward by Thomas Young in 1802, further developed by Hermann von Helmholtz in 1850, and proposed for photography by the physicist James Clerk Maxwell in 1855. The idea was that any colours can be made up from a small number, probably three, of primary colours. The artists’ primaries are normally taken to be red, yellow and blue. Actually the idea of primary colours is somewhat complex and messy; I will return to it below. But if we assume in the meantime that the idea is good, then we have in principle a natural way to build a colour photograph—take three separate photographs, with red, yellow and blue filters, and then print the three resulting images, in red yellow and blue, superimposed. In terms of the ideas discussed above, the full continuous colour spectrum can be reduced to just three discrete components.
But once again, actually doing this is a little tricky. Maxwell’s attempt in 1861 was not very successful: the idea had to wait until the 1890s to be developed into an even remotely practical form, and till 1907 for a truly commercial process. In the Autochrome system introduced by the Lumière brothers in 1907, the photographic plate included an integral screen of small dyed potato starch grains, distributed irregularly, but small enough that the eye would not distinguish individual grains. The area of plate under a coloured grain would respond to that coloured light, and not to the colours that had been filtered out. When developed (including a reversal process to get back from a negative to a positive image), each area of the image would be seen through the correct coloured filter, the same that it had been exposed through. Despite a number of disadvantages, this was a successful system that lasted until the 1950s.
In the 1930s, two successful classical musicians working for Kodak developed a process (Kodachrome) with different light-sensitive emulsions, responding to red, green and blue light respectively, all on the same plate. This became essentially the dominant system of colour photography (both still photography and cine film) until digital took over.
Other Victorian ideas
Another idea that emerged in Victorian times was that of 3D images. Here the basic principle predates photography: Charles Wheatstone demonstrated a stereoscope in 1838. It was a device that presented each eye with a picture (he used drawings), the two pictures being slightly different, in a way which caused the viewer to merge the two into a three-dimensional scene. Although some of our depth perception comes in other ways, an important component comes from our binocular vision, and Wheatstone’s device both relies on and demonstrates this fact.
Almost as soon as it was possible to do so, various systems using two cameras were developed, allowing the viewer to see commercially-prepared still 3D photographic images of places and scenes. There are several different methods of causing the images presented to the two eyes to differ, but the principle is the same, right up to and including modern 3D film and television.
Another concern was to be able to print photographs in newspapers. Newspaper ink is either on or off—it is not possible to print shades of grey directly in the newspaper printing process. Newspapers of the time sometimes used etchings, which could be prepared with a lot of effort, and could represent greys by hatching and other devices; but to produce an etching from a photograph (essentially an artist’s copy of the photograph) was not ideal. Already in the 1850s, Talbot had an idea for how to produce a printing plate directly from a photograph, although once again it took a little while to be made practical. The idea is to reduce the picture to a grid of black dots, varying in size. In areas of the picture where the dots are small, the eye sees mostly the white paper; in those areas where the dots are large, the eye sees dark grey. The first printed halftone pictures appeared in the 1870s, and in the 80s commercially successful methods were developed. Similar methods are still in use, including for printing colour pictures.
Facsimile transmission
We have seen how. for some purposes to do with images, we need to discretise some smoothly varying part of the image. We have already discretised both time (for cine film) and the colour spectrum (for colour images); now we need to turn our attention to other smoothnesses.
A (two-dimensional) picture or image has... well, two dimensions. If you are at all familiar with graphs, then you might think of them as the and dimensions. is the left-right component, and is the up-down component. Thinking for the moment only of monochrome still images, over each of these dimensions, the picture may vary anywhere between black and white, that is it may take any shade of grey. This (brightness) represents a third smooth variable to add to the two dimensions.
If you want to transmit anything over a telephone line or a radio channel, you have essentially only two smooth variables to play with: the level of the signal, and time. For (single channel) sound, this is all you need: as we saw above, a microphone turns time and air pressure variation into time and electrical current variation, which can be transmitted over a telephone wire or over a radio channel. But for pictures, we have a third variable. It follows that we must do something different with one of them.
Once again, the Victorians identified the challenge—the first serious experiments in fax transmission were by a Scotsman, Alexander Bain, in the 1840s (that is, well before the invention of the telephone!). His basic idea, which remained the dominant method right up to modern fax machines, was to scan the original, in a line from side to side, and then move down a small distance and scan a new line very close to the previous one. The whole image would be covered by a succession of lines.
Bain’s originals had to be specially prepared for this purpose, and would only deal in black-and-white. It would take quite a few more years, to the 1880s, before one could scan an existing photograph, in shades of grey, and longer still for any kind of commercial fax transmission. Nevertheless, there were successful commercial systems in the 1920s.
We now see that what Bain did was to discretise the dimension, leaving the dimension to be represented in analogue by time, and the brightness in analogue by the level of the signal.
Television
So the next thing to invent is the transmission (along wires or over radio) of moving pictures. But we already have the ingredients for this: if we discretise both the dimension and the time dimension of the moving image, we are left with just two dimensions needing analogue representation.
The process of line-by-line scanning for moving images has a name—raster scan. (For some reason this word is not usually used in the fax context, though the principle is exactly the same.) In an old-fashioned television tube, the cathode ray beam that causes the phosphor on the screen to glow follows the same raster process to regenerate the image.
The idea of using such a method for television transmission is also Victorian. An electromechanical method of raster scanning was patented (but not actually developed) in the 1880s. Again, development of commercial systems (as opposed to demonstrations) took a little longer; the name most closely associated with the invention of television is John Logie Baird, in the 1920s and 30s. The BBC made its first television transmission in 1929, and began regular transmissions in 1932. Initially the raster scan was based on electromechanical processes, and used 30 lines per image, building up to 240 lines in 1936. But electronic methods were already in the air, and in the same year the BBC switched to a 405-line electronic system. This was replaced in the 1960s by a 625-line version.
How about colour television? Again, we already know in principle how to do it—we need three colour components, so each frame has to be transmitted three times, once for each colour. Various schemes were devised to do this, but commercial systems started in the 1950s.
There is an interesting problem at the display end. We now have a cathode ray tube with three separate cathode ray guns constructing a raster pattern on the screen, which now has to have three different coloured phosphors. How to ensure that the right ray hits only the right phosphor? The usual way to do this is to have the phosphor in closely packed dots, and a metal filter screen just behind it, with a pattern of holes. These are aligned so that the ray corresponding to red can only reach the display screen where there are red phosphor dots, and so on. We can think of this as a sort of last-minute discretisation of the dimension.
Full digitisation
Now, of course, almost all of our sound (recorded and/or transmitted), and almost all of our still and moving images (ditto), are fully digitised. Digital cameras, both still and moving, contain grids of tiny photo-receptors, which record light intensity digitally in three colours. Display and printing devices turn pixel-based data back into visible images. In between, all sorts of processing can take place, entirely in the digital domain. Telephones, radio, and recorded sound are similarly treated. Your mobile phone digitises the sound itself, and received digital sound from the other end. Your landline probably doesn’t yet—it sends an analogue signal to the exchange, where it is probably digitised, and receives an analogue signal back.
If you go back in your time machine to the 1840s, to fetch Talbot and bring him forward in time, stop first in the 1980s. At this point he would be totally astonished by many things, including miniaturisation and mechanisation, although if you showed him the machine at your local pharmacy which was used to develop and print your photos, he would be able to get some grasp of the chemical and optical processes involved. But if you bring him here to the third decade of the twenty-first century, he would recognise nothing whatever of any part of the process, at any stage between the camera lens and the display on your screen.
