Achilles and Ajax playing a board game overseen by Athena (c. 510 BCE). Photograph by Aisha Abdel (2018), Wikimedia, Public Domain, https://commons.wikimedia.org/wiki/Category:Black-figure_pottery#/media/File:Attic_Black-Figure_Neck_Amphora_-_Achilles_and_Ajax_playing_a_board_game_overseen_by_Athena.jpg

10. Metaphors to Think by: The Sun and Divided Line Analogies, Book VI

The analogies we looked at in the last chapter are interesting, but they are merely appetizers to the metaphorical feast Socrates soon serves, which features the Sun, Line, and Cave analogies (the last of which we will cover in the next chapter). It is philosophical fare of the highest order, since the topic is ‘the most important subject’ which is ‘even more important than justice and the other virtues’ (6.504d)—the Form of goodness itself: ‘the form of the good is the most important thing to learn about [… since] it is by their relation to it that just things and the others become useful and beneficial […] [but] we have no adequate knowledge of it’ (6.505a).

The Greek rendered by ‘the form of the good’ is ἡ τοῦ ἀγαθοῦ ἰδέα (hê tou agatou idea)—literally, the idea of the good. As noted earlier, for Plato an ἰδέα is not an idea in our ordinary sense but rather something that is not only mind-independently real but is actually more real than the many particular instances of it. The metaphysical elevator goes all the way up to Level Four, though here Plato implies that there is yet another floor, where a very special Form, the Form of the good, resides.

To get a sense of the importance of the Form of the good, consider first the distinctive virtue of the philosopher-rulers, political wisdom. Political wisdom is knowledge of what is best for the city, but one cannot know what is superlatively good for the city without understanding what goodness itself is: ‘I do not suppose that just and fine things will have acquired much of a guardian in someone who does not even know in what way they are good. And I divine that no one will have adequate knowledge of them until he knows this’ (6.506a).

Although one can believe that something is good without grasping why it is, one cannot know that something is good without knowing why that thing is good—and one cannot know this, Socrates thinks, without knowing what goodness itself is. A ruler who does not understand what goodness itself is will at best have true beliefs about what is good for the city, but that falls far short of the knowledge required for genuine wisdom.

So what is the Form of the good, goodness itself?

What the Good Is Not (6.505a-d)

Socrates does not claim to know what the good is, but he does think he knows what it is not. Narrowing the field by excluding unworkable options is a kind of intellectual progress, and so he begins with two untenable accounts of the nature of the good. The first view, held by ‘the majority’ is the view that ‘pleasure is the good’ (6.505b). This is hedonism, the view that pleasure is the only thing that is good in itself. Any other thing that is good is good extrinsically, by being a means to the one intrinsically good thing, pleasure. Although they often run in the same harness, hedonism is distinct from egoism, the view that one’s interests count for more than the interests of others (perhaps because others’ interests do not count at all). Classical utilitarians such as Jeremy Bentham and John Stuart Mill were hedonists but not egoists. They regarded total net pleasure, the result of subtracting the pain an action produces from the pleasure it produces, as the standard of right action, where the interests of all parties affected by the action are given equal weight.

Socrates immediately locates a problem for hedonism: ‘there are bad pleasures’ (6.505c), which even hedonism’s advocates will concede. Although he does not give any examples, they are not hard to come by. Imagine a peeping Tom who is very careful not to be seen; he derives a great deal of pleasure from spying on his neighbors through his high-powered (and well-hidden) telescope, and they are none wiser, so there is no pain he is inflicting to offset the pleasure he produces for himself. But his action still seems wrong, and his pleasure is an evil pleasure, as almost anyone would think. Even though philosophical questions are not best settled by majority vote, anyone who concedes that the peeping Tom’s pleasure is bad should reject hedonism, for how can pleasure be what is good in itself if there are pleasures that are bad in themselves?

The second view Socrates considers has a bit more going for it than hedonism; if nothing else, it is held by ‘more sophisticated’ folks. It is the view that ‘the good […] is knowledge’ (6.505b), which we might awkwardly dub ‘Epistemicism’ (from the Greek word for knowledge, epistemê). This seems like a view that Socrates would find attractive, given the centrality of knowledge to philosophy, but he quickly dismisses it—not, as with hedonism, because there are instances of bad knowledge (though presumably there are) but because Epistemicism leads to an infinite regress (or, more properly, an infinite progress). Knowledge always has an object, he reminds Glaucon. If I have knowledge, I have knowledge of or about something; there is no such thing as mere, objectless knowledge. The various crafts are similar in being knowledge of how to do certain things, but they are distinguished by their objects: farmers know how to farm, doctors know how to heal, etc. Similarly, the grammarian and mathematician both possess the same kind of knowledge—theoretical or propositional knowledge that certain propositions are true, as opposed to knowledge of how to do things—but they too are distinguished by their objects. If we ask the sophisticates who hold that the good is knowledge what that knowledge’s object is, they will reply, Socrates thinks, that ‘it is knowledge of the good’ (6.505b). This is highly problematic, and not just because it is circular. If the good is identical to knowledge, then for every occurrence of ‘the good’ we can substitute ‘knowledge’, just as we can substitute ‘2+1’ for any instance of ‘3’ in a mathematical formula (e.g., since 32 = 9, it follows that (2+1)2 = 9). But if the knowledge in question is knowledge of the good, then the Epistemicist’s core claim,

(E) The good = knowledge.

becomes

(E*) The good = knowledge of the good.

But by substituting ‘knowledge of the good’ for ‘the good’, (E*) generates

(E**) The good = knowledge of the good knowledge of the good,

which in turn generates

(E***) The good = knowledge of knowledge of knowledge of the good,

and so on, with no end in sight!

Clearly, Socrates thinks knowledge is good. But it is a good, not the good. It is one of philosophy’s distinctive goods, but knowledge is not the good—it is not what goodness is. But even if we do not know what the good is, Socrates thinks we know two things it is not, and that is at least a start. So what does Socrates think the good is?

The Analogy of the Sun (6.506d–509d)

Socrates does not answer this question directly, but not because he is being cagey, as Thrasymachus might suggest. And not (at least not explicitly) because he thinks the good cannot be defined in any non-circular way. The eighteenth-century philosopher Joseph Butler remarked that ‘Everything is what it is, and not another thing’, which the twentieth-century philosopher G.E. Moore quoted at the outset of his Principia Ethica before arguing that any attempt to give a real definition of goodness was doomed to fail. Cinema lovers may recall a memorable exchange in the film The Deer Hunter between Mike (Robert De Niro) and Stanley (John Cazale), in which Mike, holding up a bullet, says, ‘Stanley, see this? This is this. This ain’t something else. This is this’.1 Stanley does not understand the lesson, but I suspect Socrates, Butler, and Moore would all be sympathetic to Mike’s point, since the good is what it is and not some other thing.

So why does Socrates not provide a value for x in the philosophical equation the good = x? Why does he choose to ‘abandon the quest for what the good itself is for the time being’ (6.506d)? Although antagonists like Thrasymachus will scoff, I believe it is because Socrates possesses the virtue of epistemic humility: he claims not to know what the good is and insists that one should not ‘talk about things one does not know as if one does know them’ (6.506c), which is what he’d be doing if he responded directly to Adeimantus’ request for an account of the good. But while he cannot say what the good is, he thinks he can say something about what it is like, which brings us to the Sun Analogy. In Book VII Socrates will suggest that dialectic—rigorous, Forms-based philosophical reflection—is the only avenue to genuine knowledge. As he did earlier in Book VI, he reminds Glaucon and company that they will be avoiding this ‘longer road’ (6.504c) and proceeding in a less exact, hypothetical way which will give them a sense of what the good is, but which will fall well short of full-blown philosophical knowledge of it.

Socrates’ plan is to explain the Form of the good in terms of something more readily understandable: the sun. He suggests that the good—the Form or essence of goodness itself—plays the same role in the intelligible realm that the sun plays in the visible realm. Strictly speaking, the focus is the sun’s role in the sensible realm, the world of sense-experience, but we will follow Socrates in using ‘visible’ to designate this realm, which also includes what he can hear, touch, taste, and smell as well as what we can see. While he cannot say what the good is, he can say what he thinks the good does. His idea is that the sun: the visible world :: the good: the intelligible world—the roles the sun and the good play in their respective worlds are analogous. In the visible world, the sun by its light enables us to see the many particular things—and also enables their existence. In the intelligible world, the good by its truth enables us to know the Forms—and also enables the existence of the Forms. Seeing something requires both a visible object and the power of sight. But it also requires ‘a third kind of thing’ (6.507d)—light. Without light to illuminate the object, the power of sight will not reveal that object to us. The sun is the main and most obvious source of light, so the sun enables us see visible objects. But it does more than enable their being seen, Socrates thinks; it enables their very existence. This is certainly true of living things, which depend for their existence on the light of the sun. (It is less clear that this is true of rocks, but we need not be sticklers about this.) The same goes for the Form of the good:

what gives truth to the things known and the power to know to the knower is the form of the good. And though it is the cause of knowledge and truth, it is also an object of knowledge […] not only do the objects of knowledge owe their being known to the good, but their being is also due to it. (6.508e–9b)

So, just as the sun provides the light that enables us to see visible objects, the Form of the good provides the truth that enables us to know intelligible objects, which of course are the forms: ‘the many beautiful things and the rest are visible but not intelligible, while the [F]orms are intelligible but not visible’ (6.507b). Beautiful things owe not only their being seen but also their very existence to the sun. Similarly, the Form of beauty depends for both its knowability and its very existence on the Form of the good.

Thus the Form of the good plays a foundational role in Plato’s epistemology, since it is the condition of all knowledge, and also in his metaphysics, since it is the condition of the existence of the other Forms and in turn the existence of concrete particular objects. Particular beautiful things are beautiful because they partake, if only temporarily, in the Form of beauty; they are temporary, spatiotemporal images or copies of the Form of beauty itself. Similarly, a particular just action or soul is just because it participates in the Form of justice, and so on. And since beautiful things and just actions are good and useful, they must also participate in the Form of the good: ‘it is by their relation to [the Form of the good] that just things and the others become useful and beneficial’ (6.505a). Thus the Form of the good subsumes the Forms of justice, wisdom, courage, etc.; not only would they not be good without it, they would not exist without it. So goodness is at the core of Plato’s conception of the universe, both epistemologically and metaphysically.

The Divided Line (6.509e–511e)

Socrates follows the Sun Analogy with a linear perspective on how the visible and intelligible worlds differ. His focus here is largely epistemological, though as we might expect metaphysics looms in the background. Having already said a bit about how knowledge and belief differ, here Plato goes into more detail, saying more about their distinct objects (thus drawing on the ill-fated Powers Argument) and also making distinctions between different kinds of knowledge and belief. We can think of the line as a sort of epistemological companion to the Metaphysical Elevator, in which one ascends epistemologically from belief to knowledge and metaphysically from concrete particular objects to the Form of the good.

Start a line segment and divide it unevenly, as below, into two sub-segments. Let one segment represent the visible world and the other the intelligible world:

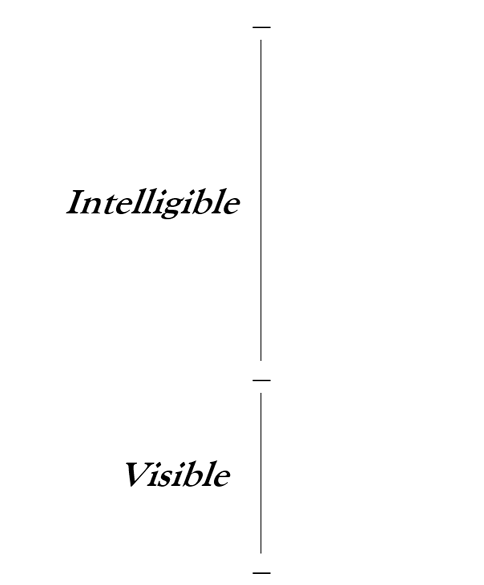
Fig. 1. The Visible World and the Intelligible World

Belief is the epistemic state (or, as Socrates would have it, the power) that operates in the visible world, while knowledge governs the intelligible world. Since length corresponds to ‘relative clarity and opacity’ (6.509d), the line segment representing the intelligible realm will be longer than the segment representing the visible realm. This should make sense, given Plato’s view that the Forms, which are at home in the intelligible realm, are both more real than the particulars and are epistemically clearer: the Forms are objects of knowledge, while the particulars are objects of belief. Belief, while clearer than ignorance, is darker and opaquer than knowledge, as Socrates claimed earlier (5.478c). So, even though there are more objects in the visible world than in the intelligible world, since the relation between particulars and their Forms is a relation of many to one, the segment representing the intelligible realm is longer than the segment representing the visible realm.

Now here comes a slightly tricky part: divide each sub-segment again by the same ratio as the entire line was divided:

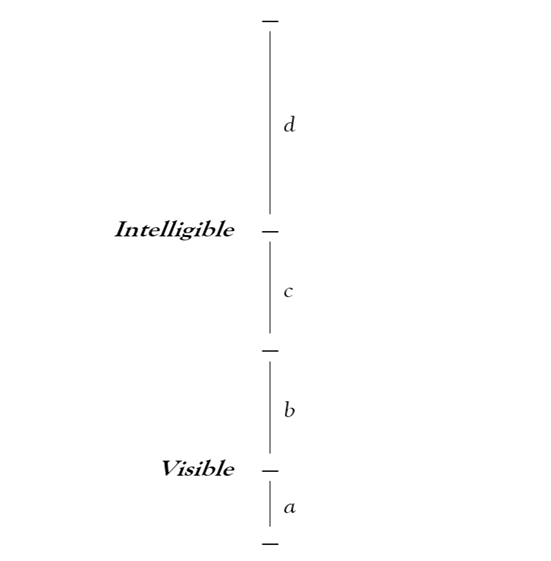
Fig. 2. The Visible World (a and b) and the Intelligible World (c and d)

So now the visible world comprises sub-segments a and b and the intelligible world comprises c and d, and with the ratios of both a to b and c to d identical to the original ratio of Visible to Intelligible. An obvious consequence of this is that a:b :: c:d. A less obvious consequence, which Socrates either does not notice or notices but does not mention, is that b and c turn out to be the same length. Given that the line is arranged in terms of ‘relative clarity and opacity’ (6.509d), the equality of b and c suggests an epistemic and metaphysical parity between the highest visible and lowest intelligible sub-sections of the line, and it is hard to see Socrates endorsing such a view. This is at least a wrinkle in the Divided Line analogy, but let us assume that it is a wrinkle that can be ironed out and move on.

Now we will see the parallel between metaphysics and epistemology. Plato further divides the main epistemic states or powers, Belief and Knowledge, which appear on the line’s right side in Fig. 3:

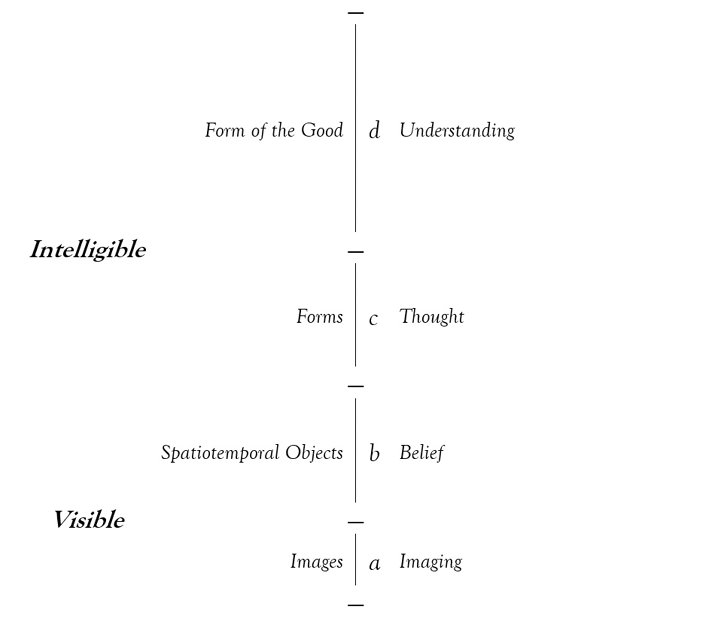
Fig. 3. The Visible World and the Intelligible World: Belief and Knowledge

The two bottom sub-segments of the line, a and b, which together make up the visible realm, have different objects. The lowest level, a, has images (εἰκόνες [eikones]) for its objects—shadows and reflections and, presumably, the analogies and metaphors of the sort that Socrates is so ‘greedy for’ in Book VI, as well as the paintings, sculptures, and poems that he will criticize in Book X. The second lowest level, b, comprises the original items of which those images are copies. The bed in which Van Gogh slept in his room at Arles, which served as the model for his famous paintings of it, would be an object appropriate to b, while the paintings of the bed, being copies of that spatiotemporal object, belong in a. In addition, we might think the second-hand opinions that many of us have, opinions we merely parrot from our favorite news source, belong here in a. Many readers active on Facebook or Twitter will be familiar with someone whose social media mission seems to be reposting or re-tweeting stories and memes that express the views they have gotten from others. (When someone says, ‘I have thought about this a lot’, one hopes they mean this literally, where ‘thought’ is a verb, and they have scrutinized and analyzed and seen implications of the point in question. What we are often saying, alas, is ‘I have a thought about this, and I think that thought a lot’, where ‘thought’ is a noun, and thinking that thought does not require critical examination of the idea’s merits and demerits, etc.) In addition to their different objects, a and b also differ in terms of the epistemic or cognitive states operating in them. While Plato generally talks of belief (δόξα [doxa]) as operating in the visible realm, here he distinguishes between εἰκασία [eikasia], imagining (or merely imaging) and πίστις [pistis], which is translatable as ‘belief’ but which suggests credence, trust, and sincerity as well.

The intelligible realm is where the Forms live. While the sub-segments of Visible had different kinds of objects, here the objects are the same: Forms (although the Form of the good operates in d, the highest level). Segments c and d—Thought (διάνοια [dianoia]) and Understanding (νόησις [noêsis]), respectively—are distinguished by how knowers are related to the Forms that populate the intelligible world.

Hypotheses and First Principles in the Divided Line

A crucial difference between Thought (c) and Understanding (d) is the role that hypothesis (ὑπόθεσις [hypothesis], literally, what is placed or set under something) plays. Mathematicians, who occupy themselves in Thought, employ hypotheses in their thinking: they ‘hypothesize the odd and the even, the various figures, the three kinds of angles’ (6.510c), etc. But, Socrates thinks, they ‘do not think it is necessary to give any account (λόγος [logos]) of them’ (6.510c), presumably because these hypotheses seem so obviously true that no justification is needed. Just as mathematicians take it for granted that there are numbers and triangles, physicists assume the existence of an external world of spatiotemporal objects, whose properties and behavior they study without feeling the need to justify this assumption. They treat their hypotheses as ‘first principles (ἀρχή [archê]))’ (6.510d)—as foundations—and draw conclusions from them. The mathematicians’ conclusions are not about the particular triangle or circle drawn on the blackboard; the physicists’ are not about the particular electrons in this particular cloud chamber; rather, they are about triangles and circles in themselves, or about electrons in themselves. Both try to prove things about the Forms, on the model of inquiry depicted by the Divided Line.

By contrast, the philosopher, who roams the realm of Understanding, recognizes hypotheses as hypotheses; they do not think of their hypotheses and assumptions as self-evidently true first principles requiring no justification. Unlike their mathematical and scientific cousins, the philosopher does not treat a hypothesis as an unassailable foundation or ‘first principle’ but rather as something that stands in need of a logos, a justification or rationale. The hardest part of philosophy, Socrates says, ‘has to do with giving a rational account’ (6.498a). It is not that mathematicians and scientists are too lazy to justify their hypotheses, but rather that they do not feel the need to do so, since their assumptions seem so obviously true. But so long as the foundational hypothesis is unaccounted for, what follows cannot fully count as knowledge, on Socrates’ view, even though it involves grasping mathematical Forms: ‘What mechanism could possibly turn any agreement into knowledge when it begins with something unknown and puts together the conclusion and steps in between from what is unknown?’ (7.533c)

Socrates implies here that mathematicians can give valid arguments (arguments whose conclusions must be true if their premises are true), but that the conclusions of their arguments are merely conditionally and not absolutely true. That is a far cry from giving an argument whose conclusion must be true, period, which would require showing that the hypotheses in question are true and do not merely seem to be true. While the mathematician’s valid arguments might be sound, the mathematician is never in a position to know whether their arguments are sound or not until they justify the hypothesis—the if—on which the conclusion ultimately rests.

To get a sense of what is at stake, consider a hypothesis that many readers encountered in high school geometry class, Euclid’s parallel postulate. That parallel lines extended indefinitely in space will never meet seems so intuitively obvious as to be axiomatic. No wonder geometers do not try to ‘give an account’ of this hypothesis. Doing so seems a waste of time, and developing a geometry that rejects that postulate seems a fool’s errand. But, as many readers know, the geometry required for Einstein’s general theory of relativity is non-Euclidean, geometry that rejects the parallel postulate. Space, on Einstein’s view, is curved, so Euclidean geometry misdescribes it. The assumption that parallel lines indefinitely extended in space would never touch seemed too obvious to need a justification, but it turns out to be false. That is the kind of worry Socrates has about the realm of Thought.

Dialectic and Understanding

It is not that hypotheses are dispensed within the realm of Understanding. Instead, they are treated as hypotheses, as needing justification, rather than as first principles requiring no justification:

It does not consider these hypotheses as first principles but truly as hypotheses—stepping stones to take off from, enabling it to reach the unhypothetical first principle of everything. Having grasped this principle, it reverses itself, and, keeping hold of what follows from it, comes down to conclusion without making use of anything visible at all, but only of forms themselves, moving on from forms to forms, and ending in forms. (6.511b)

Understanding is the result of what Socrates calls ‘dialectic’—that is what the initial ‘it’ in the quotation just above refers to. Dialectic is the longer, harder road that Socrates chooses not to travel in the Republic, opting instead for a discussion relying on analogies and metaphors. Dialectic is like mathematical thinking in having the Forms for its objects, but, as we just noted, dialectic treats hypotheses and assumptions differently than mathematical thinking. Here are some of dialectic’s distinctive features, which ground ways in which Understanding differs from Thought:

1. Giving an account. The dialectician—i.e., the genuine philosopher—‘is able to give an account of the being of each thing’ (7.534b). In addition to being able to grasp the essence of the thing under discussion, the philosopher is also able to explain that essence, to give an account of it. ‘Someone who is able to give an account of the being of each thing [is] dialectical’, Socrates says. ‘But insofar as he is unable to give an account of something, either to himself or to another […] he has [no] understanding of it’ (7.534b). Book V’s lovers of sights and sounds may have many true beliefs about which objects are beautiful, but being unable to grasp the Form of beauty, they are unable to explain why a beautiful thing is beautiful, and thus lack knowledge. Similarly, the geometer who assumes that the parallel postulate is true but who is unable to justify that assumption lacks Understanding: they think with concepts they do not fully understand.

2. Integrated knowledge. Presumably, the mathematician is able to give an account of the various mathematical objects she concerns herself with. But the dialectician is also able to see connections between the individual Forms: she sees ‘their association and relationship with one another’ (7.531c) and so achieves a unified intellectual vision. ‘Anyone who can achieve a unified vision is dialectical’, Socrates says, ‘and anyone who cannot is not’ (7.537c). A geometer is probably able to achieve a unified grasp of the various geometric Forms; it is hard to imagine someone specializing in, say, rectangles who knows nothing about circles or spheres or trapezoids. But the philosopher—the dialectician—is able to unify different domains of study, understanding not just geometry and physics or game theory and biology in themselves, but grasping how these disciplines and the Forms they study are interrelated. In short, the philosopher sees and makes connections between disparate domains.

3. Purely formal reasoning. Thought relies on visual aids: the geometer’s object in trying to prove a theorem about the nature of triangles is the Form of triangularity, but they draw particular triangles on particular chalkboards as an aid for grasping the triangle’s essence. Those drawings are aids borrowed from the visible realm. Understanding, by contrast, proceeds ‘without making use of anything visible at all, but only of Forms themselves, moving on from forms to forms, and ending in forms’ (6.511b). The dialectician is able to think with the Forms alone: her seeing is purely intellectual, and does not involve any objects from the visible realm at all, or the kinds of metaphors Socrates employs to make sense of the Form of the good. Dialectic ‘tries through argument and apart from all sense perceptions to find the being of things and does not give up until he grasps the good itself with understanding itself’ (7.532a).

4. The Form of the good. Perhaps dialectic’s most distinctive feature, and thus the most important difference between Understanding and Thought, is that dialectic involves seeing how the various Forms are related to the Form of the good. Thus dialectic requires the most complete kind of intellectual integration possible. This integration is both horizontal, so to speak, understanding how Forms are related to each other, and also vertical, understanding how these Forms are related the Form of the good, which, as the condition of both the knowability and existence of the Forms, is at a level higher than them—Level Five, so to speak, on Plato’s Metaphysical Elevator. Plato’s universe is fundamentally ordained toward the good: the Form of the good is ‘the unhypothetical first principle of everything’ (6.511b), and one does not fully grasp a thing’s essence until one grasps the end it aims at, as well. Dialectical understanding is thus a very tall order.

5. Foundationalism. The contemporary epistemological distinction between foundationalism and coherentism sheds light on the difference between Thought and Understanding. Even though Plato does not think of knowledge as justified true belief, his concern with giving an account implies that a discussion of justification is not completely out of order. A coherentist holds that a belief’s being justified is a matter of its being properly related to other beliefs: one’s beliefs hang together in a coherent way, with minimal inconsistency between beliefs. Presumably some inconsistency has to be allowed; otherwise no one’s beliefs would be justified, since we all unknowingly have beliefs that are at odds with each other. The foundationalist, by contrast, thinks that at least one belief must be justified in a non-inferential way, not getting its justification from another belief. Such a belief is the foundation—the archê—of the justification of all other beliefs.

The realm of Thought is coherentist: the mathematician’s conclusions are ‘in full agreement’ with the hypotheses they treat as first principles. The realm of Understanding, by contrast, is foundationalist: it rests ultimately on the Form of the good, which is the source of the intelligibility (and indeed the existence) of the other Forms. Ironically, the procedure for determining whether one grasps this foundation seems itself coherentist: ‘Unless someone can distinguish in an account the form of the good from everything else, can survive all refutation, as if in a battle […] and can come through all of this with his account still intact, you’ll say that he does not know the good itself’ (7.534bc). We have witnessed this procedure, elenchus, throughout the Republic, starting with Cephalus’ and Polemarchus’ and Thrasymachus’ accounts of justice. We saw it most recently in the two accounts of the good that Socrates rejected earlier in Book VI. Socrates seems to suggest that what makes an account of x true is that it can survive the sort of cross-examination we have seen so far in the Republic. But his actual view, I think, is not that coherence constitutes the correctness of an account, but rather that coherence is the best criterion of correctness: an account is not made true by its having no internal inconsistencies and no false implications or entailments; instead, its consistency and coherence are good evidence—and perhaps the best evidence—that it is true.

Readers familiar with Plato’s Euthyphro will find there a helpful example of this distinction between constitution and criterion. One of the Euthyphro’s main questions is whether the gods love holiness because it is holy or whether holiness is holy because the gods love it. That is, do the gods’ loving x make x holy or constitute x’s holiness, so x’s holiness is due to the external fact that the gods love it rather than some of its internal features? Or is the gods’ loving x simply good evidence that x is holy, their love for x being a criterion of x’s being holy, but not what constitutes x’s holiness? In short, is x loved because it is holy, or holy because it is loved?

That an account of the good or any important concept is maximally coherent suggests that it is correct, but coherence is criterial rather than constitutive of its being true. What makes an account true is its connection to the Form of the good.

Socrates’ Hypothetical Method

Before moving on, we should note how transparent Socrates has been in employing hypotheses in the Republic, reminding Glaucon and company of the conditional nature of any conclusions they draw from their hypotheses. For example, when offering the Opposition Principle as the basis for dividing the soul (4.436b), he remarks, ‘let us hypothesize (ὑποθέμενοι [hypothemenoi) that this is correct and carry on. But if we agree that it should ever be shown to be incorrect, all the consequences we have drawn from it will also be lost’ (4.437a). Socrates is reminding us that by employing hypotheses and analogies we are travelling on a less rigorous path, one that will give us a sense of what the good is but will not let us look on it directly. This should make sense, for even if Socrates is a genuine philosopher-king (though he claims otherwise), the rest of us—Glaucon, Polemarchus, you, me—are not, and we would be blinded by trying to look directly at the good, just as we would be blinded if we looked directly at the sun. So Socrates opts for the hypothetical, analogical method, which allows us to think about the good without understanding it. For that, dialectic is needed.

Dialectic: It’s No Game

Socrates appeals to dialectic to distinguish genuine from counterfeit philosophers, as his response to the Third Wave requires of him. It also enriches his explanation of the negative view of philosophers so many Athenians have. The trouble is that ‘a great evil comes from dialectic as it is currently practiced’ (7.537e), since the young people who practice it imitate Socrates’ method of intellectual cross-examination but ‘misuse it by treating it as a kind of game of contradiction’ (7.539b). A genuine philosopher, who loves and reveres the truth, regards dialectic as the best means of getting at the truth and employs it in that spirit. But without reverence for the truth, dialectic becomes merely a game aimed at humiliating the bloviating pretender to knowledge and thus showing how clever its practitioner is. It is no wonder, then, that his fellow citizens regard Socrates as a bad influence on the young people who flock to him.

Unsurprisingly, Socrates employs yet another metaphor to address the dangers of dialectic when it is not practiced with the love of truth. Imagine a bright young person ‘brought up surrounded by much wealth and many flatterers […] who finds out, when he has become a man, that he is not the child of his professed parents and that he cannot discover his real ones’ (7.538a). This turns the young person’s world upside down: core beliefs about who they are turn out to be false, they regard their adoptive parents as liars and no longer live as they were raised to do. This is what it is like to be a young person whose core moral beliefs are challenged. A person who is properly raised will, like Glaucon and Adeimantus, believe that the just life is happier, that they ought to be motivated by what is fine and noble rather than by narrow self-interest, but they do not know why the just life is happier or what the fine and noble really is. Dialectic as practiced by counterfeit philosophers ‘shakes him from his convictions, and makes him believe that the fine is no more fine than shameful, and the same with the just, the good, and the things he honored most’ (7.538d). It induces a kind of intellectual and moral vertigo: values and ways of life that seemed so certain now seem flimsy and evanescent. Improperly deployed, dialectic turns young people into relativists or nihilists who think of traditional moral virtues such as justice as shams in much the same way Thrasymachus did back in Book I: as tools clever people use to dupe simpletons like the unknowing orphan until the scales fall from their eyes. That so many of Plato’s dialogues end without discovering the nature of the virtue in question—that is, in aporia: difficulty or befuddlement—probably does not help, either. Rather than thinking that eliminating wrong accounts is a kind of progress, the clever game-player thinks he is shown that there is no answer.

Socrates thinks that few young people are sufficiently ‘orderly and steady by nature’ (7.539d) to practice dialectic properly; instead of being ‘willing to engage in discussion in order to look for the truth’, the bright young person ‘plays at contradiction for sport.’ (7.539c) They will imitate and thus internalize the wrong models (7.539bc), which echoes the concerns Socrates raised when discussing how and why ‘the storytellers’ needed to be ‘supervised.’ Thus in the advanced education for would-be philosopher-queens and -kings that we will look at after discussing the Cave Analogy, students are not trained in dialectic until they reach the age of thirty (7.537d).

So dialectic is no game. It is dangerous if practiced without a love of truth, capable of doing real damage to both its practitioner and its victims. But it also promises great cognitive benefit, as it is the genuine philosopher’s tool par excellence, a tool enabling full understanding. This understanding goes far beyond the kind of understanding Socrates’ analogies can yield, which Glaucon claims at the close of Book VI. He understands (μανθάνω) Understanding (νόησις), but he does not Understand it.

Some Suggestions for Further Reading

Readers interested in exploring the Sun and Line analogies in greater depth and detail might try Nicholas Denyer, ‘Sun and Line: The Role of the Good’, in The Cambridge Companion to Plato’s Republic, ed. by G. R. F. Ferrari (New York: Cambridge University Press, 2007), https://doi.org/10.1017/ccol0521839637, pp. 284–309, or Chapter 10 (‘Understanding the Good: Sun, Line, and Cave’) of Julia Annas, An Introduction to Plato’s Republic (New York: Oxford University Press, 1981), pp. 242–71, which is reprinted in Plato’s Republic: Critical Essays, ed. by R. Kraut (Lanham, MD: Rowman & Littlefield, 1997), pp. 143–68.

Readers interested in the ‘wrinkle’ in the Line (that segments b and c have the same length) might first see Chapter 9 (esp. pp. 203–4) of R. C. Cross and A. D. Woozley, Plato’s Republic: A Philosophical Commentary (New York: St. Martin’s Press, 1964), pp. 196–230.

Readers interested in exploring the distinction between coherentism and foundationalism might start with the first section of Erik Olsson’s ‘Coherentist Theories of Epistemic Justification’, in the Stanford Encyclopedia of Philosophy (https://plato.stanford.edu/entries/justep-coherence/). Susan Haack, Evidence and Inquiry: A Pragmatist Reconstruction of Epistemology, 2nd ed. (Amherst, NY: Prometheus Books, 2009) seeks a middle ground between the two, which she dubs ‘Foundherentism.’ William Alston, Epistemic Justification: Essays in the Theory of Knowledge (Ithaca: Cornell University Press, 1989) contains excellent essays on justification by one of the leading epistemologists of the last century.

---