15. Constructing Figures: A Tricky Art?
© Gábor L. Lövei, CC BY 4.0 https://doi.org/10.11647/OBP.0235.15
Clear graphics aid, and show, clear thinking about what data mean.
Valiela (2009)
A good graph is a well-designed presentation of interesting data, communicating complex ideas with clarity, precision, and efficiency. It gives the viewer the greatest number of ideas in the shortest time, with the least ink in the smallest space. Statistical graphics can: show the data, and induce the viewer to think about the substance, and not about methodology, design, or technology (Tufte, 1994). They also avoid distorting what the data have to say, present many numbers in a small space, and make large data sets coherent by encouraging the eye to compare different pieces of data, while revealing data at several levels of detail. A good figure also serves a clear purpose: description, exploration, or tabulation. Figures also have to be closely integrated with statistical and verbal description of a data set.
Terminology
Scientific graphs can take many forms. The most common ones depict the relationship between a response variable and one (exceptionally more, see later) explanatory variable(s). In their most common form, they are two-dimensional, using the Descartes coordinate system. Thus, there is usually a horizontal axis (often denoted the “x axis”, Figure 1), and a vertical (or “y”) one. According to tradition, the independent (explanatory) variable is presented along the horizontal, and the dependent (response) variable along the vertical axis. The axes are usually drawn to correspond to the range of values along them. The area thus indicated is called the data rectangle. Axes have ticks to indicate the scale, and tick labels to identify the scale values. The axes themselves have to be named using axis labels. The data series are represented by various symbols, and their meaning is given in the legend or key. The figure is accompanied by a caption: text that is printed below the figure, describing what is pictured. There can be multiple panels on the figure, making it a multi-panel figure (see below).
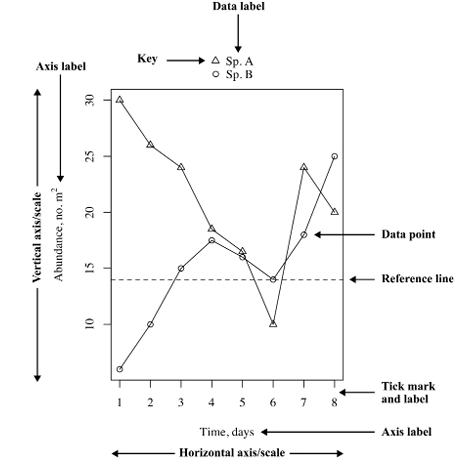
Fig. 1 Figure terminology. The square area defined by the two axes and their parallel lines is called the ‘data rectangle’. Image by author (2020).
General Rules of Scientific Graphs
There are general design rules for figures that are worth mentioning here. The first is the prohibition of double data presentation. A set of data can be presented in only one way — either in text, on a figure, or in a table. Single values and trends can be mentioned and discussed in the text, but larger parts of the whole dataset cannot be presented in more than one way.
A second rule is that figures, together with their captions, have to be self-explanatory: the reader should understand what is pictured on the figure, without reference to the text or to other figures. Note that the interpretation of the figure does not need to be given here — that goes into the text (of the Results section, see Chapter 11). All axes have to be identified, including the precise naming of the measurement units, even if this may seem redundant (such as “time, days”). The data rectangle is for the data only: viewers instinctively try to interpret everything within the data rectangle as coded data.
The simplicity of coding principle has to be mentioned here, too: figures are coded information par excellence and, if there is a new symbol, code, or colour, which constitutes visual novelty, this should be understood first, before the data can be interpreted. This gives rise to rule no. 3: keep visual novelty to the necessary minimum.
Principles
There are three basic principles in the graphical presentation of data: economy, integrity and clarity. Figures should be designed to present the data in a clear, uncluttered, and honest way.
Economy
Presentation of data should be as simple and clutter-free as possible. However, this should be realised with economy: a figure should neither be bigger nor use more ink than necessary. The principle of maximising data and minimising ink (maximising the data:ink ratio) was suggested by Edward Tufte, and was aptly named the “Tufte Principle” by Valiela (2009). The principle of economy should also be considered when deciding the best way to present your data: in text, in a figure or in a table? The option occupying the least space is usually preferred.
An important first point here is that uninformative, decorative motives should not be used. Unnecessary decoration, shading, cute pictures and other uninformative elements justly acquired the name “chartjunk” (Tufte, 2003). They mostly serve to disguise shallow thinking, and they betray a lack of belief in the data and a profound disdain for the intellect of the reader. Unfortunately, most graphical computer programs offer a vast range of chartjunk; ignore those.
Figures are expensive, and they should convey complex, often multi-layered data that need, and reward, scrutiny. Therefore, space is at a premium. Data should stand out, and everything on a figure should serve the data.
In the first instance, this means that the data rectangle should be filled with the data, to the largest extent possible. This requires a careful selection of the intervals to be included on both axes. They should only encompass the range within which there are actual data, and not beyond. Doing otherwise would simply be a waste of space. Using semi-logarithmic or double logarithmic scale often allows a more even fit of the data within the data rectangle (Fig. 2).
The most important additional information consists of the tick marks and labels on the axes. They should be sufficient to interpret the data — and no more. A common mistake is that figures have too many tick marks, and too many tick labels (Fig. 3). Not every tick mark needs a label — only so many as are necessary for understanding the data range. Tick marks should point outside, not into the data rectangle — at first glance we interpret everything within the data rectangle as data. Data points cannot be read with precision from figures, anyway — the function of a figure is not to show precise values, but relationships.
When designing or revising your own graphs, seek to improve the “data:ink ratio”. Sometimes even deleting ink can increase the information content on the graph. Examples include the range-frame graphs (Fig. 4) where an axis is only drawn where there are data points along the axis, or when the value of the mean along the axis is denoted by a small gap on the axis (Fig. 4). A particularly elegant example of retaining information, but using less ink, is when a traditional box plot is replaced by the Tufte plot (Fig. 5).
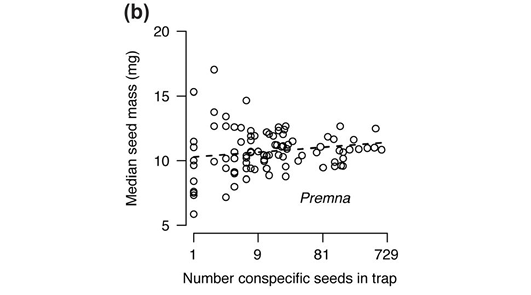
Fig. 2 Using a semi-logarithmic axis can fill the data rectangle more evenly. Here logarithmic values on base 3 was used. From Fricke et al. (2019), https://doi.org/10.1111/oik.06494. © 2019 Nordic Society Oikos. Published by Elsevier GmbH. All rights reserved. Permission for further reuse must be obtained from the relevant holder of the exclusive rights.
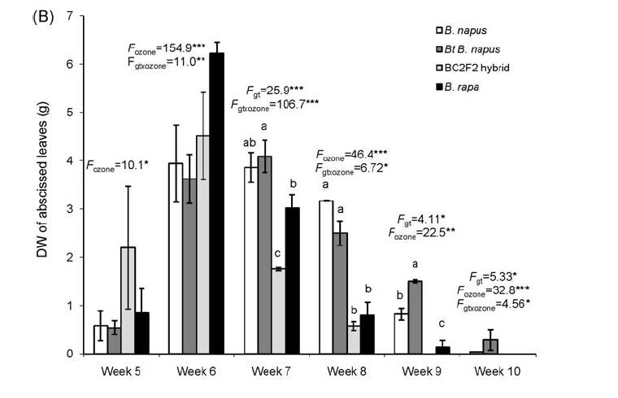
Fig. 3 Too much explanation within the data rectangle can draw the attention away from the data. From Himanen et al. (2010), https://doi.org/10.1016/j.baae.2010.06.00. © 2010 Gesellschaft für Ökologie. Published by Elsevier GmbH. All rights reserved. Permission for further reuse must be obtained from the relevant holder of the exclusive rights.
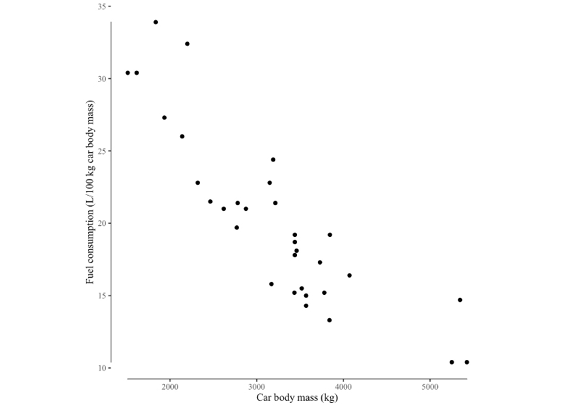
Fig. 4 A range-frame figure. Instead of the traditional axes, axis lines are only drawn within the range of data along that axis. Data modified from the mtcars R dataset, version 3.6.2. Image by author (2020).
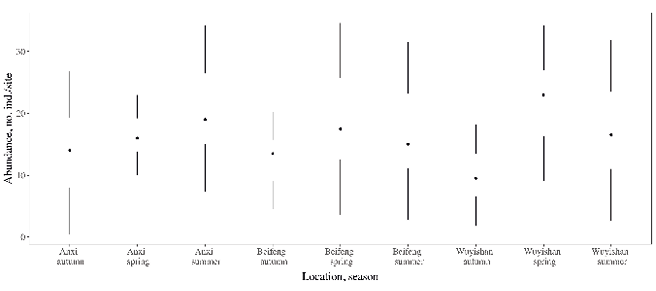
Fig. 5 A Tufte plot. An elegant way to show comparisons in descriptive statistics — in this case, the median, the central quartiles and the range. Data from Imboma et al. (2020), http://doi.org/10.3390/insects11040212. CC-BY 4.0 (http://creativecommons.org/licenses/by/4.0).
Integrity
Integrity requires that the kind of data pictured should always be truthful and unequivocally identifiable. All axes should have an axis label, even if it seems superfluous. This should contain both what was measured (what is pictured along that axis) and the measurement unit, if there is one. Sometimes we picture dimensionless numbers or indices. These have no measurement unit.
Integrity also requires truthfulness in relation to data dimensions. Data should not be pictured with “pseudo-dimensions”. A common mistake is to present two-dimensional data “in space”, using a third dimension (Fig. 6). The “thickness” of the cake on Figure 6 is totally irrelevant — it carries zero information — because, by intent, the area and not the volume of the various slices are to be compared. This is called a pseudo-dimension, because the same data can be presented in one, or even two fewer dimensions without loss of information. Data dimensionality and figure dimensionality should be consistent. We struggle, in any case, to picture anything beyond three dimensions — the three that we have should be used wisely.
There is also a sensory physiological reason for not exceeding the necessary number of dimensions: the human eye is very good at perceiving even minute differences in linear dimensions. We are much poorer in distinguishing area differences, and almost hopeless when it comes to judging differences in volume. Do not use more than the necessary number of dimensions to present your data (see more about this later in this chapter).
Data differences, and their representation, should be truthful: if the difference in your data is 50%, presenting this as a 100% difference would give a false impression to the viewer. This has been called the “lie factor” (Tufte, 2006), and is defined as the ratio between the difference in representation divided by the difference in measured values.
No axis breaks are allowed. The eye instinctively connects these gaps along the minimum chord and, thus, we get a false impressions of trend lines (Fig. 7). When interpreting figures, we estimate shape, length, etc. and make comparisons. Often there are several graphs that are to be compared. The axes should be consistent among such comparable panels. We should be careful here, because primitive graphing programs present any graph panel in the same size, irrespective of the axis range.
If such consistent axes are not possible, or if they grossly violate the principle of filling the data rectangle with data, units of change should be physically identical (Fig. 8).
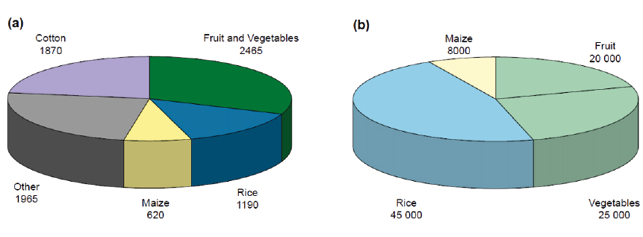
Fig. 6 An example of a superfluous third dimension, which carries no information at all — the area of the circle diagram is related to the number represented. Notice also the double data presentation. From de Maagd et al. (1999), https://doi.org/10.1016/S1360-1385(98)01356-9. © 1999 Elsevier Science Ltd. All rights reserved. Permission for further reuse must be obtained from the relevant holder of the exclusive rights.
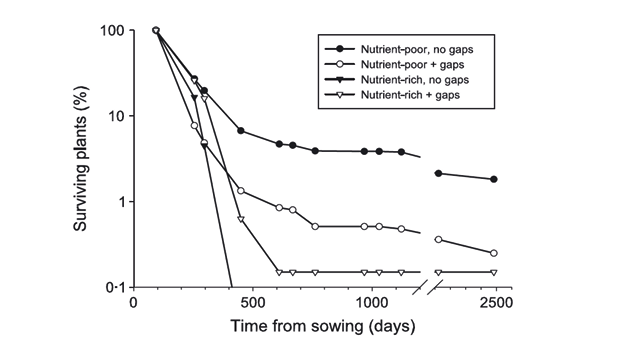
Fig. 7 When the axis is broken, we cannot correctly judge the slope of the curve. Source: Fig. 3 from Reckinger et al. (2010), https://doi.org/10.1111/j.1526-100X.2009.00522.x. © Society for Ecological Restoration International. All rights reserved. Permission for further reuse must be obtained from the relevant holder of the exclusive rights.
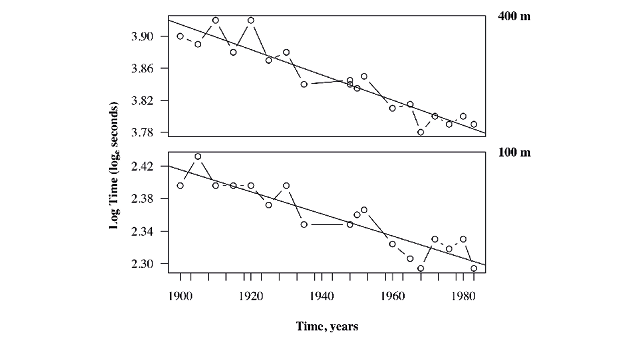
Fig. 8 When multi-panel figures are presented, their axes must be identical, or at least comparable. In this example, different sections of the same scale are used on the vertical axis. Data show the (natural logarithms of) winning times at 20th century Olympic Games at 100m and 400m sprint distances. Image by author (2020). Data modified from Cleveland (1993).
Clarity
Allow for reduction
Figures are almost never reproduced in their original size. A majority of figures is reduced when reproduced in a journal; reduction always results in loss of sharpness, definition, and detail. Consequently, figures should be designed to withstand reduction. If in doubt, use a photocopier to generate a reduced-size figure. Consider that reducing the length of axes by half would result in a figure size of 25% of the original. Also, consider the final dimensions of figures that can be reproduced in the journal. If possible, try to fit to these dimensions — but remember, the journal is the medium, and the information is the message. The medium should never take precedence over the message — if your figure must be an odd size, then so be it. You will, though, have to justify your choice of dimensions to the editor.
Data should stand out
The size of data points should always be large enough to identify where, and how many, they are. A continuous line without data points suggests an endless number of measurements, which is rarely the case.
Data visibility: symbols, overlap, axis interference
When presenting several data series on one graph, we should use symbols that easily and correctly identify data groups (see Box 10).
More than five sets of data can rarely be pictured within the same data rectangle. Use a multi-panel graph in such cases, possibly with a background grid to ease comparison; remember the comparable axes.
In cases where there are precisely overlapping measurements, the true impression of the distribution of the data requires that these data should be recognised as separate measurements. This requires the use of empty circles as symbols, because they can be recognised as separate even when they show >90% overlap. Writing a number by the data point is not an acceptable solution (see Fig. 8a as a bad example) as we cannot mentally transform a number into that many separate symbols. If there are only a few overlapping data points, they can be drawn close to each other, even touching (Fig. 9). The best way, however, is a process called “jittering”. This process adds a small random number to the data, and the graphing program subsequently treats them as separate points. Following this method, we can obtain a reasonably correct impression of the data distribution (Fig. 10). Naturally, this method should only be used to graph your data.
Sometimes we have data sitting on the x or y axis (Fig. 11). The emphasis on the data points allows the axis to be moved away (Fig. 12). This makes the interpretation of the data easier.
The principle of clarity requires that the emphasis is on the data. The data rectangle should be filled by the data only. At first glance, we try to interpret anything in the data rectangle as data. Therefore, any additional elements, including tick marks, legend, etc. should, where possible, always be outside the data rectangle. This helps us to interpret the figure. Marks, labels, and tick marks pointing into the data rectangle may generate confusion.
Comparing different panels can be difficult, and background grid lines (Fig. 13) and complementary marks can be useful. Such marks should be clearly different (lighter) from data and lines so as not to confuse the reader.
Data are interesting. People designing “interactive”, “interesting” data presentation methods try to move the emphasis from content to form — a bad design principle. Such practice often tries to disguise shallow thinking and/or an underestimation of the viewer. If you believe do not have interesting data, the wrong type of data was measured, and no amount of decoration will make them interesting.
Graphs with two dimensions can be wider than tall, as well as taller than wide. Which one is better? Our eyes are instinctively used to scanning horizontally, so we find the wider-than-tall shape easier to interpret. This is especially so if we have a data with a lot of variability, creating a curve that is “wiggly”. We can make a curve easier to interpret if the diagonal sections are as close to 45 degrees as possible. This is useful because our eyes can also detect small deviations from the diagonal. This technique is called “banking to 45 degrees”, and is automatically generated by more sophisticated graphing software. This is done iteratively by changing the height and width of a graph until most of the diagonal lines are as close to 45 forty-five degrees as possible.
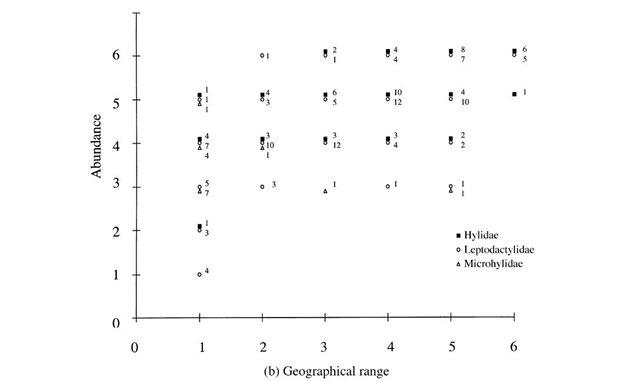
Fig. 8a When identical data points are to be represented, do not combine two forms of data presentation as here (symbols accompanied by numbers). This cannot be correctly interpreted. Fig. 2 from Murray et al. (1998), https://doi.org/10.1046/j.1365-2656.1998.00217.x. © British Ecological Society. All rights reserved. Permission for further reuse must be obtained from the relevant holder of the exclusive rights.
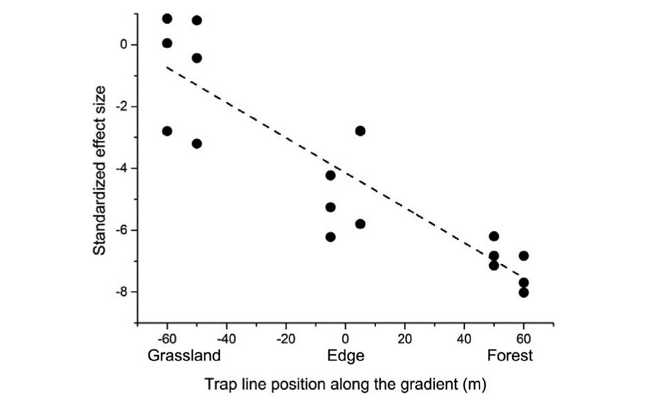
Fig. 9 When there are few identical data points, you can draw them touching each other, as the two data points here at x=50 and 60. The resulting distortion is not large. From Magura & Lövei (2019), http://doi.org/10.1111/1744-7917.12504. © 2017 Institute of Zoology, Chinese Academy of Sciences. All rights reserved. Permission for further reuse must be obtained from the relevant holder of the exclusive rights.
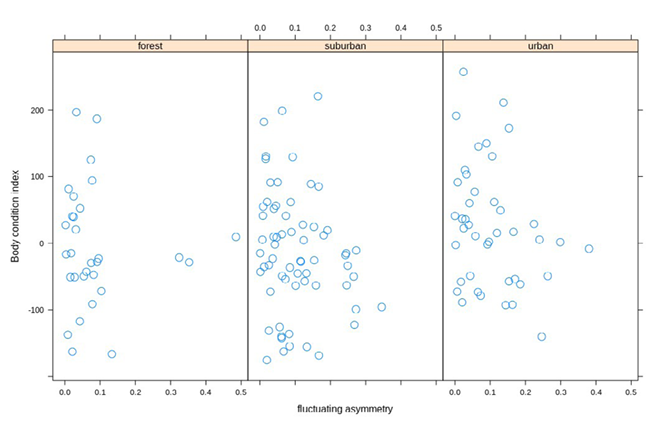
Fig. 10 When numerous data points overlap, drawing them as touching points would grossly distort graphical perception. In such cases, a judicious degree of jittering allows the viewer to distinguish between identical points with minimum distortion in trend perception. Modified from Elek et al. (2017), https://doi.org/10.1556/168.2017.18.3.4. CC-BY 4.0 (http://creativecommons.org/licenses/by/4.0).
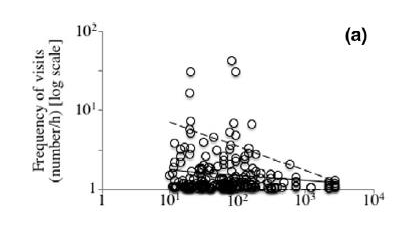
Fig. 11 Too many data points sitting on the horizontal axis make this graph cluttered. From Godinez-Alvarez et al. (2020), https://doi.org/10.1002/ece3.6285. CC-BY 4.0 (http://creativecommons.org/licenses/by/4.0).
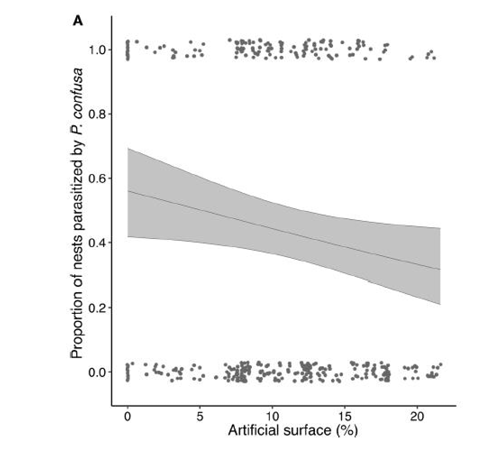
Fig. 12 Moving away the horizontal axis increases clarity. Note, however, that full dots are suboptimal symbols — close-lying data points are not easy to distinguish. Figure from Audusseau et al. (2020),https://doi.org/10.3390/insects11080478. CC-BY 4.0 (http://creativecommons.org/licenses/by/4.0).
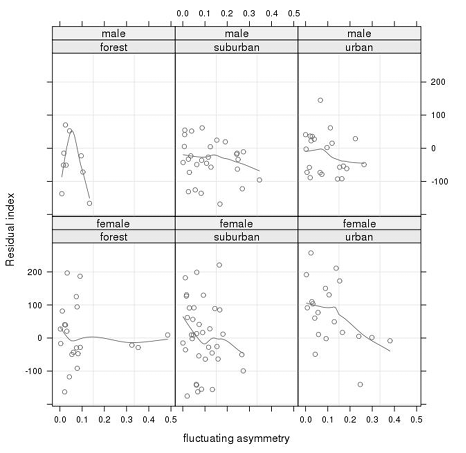
Fig. 13 An identical, visually gentle background grid helps to compare the position of the data points on different panels. Figure from Elek et al. (2017), https://doi.org/10.1556/168.2017.18.3.4. CC-BY 4.0 (http://creativecommons.org/licenses/by/4.0).
Clutter is generated when different elements of text, of various size and font type, are used in the graph. Often, there is simply too much explanation (Fig. 3), drawing attention away from the data points themselves.
Graph Types to Avoid
Bar chart
The bar chart is one of the oldest types of scientific figures (Playfair, 1622), and it is still one of the main types of figure used in published articles. The data value is represented by the height of a column — the width of the column is irrelevant. Note that there is a difference between a histogram and a bar chart, even if they seem superficially similar — in the former the width has a meaning. Bar charts can often be replaced by a simple dot, appropriately placed. An additional problem that many programs create is that, on the horizontal axis of a bar chart, the axis variable is categorical — but the program might arrange them at even distances, sometimes falsifying the time trend (Fig. 14).
Bar charts should be avoided because they use two dimensions to present one-dimensional data (the bar has a height and a width — but only the former carries any information), thus violating the principle of economy.
When bars are grouped into a composite bar chart, comparison between them becomes complicated and it is not possible to clearly perceive what they are telling us (Fig. 15). In the case of stacked bar charts (Fig. 16), comparison becomes even more is difficult because the different segments start, as well as end, at various heights, and we cannot judge the lengths correctly. Both should be avoided.
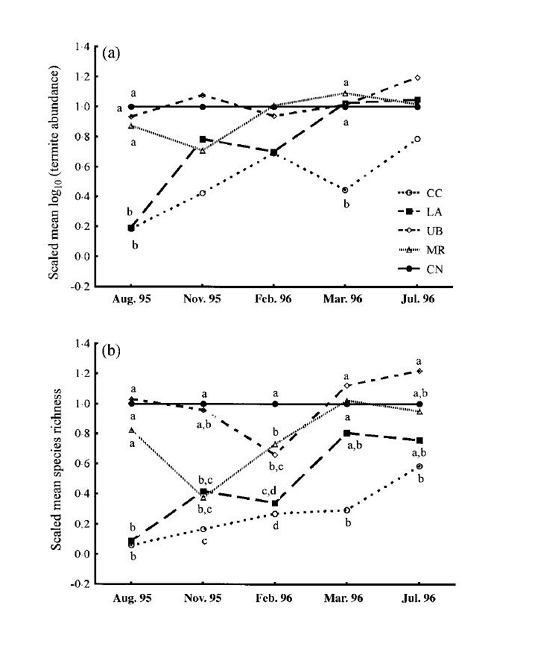
Fig. 14 Due to the incorrect scale on the horizontal axis, the rate of change cannot be correctly perceived. From Davies et al. (1999), https://doi.org/10.1046/j.1365-2664.1999.00450.x. Reproduced with permission.
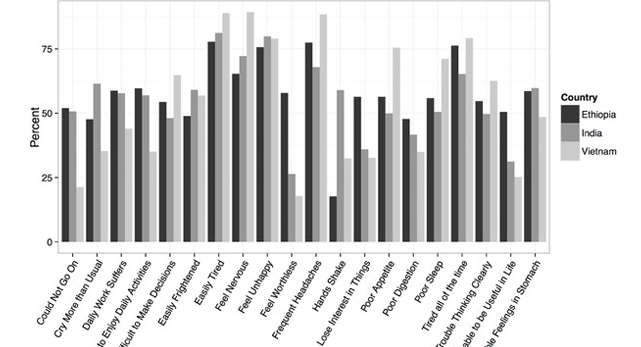
Fig. 15 A grouped bar chart. The same type of data from the three countries can be easily compared but a “country profile” is nearly impossible to perceive. Note also that the horizontal organisation, alphabetical by labels, is suboptimal. From Gausman et al. (2020), https://doi.org/10.1371/journal.pone.0228435. CC-BY 4.0 (http://creativecommons.org/licenses/by/4.0).
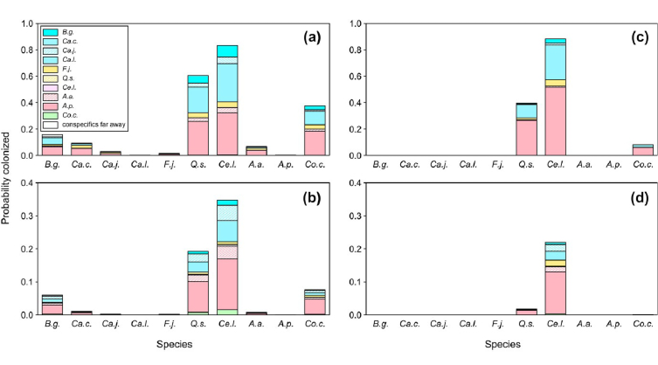
Fig. 16 A stacked bar chart. Due to the constantly shifting baselines, the smaller differences are difficult to interpret. From Masaki et al. (2019), https://doi.org/10.1111/oik.06236. CC-BY 4.0 (http://creativecommons.org/licenses/by/4.0).
Pie chart
Pie charts are frequently used in business and on “pseudo-scientific” graphs. This is a bad design overall, because we are asked to make judgements based on the area occupied by the segments. Our eye cannot judge differences in area well, and only the biggest differences can be identified correctly. That renders this figure type virtually useless. This fact is inadvertently admitted by the common practice of dividing the pie into a few sections only, as well as by writing the actual values of the pie chart segments near the segments themselves (and the common program option that allows one to generate such figures) — thus also breaking the principle of “no double data presentation” (Fig. 17).
There are now several new methods of data presentation available, developed during the last 30 years. Many of these were pioneered by the team at Bell Laboratories, with the leadership of William Cleveland.
The preferred graph to present one-dimensional data should be the dot plot. The dot plot is a relatively new graphical method, even if it is beguilingly simple — the first dot plot was apparently published in 1984 (Cleveland, 1993). This is eminently suitable to present one-dimensional data, where other variables are categorical ones. Traditionally, the measured variable is pictured along the horizontal axis, and the labels are outside the panel, along the vertical axis (Fig. 18). If there is more than one categorical variable, the multi-way dot plot can be used (Fig. 19). In such cases, carefully consider the primary vs. secondary comparisons (Fig. 20).
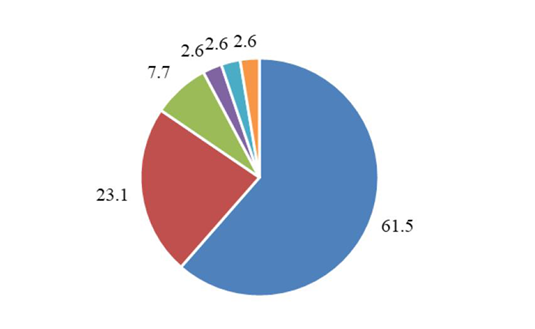
Fig. 17 A circle diagram with numbers: a case of double data presentation. From Klimek-Kopyra et al. (2020), https://doi.org/10.3390/agriculture10080314. CC-BY 4.0 (http://creativecommons.org/licenses/by/4.0).
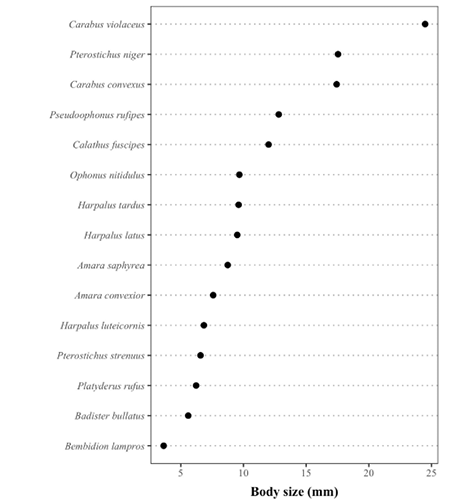
Fig. 18 A sample dot plot. Differences are presented along one dimension, e.g. length. This allows a precise perception of pattern as well as individal differences, even small ones. M. Ferrante, unpublished data. Image by author (2020).
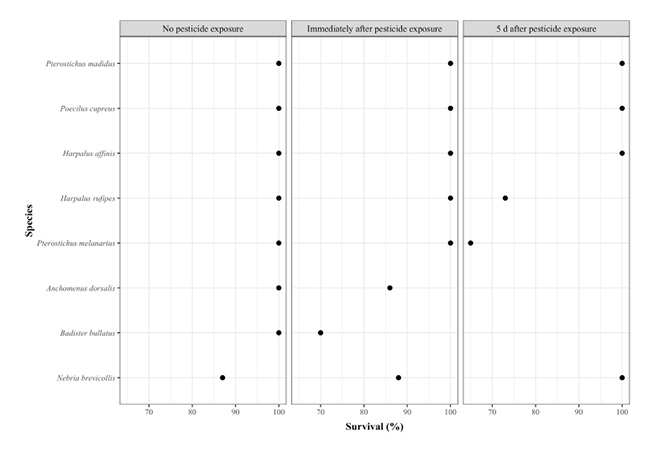
Fig. 19 A multi-way dot plot, presenting survival data by various ground beetle species exposed to pesticides. The emphasis here is on the effect of treatments on the different species. Data from Greenop et al. (2020). Image by author (2020).
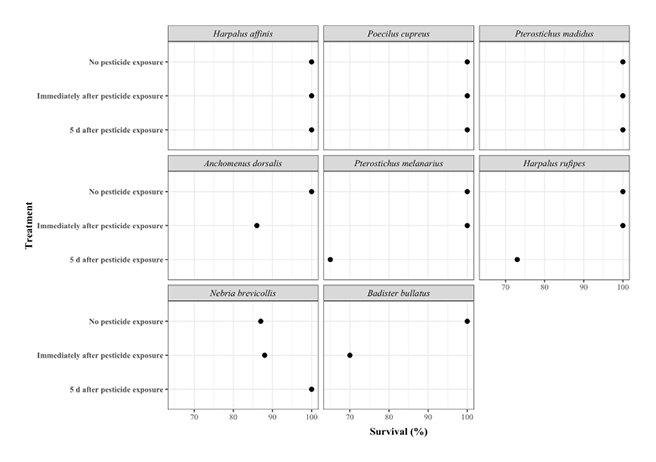
Fig. 20 An alternative multi-way dot plot of the same data as on Figure 19. Now the reaction by the different ground beetle species to the treatments is the focal comparison. Data as for Figure 19. Image by author (2020).
Within the panel, the largest values should be near the top of the panel, sequentially followed by smaller ones. This is useful for Gestalt (shape) perception. In multi-way dot plots, an optimisation algorithm should be employed, so that the larger values appear most frequently near the top (Cleveland, 1994).
Two-dimensional data are the most common type, and a line-and-symbol plot is suitable for presenting such data. There are several additional methods, especially useful for data exploration, including the locally weighted regression (loess or lowess), the conditional plot, or co-plot, and the scatterplot matrix. These and other useful graphical methods can be found in Cleveland (1993, 1994).
Figures in papers vs. figures used in talks
Never use a figure published in a paper as illustration in an oral presentation. The reason is that the first one will be printed, and readers can absorb and evaluate it at their own pace. It will not vanish. When a figure is used in a talk, it must be understood over a shorter period of time, set by the speaker — the figure is only visible while it is projected during the talk. Consequently, these two types of figures are not interchangeable: a good figure for a paper usually contains too much information to be useful in a talk. In the same way, a figure that is useful in a talk rarely has sufficient information to be worthwhile as a figure in a paper. Complex information can be conveyed by a single, carefully designed figure. The same information needs several figures in a talk.
Furthermore it is possible, and advisable, to use colour in a figure used in a talk, while the use of colour is usually prohibitively expensive to publish in a paper. Figures in a paper should usually be black-and-white.
Therefore, prepare different, specially tailored figures for a paper and a talk, even if the same data are to be presented. When thinking of figures that will be published in a paper, think black and white. Consider the careful use of colour for figures to be projected during a talk. Internet publishing often allows authors to publish colour figures at no extra cost. However, the above constraints on complexity vs. time allocated to interpret figures mean we should still not use a published colour figure in an oral presentation.
The same goes for a poster, mainly due to the type of setting in which a poster is typically presented. At a conference, too many posters usually compete for the participants’ attention, and they cover too many different things. In theory, viewers can spend unlimited time in front of a poster but, in reality, they rarely do so. Therefore, a poster is closer to a talk than to a paper.
Colour
The use of colour used to be rare in scientific journals. The reason was cost: printing black-and-white text, figures and photos is more expensive than printing text, but much cheaper than printing the same in colour, mostly because better quality paper and more sophisticated printing machines had to be used. Moreover, printing is done on sheets of paper, usually equivalent to 16 pages (these are cut up after printing). Consequently, those 16 pages all had to be printed using the same machine, even for only a single colour figure. The extra cost, which was nearly always passed on to the author, was usually over USD 1,000. This made colour illustrations very rare in the scientific journals. This is changing: many journals publish colour in their digital issues for free, while they still print the same figures in black-and-white in the printed edition. However, this is becoming less and less justifiable, as the cost of printing in colour vs. black-and-white is no longer so different.
Use colour to help understanding, not for decoration. Modest use of colour is very helpful, but do not abuse the technical possibilities to generate many different colours. Try to use harmonious combinations for maximum contrast. These are formed by colours at opposite positions on the colour wheel. Differences in shade can work, but they are very much equipment-dependent. What appears a nice shade on your own screen, could turn to a garish colour on a projector, if driven by a different computer.
There are several helpful programs on the Internet to help choose appropriate colour combinations. The Colour Scheme Designer (www.colorschemedesigner.com, now migrated to www.paletton.com) also allows you to check how people with various colour-related vision impairments will see your chosen colour scheme.
Proportion, Scale and Appearance
Graphs should tend towards horizontal, being wider than tall. Our eye is naturally practised in detecting deviations from the horizon. This also helps with ease of labelling. Avoid labels aligned in various directions. In keeping with reading direction (left to right), we can look up the impact of the cause (independent variable) on the effect (dependent variable) along the horizontal axis. When the cause is presented on the horizontal axis, you have horizontal depth, i.e. space to elaborate.
Box 11. Reviewing/evaluating figures
1. The first question must be: Do the data justify a figure? Should these data be put into a table, or can they be written in the text?
2. Is the type of figure acceptable? Is a better type of figure necessary? (dot plot, multiple dot plots, co-plot, scatterplot vs. histogram or pie chart)
Economy:
How is the data/ink ratio? Can this be improved?
Is the data rectangle well filled with data? Are any elements that do not belong there?
Integrity:
Is data dimensionality observed? Are the axes appropriate? Is context provided? If multi-panel figure, is the comparability of panels observed?
Clarity:
Are the axis scales appropriate? Are the ticks, tick labels, and symbols OK? Are both axes clearly labelled, with units of measurements? Can ink be eliminated and information retained?
Format: is the size of the figure, the font size and type, the width: height ratio of the figure acceptable?
Is banking to 45 o to be employed? Is there no superficial decoration, unnecessary visual novelty? Are the symbols well chosen and visible? Are there overlapping symbols, or symbols sitting on axes — if so, are the axes moved to make these symbols visible? Does the figure withstand reduction when printed?
Photographs
Photographs can be a useful addition to your paper. However, they are not decoration — they should be informative. Photos are more expensive than text to produce, so editors are vigilant when it comes to including photographs. The editor will almost always ask if you really do need a photo — so you had better have a reason to justify your request. Photos of habitats, organisms, occasionally of equipment can be useful. In some cases, a microphotograph, a gel photo, or a crystallogram is the vital piece of evidence, and it should be included.
If you decide your paper needs a photo, carefully check the reproduction standard of the chosen journal. Only high-quality photos are worth including — but the printing quality will also have to be high. Colour photos are nearly always at your expense, and they can be very costly.
Black-and-white photos usually do not cost you extra. Many journals have both electronic and printed versions, and such journals often allow you to include a colour photo, at no extra expense, in the electronic version of your paper, while the printed version will carry a black-and-white photo. In that case, it is best to submit two versions of the photo; one in colour, and the other one in black and white.
As mentioned earlier, figures are almost inevitably reduced in size when printed. This always causes a loss of detail and definition. You can plan for this in the relatively simple line graphs (although it does need attention), but such diminishment may be fatal to photos: so how can you control photo quality? The best result is achieved if there is no reduction or enlargement. It is very rare that every square centimetre of your photo is vital, so experiment with cropping, i.e. selecting the part of the photo that is important (this is often only a small part of the photo). Many photographic programs enable this. Suitably cropped photos can be reproduced without reduction, thus retaining the original level of detail, but it is useful to consider the dimensions of the journal. If you manipulate your photo electronically, this must be declared on the caption.
When multiple photos are presented, they can be compiled into a set of images (a plate). If appropriate, you can place a scale on the photographs. If you choose to label your photos with letters, make sure these are visible. Indicate the magnification, too, in the caption.
Today, most journals work with digital photos. This part of the process is, as yet, rather shaky due to the occasional transferability problems between programs and figure formats and, thus, there are very detailed instructions on how to prepare and submit a digital photograph. Read these instructions very carefully. Check acceptable or preferred file formats; you can contact the technical editor for clarification. This will be seen as co-operation, not hindrance. This, however, is something to consider at the stage when your manuscript has been accepted for publication.
If you are asked to provide hard copies of your photos, write appropriate information on the back of the photo, in soft pencil. This in-photo information should indicate the manuscript number, the photo number, and the orientation. Do not think it is obvious — the printer is not a scientist, so do not expect her to be able to interpret the photo. Indicate the desired position of the photo in the text.
Do not forget about pen and ink illustrations. They can be very useful, but must be drawn by a professional illustrator. Use them even if you have to pay for the drawing out of your own pocket. It does not cost the earth, and you will not regret the expense.
