16. Analysis of Sample Graphs
© Gábor L. Lövei, CC BY 4.0 https://doi.org/10.11647/OBP.0235.16
It may sound surprising but, once you develop an eye for good graphs, you will notice the occasional mistake in graphing practice. Several scientific editors agree. Per Enckell, the then-editor of one of the prime journals in the field of ecology, Oikos, re-published in the journal a chapter from the book by Edward Tufte, the eminent practitioner of presenting visual information (Tufte, 1990). Alas, this gesture did not revolutionise graphing practice. Valiela (2001) has also devoted a chapter to provide suggestions for designing scientific graphs. He selected published graphs, analysed their imperfections, and suggested improvements. The same approach is followed in this chapter. Below, you will find some of the most frequent mistakes: too few data to merit a figure (example 1), problems with the integrity of the figure, making appropriate comparisons difficult (example 2), inappropriate coding that impedes understanding (examples 3 and 5), and clutter (example 4). In each case, I present a more acceptable version of the same figure. Box 11 also lists some of the criteria to consider when designing your graph.
Example 1. The Graph that Need Not Exist
This graph presents the survival probabilities of elephant seal juveniles (1-3 years old) and adults (4 years or older) on two sub-Antarctic islands, Macquarie and Marion (Fig. 21; Fig. 7 in McMahon et al., 2003).
There are several deficiencies in the figure concerning economy, integrity and clarity:
- the figure is too wide. It can easily be made narrower to fit into one column, saving ca. 50% of space.
- the data rectangle is not filled by data — a large part on the left is only there to accommodate the legend. This is needless — legends should be placed above the figure, so that the figure is not wider than necessary. There is no need to abbreviate “Macquarie Island”. The frame around the legend is superfluous. If the legend were above the figure, the vertical axis could start at p = 0.72, saving more space.
- there is double data presentation: mortality values are represented by symbols, but precise values are also written on the figure. This is wrong, as the same data cannot be presented twice.
- there is also double coding: not only are the symbols different but the vertical lines marking the confidence intervals are all different
- the axis labels are not appropriate or are completely absent. The vertical axis should probably be “Estimated survival, %” or “Estimated probability of survival”
- the labels of the two groups, juveniles and adults, do not line up with their respective data points
- the symbols are too small — and hardly visible. The tick points are inside, whilst secondary ticks would be helpful to allow the readers to make a better estimate of the values. The lettering on the figure is a little too small, which decreases readability.
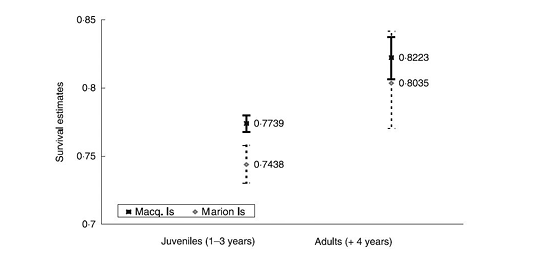
Fig. 21 A figure with too few data points. From McMahon et al. (2003), https://besjournals.onlinelibrary.wiley.com/doi/pdfdirect/10.1046/j.1365-2656.2003.00685.x. © 2003 British Ecological Society. Reproduced with permission.
Overall, however, the main problem is that this figure contains too little information: four data points and their relative 95% confidence intervals. The same information can be presented more economically in the text, therefore, there is no reason to construct a figure here.
Example 2. Small Effect, Big Effect: Misleading the Reader
This example is from a study on the winter mortality of Redshanks (Tringa totanus), in an area of Great Britain where there is a large population of wintering birds that are harassed by European Sparrowhawks (Accipiter nisus) preying on them (Fig. 22, Fig. 3 in Whitfield, 2003).
The first impression from the figure is that bigger flocks suffer higher winter mortality, and this relationship is steeper in the case of adults than juveniles. A close analysis of this figure shows, however, that this conclusion is not necessarily correct. The distortion arises because the physical size of the two panels are identical, yet their vertical axis scale is drastically different: on the top panel, presenting data on juvenile mortality, the range is from about 19% to 58%, while the lower panel, with the adult mortality data, ranges from about 3% to 18%. Considering the three graphing principles, other imperfections arise:
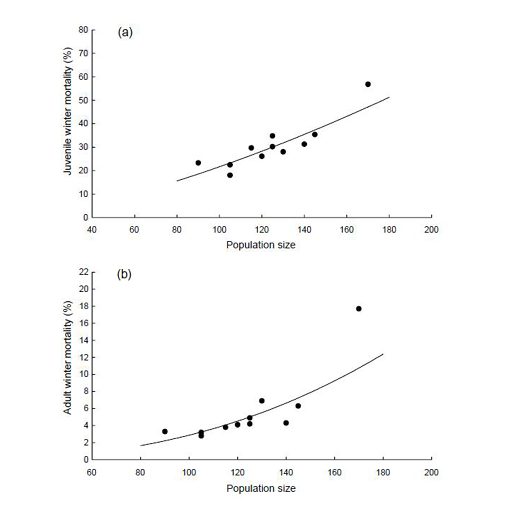
Fig. 22 A figure with two incomparable panels. From Whitfield (2003), https://doi.org/10.1046/j.1365-2656.2003.00672.x.
From the point of view of economy:
- uneconomical use of space, due to bad choice of axis intervals. There are no measurements below 90 on the horizontal axis, and nothing above 170. On the vertical axis of the upper panel, no values appear below 15 and above 60, while the range of the y values on the lower panel are from 2.5 to 18. This also forced the typesetter to place the figure between two columns, thus wasting even more space. Modifying the axes would save a lot of space;
- the full circles are not the best symbols, due to overlap on the lower panel;
- using range-frames can save some ink;
- there are more than the necessary number of tick labels on the vertical axis, especially on the lower panel;
- the vertical axis labels allow the precise identification of the data on the panel, thus the panel labels (the letters a and b) are not needed.
Concerning integrity, the two panels are not comparable: they present very different ranges, yet their physical size is identical. This misleads the reader, who is not able to correctly interpret the relationship between flock size and mortality in adults vs. juveniles.
From the point of the third principle, clarity:
- the ticks point inside, into the data rectangle. The data rectangle should be reserved for data only;
- the symbol sizes, axis labels, and tick labels are all a little too small, just about readable in the original paper. Reducing the number of tick labels not only improves the economy of the figure, but would also allow an increase in the size of the tick labels, making them more readable;
- there are no measurement units on the horizontal axis label. It probably should read “Population size, no. of individuals”.
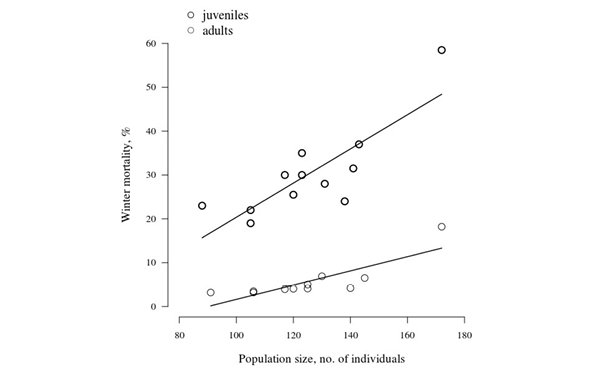
Fig. 23 Data from Figure 22, re-drawn. The two data series are now straightforwardly comparable, and the trends can be truthfully interpreted. Image by author (2020).
On the redesigned figure (Fig. 23), both the measurement series appear on the same graph, because they do not overlap. Now it is obvious that both fit a linear regression, and the relationship between mortality and population size is steeper in the case of juveniles compared to adults. The axis intervals are reduced, and the two axes do not touch. Empty circles are used as symbols, with increased sizes; letter size is increased, and a serif font is used, which has better readability than the original sans serif. A small simplification is that the axis label units are not in parentheses, but are separated from the measured parameter by a simple comma.
The highest mortality values in both age classes appear in the largest population. The difference is so great that these almost seem like outliers. Due to the lack of more data points from larger populations, however, the suspicion must remain unconfirmed that there may be a threshold size over which predation pressure radically increases.
Example 3. The Chaotic Figure — Coding Can Stand in the Way of Understanding
This paper reports on the effect on termites of various understory treatments in a tropical forest (Davies et al., 1999), from complete clearance to selective clearing up of termite mounds and undergrowth. Figure 24 (Fig. 2 of the original paper) presents the changes in density and species richness of termites over a one-year period, considering the changes in the untreated control area as baseline. The trends are not simple, the lines criss-cross each other, but the figure design does not allow fast and effective decoding.
The biggest mistake concerning the economy of this figure is the double coding: the treatments are marked by different symbols; in addition, they are connected by different lines. This is needless and breaks the “no double coding” principle. The figure has more visual novelty than necessary for swift decoding.
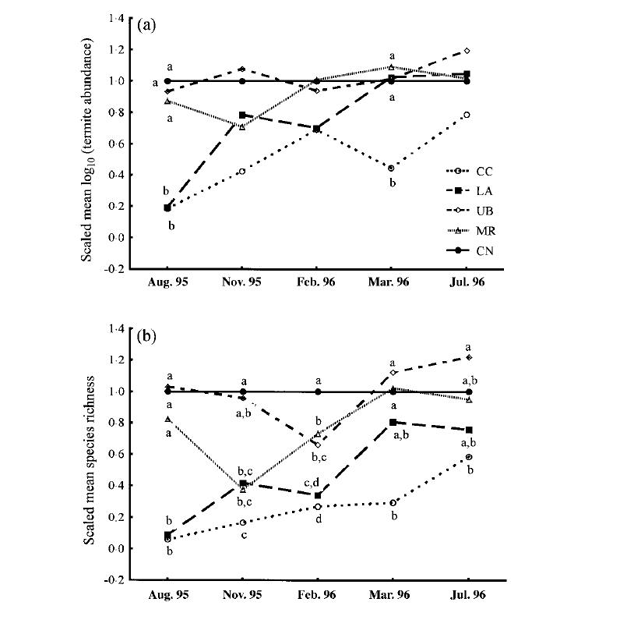
Fig. 24 A cluttered figure with faulty horizontal axis. From Davies et al. (1999), https://doi.org/10.1046/j.1365-2664.1999.00450.x. Reproduced with permission.
The axis lengths are also longer than necessary, probably to accommodate the legend which should be outside the data rectangle, anyway; the vertical axis starts at -0.2, (which is an impossible value in this context). Thus, the figure uses more space than justified. The horizontal axis is also longer than optimal: it starts before the first, and runs after the last sampling occasion, making the figure wider than needed. Consequently, the printer was forced to use the full width of the page to place the figure, creating large empty spaces on the page on both sides.
From the points of integrity, there are two points to mention:
- the horizontal scale is wrong: the equidistantly marked sampling occasions suggest that they were taken at equal time intervals. The period between two sampling occasions varies from one month (February-March, 1996) to four months (March — July, 1996). Consequently, the figure distorts the time trend, misleading the reader;
- measures of variance are missing — as the values are means, according to the axis labels, some measure of variance is necessary. There are labels on the graph, indicating the significance of differences between data points, but this is neither complete, nor easy to interpret.
The clarity of the figure is also suboptimal:
- ticks point inside the data rectangle. Due to the larger-than-necessary area occupied by the figure, these do not obscure data, but this may change when the data rectangle is reduced to its necessary minimum size. There are too many tick labels on the vertical axis, while the horizontal axis label is missing. The symbol sizes are too small, and not easily distinguishable. This is partly due to symbol choice — several of them are too similar to allow fast and precise identification of the individual treatments. The legend is placed opportunistically inside the data rectangle, but the data rectangle had to be increased, otherwise the legend would not fit. The codes are cryptic, and their meaning is not given in the caption, either. This breaks the principle that a figure, in combination with its caption, must be understandable without reference to other parts of the article;
- the reference line appears with codes that serve no clear purpose. The codes for statistical comparisons are also complicated.
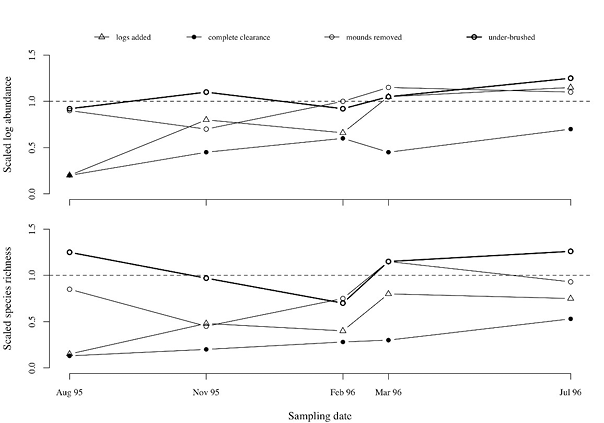
Fig. 25 The horizontal axis with true-to-time indicates a sudden change in some sites between February and March. Image by author (2020).
This figure can benefit from a range of improvements. The treatment coding can be written out, instead of using cryptic abbreviations. The legend can be placed above the data rectangle, reducing clutter. The control is coded simply as a horizontal line. The horizontal axis is modified to indicate correctly the dates when samples were taken, thus depicting the proper time trend. Now, the sudden change between February and March is very clear, hinting at an important seasonal factor change. The double coding is eliminated. The curves and lines are simplified. The two panels have the same vertical scale. The size of the symbols is increased; the font is larger and is changed to a serif font for easier readability. The axis labels are modified to indicate the parameter as well as the measurement unit. The tick labels are fewer and point outside. The coding of the differences between treatments is also simplified: letter codes appear only by those data points that are significantly different from the reference (control) value.
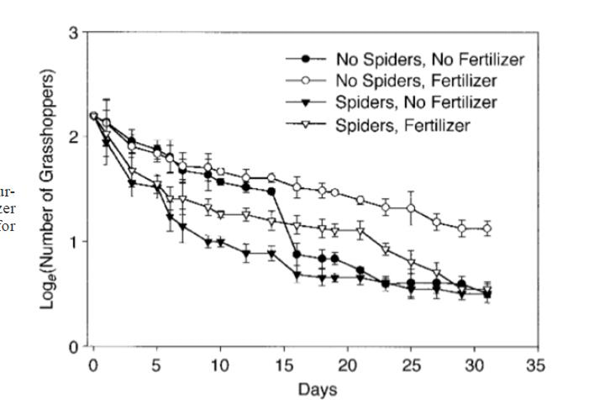
Fig. 26 A figure with a seemingly unavoidable clutter. From Oedekoven & Joern (2000) https://doi.org/10.1890/0012-9658(2000)081, © 2000 by the Ecological Society of America. All rights reserved. Permission for further reuse must be obtained from the relevant holder of the exclusive rights.
Example 4. Reducing Clutter
We often study an effect that unfolds over time. In such cases the starting conditions should be identical, so that the effects of the different treatments are comparable. Once the treatment starts to affect the response variable, differences appear and gradually become larger — but in the early phases of the experiment, the differences are small. Presenting such data using a figure poses a special problem, because overlap between the different values/curves is almost inevitable. Such is the case in the experiment reported by Oedekoven and Joern (2000), who examined the effect of spiders and use of fertiliser on grasshopper density on host plants. However, the resulting figure — Figure 3 in the original, here Figure 26 — contains several problems.
From the point of economy, the figure occupies more space than is justified. To reduce overlap among the response curves, the figure is wider than it is tall. Unfortunately, this graph was designed without considering the page size of the publishing journal: the figure is wider than one column, but not quite wide enough to span the whole width of the page. A large, ugly, empty space remains, and the typographer selected an unfortunate solution: placing the caption in the middle of the space to the left of the data rectangle. The data rectangle is also larger than necessary, to accommodate the legend and due to the excessive vertical scale. The vertical scale could start at 0.5 and end at 2.5; in which case, the data rectangle would be smaller and better filled, but, apparently, the graphing program did not allow such scaling. Evidently, this deficiency was not judged an important enough issue, by either the authors, or the journal editors, to be corrected.
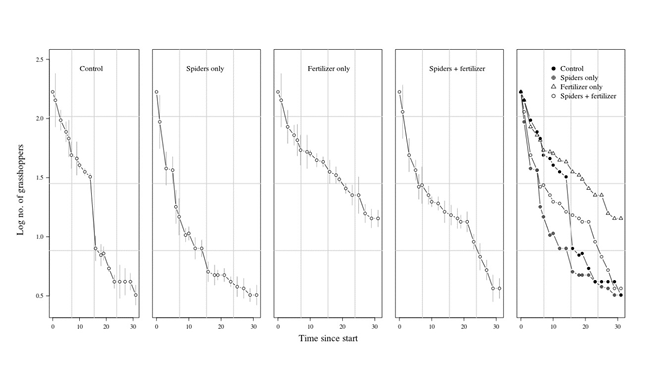
Fig. 27 The clutter on Figure 26 can be removed by plotting individual treatments separately. The background grid makes the different panels easily comparable. Image by author (2020).
The clarity of this figure is hampered mainly by the large overlap of the different curves, especially in the early days of the experiment but, also, near the end, where the curves again start to converge. Cleveland (1994) suggested that although, in general, figures should be wider than tall, when the curve is not very “wiggly”, the figure can be made taller than wide.
This figure can be improved by presenting the responses of grasshoppers to the individual treatments on separate panels, where the variability data are clearly visible (Fig. 27). Panel sizes have been reduced, achieving better economy. The same symbol type can now be used on the various panels, and the common background grid helps the between-panel comparisons. Comparison is further eased by the fifth panel, where only the means are presented, without the variability data and, thus, without clutter.
Example 5. Complicated Coding Hinders Interpretation
Cho and Lee (2019) analysed the microbiota in three species of Arctic birds: the Pink-footed goose (Anser brachyrhynchus), the Sanderling (Calidris alba) and the Snow bunting (Plectrophenax nivalis). Their figure 3 presents information on the relative abundances of dominant bacterial phyla identified in the digestive tract of a few individuals belonging to the three species (Fig. 28). This is on a divided bar chart, expressed as a percentage of relative abundance per phylum.
The bar chart is the oldest documented type of scientific graph, first used by Scottish economist William Playright (Tufte, 2001). Since then, it has remained a frequently used type of scientific graph, yet it is not always the best one to present complex data; this example displays several of the disadvantages.
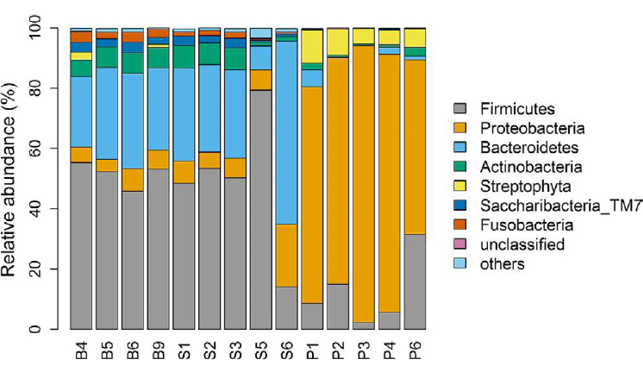
Fig. 28 Relative abundances of dominant bacterial phyla in the faeces of three arctic birds (B4, B5, B6, B9-Snow bunting; S1, S2, S3, S5, S6-Sanderling; P1, P2, P3, P4, P6-Pink-footed goose). The divided bar chart does not allow the reader to interpret small differences; only the big trends are decipherable. Fig. 3 from Cho & Lee (2020), CC-BY 4.0 (http://creativecommons.org/licenses/by/4.0), https://doi.org/10.1002/ece3.6299.
This dataset is one-dimensional: there are three variables, two of which are nominal (taxonomic names or bird identities). Only the percentage of relative abundance is a measured variable (to which a measurement unit can be attached, which is %). To use two dimensions to present the data, as on the original figure, is an abuse of dimensions — and, here, as in most cases, the width of the individual columns is indifferent — the second dimension, the column width, carries zero information. Only the length/height of different segments is important. Interpretation is made near-impossible by the continuously shifting baselines: many segments start at various positions within the columns, and this lack of a common baseline allows only crude comparisons. The colour coding does not help — several of the shades used are not easy to separate. In short, we are unable to perceive any pattern except the crudest differences — for which one does not need a figure. A different type of figure is called for.
A better method to present such data is the multi-way dot plot (Fig. 29). This allows the clear coding and separation of the various categories of endangerment of the groups of shrimps, and the measured variable is presented by a linear length with a common (vertical) baseline. In such cases, Gestalt perception is also easy. There is no need to use colour, and within-panel comparisons are swift and precise.
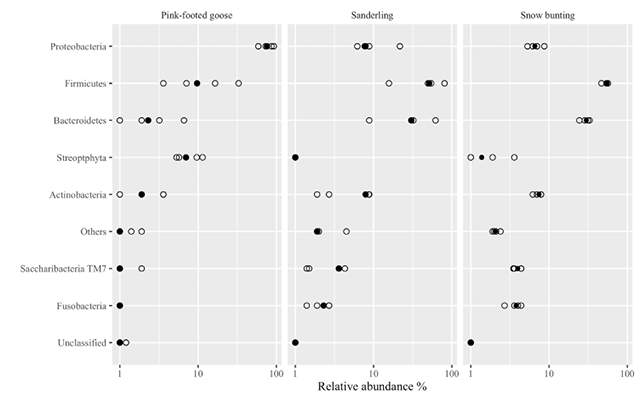
Fig. 29 A multi-way dot plot makes Gestalt recognition possible, as well as comparing microbiome profiles within and between the studied species. Data from Cho & Lee (2020) redrawn. Note the logarithmic scale on the horizontal axis. The empty circles indicate samples from individual birds; filled dots indicate the means. Image by author (2020).
