16. Ageing in the Wild, Residual Demography and Discovery of a Stationary Population Equality
© 2024 James R. Carey, CC BY 4.0 https://doi.org/10.11647/OBP.0251.16
In the late 1990s, while exploring methods for estimating population age structure using the post-capture longevity of fruit flies sampled from the wild (referred to as residual demography), I discovered an identity in which the fraction of individuals x days old in a stationary population equals the fraction that die x days later. I co-authored a paper containing this identity in 2004 as part of a larger publication with my biodemography colleagues, in which we extended the concept for practical application. In 2009, demographer James Vaupel published a proof of this identity and referred to it using the eponym Carey’s Equality. The Vaupel paper was then followed six years later (2015) by a surprise — the identity had been published in French thirty years earlier in the grey literature by demographer Nicolas Brouard. Remarkably the identity had never been cited in either the searchable (journal) literature or in any of the mainstream demography texts, treatises, encyclopaedias or reference books. Here I tell the story of how I discovered this identity, why it is important, implications for human demography and lessons learned along the way.
Introduction
A feature of many interdisciplinary fields such as biodemography is that questions are often asked that had previously not been considered by scientists in either of the “parent” disciplines (i.e. demography and biology). Presumably this is because the questions were not thought of in the first place, or, alternatively, because the answers were perceived in the respective fields to be of no general interest, to serve no conceptual purpose or to solve no pertinent problem.
In this chapter I describe a personal experience in which a question emerged during discussions with several of my biodemography colleagues in the late 1990s that appeared not to have been asked before (at least in the same way): What can information gathered on field-captured Mediterranean fruit flies (medflies) monitored through death in the laboratory tell us about population ageing in the wild? This question was the precursor that, in the late 1990s, led to my discovery of a mathematical identity unique to stationary populations stated as “the fraction of individuals x days old in a stationary population equals the fraction of individuals that die x days later.” This identity was published in a jointly-authored paper with Hans Müller, Jane-Ling Wang and other colleagues (Müller et al., 2004), followed six years later by its proof the Carey’s Equality eponym (Vaupel, 2009a), which, in turn, was followed by a paper with original analytical concepts and new theoretical insights into the identity (Rao and Carey, 2015).
The story thread focuses primarily on my quest to find a practical method for estimating age structure in medfly populations that, along the way, yielded the serendipitous discovery of this population identity. For important context, this journey was preceded by an earlier one that started when I was a participant in a 1987 workshop supported by the National Institute on Aging (NIA) that was spearheaded by the late Richard Suzman (who was then Associate Director of the NIA Division of Behavioural and Social Research) and organized by demographers Sheila Ryan Johannson and Kenneth Wachter at the University of California, Berkeley (Carey and Vaupel, 2019). Titled “Upper limits to human life span”, this workshop brought together biologists and demographers to discuss issues concerning ageing and longevity in the oldest-old (persons > 85 years old), but with a particular focus on the question concerning the existence of a specific lifespan limit in humans.
These discussions ultimately led to my involvement as a principal investigator in two different NIA-funded programs. One of these focused on oldest-old mortality (directed by James Vaupel) and the other focused on ageing in the wild (directed by myself). One of the major findings from one of the studies my colleagues and I conducted in the Vaupel-directed program was that mortality in a 1.2 million medfly cohort slowed at older ages (Carey et al., 1992). This outcome supported the hypothesis that medflies and likely many other species including humans do not possess specific limits to lifespan. Because this study used the medfly as a model system in the laboratory, the theme of the NIA-funded program that I directed was concerned with ageing in the wild. The results of these field studies on the medfly were designed to complement the laboratory studies as well as expand perspectives on ageing in evolutionarily-relevant (i.e. natural) environments.
Importance of Age in Demography and Biology
Arguably the greatest difference between population studies of humans and population studies of non-human species is the gulf in the availability of age-specific data. Whereas it is nearly ubiquitous in the former, it is mostly absent in the latter.
Without age information, human demography would be unimaginable in some types of studies and impossible in others, e.g. constructing Lexis diagrams, disaggregating age-period-cohort effects, tabulating actuarial rates, predicting future births and deaths, analysing migration trends, projecting population numbers or developing population policies. Indeed, demographers concerned primarily with human populations consider age as central to and as inextricable from their discipline as the concept of supply and demand is to economists, Darwinian selection is to evolutionary biologists and differential calculus is to mechanical engineers. Without age data, the field of demography would be reduced to a shadow of its current self at best and completely disappear at worst. Aside from population studies in a few sub-specialties in human demography (e.g. remote indigenous peoples), the absence of age data in human population studies is the rare exception.
The situation is the near-exact opposite in the vast majority of population studies concerned with non-human species. For example, the accuracy is extremely low and the costs generally extremely high for virtually all of the methods used to estimate insect age (Lehane, 1985) including wear-and-tear (Tyndale-Biscoe, 1984), cuticular hydrocarbon layering (Gerade et al., 2004), accumulation of bio-compounds (Lehane, 1985), and transcriptional profiling (Cook, McMeniman, and O’Neil, 2008; Cook and Sinkins, 2010). No ageing method has ever been routinized as part of a standardized surveillance program in applied insect ecology such as for monitoring insect disease vectors (mosquitoes, tsetse flies) where insect age is an extremely important component in disease transmission (Cook, McMeniman, and O’Neil, 2008). For vertebrates there are some exceptions including (1) long-term mark-recapture studies on selected species of birds and large mammals (Nussey et al., 2006; Ozgul et al., 2009) and (2) ecological studies spanning many taxa that use post-mortem techniques to estimate age including otolith layering in fish (Campana and Thorrold, 2001; Limburg et al., 2013) and tooth wear in wildlife (Dinsmore and Johnson, 2012). Although there are a number of relatively recent papers for estimating age- and stage-specific life history parameters (Cochran and Ellner, 1992; Metcalf et al., 2009; Davison, 2011; Horvitz and Tuljapurkar, 2008), this is a different concept than that for estimating the age of individuals.
The profundity of not having information on individual and population age in studies of non-human species is not recognized by the majority of mainstream demographers because of their exclusive focus on humans. But this lack is deeply frustrating to the majority of population biologists and applied ecologists. This is because the absence of information on age and age structure in populations of non-human species severely limits the scope and depth of demographic analysis and modelling in several important respects. Firstly, the majority of the most sophisticated demographic models in the literature are developed for and concerned with human populations. These methods both assume and require information on individual-age and population-age structure. Therefore, without age data on non-human species, many of the classical demographic models including cohort life tables and age-structured population models apply in theoretical and laboratory contexts rather than in the wild settings where they are the most relevant.
Secondly, age is a major source of risk which, as a general concept, underlies the quantification of various age-specific force-of-transitions, for example in sexual maturation, marriage and divorce, reproduction, disease acquisition, disablement, retirement and death. Because force-of-transition concepts apply to changes of state in species across the Tree of Life (Jones et al., 2014), the lack of age information limits demographic analysis.
Thirdly, the results of demographic studies in the laboratory are of marginal value without the availability of age data for cohorts and populations in the field. These limitations frequently preclude opportunities to refine, adapt and expand powerful demographic tools for use in analysis of populations of non-human species. They also restrict the range of possibilities for creating new demographic concepts and building new models based on the treasure-trove of life history (and thus demographic) characteristics observed across the Tree of Life.
In light of the near-absence of methods for estimating age structure in fruit fly populations and the importance of finding a method, several of my biodemography colleagues and I set about trying to develop new concepts for studying ageing in the wild. We believed that it might be possible to achieve a better outcome for estimating age structure in insect populations using demographic models than with costly and mostly inaccurate high-tech methods used to estimate the age of individual insects.
Discovery and Formulation in Four Stages
A retrospective examination of the process that took me from an idea to the discovery of the life table identity occurred in four stages. Remove any of the first three stages or even one of the within-stage details, and I would likely not have discovered the identity. The last stage was model formulation after having identified the key equivalency. Key parts of the following sections are taken from a paper by myself and co-workers written at approximately the same time as this one (Carey, Silverman, and Rao, 2019).
Stage I: Framing the Concept
The germ of the idea that ultimately led to the discovery of the population identity was motivated by my view, and that of many insect ecologists, that the conventional methods for estimating individual age and age structure in wild populations described earlier are sorely lacking. Thus, the question that arose in 1998 on a research retreat in Crete (Greece) involving myself, mathematical demographer Anatoli Yashin and geneticists Lawrence Harshman and Linda Partridge was: “What can be learned about aging in the wild from information gathered on field-captured fruit flies of unknown age monitored in the laboratory?” This initial question, the concept of which is illustrated in Figure 1, was framed around the potential use of biological information in what Partridge referred to as “residual demography”, e.g. the post-capture levels and patterns of egg laying; challenge assays such as starvation and desiccation resistance; health status and remaining longevity. None of us had an inkling that this biological idea would lay the groundwork for the discovery of a population identity.
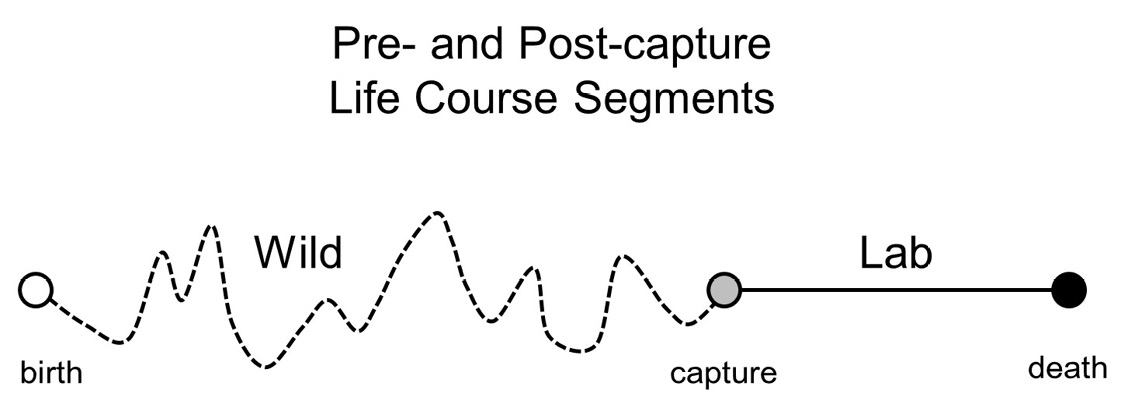
Fig. 1 Schematic diagram of the captive cohort concept in which the life course of an individual is divided into pre- and post-capture segments. An individual is born (open circle), lives an unknown fraction of its life in the wild (dashed line), is captured (shaded circle), and is monitored through death (black-filled circle).
Stage II: Simulation Studies
Inasmuch as I am trained as an insect ecologist and not as a mathematical modeler per se, I asked several of my mathematical demography colleagues what statistical concepts would be required to estimate the age structure of a fruit fly population using the post-capture survival information of wild-caught individuals of unknown age.
Suppose a fly of unknown age is captured in the wild and lives for twenty-three days in the laboratory. Assuming Gompertzian mortality rates and a maximum lifespan in the laboratory of sixty days for this (hypothetical) species, what is the best estimate of the age of this individual fly when it was captured, and the confidence intervals for this estimate?
The consensus among my colleagues was that answering this question would require development of a sophisticated Bayesian statistical model. Given the time and statistical expertise required to build a model designed to answer this type of question, the biological studies needed to both parameterize and validate it species-by-species, and the likelihood that both the accuracy and precision of the model would be low, I decided that statistical model-building should not be my next step. Instead, I decided my most parsimonious next step should be simulation studies designed to answer the question: “What are the survival patterns of a group of fruit flies that are each captured at random ages in a computer-generated stationary population?”
Example results of simulations based on laboratory data collected on 1,000 individual medflies (Carey et al., 1998) revealed distinct patterns that were much different than those for a cohort of newly-enclosed fruit flies (Figure 2). This was no surprise, since survival of the group involved individuals of different ages and thus different composite mortality rates. But on seeing the consistency of the survival patterns, my immediate thought was that there had to be a mathematical explanation that would account for their similarity. Follow-up simulations using replicates with sample sizes in the many thousands of individuals yielded virtually identical post-capture survival curves thus confirming the idea not only that there existed an underlying mathematical model, but that it might be simple. Although in retrospect the results of these simulations now appear obvious, they were not obvious to me at the time.
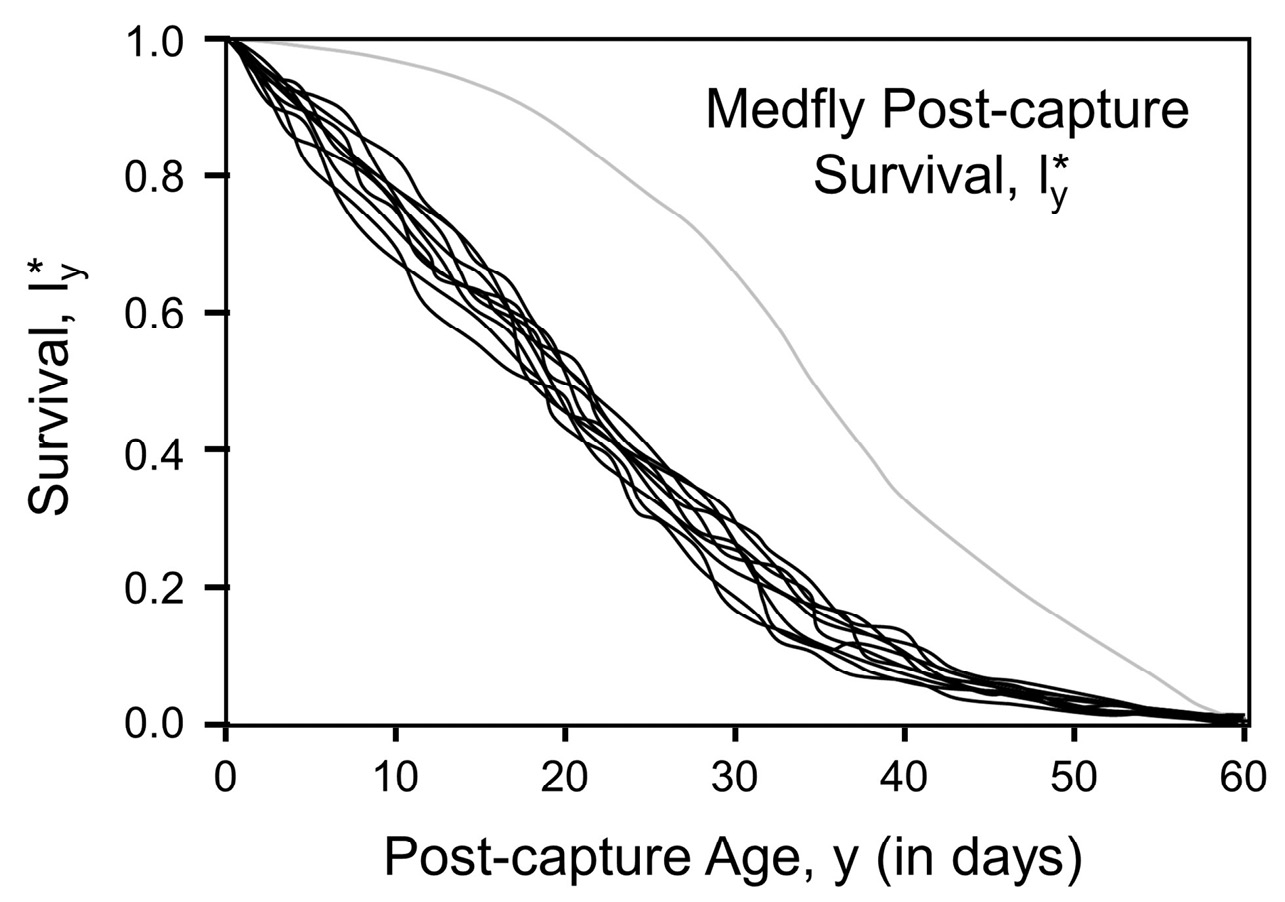
Fig. 2 Survival (l*y) curves generated from simulation studies consisting of 10 replicates of 100 medflies sampled at random ages and monitored through their remaining lifetimes (i.e. post-capture segments, see Fig. 1). The grey line is the age-specific survival schedule of a birth cohort where age is in chronological rather than post-capture time (denoted y). Medfly survival data used for simulation from Carey and co-workers (Carey et al., 1998).
Stage III: Construction of a Heuristic Life Table
In order to move from a field sampling concept to the development of an analytical framework, I decided to construct a simple heuristic pencil-and-paper life table model as an aid to understanding the relationship between the population as a whole and what I was then referring to as the captive cohort — the group of individuals of mixed ages that were survived forward from their age of capture through death. Ultimately this framework elucidated the connection between population age structure and the captive cohort death distribution.
Shown in Table 1, the life-table-based model consisted of sub-components framed as separate but interconnected sub-tables. The first of these sub-tables (columns 1–4 in Table 1) contains the basic metrics of the stationary population with age x in column 1, and the number in the population at each age (Nx) in column 2 (i.e. 40, 30, 25, 5 and 0 individuals at ages 0, 1, 2, 3, and 4, respectively). The corresponding survival lx within this population and its age structure cx are given in columns 3 and 4, respectively.
The framework for the second sub-component of the model in Table 1 (columns 5–9) was central to the eventual discovery of the population identity for three reasons. Firstly, it includes a new age index for the newly-formed group referred to as captive age, denoted y, defined as the time units from capture (y = 0) through death of the last individual in the sample cohort. Secondly, it revealed the initial age structure of the sample based on the assumption of random sampling. This is shown in the first row for columns 6 through 9, the fractions of which correspond to the proportion of the population sample for each of the respective ages. For example, I assumed that if 0.30 of the stationary population in the wild is in age class 1 then (on average) there will be 0.30 of the captive sample in this age class. Thirdly, these proportions are then subject to their respective age-specific survival rates. For example, the 0.30 individuals in age class 1 at captive age ly* are reduced to 0.25, 0.05 and 0.00, respectively, for captive ages 1, 2 and 3, respectively. This sub-table helped me visualize the internal mortality dynamics of the population sample.
The concept for the third subcomponent of Table 1 (columns 10–11) was to bring life table methods to bear on the captive cohort. Inasmuch as the sum of the fractions surviving in each of the sample sub-cohorts at each captive age (y) represents the total of the original surviving, these sums represent the survival schedule of the captive cohort, ly*. Although I found the survival column (column 10) interesting, it revealed nothing about the deeper mathematical connection between the population and the captive cohort. It was only when I computed the dy*column did I experience a Eureka moment — the values for the death distribution (column 11) were exactly equal to the values in the age distributions (column 4).
In his fascinating paper on the role of serendipity in science, Yaqub (2018) would likely classify my discovery of this stationary population equality as a “Mertonian serendipity” — discovery as the outcome of a targeted search that solved a problem in hand (age-structure estimation) via an unexpected route. The expected route would have been through the use of Bayesian models.
Stage IV: Model Formulation
In a section titled “A key demographic identity” my statistical colleagues Hans Müller and Jane-Ling Wang formulated a mathematical model based on the framework and concepts that I developed as given in Table 1 (Müller et al., 2004). Assuming population stationarity in this hypothetical case, the fraction of individuals age x in the population is given by cx = lxΣly = c0lx. The death rates in the marked sample life table at captive age xʹ are by definition d*y = l*y − d*y+1. These death rates are generated by subjects that enter the marked sample life table at various unknown ages, and survive to captive age y. For all individuals that enter the marked sample cohort at age z, the contribution to d*y is therefore
cz …
…  (1 −
(1 −  ) = cz(
) = cz( −
−  ) = c0(lz+y − lz+y+1)
) = c0(lz+y − lz+y+1)
where lz refers to the survival of the captured individuals at age z.
The contributions of individuals entering the marked sample life table at various ages are additive. Therefore, adding the contributions over all ages of entry z:
d*y = Σ c0(lz+y − lz+y+1) = c0/ly
and therefore
d*y = Σ cx
This formula states that the fraction of a population age x days equals the fraction of the population that die x days later. The shorthand for this equality is age structure equals death distribution. In his proof of this equality, Vaupel expressed the relationship differently — the proportion of the population with x years of life remaining is equal to the proportion dying x years in the future (Vaupel, 2009a; p. 8). The shorthand for this expression of the same equality is life lived equals life left.
Vaupel notes that since births equal deaths in a stationary population, Carey’s Equality generalizes this relationship by showing that the proportion of individuals younger than x equals the proportion whose remaining lifespan is less than x. Similarly, the proportion of individuals x or older is equal to the proportion of individuals who will still be alive in x days (years).
Table 1 Illustration of the relationship between the age structure in a stationary population (columns 1–4), the captive (sample) cohort life (columns 5–9), and the captive cohort life table (columns 10–11). Framework from Table 1 in Hans Müller and others (Müller et al. 2004). The identity illustrated in this table as well as one for medfly stationary populations are visualized in Figs. 3–5 of the paper by Carey et al. (2019).
|
Wild Population |
Captive Cohort (mixed chronological ages) |
|||||||||
|
Post-capture Age (time since capture) |
Population Sample at Capture |
Captive Life Table |
||||||||
|
Age |
Number age x |
Survival |
Age structure |
Age 0 |
Age 1 |
Age 2 |
Age 3 |
Survival to age y |
Deaths at age y |
|
|
x |
Nx |
lx |
cx |
y |
x = 0 |
x = 1 |
x = 2 |
x = 3 |
ly* |
dy* |
|
(1) |
(2) |
(3) |
(4) |
(5) |
(6) |
(7) |
(8) |
(9) |
(10) |
(11) |
|
0 |
40 |
1.000 |
0.40 |
0 |
40 |
30 |
25 |
5 |
1.00 |
0.40 |
|
1 |
30 |
0.750 |
0.30 |
1 |
30 |
25 |
5 |
0.60 |
0.30 |
|
|
2 |
25 |
0.625 |
0.25 |
2 |
25 |
5 |
0.30 |
0.25 |
||
|
3 |
5 |
0.125 |
0.05 |
3 |
5 |
0.05 |
0.05 |
|||
|
4 |
0 |
0.000 |
0.00 |
4 |
0 |
0.00 |
0.00 |
|||
|
100 |
1.00 |
100 |
60 |
30 |
5 |
1.00 |
||||
A Surprise Retrospective Story
Given the depth and scope of the demography literature in general (Poston and Micklin, 2005) and of the mathematical demography (Land, Yang, and Yi, 2005) and life table literature in particular (Guillot, 2005), I was interested to know whether this identity had already been published in some form. My online searches in the demography, statistics and mathematical biology literature revealed that there were no previous papers on this identity in either the primary literature or in the searchable secondary and grey literature. Later perusals of demography texts (Preston, Heuveline, and Guillot, 2001; Keyfitz and Caswell, 2010), handbooks (Poston and Micklin, 2005), methods books (Siegel and Swanson, 2004; Caswell, 2001), dictionaries (Peterson and Peterson, 1986), encyclopaedias (Demeny and McNicoll 2003a, 2003b) and treatises (Caselli, Vallin, and Wunsch, 2006f) also indicated that this result was not present in the earlier literature.
To my astonishment, three years ago I learned from Tim Riffe that he had discovered a 1986 paper describing an equality in stationary populations that was expressed differently than mine but similarly to Vaupel’s life-lived and left version (Riffe, 2015). In his article, titled “Structure et dynamique des populations. La pyramide des années à vivre, aspects nationaux et exemples régionaux”, French demographer Nicolas Brouard (1986; pp. 160–61) wrote:
La population stationnaire a un intérêt pour le sujet qui nous préoccupe, car dans une population rigoureusement stationnaire la pyramide des âges est aussi égale à la pyramide des années à vivre. On montre [2] en effet que dans une population stationnaire, il y a autant d’individus ayant vécu x années que d’individus ayant x années à vivre.
[The stationary population has an interest in the subject that concerns us, because in a strictly stationary population the age pyramid is also equal to the pyramid of the years to live. It is shown [2] that in a stationary population, there are as many individuals having lived x years as individuals having x years to live.]
Although this description of the identity differs from mine (i.e. age structure equal death distribution), it is virtually identical to the description presented by James Vaupel (i.e. life lived equals life left; Vaupel, 2009a). In correspondence with Brouard (Brouard, 2018) I learned that, in an exercise of the final examination (February 1984) at the Institut de Formation et Recherche Démographiques (IFORD), he asked the students to prove the identity in discrete time. Also, Brouard inserted the proof of the theorem in continuous time in the chapter entitled “Infinitesimal approach of mortality” of his mimeographed manual “Mouvements et modèles”. I learned from Brouard that at that time not only were French demographers required to first publish their findings in French, but, interestingly, young researchers like him did not have ready access to IBM Selectric typewriter math typeballs — the state-of-technology in personal typesetting at the time. He thus implied in his correspondence that otherwise he would have published the book containing his identity “Mouvements et modèles” earlier. His book was not published until 1989 when the word-processing software LaTeX became widely available. However, its distribution was extremely limited because it was published as a training manual for IFORD in the African country of Cameroon. Brouard noted in his correspondence with me (Brouard, 2018):
Others were not interested by the equality which […] appeared not very useful per se […] after the weak response of [more senior] French demographers to my articles I moved away from formal demography[.]
Brouard’s story reveals how his limited access to typesetting technology, the restricted distribution of the publications, the necessity of publishing in French rather than in English, the perceived absence of any utility of the identity and the lack of interest by his more senior colleagues conspired to keep his discovery (Brouard’s Theorem) hidden from mainstream demography for thirty years.
Discussion
The need to find a method to estimate age structure in insect populations was the driving force behind development of the methodological component of my research program on ageing in the wild in the late 1990s. One of the important outcomes of the quest was the discovery of the identity that Vaupel referred to as Carey’s Equality. Although this discovery and its connection with Brouard’s earlier publication was important from the standpoint of basic demography, the identity itself could not be used to estimate age structure in actual wild fruit fly populations because: (1) like most field populations, fruit fly populations in the wild violate the assumption of stationarity; and (2) conditions flies experience pre-capture (field) are different than those they experience post-capture (laboratory). Nonetheless, the discovery of the identity was important, especially from a practical standpoint because it established the theoretical foundation for using the post-capture death distribution of individuals of unknown ages to estimate age structure in the populations from which they once belonged. More realistic models to estimate age structure in actual field populations of fruit flies were developed by my UC Davis statistical colleagues, Hans Müller and Jane-Ling Wang, and their students, based on the use of mortality data from reference fruit fly life tables and iterative mathematical methods (Müller et al., 2007; Müller et al., 2004). Example applications of these methods for estimating age structure in wild populations of insects along with their constraints are given in the papers by Carey, Papadopoulos and their colleagues (Carey et al., 2008; Carey et al., 2012; Papadopoulos et al., 2016).
Papers related either to this identity, similar concepts or stationary population theory more generally, which were published many years prior to the paper that described this identity (Müller et al., 2004), include the two papers by Brouard (Brouard, 1986, 1989), the classic papers by Ryder (1965, 1973, 1975) on replacement populations, the article by Kim and Aron (1989) showing the equivalency of the average age and average expectation of remaining life in a stationary population, the book section by Keyfitz (1985; p. 74) containing a general formula for the average expectation of life in a stationary population, and the demography text by Preston and his co-authors (Preston, Heuveline, and Guillot, 2001; pp. 53–58) outlining the basic properties of a stationary population. More recent papers connecting life lived to life left (or age structure to death distributions) include one by Goldstein (2009) proving the earlier finding of Kim and Aron (1989) but in a different way; a paper by Rao and Carey (2015) with original approach and new conceptual insights into Carey’s Equality; symmetries between life lived and left in finite stationary populations (Villavicencio and Riffe 2016a); the relationship of random age and remaining lifetimes by Finkelstein and Vaupel (2014); and the paper by Vaupel and Villavicencio (Vaupel and Villavicencio, 2018) in which they extend stationary population identity to the stable, non-stationary case.
Although Brouard’s Theorem and Carey’s Equality both describe the same demographic identity, the contexts in which they were discovered and the concepts upon which they are based are fundamentally different. From my experience working with scientists in the professional worlds of both human (classical) demography and biodemography, the conceptual differences between the two flow naturally from these two worlds — the “life lived equals life left” perspective from demography, and the “age structure equals death distribution” perspective from biodemograpy. Indeed, until James Vaupel published the proof of the stationary population identity (Vaupel, 2009), I had never before thought of age structure (denoted cx) as a “life lived” concept, or of the death distribution (denoted dx) as a “life left” concept. Even though they are literally identical, they are neither semantically nor conceptually identical.
As a biodemographer working through each of the stages in the discovery process that I described earlier, my focus was on the potential use of life table theory as a basis for estimating the age structure of a life table (stationary) population. I am reasonably certain that I would never have conceived of measuring ‘life left’ as a way to estimate ‘life lived’ instead of the use of the conventional and more transparent life table concepts in which the death distribution provides a means to estimate age structure.
I consider development of the general idea of using the death distribution of wild-caught fruit flies to estimate population age structure distribution to be the single most important concept that emerged from brainstorming sessions on ‘residual demography’ with my colleagues two decades ago. The ‘accidental’ discovery of the stationary population identity itself is personally gratifying for several reasons. These include bringing Nicolas Brouard’s original contribution to light and thus providing him with due credit, contributing to the basic demographic literature so that the basic identity becomes part of the demography pedagogy (e.g., Wachter, 2014), and using it as the conceptual basis for the development of the captive cohort method as a new technique for estimating age structure in wild populations. These contributions all resulted from the original discussions with my colleagues in Crete when we asked the question situated within the inter-zone between biology and demography: what can residual demography tell us about ageing in the wild?
Implications for Human Population Studies
A career-altering decision I made in my first year as an assistant professor of entomology at the University of California Davis in 1980 was to audit Kenneth Wachter’s course in introductory demography at the University of California, Berkeley. Although this required a half-day’s commitment several days each week for three months (i.e. the Davis-Berkeley round trip), the experience exposed me to methods of formal demography that had been expressly developed for and applied to human populations, tied me into a network of professional demographers and motivated me to join several population associations (e.g. Population Association of America; International Union for the Scientific Study of Populations) and present papers at their meetings. It also gave me both the incentive and the confidence to, where possible, generalize my findings on non-human species in order to contribute to the mainstream demographic literature, particularly as they apply to human populations (e.g., Carey, 1997; Judge and Carey, 2000; Carey and Judge, 2001; Carey, 2003).
I believe the stationary population identity that I discovered in the context of medfly research has a number of important implications in both basic and applied contexts for human demography. I briefly describe several of these next.
Human Evolution
It is virtually certain that the population growth rates of various species of early hominids (e.g. Australopithicus spp.) in general and of prehistoric Homo sapiens in particular were stationary, or nearly so, the vast majority of the time (Johnson and Brook, 2011; Lee and Tuljapurkar, 2008; Boone, 2002). Indeed, it is estimated that during most of the Holocene, human populations worldwide grew at a long-term annual rate of 0.04% (Zahid, Robinson, and Kelly, 2016) which, for practical purposes, have age structures that are nearly indistinguishable from stationary populations.
Using the concept of the stationary population identity, life-table rates of prehistoric populations (Gage, 1998; Kaplan et al., 2000) imply that up to half of the population is 20 years old or greater, and at least a quarter are over 30 years old. This implies (from the identity) that 50% and 25% of the prehistoric populations had respectively 20 and 30 years remaining to live together. These basic demographic metrics provide important perspectives on the extent to which individuals in prehistoric societies shared lives (and thus their skills, language, stories, art, music and culture).
Historical Demography
An interesting application of the population identity, similar to its original application in fruit fly demography, was offered by Villavicencio and Riffe (2016b), who suggested that the concept might be applied to incomplete historical data. In the Barcelona Historical Marriage Database — which collects information about marriage licenses of Barcelona (Spain) from the mid-fifteenth century until the early twentieth century — individuals are first identified in their marriage record and then followed up. But no information is available about their birth date or their age at marriage (Villavicencio, Jordà, and Pujadas-Mora, 2015). Interestingly they used a Bayesian statistical modelling approach (Colchero and Clark, 2012; Colchero, Jones, and Rebke, 2012) as was first suggested by me for estimating the post-capture lifespans of fruit flies. The alternative that Villavicencio and Riffe suggested was the possibility of using the life-table identity to estimate the pre-marriage ages of this historical population.
Demographic Principles
Inasmuch as stationary population theory and basic concepts are inextricably linked to population stationarity (Preston, Heuveline, and Guillot, 2001), the stationary population identity contributes to a number of fundamental principles upon which the field rests. For example, demographic transition theory is based on the concept of offsetting birth and death rates at the beginning and end of the transition (Mesle and Vallin, 2006); population momentum is based on the concept of stationarity as its end point (Caselli, Vallin, and Wunsch, 2006a); and zero population growth (ZPG) is, by definition, based on the concept of the cessation of population growth (Caselli, Vallin, and Wunsch, 2006a), and thus implies stationary populations. The stationary population identity can now be integrated into each of these basic demographic principles.
Replacement-level Populations in the Twenty-first Century
To study the world population today is to study many countries whose populations are essentially quasi-stationary. For example, the Population Division of the United Nations noted that in 2010–15 there were eighty-three countries with below-replacement fertility that accounted for nearly half (46%) of the world’s population (UnitedNations, 2017). The vast majority of European countries are experiencing population growth rates within +0.5% of replacement-level change. And, with nearly 20% of the world’s population, China’s population growth rate, currently at slightly over 0.5%, is not far from replacement-level and is predicted to fall to zero by mid-century. Extending Vaupel’s example (using 2005 life table rates for the United States) to the quasi-stationary populations of the world shows that around 50% of hypothetical individuals are 41 years old or older. Since the population change in nearly half of the world’s population is near replacement, this implies that around a quarter of the world’s “life-table populations” will be alive in 2060, a date approximately forty-one years from now that is often considered as being in the distant future.
Future World
One of the most fascinating contributions in the 143-chapter treatise in population studies (Caselli, Vallin, and Wunsch, 2006b, 2006c, 2006d, 2006e) is Chapter 78 by Vallin and Casalli entitled “The Future of Mankind” (Vallin and Caselli, 2006). In exploring one variant of the scenario of a “one-child, 150-year life expectancy” world, they note that up to 84% of the population would be made up of centenarians alone. Applying the stationary population identity concept suggests that more than eight out of ten individuals in this hypothetical futuristic population would share one hundred years of life together. This scenario illustrates an extreme case of Joel Cohen’s concept of Methuselah’s choice (Cohen, 1995) — the necessity of an extraordinarily low birth-rate (=1/150) in a stationary world of long-lived individuals.
Concluding Thoughts
I believe there are several lessons that can be learned from this story. The first is that the proverb “necessity is the mother of invention” can also be reframed as “… the mother of discovery”. My quest to find a practical solution to the problem of population age structure estimation led to the discovery of the basic stationary population identity. A second lesson pertains to the virtues of pencil-and-paper modelling in science — it is both immediate and simple (Wong and Kjaergaard, 2012). This step forced me to think about the essence of the problem rather than becoming buried in its complexities. Simple is not the same as simplistic. A third lesson pertains to the discovery of new demographic principles. If the stationary population identity remained hidden for most of the 350-year history of the life table, there are almost certainly more undiscovered ones. I believe the most fertile ground for new demographic discoveries will be within the interdisciplinary paradigm of biodemography.
I will close with what I consider to be the wonderment of the discovery. How could this particular mathematical property of (arguably) the most studied of all demographic models — the life table — have remained hidden for so long? And once discovered, still not have found its way into the mainstream demographic literature for thirty more years? Why do all deaths that occur in a stationary fruit-fly population at twenty-five days post-capture, for example, sum exactly to the number that were precisely twenty-five days old in the original population? How is it possible to compute precisely the age structure of a stationary population without age data on even a single member? Think about that.
The concept appears not to make sense on its face. It is a discovery that is not obviously true. But once proven (Brouard, 1989; Vaupel, 2009b) becomes one that obviously is true.
Acknowledgments
Many of the findings that inform this chapter were supported in part by the National Institute on Aging grants P01 AG08761-10 and P01 AG022500-01, and through UC Berkeley CEDA grant P30AG0128. I thank Lawrence Harshman, Linda Partridge and Anatoli Yashin for lively discussions on residual demography in the late 1990s, and my UC Davis colleagues Hans Müller and Jane-Ling Wang for their formulations and insights. I am especially indebted to James Vaupel for recognizing the importance of this identity in the first place, for his mathematical proof, and for crediting me with its (re-) discovery. I am grateful to Arni Rao for his energy and enthusiasm for doing collaborative work with me on this identity as well as for his theoretical insights and innovative ideas after having first met him at the Nathan Keyfitz Memorial Symposium at Ohio University in 2013. I thank Tim Riffe for bringing Brouard’s Theorem to my (indeed the world’s) attention and, along with Francisco Villavicencio, for their insightful and constructive comments on an earlier version of this chapter. I am grateful to Nicolas Brouard for background information he provided me about the circumstances of his original discovery. Finally, I thank Raziel Joseph Davison for her constructive review of an earlier version of this paper, and Rebecca Sear, Ronald Lee and Oskar Burger for their encouragement, feedback and patience.
References1
Boone, James L. 2002. ‘Subsistence Strategies and Early Human Population History: An Evolutionary Ecological Perspective’, World Archaeology, 34.1: pp. 6–25, https://doi.org/10.1080/00438240220134232
Brouard, N. 1986. ‘Structure et Dynamique des Populations La Pyramide des Annees a Vivre, Aspects Nationaux et Examples Regionaux [Structure and Dynamics of Population Pyramids of the Years to Live, National Aspects and Regional Examples]’, Espace, populations, sociétés, Visages de la population de la France, 4: pp. 157–68, https://doi.org/10.3406/espos.1986.1120
—. 1989. ‘Mouvements et modeles de population [Population movements and models]’, in Institut de Formation et de Recherche Démographiques, Yaoundé, Cameroun. [Clarification requested: is this a report from the institut?] https://sauvy.ined.fr/brouard/enseignements/iford/mouvementetmodeles.pdf
—. 2018. Personal correspondence. Email January 22, 2018.
Campana, S. E., and S. R. Thorrold. 2001. ‘Otoliths, Increments, and Elements: Keys to a Comprehensive Understanding of Fish Populations?’, Canadian Journal of Fisheries and Aquatic Science, 58.1: pp. 30–38, https://doi.org/10.1139/f00-177
Carey, J. R. 1997. ‘What Demographers Can Learn from Fruit Fly Actuarial Models and Biology’, Demography, 34.1: pp. 17–30, https://doi.org/10.2307/2061657
—. 2003. ‘Life span: A conceptual overview’, in Life Span: Evolutionary, Ecological, and Demographic Perspectives (Supplement to Population and Development Review 29), ed. J. R. Carey, and S. Tuljapurkar (New York: Population council),
J. R. Carey and S. Tuljapurkar (eds.). 2003. Life Span: Evolutionary, Ecological, and Demographic Perspectives, A Supplement (New York: Population Council), XXIX.
Carey, J. R., and D. S. Judge. 2001. ‘Life Span Extension in Humans is Self-Reinforcing: A General Theory of Longevity’, Population and Development Review, 27.3: pp. 411–36, https://doi.org/10.1111/j.1728-4457.2001.00411.x
Carey, J. R., P. Liedo, H.-G. Müller, J.-L. Wang, and J.-M. Chiou. 1998. ‘Relationship of Age Patterns of Fecundity to Mortality, Longevity, and Lifetime Reproduction in a Large Cohort of Mediterranean Fruit Fly Females’, Journal of Gerontology Series A: Biological Sciences and Medical Sciences, 53A.4: B245-B51, https://doi.org/10.1093/gerona/53a.4.b245
Carey, J. R., P. Liedo, D. Orozco, and J. W. Vaupel. 1992. ‘Slowing of Mortality Rates at Older Ages in Large Medfly Cohorts’, Science, 258.5081: pp. 457–61, https://doi.org/10.1126/science.1411540
Carey, J. R., N. T. Papadopoulos, H-G. Müller, B. I. Katsoyannos, N. A. Kouloussis, J-L. Wang, K. Wachter, W. Yu, and P. Liedo. 2008. ‘Age Structure Changes and Extraordinary Life Span in Wild Medfly Populations’, Aging Cell, 7.3: pp. 426–37, https://doi.org/10.1111/j.1474-9726.2008.00390.x
Carey, J. R., N. T. Papadopoulos, S. Papanastasiou, A. Diamanditis, and C. T. Nakas. 2012. ‘Estimating Changes in Mean Population Age Using the Death Distributions of Live-Captured Medflies’, Ecological Entomology, 37.5: pp. 359-69, https://doi.org/10.1111/j.1365-2311.2012.01372.x
Carey, J. R., S. Silverman, and A. S. R. S Rao. 2019. ‘The Life Table Population Identity: Discovery, Formulations, Proof, Extensions and Applications’, in Handbook of Statistics: Integrated population biology and modeling Vol. 39, ed by. Arni S. R. Rao (Amsterdam: Elsevier), XXXIX.
Carey, J. R., and J. W. Vaupel. 2019. ‘Biodemography’, in Handbook of Population, ed. by D. Poston and M. Micklin (New York: Kluwer Academic/Plenum Publishing).
Caselli, C., J. Vallin, and G. Wunsch, 2006a. ‘Population models’, in Demography: Analysis and Synthesis, ed. by C. Caselli, J. Vallin and G. Wunsch (Amsterdam: Elsevier).
—. 2006b. Demography: Analysis and Synthesis. A Treatise in Population Studies (Amsterdam: Academic Press:), I.
—. 2006c. Demography: Analysis and Synthesis. A Treatise in Population Studies (Amsterdam: Academic Press), II.
—. 2006d. Demography: Analysis and Synthesis. A Treatise in Population Studies (Amsterdam: Academic Press), III.
—. 2006e. Demography: Analysis and Synthesis. A Treatise in Population Studies (Amsterdam: Academic Press), IV.
—. 2006f. Demography: Analysis and Synthesis. A Treatise in Population (London: Academic Press), I, II, III, IV.
Caswell, H. 2001. Matrix Population Models (Sunderland, Massachusetts: Sinauer Associates, Inc.).
Cochran, M. E., and S. Ellner. 1992. ‘Simple Methods for Calculating Age-Based Life History Parameters for Stage-Structured Populations’, Ecological Monographs, 62.3: pp. 345–64, https://doi.org/10.2307/2937115
Cohen, J.E. 1995. How Many People Can the Earth Support? (New York: W.W. Norton & Company).
Colchero, Fernando, and James S. Clark. 2012. ‘Bayesian Inference on Age-Specific Survival for Censored and Truncated Data’, Journal of Animal Ecology, 81.1: pp. 139–49, https://doi.org/10.1111/j.1365-2656.2011.01898.x
Colchero, Fernando, Owen R. Jones, and Maren Rebke. 2012. ‘BaSTA: an R Package for Bayesian Estimation of Age-Specific Survival from Incomplete Mark–Recapture/Recovery Data with Covariates’, Methods in Ecology and Evolution, 3.3: pp. 466–70, https://doi.org/10.1111/j.2041-210X.2012.00186.x
Cook, P. E., C. J. McMeniman, and S. L. O’Neill. 2008. ‘Modifying Insect Population Age Structure to Control Vector-Borne Disease’, in Transgenesis and the Management of Vector-Borne Disease, in Experimental Medicine and Biology, ed. by Serap Aksoy (New York: Springer), pp. 126–40, DCXXVII, https://doi.org/10.1007/978-0-387-78225-6_11
Cook, P. E., and S. P. Sinkins. 2010. ‘Transcriptional Profiling of Anopheles Gambiae Mosquitoes for Adult Age Estimation’, Insect Molecular Biology, 19.6: pp. 745–51, https://doi.org/10.1111/j.1365-2583.2010.01034.x
Davison, R. J., 2011. ‘Stage-structured demography in stochastic environments: an investigation into the role of variability in driving population dynamics’, PhD thesis, University of Stanford, https://purl.stanford.edu/qh169rj6400
Demeny, P., and G. McNicoll (eds.). 2003a. Encyclopedia of Population (New York: The Gale Group Inc.).
—. 2003b. Encyclopedia of Population (New York: The Gale Group Inc.).
Dinsmore, S. J., and D. H. Johnson. 2012. ‘Population Analysis in Wildlife Biology’ in The Wildlife Techniques Manual. Research, ed. by N. J. Silvy (Baltimore: The Johns Hopkins University Press).
Finkelstein, M., and J. Vaupel. 2014. ‘On Random Age and Remaining Lifetime for Populations of Items’, Applied Stochastic Models in Business and Industry, 31.5: pp. 681–89, https://doi.org/10.1002/asmb.2073
Gage, T. B. 1998. ‘The Comparative Demography of Primates: With Some Comments on the Evolution of Life Histories’, Annual Review of Anthropology, 27: pp. 197–221, https://doi.org/10.1146/annurev.anthro.27.1.197
Gerade, B. B., S. H. Lee, T. W. Scott, J. D. Edman, L. C. Harrington, S. Kitthawee, J. W. Jones, and J. M. Clark. 2004. ‘Field Validation of Aedes Aegypti (Diptera: Culicidea) Age Estimation by Analysis of Cuticular Hydrocarbons’, Journal of Medical Entomology, 41.2: pp. 231–38, https://doi.org/10.1603/0022-2585-41.2.231
Goldstein, J. R. 2009. ‘Life Lived Equals Life Left in Stationary Populations’, Demographic Research, 20: pp. 3–6, https://doi.org/10.4054/demres.2009.20.2
Guillot, M. 2005. ‘Life Tables’, in Handbook of Population, ed. by D. Poston and M. Micklin (New York: Springer).
Horvitz, C. C., and S. Tuljapurkar. 2008. ‘Stage Dynamics, Period Survival, and Mortality Plateaus’, The American Naturalist, 172.2: pp. 203–15, https://doi.org/10.1086/589453
Johnson, Christopher N., and Barry W. Brook. 2011. ‘Reconstructing the Dynamics of Ancient Human Populations from Radiocarbon Dates: 10 000 Years of Population Growth in Australia’, Proceedings of the Royal Society B: Biological Sciences, 278.1725: pp. 3748–54. https://doi.org/10.1098/rspb.2011.0343
Jones, Owen R., Alexander Scheuerlein, Roberto Salguero-Gómez, Carlo Giovanni Camarda, Ralf Schaible, Brenda B. Casper, Johan P. Dahlgren, Johan Ehrlén, María B. García, Eric S. Menges, Pedro F. Quintana-Ascencio, Hal Caswell, Annette Baudisch, and James W. Vaupel. 2014. ‘Diversity of Ageing Across the Tree of Life’, Nature, 505.7482: pp. 169–73, https://doi.org/10.1038/nature12789
Judge, D. S., and J. R. Carey. 2000. ‘Postreproductive Life Predicted by Primate Patterns’, Journal of Gerontology: Series A, Biological Sciences and Medical Sciences, 55A.4: pp. B201-B09, https://doi.org/10.1093/gerona/55.4.B201
Kaplan, H., K. Hill, J. Lancaster, and A. M. Hurtado. 2000. ‘A Theory of Human Life History Evolution: Diet, Intelligence, and Longevity’, Evolutionary Anthropology, 9.4: pp. 156–85, https://doi.org/10.1002/1520-6505(2000)9:4<156::AID-EVAN5>3.0.CO;2-7
Keyfitz, N. 1985. Applied Mathematical Demography (New York: Springer-Verlag).
Keyfitz, N., and H. Caswell. 2010. Applied Mathematical Demography (New York: Springer).
Kim, Y. J., and J. L. Aron. 1989. ‘On the Equality of Average Age and Average Expectation of Remaining Life in a Stationary Population’, SIAM Review, 31.1: pp. 110–13, https://doi.org/10.1137/1031005
Land, K. C., Y. Yang, and Z. Yi. 2005. ‘Mathematical demography’, in Handbook of Population, ed. by D. Poston and M. Micklin (New York: Springer).
Lee, Charlotte T., and Shripad Tuljapurkar. 2008. ‘Population and Prehistory I: Food-Dependent Population Growth in Constant Environments’, Theoretical Population Biology, 73.4: pp. 473–82, https://doi.org/10.1016/j.tpb.2008.03.001
Lehane, M. J. 1985. ‘Determining the Age of an Insect’, Parasitology Today, 1.3: pp. 81–85, https://doi.org/10.1016/0169-4758(85)90048-1
Limburg, K. E., T. A. Hayden, W. E. PineIII, M. D. Yard, R. Kozdon, and J. W. Valley. 2013. ‘Of Travertine and Time: Otolith Chemistry and Microstructure Detect Provenance and Demography of Endangered Humpback Chub in Grand Canton, USA’, PLOS ONE, 8: p. e84235, https://doi.org/10.1371/journal.pone.0084235
Mesle, F., and J. Vallin. 2006. ‘The Health Transition: Trends and Prospects’, in Demography: Analysis and Synthesis, ed. by C. Caselli, J. Vallin and G. Wunsch (Amsterdam: Elsevier).
Metcalf, C. Jessica E., Carol C. Horvitz, Shripad Tuljapurkar, and Deborah A. Clark. 2009. ‘A Time to Grow and a Time to Die: a New Way to Analyze the Dynamics of Size, Light, Age, and Death of Tropical Trees’, Ecology, 90.10: pp. 2766–78, https://doi.org/10.1890/08-1645.1
Müller, H. G., J-L. Wang, J. R. Carey, E. P. Caswell-Chen, C. Chen, N. Papadopoulos, and F. Yao. 2004. ‘Demographic Window to Aging in the Wild: Constructing Life Tables and Estimating Survival Functions from Marked Individuals of Unknown Age’, Aging Cell, 3.3: pp. 125–31, https://doi.org/10.1111/j.1474-9728.2004.00096.x
Müller, H. G., J-L. Wang, W. Yu, A. Delaigle, and J. R. Carey. 2007. ‘Survival in the Wild Via Residual Demography’, Theoretical Population Biology, 72.4: pp. 513–22, https://doi.org/10.1016/j.tpb.2007.07.003
Nussey, D. H., L. E. B. Druuk, A. Donald, M. Fowlie, and T. H. Clutton-Brock. 2006. ‘The Rate of Senescence in Maternal Performance Increases with Early-Life Fecundity in Red Deer’, Ecology Letters, 9.12: pp. 1342–50, https://doi.org/10.1111/j.1461-0248.2006.00989.x
Ozgul, A., S. Tuljapurkar, T. G. Benton, J. M. Pemberton, T. H. Clutton-Brock, and T. Coulson. 2009. ‘The Dynamics of Phenotypic Change and the Shrinking Sheep of St. Kilda’, Science, 325.5939: pp. 464–67, https://doi.org/10.1126/science.1173668
Papadopoulos, N., J. R. Carey, C. Ioannou, H. Ji, H.-G. Müller, J.-L. Wang, S. Luckhart, and E. Lewis. 2016. ‘Seasonality of Post-Capture Longevity in a Medically-Important Mosquito (Culex Pipiens)’, Frontiers in Ecology and Evolution, 4: p. 63, https://doi.org/10.3389/fevo.2016.00063
Peterson, W., and R. Peterson. 1986. Dictionary of Demography: Terms, Concepts, and Institutions A-M (New York: Greenwood Press).
Poston, D., and M. Micklin (eds.). 2005. Handbook of Population (New York: Springer).
Preston, S.H., P. Heuveline, and M. Guillot. 2001. Demography: Measuring and Modeling Population Processes (Malden: Blackwell Publishers).
Rao, A. R. R. S., and J. R. Carey. 2015. ‘Generalization of Carey’s Equality and a Theorem on Stationary Population’, Journal of Mathematical Biology, 71: pp. 583–94, https://doi.org/10.1007/s00285-014-0831-6
Riffe, R. 2015. ‘The Force of Mortality by Life Lived is the Force of Increment by Life Left in Stationary Populations’, Demographic Research, 32: pp. 827–34, https://doi.org/10.4054/demres.2015.32.29
Ryder, N. B. 1965. ‘The Cohort as a Concept in the Study of Social Change’, American Sociological Review, 30.6: pp. 843–61, https://doi.org/10.2307/2090964
—. 1973. ‘Two Cheers for ZPG’, Daedalus, 102: pp. 45–62.
—. 1975. ‘Notes on Stationary Populations’, Population Index, 41.1: pp. 3–28, https://doi.org/10.2307/2734140
Siegel, J. S., and D. A. Swanson. 2004. The Methods and Materials of Demography (Amsterdam: Elsevier Academic Press).
M. Tyndale-Biscoe. 1984. ‘Age-Grading Methods in Adult Insects: A Review’, Bulletin of Entomological Research, 74.3: pp. 341–77, https://doi.org/10.1017/s0007485300015637
United Nations. 2017. ‘World Population Prospects: The 2017 Revision’, Department of Economic and Social Affairs, Population Division, Working Paper No. ESA/P/WP/248.
Vallin, J., and C. Caselli. 2006. ‘The Future of Mankind. Looking Ahead After the Transition’, in Demography: Analysis and Synthesis, ed. by C. Caselli, J. Vallin and G. Wunsch (Amsterdam: Elsevier).
Vaupel, J. W. 2009a. ‘Life lived and left: Carey’s equality’, Demographic Research, 20: pp. 7–10, https://doi.org/10.4054/demres.2009.20.3
Vaupel, J. W., and F. Villavicencio. 2018. ‘Life Lived and Left: Estimating Age-Specific Survival in Stable Populations with Unknown Ages’, Demographic Research, 39: pp. 991–1008. https://doi.org/10.4054/demres.2018.39.37
Vaupel, James W. 2009b. ‘Life Lived and Left: Carey’s Equality’, Demographic Research, 20: pp. 7–10. https://doi.org/10.4054/demres.2009.20.3
Villavicencio, F., and T. Riffe. 2016a. ‘Symmetries Between Life Lived and Left in Finite Stationary Populations’, Demographic Research, 35: pp. 381–98, https://doi.org/10.4054/demres.2016.35.14
Villavicencio, Francisco, Joan Pau Jordà, and Joana M. Pujadas-Mora. 2015. ‘Reconstructing Lifespans Through Historical Marriage Records of Barcelona from the Sixteenth and Seventeenth Centuries’, in Population Reconstruction ed. by Gerrit Bloothooft, Peter Christen, Kees Mandemakers and Marijn Schraagen (Cham: Springer International Publishing).
Villavicencio, Francisco, and Timothy Riffe. 2016b. ‘Symmetries Between Life Lived and Left in Finite Stationary Populations’, Demographic Research, 35: pp. 381–98. https://doi.org/10.4054/demres.2016.35.14
Wachter, K. W. 2014. Essential Demographic Methods (Cambridge, Massachusetts: Harvard University Press).
Wong, B., and R. S. Kjaergaard. 2012. ‘Points of View: Pencil and Paper’, Nature Methods, 9: p. 1037, https://doi.org/10.1038/nmeth.2223
Yaqub, Ohid. 2018. ‘Serendipity: Towards a Taxonomy and a Theory’, Research Policy, 47.1: pp. 169–79, https://doi.org/10.1016/j.respol.2017.10.007
Zahid, H. Jabran, Erick Robinson, and Robert L. Kelly. 2016. ‘Agriculture, Population Growth, and Statistical Analysis of the Radiocarbon Record’, Proceedings of the National Academy of Sciences, 113.4: pp. 931–35, https://doi.org/10.1073/pnas.1517650112
1 Note this chapter has been posted on the Open Science Framework website since 20/06/2019, after it was accepted for publication, so the references will reflect when the chapter was written and not the OBP publication date.
