9. My Family and Other Animals:
Human Demography Under a Comparative
Cross-Species Lens

Owen R Jones, Thomas H G Ezard, Claire Dooley, Kevin Healy,
Dave J Hodgson, Markus Mueller, Stuart Townley and
Roberto Salguero-Gomez

© 2024 Owen R Jones et al., CC BY 4.0 https://doi.org/10.11647/OBP.0251.09

Like all species, the demography of humans has been shaped under the framework of natural selection. Our understanding of human demography can thus be enhanced by viewing it through a comparative, cross-species, lens and exploring the position of humans among other animal species. Here we use demographic data in the form of matrix population models (MPMs) from humans and 90 other animal species to contextualize patterns of human evolutionary demography. We conduct an additional analysis using human MPM data derived from raw census data from 96 countries over a period spanning 1780 to 2014. For each MPM, we calculate a suite of demographic variables that describe multi-component life history strategy, and use principal component analysis (PCA) to contextualize human populations among the other vertebrates. We show that, across species, life history strategy can be described by position across two dominant axes of variation, and that human life history strategy is indeed set apart from that of other animals. We argue that life history architecture — the set of relationships among life history traits, including their correlations and trade-offs — is fundamentally different within humans than across all animal species, perhaps because of fundamental distinctions in the processes driving within-species and among-species differences. We illustrate strong general temporal trends in life history strategy in humans and highlight both striking commonalities and some differences among countries. For example, there is a general for traversal across life history space that reflects increased life expectancy and life span equality, but there is also among-country variation in the trajectories that remains to be explained. Our approach of distilling complex demographic strategies into principal component axes offers a useful tool for the exploration of human demography.

Introduction

A literature search will reveal thousands of articles with titles containing “… humans and animals …”, loaded with the implication that humans are not animals, but that they rather belong to a very distinct group. But humans are certain animals: we may be exceptional in many ways, but perhaps not in terms of our demographic traits. Consider life span: the longest-lived human on record (Jean Calment, died aged 122 (Jeune and others, 2010)) was nowhere near as old as the longest-lived invertebrate, or vertebrate. Those records belong to the humble quahog (Arctica islandica), a bivalve, (>507 years; Butler and others, 2013) and Greenland shark (Somniosus microcephalus) (270 years; Nielsen and others, 2016) respectively. The reproductive output of humans is fairly modest: the highest total fertility rates (~11 children per woman) have been recorded for Hutterite populations of North America (Robinson, 1986), pales into insignificance compared to most non-human animal species, even if some approach our relatively low fertility rates (e.g., elephants, whales). Humans are admittedly unusual in the extended period of post-menopausal survival experienced by women, but there is evidence for this in some other species too (Cohen, 2004; Ellis and others, 2018).

Niko Tinbergen pioneered a multifaceted approach to the study of animal behaviour when he argued that behavioral questions could be addressed at both an ultimate and a proximate level, and in a dynamic or static context (Tinbergen, 1963). Although the answers to questions posed from these four perspectives will be different, they are entirely consistent with each other. In this chapter, we view the demographic behaviour of animals from the dynamic and ultimate perspective: the evolutionary lens. We aim to put human demography and their variable life histories (i.e., key demographic events in their lifecycle) in the broader evolutionary and comparative context by analyzing demographic patterns across the animal kingdom, and exploring the position of humans among other animal species in ‘life history space’.

Like all other animals (and indeed species from the other Kingdoms), our characteristics have been shaped under the evolutionary framework of natural selection. Natural selection functions as an optimization algorithm: fitness is maximized under the long-term conditions experienced by the population (Cole, 1954; Gadgil and Bossert, 1970) and differences among species can, in theory, be explained by variation in the conditions in which they live, the conditions experienced in the past, and constraints of ancestry and genetic architecture. Thus, understanding the origins, the current context, and plausible future for human demography is enhanced by an explicit consideration of other animal species, and the relationships among them.

A great deal of variation exists among animals in traits such as somatic growth rate, age at maturity, life span, number and frequency of offspring produced, survival rates at particular ages or stages, and so on. These traits, collectively known as life history traits, describe the life cycle of an organism. These traits are the focus of the field of life history evolution (Stearns, 1992) and can be estimated using demographic methods (Caswell, 2001; Cochran and Ellner, 1992). Two of the most widely used in demography, both of which integrate schedules of survival and reproduction, are the life table (Chiang, 1984), and the matrix population model (MPM) (Caswell, 2001). MPMs have proved most popular among demographers studying non-human animal populations (Salguero-Gómez and others, 2016a).

The use of MPMs as descriptors of life cycles has a long and distinguished history. Their utility was first outlined by Leslie (1945) for age-structured models, and later extended by Lefkovitch (1965) to include stage-structured models, which can describe cycles based on size, ontogeny, and other phenotypic properties. Both types of MPM describe the dynamics of populations over a discrete time interval (often a year): n(t+1) = A*n(t), where n is the population vector containing the number (or sometimes the relative frequencies) of individuals at each (st)age at time t or t+1, and where A is the MPM (also known as the population projection matrix), which describe rates of transition among (st)ages (i.e., probabilities of survival, ontogenetic development, and reproductive output). The major reason for the rapid adoption and widespread use of MPMs arises from their tractability and well-understood mathematical properties (Caswell, 2001; Caswell and others, 2018), and the fact that a large diversity of useful analytical outputs can be derived from them. These analytical outputs include metrics of population dynamics, including the rates of population growth, population structure, metrics for transient dynamics (Stott and others, 2011), the evaluation of the absolute (sensitivities) and relative (elasticities) importance of demographic processes and covariates onto population-level metrics (de Kroon and others, 2000) (among others), and a range of life history metrics including generation time, life expectancy, measures of entropy (e.g., equality in the age at death, or in the age of reproducing females), and so on (see Morris and Doak, 2002; Caswell, 2001; Caswell and others, 2018 for more details). The widespread use of MPMs to describe species population dynamics and the broad range of life history metrics that can be derived from them enables meaningful comparisons of life history across a wide taxonomic scope: a task made easier by the release of the COMPADRE Plant Matrix Database (Salguero-Gómez and others, 2015) and COMADRE Animal Matrix Database (Salguero-Gómez and others, 2016a), and associated functionality (e.g., the Rage and Rcompadre R packages (Jones and others, 2022))

In this chapter, we use MPMs for a subset of vertebrate species from the COMADRE Animal Matrix Database alongside human MPMs derived by applying an iterative scheme that estimates life tables from raw census data from 96 countries (Keyfitz, 1966). We compare these sets of MPMs to contextualize the patterns of human evolutionary demography. We carefully select a set of life history traits that describe the multi-component life history strategy and use multivariate statistical analysis to contextualize the uniqueness (or otherwise) of human populations among the other vertebrates.

We illustrate that, across species, these life history strategies can be understood by examining their distribution across two major independent axes, one associated with the pace of life (in the demographic sense (see Nettle and Frankenhuis, 2019)), and the other associated with reproductive strategy. Demographic strategy, defined by position on these two axes, is not strongly structured by taxonomic affiliation. Humans sit apart from the other mammals, but not exceptionally so. We also show that within humans, the structuring of demographic strategies is markedly different from the cross-species patterns. This difference may reflect differences in the biological processes driving variation.

Methods

We obtained data on the demography of humans and 90 other animal species across 84 genera, 50 families, 25 orders and 3 vertebrate classes. All of the data included are in the form of matrix population models (MPMs) with a dimension ranging from 2 to 60. MPMs describe the life cycle of an organism as a set of discrete stages, or ages, with transitions from (st)age-to-(st)age expressed as probabilities or recruitment (Figure 1). For our study, MPMs have a distinct advantage over life tables because they are far more widely available in non-human animal studies (Salguero-Gómez and others, 2016a), thus expanding our comparative evolutionary context. Like life tables, the properties of MPMs are well-understood (Caswell, 2001). From MPMs, one can calculate a broad range of metrics ranging from population dynamics measures, such as long-term population growth rate, to short-term dynamics descriptors, such as reactivity and damping ratio which quantify population responses to perturbation (Stott and others, 2011), to measures which may be better described as life history traits such as life expectancy and reproductive strategy (e.g., frequency and quantity of reproduction). Collectively these suites of demographic and life history parameters fully describe the life history demography of the population concerned at the time and place of study.

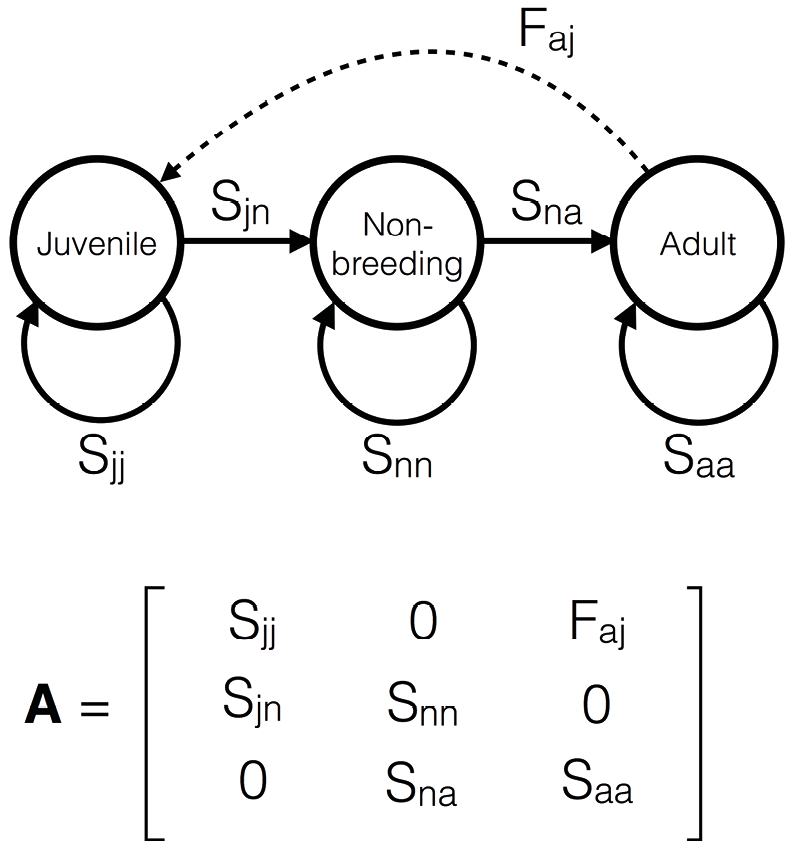
Figure 1. An example of a matrix population model (MPM) and its associated life cycle diagram. This model has three stages defined by ontogeny. In the life cycle diagram, the arrows represent transitions from stage-to-stage in one time step (usually a year). The unbroken arrows represent survival, while the broken arrow represents recruitment to the juvenile stage. The letters next to the arrows indicate the relationship between processes described by the life cycle diagram and the matrix model below it. Thus, for example, Sjn represents a transition probability (survival) from the juvenile stage (j) to the non-breeding stage (n); Saa represents adult survival; and Faj represents the average number of recruits to the juvenile stage produced by an adult.

We obtained the non-human MPMs from the COMADRE Animal Matrix Database (Salguero-Gómez and others, 2016a). This database contains several thousand MPMs from hundreds of species and we use only a subset of these here. Specifically, we filter the matrices to include only tetrapods (mammals, reptiles and birds1) partly due to data availability and partly because we wanted to focus on unitary (non-modular) organisms with no clonality or retrogression (i.e., ‘rejuvenation’), which pose numerous analytical and conceptual complications. In addition, we only include ‘mean matrices’ (i.e., the models parameterized with field data that represent the average dynamics expressed by a population across study periods and sites), where the data were collected under unmanipulated and non-captive conditions with a projection interval of one year, and where the matrix could be split into sub-matrices according to demographic processes of growth/survival and sexual reproduction (termed the U and F matrices respectively). We further tested these matrices to ensure they satisfied the mathematical conditions of irreducibility and primitivity, which are necessary for some of the calculations performed (Stott and others, 2012). Application of these criteria resulted in a dataset of 200 MPMs for 87 non-human species. Most species were only represented by a single matrix, but for others, where studies on a particular species have been published from more than one location or time period, there were several matrices available (median = 1, mean = 2.157, range = 1–16).

To this set, we added 1,657 human MPMs obtained from age-specific female population size, birth, and death data.2 These data were sourced from three population atlases (Keyfitz and Flieger, 1968, 1990, 1971), on the Eurostat server (http://ec.europa.eu/eurostat), as described by Nicol-Harper et al. (2018), or from the Australian Bureau of Statistics, Official Statistics of Japan, Statistics Canada, Statistics New Zealand and the United States Census Bureau. These sources contain different data resolutions (the Eurostat data is age-specific, whereas the others group specific ages into five-year intervals) and different maximum ages, so all were treated using an iterative scheme (Keyfitz, 1966) to generate a ‘common currency’ of comparable matrices with five-year projection intervals. Keyfitz’s iterative scheme takes snapshot data provided in population censuses and infers rates of survival (l_x) and fertility (m_x) assuming a stationary population structure. In other words, ‘a life table that agrees with the data’ (Keyfitz, 1966). Mueller et al. (to appear as Mueller, M., Packman, D. Townley, S., Hodgson, D., Dooley, C.A., Bijak, J., and Ezard, T.H.G, R and MATLAB functions to convert demographic census data to Life Tables and Leslie Matrices, Wellcome Open Research) give further discussion on the implementation of Keyfitz’s iterative scheme (1966) as well as open-source code for MATLAB and R. The R functions are also available within the COMPADRE GitHub repository. These MPMs span 1780 to 2014 across 96 countries. For most countries, just a few MPMs were available (median = 6). For others, multiple years were available (e.g., 90 years for Sweden, 33 years for France, 15 years for Japan), which then allowed us to study how human populations have navigated through time within an organizational framework that contextualizes their demography to that of the other vertebrate species examined here.

We calculate six life history traits from each MPM, which we first list here, but then define more precisely in subsequent paragraphs (Table 1). These life history traits are broadly divided into measures relating to pace and shape of aging (Baudisch, 2011), as well as to reproduction and its distribution throughout the life course. In the former category, we included mean life expectancy (e₀), exceptional life span (Ω), and distribution of mortality risk (quantified by Keyfitz’ life table entropy, H). We also included a measure which quantifies the degree of iteroparity: Demetrius’ evolutionary entropy, S. Degree of iteroparity quantifies the spread of reproduction over the life course. Species with a very low degree of iteroparity reproduce only once before death,3 while species with a higher degree of iteroparity reproduce numerous times. Finally, we include the basic reproduction number (R₀). Most of these metrics can be calculated directly from the MPMs, but the two entropy measures required that we first calculate a life table from the MPM. We accomplished this using the ‘age-from-stage’ methods developed by Cochran & Ellner (1992) and Caswell (2001). For the human MPMs, e₀ is a direct output of the iterative scheme implemented to calculate the lifetable (i.e., the conversion to MPM is redundant).

Mean life expectancy (e₀) is a measure of the average time an organism can be expected to live. We calculated mean life expectancy from birth (i.e., from entering the first stage of the life cycle described by the MPM) using a Markov chain approach, which focuses on the time individuals spend in different states (i.e., life stages) as they pass through the life cycle. The primary tool for this analysis is the fundamental matrix (N) of the MPM (A), which provides a measure of the expected residence time in each state in a Markov chain (see Caswell 2001 for further details). The first column of N thus represents time that an individual that was originally in the first stage spends in each subsequent stage and, therefore, the sum of the column is an estimate of life expectancy across all the stages. We calculated exceptional life span (Ω) as the number of time steps (i.e., years in this case) that it would take a population vector of 1000 individuals in the first stage and zero in all other stages to reach a population size of less than 10 (summation of the population vector n < 10) when multiplied iteratively following the chain rule of n(t + 1) = A*n(t) (described in Caswell, 2001, and Morris & Doak, 2002). For the human MPMs, the calculation of exceptional life span was not possible because the oldest age class (80+ years) did not include a stasis transition (i.e., surviving within the age class). Thus, our analysis of the human MPMs alone excluded this variable; for our cross-species comparison we used an exceptional life span value of 100 years, based on an examination of life tables from the human mortality database (HMD). The exact value of exceptional life span varies among populations and time periods, and we therefore checked that varying the value used between 85 and 120 did not qualitatively influence our results. There are several measures of generation time (T), but we use the time taken for a population to increase by a factor of R₀, i.e. T = log R₀/log λ₁, which is straightforward to calculate from stage-classified matrix models (Caswell, 2001).

We included two entropy measures. First, Keyfitz entropy (H, also known as life table entropy (Keyfitz, 1985)) is a measure that describes the way that mortality risk is distributed over the life course. Where mortality risk remains constant through life H = 1, where mortality risk is relatively high early in life and declines with age (as in, for example, teleost fish) H > 1, and where and where mortality risk increases with age (as in humans) H < 1. In the extreme case where there is zero mortality until all individuals die at the same time, H = 0. H can therefore be interpreted as a measure of the shape of the survivorship curve, and of the mortality trajectory, and thus the ‘shape’ of senescence (sensu Baudisch, 2011) (See Figure 2A). In addition, it is useful to note that H is also a descriptor of the distribution of the age at death, or lifespan equality, with low values of H corresponding to high life span equality, where most individuals die at a similar age (Colchero and others, 2016). Note that H is well-correlated with numerous other viable candidate measures of the shape of the mortality trajectory — and consequently the distribution of the ages at death (Wrycza and others, 2015). Secondly, Demetrius’ evolutionary entropy (S), quantifies the degree of iteroparity, or the spread of reproduction across the life course and can also be interpreted as the uncertainty in the age of the mother of a randomly chosen newborn (Demetrius, 1974). Organisms that reproduce in a single reproductive bout (e.g., semelparous species) have low values of S (S ≈ 0), and those that reproduce steadily throughout their life course have high values of S (S >> 0) (Figure 2B).

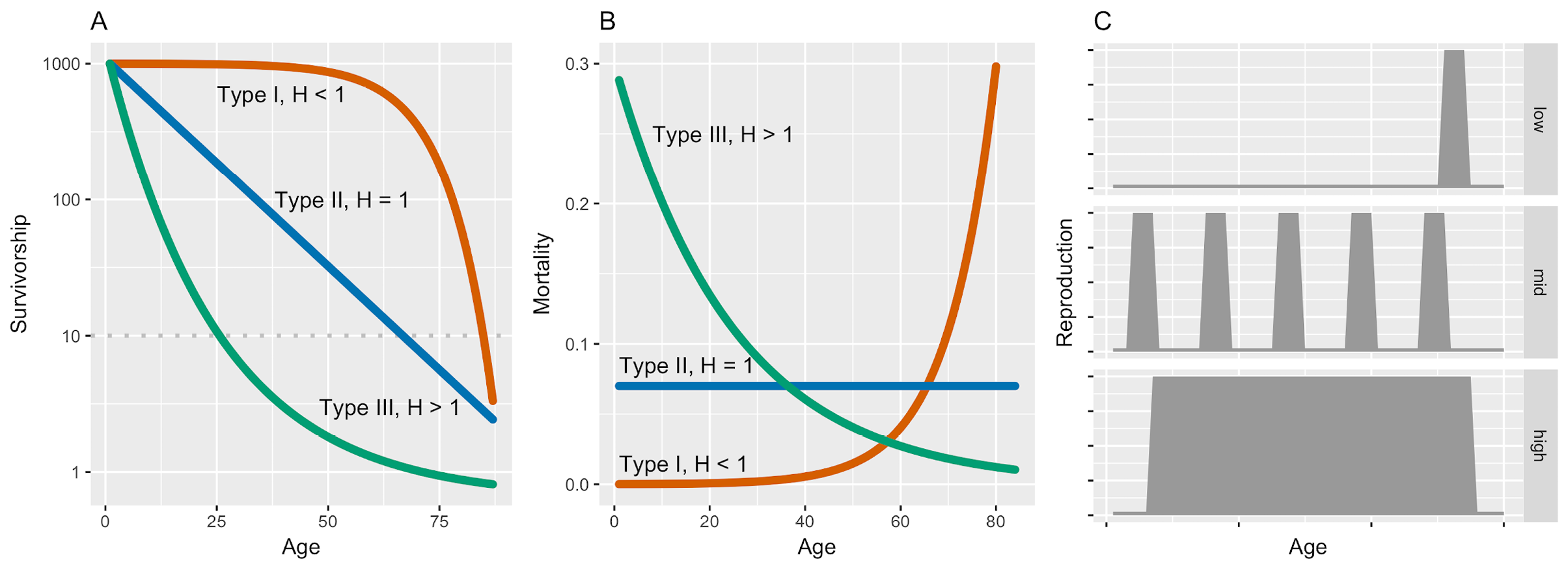
Figure 2. The relationship between survivorship curves and the distribution of mortality risk over the life course as quantified by Keyfitz’s life table entropy (A) and the corresponding mortality trajectories (B). In this case, the entropy values are 0.16, 1.00 and 1.28 for Type I, II and III respectively. C illustrates the relationship between distribution of reproductive output and degree of iteroparity measured using Demetrius’ evolutionary entropy ranked from low entropy in the top panel to high entropy in the bottom panel.

Finally, to calculate the basic reproduction number (R₀), which is the average number of offspring produced over the lifetime of an individual, we used the methods described by Caswell (2001). Thus, we first calculated a matrix, R, as the matrix product of the fundamental matrix (N) and the F matrix (sexual reproduction). Then we calculated R₀ as the dominant eigenvalue of the matrix R. Collectively, these metrics provide a well-rounded description of the life history strategy of the species and populations in our study.

Phylogenetic trees describe the hypothetical evolutionary relationships of groups of organisms with a single common ancestor. They are necessary in comparative analyses across species, because (i) common statistical approaches assume independence of errors, which is not the case in analysis where each datapoint is related in some structured hierarchical way to all others, and (ii) it is useful to gain insight of how trait values are structured by the phylogeny (Blomberg and others, 2003; Freckleton and others, 2002). We use a species-level phylogeny constructed by Healy et al. (2019) based on available phylogenies for birds (Jetz and others, 2012), mammals (Kuhn and others, 2011) and reptiles (Pyron and Burbrink, 2014).

Statistical Methods

Our statistical methods differed between our central cross-species analysis, which includes all available species data, and the analysis we performed on solely the human data. For the cross-species analysis, we heed the well-known observation that demographic parameters scale with body mass. We therefore obtained body mass for our species from Myhrvold et al. (2015) and regressed each demographic trait against body mass in a phylogenetic generalized least squares (PGLS) regression. In addition, we controlled for matrix dimension, which can potentially confound comparative analyses (Salguero-Gómez and Plotkin, 2010), by adding it (log10 transformed) as a covariate. We used the residuals from this relationship, which describe each trait’s departure from expectation given body mass, phylogenetic relationships, and matrix dimension in a principal component analysis (PCA) (Gaillard and others, 1989). For the human-only analysis we did not need to account for phylogeny, body mass or matrix dimension in this way since the subjects are all populations from a single species, with approximately the same body mass and from matrices of equal size. Nevertheless, we acknowledge that the human data has numerous structural dependencies that may influence mortality and fertility patterns, and these are the subject of ongoing work.

Principal Component Analysis (PCA)

Principal component analysis (PCA) is a statistical technique that reduces complex, multidimensional data to a smaller number of dimensions (hereafter, ‘axes’) that are linearly uncorrelated (Legendre and Legendre, 2012; Mardia and others, 1979). We use PCA to characterize our complex life history data by using either the residuals from our cross-species regression models or the actual demographic estimates for the analysis of humans alone. For the cross-species analysis, to avoid swamping the analysis with human data, we used representative data from a subset of the human MPMs. Specifically, we used the mean demographic trait values for each of the 84 countries for which we had data. We fitted the PCA using the prcomp function in the stats package of R, and took the standard approach of z-transforming the data (mean centered at 0 with a standard deviation of 1 (Legendre and Legendre, 2012)). We determined the number of principal component axes to retain using Horn’s parallel analysis (Horn, 1965; Dinno, 2009). We then used those retained axes to define the life history strategy space onto which we will contextualize the demographic behaviour of the species and populations included in our analysis.

We conducted several PCA analyses to explore life history variation both across species and within humans. First, in order to define the framework for comparisons between humans and other vertebrates, we carried out a PCA across all species (including humans). A large body of previous work (Stearns, 1992; Jones and others, 2008; Gaillard and others, 2005) has suggested the existence of a ‘fast-slow continuum’ of life history. In this putative continuum, species’ demographic strategy can be adequately described by position along a single axis of variation with species with high allocation to reproduction at one end, and those with low allocation at the other end. We therefore hypothesized that there would be clear evidence of a major fast-slow life history continuum, with traits relating to time aligning with the first PC axis. We also expected to see an orthogonal axis related to the range of reproductive strategies available, based on previous work in plants and animals (Salguero-Gómez and Jones, 2016; Salguero-Gómez and others, 2016b). In this second axis, at one extreme are highly-fecund, highly-iteroparous species while at the other extreme are semelparous species that reproduce only once.

Second, we conduct a PCA focused on human populations to evaluate how the life history structuring of our species differs from life history structuring across the vertebrates. For three human populations with high temporal replication, we examined how their relative positioning within the PCA life history strategy space has shifted through time. Broadly we expect to see a similar structuring — with pace of life being a dominant axis. When looking at changes through time in particular populations, we expect to see clear traversal through life-history strategy space reflecting the well-known increases in life expectancy and life spans alongside a reflection of changes in life table entropy that have accompanied changes in the distribution of age at death.

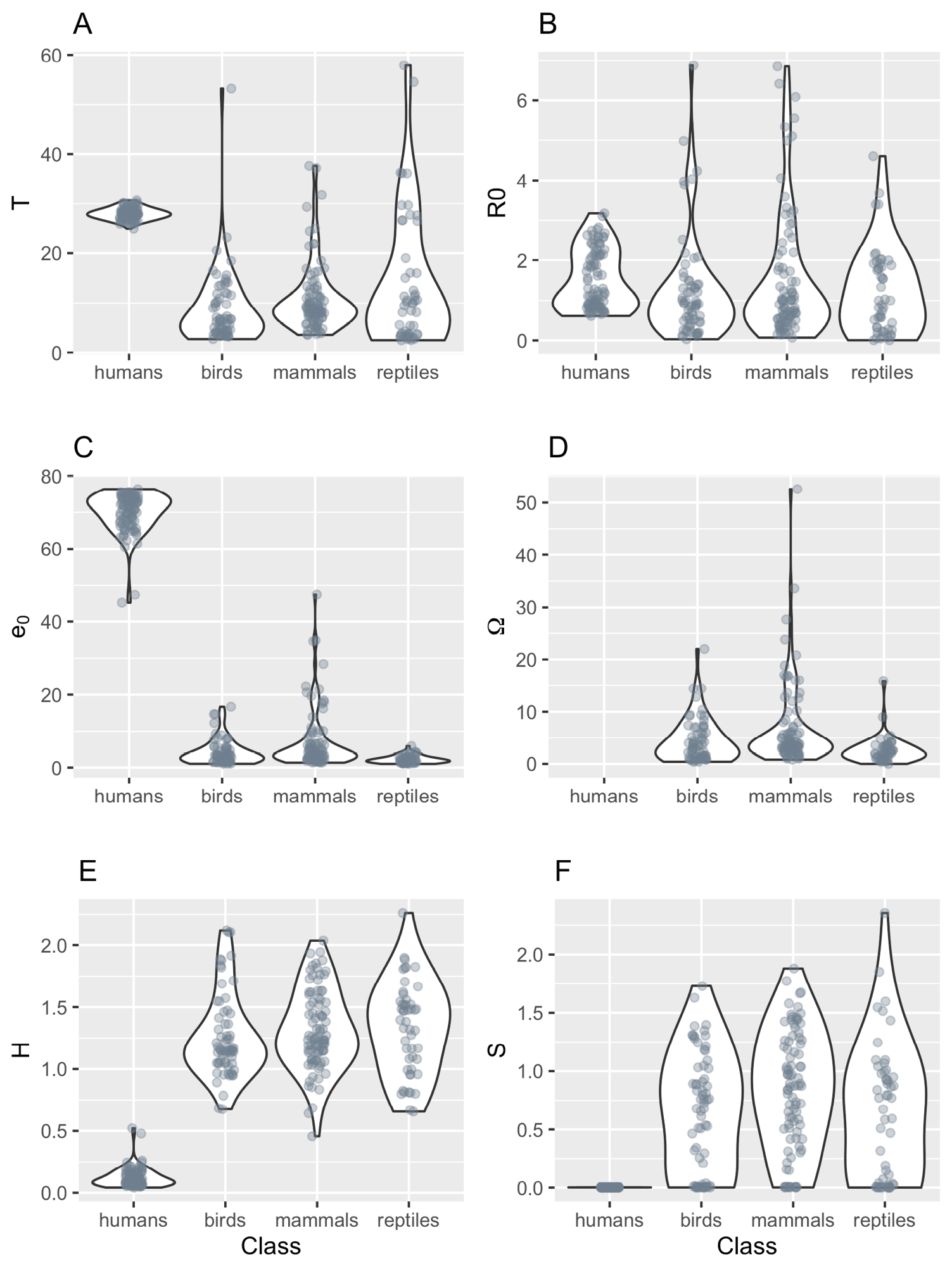
Figure 3. The distribution of six demographic trait values in MPMs used in this study for humans, birds, non-human mammals, and reptiles. A. generation time (T); B. basic reproduction number (R₀); C. mean life expectancy (e₀); D. exceptional life span (for non-humans only) (Ω); E. distribution of mortality risk (H); F. degree of iteroparity (S) — see text for details. Each point represents a single estimate derived from an MPM. Non-human species are represented by between 1 and 16 estimates (mean = 2.157, median = 1), humans are represented by 96 measurements which are the arithmetic means for each country in the available dataset. The values for S in humans were all very low (range: 0.0012–0.0030).

Results

Across the taxonomic groups the demographic trait distributions overlap for the non-human animals, though it is clear that the longevity and life expectancy of some mammals greatly exceed those of the other two classes (Figure 3). It is also very clear that humans are rather exceptional when considering these life history trait values, with trait distributions that are far-removed from the other mammals in most cases (Figure 3).

The strength of phylogenetic signal in the relationships between body mass and the demographic traits varied considerably, and the estimates were rather uncertain in many cases. In descending order of signal strength, the values were: generation time (0.96, 95% CI = 0.82–1.00), life expectancy (0.64, CI = 0.36–0.82), life table entropy (0.51, 95% CI = 0.04–0.83), exceptional life span (0.47, 95% CI = 0.04–0.73), R₀ (0.10, 95% CI = 0.00–0.63), and evolutionary entropy (0.00, 95% CI = 0.00–0.71).

Principal Components Analysis: All Species

The PCA analysis (Figure 4) revealed that the life history strategy of the animals in our dataset is adequately described by two principal component axes, according to Horn’s parallel analysis (Horn, 1965; Dinno, 2009). Together these two axes explain 70.59 % of variation in demographic traits (45.85 and 24.74 % for PC 1 and 2 respectively). The analysis also revealed that all taxonomic classes (birds, reptiles, and mammals) cluster together in demographic PCA-space (Figure 4), and that the humans are to be found outside the 95% CI bivariate ellipse that represents the limits of mammalian life history strategy. The loadings (Figure 4 and Table 2) indicate that three of the six variables (exceptional life span (Ω), mean life expectancy (e0) and generation time (T)), align well with PC1 and two align well with PC2 (distribution of mortality risk (H), degree of iteroparity (S)). Basic reproduction number (R0) appears to align approximately halfway between the two major PC axes. Since generation time, life expectancy, and exceptional life span are related to the timing of key life events we interpret this first major axis as being strongly associated with the fast-slow continuum (Stearns, 1992; Jones and others, 2008). The second axis (PC2) can be interpreted as representing the probability distribution of key events in the life course: reproduction (indicated by S) and mortality risk (indicated by H). For example, mortality risk may be distributed evenly (negligible senescence), or may increase or decrease with age (senescence or negative senescence). Likewise, reproduction can be concentrated within a particular part of the life course (as in humans) or distributed more evenly.

Table 2: Variable loadings for the first two principal components of the PCA analyses. e₀ = life expectancy; Ω = exceptional life span; T = generation time; R₀ = basic reproduction number; H = distribution of mortality risk; S = degree of iteroparity. SD = standard deviation. All variables were mean standardized before analysis. See Table 1 and main text for details.

Analysis	PC	SD	e0	Ω	T	R0	H	S
Cross-species	PC1	1.659	0.525	0.566	0.390	0.300	0.119	0.384
	PC2	1.218	0.359	0.178	0.102	−0.140	−0.736	−0.518
Human (all)	PC1	1.750	0.514	–	−0.006	−0.481	−0.505	−0.500
	PC2	1.014	−0.131	–	−0.940	−0.214	0.195	−0.138

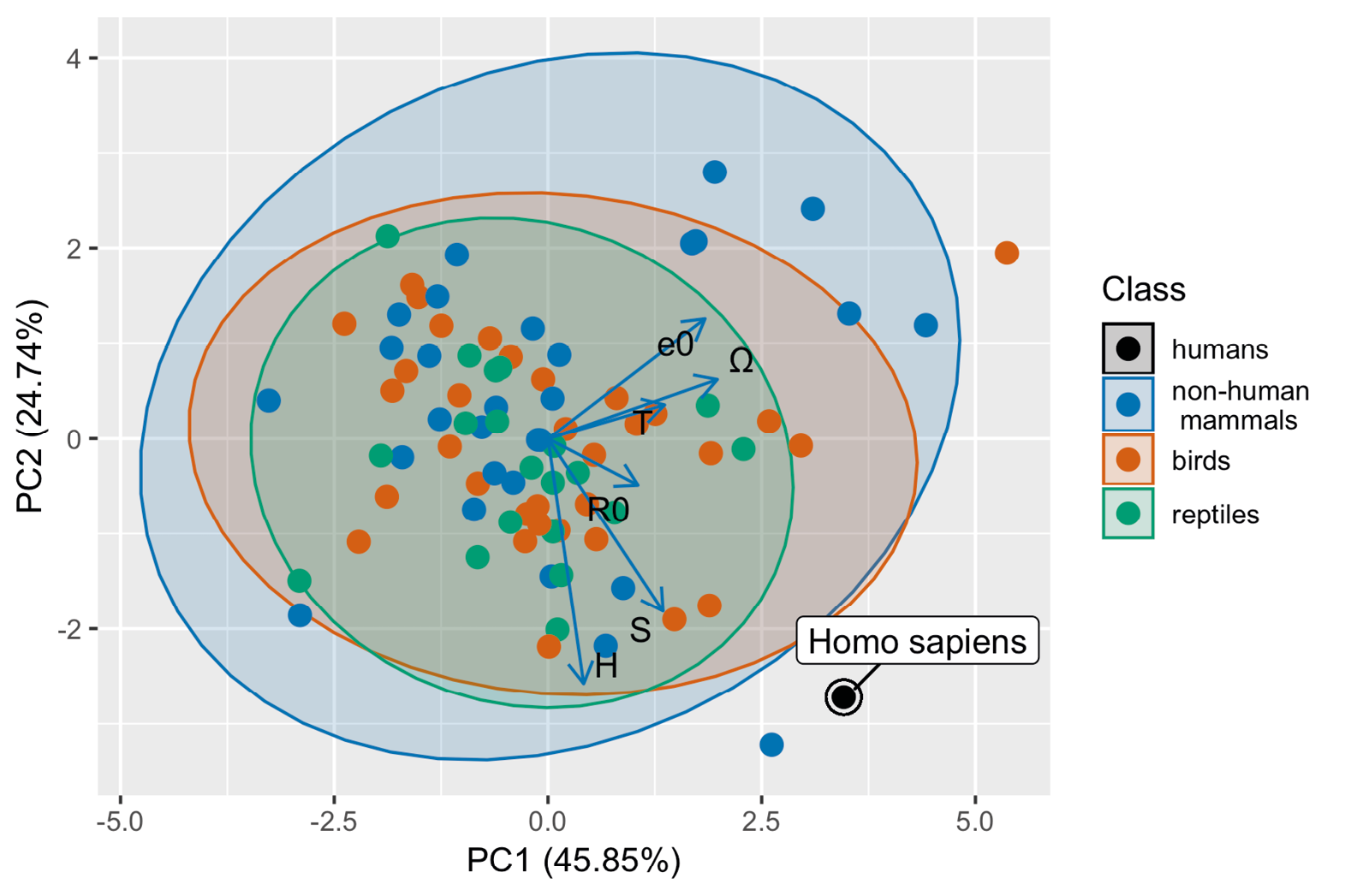
Figure 4: Principal components analysis of demographic behaviour for 34 bird species, 33 mammal species (including humans), and 19 reptile species. The ellipses illustrate the life-history strategy space occupied by these taxonomic groups (excluding humans), and are defined by the 95% bivariate confidence interval associated with the PC scores for each group. The arrows represent the principal component loadings for each of the demographic variables in the analysis: T = generation time; R₀ = basic reproduction number; e₀ = mean life expectancy; Ω = exceptional life span; H = distribution of mortality risk; S = degree of iteroparity — see text for details. See Table 2 for variable loading values. The outlier point for the non-human mammals is the blue monkey (Cercopithecus mitis), and the outlier for the birds is European honey buzzard (Pernis apivorus).

Principal Components Analysis: Humans Only

Examining the PCA for humans reveals a markedly different picture. Although again, the first two PC axes were sufficient to explain most 81.81% of the variation (61.26% and 20.55% for PC 1 and 2 respectively), these axes were less-readily identifiable as clear ‘pace of life’ and probability distribution of life events (or indeed “reproductive strategy”) axes (Figure 5A). The loading for T is markedly larger than all others, and dominates PC2, but the relationship between T and other variables (as we will show below) is dependent on the time period analyzed. Interestingly, although the loadings for e₀ and H were orthogonal in the cross-species analysis, they were in opposition in the human analysis, indicating that increased average life span is associated with a decline in entropy (i.e., an increase in the equality of age at death). The closest association among loadings was between R₀ and S highlighting the close positive association between these traits.

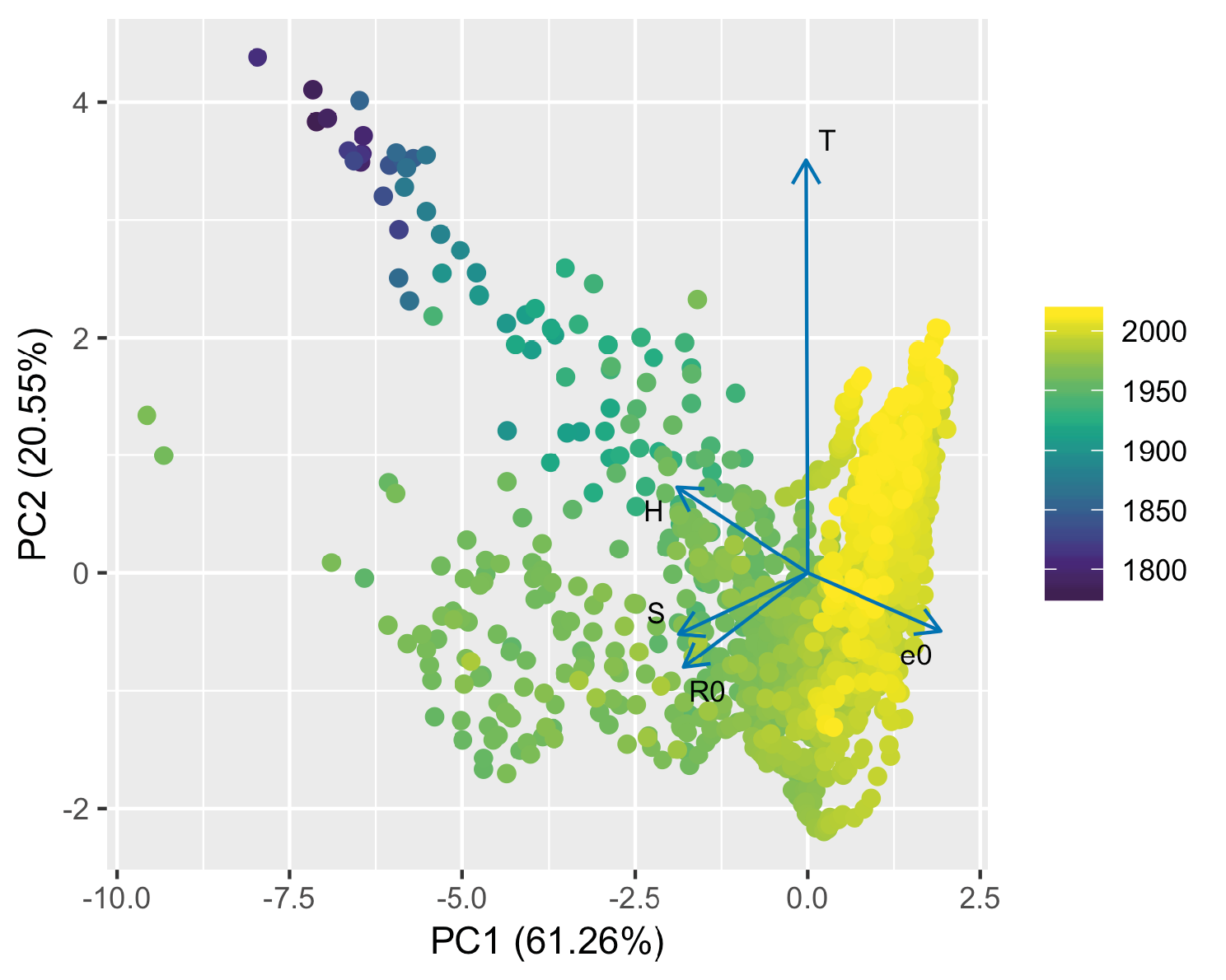
Figure 5: Principal components analysis (PCA) of demographic behaviour for 1657 MPMs for humans. There are 96 countries represented by between 1 and 90 matrices (mean = 17.26, median = 6), representing populations from years between 1780 and 2014. The points are colour coded, with older points being dark purple and more recent points being bright yellow. The principal component loadings for each of the demographic variables are represented by blue arrows: T = generation time; R₀ = basic reproduction number; e₀ = mean life expectancy; H = distribution of mortality risk; S = degree of iteroparity — see text for details. The key points to observe here are the strength and associations of the principal component loadings (i.e., which arrows sit together, and which are in opposition or orthogonal to each other). See Table 2 for variable loading values.

A particularly striking phenomenon clear from Figure 5 is the shift across demographic strategy space that has occurred through time that is apparent from the colour coding of the data points by year. This shift, from the top-left towards the bottom-right of the figure indicates, broadly speaking, that populations have trended towards increased life expectancy, decreased entropy (with mortality more concentrated towards the end of life), and with a shorter generation time. These trends can perhaps be seen more clearly by examining how some exemplar countries, Sweden, France, Japan, and Bulgaria have “moved” across PCA life history strategy space through time (Figure 6).

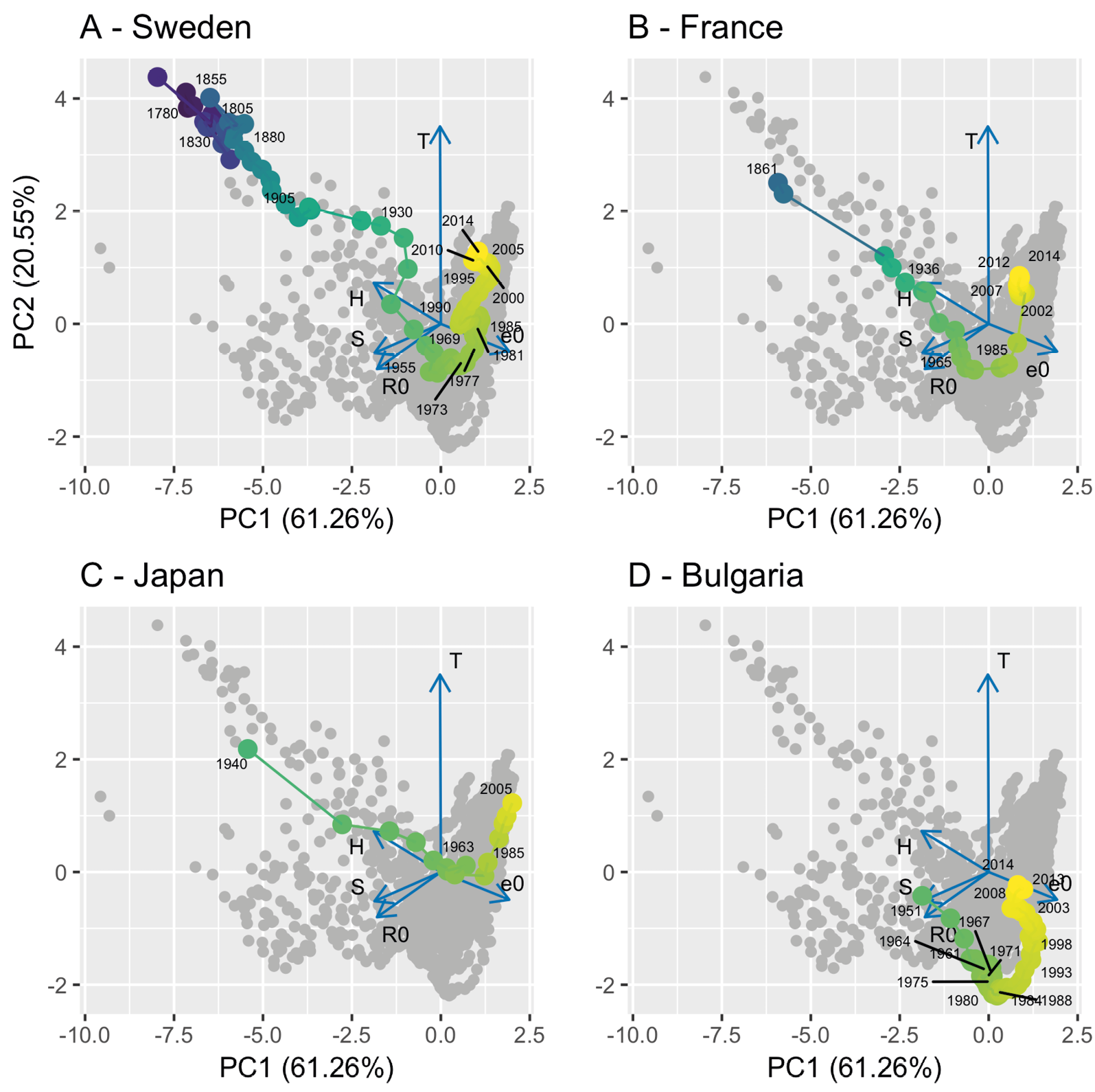
Figure 6: The traversal of demographic PCA-space by four example countries, (A) Sweden, (B) France, (C) Japan, and (D) Bulgaria. The grey points are the points for the non-focal countries while the coloured points represent the focal country. The points are colour coded to represent time, using the same scale as in Figure 5. The blue arrows represent the principal component loadings for each of the demographic variables in the overall analysis: T = generation time; R₀ = basic reproduction number; e₀ = mean life expectancy; H = distribution of mortality risk; S = degree of iteroparity — see text for details.

Discussion

We aimed to explore where the demography of humans fits in to the bigger evolutionary picture of other vertebrate species. The distribution of demographic behaviour among species is of profound interest to evolutionary biologists with researchers questioning whether, and how, species with certain combinations of demographic traits are restricted to particular habitats (Southwood, 1988). One of the dominant frameworks that has been used to study this topic is the fast-slow continuum, which focuses on the trade-off between survival (or somatic maintenance) and reproduction (Stearns, 1992). This trade-off proposes that the entire range of life histories can be described by position along a single axis with proportionally high allocation to reproduction at one end and low allocation at the other end. The existence of this fast-slow life history framework has received considerable support (Gaillard and others, 2005; Jones and others, 2008; Oli, 2004; Sæther, 1987), but the picture has been complicated by research revealing additional axes that structure observed life-history variation among species (Salguero-Gómez and Jones, 2016; Bielby and others, 2007; Gaillard and others, 1989).

Our examination of the principal components axes of humans, mammals (including humans), birds, and reptiles supports our hypothesis, confirming that the distillation of the great variety of demographic behaviour requires two major axes. These two axes explain a large proportion (~70%) of the variation life history across species. This figure is markedly larger than found across the plant kingdom (55%) by Salguero-Gómez et al. (2016b), but less than the 80% reported by Salguero-Gómez & Jones (2016) for an analysis across both plant and animal kingdoms. However, the life-history traits included differ among these three analyses making over-interpretation of these differences unwise. A more appropriate comparison is with the result of the human-only PCA conducted for this chapter, where we used the same approach and variables (with the exception of exceptional life span), and for which the PCA explained 82% of demographic variation. The result that a cross-species analysis explains less variation than a within species analysis is likely caused by the more constrained repertoire of available life history strategies within- rather than among-species.

Previous cross-species studies in plants and animals (Salguero-Gómez and Jones, 2016; Salguero-Gómez and others, 2016b) interpreted the two dominant principal component axes as (i) the pace of life and (ii) the reproductive strategy axes. The former axis relates to the timing of life events such as generation time (which is tightly linked to age at maturity), life expectancy, and life span, while the latter axis is related to the amount and distribution of reproductive output. As expected, we find good evidence for the existence of a dominant ‘pace of life’ axis in the cross-species analysis. However, we make a slightly broader interpretation of the second axis, which we interpret as indicative of the ‘distribution of life events’. Our interpretation here is driven by the fact that both life table entropy (indicative of distribution of mortality) and degree of iteroparity (indicative of distribution of fertility) align well with this axis. The almost total overlap of the three taxonomic classes in life history strategy space occupied indicates that life history strategy is not structured taxonomically. It is striking that although humans may not be exceptional in terms of some individual demographic traits, when considered collectively in a PCA these traits reveal that our demographic behaviour falls some way outside of the norm for mammals. It is worth considering, however, that the data we are using in this study may not reflect the ancestral state of humans because they are dominated by contemporary populations with low mortality and fertility. In future work it will be interesting to explore how populations that may be closer to the ancestral state fit into this schema (e.g., using data on contemporary hunter gatherers).

The direction and magnitude of the PCA loadings illustrate the ‘life history architecture’ — the complex of correlations among our chosen set of demographic traits. They show that across species the traits we included in our analysis can be divided into two orthogonal sets of highly-correlated traits: (i) life expectancy, exceptional life span, and generation time, and (ii) distribution of mortality risk, and degree of iteroparity. Net reproductive output fell in between these two major axes. Within these trait groups, as one trait has evolved, the others have ‘hitched a ride’ due to mathematical association or genetic correlation: e.g., as life expectancy has increased, so has exceptional life span and generation time. The orthogonality of these two groups suggests that although the within-group traits are tightly correlated, the traits in different groups are not, and have the capacity to evolve more-or-less independently. For example, it seems that species with short or long exceptional life spans (or life expectancies, or generation time) can have any type of mortality trajectory (indicated by the distribution of mortality risk, life table entropy). Since life span and life expectancy are measures of the pace of mortality, while entropy is a measure of the shape of mortality, this supports Baudisch’s (2011) assertion that pace and shape are likely to be independent aspects of the mortality trajectory. We note, however, that exceptional life span and life expectancy are not perfectly aligned. This indicates that these measures do not scale together, but rather that as exceptional life span increases, life expectancy does not keep pace, which leads to a tendency for increased values of H (e.g., moving from a Type I towards a Type II or III survivorship curve, or towards greater inequality in age at death). This observation is supported by the result that the loading for H is not perfectly orthogonal to life expectancy.

An examination of the PCA for humans alone reveals that life history architecture within our species is rather different to the cross-species PCA. Our interpretation of the dominant axes as pace-of-life and distribution of life events are now far less clear cut. Furthermore, rather than the traits being divided fairly neatly into two approximately orthogonal groups, the situation of humans appears to be more complex. Nevertheless, there are some interesting observations: life expectancy is directly opposed to the distribution of mortality risk (H), indicating a close positive association between life span equality and life expectancy. This observation supports recent work on humans and our close primate relatives that shows a striking linear relationship between life expectancy and life span equality (Colchero and others, 2016). The marked shift in position in the life history space (PCA-space) begs the question: has life history architecture changed through time? Such changes in the demographic variable loadings might be expected given the well-known and dramatic reductions in infant and childhood mortality (Vaupel, 1986; Hill and others, 2012) and the occurrence of the demographic transition from high birth and death rates to low birth and death rates as societies industrialize (Kirk, 1996). However, this analysis is non-trivial given the within-country dependencies and the different geographic coverage of the data through time, and it would be difficult to disentangle temporal changes common across countries from compositional changes.

The clear differences between the cross-species and within-species analysis are enigmatic, but it is important to bear in mind that the processes leading to differences among data points in these two analyses are fundamentally distinct. Indeed, this distinction between, within-,and among species analyses have led some to question the wisdom of invoking life history theory, and, in particular continua, such as the fast-slow continuum, to explain variation within species (Zietsch and Sidari, 2019). The relationships and differences among traits in the cross-species analysis are primarily the result of evolution. Selection pressures vary among species resulting in different optima for demographic traits depending on environmental conditions. Within humans (i.e., variation across human populations and through time), the observed demographic variation and structuring are likely the result of phenotypic plasticity (the capacity of a genotype to exhibit different phenotypes depending on the environment), rather than natural selection. This plasticity has resulted in some striking patterns in the within-human analysis.

The remarkable plasticity of demographic behaviour in modern humans is clearly seen with the passage through time of our four example countries across life history strategy space. The tendencies towards longer exceptional life spans and longer life expectancies are well-known among human demographers (Oeppen and Vaupel, 2002). So too is the trend that mortality distribution has shifted leading to greater equality in the age at death (Colchero and others, 2016; Gillespie and others, 2014). There is clearly a rather large difference among populations in the speed that life history strategy space is traversed. For example, it took Japan a fraction of the time to traverse this space than that taken by France and Sweden. Another striking feature is the non-linear U-shaped trajectory seen in all four of our example countries. It is possible that this may be driven by the advent of birth control methods in the 1960s-70s, but further investigation is needed to support this. Although the qualitative pattern shown in the different countries are similar, there are qualitative differences that will be fascinating to explore.

Our approach of distilling demographic strategy into principal component axes, which is derived from workers focusing on the life history evolution of non-human species (Gaillard and others, 1989), offers a useful tool for the exploration of human demography. First, it allows us to see how our life history strategy compares with other species; the results reveal we are a mammalian demographic outlier. Second, it offers a tool for tractably exploring how complex strategies are influenced by environmental drivers. For example, it would be interesting to explore the impact of technological and public health developments, wealth, and income equality on human life history strategy rather than single demographic variables. The comparably vast wealth of data available across diverse human populations represent a treasure trove to help us understand the development of life history strategies.

Acknowledgements

Appendix: Species List

References4

Baudisch, A. 2011. ‘The Pace and Shape of Ageing’, Methods in Ecology and Evolution, 2.4: pp. 375–82. https://doi.org/10.1111/j.2041-210x.2010.00087.x

Bielby, J., G. M. Mace, O. R. P. Bininda-Emonds, M. Cardillo, J. L. Gittleman et al. 2007. ‘The Fast-Slow Continuum in Mammalian Life History: An Empirical Reevaluation’, The American Naturalist, 169.6: pp. 748–57. https://doi.org/10.1086/516847

Blomberg, S. P., T. Garland Jr, and A. R. Ives. 2003. ‘Testing for Phylogenetic Signal in Comparative Data: Behavioral Traits Are More Labile’, Evolution, 57.4: pp. 717–45. https://doi.org/10.1554/0014-3820(2003)057[0717:tfpsic]2.0.co;2

Butler, P. G., A. D. Wanamaker, J. D. Scourse, C. A. Richardson, and D. J. Reynolds. 2013. ‘Variability of Marine Climate on the North Icelandic Shelf in a 1357-Year Proxy Archive Based on Growth Increments in the Bivalve Arctica Islandica’, Palaeogeography, Palaeoclimatology, Palaeoecology, 373: pp. 141–51. https://doi.org/10.1016/j.palaeo.2012.01.016

Caswell, H. 2001. Matrix Population Models: Construction, Analysis, and Interpretation (Sunderland, MA: Sinauer Associates Incorporated).

Caswell, H, C. de Vries, N. Hartemink, G. Roth, and S. F. van Daalen. 2018. ‘Age × Stage-Classified Demographic Analysis: A Comprehensive Approach’, Ecological Monographs, 88.4: pp. 560–84. https://doi.org/10.1002/ecm.1306

Chiang, C. L. 1984. The Life Table and Its Applications (Malabar, FL: Krieger Publishing Company).

Cochran, M. E., and S. Ellner. 1992. ‘Simple Methods for Calculating Age-Based Life History Parameters for Stage-Structured Populations’, Ecological Monographs, 62.3: pp. 345–64. https://doi.org/10.2307/2937115

Cohen, A. A. 2004. ‘Female Post-Reproductive Lifespan: A General Mammalian Trait’, Biological Reviews of the Cambridge Philosophical Society, 79.4: pp. 733–50. https://doi.org/10.1017/s1464793103006432

Colchero, F., R. Rau, O. R. Jones, J. A. Barthold, D. A. Conde et al. 2016. ‘The Emergence of Longevous Populations’, Proceedings of the National Academy of Sciences of the United States of America, 113.48: pp. E7681–90. https://doi.org/10.1073/pnas.1612191113

Cole, L. C. 1954. ‘The Population Consequences of Life History Phenomena’, The Quarterly Review of Biology, 29.2: pp. 103–37. https://doi.org/10.1086/400074

Demetrius, L. 1974. ‘Demographic Parameters and Natural Selection’, Proceedings of the National Academy of Sciences, 71.12: pp. 4645–47. https://doi.org/10.1073/pnas.71.12.4645

Dinno, A. 2009. ‘Exploring the Sensitivity of Horn’s Parallel Analysis to the Distributional Form of Random Data’, Multivariate Behavioral Research, 44.3: pp. 362–88. https://doi.org/10.1080/00273170902938969

Ellis, S., D. W. Franks, S. Nattrass, M. A. Cant, D. L. Bradley et al. 2018. ‘Postreproductive Lifespans Are Rare in Mammals’, Ecology and Evolution, 8.5: pp. 2482–94. https://doi.org/10.1002/ece3.3856

Freckleton, R. P., P. H. Harvey, and M. Pagel. 2002. ‘Phylogenetic Analysis and Comparative Data: A Test and Review of Evidence’, The American Naturalist, 160.6: pp. 712–26. https://doi.org/10.1086/343873

Gadgil, M., and W. H. Bossert. 1970. ‘Life Historical Consequences of Natural Selection’, The American Naturalist, 104.935: pp. 1–24. https://doi.org/10.1086/282637

Gaillard, J-M, N. G. Yoccoz, J-D Lebreton, C. Bonenfant, S. Devillard et al. 2005. ‘Generation Time: A Reliable Metric to Measure Life-History Variation among Mammalian Populations’, The American Naturalist, 166.1: pp. 119–223. https://doi.org/10.1086/430330

Gaillard, J-M, D. Pontier, D. Allainé, J. D. Lebreton, J. Trouvilliez et al. 1989. ‘An Analysis of Demographic Tactics in Birds and Mammals’, Oikos, 56.1: pp. 59–76. https://doi.org/10.2307/3566088

Gillespie, D. O. S., M. V. Trotter, and S. D. Tuljapurkar. 2014. ‘Divergence in Age Patterns of Mortality Change Drives International Divergence in Lifespan Inequality’, Demography, 51.3: pp. 1003–17. https://doi.org/10.1007/s13524-014-0287-8

Healy, K. T. Ezard, O. R. Jones, R. Salguero-Gómez, and Y. M. Buckley. 2019. ‘Animal life history is shaped by the pace of life and the distribution of age-specific mortality and reproduction’, Nature Ecology & Evolution, 3.8: pp. 1217–24. https://doi.org/10.1038/s41559-019-0938-7

Hill, K., D. You, M. Inoue, and M. Z. Oestergaard. 2012. ‘Child Mortality Estimation: Accelerated Progress in Reducing Global Child Mortality, 1990–2010’, PLoS Medicine, 9.8: e1001303. https://doi.org/10.1371/journal.pmed.1001303

Horn, J. L. 1965. ‘A Rationale and Test for the Number of Factors in Factor Analysis’, Psychometrika, 30.2: pp. 179–85. https://doi.org/10.1007/bf02289447

Jetz, W., G. H. Thomas, J. B. Joy, K. Hartmann, and A. O. Mooers. 2012. ‘The Global Diversity of Birds in Space and Time’, Nature, 491.7424: pp. 444–48. https://doi.org/10.1038/nature11631

Jeune, Bernard, Jean-Marie Robine, Robert Young, Bertrand Desjardins, Axel Skytthe et al. 2010. ‘Jeanne Calment and Her Successors. Biographical Notes on the Longest Living Humans’, in Demographic Research Monographs, ed. by H. Maier, J. Gampe, B. Jeune, J. M. Robine, J. Vaupel (Berlin, Springer), pp. 285–323.

Jones, O. R., J-M Gaillard, S. Tuljapurkar, J. S. Alho, K. B. Armitage et al. 2008. ‘Senescence Rates Are Determined by Ranking on the Fast-Slow Life-History Continuum’, Ecology Letters, 11.7: pp. 664–73. https://doi.org/10.1111/j.1461-0248.2008.01187.x

Jones, O. R., P. Barks, I. Stott, T. D. James, S. Levin et al. (2022). ‘Rcompadre and Rage — Two R packages to facilitate the use of the COMPADRE and COMADRE databases and calculation of life‐history traits from matrix population models’, Methods in Ecology & Evolution, 13: pp. 770–81. https://besjournals.onlinelibrary.wiley.com/doi/pdf/10.1111/2041-210X.13792

Keyfitz, N. 1966. ‘A Life Table That Agrees with the Data’, Journal of the American Statistical Association, 61.314: pp. 305–12. https://doi.org/10.1080/01621459.1966.10480866

—. 1985. Applied Mathematical Demography (New York: John Wiley & Sons).

Keyfitz, N., and Wilhelm, F. 1968. World Population: An Analysis of Vital Data (Chicago: University of Chicago Press).

—. 1971. Population: Facts and Methods of Demography (San Francisco: W. H. Freeman & Co.).

—. 1990. World Population Growth and Aging: Demographic Trends in the Late Twentieth Century (Chicago: University of Chicago Press).

Kirk, D. 1996. ‘Demographic Transition Theory’, Population Studies, 50.3: pp. 361–87. https://doi.org/10.1080/0032472031000149536

de Kroon, H., J. van Groenendael, and J. Ehrlen. 2000. ‘Elasticities: A Review of Methods and Model Limitations’, Ecology, 81.3: pp. 607–18. https://doi.org/10.1890/0012-9658(2000)081[0607:earoma]2.0.co;2

Kuhn, T. S., A. Ø. Mooers, and G. H. Thomas. 2011. ‘A Simple Polytomy Resolver for Dated Phylogenies’, Methods in Ecology and Evolution, 2.5: pp. 427–36. https://doi.org/10.1111/j.2041-210x.2011.00103.x

Lefkovitch, L. P. 1965. ‘The Study of Population Growth in Organisms Grouped by Stages’, Biometrics, 21.1: pp. 1–18. https://doi.org/10.2307/2528348

Legendre, P., and L. F. J. Legendre. 2012. Numerical Ecology (Amsterdam: Elsevier).

Leslie, P. H. 1945. ‘On the Use of Matrices in Certain Population Mathematics’, Biometrika, 33.3: pp. 183–212. https://doi.org/10.1093/biomet/33.3.183

Mardia, K. V., J. T. Kent, and J. M. Bibby. 1979. Multivariate Analysis (London: Academic Press).

Morris, W. F., and D. F. Doak. 2002. Quantitative Conservation Biology: Theory and Practice of Population Viability Analysis (Sunderland, MA: Sinauer Associates Incorporated).

Myhrvold, N. P., E. Baldridge, B. Chan, D. Sivam, D. L. Freeman et al. 2015. ‘An Amniote Life-History Database to Perform Comparative Analyses with Birds, Mammals, and Reptiles’, Ecology, 96.11: pp. 3109–09. https://doi.org/10.1890/15-0846r.1

Nettle, D., and W. E. Frankenhuis. 2019. ‘The Evolution of Life-History Theory: A Bibliometric Analysis of an Interdisciplinary Research Area’, Proceedings of the Royal Society B, 286.1899: pp. 20190040. https://doi.org/10.1098/rspb.2019.0040

Nicol-Harper, A., C. Dooley, D. Packman, M. Mueller, J. Bijak et al. 2018. ‘Inferring Transient Dynamics of Human Populations from Matrix Non-Normality’, Population Ecology, 60.1: pp. 185–96. https://doi.org/10.1007/s10144-018-0620-y

Nielsen, J., R. B. Hedeholm, J. Heinemeier, P. G. Bushnell, J. S. Christiansen et al. 2016. ‘Eye Lens Radiocarbon Reveals Centuries of Longevity in the Greenland Shark (Somniosus Microcephalus)’, Science, 353.6300: pp. 702–04. https://doi.org/10.1126/science.aaf1703

Oeppen, J., and J. W. Vaupel. 2002. ‘Broken Limits to Life Expectancy’, Science, 296.5570: pp. 1029–31. https://doi.org/10.1126/science.1069675

Oli, M. K. 2004. ‘The Fast–slow Continuum and Mammalian Life-History Patterns: An Empirical Evaluation’, Basic and Applied Ecology, 5.5: pp. 449–63. https://doi.org/10.1016/j.baae.2004.06.002

Pyron, R. A., and F. T. Burbrink. 2014. ‘Early Origin of Viviparity and Multiple Reversions to Oviparity in Squamate Reptiles’, Ecology Letters, 17.1: pp. 13–21. https://doi.org/10.1111/ele.12168

Robinson, W. C. 1986. ‘Another Look at the Hutterites and Natural Fertility’, Biodemography and Social Biology, 33.1–2: pp. 65–76. https://doi.org/10.1080/19485565.1986.9988623

Sæther, B-E. 1987. ‘The Influence of Body Weight on the Covariation between Reproductive Traits in European Birds’, Oikos, 48.1: pp. 79–88. https://doi.org/10.2307/3565691

Salguero-Gómez, R., and O. R. Jones. 2016. ‘Life History Trade-Offs Modulate the Speed of Senescence’, in The Evolution of Senescence in the Tree of Life, ed. by Richard Shefferson, Owen R. Jones, and Roberto Salguero-Gómez (Cambridge: Cambridge University Press), pp. 403–21.

Salguero-Gómez, R., O. R. Jones, C. R. Archer, C. Bein, H. de Buhr et al. 2016a. ‘COMADRE: A Global Data Base of Animal Demography’, Journal of Animal Ecology, 85.2: pp. 371–84. https://doi.org/10.1111/1365-2656.12482

Salguero-Gómez, R., O. R. Jones, C. R. Archer, Y. M. Buckley, J. Che-Castaldo et al. 2015. ‘The COMPADRE Plant Matrix Database: An Open Online Repository for Plant Demography’, Journal of Ecology, 103.1: pp. 202–18. https://doi.org/10.1111/1365-2745.12334

Salguero-Gómez, R., O. R. Jones, E. Jongejans, S. P. Blomberg, D. J. Hodgson et al. 2016b. ‘Fast-Slow Continuum and Reproductive Strategies Structure Plant Life-History Variation Worldwide’, Proceedings of the National Academy of Sciences, 113.1: pp. 230–35. https://doi.org/10.1073/pnas.1506215112

Salguero-Gómez, R., and J. B. Plotkin. 2010. ‘Matrix Dimensions Bias Demographic Inferences: Implications for Comparative Plant Demography’, The American Naturalist, 176.6: pp. 710–22. https://doi.org/10.1086/657044

Southwood, T. R. E. 1988. ‘Tactics, Strategies and Templets’, Oikos, 52.1: pp. 3–18. https://doi.org/10.2307/3565974

Stearns, S. C. 1992. The Evolution of Life Histories (Oxford: Oxford University Press).

Stott, Iain, David James Hodgson, and Stuart Townley. 2012. ‘Beyond Sensitivity: Nonlinear Perturbation Analysis of Transient Dynamics’, Methods in Ecology and Evolution, 3.4: pp. 673–84. https://doi.org/10.1111/j.2041-210x.2012.00199.x

Stott, I., S. Townley, and D. J. Hodgson. 2011. ‘A Framework for Studying Transient Dynamics of Population Projection Matrix Models’, Ecology Letters, 14.9: pp. 959–70. https://doi.org/10.1111/j.1461-0248.2011.01659.x

Tinbergen, N. 1963. ‘On Aims and Methods of Ethology’, Zeitschrift Für Tierpsychologie, 20.4: pp. 410–33. https://doi.org/10.1111/j.1439-0310.1963.tb01161.x

Vaupel, J. W. 1986. ‘How Change in Age-Specific Mortality Affects Life Expectancy’, Population Studies, 40.1: pp. 147–57. https://doi.org/10.1080/0032472031000141896

Wrycza, T. F., T. I. Missov, and A. Baudisch. 2015. ‘Quantifying the Shape of Aging’, PloS One, 10.3: e0119163. https://doi.org/10.1371/journal.pone.0119163

Zietsch, B. P., and M. J. Sidari. 2019. ‘A Critique of Life History Approaches to Human Trait Covariation’, Evolution and Human Behavior, 41.6: pp. 527–35. https://doi.org/10.1016/j.evolhumbehav.2019.05.007