2. Theories and Models: Understanding and Predicting Societal Collapse

Sabin Roman

There have been numerous arguments put forth to explain why societies collapse. In this chapter we consider different approaches to understanding the risk of societal collapse. According to Joseph Tainter, collapse is a rapid and significant loss of an established level of socio-political complexity of a society.1 A complex society usually exhibits a degree of social stratification and differentiation; specialisation of economic functions and occupations at the individual, group, and territorial level; centralised control, i.e. elites that regulate and integrate economic and political activity; regimentation and behavioural control (e.g. rule of law); investment in cultural property (e.g. monumental architecture, literary, and artistic creation etc.); information flow between individuals (e.g. education), between economic and political groups, and between centralised structures and the periphery; trading and redistribution of resources; the general coordination and organisation of individuals and groups; and a single political unit which integrates an extended territory. Practically, collapse is signalled by (or has been associated with) the disappearance or significant decline in these indicators of complexity.

A simple example of quantitative reasoning that gives some insight into the long-term future of our society is the doomsday argument. In 1964 the American cultural theorist Albert Goldman proposed ‘Lindy’s Law’ after spending time in Lindy’s delicatessen in New York listening to comedians try to predict how long each other’s shows would run for. According to this law, “the life expectancy of a television comedian is proportional to the total amount of his exposure on the medium”, based on the observation that many comedians would overexpose themselves in ways that would ultimately prove unsustainable in the long run. This principle was later formalised by the mathematician Bernard Mandelbrot2 and then generalised by Nassim Taleb into the idea that non-perishable things (like human projects and ventures, up to and including human civilisations, but not people or artefacts) ‘age’ in reverse so that “every year that passes without extinction doubles the additional life expectancy” and “the robustness of an item is proportional to its life”.3 Of course, this does not mean we can predict when any given society will collapse, but it does allow us to gain some indication of how long societies in general can be expected to survive, and also potentially which aspects of any given society will outlast which others.

A similar kind of argument was developed by J. R. Gott to consider future prospects for our species.4 This is not based on assumptions about the way that things do or don’t age, but rather on a Bayesian argument about what we can infer from the fact that we ourselves have observed something existing. The idea is that, if an item can only be observed for a finite length of time (e.g. the period of time during which it exists) then, unless we have some prior belief that we are observing it at a special time in its life (e.g. we are actually observing its creation or demise) we should expect our observation of that thing to be located randomly within this period. Thus, we might reason that there is a 95% probability that we will not be observing it at either the first or last 2.5% of its life, and an equal chance that we are observing it in the second half of its lifespan as in the first. Gott goes on to evaluate this argument against his observations of different aspects of civilisation, including Stonehenge, the Berlin Wall, the USSR, and the journal Nature (in which he was publishing). He also applied this argument to our observation of the existence of humanity itself, concluding that we should have 95% confidence that our species will survive between 5,100 years and 7,800,000 years into the future.

Gott, and most other theorists of the subject, were actually more interested in further development of the doomsday argument, which depends not on the temporal location of our observation of the existence of humanity, but rather on our own demographic location within the species itself. The argument is as follows: from a total of N humans that will be born, any one person is equally likely to find themselves at any position n of the total population N. So, the distribution of n/N is uniform over [0; 1]. There is a 95% chance that n/N is within [0.05; 1], so n/N > 0.05, which implies that N < 20n. This places an upper limit on the total expected number of people that will ever be born. With different assumptions on birth rates, we can then determine the total time that humanity has to exist. If 60 billion people have been born by now, then a total of 1.2 trillion people is to be expected overall. This argument has been analysed from various perspectives. However, it has too many moving parts to give a robust time horizon for the end of humanity. The total number of humans up to the present day needs to be estimated, as well as the fraction this constitutes of the total N, and the likely population levels and birth rates over time. For example, population levels for humanity have varied from a few million (for most of our history) to billions (after 1800). Hence, depending on these estimates, the time our species has left can vary from thousands to millions of years so that, irrespective of its validity, the argument is simply not that informative.

While Lindy’s Law and the temporal version of the doomsday argument have fewer moving parts, allowing timescales to be estimated with less uncertainty, the arguments still do not prove to be that informative, with the estimates for the future lifespan of our civilisation or species ranging over at least three orders of magnitude (similar to the demographic case). Nevertheless, the argument is not necessarily void, as the upper bound of its predictions are comparable with estimates of mammal species’ lifetimes.

What makes the doomsday argument informative is its use of the 95% confidence interval, but this is not necessarily justified. Assuming that all the humans born up to the present moment (or the amount of time our species has existed for) amounts to 5% of the total is rather arbitrary. Nevertheless, since Sir Ronald Fisher introduced the 95% confidence interval, there has been a tyranny of the 5% in statistical testing.5 The 5% feels like a ‘safe’, modest quantity to reference and changing the doomsday argument to use more than 10% (which crosses a psychological boundary for a civilisation with a decimal system) would likely be viewed with suspicion and unease.

Regardless of their potential value, however, Lindy’s Law and the doomsday argument offer us only one way to assess the likely future of our species, and their axioms are limited by being almost entirely neutral regarding evidence that might shed light on this question (apart from the date at which our species/civilisation first emerged and the total size of previous populations, both of which are highly contestable and hard to determine with any precision). At its core, the doomsday argument relies on the assumption that there is some natural regularity that governs the past and future lifespan of humanity and our projects, arguing that we have no reason to consider our current observations of them to be special in history. Given the rapid changes that have been experienced in recent decades—in everything from the global population to the pace of technological development—both of these assumptions appear highly questionable.

However, we do not, in fact, need to adopt such an evidence-neutral approach. There have been numerous studies that address societal collapse within the field of archaeology (see the work of Tainter’s The Collapse of Complex Societies and references therein)6 and from an ecological perspective.⁷ In the next sections, we review the main categories of theories put forward to explain societal collapse.

Exogenous factors and one-shot explanations

A popular reason that is proposed for the collapse of complex societies is the depletion of natural resources, which can take various forms, such as deforestation (as Jared Diamond has argued in the case of Easter Island)8 or degradation of soil quality for the Maya.9 This is a recurrent topic of concern for modern society, with emphasis ranging from water scarcity¹⁰ to phosphorus shortages,¹¹ or, quite frequently, energy production.¹² The problem is often phrased in terms of reaching peak production of a certain resource, such as metals¹³ or fossil fuels.¹⁴

The loss of resources can be gradual or rapid (such as in the case of a fast onset of environmental changes, with historic examples being the floods of the Nile river that favoured crop parasites in the Middle Kingdom of Egypt¹⁵ or droughts for the Maya).16 A contemporary example is climate change, which can lead to reduction in glacial cover and threaten freshwater supplies17 or loss of arable land due to changes in temperature and precipitation.¹⁸ Disruption via the loss of resources can also take the form of a shift to a new resource base that can destabilise prior social order and contribute to collapse.19 A notable example for the modern world is the change to renewable energy resources and the move away from fossil fuels. A genuine transition to renewables is likely to be tumultuous.²⁰

The general difficulty with natural resource arguments for the collapse of societies is that administrative structures, the allocation of labour, and numerous innovations are often developed and geared towards dealing with possible resource shortages and deteriorating environmental conditions.21 Thus, the scarcity of resources first leads to an increase of the complexity of a society, rather than its collapse. While this can be a contributing mechanism to collapse, by itself it is not enough to adequately explain collapse. Overall, theories of collapse that rest on the depletion or scarcity of natural resources propose an almost paradoxical hypothesis that societies collapse in conditions they have been adapting to and dealing with since their inception.

Another broad category of explanations for collapse is focused on competition between societies, which can also take multiple forms. Historical cases that have been included in this category are the demise of the Huari and Tiahuanaco.22 A common instance of competition is invasion from outsiders, which includes the Germanic invasion of the Roman Empire,23 or the invasion of the Hittite Empire by seafaring nomads,²⁴ or contact with Europeans (in the case of Easter Island).25 In recent history, the possibility of collapse via this competitive route has notable examples, such as the collapse of the Soviet Union in competition with the US.26

While appealing in its simplicity and the identification of a ‘smoking gun’ for collapse, this class of arguments misses an important point. Throughout its history, any given society has likely encountered many external threats, such as competition with several other societies on economic terms or, more directly, as conflict and warfare. None of these instances led to its collapse, but rather to a further increase in its complexity. Thus, blaming collapse on a certain instance of competition with another society is a type of cherry-picking.

Catastrophes are also a frequently quoted cause of collapse, with examples including the volcanic eruptions and earthquakes for the Minoan Civilisation,27 major epidemics for the Maya,28 or rat infestation for Easter Island.29 Catastrophes can be classified as extreme cases of contingent events, which form another class of explanations, where a sequence of detrimental events led to the collapse. The events need not be causally related, but represent a string of losses experienced by the society that weaken it and lead to its breakdown or collapse. Again, these types of arguments neglect the adaptive capacity a society has in managing shocks to its function. While a sizable catastrophe can effectively destroy an entire social system, such as with Pompeii,30 they rarely have the geographical reach to lead to widespread collapse.

A related theory of collapse considers societies to be vulnerable and incapable of adaptation, so they cannot provide adequate and sufficient responses to their challenges and circumstances, e.g. the Aztec and Inca Empires.31 If a society could not find and implement effective solutions to its problems, what prevented it from doing so? While these types of theories postulate the natural implication that if a society is not able to respond adequately to problems it will collapse, they do not account for the state of fragility.

For modern society, there are several examples of catastrophes that are threatening: the case of a solar flare, or asteroid impact, or a series of volcanic eruptions. While these can prove damaging worldwide in various regards (demographically, economically) it is questionable if they would pass the necessary threshold to lead to global collapse. The critical features lie in social organisation and how we are using the environment that gets impacted. In the case of the dinosaurs, the asteroid hitting the planet led to the destruction of their ecological niches and thus to their extinction,32 but some species of mammals did survive. Thus, for the systems our society uses, our concern for their collapse does not necessarily stem from the gravity of any given catastrophe, but rather the high level of fragility we see they have. As with the ancient historical cases, to understand the vulnerability of the modern world in facing external threats, we need to account for its internal dynamics, which is of much higher complexity, and thus a greater challenge than any historical example. This is well exemplified by climate change, where the main driver of the phenomenon has been human activity since the start of the industrial revolution.

Overall, arguments based on competition with other societies, intruders, or catastrophes neglect the fact that these types of events have previously been encountered by a given society but no collapse occurred, e.g. earthquakes in the Minoan civilisation, barbarian attacks on the Roman front, or competition between the Mayan centres. In addition, these theories have the added difficulty of placing the drivers of the collapse outside of the society in question, which is incomplete from an epistemological perspective without accounting for changes in social structure and dynamics.

Some of the earliest proposed causes for the collapse of civilisations have been the conflict between social classes and the mismanagement by elites. Compared to the arguments above, one of the strengths of this class of explanations lies in placing the mechanism of collapse within the society in question. However, these explanations are accompanied by some mystical (vague, unmeasurable) factors underlying the collapse, e.g. a loss of social unity or of civic virtue.

One early theory of societal decline and collapse was put forward by Ibn Khaldun in 1377, who proposed a cyclical model for the rise and fall of civilisations.33 Khaldun introduces the notion of ‘asabiyyah’, which roughly translates to social cohesion and unity. The theory can be summarised as follows: asabiyyah is strongly felt in the early stages of a society, but diminishes as the society grows and the leadership becomes too removed from the concerns of the majority of people. If a group at the periphery of the society enjoys a greater degree of social solidarity, it can grow in dominance and eventually lead to a change in the leadership. Then, a new cycle can start. One notable application of the theory has been to the Ottoman Empire to understand its development, which started at the periphery of the Byzantine Empire and grew to prominence.34

In the 18^th century Edward Gibbon, in Decline and Fall of the Roman Empire, argued that the “virtue” of the citizens degraded, as they were less willing to protect their borders and outsourced their military defences to barbarian mercenaries.35 In addition, he stated that Christianity diminished the martial spirit of the Romans, and belief in the afterlife made them reluctant to sacrifice themselves for the empire. We can observe that both Khaldun and Gibbon give explanations that rely on the loss of social cohesion—either due to the leadership or amongst the masses—and the subsequent invasion/replacement by an outside force.

As archaeology developed as a scientific field, the explanations based on class conflicts gained new popularity. A major systematic study, with a comprehensive review and integration of historical knowledge on societal development and collapse, was Arnold Toynbee’s A Study of History, published in 1961, with volumes IV-VI covering the ‘breakdown’ and ‘disintegration’ of civilisations.36 Toynbee does not consider environmental degradation or external invading forces as a root cause of the breakdown of a society. Rather, he argues that the mechanism behind the collapse is internal to the society and develops a theory of how this unfolds (as follows).

A “creative minority” is responsible for problem-solving within a society that leads to its growth and development, but eventually it ceases to be innovative, at which point it turns into a “dominant minority” which simply imposes rules and forces the majority into obedience. The majority is called the “proletariat” and is further divided into internal and external categories. The internal proletariat is under direct subjugation of the dominant minority, whereas the external one is left in poverty and disorganised. This state of affairs creates a tension that eventually leads to the disintegration of the social order. Toynbee applies the above theory to an extensive set of examples, including the Roman Empire, the Mayan civilisation, and the Old Egyptian Kingdom.

Recent applications of the class conflict hypothesis include Easter Island37 and the Maya.38 In the case of the modern world, we see a significant degree of social upheaval in the 18^th and 19^th century based on class conflict,³⁹ which (in part) likely inspired this category of theories for societal collapse. The main difficulty with theories of internal conflict and elite mismanagement is that these types of tensions and inefficiencies always exist in societies.40 It is questionable that only at a certain point in a society’s history did these recurrent themes cause the social structure to break down completely.

Prior to collapse, a high degree of social conflict can be present, as was the case with certain Chinese dynasties,41 but direct causation cannot be inferred from this temporal succession. Similar to theories of resource depletion, the class conflict arguments encounter the difficulty that these types of challenges are characteristic to the structuring and functioning of a society since its inception. Similar to arguments based on external threats, the occurrence of internal conflicts is so common that explaining collapse based on the social upheaval happening just before collapse amounts to cherry-picking of events. Arguably, there is a long chain of events, with both internal and external factors, which occur throughout a society’s history that are causally connected and can amount to its collapse. While the class conflict hypothesis highlights an important category of such contributing events, the causal structure is still short-sighted and the connection with other factors is neglected.

As seen above, most common theories of societal collapse either focus on factors that are not internal to the society in question or, in cases where the causes are intrinsic to the society, they refer to social conditions that have been characteristic to the society since its formation. The main difficulty in the explanations above is that they force the cause to be considered a single factor and posit the causal mechanism as a direct, linear process. Given the complexity of the systems involved, collapse is often a multi-faceted process that requires accounting for multiple interrelated factors. Simply listing the different contributing phenomena is insufficient to give us additional insight, but what can bridge the epistemological gaps is establishing the connection and causation between the different aspects affecting the operation of a society, such as its resource usage, its social organisation, main paradigms, norms, and institutions, and how it adapts to external threats. A consistent way to map these factors into one conceptual scheme is the identification of feedback mechanisms and the use of causal loop diagrams to illustrate the relationships that form and manifest over time.

The case of feedback mechanisms

A feedback mechanism is a multi-causal relationship between two or more variables. It can be represented by a causal loop diagram (CLD), where the different variables are listed and connections are illustrated with arrows. The variables are called stocks and represent quantities that change over time.

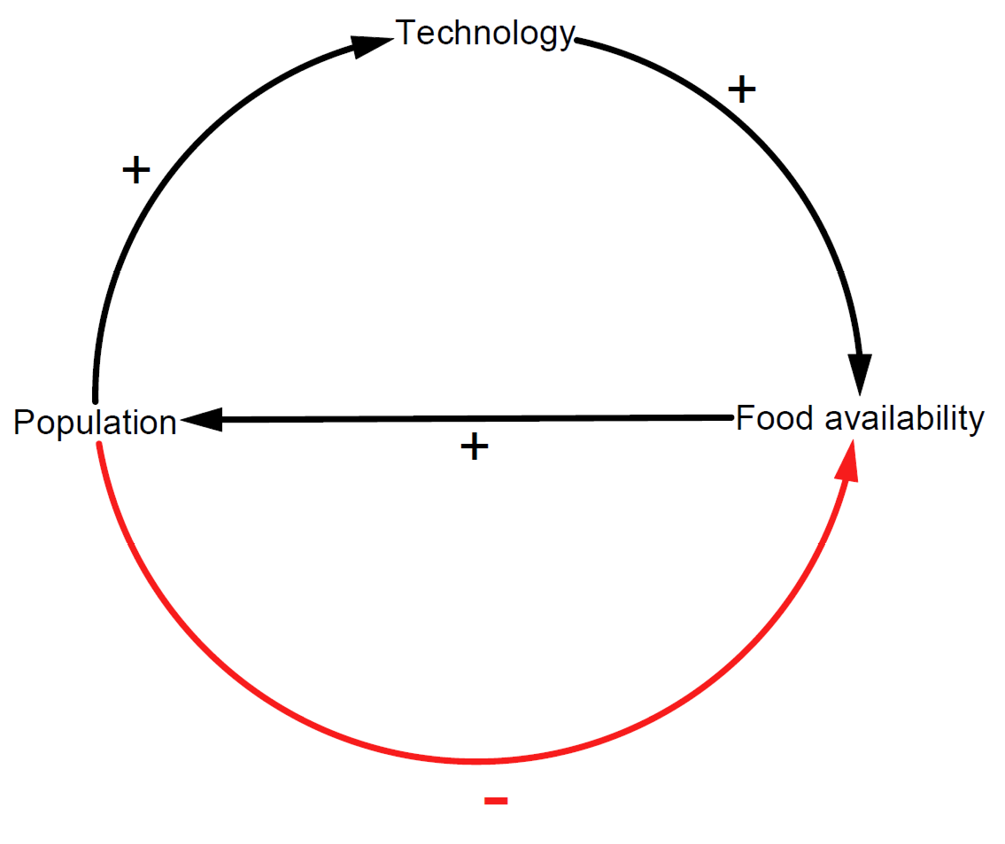
Fig. 1. A causal loop diagram (CLD) illustrating the relationship between population and food availability posited by Malthusian theory (lower half). An increase in population leads to a decrease in availability of food due to larger consumption. An increase in available food spurs an increase in population due to the higher amount of resources. The feedback tends to stabilise: any increase in population comes with a decrease in available food, which leads to a lower population. Boserup considers technology as adding a positive feedback loop (upper half), wherein a greater population leads to more technological innovation which allows more food production.42

The influence of one stock on another is shown through an arrow with a + (plus) or - (minus) depending on the growth of the starting stock, which leads to increase (+) or decrease (-) in the target stock. A CLD of a process can highlight its non-linear nature, represent how multiple factors influence each other, clarify the conceptual model of the dynamics, and be a stepping stone to a quantitative description.43 Numerous physical, biological, social, and technological processes can be described through CLDs,⁴⁴ and they represent a natural explanatory framework for a process as complex as societal collapse.

An early example of a feedback mechanism applied to the sustainability of human society can be found in the 1798 work of Thomas Malthus, whose main argument can be summarised in the CLD of Fig. 1 (lower half).⁴⁵ The CLD can be understood as follows: an increase in population leads to a decrease in available food, while an increase in available food leads to an increase in population. The feedback mechanism is balancing, meaning that an increase in population leads to a decrease in available food, which would imply a decrease in the population. Thus, the variables tend to stabilise to certain values, because significant growth in one then leads to a counter-acting response from the other. The CLD only illustrates the simplest instance of Malthusian ideas, but does convey the point that population overshoot implies a later, possibly sharp, population decline.

An additional aspect Malthus points out is that population grows in exponential fashion, whereas agricultural production can only grow linearly. As described above, the mismatch will cause population levels to return to sustainable levels. In addition to food scarcity, with increasing population density, the chance of war breaking out increases, diseases are more easily transmitted, and general livelihood become harsher, which makes the bearing and raising of children more difficult. From the economic viewpoint, we can interpret this as saying that the costs of sustaining the population are growing faster than the capacity to sustain them.

With the industrial revolution, it became increasingly clear that technology could help eliminate—or at least delay—the negative population pressure Malthus hypothesised. Eventually, an alternative theory appeared with E. Boserup’s The Conditions of Agricultural Growth: The Economics of Agrarian Change Under Population Pressure, which argued that, under conditions of rapid population growth and low land productivity, new, more intensive, agricultural technology would be developed to provide sufficient food.46 Behind Boserup’s thesis is the old tenet that ‘necessity is the mother of all invention’. For example, the Mayan civilisation employed intensive agricultural practices (field-raising, terrace-building, etc.) and better irrigation and water management systems (e.g. building reservoirs) to cope with rainfall variability (including droughts) and their growing population.47

In Fig. 1 (upper half) we can see the CLD associated with Boserup’s idea: an increase in population leads to an increase in technological development, that leads to an increase in food production. Thus, the decrease in food availability due to a large population growth can be compensated for through technological means. When conventional farming methods prove insufficient, the short-term response is likely the diversification and intensification of agricultural practice to compensate for any likely shortfall in production. But, as the Mayan case illustrates, on much longer time scales, the (ultimately) finite carrying capacity of the environment would constrain population growth (assuming all other factors are unchanged).48 Thus, the theories of Malthus and Boserup can operate at different timescales, with a Malthusian catastrophe not necessarily avoided in the long term.

The question is then if technological innovation can continue to overcome environmental and production problems associated with the availability of food (and other necessary resources). Despite challenging Malthus by arguing that productivity per unit of land increases under intensification, Boserup argues that productivity per unit of labour actually decreases. Through factors such as preparation, fertilisation, and irrigation, human labour per unit of agricultural output increases but continues to be undertaken due to the growing population size. The work of Boserup received quantitative support through the data compiled by Clark and Haswell49 and Wilkinson,⁵⁰ who show that the average and marginal return on agriculture does indeed decline with increasing labour.

Tainter generalises Boserup’s observation of declining productivity per unit of labour to all problem-solving endeavours, not just procurement of food.51 Specifically, Tainter posits that there are diminishing returns to investments in complexity (all activity geared towards problem-solving). In particular, this trend holds for technical innovation, e.g. to reach the same number of patent applications in 1958 as in 1946, the US required twice as many scientists and engineers, and three times as much investment as 12 years before.52 Similar trends continue up to the present,⁵³ with examples including the decreasing number of patents per inventor,⁵⁴ the reduction in energy return on investment in oil production,⁵⁵ Eroom’s law in pharmaceutical discoveries showing a decrease in R&D efficiency by a factor of 100 from 1950 to 2010,⁵⁶ and the rising economic and environmental costs of deep learning.⁵⁷

The theories of Malthus, Boserup, and Tainter are not only applicable to modern society but also to past societies, and can (in part) account for historical cases of collapse, at least in cases relating to resource-harvesting in a fragile environment, such as for Easter Island58 and the Classic Lowland Maya.59 The idea of diminishing returns to investments in problem-solving is well exemplified by the Roman Empire,60 whose early conquests were very profitable and allowed for the elimination of taxes for the citizens. With the expanding territory, the military and administrative costs grew as well.

At a certain point, further conquests/conflicts proved less beneficial and even amounted to a loss of resources, like the wars with the Germanic tribes. Maintenance of the empire ended up having larger costs than revenue, and territory was gradually lost. The Roman currency, the denarius, was being debased to expand the money supply and cover the costs (at least temporarily).61 Throughout a period of 400 years, these negative returns manifested as a collapse. Similar arguments have been forwarded regarding the Chinese dynastic cycle,62 the Ottoman Empire,63 and the Maya.64

More generally, as was the case with the Roman Empire, the maintenance of a complex socio-political system requires resources and energy in various forms. Each new problem leads to an increase in the system’s complexity due to the new institutions, more people, and different specialisations required to implement a solution. The increased complexity carries additional energy costs. The previously existing structures are not radically reformed but are expanded to incorporate new functionality, or additional ones are created.

So, the complexity tends to add increase with time, and hence, so do the costs of its maintenance. Furthermore, the benefits incurred in this enterprise suffer from the law of diminishing returns.65 As such, “investment in socio-political complexity as a problem-solving response reaches a point of declining marginal returns”.66 At an advanced stage of socio-political growth, a society uses up most of its energy to maintain all the previously implemented solutions, and has very low returns on solving new problems. Thus, it becomes increasingly sensitive to—and incapable of—tackling internal or external threats and perturbations. In these conditions, collapse is a likely outcome, irrespective of specific factors or circumstances.

Another theoretical framework that significantly extends Malthus’ work is structural demographic theory.67 Beyond the population, the theory considers the role played by state structures and elites in stabilising or destabilising social order and dynamics. Multiple feedback mechanisms are posited within the social hierarchy, and several causal pathways are found for the emergence of political and wider social instability. The theory was developed by Peter Turchin and others to explain the emergence of rebellions and revolutions within a state, and it has led to numerous quantitative models that capture these phenomena in mathematical form.68

A theory of collapse built on feedback mechanisms describing social dynamics is consistent with the nature of a complex system, wherein multiple interacting factors are present, the evolution is non-linear, and causality cannot be assigned to singular aspects of the system. The frameworks outlined above are examples of influential theories on long-term sustainability (and collapse) that can be formulated as feedback mechanisms. While bridging epistemological gaps found in prior types of arguments, we can ask if these theories can provide specific predictions or remain as explanatory frameworks with no clear time horizons for their insights.

To achieve specific, reliable, and quantitative predictions, it is necessary to formulate mathematical models of societal dynamics and evolution, such as within structural demographic theory.69 Qualitatively describing the structure and dynamics of societies through feedback mechanisms is an important stepping stone towards the developments of realistic mathematical models.70 A mathematical model can encapsulate the non-linear features of the relationships and dynamics found within a social system, and quantify and predict the time evolution of relevant variables (such as population levels, resource usage, economic metrics, etc.).

There are several different modelling methodologies that are commonly employed, and they differ in their complexity and calibration. There are large-scale models that attempt to capture multiple socio-environmental factors in a fine-grained fashion. These models fall into two broad classes:

(a) agent-based models (ABMs), which represent individuals (or communities) as agents with set attributes and behavioural rules, such that a realistic rendering of relevant behaviour is desired with the aim of obtaining larger scale emergent phenomena. Often, they also explicitly model the spatially extended features, such as terrain; and

(b) integrated world models, which employ a wide variety of modelling techniques (system dynamics, econometrics, etc.) and aim for an accurate, detailed representation of the system under study. They are complex models that use a large number of variables and parameters.

Early agent-based models were formulated and implemented in the 1970s and 80s. One of these models which we will mention is Schelling’s model of racial segregation,71 the iterated prisoner’s dilemma,⁷² and Craig Reynolds’ “Boids” computer programme.73 In the 1990s, the method expanded significantly, and became widely applied to modelling social and economic phenomena. Of particular interest is the Sugarscape model that is built up gradually and grows increasingly complex, when more realistic phenomena start to emerge (like wealth inequality, trade relations, and conflict).74 This example is an excellent illustration of the general, non-trivial, and useful insights ABMs can provide by building social structure from the bottom-up.

There are several notable examples of agent-based models that address the dynamics of past societies and human activity (trade, migration, etc).75 Arguably, the first significant effort in this sense was by Dean et al.,⁷⁶ Axtell et al.,⁷⁷ and Gumerman et al.,⁷⁸ who modelled the Kayenta Anasazi that lived in the Long House Valley in the Black Mesa area of north-eastern Arizona (US) from about 1800 BCE to 1300 CE. Other agent-based models focus on the Mayan civilisation79 and the Bronze Age collapse,80 but beyond the cases listed, agent-based models that aim to reproduce the archaeological records of complex, past societies are scarce. Effort in this area is directed more towards understanding prehistoric social dynamics and organisation.81

Given the large number of parameters and the many specific modelling choices that have to be made when designing such a high-resolution model, the problem of validating it is quite difficult. How many other parameter values and design decisions are compatible with the output of the model? To what extent are these possible models equivalent and insightful about the actual historical behaviour, decisions, and events? These questions cannot be answered in general, and despite the significant effort put into developing a realistic ABM, the whole endeavour can be at risk of becoming a very sophisticated curve-fitting exercise that provides little historical insight. Still, a variety of empirical approaches have been applied to ABMs, and this has led to a continued debate regarding their validation.82

The first major examples of mathematical models developed to account for collapse have not been aimed at ancient societies, but rather at modern society. The first global integrated models were initiated after the sustainability movement of the 1960s, when the Club of Rome was established by a group of economists and scientists with the goal to pursue a holistic understanding of—and solutions to—the world’s major social and environmental problems.83 In the mid-1950s, Professor Jay Forrester at MIT developed system dynamics, a diagrammatic method to aid the development of large-scale models consisting of differential equations.84

At the request of the Club of Rome, Forrester developed the World1 and World2 models, which incorporate complex feedback that characterises modern industrial society.85 Eventually, the World3 model was developed, which led to the ‘Limits to Growth’ (LTG) study, led by Donella Meadows, that attempted to understand the development of society by taking into account a wide range of phenomena, including food production, pollution, economic wellbeing, population growth, and industrial output.86 ‘Limits to Growth’ is based on the World3 model, which consists of 16 state variables (e.g. population, pollution, arable land) and 80 fixed parameters. The timeframe of the model is 200 years, between 1900 and 2100. The study focused on three scenarios: a base case with parameters best fitted to historical data, an environmentally sustainable case, and a technologically driven, industry-intensive scenario.

The first and third scenarios led to a peak in industrial output in the 21^st century and a subsequent decline in economic activity and demographic levels. The sustainable case manages to reach a steady state with little loss of life, but it requires parameter choices that, in the real world, would require drastic action to curtail pollution and population growth. Given its dire outlook, the LTG study has received harsh criticism from economists,87 but in recent years the standard run of the model has been found to match well with historical trajectories.⁸⁸ Since LTG was published, several other models have been developed, which are aimed at integrating social, ecological, and technological factors into a coherent whole to provide policy recommendations.89

There is another category of models where low-dimensional dynamical systems are employed to represent the dynamics of the system in an aggregated way. The models generally fall into one of two methodological approaches:

(a) economic-based models, in which individuals of the society are modelled as rational, utility-maximising agents. Typically, a utility function is chosen dependent on labour and land, and maximised under certain constraints. The relations that are obtained later inform the choice of dynamical system and parameters that influence the societal dynamics; and

(b) ecologically inspired models, which employ functional forms used in ecology to build the dynamical system and do not rely on neo-classical assumptions of consumer behaviour. The choice of dynamical system in this case is made by attempting to match the model structure to a theoretical framework (sociological or archaeological), along with empirical observations and measurements.

A broader trend started in the late 1990s—developing simple dynamical systems to model societal evolution. Renewed interest in the mathematical modelling of societal development (and collapse) was sparked by the work of Brander and Taylor.90 Several papers that appeared following Brander and Taylor’s also employed the economic methodology and analysed how different factors—such as property rights, technology, or growth—could have impacted and possibly modified the outcome on Easter Island.

With regard to economic models of societal dynamics, we can identify three weaknesses: (i) the fundamental assumption of rational human behaviour is not justified empirically,91 (ii) the literature did not aim to improve the archaeological fit of the initial model by Brander and Taylor, and (iii) the models have increased in complexity over time with no discernible, testable features—e.g. more parameters were added or more complicated objective functions were proposed. Models which were developed on ecological and archaeological grounds, which we detail next, do not share these difficulties.

Some models do not employ an economic approach to modelling societies, but rather develop the dynamical systems more heuristically, from either ecological considerations or society-specific features consistent with the archaeology. In mathematical ecology, similarly to economics, an adequate representation of a system by a model is achieved by following certain general modelling principles.92 But with regard to historical processes, there has not yet been a consensus on the appropriate modelling techniques. A new field called ‘cliodynamics’93 seeks to provide such a common framework for modelling historical processes, but the field is still in its infancy.

We have reviewed the main theories put forward to explain how societies collapse, starting with qualitative theories with a focus on single exogenous factors, such as resource depletion, competition and conflict with other societies, catastrophes, and contingent events. Then, we considered theories with an endogenous explanation of collapse, which focus predominantly on class structures and elite mismanagement. In this regard, the theories of Khaldun, Gibbon, and Toynbee were highlighted as notable examples throughout the history of the field. The theories considered up to this point posit that collapse occurs in conditions that have been recurrent throughout the history of societies. Hence, taking any one given event (e.g. resource shortage, war, rebellion, etc.) as being the cause of the collapse means ignoring similar historical precedents and not accounting for how the society became susceptible to collapse.

Then, we considered theories that can be formulated as feedback mechanisms operating within societies. Historically, Malthus’ theory provides an early example, upon which several refinements were made, notably by Boserup and Tainter, and later in structural demographic theory. These later theories provide frameworks compatible with the nature of a complex system (such as a society) and do not have the epistemological problems of previously mentioned theories, as they provide a mechanism and causal pathway for increased vulnerability to collapse. Furthermore, they provide a stepping stone to mathematical modelling of collapse, which moves beyond qualitative considerations and gives quantitative insight into the phenomenon.

Quantitative models of societal dynamics and collapse broadly fall into the following categories: agent-based models, integrated world models, and low-dimensional dynamical models. Agent-based models offer a bottom-up approach to understanding a system’s structure and behaviour. The insight these models can provide is how basic building blocks of the system in question behave. The difficulty lies in matching underlying agent behaviour with large-scale features with the data, and discriminating between alternative assumptions regarding the agent’s characteristics. Integrated world models have a high degree of complexity (many variables, equations, mechanisms, and sub-models) that hinder understanding and communication. Nevertheless, due to their complexity and comprehensiveness they are also the most realistic models, and are used in policy-making.

Low-dimensional dynamical systems models have been widely used to capture societal mechanisms from a top-down perspective.94 The different schools of thought on the methodology of developing these models can be divided into either economically or ecologically focused; each one has different emphases and strengths. The advantage of low-dimensional models is that they can capture a specific idea or theory on how societal evolution takes place. This, plus their smaller number of variables, allows for comparison with the archaeological record. The main shortcoming of these models is the potential over-simplifications they make in describing the systems under study. However, searching for models at a mesoscopic scale of intermediate complexity can be advantageous, as sufficient societal elements can be accounted for to reproduce known data, but the model can also be kept manageable, so that it can be understood analytically and communicated more easily.

Still, the topic of societal collapse has generally been approached from a mostly qualitative perspective, which presents arguments in a narrative form without a mathematical understanding of the underlying dynamics. In some cases, there even appears to be an aversion to quantitative models.95 Tainter argues that quantitative models are inadequate to capture the full scope of societal complexity and the underlying drivers of its evolution.96 Turchin disagrees, and argues that “a discipline usually matures only after it has developed mathematical theory” especially if the discipline deals with dynamical quantities.97 Informal verbal models are appropriate if the underlying mechanisms are sufficiently simple (acting in a linear and additive manner), but generally misleading if the system exhibits non-linear feedback and time lags.98

Casting hypotheses into quantitative models can help in illuminating uncertainties regarding the system, expose prevailing wisdom as incompatible with available data, guide data collection, or uncover new questions.⁹⁹ Mathematical models can thus be “indispensable when we wish to rigorously connect the set of assumptions about the system to predictions about its dynamics behavior”.¹⁰⁰ However, as with Lindy’s Law and the doomsday argument, there remains the general difficulty (as with any mathematical model) of choosing and calibrating its parameters. In addition, given the overall complexity of any given society, any proposed qualitative or quantitative description (feedback mechanism, models, etc.) can only aim to provide a partial description of societal dynamics and collapse. Establishing cause-effect relationships requires both empirical support and validated modelling, and remains subject to much debate. Applying this methodology to modern society comes with additional difficulties due to the system’s highly interconnected nature, but progress is being made with regard to threats such as climate change.101

The use of quantitative models to test the validity of hypotheses has not been common in social sciences historically, and a new field called ‘cliodynamics’ has emerged to tackle this issue102, and provide historical and current insight into social processes and emerging instability.¹⁰³

Cliodynamics has the potential to follow in the footsteps of theoretical physics and mathematical biology in providing a robust, reliable modelling framework. The framework would be applicable to societal dynamics for ancient and modern cases. While the validation of any given model is difficult and debatable, by building a significant number of models with diverse features, a mathematical dictionary can be constructed that allows diverse social phenomena to be translated into equations or computational models. While economics provides one possible framework for modelling human behaviour, the models can be overly limiting in their underlying assumptions, whereas cliodynamics is more open to a diversity of assumptions from either an ecological or historical perspective.

Each term in an equation or rule in an agent-based model can form a foundation and a set of building blocks to obtaining certain emergent behaviours. For example, the law of mass action is a common functional term employed to model predator-prey interactions in population biology or population interactions in epidemiology. Similarly, the relationships between state resource, population, and war;104 the impact of wealth on birth rates;¹⁰⁵ population shifts between specialisations;106 the territory conquered by an army;¹⁰⁷ or transitions between a unified or turbulent period in history can be modelled through specific terms and equations proposed in the literature.¹⁰⁸ If a common set of historical mechanisms can be found throughout multiple time periods and a modelling framework with a toolkit of different methodologies adaptive to different scenarios can be built, then the science-fiction discipline of psychodynamics that Asimov imagined would be within reach.