11. Waves of Enlightenment

I dare say poor Fresnel, if he had lived, would have preferred his share of the honour as much as I do mine. It was before I knew you that mine was earned; and acute suggestion was then, and indeed always, more in the line of my ambition than experimental illustration.

Young, letter to his sister-in-law Emily Earle, 1827 [310]

Among long-known optical phenomena yet to be convincingly explained by the wave theory of light in the 1810s was something called double refraction. Anyone who has seen the effect of a colourless, transparent crystal of Iceland spar—a form of calcite so called because it was first produced in Iceland in the seventeenth century—will know this phenomenon. If you place a thin slice of Iceland spar on top of a printed page and orient it in a particular way, you see a double image of the printed letters underneath the crystal. Iceland spar bends an incident ray of light into two refracted rays, not just the usual single refracted ray observed when light is incident on glass or water (see Figure 11.1).

One of these rays is known as the ordinary (or regular) ray. It behaves like the usual refracted ray, with its angle of incidence and its angle of refraction related to each other by Snell’s law (as mentioned in Chapter 7, ‘Let There Be Light Waves’). The other ray is known as the extraordinary (or irregular) ray. Its refraction is not governed by Snell’s law. This is because the nature of the ordinary ray and the extraordinary ray differs in one fundamental respect, as we shall now come to understand.

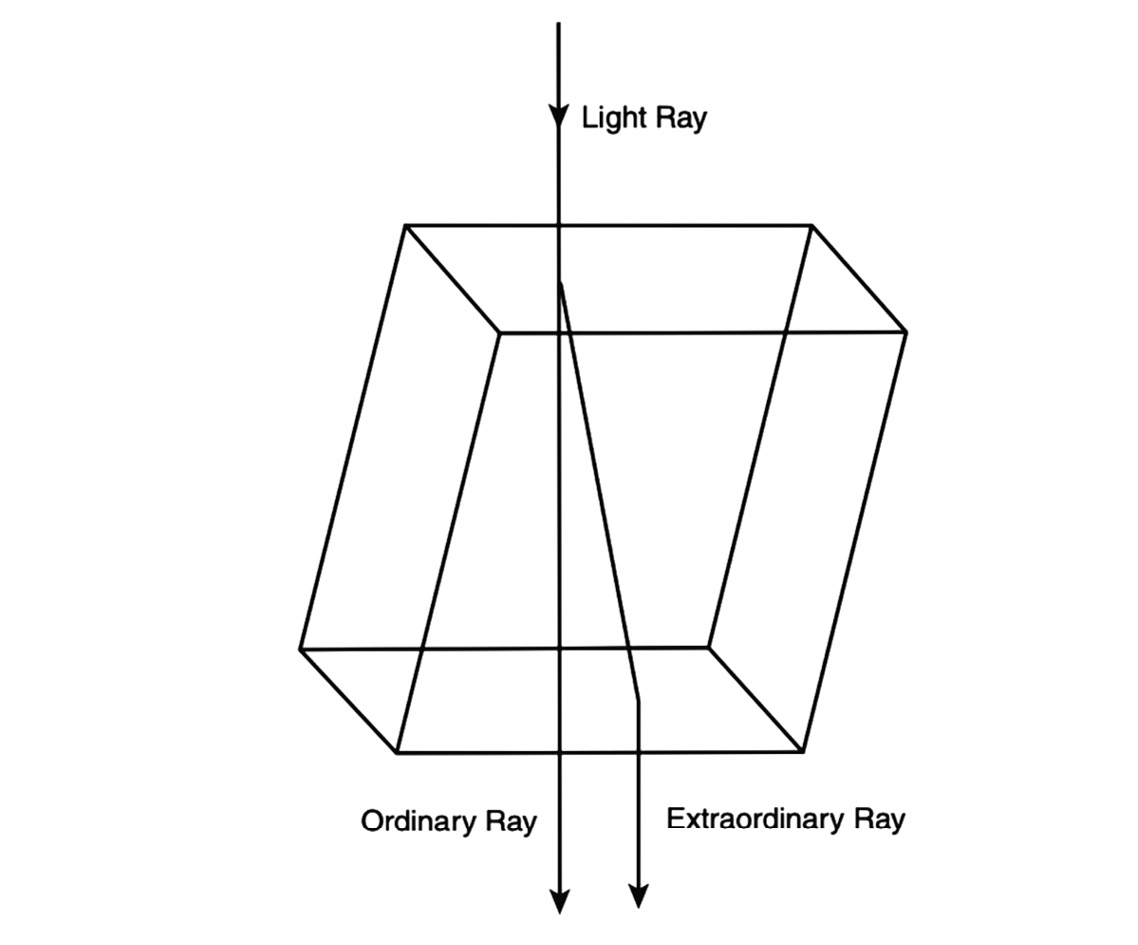
Fig. 11.1 Double refraction of a light ray incident at right angles to one face of a calcite crystal. It was first observed with Iceland spar.

Double refraction was first described in detail by Erasmus Bartholin in 1670. Soon after, Christiaan Huygens performed his own experiments with Iceland spar and observed an additional peculiarity. When Huygens used two identical, flat, polished plates of the special crystal to view a small object, he saw the object either doubled or quadrupled, depending on the relative position of the two plates. It seemed that in some positions, the lower plate had the power to split the two rays from the upper plate into four rays, but not in other positions. When Huygens rotated the lower plate, keeping the upper plate still, the double image and the quadruple image alternated: he saw two images, then four images, then two images, then four images, and so on, as he kept turning the plate. Why should the lower plate of Iceland spar apparently lose its power to split light rays and produce only a double image in certain positions? Unable to theorise this, Huygens hazarded the comment: ‘It seems as though, as it passes the upper plate, the [regular] ray has lost something that is necessary to bring the matter into motion, which is needed for the irregular refraction [in the lower plate]. But to say how that operates—up until now I have discovered nothing that satisfies me.’[311]

More than a century later, Young repeated the experiment and wrote about the puzzle in his Natural Philosophy in 1807:

The most singular of all the phenomena of refraction is perhaps the property of some natural substances, which have a double effect on the light transmitted through them, as if two mediums of different densities freely pervaded each other, the one only acting on some of the rays of light, the other on the remaining portion. These substances are usually crystallised stones, and their refractions have sometimes no further peculiarity; but the rhomboidal crystals of calcarious spar [the name calcite was not coined until 1845], commonly called Iceland crystals, possess the remarkable property of separating such pencils of light, as fall perpendicularly on them, into two parts, one of them only being transmitted in the usual manner, the other being deflected towards the greater angle of the crystal. […] It is also remarkable, that the two portions of light, thus separated, will not be further subdivided by a transmission through a second piece [of Iceland spar], provided that this piece be in a position parallel to that of the first; but if it be placed in a transverse direction, each of the two pencils will be divided into two others; a circumstance which appears to be the most unintelligible of any that has been discovered respecting the phenomena of double refraction.[312]

Experiments with double refraction using various kinds of crystal done by others around this time were still more confusing. If light was shone on the coloured mineral tourmaline, the ordinary ray was seen to be absorbed after passing through a small thickness of the crystal, while the extraordinary ray was transmitted by the crystal. When two sections from one crystal of tourmaline were put one behind the other in exactly the same orientation as they had before they were cut, light passed through both of them. But if the second section of tourmaline was now turned through ninety degrees, no light passed: the extraordinary ray was stopped. However, when the second slice was turned through a further ninety degrees, the extraordinary ray again passed through it.

If the second crystal of Iceland spar in Young’s experiment was replaced by a thin slice of tourmaline (thin enough for the ordinary ray not to be totally absorbed), a further intriguing effect was observed. With the slice in one particular position, it transmitted only the ordinary ray from the Iceland spar and cut off the extraordinary ray. But when the slice was turned through ninety degrees, the situation was reversed and the extraordinary ray was transmitted while the ordinary ray was cut off. At intermediate angles, the tourmaline transmitted part of the ordinary ray and part of the extraordinary ray.

In our own time, a similar effect is well known with so-called Polaroid sunglasses, which are designed to reduce glare. If you look at a sunny scene through two pairs of Polaroid sunglasses held in the same orientation, light passes through both sets of lenses. But if you turn one pair of sunglasses through ninety degrees, keeping the two lenses for the right (or the left) eye superimposed, the sunlight is almost entirely cut off before it can reach the eye. At an intermediate angle, part of the sunlight remains visible.

From these observations, it is clear that light has some kind of orientation in addition to its direction of propagation, and that different light rays can have different orientations. Today, the extraordinary ray in double refraction is said to be differently polarised from the ordinary ray. Polaroid sunglasses work by eliminating as much horizontally polarised light as possible, since glare consists largely of horizontally polarised light, and transmitting vertically polarised light.

In the seventeenth century, Huygens and Newton did not refer to ‘polarisation’ as such—the term was introduced only in 1809 by Etienne Malus—but they accepted as a fact the orientability of light. Their problem, and the problem of their early nineteenth-century followers, was how to explain this fact theoretically. How could a light corpuscle—as imagined by Newton or Pierre-Simon Laplace (a convinced corpuscularist)—or a light wave—the concept preferred by Huygens or Young—be physically oriented, other than in the direction of propagation of a light ray?

Newton’s Opticks devotes a number of pages to a discussion of double refraction, but Newton plainly felt frustrated by it. Query 26 in this section of his great work reads: ‘Have not the rays of light several sides, endued with several original properties?’[313] The idea of ‘sides’ for light was Newton’s stab at the future concept of polarisation. Query 27 sums up: ‘Are not all hypotheses erroneous which have hitherto been invented for explaining the phenomena of light, by new modifications of the rays? For those phenomena depend not upon new modifications, as has been supposed, but upon the original and unchangeable properties of the rays.’[314] The only plausible hypothesis that corpuscularists could propose to account for double refraction was that corpuscles were sorted into two rays—ordinary and extraordinary—by the structure of a crystal, according to a corpuscle’s shape; and that a second crystal then filtered them again according to their shape, blocking some and letting through others. ‘It would be like trying to put square pegs into square holes; they only fit if oriented certain ways,’ writes the physicist Arthur Zajonc.[315] But nobody in this early period had any credible notion as to why the various corpuscles in a given light ray should vary in shape (in itself unlikely) and what this might entail in mechanical terms. If the corpuscles really were similar to bullets from a gun, there seemed to be no compelling reason why they should not all be identical in shape and oriented in only one direction.

Huygens, by contrast, gave the wave theory a small advantage over the corpuscular theory. He came up with a mathematical model that enabled him to calculate, for a given substance, the direction of the extraordinary ray; and his results agreed with experiment. His model assumed that the ether inside the double-refracting crystal propagated two light waves—one spherical (the ordinary ray), the other ellipsoidal (the extraordinary ray); the latter was ellipsoidal because its velocity was different in different directions. This assumption seemed reasonable given the fact that the various kinds of crystals exhibiting double refraction were known to have other properties, too, such as thermal conductivity and mechanical elasticity, that varied with the orientation of the crystal. (Tourmaline is today used in piezoelectric devices, because, along particular axes, a tourmaline crystal generates an electric charge when put under mechanical stress and also changes its shape when a voltage is applied to it.) But Huygens’s wave model was completely unable, like the corpuscular model, to account for the strange behaviour of polarised light when it was incident on a second double-refracting crystal.

Thus in 1807, when Young published his Natural Philosophy, neither theory—corpuscular or undulatory—gave much of an account of polarisation; or for that matter a fully satisfactory account of reflection, refraction and diffraction, as discussed in Chapter 7. The only experiments that seemed to favour the wave theory unequivocally were Young’s experiments on interference, but, as presented in Natural Philosophy, they lacked the kind of precision and mathematical rigour increasingly expected by physicists. In bald truth, Young’s theory of interference made so little initial impression that there is hardly a single allusion to the interference of light in any work on optics published in Britain or abroad between the time of Henry Brougham’s attack in 1802–1804 and the more mathematical, rigorous work of Augustin Fresnel and Dominique Arago in 1816; when the astronomer William Herschel (father of John) communicated three papers on Newton’s rings to the Royal Society in 1807, 1809 and 1810, Herschel did not even mention Young’s interference explanation of the colours of the rings published by the Royal Society in 1802.

During the next decade or so, however, from 1808, there was an explosion of new experimental evidence in optics and attempts at theoretical explanation, as the debate heated up between corpuscularists and undulationists. Much of the experiment and argument focused on polarisation, and in the 1820s, it would be the undulatory explanation of this particular phenomenon that would convert all but the most fanatical of corpuscularists (who of course included Young’s detractor, Brougham). George Peacock, who was a young Cambridge mathematician in this period of flux and ferment, catches the excitement among physicists generated by these developments—most of which came out of France—in his biography of Young:

In the intermediate period Laplace [a corpuscularist] published his celebrated memoir on the double refraction of Iceland spar [in 1809]: Malus [an undulationist] had discovered the polarisation of light by reflection, and was engaged in a brilliant series of researches connecting his discovery with the optical properties of crystalline bodies, when a premature death brought his labours to a close: [David] Brewster [a corpuscularist] was enriching every department of experimental optics with the most remarkable speculations and discoveries: Arago [an undulationist] had found out the colours of crystalline plates produced by polarised light, and though less fertile than some of his contemporaries in the number of his contributions to the science, he was second to none of them in the critical sagacity with which he analysed their labours: [Jean-Baptiste] Biot [a corpuscularist] was combining theoretical and practical researches with a success and ingenuity which seemed to promise him the first place amongst optical discoverers, when it was his misfortune to waste his energies and compromise his reputation in the proposition and obstinate maintenance of his theory of moveable polarisation: at a later period [from 1815 onwards], the labours of Fresnel [an undulationist], who—though treading generally in the footsteps of Young, required no foreign aid either to guide or support him—were destined to give unity and system to the vast mass of facts and theories which his predecessors had accumulated and prepared.[316]

Young himself, in this period, was trying to establish his credentials as a physician, rather than as a physicist. He did few optical experiments after 1807, but he was keenly interested in the optical works of others and wrote several anonymous reviews of them and a major article, ‘Chromatics’, for the Encyclopaedia Britannica. Although he never wavered in his belief in the undulatory theory, its intractable experimental difficulties disturbed him.

Reviewing Malus’s work on polarisation in 1810, for instance, Young commented somewhat pessimistically, despite the fact that Malus himself did not draw the same conclusion as he did: ‘This statement appears to us to be conclusive with respect to the insufficiency of the undulatory theory, in its present state, for explaining all the phenomena of light. But we are not therefore by any means persuaded of the perfect sufficiency of the projectile [corpuscular] system […] [Much] more evidence is still wanting before [the question] can be positively decided.’[317]

Five years later, in a letter to Brewster in 1815, Young stated: ‘With respect to my own fundamental hypotheses respecting the nature of light, I become less and less fond of dwelling on them, as I learn more and more facts like those which Mr Malus discovered: because, although they may not be incompatible with these facts, they certainly give us no assistance in explaining them.’[318]

And in his article in the Encyclopaedia Britannica, written in late 1817 in the heat of the debate, Young began:

But notwithstanding all that has hitherto been done, it appears to be utterly impracticable, in the present state of our knowledge, to obtain a satisfactory explanation of all the phenomena of optics, considered as mechanical operations, upon any hypothesis respecting the nature of light that has hitherto been advanced: it will therefore be desirable to consider the facts which have been discovered, with as little reference as possible to any general theory […]

[A]t the same time, it will be absolutely necessary, as a temporary expedient, to borrow from the undulatory system Dr Young’s law of the interference of light, as affording the only practicable mode of connecting an immense variety of facts with each other, and of enabling the memory to retain them; and this adoption will be the more unexceptionable, as many of the most strenuous advocates for the projectile [corpuscular] theory have been disposed, especially since the experiments of Mr Arago and Mr Fresnel, to admit the truth of the results of all the calculations, in which this law has been employed.[319]

Reviewing Laplace’s highly mathematical, corpuscular explanation of double refraction, with which he pungently disagreed, Young made a significant suggestion. The acoustician Ernst Chladni had observed that sound travelling through wood—a rod of Scotch fir in particular—had a slightly higher velocity in one direction, along the grain, than in another direction, at an angle to the grain, due to the wood’s being more elastic in the first direction than in the second. (The ratio of the different velocities is about five to four.) Perhaps, wrote Young, in double refraction there is a similar kind of difference in the ‘structure of the elementary atoms of the crystal’[320] as in the grain of the wood? This would produce the ellipsoidal wave motion suggested by Huygens, and account for the extraordinary ray. But acute as Young’s analogy was, it suffered from the crucial disadvantage that it did not account for the existence of the ordinary ray.

It also shows how he was misled by his persistent comparisons of light and sound. Light and sound could both be reflected, refracted and diffracted. They could also interfere with themselves, as shown by the double-slit experiment and by the phenomenon of beats (described in Chapter 7). Sound was long established to be an alternating compression and rarefaction of the air (a true vacuum is, of course, soundless)—a pressure wave that transmitted itself longitudinally, that is, along the path of the sound’s propagation. By analogy, light was therefore thought by Young to be a longitudinal compression and rarefaction of the ether, in the direction of the light ray. But if this assumption were correct, it would provide no explanation for the polarisation of light. Sound does not exhibit any polarised phenomena; there is, for example, no double refraction of sound, with an ‘ordinary’ sound wave and an ‘extraordinary’ sound wave. For sound, being a longitudinal wave, by definition, can have only one intrinsic orientation, along the line of propagation.

For a long time, the analogy with sound ‘blinded’ Young and others, including Arago, to the ‘secret of polarisation’, in the words of his biographer Alex Wood.[321] In ‘Chromatics’, Young writes: ‘It is certainly easier to conceive a detached particle, however minute, distinguished by its different sides, and having a particular axis turned in a particular direction, than to imagine how an undulation, resembling the motion of the air which constitutes sound, can have any different properties, with respect to the different planes which diverge from its path.’[322] In other words, profoundly unsatisfactory though the corpuscular theory of polarisation was, Young found it impossible to explain polarisation on the undulatory theory, because he imagined that light waves in the ether must be transmitted longitudinally, like sound waves in air, along the path of a light ray.

I have […] been reflecting on the possibility of giving an imperfect explanation of the affection [refraction] of light which constitutes polarisation, without departing from the genuine doctrine of undulations. It is a principle in this theory, that all undulations are simply propagated through homogenous mediums in concentric spherical surfaces like the undulations of sound, consisting simply in the direct and retrograde motions of the particles in the direction of the radius, with the concomitant condensation and rarefactions. And yet it is possible to explain in this theory a transverse vibration, propagated also in the direction of the radius, and with equal velocity, the motions of the particles being in a certain constant direction with respect to that radius; and this is a polarization.[323]

The key word here is transverse; we should not bother too much about the precise wording of the rest of Young’s explanation (which again drags in an analogy with sound). A water wave is a transverse vibration; a sound wave is not—it is longitudinal. The water moves up and down transversely, that is, at right angles to the direction of propagation of the wave; the air molecules move longitudinally, in the same direction as the sound propagates. Young was making the radical proposal to Arago that light might be a longitudinal wave with a transverse component.

Polarisation would be explicable, at least in principle, with a transverse wave. A transverse wave vibrates in a plane perpendicular to the axis of propagation; however, within this perpendicular plane, the vibration can take any orientation at all with respect to the axis. It can, for instance, be vertically polarised, like a water wave, and not vibrate at all at any other angle to the axis, including horizontally. Or it can be horizontally polarised, and not vibrate at all at any other angle to the axis, including vertically. We can imagine these two situations with an elastic cord. You fix one end of the cord to a hook on a wall, and then you make waves in the cord. If you move your hand rhythmically up and down—that is, vertically—you can create a transverse wave in the cord that is vertically polarised. If instead you move your hand from side to side, horizontally, you get a horizontally polarised transverse wave (if you ignore the inevitable sagging of the cord). Then imagine threading the cord through a slit in a card located between you and the hook. If the slit is held vertical, the vertically polarised wave will pass through the slit, whereas the horizontally polarised wave will be stopped by it. Turn the slit through ninety degrees so that it is horizontal, and the horizontally polarised wave will be transmitted, whereas the vertically polarised wave will be cut off. The crystal structure of Iceland spar or tourmaline could act in a similar way to the slit, cutting off the extraordinary ray in one crystal orientation and the ordinary ray in a second crystal orientation at ninety degrees to the first one—assuming, that is, the light in the ordinary ray is polarised in a direction at ninety degrees to the light in the extraordinary ray. Hence, the tourmaline slice’s ability to cut off the ordinary ray but transmit the extraordinary ray coming from a piece of Iceland spar in one orientation of the slice, and transmit the ordinary ray but cut off the extraordinary ray when the slice is turned through ninety degrees.

Today, following the pioneering work of James Clerk Maxwell in the second half of the nineteenth century, we know that light is an entirely transverse electromagnetic wave. An electric field and a magnetic field vibrate in a plane perpendicular to the direction of propagation, with the two fields always at right angles to each other (Figure 11.2). Polarisation of light means confining the electric field (and hence the magnetic field) to a certain orientation. In plane-polarised light—as transmitted by Polaroid sunglasses—the electric field vibrates in only one direction within the plane.

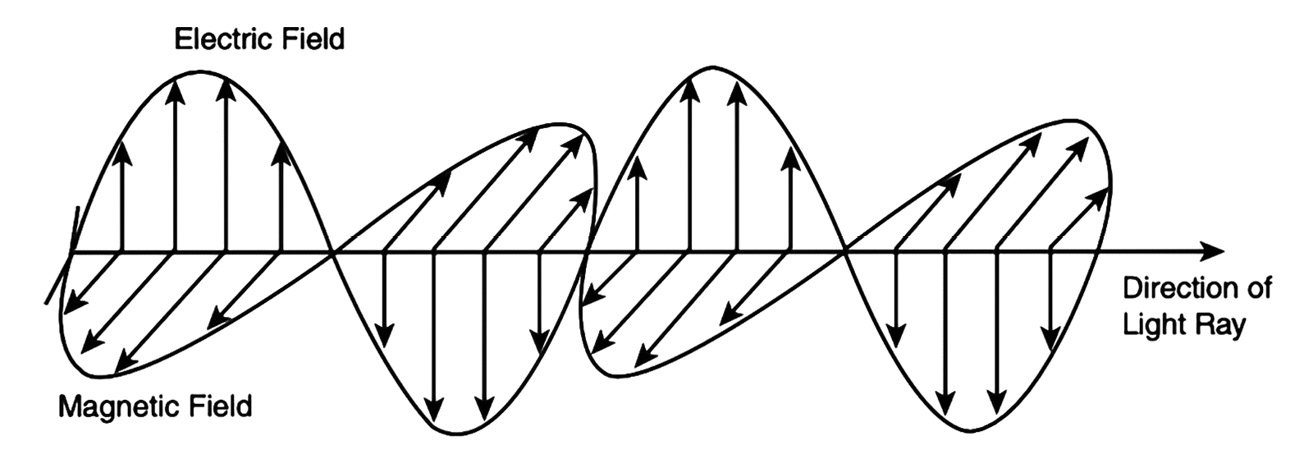
Fig. 11.2 Light is an electromagnetic wave, in which the electric and magnetic fields vibrate at right angles to each other and also at right angles to the direction of propagation of the wave, that is, transversely, not longitudinally.

Young had provided the seed concept to explain polarisation—the transverse wave—but it would not be true to say that he nurtured this into a full-blown theory. As so often with him, he laid the foundation, but left others to consolidate the theory. Fresnel, advised by Arago, had developed Young’s extensive early work on interference and diffraction into a convincing system from 1815 onwards. Now he did the same for Young’s aperçu that light could be transverse; indeed, Fresnel transformed it into a model that really worked and could rationalise many of the confusing phenomena of polarisation. In 1817, Young had proposed a small transverse component to light, but in the same breath he had retained a far larger longitudinal component. Fresnel, by 1821, was able to show via mathematical methods that polarisation could be explained only if light was entirely transverse, with no longitudinal vibration at all.

The mechanically-inclined Young was not convinced. In 1823, he wrote in the Encyclopaedia Britannica: ‘This hypothesis of Mr Fresnel is at least very ingenious, and may lead us to some satisfactory computations: but it is attended by one circumstance which is perfectly appalling in its consequences.’ Only in solids, Young emphasised, had transverse waves with ‘lateral’ (i.e., horizontal) vibrations been observed. Fresnel’s hypothesis would mean that ‘the luminiferous ether, pervading all space, and penetrating almost all substances, is not only highly elastic, but absolutely solid!!!’[324] Young was not much of a user of exclamation marks, and his point was certainly a penetrating one, which Fresnel’s theory could only ignore. Young’s criticism was not fully answered until the internal contradictions of the ether finally led to its abandonment as a medium for light waves in the time of Einstein.

There was tension between Young and Fresnel from the beginning. In 1815, Fresnel had begun his work on light by rediscovering the principle of interference, being unaware of Young’s publications of 1800–1807. He was working far from the scientific circles of Paris in his home village in Normandy using a few crude instruments made by a local blacksmith; he also did not read English. It was Arago who drew Fresnel’s attention to Young’s work, published in the Royal Society’s Philosophical Transactions and in Young’s Natural Philosophy. Fresnel acquiesced gracefully—though in truth he had little choice, given the clear-cut published evidence—telling Young in 1816 that ‘if anything could console me for not having the advantage of priority, it would be having been brought into contact with a scholar who has enriched physics with so many important discoveries, and that has contributed not a little to increase my confidence in the theory which I adopted.’[325] Young was generous in his response to Fresnel, though at times proprietorial. In the 1820s, as Fresnel made important original progress, unaided by Young, the contact between them was not always smooth, but it never degenerated into anything like the suspicion and open rivalry that would mark Young’s relationship with Fresnel’s fellow countryman Jean-François Champollion (who was almost the same age as Fresnel) during exactly the same period. Indeed, Young had a hand in the award of the distinguished Rumford medal of the Royal Society to Fresnel, just before his premature death from tuberculosis in 1827, at the age of only thirty-nine. (As foreign secretary of the society, Young sent Fresnel the medal along with an official letter of congratulation.)

An important reason for their better relationship, as compared with Young and Champollion, was that Young and Arago became close friends, and Arago acted as a trusted interpreter between Young and Fresnel. After Young’s death, an affectionate Arago wrote a memoir of Young in which he vividly recalled this aspect of his role at his first meeting with Young in Worthing:

In the year 1816, I passed over to England with my learned friend M. Gay-Lussac. Fresnel had then just entered in the most brilliant manner into the career of science by publishing his Memoire sur la Diffraction. This work, which, according to us, contained a capital experiment, irreconcilable with the Newtonian theory of light, naturally became the first object of our communication with Dr Young. We were astonished at the numerous restrictions he put upon our commendations, and in the end he told us that the experiment about which we made so much ado was published in his work on Natural Philosophy as early as 1807. This assertion did not appear to us correct, and this rendered the discussion long and minute. Mrs Young was present, and did not appear to take any interest in the conversation; but, as we knew that the fear, however puerile, of passing for learned ladies—of being designated blue-stockings—made the English ladies very reserved in the presence of strangers, our want of politeness did not strike us till the moment Mrs Young rose up suddenly and left the room. We immediately offered our most urgent apologies to her husband, when Mrs Young returned, with an enormous quarto under her arm. It was the first volume of the Natural Philosophy. She placed it on the table, opened it without saying a word at [a certain page], and pointed with her finger to a figure where the curved line of the diffracted bands, on which the discussion turned, appeared theoretically established.[326]

By 1827, the year of Fresnel’s death, the Young-Fresnel undulatory theory of light, as it would now become known, was sufficiently established to explain all the major phenomena of light—reflection, refraction, diffraction and polarisation—in a quantitative way that left little room for doubt that it was superior to the corpuscular theory. Even the magisterial corpuscularist Laplace had been won over. In Britain, the theory received a sort of official blessing in an encyclopaedia article written by Sir John Herschel. He wrote:

The unpursued speculations of Newton [about undulations in light], and the opinions of Hooke, however distinct, must not be put in competition, and, indeed, ought scarcely to be mentioned, with the elegant, simple, and comprehensive theory of Young—a theory which, if not founded in nature, is certainly one of the happiest fictions that the genius of man ever invented to grasp together natural phenomena, which, at their first discovery, seemed in irreconcilable opposition to it. It is, in fact, in all its applications and details, one succession of felicities; insomuch, that we may be almost induced to say, if it be not true, it deserves to be so.[327]

Then Herschel paid tribute to Fresnel, too:

[W]e must not, in our regard for one great name, forget the justice which is due to the other; and to separate them and assign to each his share would be as impracticable as invidious, so intimately are they blended together throughout every part of this system—early, acute and pregnant suggestion characterising the one [Young], and maturity of thought, fullness of systematic development and decisive experimental illustration, equally distinguishing the other [Fresnel].[328]

On this occasion, Young did not demur. He told his sister-in-law Emily that Herschel ‘has divided the prize very fairly’ and remarked that the lately deceased Fresnel probably would have agreed. For, he admitted, his own ambition lay always more in the direction of ‘acute suggestion’ than ‘experimental illustration’.[329] It was one of the perquisites of being a polymath—and also one of its penalties, as would become increasingly apparent to Young with age.

Notes and References

[310] Letter to Emily Earle (Nov. 1827) in Peacock: 397.

[311] Quoted in Andriesse: 273.

[312] Young, Natural Philosophy, vol. 1: 445.

[313] Newton: 358.

[314] Ibid: 361.

[315] Zajonc: 117.

[316] Peacock: 369–70.

[317] Quoted in Wood: 181.

[318] Letter to Brewster (13 Sept. 1815) in Young, Miscellaneous Works, vol. 1: 361.

[319] Young, Miscellaneous Works, vol. 1: 279–80.

[320] Ibid: 228.

[321] Wood: 186.

[322] Young, Miscellaneous Works, vol. 1: 332.

[323] Letter to Arago (12 Jan. 1817) in Young, Miscellaneous Works, vol. 1: 383.

[324] Young, Miscellaneous Works, vol. 1: 415. Fresnel’s work is thoroughly discussed by Kipnis and by Buchwald.

[325] Letter to Young (24 May 1816) in Young, Miscellaneous Works, vol. 1: 378. This translation appears in Wood: 189.

[326] Arago: 239–40.

[327] Quoted in Whewell: 349–50.

[328] Quoted in Wood: 204.

[329] Letter to Emily Earle (Nov. 1827) in Peacock: 397.