• Meta-Xenakis
  • 11. On the Link between the Exact Sciences and Music in Iannis Xenakis’s Creative Work

11. On the Link between the Exact Sciences and Music in Iannis Xenakis’s Creative Work

Pablo Araya1

© 2024 Pablo Araya, CC BY-NC 4.0 https://doi.org/10.11647/OBP.0390.13

Introduction

I will offer here two lines of reasoning that allow me to propose that, in the creative work of the Greek composer Iannis Xenakis, the metaphorical and the analogical possess an important gravitational pull between the exact sciences and music.

First Reasoning

Xenakis was neither a physicist nor a mathematician; he was a civil engineer.2 So Xenakis generated neither physics nor mathematics; rather, as he admitted in an interview, he only used them both.3 Certainly this does not seem to be a decisive detail; however, it warns us about a question that, although obvious, is still relevant: using formulas or equations to compose music does not imply establishing a fusion between art and the exact sciences, nor does it guarantee, in artistic-expressive terms, an effective construction of the work.

This explanation leaves us in a difficult place if we wish to trace the link between music and science in Xenakis’s creative work. However, to remedy this difficulty, we may think about what Raymond Nickerson explained, i.e., that one of the tasks of mathematics is to understand the structures and patterns underlying any phenomenon.4 But we need more than just this understanding, because with mathematics one also obtains, among other things, the possibility of creating various structures that may or may not be connected to physical reality.5 Hence, it could be thought that all composers, in one way or another, have been amateur mathematicians, since music is also shaped (or configured) by patterns and structures with different degrees of complexity, and, more precisely, it is composers who generate those structures with sounds.6 Therefore, if this perspective is taken into account, we understand that the use and the Xenakian application of mathematics in the field of the creative-musical (by the way, very much criticized by some specialists) does not seem to be the most admirable and remarkable.7 But then, what is the most striking quality or characteristic of Xenakis’s creative procedure, which, of course, has a very close relationship with the exact sciences? I will answer this in the following segment.

Second Reasoning

If the use of formulas or equations is not what gives a foundation to the connection between the exact sciences and music in Xenakis’s creative work, then what does? If we confine our study to Metastasis (1953–4) and Pithoprakta (1955–6), we may observe that the interdependence between music and the exact sciences tends towards the metaphorical-analogical due to the fact that the composer is seeking to model sound-musical events that possess a similarity with some phenomena of nature that are mainly dealt with by physicists: i.e., phenomena that are linked to statistical physics (e.g., the collision of millions of particles in a gas cloud).8 Let us note what Xenakis says:

But other paths also led to the same stochastic crossroads […] natural events such as the collision of hail or rain with hard surfaces, or the song of cicadas in a summer field. These sonic events are made out of thousands of isolated sounds; this multitude of sounds, seen as a totality, is a new sonic event. This mass event is articulated and forms a plastic mold of time, which itself follows aleatory and stochastic laws. If one then wishes to form a large mass of point-notes, such as string pizzicati, one must know these mathematical laws […] It is an event [sound masses] of great power and beauty in its ferocity.9

Elsewhere, he also points out:

The first step was the control of mass events and the recognition of laws which govern nature. Then I looked for the analogy of these natural phenomena in music […] I followed Maxwell’s approach step by step: what he did with the molecules I did with the sounds. Why not? I made the same simple initial hypotheses with intervals, durations and intensity; I found the formulas that determine them. Then two questions arose: is it possible to make music with fewer elements (i.e. fewer than a “mass”) and yet with the same method, that is, stochastically? And: do I have the right to make computations with elements which are not physical by nature but are linked to our senses? I was seeking to justify what I was doing—after all, I was the first to embark on this path […] That’s my contribution to the development of music: I use ideas in composing that are completely alien to music.10

The above quotations corroborate, to some extent, the hypothesis that under Xenakis’s music lies a metaphor-analogy with certain phenomena of nature that are studied and modeled by physicists (mostly statistical physics) or by some applied mathematicians. Therefore, from this point of view I consider that the most notorious of the Xenakian connections between music and the exact sciences is the cognitive mechanism linked to metaphor and analogy. However, as I will explain below, there are some obscure points in this connection.

The Metaphor-Analogy of Xenakis

Now, I will try to show (although I am not a logician or a philosopher, nor do I have great knowledge in cognition or computation) how Xenakis deployed his metaphor-analogy between the exact sciences and music. I will carry out this task in a sequential way, although I know that this entails certain risks because the cognitive mechanisms linked to creativity do not work linearly. The following methodology will be applied:

  • First, I will outline a brief definition of metaphor and analogy.
  • Then I will take as a reference a specific set of theoretical perspectives in relation to metaphor and analogy that will serve to support my hypothesis.

Brief Definition of Metaphor and Analogy

Almost all the authors and texts consulted agree that both metaphor and analogy are cognitive mechanisms, proper to human beings, that consist of explaining or understanding something from concepts and ideas that are foreign to that original something.11 Consequently, what we have is a connection (mapping) of domains that may be more or less close or very distant from each other: the domain of the origin is the source-domain, while the domain with which the source-domain is connected is the target-domain. The functions and purposes of metaphor and analogy are multiple and are linked to various areas or disciplines (law, philosophy, pedagogy, artificial intelligence, etc.). However, the metaphorical and the analogical seem to play a very decisive role in the creative field (in the exact sciences, the arts, and in all the disciplines I have just mentioned), hence my interest in delving deeper into this topic.12

First Perspective: Aspect Schema (Lakoff and Núñez)

From the linguistic perspective of George Lakoff (b. 1941), the metaphor, which connects or maps two areas or aspects of reality with different degrees of remoteness or closeness to each other, is based on a concrete, physical experience or sensation of the person.13 Thus, the metaphor and the elaboration of the concepts derived from it emerge from a series of experiences (which we could call “everyday”), rooted in the bodily and the sensory; this process or mechanism presents a specific structure called an aspect schema.14

This is not a minor fact if we relate it to Xenakis’s music: on more than one occasion, the composer expressed that his creative insight (the one linked to physics and mathematics) was influenced by experiences and impressions that were part of his daily life and that seem to have strongly marked him:

About these events that Xenakis experienced firsthand, the following should be noted: 1) they are phenomena made up of multiple (thousands or millions) components or elements; that is, they are collective or mass phenomena, which refers us back to the sound masses of Metastasis and Pithoprakta; 2) the behavior of these masses tends to be chaotic or disordered (something that is also emulated in these two works); and 3) in both pieces there is a tendency towards the inharmonic spectrum (noise).

Therefore, it seems that Lakoff and Rafael Núñez’s perspective could be plausible. But, moreover, this detracts from the idea of abstraction that Xenakis and some musicologists have given to his creative work.18 So, with the Lakoffian approach, we see that the creative imagination, whether or not it then involves a hyper-abstract cognitive work, cannot be detached from the concrete: it is first necessary to be grounded in the material-daily to then go towards regions where the intangible-abstract is what predominates. In this sense, it seems that the one (the material-daily) without the other (the intangible-abstract) is not a viable option to understand the creative act.19

Second Perspective: Creative Insights (Visokolskis and Carrión)

The work of the researchers/philosophers Sandra Visokolskis and Gonzalo Carrión tries to understand how the creative factor occurs in subjects through mathematical diagrams. However, these philosophers offer a referential framework to explain some issues that are linked to Xenakis’s creative-musical work. It should be noted that I will not make a strict interpretation of the proposal of these two specialists; I will be forced to make some adaptations.20

The first interesting aspect of the approach of these philosophers lies in their definition of creative work:

Thus, insight or ingenuity is the demonstrative ability to find the right middle term [...] The key to the ingenious act lies in connecting two extreme terms to each other through a found middle term, thus forming a mathematical proportion. The curious thing about this finding is the unexpectedness of such a connection, given that, in principle, the extreme terms are radically different from each other and it would be difficult to link them, unless an idea obtained in a perspicuous way emerges. Moreover, instead of a single middle term C, there could be a finite number n of them greater than one, establishing a continuous proportion: A: C1 :: C1: C2 :: ... :: Cn: B, with natural n.21

From the above quotation, it is clear that a novel (or ingenious) creative act requires the connection of two terms (A and B) distant from each other; however, this union or connection must find an/other term/s (C, C1, C2...Cn) in between that are the ones that make A and B connect. Beyond this, we must note two things:

  • The mathematical expression outlined by Visokolskis and Carrión contains an idea of proportionality that, for the purposes of this paper, is not very relevant (we will see why shortly).
  • The linking of terms refers to metaphor or analogy; that is, connecting A and B implies establishing a cognitive mechanism linked to the metaphorical or the analogical.

Closely related with the preceding concepts, these two researchers add something equally important: for this metaphorical-analogical connection to take place, that is, for the creative insight to be realized and ingenious, there must be a change of perspective (P), meaning a change from P (whose properties are a1, a2, ..., an) to P’ (whose properties are b1, b2, ..., bn).22 Hence, for A [C, C1, C2, ..., Cn] B to be realized, it is essential that there be a different view or appreciation in the metaphor-analogy mapping (P → P’).

Thus, keeping in mind the point of view of these philosophers, I will try to trace, not without limitations and with some deviations or inconsistencies, the creative-cognitive-musical mechanism of Xenakis. In this direction, it is evident that the Xenakian connection between A and B refers to the link between the exact sciences (A) and music (B). But what elements (C or C1, C2, ..., Cn) are there in the medium that allow A and B to be linked? I propose the following:

Xenakis hinted at the path that I propose in chapter 1 of Formalized Music called Free Stochastic Music.23 In any case, the operation A [C, C1, C2, ..., C7] B equally shows the change of perspective (the cognitive leap P → P’) in the observance of the problem, that is, in the construction of the metaphor-analogy (on Xenakis’s side), which implies that perceiving or intuiting that part of the mathematical scaffolding linked to stochastics is susceptible of being applied to music. Thus, because of this, a different panorama is obtained (P’) and the originality and uniqueness of Xenakis’s work is understood (although I only allude to Metastasis and Pithoprakta).

Finally, and it cannot be overlooked, the model provided by Visokolskis and Carrión, as far as the topic I address in this paper is concerned, is not completely satisfactory (beyond its usefulness and value in providing a framework to develop and tackle the problem of musical creativity): the introduction of the terms C, C1, C2, etc., do not always work in a balanced, proportionate way (with a predominance of terms in equal proportions and without maintaining a complex interrelation between them; between C1, C2, C3, etc. there are non-linear relations, which means that the creative process is unstable and not at all immediate). Moreover, as the terms progress, it seems that sub-analogies emerge or are generated at different spatio-temporal scales.24

Third Perspective: Degrees of Positivity/negativity and Plausibility in Xenakis’s Analogy (Bartha)

The work of Paul Bartha is truly comprehensive and complex. He presents a sort of summary of the many ways of approaching analogy. Naturally, in this paper I will not take into account all the possibilities that this philosopher offers. However, taking as a reference some of his contributions, always adapting and modifying them in some way, I will propose a perspective that can help us better understand the metaphor-analogy carried out by Xenakis. So, let us look at Bartha’s interpretation of the analogy:

S and T are the source and target domains, respectively. A domain is a set of objects, properties, relations, and functions, together with a set of accepted statements about those objects, properties, relations, and functions. More formally, a domain consists of a set of objects and an interpreted theory about them. The language of the theory has symbols for the objects, properties, relations, and functions to which the theory refers. I shall adopt the convention of using unstarred symbols (a, P, R, f) for items in the source domain and starred symbols (a*, P*, R*, f*) for items in the target domain. An analogy between S and T is a mapping between objects, properties, relations, and functions in S and those in T.25

Here, I attempt to link Bartha’s conclusions with Xenakis’s creative procedure:

Source-domain (statistical physics) – S

Target-domain (stochastic music) – T

Objects (a):

Models or mathematical formalisms represent global or collective natural phenomena.

Objects (a*):

Notational models or formalisms represent global or collective sound phenomena (sound masses).

Properties (P):

Statistical physics studies the properties of systems made up of an immense number of elements.26

Properties (P*):

Stochastic music involves the creation of works whose main characteristic lies in the fact that it is constituted of an immense number of sound events (example: pitches = notes).27

Relationships (R):

Seeks to understand the relationship between the microscopic (the properties of the constituent elements of the system; for example, molecules) and the macroscopic (collective properties of the system).28

Relationships (R*):

Relates the microscopic (the properties of the constituent elements of the system; for example, pitches or notes) and the macroscopic (collective properties of the system; example: resulting texture = sound mass).29

Functions (f):

Generates the necessary tools, from the point of view of Prigogine, to build an image of nature in which concepts such as: instability (chaos) → probability → irreversibility are incorporated; thereby tackling the problem of complexity in its various facets.30

Functions (f*):

Uses concepts and tools from statistical physics to compose musical works with a radically different creative profile.

Table 11.1 Analogical correspondence between exact sciences and music in the creative work of Iannis Xenakis, taking into account Paul Bartha’s study of analogy.

Thus, for Bartha, analogy is consolidated when there is a mapping between the objects, properties, relations, and functions of the source-domain and the objects, properties, relations, and functions of the target-domain.31 Unfortunately, he does not specify what he means by objects, properties, relations, and functions. For this reason, the mapping I have outlined above was made arbitrarily. Now, bearing this in mind, I will attempt to determine, however rudimentarily, the degree of positivity or negativity of the analogy. Also, and based on the degree of positivity or negativity I just mentioned, I will attempt to determine the degree of plausibility of such a metaphor-analogy. In any case, the result of the former (degree of positivity or negativity) as well as the latter (degree of plausibility), will depend on the mapping or correspondence between a, P, R, f and a*, P*, R*, f*:

a ↔ a* = +; one of the main objects in both domains refers to the use of models to represent and, redundantly, model the phenomena they are interested in; here there is a strong and positive reciprocity.

P ↔ P* = ±; here we observe a partial correspondence between the terms: while P studies and knows the properties of systems made up of a large number of elements or components, P* intends to use this knowledge for creative purposes; that is, there are different cognitive functions: P = knowing / P* = creating. Consequently, the reciprocity is more or less strong and positive.

R ↔ R* = +; the relationships within each domain have the same purpose: to understand how the microscopic is linked to the macroscopic, therefore, reciprocity remains strong and positive.

f ↔ f* = ±; the functions that the tools have in each domain are quite different: f tries to generate mathematical tools (statistical mechanics) to construct a different image of nature and thus obtain a greater degree of certainty in knowledge; f* only applies those mathematical tools, although it does so for creative purposes; again, these are different cognitive functions. Because of this, it follows that there is a more or less strong and positive reciprocity between f and f*.

From the above it follows that:

a ↔ a* = + (strong and positive reciprocity).

P ↔ P* = ± (more or less strong and positive reciprocity).

R ↔ R* = + (strong and positive reciprocity).

f ↔ f* = ± (more or less strong and positive reciprocity).

Thus, one has two strong and positive reciprocities and two more or less strong and positive reciprocities; therefore, the degree of plausibility of Xenakis’s metaphor-analogy is optimal.32 Likewise, the procedure I used to determine the degree of plausibility (which could be translated into the degree of strength and reciprocity between the objects, properties, relations, and functions of each domain) reminds us of the analogy of attribution proposed by the Mexican philosopher Mauricio Beuchot (b. 1950): the plausibility or strength of the analogy, which, as I already explained, has to do with the type of correspondence or reciprocity between the terms of each domain, gradually degrades, beyond a certain proportional limit, the analogy is out of context and cannot be sustained.33

Perspective Four: Similarities, Structure, and Purpose in analogies (Holyoak and Thagard)

The work of Keith Holyoak and Paul Thagard is often referred to as multi-constraint theory and is developed within the area of artificial intelligence and what Bartha calls structuralist approaches.34 Again, I will make a nearly free use of their perspective, adapted to my interests.

Holyoak and Thagard explain that, in almost any analogical reasoning, there are three basic features or conditions (constraints):

Thus, these three components (similarity, structure, and purpose/s) are what determine (in a flexible way) the establishment of the analogy/ies. So, it follows that analogy is obtained because of people’s ability to find structural patterns underlying both the source-domain and the target-domain: “On the surface, the elements are very different, but at the base [underlying] the relationship of the elements finds very similar structural patterns.”35

Of course, this theory states, contrary to the position of Lakoff and Núñez, that analogy responds to an abstract cognitive capacity.36 Beyond this particularity, I will try to apply Holyoak and Thagard’s principles in the analysis of the Xenakian metaphor-analogy.

Source-domain: Exact Sciences (statistical physics)

Target-domain: Stochastic Music (Xenakis)

Similarity between elements of the domains:

a) Phenomenon/a it deals with: statistical physics focuses on phenomena consisting of thousands or millions of elements (example: collision of particles in a gas cloud).

b) Agent/s: it is the scientist who studies and knows these natural statistical phenomena.

c) Mathematics: to know and model those phenomena susceptible of being expressed in statistical terms, the scientist uses the construction of mathematical models (I referred to this in the third perspective).

a) Phenomenon it deals with: Xenakis’s stochastic music recreates a phenomenon made up of hundreds or thousands of sound events (example: sound masses made up of, redundantly, multiple sound events).

b) Agent/s: it is the composer who perceives and creates these musical statistical phenomena (sound masses).

c) Notation: in order to reason, model or, if desired, compose the phenomenon in question (with qualities susceptible of being expressed in statistical terms), the composer uses the construction/configuration of notational formalisms (I referred to this in the third perspective).

Structural parallels (isomorphisms):

Clearly, the similarity between the elements of each domain shows us the structural parallel between, redundantly, each domain.

The same (as cell to the left).

Purposes of agents:

The agent who has purposes in the scientific domain is the scientist (a physicist or an applied mathematician). Basically, his purpose is to know and understand the phenomenon.

The agent who possesses purposes in the field of music is the composer.37 Certainly, its main purpose is to perceive and, from there, to create music.

Table 11.2 Analogical correspondence between exact sciences and music in the creative work of Iannis Xenakis, taking into account the study of Keith Holyoak and Paul Thagard in relation to analogy.

To summarize the idea discussed in the table above, please refer to the following chart:

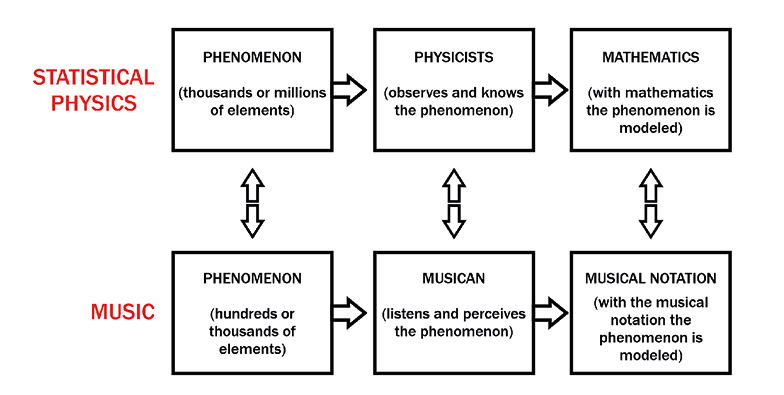
A diagram showing three boxes connected to the right by arrows, placed above another three boxes connected to the right by arrows. The upper boxes are labelled in red: Statistical Physics, and the lower boxes are labelled Music. The upper boxes and lower boxes are linked by pairs of arrows that point in each direction.

Fig. 11.1 Connection and relationship of the domains according to Holyoak and Thagard. Figure created by author (2022).

The detection of the three basic conditions of Holyoak and Thagard does not seem to be so straightforward and obvious. Why? For the simple reason that Xenakis does not establish a resemblance with statistical physics; on the contrary, the similarity is with certain natural phenomena studied by statistical physics. Then, and as Xenakis himself explained in different interviews, what he did was to take the object of study or knowledge (the phenomenon itself) of statistical physics as a reference and, based on this, he performed two operations: 1) he noticed that it was possible to connect the natural phenomenon with the musical one: the former (let us suppose it is a gas cloud, the beating of raindrops on a sheet metal roof or the singing of cicadas) was transferred to the latter (the sound masses made up of hundreds or thousands of notes of different durations); 2) he determined that the musical parameters (punctual sounds and sets of discontinuous -granulated- and continuous -glissandi- sounds) and their qualities (density, durations, registers, velocities, etc.) could be modeled mathematically with the tools of statistical mechanics (probabilities).38

The proposal I have developed above shows that the Xenakian metaphor-analogy is quite diffuse. This is because each domain involves the deployment (and acquisition), by the agents, of different abilities and cognitive mechanisms: the physicist observes the phenomenon and models it with mathematical tools and, finally, knows it; the musician (composer) listens to the phenomenon and models it with the notation system and, more than knowing it in an epistemological sense, seeks to create or re-create it. In any case, and beyond these appreciations, one could also think that Xenakis has achieved, if you will, a sort of mixture or fusion of the functions and cognitive mechanisms I have just pointed out.39

But, regardless of this: is the metaphor-analogy that Xenakis proposes totally convincing? The answer is no. It can only be partially trusted. The reason for this distrust is that, as I said, the metaphor-analogy is given with the phenomenon that physicists deal with. However, this does not mean that statistical physics and stochastic music have a clear and definite structural isomorphism: Xenakis uses or applies statistical mechanics (mathematics) to model or shape the sound, but the metaphorical-analogical correspondence is given with the phenomenon and not with the mathematics that analyzes the phenomenon. So, from this point of view, there would be no connection (or a very remote connection) between the exact sciences (statistical physics) and music.40

Final Considerations

A fact that is not minor, and which should be taken as a warning, is that the study of metaphor and analogy of almost all the authors or specialists to whom I have had recourse is directed towards the philosophical (informal logic or argumentation theory) or scientific (artificial intelligence) fields. This means that such theoretical perspectives are not always helpful to me: the subject matter I address in this text is centered on the creative-musical (within the artistic field, although music does not always fit this field),41 and not on the philosophical or the scientific. Hence, perhaps this is the reason why such theories around the metaphorical or the analogical do not quite fit with my inquiry regarding the exact sciences-music link in the work of Xenakis. In any case, and beyond this circumstance, I consider that there are two elements in common between music and the exact sciences that function as a substratum or an ultimate foundation, and that, nevertheless, are the ones which allow the Xenakian metaphor-analogy to be plausible: I am referring to the notions of measurement (the use of a notation system to reason and then model the phenomena) and of structure (with the notation system it is possible to visualize and manipulate phenomena, although, likewise, it is also possible to generate-creatively-diverse patterns, configurations, ordering criteria, or structures). In this sense, I will try to give some degree of plausibility to this way of understanding things by means of the following reasoning associated with analogy:42

So, this reasoning or “logical formalism” attempts to show that both the concept of structure and the use of a notation system (measurement) are essential components for music and the exact sciences; this statement belongs to David Bohm (1917–92), who presaged it in this way:

The consideration of the joint work of order and measure in ever wider and more complex contexts leads us to the notion of structure [...] The classes of order and measure and more complex contexts leads us to the notion of structure [...] The kinds of structures that can evolve, grow or be structures that can evolve, grow, or be built are obviously limited by the order and measure that underlie it. A new order and measure will make it possible to consider new kinds of structures. We can take a simple example from music. Here the structures we can work with depend on the order of the notes and certain measures (scale, rhythm, tempo, etc.). Evidently, new orders and measures will make it possible to create new structures in music.43

Bohm’s quotation exposes, in my opinion, the reasons and the platform on which Xenakis’s metaphor-analogy could be concretized, a matter that resulted in a musical revolution. In this sense, it must be understood that, although the metaphorical-analogical is not new in the field of music, the type of metaphor-analogy that this composer deployed is.

Now, if the interference and predominance of the metaphorical-analogical in the musical field are characteristic and undeniable, this means that the one (metaphor) and the other (analogy) must be understood as particular and relevant cognitive devices or resources to explain the creative processes in music. Also, as I explain above, metaphor and analogy play a prominent role in other activities of human endeavor.44 In order to clarify and better contextualize this approach it will be convenient to take into account the following: in his Analytic of the Beautiful, Immanuel Kant (1724–1804) established a clear division between the exact sciences and art.45 However, his separation proposed something more than a simple partition between fields; he was actually determining the cognitive mechanism that would be incumbent on each area: exact sciences/scientist = cognitive work linked to an analytical and linear process; art/artist = genius, whose cognitive-creative procedure is unknown.46 From this, Kant concluded: exact sciences/scientific = there is learning and knowledge; art/artist = genius/there is no learning or knowledge.47 Thus, through the analytical and linear procedure, the German philosopher believed that it was possible to trace and determine the cognitive mechanism of the scientist and the exact sciences. However, when facing the issue of creativity in the artistic field, he was unable to explain precisely how it worked; therefore, he invented the figure of the genius.48

But then, what is the cognitive mechanism that the artist (musician in this case) deploys? One of the possibilities, as I proposed at the beginning of this paper, is linked to the metaphorical and the analogical. Furthermore, a pioneer who made important contributions relating metaphor and analogy with music was Julio Estrada (b. 1943).49 What does this creator-researcher propose? Broadly speaking:

The Estradian approach is fundamental because it recognizes the impact that the metaphorical and the analogical have on the cognitive-creative factor: both give rise to a more personal creative experience, that is, an experience linked to one’s own imagination; and also leads to a process of reconceptualization and resignification of musical structures, something that, as we have already observed, seems to have been the main attribute of Xenakis’s creative work.50

References

ARAYA, Pablo (2018), “Objetos sonoros y configuraciones texturales dinámicas del sonido en la música instrumental contemporánea”, Pilacremus, vol. 2, no. 2, p. 97–137.

ARAYA, Pablo (2020a), Una correspondencia metafórico-analógica conceptual entre ciencia y música: la noción de sistemas complejos aplicada al análisis de obras solistas y de cámara de Julio Estrada, Luciano Azzigotti, Samuel Cedillo y Raúl Dávila, doctoral dissertation, Facultad de Artes, Universidad Nacional de Córdoba, https://rdu.unc.edu.ar/handle/11086/15729

ARAYA, Pablo (2020b), “Un diálogo entre música y ciencias exactas a partir de una correspondencia metafórico-analógica con el concepto de ‘estructuras disipativas’ de Ilya Prigogine (Phowa para flauta bajo sola, un caso de estudio)”, El oído Pensante, vol. 8. no. 2, p. 163–84, https://doi.org/10.34096/oidopensante.v8n2.8015

ARAYA, Pablo (2022), “En torno al vínculo ciencias exactas-música en el trabajo creativo de Iannis Xenakis”, Pilacremus, Centenario Xenakis 1922–2022, vol. 6, no. 6, p. 25–50.

BARREA, Andrés, “Mapas y Modelos” (2021), Grupo De Análisis Numérico Y Computación, Faculty of Mathematics, Astronomy, Physics and Computing, Universidad Nacional de Córdoba, https://sites.google.com/view/ganycfamaf/seminarios/2021?authuser=0&fbclid=IwAR0ZriJdNs6bjOHwY_TU5OUB1rwCqN0mfoS8MuFD3unF13ohhW3iEoZ2Sf8

BARTHA, Paul (2010), By Parallel Reasoning: The Construction and Evaluation of Analogical Arguments, New York, Oxford University Press.

BARTHA, Paul (2022), “Analogy and Analogical Reasoning”, in Edward N. Zalta (ed.), The Stanford Encyclopedia of Philosophy, online Summer 2022 edition, https://plato.stanford.edu/archives/sum2022/entries/reasoning-analogy/

BERAN, Jan (2004), Interdisciplinary Statistics: Statistics in Musicology, Washington, DC, Chapman and Hall/CRC Press Company.

BOHM, David (2002), La totalidad y el orden implicado, Barcelona, Kairós.

BOURGEOIS, Jacques (1969), Entretiens avec Iannis Xenakis, Paris, Boosey and Hawkes.

DUHAUTPAS, Frédérick, RENAUD, Meric, and SOLOMOS, Makis (2012), “Expressiveness and Meaning in the Electroacoustic Music of Iannis Xenakis. The case of La Légende d’Eer”, Electroacoustic Music Studies Network Conference Meaning and Meaningfulness in Electroacoustic Music, p. 1–12, http://www.ems-network.org/IMG/pdf_EMS12_duhautpas_meric_solomos.pdf

ESTRADA, Julio (1990), “Ruidos poco conocidos de Orfeo”, in Lucero Enriquez (ed.), (In) disciplinas, Estética e historia del arte en el cruce de los discursos. XXII Coloquio Internacional de Historia del Arte, Estudios de Arte y Estética, Mexico, UNAM, Instituto de Investigaciones Estéticas, p. 553–84.

GARCÍA MORENTE, Manuel (2013), Lecciones preliminaries de filosofía, Buenos Aires, Argentina, Editorial Losada.

GELFERT, Axel (2016), How to Do Science with Models: A Philosophical Primer, Switzerland, Springer.

GOEHR, Lydia (2017), “All Art Constantly Aspires to the Condition of Music—Except the Art of Music: Reviewing the Contest of the Sister Arts”, in Paul Kottman (ed.), The Insistence of Art: Aesthetic Philosophy After Early Modernity, New York, Fordham University Press, p. 19–69.

GLISSANT, Edouard (1986), “An Interview with Iannis Xenakis”, The Courier: A Window Open to the World, Unesco, no. 8, p. 4–8.

HOFSTADTER, Douglas (1995), Fluid Concepts & Creative Analogies, New York, New York, Basic Books.

HOLYOAK, Keith, THAGARD, Paul (1995), Mental Leaps: Analogy in Creative Thoughts, London, MIT Press.

KANT, Immanuel (2006), Crítica de la Facultad de Juzgar, translation, introduction, notes and appendices by Pablo Oyarzún, Venezuela-Caracas, Monte Ávila Latinoamericana Editores.

LAKOFF, George (1993), “The Contemporary Theory of Metaphor”, in Andrew Ortony (ed.), Metaphor and Thought, Cambridge, United Kingdom, Cambridge University Press, p. 202–51, https://doi.org/10.1017/CBO9781139173865

LAKOFF, George and JOHNSON, Mark ([1980] 1998), Metáforas de la vida cotidiana, translated by Carmen González Marín, Madrid, Ediciones Cátedra S.A.

LAKOFF, George and NÚÑEZ, Rafael (2000), Where Mathematics Comes From: How the Embodied Mind Brings Mathematics into Being, New York, New York, Basic Books.

OLGUÍN, Valeria and TAVERNINI, Lucía Micaela (2018), “¿Torbellino De Ideas O Razonamiento Mediante Analogías? Evaluación De La Eficacia De Dos Modos De Pensamiento Para Promover La Creatividad”, Subjetividad y Procesos Cognitivos, vol. 22, no. 1, p. 84–100.

NICKERSON, Raymond (2011), Mathematical Reasoning: Patterns, Problems, Conjectures, and Proofs, New York and London, Psychology Press.

PERLOVSKY, Lenoid (2006), “Fuzzy Dynamic Logic”, New Mathematic and Natural Computation, vol. 2, no. 1, p. 43–55.

PERLOVSKY, Leonid and KOZMA, Robert (2007a), Neurodynamics of Cognition and Consciousness, Berlin, Heidelberg, and New York, Springer Verlag,
https://doi.org/10.1007/978-3-540-73267-9

PERLOVSKY, Leonid (2007b), “The Mind vs. Logic: Aristotle and Zadhe”, Society for Mathematics of Uncertainty, Critical Review, vol. 1, no. 1, p. 30–3.

PERLOVSKY, Leonid and ILLIN, Roman (2012), “Brain. Conscious and Unconscious Mechanisms of Cognition, Emotions, and Language”, Brain Sciences, vol. 2, p. 790–834, https://doi.org/10.3390/brainsci2040790

PRIGOGINE, Ilya (2009), Las leyes del caos, España-Barcelona, Drakontos Bolsillo.

PRIGOGINE, Ilya and STENGERS, Isabelle (1990), La Nueva Alianza - Metamorfosis de la Ciencia, España, Madrid, Alianza Editorial S.A.

REALE, Giovanni and ANTISIERI, Dario (1995), Historia del pensamiento filosófico y científico, Barcelona, Herder Editorial.

REIF, Frederick (1993), Física Estadística, Barcelona, Editorial Reverté.

SOLOMOS, Makis (2004), “Xenakis’ Thought Through his Writings”, Journal of New Music Research, vol. 33, no. 2, p. 125–36, https://doi.org/10.1080/0929821042000310603

TRENCH, Máximo, MINERVINO Ricardo A. (2020), Distant Connections: The Memory Basis of Creative Analogy, Switzerland, Springer, https://doi.org/10.1007/978-3-030-52545-3

VARGA, Bálint András (1996), Conversations with Iannis Xenakis, London, Faber and Faber Limited.

VEALE, Tony, GERVÁS, Pablo, and PEASE, Alison (2006), “Understanding Creativity: A Computational Perspective”, New Generation Computing, vol. 24, no. 3, p. 203–7, https://doi.org/10.1007/BF03037331

VIGOTSKY, Lev (2007), Imaginación y creación en la edad infantil, Buenos Aires, Nuestra América Editorial.

VISOKOLSKIS, Sandra Aída and CARRIÓN, Gonzalo (2020), “El papel de la perspicacia en la construcción de patrones imaginativos en el razonamiento diagramático”, in María De las Mercedes O´Leary, Lucía Federico and Ariza Yefrin (eds.), Filosofía e Historia de la Ciencia en el Cono Sur Selección de Trabajos del XI Encuentro, Buenos Aires, AFHIC, p. 711–23.

WALTON, Douglas (2006), Fundamentals of Critical Argumentation, New York, Cambridge University Press, https://doi.org/10.1017/CBO9780511807039

WALTON, Douglas, REED, Chris, and MACAGNO, Fabrizio (2008), Argumentation Schemes, New York, Cambridge University Press, https://doi.org/10.1017/CBO9780511802034

WALTON, Douglas and HYRA, Curtis (2018), “Analogical Arguments in Persuasive and Deliberative Contexts”, Informal Logic, vol. 38, no. 2, p. 213–61, https://doi.org/10.22329/il.v38i2.4805

WIGNER, Eugene ([1960] 2004), “La irrazonable eficacia de la matemática en las ciencias naturales”, Communications in Pure and Applied Mathematics, vol. 13, no. 1, p. 1–12, https://doi.org/10.1002/cpa.3160130102

XENAKIS, Iannis (1992), Formalized Music: Thought and Mathematics in Music, additional material compiled and edited by Sharon Kanach, Hillsdale, New York, Pendragon Press.

ZAPLINTY, Michael and XENAKIS, Iannis (1975), “Conversation with Iannis Xenakis”, Perspectives of New Music, vol. 14, no. 1, p. 86–103.

  1. 1 An earlier version of this article appears in Spanish in Araya, 2022. English translation by the author.

  2. 2 Varga, 1996, p. 19.

  3. 3 Bourgeois, 1969, p. 34, quoted in Solomos, 2004, p. 128.

  4. 4 Nickerson, 2011.

  5. 5 Wigner, [1960] 2004.

  6. 6 Beran, 2004; Araya, 2018, 2020a, 2020b.

  7. 7 Zaplinty and Xenakis, 1975.

  8. 8 Solomos, 2004; Duhautpas, Meric, and Solomos, 2012.

  9. 9 Xenakis, 1971, p. 9.

  10. 10 Varga, 1996, p. 77–9.

  11. 11 Lakoff and Johnson, [1980] 2003; Lakoff, 1993; Lakoff and Núñez, 2000; Hofstadter, 1995; Holyoak and Thagard, 1995; Walton, 2006; Walton, Reed, and Macagno, 2008; Bartha 2010, 2022; Gelfert, 2016; Walton and Hyra, 2018; Visokolskis and Carrión, 2018; Olguín and Tavernini, 2018; Trench and Minervino, 2020.

  12. 12 Veale, Gervás, and Pease, 2006.

  13. 13 Lakoff and Johnson, [1980] 1998; Lakoff, 1993; Lakoff and Núñez, 2000; Bartha, 2022.

  14. 14 Bartha, 2010, p. ix; Lakoff and Núñez, 2000, p. 34–7.

  15. 15 Xenakis, 1971, and Andrew Toovey, “Iannis Xenakis (1 of 2) Filmed Interview in English with German subtitles” (28 Oct 2010), YouTube,
    https://www.youtube.com/watch?v=j4nj2nklbts&ab_channel=AndrewToovey

  16. 16 Varga, 1996, p. 54; Andrew Toovey, “Iannis Xenakis (1 of 2) Filmed Interview in English with German subtitles” (28 Oct 2010), YouTube,
    https://www.youtube.com/watch?v=j4nj2nklbts&ab_channel=AndrewToovey

  17. 17 Varga, 1996, p. 48; Suicrea unam, “Julio Estrada Y…”, Facebook,
    https://www.facebook.com/SUICREA.UNAM/videos/355215483264868

  18. 18 Varga, 1996; Solomos, 2004.

  19. 19 Estrada, 1990; Vigotsky, 2007; Araya, 2020a.

  20. 20 In the development of this segment, I will not resort to the use of a technical language linked to logic (something that Visokolskis and Carrión do contemplate); all my appreciations or deductions will be circumscribed to an intuitive and, probably, equivocal procedure. In any case, I consider that, beyond this shortcoming, the general idea of what I want to express can be grasped.

  21. 21 Visokolskis and Carrión, 2020, p. 712 [Por tanto, la perspicacia o ingenio es la capacidad demostrativa de encontrar el término medio adecuado […] La clave del acto ingenioso reside en conectar dos términos extremos entre sí a través de un término medio hallado, formando así una proporción matemática. Lo curioso de este hallazgo es lo inesperado de tal conexión, dado que, en principio, los términos extremos son radicalmente diferentes entre sí y sería difícil vincularlos, a menos que surja una idea obtenida de manera perspicua. Más aun, en lugar de un solo término medio C, podría haber una cantidad finita n de ellos mayor que uno, estableciendo una proporción continua: A: C1 :: C1: C2 :: ... :: Cn: B, con n natural].

  22. 22 As Visokolskis and Carrión explain, the properties of P’ (which are b1, b2, ..., bn) in P were something peripheral; likewise, in P’ they cease to be irrelevant and, because of this, the cognitive leap is made.

  23. 23 Xenakis, 1971.

  24. 24 Here there is an indirect reference to the Cognitive Neuro-Dynamics of Perlovsky and Kozma (2007a) that considers the brain as a complex dynamic system in perpetual motion. However, this movement is always at the edge of stability. For this reason, the mathematical modeling of the mental processes occurring in the brain, from the point of view of the Cognitive Neuro-Dynamics, resorts to nonlinear chaotic dynamics and fuzzy logic.

  25. 25 Bartha, 2010, p. 13.

  26. 26 Prigogine, 1990, 2009; Reif, 1993.

  27. 27 Xenakis, 1971.

  28. 28 Prigogine, 1990, 2009; Reif, 1993.

  29. 29 Xenakis, 1971.

  30. 30 Prigogine, 2009, p. 95

  31. 31 Bartha, 2010.

  32. 32 Note that I am not resorting to formalism or to the technical definition that Bartha (2010; 2022) deploys in his research on the concept of plausibility; for him there are two types or classes of plausibility: one in terms of degrees or gradations, and the other in categorical terms. The one I developed above could be said to attempt to approach the former.

  33. 33 See Mauricio Beuchot in Rafael Frances, “Curso sobre el método analéctico crítico 03 17/02/16. Dr. Mauricio Beuchot” (6 May 2016), YouTube, https://www.youtube.com/watch?v=rXSOim6WHcw; Araya, 2020a.

  34. 34 Holyoak and Thagard, 1995; Bartha, 2010.

  35. 35 Holyoak and Thagard, 1995, p. 19.

  36. 36 Lakoff and Núñez, 2000.

  37. 37 The chapter seeks to understand the musical cognitive-creative process of Xenakis from its relationship with the exact sciences. Consequently, my intention is to understand the composer’s perspective which, in this case, refers to Xenakis. Therefore, and beyond the fact that other important actors (performers, audience, etc.) are involved in the field of music, when I speak of purposes (in the context of Holyoak and Thagard’s research), I am unequivocally alluding to the possible purposes that Xenakis may have had at the time of making his music. Of course, one of Xenakis’s most prominent purposes, I believe, at least in this case, was to generate works that show new ways of structuring and perceiving music. Therefore, and in order to achieve this goal, Xenakis established a fruitful dialogue with the exact sciences (statistical physics). However, as will be seen in the following lines (within the main corpus of the text), this dialogue was neither direct nor simple.

  38. 38 Varga, 1996; The object or phenomenon of knowledge of statistical physics refers to events made up of thousands or millions of elements (Xenakis, 1971; Prigogine, 1990); Xenakis, 1971, p. 12–16.

  39. 39 I said that the physicist observes/knows and the musician listens/perceives: this seems excessively restrictive since the act of knowing or perceiving contemplates many and very complex sides. But, regardless of this apparent restriction, what I mean to imply is that in both cases there are some cognitive mechanisms that may be more predominant than others due to the specific disciplinary field to which they belong.

  40. 40 The discussion around this problem is not exhaustive here, since mathematical models are also understood as metaphors or analogies of reality (Barrea, 2021). If we believe this to be so, Xenakis’s metaphor-analogy would be given, then, from three consecutive steps: natural phenomenon → mathematical tool to model the phenomenon → music (sound mass).

  41. 41 Goehr, 2017.

  42. 42 Walton, Reed, and Macagno, 2008, p. 57.

  43. 43 Bohm, 2002, p. 173–4 [La consideración del trabajo conjunto del orden y la medida en contextos cada vez más amplios y más complejos nos lleva a la noción de estructura […] Las clases de estructuras que pueden evolucionar, crecer o ser construidas están limitadas evidentemente por el orden y la medida que la subyacen. Un nuevo orden y medida harán posible el considerar nuevas clases de estructuras. Podemos tomar un ejemplo sencillo de la música. Aquí las estructuras con las que podemos trabajar dependen del orden de las notas y de ciertas medidas (escala, ritmo, tiempo, etc.). Evidentemente, órdenes y medidas nuevos harán posible la creación de nuevas estructuras en la música].

  44. 44 Veale, Gervás and Pease, 2006; Visokolskis and Carrión, 2020; Gelfert, 2016; Olguín and Tavernini, 2018.

  45. 45 Kant, 2006, p. 216–18.

  46. 46 The analytical and linear procedure implies that a problem, in reference to knowledge, is first decomposed into its essential parts; then those parts will be recombined and thus the complete solution of the problem will be obtained. In short, this means that the whole is nothing more than the sum of its parts. In other words, through a series of successive and orderly steps (analysis), the final result (the whole) is reached and obtained. This way of understanding and approaching things has its origin in mathematics and in Descartes’s (1596–1650) method, but it was also used in Newton’s (1643–1727) physics. In any case, and beyond its effectiveness, the analytical and linear method was questioned by thermodynamics and nonlinear and chaotic dynamics in the 20th century (Prigogine and Stengers, 1990; Strogatz, 1994; Reale and Antisieri, 1995; García Morente, 2013).

  47. 47 Although I am simplifying the separation proposed by Kant, in essence, this is how it happened.

  48. 48 Of course, at this point no one can think that things work this way, neither for science nor for art, especially because of the latest advances and contributions of neuroscience and artificial intelligence (Perlovsky, 2006, 2007; Perlovsky and Kozma, 2007; Perlovsky and Illin, 2012; Araya, 2022a, 2022b).

  49. 49 Estrada, 1990. As far as I know, Xenakis also alluded to the metaphorical and the analogical (Glissant, 1986); however, his theoretical investigations do not seem to have delved into this topic.

  50. 50 Araya, 2020a; Suicrea unam, “Julio Estrada Y…”, Facebook, https://www.facebook.com/SUICREA.UNAM/videos/355215483264868

Powered by Epublius