As for the stage, the two works also have the same setup, with the two ensembles sharing the stage, and the conductors standing back-to-back (Figure 15.2).

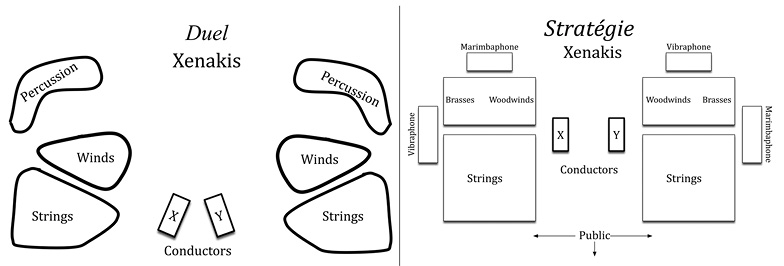
Fig. 15.2 Comparison between Duel and Stratégie stage setup. Figure created by authors.

Duel

Concerning Duel, we can notice that each orchestra is made up of three groups:

Winds: one piccolo, one oboe, one clarinet in E-flat, one bass clarinet in B-flat, one bassoon, one contrabassoon, two trumpets, one trombone.
Percussions: two bongos, three congas, one snare drum, one drum.
Strings: six first violins, six second violins, four cellos, two double basses.

The two orchestras are positioned to the left and right of the stage, with the two conductors standing back-to-back, or on two opposite podiums.

In Formalized Music,7 Xenakis presents us with a general diagram, in a very artistic way, showing the relationship between the different elements of the composition (Figure 15.3).

The Duel material comes in the form of five containers (I to V), three for the strings, one for the percussion and one for the winds. Each of these containers corresponds to a stochastic sound structure. Xenakis calls these structures tactics. The sixth container is silence.

II.

IV.

VI.

Cloud of sound grains (strings)

Sustained strings in parallel with fluctuations (strings)

Networks of crossing string glissandi (strings)

Stochastic Percussions (percussions)

Stochastic Wind Instruments (winds)

Silence

Table 15.2 Six tactics in Duel.

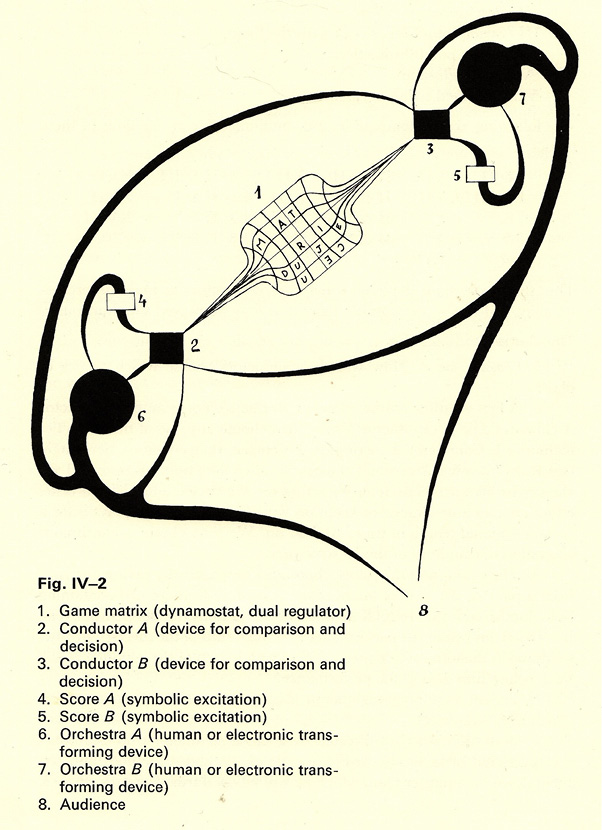
A graphic image in black ink showing two circles positioned diagonally and connected by hand drawn lines of varying thickness to create an artistic and partially symmetrical design. Parts of the image are marked with numbers, and a key to the significance of the numbers is printed underneath the image.

Fig. 15.3 Xenakis’s sketch for Stratégie 8 (reproduced with permission from Pendragon Press).

Each conductor then has six sound configurations at his disposal; i.e., six tactics, from which he will choose during the performance of the work.

Regarding the material of Duel’s containers, as shown by Benoît Gibson,9 it comes mainly from two other works by Xenakis: Syrmos (1959) for containers I, II, and III and Achorripsis (1959) for container V. The latter uses the instrumentation of Achorripsis without the percussion. As our objective is the formal structure, we will not deepen the aspect of “self-borrowing” already commented on by Gibson, but will follow an example from Duel’s score. Figure 15.4 shows the beginning of Duel’s first section, which comes from Syrmos (1959).

An extract of a music score for string orchestra written on eighteen staves. The music is barred in a la breve time, at the metronome speed half note equals sixty, and the pitch and rhythmic material is complex.

Fig. 15.4 Duel I, from Syrmos (1959). Re-notated by authors.

Game Theory

In Musique Formelles, Xenakis gives two references regarding game theory:10 La Stratégie dans les actions humaines by J. D. Williams and La théorie des jeux et programmation linéaire by Steven Vajda.11

It is important to note that in the 1950s, game theory was a booming discipline. When the Compleat Strategies was first published in 1954, the original version of Williams’s book, Game Theory was an esoteric and mysterious subject, familiar only to some researchers, especially those in the army. This indicates that Xenakis was aware of the cutting-edge developments and research of his time.12

In Chapter III of Musique Formelles,13 Xenakis describes the method for creating the matrix of Duel from subjective judgments on combinations of sound textures, or tactics (Table 15.3).

Four columns with the titles Couple, Qualification, Couple and Qualification.

Table 15.3 Table of Evaluations 14 (reproduced with permission from Pendragon Press).

These calculations lead to a matrix (Figure 15.5) describing the points for each move.

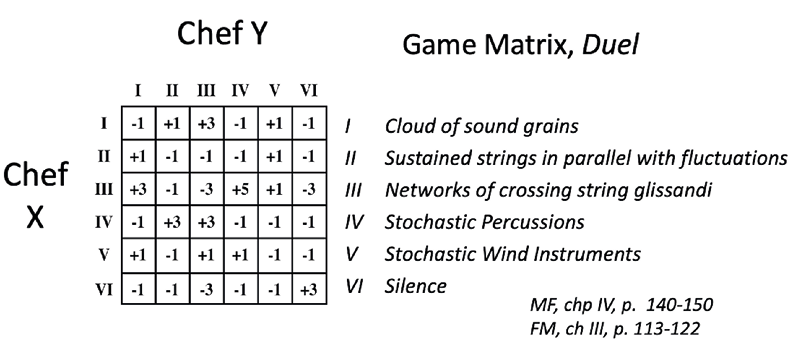
A diagram showing a six-by-six matrix labelled Chef Y for the columns and Chef X for the rows. Each row and column of the matrix is labelled one to six, and inside each box of the matrix is a number, positive or negative between one and five. The meaning of these numbers is indicated in a table to the right of the matrix.

Fig. 15.5 Original game matrix for Duel. Figure created by authors.

This matrix is the game matrix, which defines a zero-sum two-player game, a special case of mathematical game theory. A matrix gives the agents’ gains and losses (game rows or columns). Each row or column corresponds to a given tactic. In this specific case, if player X plays tactic IV, while player Y plays tactic III, the result is +3; i.e., 3 points to player X (Figure 15.6).

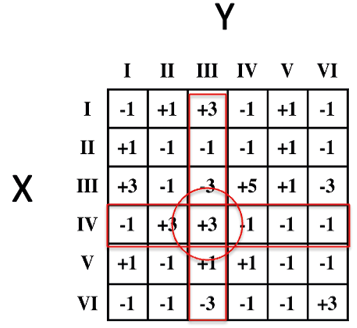
The same matrix as in figure fifteen five but with a red circle drawn around the box four down and three along, containing the number plus three.

Fig. 15.6 Specific example of a move. Figure created by authors.

Since Xenakis wants a fair game, i.e., a zero sum of winnings, he calculated the probabilities for the different tactics (rows and columns). Xenakis bases his calculations on John von Neumann’s (1903–57) minmax theorem, which is a special case of Nash’s equilibrium theorem 15 ensuring the existence of a stable solution (Figure 15.7), with a game value equal to -0.07, which means that this game is almost balanced.

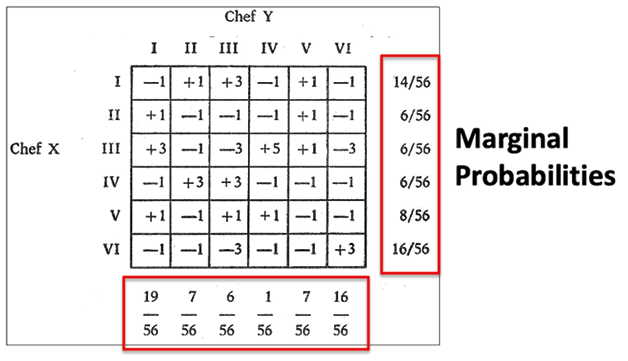
The same matrix as in figure fifteen five but with the marginal probabilities of the numbers shown within the matrix given in a red box to the right, for the rows, and to the bottom for the columns.

Fig. 15.7 Weighted random choices for each agent, marginal probabilities. Figure created by authors.16

Note that, unlike in Musiques Formelles and Formalized Music (Figure 15.5), in the score of Duel (Figure 15.8) tactics I, II, and III are replaced by A, B, and C, which are sound combinations. A can be tactic I or II or III. B will be one of the following combinations: A+IV, or A+V, or IV+V. And C will be the combination A+IV+V (all combinations of three), remembering that A is multiple. This presumably is in order to bring more variety to the games.

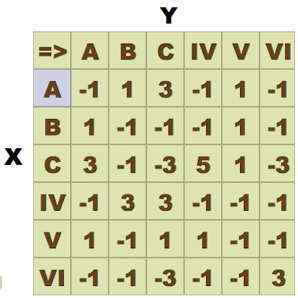
The same matrix as in figure fifteen five but with the first three rows and the first three columns labelled A B and C, with the A of the A row marked in blue.

Fig. 15.8 Matrix game in Duel’s score. Figure created by authors.

Duel—Pragmatic Performance Issues

The performance of Duel is not without difficulties and requires complex preparation from both conductors. Some preliminary decisions are necessary before playing Duel:

The allocation of rows and columns (for example by drawing heads or tails between the two conductors).
The determination of the duration (by choosing a duration in minutes, the number of moves, or the maximum number of points to obtain).
The decision of who will start.

Other elements are at the discretion of the conductors:

The places in the score to start tactics.
The duration of each move.

Xenakis is precise in pointing out that there are two ways: the “degenerate way;” that is to say, without considering the matrix, and playing in a musical or intuitive way; and the “valid” way, using the matrix and its values, as well as applying the marginal probabilities:

A degenerate game is one in which the parties play arbitrarily following a more or less improvised route, without any conditioning for conflict, and therefore without any new compositional argument. This is a false game.17

The only valid (way), the only one that brings something new, in the case of several orchestras, is the one that is sanctioned by gains and losses, by victories and defeats.18

And according to Xenakis, the winner is the one who best follows the rules of the game:

The winner won because he simply better followed the rules of the game imposed by the composer who, therefore, claims responsibility for the “beautiful” or “ugly” of his music.19

Now, considering the ways to play with the matrix, we can basically count three of them:

Random choices weighted by the marginal probabilities, those just mentioned.
Choices minimizing the opponent’s gain in the next step, minmax.
Choices maximizing its own gain, minmax-gain.

Obviously, nothing prevents mixing these strategies.

Computer Simulations of the Game

To be able to study the dynamics and the evolution of the structure of Duel, we carried out computer simulations, using each of the strategies mentioned. Figure 15.9 shows the Max software interface built for this intent.

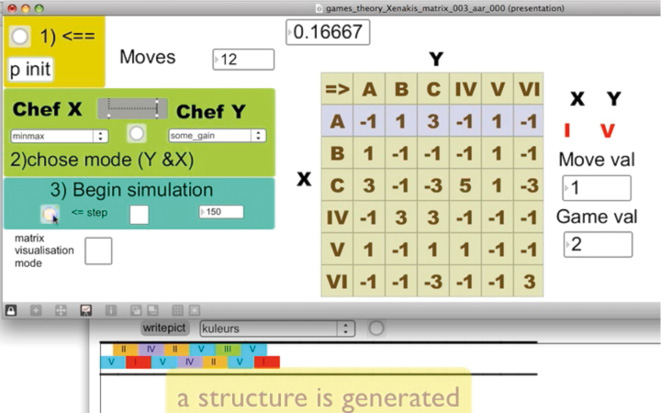
A screen shot of a an app interface showing selection options for Chef X and Chef Y and app controls in a coloured box on the left, the matrix from Figure fifteen five in the middle, and two small windows displaying live results on the right of the interface.

Fig. 15.9 Max interface for simulation. Figure created by authors.

We have also represented the result in the form of curves and a formal diagram, to help us identify the emerging structure. This simulation would converge to the value of the game after a large enough number of steps. Figure 15.10 presents an example of the carpet, our diagram, of played sequences.

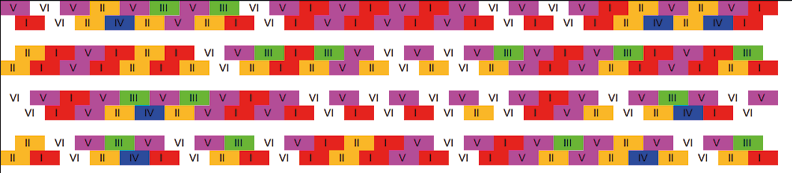
A coloured graphic showing the output of the app in two parallel lines where each numeric output is represented in a different colour. The graphic contains four rows of outputs.

Fig. 15.10 The carpet, diagram of successive moves. Figure created by authors.

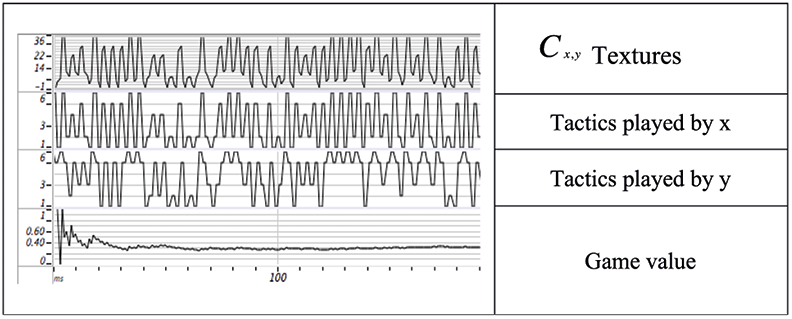
A graphic showing four sets of results as a set of line graphs, one above the other with each set of results labelled on the right as: Textures, Tactics played by X, Tactics played by Y, and Game value.

Fig. 15.11 displays the curves representing the evolution of the textures, the moves of each player, and the evolution of the value of the game. Figure created by authors.

Figure 15.11 displays the curves representing the evolution of the textures, the moves of each player, and the evolution of the value of the game. Figure created by authors. To study the dynamics of the game, we can represent (or think of) the evolution of different tactics as a sequence of mixtures (Cx,y) of two tactics, which we will call textures (Ti). Each combination of two tactics corresponds to a texture (Cx,y) ⇒ Ti ∈ {1, 2, …, 36}).

In the particular case of Duel, we can generate 36 textures resulting from the 36 combinations of the six tactics (A, B, C, IV, V, and VI) (Figure 15.12). For example, in Figure 15.13, the first combination corresponds to tactic VI played by X and by tactic V played by Y, which corresponds to the texture 35. The second combination corresponds to tactic B played by X and by tactic V played by Y, which corresponds to texture 11. The third combination corresponds to texture 8, and so on. Each texture is not a single element, but a category, an equivalence class, such that the texture i, is the texture Ti generated by a pair of x and y strokes, Cx,y .

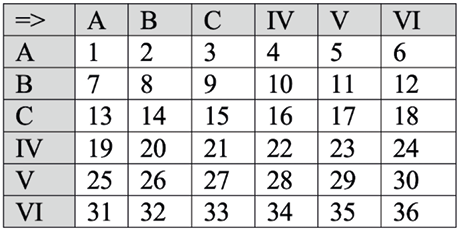
The same matrix as figure fifteen eight but with cumulative values shown in each square ranging in value from one in square AA to thirty-six in square six six.

Fig. 15.12 Textures matrix. Figure created by authors.

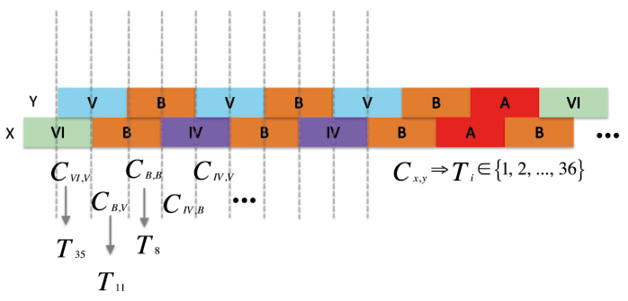
A graphic image showing two lines of values one above the other where each value is represented in a different colour. The overlapping pairs of outputs are represented as a value T below the image. The probability formula for T is indicated on the right of the image.

Fig. 15.13 Game evolution. Figure created by authors.

On the other hand, if we consider that the two orchestras are symmetrical, and that a texture resulting from a move (i, j) is identical to the texture resulting from a move (j, i), then Ci,j ≡ Cj,i , our texture matrix becomes symmetrical and only has 21 textures, Cx,y ∈ {1, 2, …, 21} (Figure 15.14)

This consideration is already taken into account by Xenakis, in his construction of the table of “subjective judgments” (Table 15.3) where it is clearly indicated that the pairs (x, y) are equivalent to the pairs (y, x). We are aware that from the listener’s point of view the setup will not always be symmetrical. On the other hand, as a first approach to the analysis, we will consider this disposition.

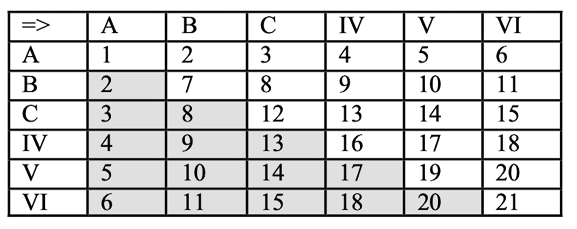
A matrix as in figure fifteen fifteen twelve but with the values one to six in both the first row and the first column, and with consequently different accumulations in the other boxes.

Fig. 15.14 Simplified texture matrix. Figure created by authors.

Let us see some simulation results.20

Simulation using Weighted Random Choices (wrc)

In this simulation we use the marginal probabilities, calculated by Xenakis (Figure 15.7) to make Weighted Random Choices. In this simulation, the game goes through the twenty-one cells, therefore through the thirty-six combinations of sounds offered. The morphology of the paths depends on the weight ratio of rows and columns and does not show special patterns (Figure 15.15). However, we notice a particular distribution in the texture histogram (Figure 15.16). A few seem favored over others, such as texture 6 over texture 16, which is to be expected since the probabilities of lines A and VI for both players are preponderant.

Output represented as a single line graph plotting a value between zero and twenty-one, showing more than two hundred and forty successive values.

Fig. 15.15 Textures’ evolution (wrc). Figure created by authors.

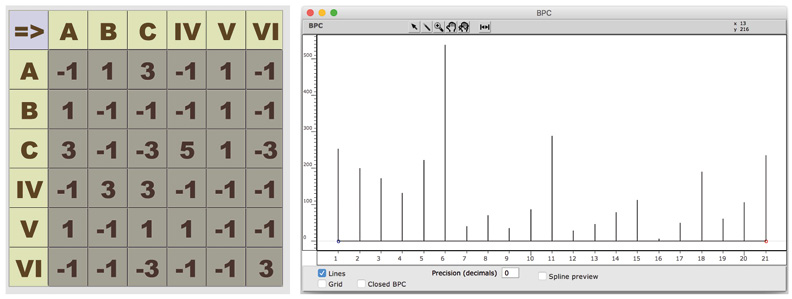
The same matrix as in figure fifteen five on the left of the image, and on the right a bar graph showing the accumulations of values between one and twenty-one.

Fig. 15.16 Textures’ coverage (wrc) and histogram. Figure created by authors.

Choices Minimizing the Gains of the Adversary (Minmax)

In this simulation, each move is supposed to minimize the opponent’s gain. The game does not cover the twenty-one cells, leaving some combinations tacet (Figure 15.17). The morphology of the paths presents cycles and almost repetitive forms (Figure 15.18).

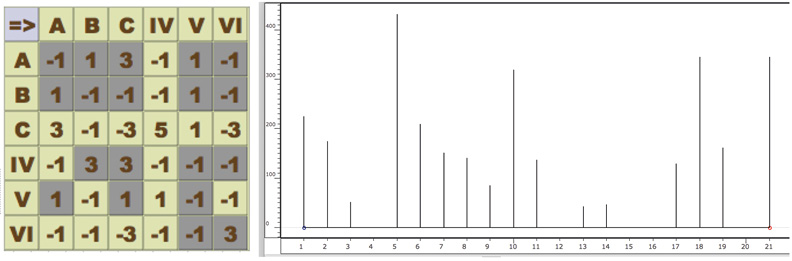
The same graphic as figure fifteen fifteen but showing different output values.

Fig. 15.17 Textures’ coverage (minmax) and histogram. Figure created by authors.

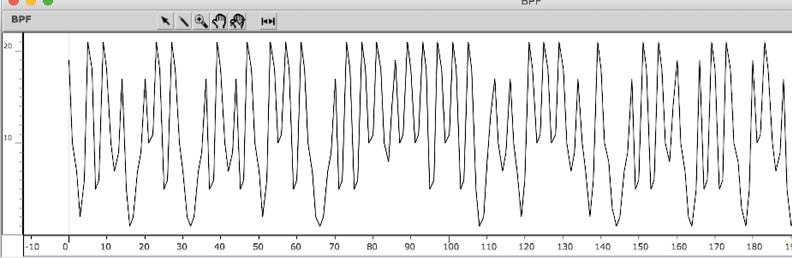
Output represented as a single line graph plotting a value between zero and twenty-one, showing more than one hundred and ninety successive values.

Fig. 15.18 Textures’ evolution (minmax). Figure created by authors.

Observing the curve of the evolution of textures, one can easily identify cycles, a kind of X A Y A’, etc.: a structure by blocks (Figure 15.19).

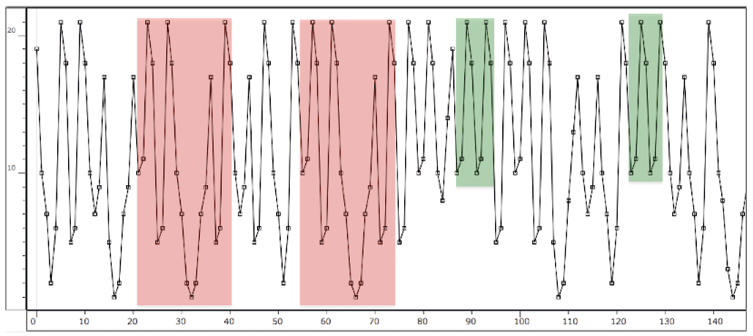
Output represented as a single line graph plotting a value between zero and twenty-one, showing more than one hundred and forty successive values. Two sections of the graph are marked in red to the left and two in green to the right where repetitions of value successions occur.

Fig. 15.19 Cycles in the textures’ evolution curve (minmax). Figure created by authors.

Choices Maximizing own Gains (Gainmax)

In this simulation, each move is supposed to maximize a player’s own gains. The game does not pass through the twenty-one cells, still leaving combinations tacet (Figure 15.20). The morphology of the patterns also presents cycles and almost repetitive forms (Figure 15.21).

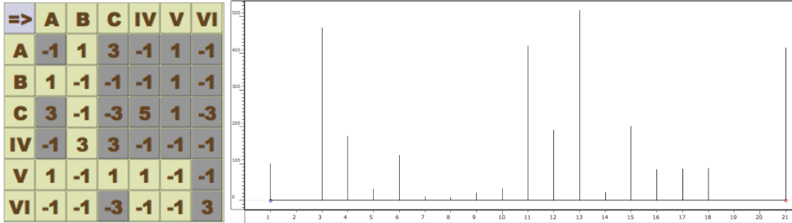
The same matrix as in figure 15.5 on the left of the image, and on the right a bar graph showing the accumulations of values between one and twenty-one, with different output to figure fifteen sixteen.

Fig. 15.20 Textures’ coverage (gainmax) and histogram. Figure created by authors.

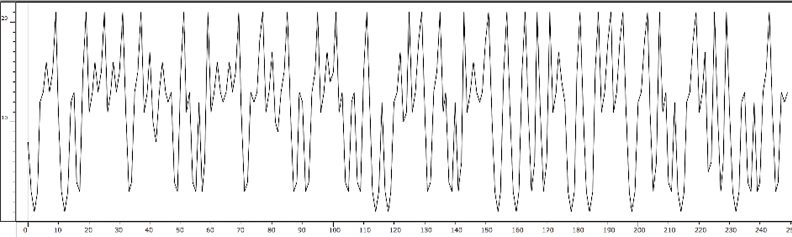
Fig. 15.21 Textures’ evolution (gainmax). Figure created by authors.

Observing the curve of the evolution of textures, we can again identify cycles (Figure 15.22).

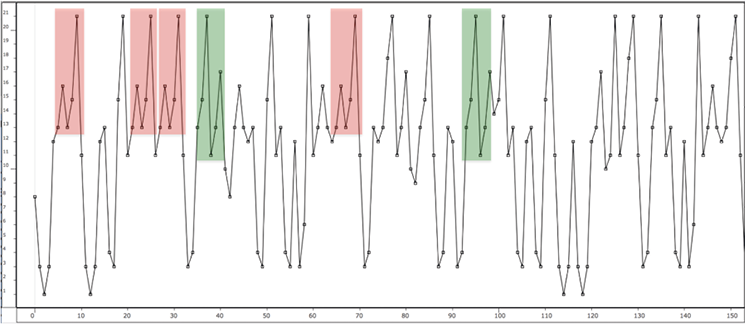
Output represented as a single line graph plotting a value between zero and twenty-one, showing more than one hundred and fifty successive values. Four sections of the graph are marked in red and two in green where repetitions of value successions occur.

Fig. 15.22 Cycles in the textures’ evolution curve (gainmax). Figure created by authors.

A Few Comments

In any case, we can perceive that the combination of VI+VI tactics, i.e., texture 21, is a silence, which articulates the sequence musically, creating blocks of more or less repetitive patterns. We find this same situation (silence) in other completely composed works (Achorripsis, N’Shima (1975), etc.). Figure 15.23, Figure 15.24, and Figure 15.25 present an excerpt from a simulation with x and y using the same type of choice, gainmax.

Fig. 15.23 Diagram of successive moves. Figure created by authors.

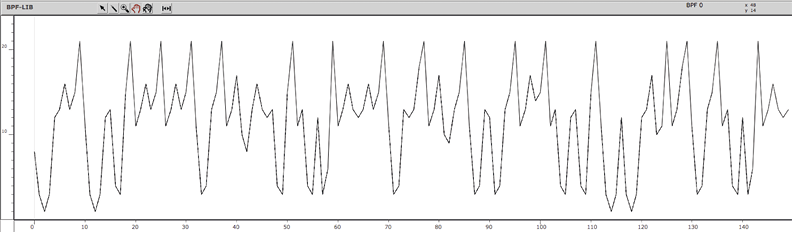
Fig. 15.24 Texture evolution curve. Figure created by authors.

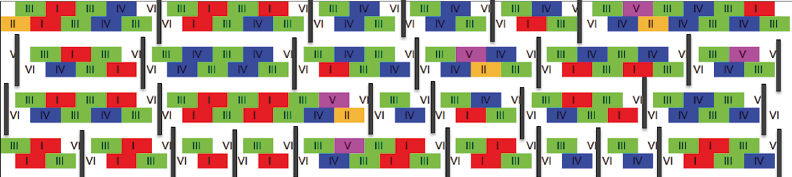
Fig. 15.25 Diagram of successive moves articulated by silences. Figure created by authors.

We can notice (Figure 15.26) that silences punctuate the sequence creating groupings of textures.

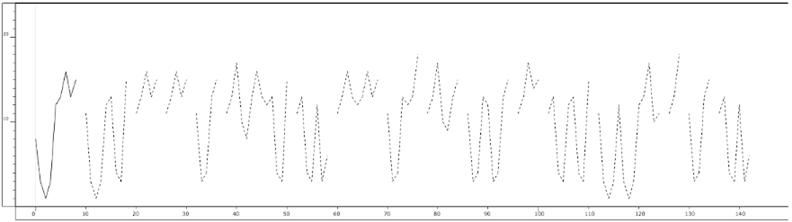
Fig. 15.26 Evolution curve of textures (Figure 15.24) articulated by silences. Figure created by authors.

Another example (Figure 15.27, Figure 15.28) with x and y using minmax moves.

Fig. 15.27 Diagram of successive moves articulated by silences. Figure created by authors.

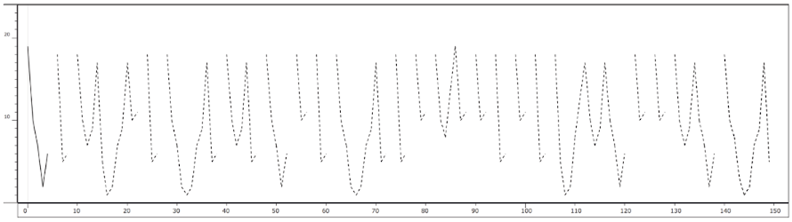
Fig. 15.28 Evolution curve of textures articulated by silences. Figure created by authors.

Conclusions

This work is the first approach to the problem, a simplification for the purposes of this study. As we mentioned, each texture is not a single element, but a category, an equivalence class; for example, the T1 texture, which is the combination of 2 tactics A, will correspond to 6 sub-textures. In addition, we know that to play each tactic, the leader/conductor can ask to start at any section. Each tactic has 23 sections. That is to say that each of these 6 sub-textures can be broken down into 23 × 23, or 529 possibilities. However, can one really hear the difference? In addition, in rehearsal, the conductors can draw on the expression and duration of each move and on the tempi.

At first glance, the choices of the conductors involve problems of a structural or formal order. The random strategy leads to a random structure. A weighted random strategy does not produce noticeable structures, but texture polarizations. And the minmax or gainmax strategies, with or without profits, lead to a game that generates more or less repetitive cycles and patterns.

This brings us to the fact that according to the choices of the conductors, one or more methods could be chosen. If they want a form with redundancies, they will choose to keep the same method as much as possible. However, if they choose to have a more varied form, changing the method helps to achieve this goal.

A final point, considering the choice of tactics, leaders/conductors should be careful of hesitation which could introduce “pauses” in the articulation during the performance, silence having a clear structural function.

It is important to make a difference between the study of the dynamics of the system proposed by Xenakis and the actualization of this system within the context of a real musical presentation. For Duel, Xenakis asks for a minimum duration of ten seconds for each move, a minimum time which can be increased or shortened by prior agreement of the leaders/conductors. For ten minutes (600 seconds), with an average time of fifteen seconds, we will have an average of eighty moves per execution. The scale of study of the two situations is very different. In practice, the form will undoubtedly vary from the theoretical form, in particular because of performance issues.

Duel (and even Stratégie) have a lot of execution issues, including choosing real-time tactics depending on the chosen method, communication between conductors and performers, and navigating through the scores. The problem of an interface for execution has already been presented on another occasion.21

For the continuation of this study, we propose to deepen the study of the calculations of Xenakis, the study of the textures (shape) dynamics, designing experiences with musicians, consulting conductors to improve the interface, complete interfaces for Duel and Stratégie, and to do a full-scale experiment.

References

ECO, Umberto (1962), Opera aperta: Forma e indeterminazione nelle poetiche contemparanee, vol. 3, Milan, Tascabili Bompiani.

GIBSON, Benoît (2011), The Instrumental Music of Iannis Xenakis. Theory, Practice, Self-borrowing, Hillsdale, New York, Pendragon Press.

MALT, Mikhail and SLUCHIN, Benny (2011), “L’interprétation assistée par ordinateur,” Le journal de l’Association des Anciens de Sciences et Musicologie, Hors-série, no. 1, April, p. 17–21.

MATOSSIAN, Nouritza (1981), Iannis Xenakis, Édition Fayard/Sacem, France.

von NEUMANN, John and MORGENSTERN, Oskar (1944), Theory of Games and Economic Behavior, Princeton, New Jersey, Princeton University Press.

SLUCHIN, Benny (2005), “Linaia Agon, Towards an Interpretation Based on the Theory”, in A. Georgaki and M. Solomos (eds.), Proceedings of Iannis Xenakis International Symposium, Athens, p. 299–311.

SLUCHIN, Benny and MALT, Mikhail (2010), “Interpretation and Computer Assistance in John Cage’s Concert for Piano and Orchestra (1957–58)”, paper presented at 7th Sound and Music Computing Conference Proceedings, Barcelona, July 21–24, https://hal.science/hal-01580136/document

SLUCHIN, Benny and MALT, Mikhail (2011a), “Open Form and Two Combinatorial Musical Models: The Cases of Domaines and Duel,” paper presented at 3rd International Conference on Mathematics and Computation in Music, Paris, June 15–17, p. 255–69, https://hal.science/hal-01580314/file/Open%20form%20and%20two%20combinatorial%20musical%20models%20-%20The%20cases%20of%20Domaines%20and%20Duel.pdf

SLUCHIN, Benny and MALT, Mikhail (2011b), “Play and Game in Duel and Strategy,” paper presented at Xenakis International Symposium, London, April, 2011.

TAZDAÏT, Tarik (2023), La science est un jeu, Paris, Classiques Garnier.

VAJDA, Steven (1959), La théorie des jeux et programmation linéaire, Paris, Dunod.

WEBB, James N. (2007), Game Theory, Decisions, Interaction and Evolution, Heidelberg, Springer.

WILLIAMS, John Davis (1956), La Stratégie dans les actions humaines, Paris, Dunod.

WILLIAMS, John Davis (1954), The Compleat Strategyst: Being a Primer on the Theory of Games of Strategy, New York, New York McGraw-Hill.

XENAKIS, Iannis (1959), Duel, Paris, Salabert.

XENAKIS, Iannis (1963), “Musiques Formelles,” La Revue Musicale, vols. 253–4.

XENAKIS, Iannis (1992), Formalized Music: Thought and Mathematics in Music, additional material compiled and edited by Sharon Kanach (rev. ed.), Stuyvesant, New York, Pendragon.

1 This text is an expanded version of an earlier publication, Sluchin and Malt, 2011b.
2 “Duel (1959),” IRCAM, https://brahms.ircam.fr/en/works/work/12797/54466
3 “Stratégie (1962),” IRCAM, https://brahms.ircam.fr/en/works/work/12878/
4 Review cited in Matossian, 2005, p. 226.
5 Seiji Ozawa, Yomiuri Nippon Symphony, Hiroshi Wakasugi, Yuji Takahashi – Orchestral Space, Label: Varèse Sarabande – VX 81060, Vinyl, LP, Recorded May 1–4, 1966, US, 1978.

6 “Orchestral Space,” RYM, https://rateyourmusic.com/release/comp/yomiuri-nippon-symphony-orchestra-seiji-ozawa-hiroshi-wakasugi-yuji-takahashi/orchestral-space/
7 Xenakis, 1963, p. 150; Xenakis, 1992, p. 124.
8 Xenakis, 1992, p. 124.
9 Gibson, 2011, p. 14–19; p. 164–71.
10 Xenakis, 1963, p. 226.
11 Williams, 1956; Vajda, 1959.
12 Williams, 1954.
13 Xenakis, 1963, p. 140–50, or Chapter IV of the English version: Xenakis, 1992, p. 110–30.
14 Xenakis, 1992, p. 114.
15 “Nash Theorem (In Game Theory),” Encyclopedia of Mathematics,
https://encyclopediaofmath.org/index.php?title=Nash_theorem_(in_game_theory)
16 Figure based on Xenakis’s original figure in Xenakis, 1963, p. 147.
17 Xenakis, 1963, p. 140; Xenakis, 1992, p. 113 [Un jeu dégénéré est celui dans lequel les parties jouent arbitrairement en suivant des parcours plus ou moins ‘improvises’, mais sans conditionnement conflictuel, donc sans valeur compositionnelle. C’est un faux jeu].
18 Xenakis, 1959, p. 4 [La seule (façon) valable, la seule qui apporte quelque chose de nouveau, dans le cas de plusieurs orchestres, est celle qui est sanctionnée par des gains et des pertes, par des victoires et des défaites].
19 Ibid., p. 5 [Le gagnant a gagné parce qu’il a simplement mieux suivi les règles du jeu imposées par le compositeur qui, par conséquent, revendique la responsabilité du ‘beau’ ou du ‘laid’ de sa musique].
20 The simulations were carried out with samples of 3,000 moves.
21 Sluchin and Malt, 2011b.

15. Game Theory and Formal Structure in Iannis Xenakis’s Duel (1959)

Mikhail Malt and Benny Sluchin1

Introduction

Historical Overview

Duel, Stratégie: Description