19. Performing Iannis Xenakis’s Polyrhythms: A Perception-informed Approach to Renotation

Imri Talgam

Introduction

Xenakis’s use of algorithmic composition often produces great difficulties for performers, especially in his solo works. These difficulties result from the use of probability distributions that generate dense and irregular textures, often bordering on the impossible both physically (as in Evryali (1973), for example) and mentally. My goal in this chapter is to address performance challenges that stem from Xenakis’s use of complex polyrhythms, which frequently appear in his works from the 1970s onwards. The solo piano piece Mists, written in 1980, serves as a particularly rich case study, with passages that prefigure the rhythmic intricacies of New Complexity. The ideas I will propose here could be applied in many other Xenakis chamber and solo pieces from this period that feature complex polyrhythms, including Dikhthas (1979), Tetras (1983), Komboï (1981), and À l’île de Gorée (1986).

In such extreme pieces, performers need to develop new learning and performance strategies to deal with the vast amount of information and extreme rhythmic complexity. I argue that to tackle these difficulties successfully, performers should renotate the score methodically, based on perceptual and cognitive criteria. By renotating the score, we can create a script for the streamlined performance of otherwise overwhelmingly complex rhythms, while keeping the result perceptually similar to the original.

Discussions of the challenges involved in the performance of complex rhythm often focus on composers identified with “New Complexity,” especially in the works of Brian Ferneyhough (b. 1943), where performers are required to decipher and calculate several layers of nested tuplets before they can begin practicing the rhythms. In many of these discussions, the emphasis is on the use of complex notation as a strategy for transforming the performer’s relation to the score, either by “psychologizing” the learning process,1 or on the meaning and feasibility of the infinitesimal nuances called for in performance, as well as the choices performers must make in interpreting these rhythms.2 In contrast to these approaches, I believe Xenakis was less interested in creating a dense text for the performer to interpret than in presenting complex stochastic rhythms without compromising his compositional ideas, even though these might not be possible to reproduce in live performance with the accuracy of a computer. Consequently, I will focus on purely practical considerations, and suggest conceptual tools that can assist performers.

Mists (1981) for Piano

Fig. 19.1 Mists (1981), Opening and Stretto. Reset in Dorico by author.

The opening of Mists consists of continuous random walks along the custom scales or pitch sieves that Xenakis designed for this piece, as shown by Ronald Squibbs.3 Initially, the random walks create a two-voice polyphonic texture, with each voice emerging from the bottom of the keyboard and gradually climbing up. Due to the distance in register, the two voices are easily streamed, forming distinct polyphonic entities. Rhythmically, each voice articulates isochronous attacks, with frequent changes of speed notated using polyrhythms. While this is rhythmically challenging due to the independent rate in each hand and the lack of common attack points, it is still manageable without any renotation.

Media 19.1 Mists, Opening and Stretto, Performance by Aki Takahashi.4 © Mode Records (2006).
https://hdl.handle.net/20.500.12434/53d33115

This sudden explosion of information and energy makes this passage extremely difficult to perform, although the polyrhythms might be more difficult to recognize aurally than in the earlier versions with two voices. The impression of polyphony is diminished due to the proximity in register of the voices, which causes them to fuse together and become a dense texture. Most performers approximate the rhythms, contributing even further to the impression of a dense sound mass with little internal structure or detail.

Looking at the Stretto passage (measures 9–11 above) more closely immediately reveals two related performance difficulties. First, the score conveys the different speed of each voice relative to sixteenth-notes, but the composite attack pattern that results from their interaction is not immediately visible. Xenakis took care to place the notes in graphically correct order, but this does not give all the information required for performance. The second difficulty is the extreme irregularity and proximity of some of these attacks, which include various gradations of “almost together,” while never repeating the same timing. As Franklin Cox notes, scores provide both too much and too little information.5 The complexity of the composite inter-onset intervals (IOIs) becomes apparent when we listen to a rhythmically perfect computer rendition of the passage.

Media 19.2 MIDI version, original tempo (eighth-note = 96) of Mists, measures 9–11.
https://hdl.handle.net/20.500.12434/9167a84e

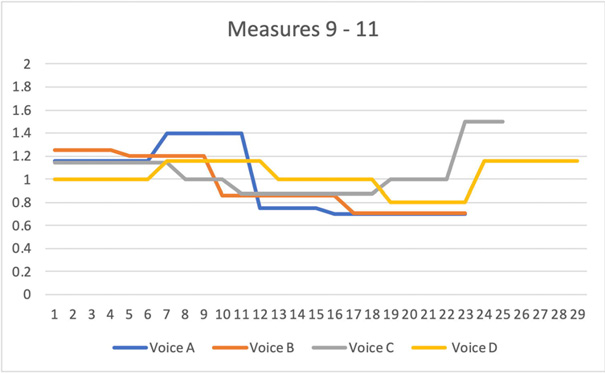
Fig. 19.2 Salient macro-features. Each voice slows down in steps (except Voice A initially), with a noticeable bump up in speed in measure 11. As a result, the overall density of events decreases. Figure created by author.

Despite the inevitable blurring of polyphony, the passage has some interesting macro characteristics that are perceptually salient, yet not immediately evident in the score. Looking at the graph, we have the tempo change in each voice over time, with the voices labeled from top to bottom: Voice A is the top voice. The X axis is time measured in sixteenth-notes, while the Y axis shows the tempo of each polyrhythm relative to sixteenth-notes, which are denoted with the value 1 (or a ratio of 1:1). Numbers greater than 1 represent polyrhythms with faster movement, such as 7:5, or 1.4 times the speed of a sixteenth. Conversely, values below 1 represent polyrhythms that are slower than sixteenth-notes, such as 5:7 or 0.714.

Fig. 19.3 Quantized arborescences and random walks, Mists, measures 14–21. Tempo changes in each of the four Voices (Y Axis). Decimals represent tempo relative to sixteenth-notes. The published score has been reset in Dorico by the author, with some errors corrected, e.g., measures 18–19 RH top voice notated 7:8 should be 7:6; measure 19 LH top voice, the 6:5 has been erroneously copied from the RH lower voice. However, all the visual alignments are correct.

The macro trend is clear: the passage begins with faster speeds in each voice and gradually slows down in steps, before bumping the speed up again at the very end. This means that the density of attacks gradually goes down, though without any corresponding drop in dynamics. The decreasing density is even clearer when listening back to the passage at half tempo:

Media 19.3 MIDI version at half tempo (eighth-note = 48) of Mists, measures 9–11.
https://hdl.handle.net/20.500.12434/366fd4a3

This type of macro rhythmic process is perceptually more salient than the isochronous polyrhythms that create the texture; in other words, listeners are more likely to notice a gradual change in density than precise polyrhythmic relations between four voices.

The next section of Mists is structured as a series of alternations between further random walks, mostly separated by simpler phrases modeled on arborescences (or melodic branching structures) using only thirty-second notes. The contrast between the rhythmic regularity of the arborescences and the complex macro rhythmic processes of the walks becomes the center of attention.

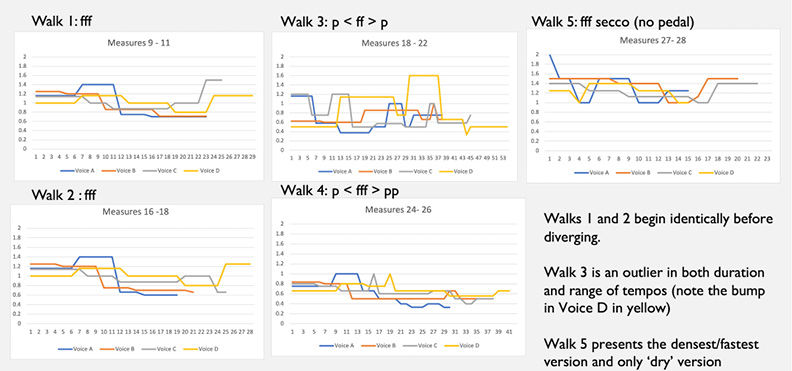
Fig. 19.4 Macro features of successive random walks, Mists, measures 14–21. Figure created by author.

Extracting these macro features can help reframe the goals of performance. Rather than attempting to realize the polyrhythms as such, and attempting to reproduce each layer isochronously, it becomes clear that performers should focus on reproducing the perceptually salient macro features that differentiate these random walks and give each of them a distinct quality. This reframing of the performance priorities is also aesthetically significant: instead of attempting an entirely deterministic realization of every single detail, the performer aims to capture the most significant statistical features. This is line with Xenakis’s compositional approach, in which the individual details are random, while the larger processes are clearly shaped by the composer.

Let us examine some possible performance responses to these difficulties, in order of increasing investment. First, we have an informal approach of keeping an eighth-note tactus and approximating the exact timings, likely only keeping the order of attacks within a beat while sacrificing precision and the isochrony in each voice. In this approach (which is the most common one among musicians due to time-constraints), the texture assumes a “generic” sound of slightly desynchronized events with little variation in average density. This often involves reducing the irregularity of the attacks to a simplified recurring pattern. This approximation often results in IOIs that are more regular than the original.

The second strategy is to calculate the Least Common Multiple (LCM) between the various layers, or renotate the polyrhythms using subdivisions. Unfortunately, this is both time-consuming and does not yield useful results, as we can see from MacFarland’s renotation of a similar excerpt from Tetras:

Fig. 19.5 Limitations of LCM or Polyrhythm Respelling Strategy. Subdivisions are too fast to be useful even without LCM. From McFarland’s, “Second Generation Performances of Xenakis’ String Quartets,” in Kanach, 2010, p. 254 (reproduced with permission).

This is not useful because the subdivisions are so fast that we cannot count them at the notated tempo, suggesting we need to simplify things somewhat to produce a useful score. This brings us to the strategy I advocate, a renotation informed by perception.

Fig. 19.6 Polyrhythms converted to decimal values (7:6 example). Reset in Dorico by author.

As a preliminary stage, we can translate the polyrhythms into decimals, which helps us determine the relation between attack points in different voices without a LCM. For example, in the top voice the ratio 7:6 denotes 7 attacks in the time of 6 sixteenth-notes. 6 divided by 7 is 0.857—the time point for the second note in the 7:6 group, right before the second sixteenth-note of the passage (timepoint 1). This can be made more intuitive by adding an offset of 1, so that we can start counting from 1 instead of 0 and can refer the decimal time-points to sixteenth-note subdivisions in the published score. By doing this with each voice, we can start investigating the composite attack pattern, or the IOIs between different voices. Another important feature this reveals is the ‘horizontal’ behavior of each voice as it changes from one polyrhythm or ratio to another. For example, Voice 1 (top) switches from 7:6 (0.857) to 7:5 (0.714), so it is noticeable faster.

Before renotating, it is necessary to define some thresholds for the perception of rhythmic differences, to ensure the simplified version will still sound very much like the original. In a sense, this is like the data-compression of an mp3 format, which uses perceptual coding to make sure the compressed file reproduces the perceptually salient features, while removing a considerable amount of information.6

To simplify the rhythm, while preserving the same perceptual features, we must define a threshold for distinction between events. Hirsh found that two milliseconds (ms) are required to discern that two tone onsets are present, while a considerably greater interval of around 20 ms is required for listeners to determine the order of the note onsets correctly.7 This suggests that within the 20 ms range, we need not worry about the rhythmic definition of IOIs between voices, or even the exact order. With some additional inaccuracy in performance, the result will be perceptually very similar.

The absolute limit to metric subdivision is considerably higher. Justin London proposes a limit of about 100 ms for the fastest subdivision of a tactus, under which we can no longer expect precise performance or listening.8 In the prescribed tempo of eighth-note = 96 (m.m. or BPM), the duration of one thirty-second-note is 156 ms, well within the possibility of metric subdivision. However, sixty-fourth-notes last 78ms, already too fine for metric definition.

Fig. 19.7 Perception-based constraints and tempo values. Reset in Dorico by author.

On this basis, we can formulate a quantization strategy for renotation. The lowest level of metric subdivision should be thirty-second-notes, with all attacks on time-points under this level defined using a combination of grace notes (occurring right before a metrically defined attack) or arpeggiation (which we can use to denote events right after a metric point). Using the decimal time-point values for all voices, we can calculate IOIs in milliseconds and round off values to the nearest metric position, and then translate them to a grace note or arpeggio relative to that position. In cases that an attack falls very close to a sixty-fourth-note subdivision, this notation may be used as well to avoid even cruder approximation.

Although all voices could be quantized in this way, I find it better to retain one more polyrhythmic layer in addition to the sixteenth-note pulse. In this way two voices remain metrically defined, while the two others are converted to a-rhythmical grace-notes and arpeggiations. This assumes that it is possible to perform a polyrhythm between two voices relatively easily, as in the earlier two-voice texture. To limit the number of possible renotations from the combinations of rhythmic and arhythmic voices, we can add two more constraints based on practical considerations. First, we should keep any voice that articulates sixteenth-notes, as these provide the easiest means of orientation and as a subdivision of the eighth-note tactus established at the opening. Second, each hand should have at least one layer that is metrically defined, to ensure synchronization with the other hand.

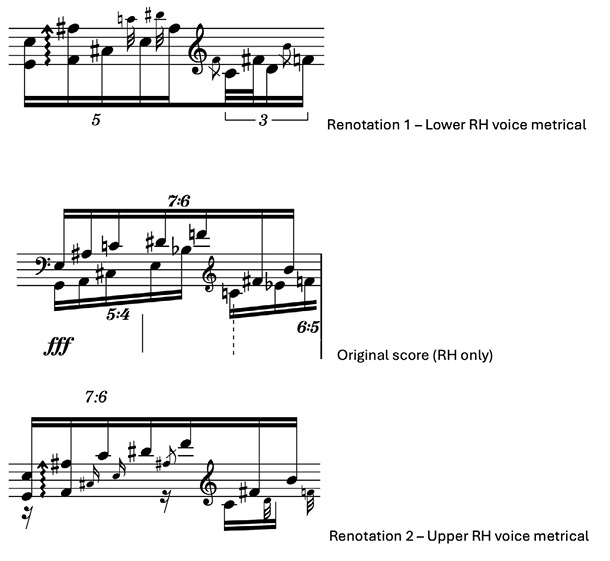
Fig. 19.8 Two possible renotations (right hand only). Reset in Dorico by author.

Looking at the beginning of this passage again, we have two possible renotations. For the sake of clarity, we will focus on the right-hand part only. There are two possible renotations depending on which layer of the right hand we choose to be metrical. In the middle we have the original notation, with the two alternative notations above and below. In the renotation above, the lower voice (5:4) is metrical and the upper one is translated to grace notes; the lower renotation takes the upper voice 7:6 as metrical and translates the 5:4 to grace notes.

The preference for one of these two versions is less clear-cut and would often involve contextual performance considerations. For example, in most cases we might find a renotation that preserves the metric identity of the faster moving voice to be more intuitive. In most cases, it is best to take a faster moving layer as metrical one, since it is easier to accurately fit in a slower series of pulsations on to a faster one than the opposite. Additionally, faster-moving layers also tend to draw more attention and are easier to entrain to, meaning listeners are more sensitive towards deviations from their isochronous values relative to deviation in slower-moving layers. On the other hand, perceptual considerations might influence this; for example, in case a slower moving layer is set in a register that helps segregate it from the texture, making listeners more sensitive to its isochrony.

Fig. 19.9 Other strategies used. On the left side, the 4:5 polyrhythm is converted to a composite attack pattern using LCM-based respelling. On the right, a similar integration into a composite pattern in which a subdivision of the upper voice approximates the position of the third note in the lower voice. Reset in Dorico by author.

Two other strategies used here should be mentioned in passing: a) Some attack points can be rounded off to a subdivision of a polyrhythm in one of the metrical layers, as can be seen on the right, with the lower voice assimilated into the upper polyrhythm; b) Some polyrhythms can be translated into a composite attack pattern, as in the 4:5 in the left hand towards the end of the passage. In both cases, the principle is the integration of different rhythmic layers into a composite attack pattern.

Finally, the choice of renotation should make sure to preserve details in rhythmic layers that contribute to the macro identity. Looking again at Walk 3, we noted the abrupt bump in Voice D to a higher speed towards the end of the passage as a unique feature of this Walk. Accordingly, the renotation should preserve the metric identity of this voice to avoid obscuring this feature.

Fig. 19.10 Final renotation of Walk 1, Mists, measures 9–11. Renotation (above) followed by measures 10–11 in the original score (below). Reset in Dorico by author.

I think this renotation offers some immediate benefits compared to the original. The introduction of metric hierarchy facilitates learning and allows the performer to read the passage in more conventional way. It is also possible to read the approximate composite rhythm without being dependent on the extremely small differences in graphic spacing. In addition to conveying the composite rhythmic pattern more directly, the renotated score helps to divide the information in relation to physical actions (for example by highlighting points of synchronization between the hands). In this way, one could see it as a graphic representation of the embodied navigation of the score, as described for example by Antoniadis.9

As a data-compression strategy, this renotation results in loss of information; only two of the four layers have preserved a precise definition, while the other two have become approximations and fail to convey their isochrony. However, we can see this as a practice and learning strategy rather than a replacement of the original score. While the renotated score loses some fine detail, it was the excess information in the original notation that led performers to informal approximations and unconscious normalization of rhythms. At the same time, the new score also adds useful information as a script for performance. In a sense, it spells out the mental process that performers would otherwise leave unarticulated.

A second problem is less obvious: the renotation can skew the dynamics by emphasizing the rhythmic layers. Attacks that fall on the beats tend to be emphasized, owing both to habits associated with traditional Western tonal music and to the connection between metric entrainment and sensorimotor performance.10

The loss of isochrony is less crucial than it seems, due to the fused nature of texture in this passage. The proximity in register and the uniform timbre between voices cause a destructive interference that prevents the perception of separate isochronous voices even in a perfectly timed computer performance. It is important to note that this is a highly contextual issue, and that in cases that allow entrainment to one of the layers, distorting the isochrony of each layer becomes much more problematic. For example, if each rhythmic layer articulated a single pitch or unique timbre, this could result in the perception of polyphony individual voices and improve our sensitivity to inaccurate performance. However, in this case both the decreased isochrony and dynamic skewing can be counteracted by conscious practice, or by switching back and forth between different versions of the score and choosing to focus on a previously neglected rhythmic layer.

The most significant issue with this renotation strategy is its time-consuming character when done by hand. The process could be automated using software that outputs symbolic notation, such as OpenMusic or Max/MSP’s Bach package. This would offer the further advantage of having variable resolution for the quantization, from very crude approximations (which might be useful early in the learning process) to finer ones as goals for final performance.

Renotation of Stochastic Clouds

As Squibbs notes, Mists also contains two other types of textures in addition to the continuous random walks of the opening pages.11 The second texture type to appear is arborescences, characterized by branching pitch structures, which first appear in measures 14–16 and then in two subsequent variants in measures 22–4 and 28–30. In contrast to the independent rates of each voice in the opening, this first group of arborescences “snaps” to a thirty-second-note rhythmic grid and presents no special rhythmic challenge for performers. Later arborescences, however, make use of the polyrhythmic writing of the opening and once again present extreme complexity, which can be addressed in the same way through renotation as the opening materials discussed above.

The last type of texture is discontinuous random walks, or stochastic clouds, which dominate the majority of the piece and give it its name. The random walks are discontinuous in both pitch and rhythm; unlike the previous figurations, they do not feature any isochronous attacks or metric organization, but only changes in rhythmic density and range of pitches in each cloud.12 For the sake of clarity, Xenakis chose to notate these without metric values, with the notes placed spatially inside a sixteenth-note rhythmic grid for orientation instead.13

Interestingly, this notation presents performers with the opposite situation from the opening polyrhythms. While the former presents performers with too much information and requires some simplification and selective removal of rhythmic definition, the latter presents too little information, making it difficult for performers to learn and retain. In this case, it is advantageous to insert some rhythmic organization, particularly in higher density situations, where a notated rapid succession of slightly asynchronous attacks can be substituted with a (synchronous) rhythmic subdivision which approximates it closely. Although this strategy risks introducing more rhythmic regularity than the spatial notation suggests, it can help performers approximate the changes in density, which are perceived as an average that changes over longer time stretches of a few seconds.14

Fig. 19.11 Renotation stochastic cloud, Mists, measures 66–8. Reset in Dorico by author.

Once more, this strategy sacrifices some rhythmic detail by simplifying highly irregular, infinitesimally differentiated attack patterns in order to make it possible to convey the macro process of entire passages, such as changes in density and degree of irregularity between successive groups. In this particular case, the differences between an ideal asynchronous version and a live performance of the synchronous renotation are miniscule, especially considering the possibility that a human performer adds some small degree of randomness to the timing in a performance.

To review briefly the renotation methodology: the first step was to identify the source of difficulty, and then as a second step to define the perceptually salient characteristics that need to be conveyed. The third step was establishing limits to the precision and complexity that performance should aim for, based on both the performer’s limitations as well as listeners’ sensitivity threshold. With these perceptual considerations used to define the rhythmic grid, the rest of the renotation proceeds, based on practical considerations to choose which layers to define metrically and which to approximate.

The overwhelming amount of information in the original score of measures 9–11 leads performers to simplify it by normalizing some of the IOIs, resulting in more regularity than there should be. By contrast, in the renotated score, the deliberate loss of some information inserts a certain amount of noise into the rhythmic performance, which guarantees irregularity. In other words, in this case it might be better to replace the noise generated by an approximate reading of a complex and precise score with a noiseless realization of a score that has some noise (or rhythmic approximation) already built into it. This can be seen as abandoning the high modernist ideal of performance as “noiseless” transmission15 and replacing it with a model that recognizes the limitations of live performers and listeners alike. In the case of Xenakis, the introduction of some additional rhythmic noise seems well within the composer’s aesthetics.

References

ANDREATTA, Moreno (2020), “On Two Computational Models of the Pitch-Rhythm Correspondence. A Focus on Milton Babbitt’s and Iannis Xenakis’s Theoretical Constructions,” Gegliederte Zeit, no. 15, Jahreskongress der Gesellschaft für Musiktheorie Berlin 2015, https://hal.science/hal-03031219

ANTONIADIS, Pavlos (2011), “Physicality as a Performer-specific Perspectival Point to I. Xenakis’s Piano Work: Case Study Mists,” paper presented at Proceedings of the I. Xenakis International Symposium 2011, 1–3 April.

BARTHEL-CALVET, Anne-Sylvie (2020), “Categories of Rhythmic Organization in Xenakian Textures,” Gegliederte Zeit, no. 15, Jahreskongress der Gesellschaft für Musiktheorie Berlin 2015, p. 260.

BRESSON, Jean, AGON, Carlos, and ASSAYAG, Gérard (2011), “OpenMusic—Visual Programming Environment for Music Composition, Analysis and Research,” in Proceedings of the ACM Multimedia Conference and Co-Located Workshops, New York, Association for Computing Machinery, p. 743–6, https://doi.org/10.1145/2072298.2072434

COX, Franklin (2002), “Notes Toward a Performance Practice of Complex Music” in Claus-Steffen Mahnkopf et al. (eds.), Polyphony & Complexity (1st ed.), Hofheim am Taunus, Wolke Verlag, p. 70–132.

DUNCAN, Stuart Paul (2010), “To Infinity and Beyond: A Reflection on Notation, 1980s Darmstadt, and Interpretational Approaches to the Music of New Complexity,” Journal for New Music and Culture, vol. 7, http://www.searchnewmusic.org/duncan.pdf

FERNEYHOUGH, Brian (1981), Lemma-Icon-Epigram for solo piano (score EP7233), London, Peters Edition.

GIBSON, Benoît (2022), “The Use of Stochastic Distributions in the Instrumental Works of Iannis Xenakis: Between Chance and Intuition,” in Anastasia Georgaki and Makis Solomos (eds.), Centenary International Symposium XENAKIS 22. Lectures Workshops Concerts, Athens, Spyridon Kostarakis, p. 1–14.

HIRSH, Ira J. (1959), “Auditory Perception of Temporal Order,” The Journal of the Acoustical Society of America vol. 31, no. 6, p. 759–67.

LONDON, Justin (2002), “Cognitive Constraints on Metric Systems: Some Observations and Hypotheses,” Music Perception, vol. 19, no. 4, p. 529–50.

LONDON, Justin (2012), Hearing in Time: Psychological Aspects of Musical Meter, Oxford, Oxford University Press.

SCHICK, Steven (1994), “Developing an Interpretive Context: Learning Brian Ferneyhough’s Bone Alphabet,” Perspectives of New Music, vol. 32, no. 1 (Winter), p. 132–53.

SQUIBBS, Ronald (2002), “Some Observations on Pitch, Texture, and Form in Xenakis’ Mists,” Contemporary Music Review vol. 21, no. 2–3, p. 91–108.

VARGA, Bálint András (1996), Conversations with Iannis Xenakis, London, Faber and Faber.

XENAKIS, Iannis (2006), Xenakis Edition 4—Piano Works, Aki Takahashi, piano (CD mode 80), New York, Mode Records, https://moderecords.com/catalog/080xenakis/ and https://iannisxenakis.bandcamp.com/album/xenakis-edition-4-works-for-piano-mode80

XENAKIS, Iannis (1992), Formalized Music: Thought and Mathematics in Music, additional material compiled and edited by Sharon Kanach (rev. ed.), Stuyvesant, New York, Pendragon.