23. Polytropos: Iannis Xenakis, Engineer in Music and Architecture
Panayotis Tournikiotis
© 2024 Panayotis Tournikiotis, CC BY-NC 4.0 https://doi.org/10.11647/OBP.0390.25
Iannis Xenakis’s contribution to architecture uniquely intertwines the work of Le Corbusier (1887–1965) with his own musical explorations. However, it has a special experimental dimension, combining morphogenesis with structural design and construction. His contributions are created, not born, and seek a cosmic relation with the earth. Starting from his civil engineering studies in Athens, he developed a mathematical thinking that fertilized the morphological search of Le Corbusier and gave an unprecedented material and spiritual dimension to buildings that are now landmarks and part of the world cultural heritage. He was equally creative in music and in the creation of spatial events that linked music and architecture. Xenakis was a polytropos: a “much-traveled” man, like Odysseus, resourceful and inventive, a traveler to unknown seas.

Fig. 23.1 Xenakis in front of the School of Civil Engineering, National Technical University of Athens, in 1945. National Technical University of Athens—School of Architecture, CC BY-NC-ND.
Engineer
Xenakis studied at the School of Civil Engineering of the National Technical University of Athens (Polytechnic University) from 1940 to 1947.
This was a school that was very advanced in the studies of reinforced concrete. Not many documents from his studies have survived. However, there is one that he kept throughout his life, likely because it held great importance to him and to the computational shaping of his thinking. It is a graphic calculation of a productive reinforced concrete beam with a single connection, on the left side only.
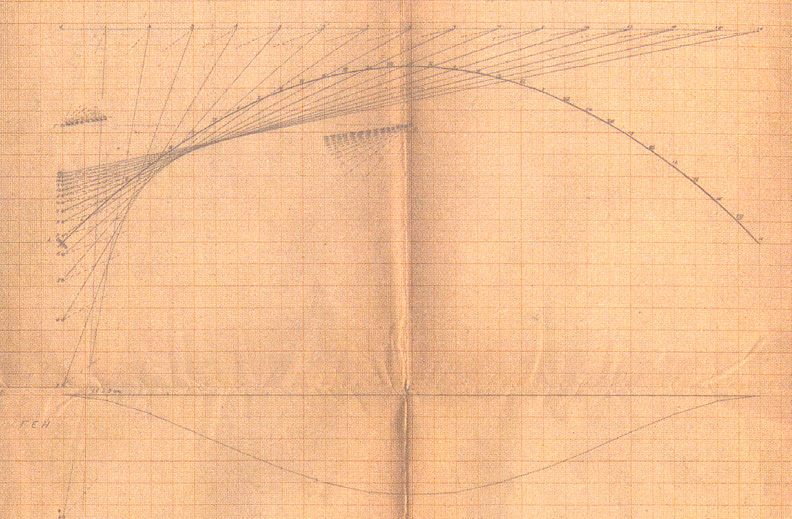
Fig. 23.2 Detail of a drawing of graphic calculation during Xenakis’s studies at the School of Civil Engineering, Athens, signed 16 January 1947 (excerpt, Olivier Revault d’Allonnes, 1975, p. 44).
It is a parabolic arc, a graphical and not a mathematical solution of the calculation. Xenakis had a great love for mathematics, but here he solves his problem graphically and uses an approach on millimeter paper that is typical for the time. This is the approach of a civil engineer drawing with Cartesian coordinates on a piece of paper divided in millimeters. The architect’s approach is inherently different because he is working on transparent paper with no reference points.1
The Atelier of Le Corbusier

Fig. 23.3 Xenakis and Le Corbusier at the Atelier, 35 Rue de Sevres, 1951. Courtesy of Fondation Le Corbusier.
Xenakis received his diploma in June 1947 and made sure that in July of the same year he obtained an official translation in French, clearly intending to leave immediately for France. He had to enlist in the army compulsorily in July, but he managed to escape to Paris and joined Le Corbusier’s atelier at the end of 1947. Of course, he was convicted of desertion. Le Corbusier was famous among architects from the 1930s. Graduates of the School of Architecture of Athens had gone to work in his atelier immediately after their studies in 1930, and Le Corbusier came to Athens in 1933. He gave the lecture “Air, Sound Light” in front of the School of Architecture in the framework of the 4th International Congress of Modern Architecture. Several of the students who heard him then left civil war-torn Athens for Paris in 1945, and some of them joined Le Corbusier’s atelier. George Candilis (1913–95) and Aris Provelengios (1914–99), for example, were both architects, but Stelios Moussiopoulos (1921–2003) and Nicholas Hatzidakis (1920–2004) were civil engineers. By 1945, Le Corbusier had begun to undertake major projects, and one of the first was the Marseille apartment block (Unité d’habitation de Marseille), where civil engineers were needed for the complex reinforced concrete calculations.2 Xenakis, who had just graduated, was immediately involved with the Marseille project, contributing to the construction as a civil engineer, and he was mainly employed this way, as part of the ATBAT (Atelier des Bâtisseurs or “Builders” Studio), a sort of subsidiary created by Le Corbusier for the housing project commissions he was receiving from the French Ministry of Reconstruction following World War II. Nevertheless, during his entire time in Le Corbusier’s atelier, from 1948 to 1959, he worked systematically on various projects.
Le Corbusier kept a systematic record of what he commissioned, noting whom he assigned them to and when he received the results. For instance, Xenakis was commissioned by him on 28 February 1952, with sections for the Chandigarh High Court. Much later, in 1956, he was involved with drawings in the Chandigarh project, the Philips Pavilion, the Firminy Cultural Center, and the Baghdad Stadium. In a very interesting certificate, obtained in July 1958, Le Corbusier confirms that Xenakis has been employed at the Atelier since 1948:
[…] in the capacity of architectural-engineer, head of studies. His attitude since then has been that of a perfect and indispensable collaborator, always very assiduous in his work, taking on ever-increasing responsibilities for which the direction [of the atelier] has long given him its full confidence, given his high professional abilities and scrupulous honesty.3
It was therefore a long collaboration in which architecture and the art of engineering were intertwined, while Xenakis was truly trusted by Le Corbusier.
Xenakis’s first major contribution to Le Corbusier, however, was not in building but in theory. Xenakis’s interest in mathematics, the golden ratio, and mathematical series, especially the Fibonacci sequence,4 met Le Corbusier’s interest in a global system of harmony in architecture based on man. Xenakis elaborated many of Le Corbusier’s investigations contained in the Modulor,5 but he does not sign them because he is just a collaborator in the atelier and, like all collaborators, he contributed to individual areas of an investigation that was a complex collective work. References to Pythagoras (ca. 570–500/490 BCE) and Plato (428/7–348/7 BCE) link music with architecture, seeking a harmony that transcends them, claiming a cosmic relationship. The Fibonacci sequence develops in the Modulor the relationship of the golden ratio to a spiral ascent following a red and a blue scale. Each step produces a dimension that is harmonious in relation to all the others, and at the same time different from all the others. That is, all elements differ from each other but are, at the same time, connected by a common rule. They harmonize following another kind of order. In Le Corbusier’s mind, this starts with the average height of a human being, centered on the navel, and a series of data that harmonize and produce the overall work of art that is the Unité d’habitation of Marseille, and then other works in which dimensions are likewise harmonized. Of course, you cannot see this harmony. It is not obvious. It is something inherent that gives a reason to architecture, but is lost in mind and matter.
Chandigarh
During these twelve years, Xenakis worked on many projects, some more and some less important. I will mention three of them, to shed light on his participation in Le Corbusier’s atelier, which I think was mutually important for both Xenakis and Le Corbusier. The first is the Parliament of Chandigarh. Le Corbusier undertook a gigantic project, an entire city with an administrative center, the Parliament, High Court and more, in the newly independent India. His aim was a symbolic work that could express the modernity that India was then striving for vis-à-vis the Western European world. The Parliament was built on almost deserted land, from which it emerges as a geometric form of sculptural reinforced concrete. A pyramid dominates the top of the roof, alongside a strange hyperboloid structure, which is inexplicable at first glance.

Fig. 23.4 The Parliament of Chandigarh (c. 1959). Courtesy of Fondation Le Corbusier.
Le Corbusier had told Xenakis that, while flying over Ahmedabad, India, to go to Chandigarh, he had seen a nuclear power station that was just being finished, with reinforced concrete towers, built to cool the decay of the atom.6 From this was born the idea that the great hall of democracy in the Parliament should receive the cosmic light through a hyperbolic release to the sky to illuminate the representatives of the people. Xenakis undertook to support this peculiar solid on a horizontal plate. It was not at all simple to define and calculate such forms at that time. Xenakis followed an experimental method that had been tested in civil engineering laboratories, constructing a scale model that accepts loadings and allows a proportional sizing of the real structure. Surviving photographs of this model show the young Xenakis clearly contented alongside the mature Le Corbusier.

Fig. 23.5 The model of the hyperboloid on the roof of the Parliament of Chandigarh. The last picture in the series shows Le Corbusier with Xenakis (c. 1956). Courtesy of Fondation Le Corbusier.
Xenakis worked systematically to calculate, in geometric terms, the shape of this solid. He developed the model and made large drawings, which are signed “dessiné par Xenakis” (drawn by Xenakis).

Fig. 23.6 Detail of the drawing 5451 for the Parliament of Chandigarh, “dessiné par Xenakis” 5-11-1956. Courtesy of Fondation Le Corbusier.
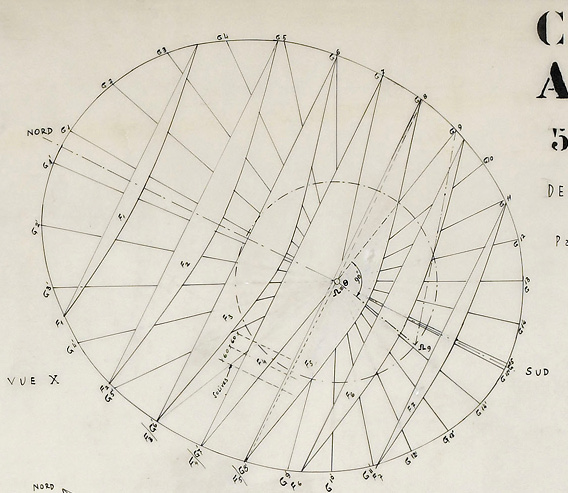
Fig. 23.7 Detail of the drawing 5451 for the Parliament of Chandigarh, 5-11-1956. Courtesy of Fondation Le Corbusier.
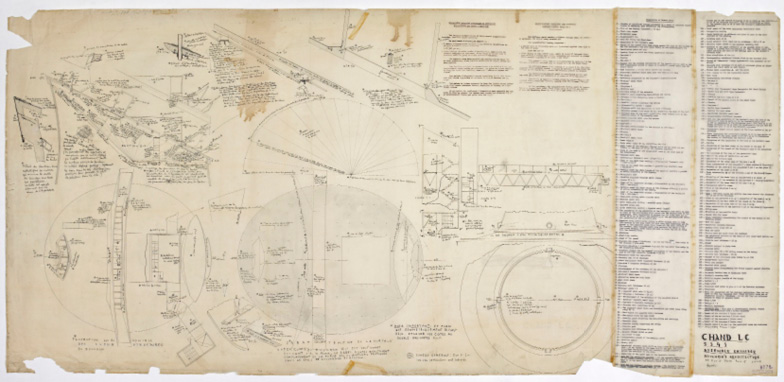
Fig. 23.8 The Parliament of Chandigarh, drawing 5545, signed Xenakis, 6-12-1957. Courtesy of Fondation Le Corbusier.
It was not easy to build the glass barrier on the roof of the hyperbola. Xenakis was also asked to design and calculate the metal trusses that were necessary to meet the technical problem. Looking at the details, we realize that there are dynamic proportions, which follow the square root of two or the golden ratio, and produce increasing spirals and ellipsoidal forms. The design includes the calculation of the structural reinforcement. That was Xenakis’s job in the office. However, something else is particularly important: Xenakis does not simply consider how a particular concrete form will stand; he draws the form following the diagram of the static function and gives computational form to the building. Xenakis was deeply involved in the construction of these complex and innovative forms, which were unprecedented in large public buildings. While his signature is certainly on all the drawings he undertook, there is no doubt that these drawings, numbered Chand LC 5451 or 5545, relate to Le Corbusier’s Chandigarh project. Though this was a collective work of Le Corbusier’s atelier, these specific drawings can be attributed to Xenakis’s contributions.
La Tourette
The second project is the Couvent Sainte-Marie de La Tourette, a Dominican monastery in which Xenakis played a leading role as “project manager.”7 In Chandigarh, he had not concerned himself with the overall work but mainly with one feature at a time, such as the hyperbolic roof. At the convent of La Tourette, Xenakis took pride in his approach to the work of the Dominican monks, a centuries-old lineage rooted in the Middle Ages and scholastic thought. This form of scholasticism has deep philosophical roots and differs from the contemporary understanding of the term. In its Dominican version, it links Christianity with ancient Greek philosophy, Aristotle (348–322 BCE) or Plato. Xenakis’s contribution to the monastery is mainly known because he undertook the design of the glazing on the large horizontal glass panels on the façade of the building, called “pans de verre ondulatoires,” i.e., undulating glass panes.8

Fig. 23.9 The Dominican monastery of Sainte-Marie de La Tourette (1954–60). On the right, undulating glass walls; to the left, the curved volume and the “light cannons” that bring light into the crypt. Photo by author (1999), CC BY-NC-ND.
In these glazing units there are vertical and horizontal dividers defining the dimensions of the rectangular windows without it being clear how. In fact, Xenakis applied Fibonacci’s mathematical sequence, which is the basis of the Modulor. The distances between the separating elements are calculated so that there are no two panes with the same dimensions, but all dimensions are harmonized with each other, that is, well-tempered. This produces a chaos that is orderly and mathematically calculated as a whole. Xenakis also designed the internal routes, in which you move around within glass walls on the right or left, following the same principle. When you walk through the corridors you are struck by the complexity and variation of forms, and the changing dimensions of the vertical and horizontal elements, in which develops the geometry of the common harmonious rule. At this time, he also composed Metastasis (1953–4), which is in a way the musical expression of his architectural discourse.
Looking through the glass walls, into the courtyard, there is a cube of bare, reinforced concrete on which sits a pyramid. It is a chapel.

Fig. 23.10 The oratory in the courtyard of the monastery of Sainte-Marie de La Tourette. Photo by author (1999), CC BY-NC-ND.
At the edge of the cube there is a slit, like a black line, through which, alone, natural light enters the interior. Quite conversely, the inner edges that are blind are accentuated with thin bright lines of colored neon. It is worth keeping this illuminating intervention in the space of prayer in mind for the later discussion of polytopes and the relationships between space, time, and light in music and architecture.
The La Tourette project was a crucial turning point in Xenakis’s career as an architect, for an additional reason. During construction, André Wogensky (1916–2004), the architect and manager of Le Corbusier’s atelier, delegated responsibility for the project and communication with the Dominican monks to Xenakis. Consequently, in 1956, Xenakis became responsible for the entire project and supervised the construction on site. He thus became a decisive collaborator of Le Corbusier.
In the church of the monastery, one of the most impressive places I have entered in my life, there is a crypt to the left of the holy altar and a red sloping surface to the right. The crypt, one level below the holy altar, extends outside the rectangular prism of the building, defining a curved volume in the shape of a grand piano’s tail, with three conical forms on its roof, the “light cannons,” designed to bring natural light into the small chapels of the crypt where the monks go to worship. The interior of the conical forms is brightly colored in Le Corbusier’s primary colors, which tint the natural light, giving a cosmic dimension to the sanctity of the monastery.

Fig. 23.11 The conical forms bringing colored light in the crypt of the monastery of La Tourette. Photo by author (1999), CC BY-NC-ND.
To the right of the altar, the sloping surface is red, while the rest of the church’s surface, which is of bare concrete, is dark grey. Above the red surface there are seven light collectors, the ‘machine guns’, that bring in the sun and are tuned so that the sun completely covers the surface at the two equinoxes.

Fig. 23.12 The sloping surface in the church bringing red light to the holy altar. Photo by author (1999), CC BY-NC-ND.
The red then spreads and fills the whole area of the holy altar. The scene could refer to the Apocalypse. Remember that there is blood in this story, which has a deeper symbolic meaning.
Let’s leave metaphysics inside the church and go to the roof. There is, of course, no reason to go to the roof, but if you get there you will find an extension of the staircase, a “stairway to heaven:” a rectangular prism, with openings that combine horizontal and vertical elements in an order that we cannot clearly define.

Fig. 23.13 Stairway to heaven: the neume of the window οn the rectangular prism offering access to the roof of La Tourette. Photo by author (2003), CC BY-NC-ND.
It seems incomprehensible. For Xenakis it is a neume in French, from the Greek word νεύμα, which means “nod” or “sign.” The neume refers to the harmony of Gregorian music, which predates classical harmony. The neumes, which are motions of the head, eyes, and eyebrows, become symbols of ascent and descent, which are written over the words to indicate the melodic curve and later evolve into notes of a four-line musical notation. Xenakis implies a melismatic relationship between the interior and the cosmic space, dependent on sunlight, which is subject to a neume. Turning our gaze to the other side of the terrace, we discover another symbolic geometry, a pyramid.

Fig. 23.14 A garden of symbolic geometry on roof of La Tourette. Photo by author (2003), CC BY-NC-ND.
One does not see it, nor the sculptural forms and the staircase that are organized in total harmony. Only God sees them. No one else.
Philips Pavilion
The third building I will refer to is the Philips Pavilion at the Brussels World’s Fair in 1958, which was commissioned by Le Corbusier, who chose Xenakis as his main partner, and which ultimately became the apple of discord between them. The design is primarily due to Xenakis, who devised a parabolic hyperboloid to define thin, shelled, reinforced concrete surfaces. The graphic design of the form is the same as the graphic design of the static structure, so that the form and the static function form a single system. However, construction difficulties did not allow the implementation of the initial design, which was done conventionally with prefabricated slabs on a load-bearing metal frame.9
In order to refine his conception, Xenakis resorted to mathematical objects and sought an overall harmony. A platonic polyhedron is hung inside the pavilion as a dominant element of its architecture. Of great interest are the patterns of rotation of the planes to produce the curved surfaces of the parabolic hyperbola on the base of straight lines. Indeed, in each point of the composite curve rests a straight line. However, what is complex is at the same time as simple as its graphical representation.

Fig. 23.15 The Philips Pavilion, detail of the drawing 5439, “dessiné par Xenakis,” signed Le Corbusier, 19-10-1956. Courtesy of Fondation Le Corbusier.
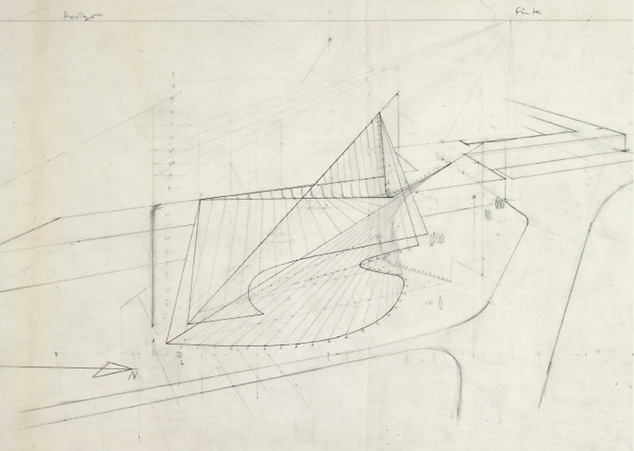
Fig. 23.16 The Philips Pavilion, detail of the drawing 5439, 19-10-1956. Courtesy of Fondation Le Corbusier.
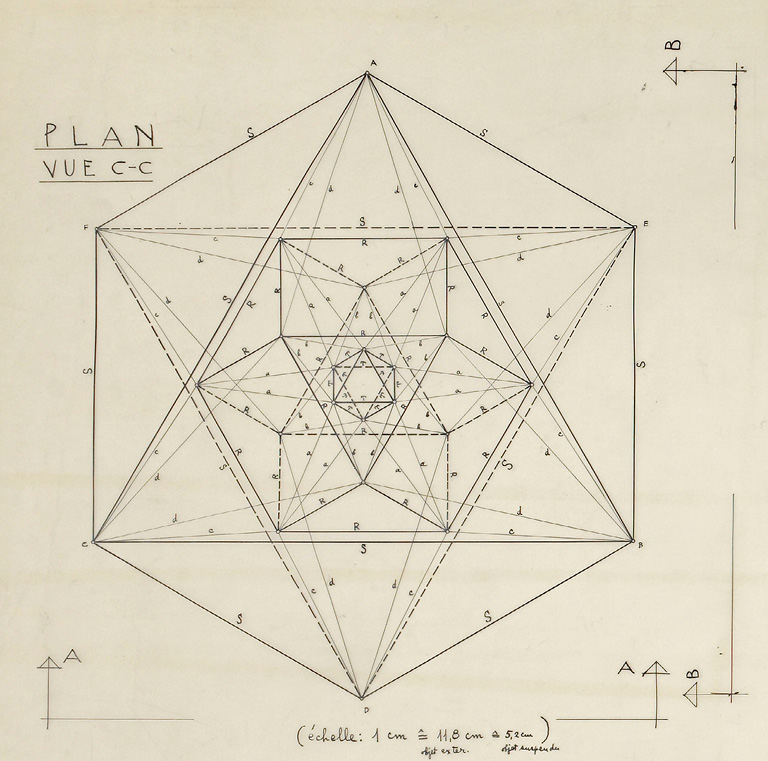
Fig. 23.17 The Philips Pavilion: mathematical object. Detail of the drawing 5547, 3-3-1958. Courtesy of Fondation Le Corbusier.
Inside the pavilion a multimedia event was organized, i.e., an early polytope, the Poème électronique (1957–8) (or Electronic Poem) to music by Edgard Varèse (1883–1965), but at the entrance and exit you could hear Xenakis’s Concret PH (1958), developing “nuages de poussière de sons” (clouds of dust of sound). PH stands for [p]araboloid [h]yperboloids and for [Ph]ilips; concret for reinforced concrete and musique concrète. The cloud of Xenakis’s concret sounds, the sound of smoldering coals, is a disorder that has another kind of order.
The Philips Pavilion period was, however, difficult for Le Corbusier’s relations with Xenakis, as well as for Le Corbusier’s relations with the other partners in the atelier. No doubt, Le Corbusier was growing up as well. In a very interesting, handwritten note entitled “Xenakis’s personal expenses,” that was sent by Xenakis to Le Corbusier on 11 February 1957, he writes to him:
[…] for rent, for food, for the maintenance of my father who is seventy-nine years old, for taxes, and for laundry, there is no money for more clothes, for books, for my wife and for my daughter. I am forty years old.
Le Corbusier replies to him in handwriting also just below:
[…] forty years old? What do you think I did when I was forty? I was trying to build the building of the League of Nations. Nobody was paying me. I had nothing to eat; I lived in a room with no bathroom and no running water. How do you think things are done?

Fig. 23.18 An informal exchange of complaints between Xenakis and Le Corbusier, 11 February 1957. Courtesy of Fondation Le Corbusier.
Le Corbusier kept it, and that is how we can read it today, but we do not know if Xenakis ever got that answer. Nevertheless, this is a father-son fight, not an employer-employee dispute. Then, of course, things took a different turn, about which much has been written. Xenakis received on 31 August 1959, a letter from Le Corbusier, which for me is lovely because it expresses both sincerity and appreciation, with which Xenakis was fired. It is extremely interesting to read this letter, but it is equally noteworthy that a similar dismissal letter went to the entire office. Le Corbusier fired them all! He no longer wanted to have an atelier with associates. He had other things on his mind. He wrote:
Dear Xenakis. Modern architecture in France has triumphed; it has finally been adopted. Now, it is possible for you to find new fields to apply what you have learned by yourselves, as well as what your work with me has brought you. I believe it behooves each of you to take advantage of any opportunity that arises or that you may induce. Therefore, I hereby render you free as of September 1, 1959.10
This letter has often been seen as an unfair rejection of Xenakis by Le Corbusier at a time when Xenakis was actually responsible for Le Corbusier’s architecture. I would not see it that way. For Le Corbusier it is an end, and for Xenakis a new beginning. Xenakis was born in 1922 and Le Corbusier in 1887. When Xenakis arrived at Le Corbusier’s atelier in 1947, he was twenty-five years old and Le Corbusier was sixty, world famous, and important. When Xenakis left the office in 1959, the age difference remained. Le Corbusier was seventy-two and Xenakis was thirty-seven. The difference was great, and was more akin to the distance between a father and a son than it that of a teacher and a student. Le Corbusier passed the baton and began the struggle to establish the Le Corbusier Foundation to protect his work, concerned with its future legacy. For Xenakis, this marked a pivotal moment as he shifted his focus towards music.
Music
I will not go into the depth of the relationship between music and architecture, as those deeply involved in music are likely more versed in this connection. Instead, I will revisit my starting point: the drawing of a parabolic arc on millimeter paper, a task essential in civil engineering but typically outside the architect’s scope. Xenakis began to write music, starting with Metastasis, using graphics and parabolic arcs on millimeter paper, when he was working at La Tourette. In fact, the way in which he develops the drawings of his music on standard graph paper is analogous to the curves that define the calculation of reinforced concrete, and the form of the buildings he designed for Le Corbusier.11
He was an engineer in music. He reasonably had many doubts about these musical drawings, and so one day, he recounts, he took a pile of papers and went to Hermann Scherchen (1891–1966), a famous French/German musician of the time, to show them to him and ask if they were worthwhile. He describes the scene in detail, but what is significant is that Scherchen tells him, “I’m interested in your music because it’s made by someone who comes from outside of music.”12 Similarly, one could argue, substituting architecture for music, that the architecture Xenakis created “came from outside of architecture.” He did not use the tools of an architect’s education; he used other tools, with which he gave form to the materials. He was an engineer in architecture. Thus, Xenakis’s music and architecture have a very important element in common. They develop beyond their field, and there they meet because they eventually develop in the same way, by the same mind, with the same approach, gradually escaping into a constant search for order in chaos, as clouds are organized. Of course, a cloud has a form. As do even sound and light.
Cosmos
The Cosmic City is the design of a utopian city. It is due to an initiative of Françoise Choay (b. 1925), who was compiling a book in the early 1960s about utopias and realities in urban planning, and commissioned Xenakis to design a utopia, i.e., to imagine how we could live in the distant future.13 Xenakis called this city “la ville cosmique” (Cosmic City). The word cosmique refers to the philosophical concept of cosmos, which is the universe, and indirectly to the philosophical ideas of Kostas Axelos (1924–2010), another Greek who left Athens like Xenakis, and was linking the future of the cosmos to pre-Socratic philosophy.14 Xenakis’s Cosmic City consists of giant parabolic hyperboloid buildings in a meadow landscape that remains essentially intact. The buildings, like skyscrapers, were meant to disappear into the clouds, as he describes in the text accompanying the drawing. It is hard not to remember the utopia of the city of birds, that is Aristophanes’s (450–388 BCE) city-in-the-sky, or literally ‘cloud-cuckoo-land’ (Νεφελοκοκκυγία). At the top right of a drawing by Xenakis of his Cosmic City is a black star.15 I cannot say for sure if it is the moon or the sun, but we are up high, and underneath, grows a land that is a utopian return to nature, a meadow. I will revisit the meadow later on discussing the myth of Eer in Plato’s Republic. In the meantime, let us keep in mind that Xenakis was not content with a text and drawing for Choay’s book. He spent a lot of time calculating the giant towers of his Cosmic City, reminiscent of the hyperboloids of the nuclear towers he was inspired from in Chandigarh, the parabolic hyperboloids of the Philips Pavilion, the graph-based design of his music and architecture.
Polytopes
Around 1970, Xenakis, definitely free from Le Corbusier, becomes increasingly involved in something that is again beyond music. He designs sound, light, color, and space during live performances. The Polytopes are installations in Montreal (1967), Paris (Cluny 1971–2), Persepolis (1971), and Mycenae (1978), while the Diatope (1978), in Paris, is developed as an “offspring” of the Philips Pavilion event some twenty years earlier, with light and sound effects in special viewing conditions for spectators, who lie down and experience a cosmic event. The Diatope was an ephemeral tense form that followed the principles of the Philips Pavilion on flexible surfaces.16

Fig. 23.19 Xenakis, A Gesture of Light and Sound, the Diatope. Centre Georges-Pompidou, Paris, 1978. Scanned booklet from author’s collection.
Inside the Diatope, an event was held: La Légende d’Eer. Eer is a mythical hero, in the last part of Plato’s Republic (614–616), who has experienced what happens when you die. After death, there is a court: there are the righteous who go to the meadow, and the unjust who go to the Tartarus. Plato explains how all this happens; the most striking detail is that in the meadow, a grassy place like paradise, where souls are gladly encamped as at a festival, there are rays of light that connect the ground to the sky and other flares, giving, with their colored light interference, a lightning version of paradise. In addition, eight Sirens stand in a rotating circle, emitting sounds to create the symphony of a single harmony. The use of lasers in Xenakis’s polytopes is part of this modern yet metaphysical approach, with many flashes, flares, and sounds that rival the stars and the Sirens.
The Polytope of Mycènes in the summer of 1978 was a transgression of the myth of Eer in the world of the Atreides. Those who experienced it can recount the convergence of masses of spectators amid prehistory and myth, ruined antiquities, goats, and sheep in the midst of a hot summer landscape, full of laser lights, percussion, and computer sounds. It is impossible to reproduce this unique event. Xenakis introduced the electroacoustic sound of Mycènes Alpha, a composition that converts hand-generated graphics into music with the help of a computer. To make that happen, he invented a horizontal surface engraved with the Cartesian geometry of millimeter paper, on which a stylus or a hand moves to produce music. The music is produced by the movement of the hand on a drawing surface, such as an architectural drawing board, and this movement makes the gesture graphical and transcribes it into sounds.

Fig. 23.20 Iannis Xenakis in Salzburg with UPIC (Centre Acanthes, 1985). Photo by Henning Lohner, courtesy of CIX Archives, Lohner collection.
The machine is UPIC (Unité Polyagogique Informatique du CEMAMu, the Centre for Studies in Mathematical and Automated Music), which digitally converts graphics into sound. It marked a new era for Xenakis, but at the same time represented an impressive meeting of Mycenae with pioneering pursuits that literally go outside the field of music, outside the field of architecture; outside.
Amorgos
The house on Amorgos is one of Xenakis’s most interesting works, his only building in Greece, also constructed in his absence during the Greek dictatorship. It is a holiday home for François-Bernard Mâche (b. 1935), friend and musician, in a deserted area of Amorgos, not at all like other houses. It is a series of curvilinear volumes, randomly twisted or arranged in excessive order, which develop in space like a dice roll or a skillful gesture and, at the same time, embrace vital functions within them. The relationship between inside and outside passes through the uncommon geometry of the openings similar to those we saw on La Tourette’s terrace, with the neume coming back as an order of cosmic harmony, and indeed, a reinterpretation of the relations between inside and outside.

Fig. 23.21 Xenakis, holiday house in Amorgos, 1966–77. Photo by Elina Loukou (2005).

Fig. 23.22 Xenakis, holiday house in Amorgos, 1966–77. Photo by Elina Loukou (2005).

Fig. 23.23 Xenakis, holiday house in Amorgos, 1966–77. Photo by Elina Loukou (2005).
What is the opening, what is the wall, what is the window? The openings are designed with mathematical relationships and dimensions, revealed depending on how and where you sit, at what height, and how your eyes see horizontally, in and out, or how the sun and moon move. The house as a periscope or observatory creates an unfolding event of cosmic harmony in the prehistoric land of Amorgos.
Corsica
Xenakis lived with his wife Françoise and their daughter Mâkhi in various apartments in Paris. Describing her relationship with her father, Mâkhi writes that every time they entered an apartment, Xenakis would change it as much as he could. He was tearing down walls, changing colors, installing tense, textile surfaces, etc… that formed spatial structures. Most interesting in these domestic architectures, however, is the way he designed a holiday home for himself, his wife, and their daughter in Corsica. The two-story, tower-like structure rests on an ellipsoidal foundation, with a peripheral development of vertical openings arranged in a mathematical order reminiscent of the La Tourette monastery. The design allows for climbing to the roof, where one can sit in the evenings and look at the stars: to be in touch with the universality of a meadow, overlooking the sea, with a kayak on the beach as a measure of freedom and escape…

Fig. 23.24 Xenakis, holiday house in Corsica, 1996–7. Photo by D. Gainet (2005).
Back Home
Although a civil engineer, Xenakis was much more appreciated in the School of Architecture of the National Technical University of Athens. Students sought him out from the first time he returned to Greece, in November 1974, immediately after the dictatorship, demanding to learn about architecture, music, and his collaboration with Le Corbusier, and the school proclaimed him an honorary doctor honoris causa on 18 September 1992, in the large hall of the main neoclassical building. In front of the same building where Le Corbusier found himself in 1933 during the 4th CIAM (Congrès international d’architecture moderne), Xenakis stood in 1944, during the civil battle of Athens, amidst the rattling of bullets that left scars on both marble and people. Against the backdrop of bright anti-aircraft fire, the sky bore witness to the first flares of the composer’s future polytopes. In awarding the doctorate to Xenakis, the President of the School, Professor Dionysis Zivas (1928–2018), proposed an interpretation of the decision, which concluded with this righteous statement:
The honor is awarded to a graduate of the Institution who, first of all, as a civil engineer initially and with the dynamics that things themselves determine as an architect later, contributed to the conception of important and well-known architectural projects and to the solution of the corresponding problems with internationally recognized success. At the same time, this honor is given to the man who opened his own, new, and personal path in contemporary music, which has also received international recognition and acclaim. The synthesis of all these different in terms of expression, but perhaps not such different constituent parts, the synthesis in other words of science, art, and technology in such an original and creative way, determines the special dimension and uniqueness of the personality and the work of Iannis Xenakis. That is the reason behind our decision. This is what bridges Xenakis: a civil engineer with music and architecture. With the whole world.17
Polytropos
Polytropos is the very first adjective and main attribute Homer (ca. eighth century BCE) applies to Odysseus in his Odyssey. Literally it means “much-traveled” or “much-wandering,” but it can be used metaphorically as “turning many ways,” resourceful, inventive and complicated, militant, creative and adventurous, a traveler to unknown seas, armed with rationalism, and driven by cosmic geometry: that of constellations. Homer, of course, intended both senses of the word. Xenakis was as polytropos as Odysseus. He was first an engineer, but he was an engineer of music and architecture, a navigator without limits, certainly free, but with a constant return to his ideal Greek origin, his eternal homeland, along with his flight into the cosmos. Polytropos and Polytopos.
References
AXELOS, Kostas (1962), Héraclite et la philosophie: La première saisie de l’être en devenir de la totalité, Paris, Les Éditions de Minuit.
AXELOS, Kostas (1964), Vers la pensée planétaire: Le devenir-pensée du monde et le devenir-monde de la pensée, Paris, Les Éditions de Minuit.
CHOAY, Françoise (1965), L’Urbanisme, utopies et réalités, Paris, Seuil.
LE CORBUSIER (1950), Le Modulor, essai sur une mesure harmonique à l’échelle humaine applicable universellement à l’Architecture et à la mécanique, Paris, Éditions de l’Architecture d’Aujourd’hui.
LE CORBUSIER (1955), Le Modulor 2, Paris, Éditions de l’Architecture d’aujourd’hui.
MATOSSIAN, Nouritza (2005). Xenakis, Nicosia, Moufflon Publications.
Pyrforos [n.a.], vol. 4, (1992), p. 114.
REVAULT D’ALLONNES, Olivier (1975), Les polytopes, Paris, Balland.
SOLOMOS, Makis (ed.) (2022), Révolutions Xenakis, Montreuil and Paris, Éditions de l’Œil and Philharmonie de Paris—Musée de la musique.
XENAKIS, Iannis (2008), Music and Architecture: Architectural Projects, Texts, and Realizations, translated, compiled and presented by Sharon Kanach, Hillsdale, New York, Pendragon Press.
XENAKIS, Mâkhi (2022), Iannis Xenakis, Un père bouleversant, Paris, Actes Sud.
1 See also Xenakis, 2008, p. 4, for another example of such a drawing.
2 See Xenakis, 2008, Chapter 1.04.
3 Solomos, 2022, p. 202.
4 The Fibonacci sequence is a sequence of numbers where each number is the sum of the two preceding numbers. The Fibonacci sequence, strongly related to the golden ratio, reflects various patterns in nature like the perfect spiral of a nautilus shell. The Italian mathematician Leonardo Bonacci da Pisa (ca. 1170–ca. 1242) who introduced the sequence to Western European mathematics in his 1202 book Liber Abaci, was nicknamed Fibonacci in the nineteenth century.
5 See Le Corbusier, 1950; 1955.
6 Xenakis, 2008, p. 22.
7 Xenakis, 2008, Chap. 1.14
8 Xenakis, 2008, Chapters 1.11 and 1.12.
9 See Revault d’Allonnes, p. 126–9.
10 Xenakis, 2008, p. 5–6.
11 See “Metastasis, partition graphique sur papier calque, OM 1/4 p.28, Coll. Famille IX DR,” Les Amis de Xenakis, https://www.iannis-xenakis.org/archives/
12 See Xenakis, 2022, p. 103; Matossian, 2005, p. 88–9.
13 Choay, 1965.
14 Axelos moved to Paris in 1945 together with about two hundred grantees of the French government, including most of the Greek architects and civil engineers whom Xenakis met in the atelier of Le Corbusier. Ηis critical thinking has been reflected in many philosophical essays, with regard to pre-Socratic philosophy and planetary thinking; see Axelos 1962, 1964.
15 See The Outpost, “IANNIS XENAKIS AND THE NOTION OF A COSMIC UTOPIA” (21 February 2018), Wilderutopia, https://wilderutopia.com/sustainability/land/iannis-xenakis-and-the-notion-of-a-cosmic-utopia/
16 Xenakis, 2008, Chapters 4.16–4.21.
17 Pyrforos [n.a.], 1992, p. 114. Pyrforos means “torchbearer” and refers to Prometheus-as-torchbearer, which is the emblem of the National Technical University of Athens (NTUA). Pyrforos was the journal of the NTUA from 1992 to 2003.
