33. Xenos: A Xenharmonic Dynamic Stochastic Synthesis Virtual Instrument

Raphael Radna

Introduction

Xenos is a virtual instrument that implements and extends Dynamic Stochastic Synthesis (DSS), a direct digital synthesis method devised by Iannis Xenakis. Xenos adapts DSS for use in contemporary computer-based composition environments; written in C++ with the JUCE framework, it offers efficiency, cross-platform compatibility, and ease of use. As a plugin, Xenos leverages host software features, such as MIDI input and parameter automation, to increase the applicability of DSS to a broad range of computer music composition and performance contexts.

Xenos also introduces a novel pitch quantization feature to DSS. While traditional DSS produces continuous pitch, Xenos can optionally be tuned to an arbitrary scale, enhancing the algorithm’s suitability to compositional styles that require fine control of pitch organization. Furthermore, the Xenos pitch quantizer can use microtonal and xenharmonic scales: any scales comprised of intervals that deviate substantially from those of the equal-tempered chromatic scale. Several scale presets are included, and it is also possible to load custom scales in the Scala format: a popular interapplication exchange standard for musical scale specification.1

In Greek, xenos means “foreigner” or “stranger.” It is one root of the term xenharmonic, meaning “foreign harmony.” Xenos was given this name as commentary on the marginal position of direct digital methods within the domain of sound synthesis, in reference to its xenharmonic quantization capabilities, and in homage to Xenakis. However, Xenos does not aim to replicate Xenakis’s compositional methods but rather to preserve and extend DSS, abstract it from any particular style of composition, and make it eminently accessible to composers engaging with diverse musical aesthetics. Xenos is therefore released as free and open-source software, with the hope that it might increase awareness and usage of this nonstandard sound synthesis technique and important part of Xenakis’s legacy.2

Background

Xenakis and Stochastic Music

At his centennial, Xenakis remains among the most influential avant-garde composers of the twentieth century. An innovator in the integration of mathematical concepts and procedures with the arts, he pioneered the field of stochastic music: the application of statistical probabilities to music composition. He employed this technique in much of his published music, including the early orchestral works Metastasis (1953–4) and Pithoprakta (1955–6), which, contrasting the prevailing serial methods of the time, he conceptualized as masses formed by the statistical means (probabilities) of independent sound events.3

From the 1960s onwards, Xenakis used computers to execute the numerous calculations required by his compositions.4 As advancements in computing surged in the late 1960s, the potential of digital sound synthesis rapidly became apparent. New computer music capabilities would, for the first time, enable stochastic procedures to touch the shortest timescales of music, inaugurating the domain of stochastic timbre generation. It is in this context that Xenakis developed a theory of the stochastic synthesis of audio waves. He published some germinal ideas in “New Proposals in Microsound Structure,” the final chapter of the 1971 edition of Formalized Music, which presents several time-domain methods of digital synthesis that use probability distributions to produce noisy, complex timbres.5 Xenakis first employed these techniques in the Polytope de Cluny (1972); later, he consolidated and developed them into the Dynamic Stochastic Synthesis algorithm, which debuted in La Légende d’Eer (1977).6

Xenakis returned to stochastic synthesis in the late 1980s. With Marie-Hélène Serra, he created the GENDY program,7 which implemented a variation of the original DSS algorithm. Xenakis used this software to compose Gendy3 (1991), a fully automated computer music composition with DSS as its only sound source. Gendy3 is arguably Xenakis’s most purely algorithmic work, as its pitches, timbres, textures, and form are all generated by software-controlled stochastic processes without intervention by the composer beyond initial parameter selection. Its low-level sonic activity and high-level formal structure are thus unified by their basis in the same theory, an important implication and attraction of stochastic composition.8

Theory of Dynamic Stochastic Synthesis

DSS is a type of direct digital synthesis: a group of techniques founded on the properties of the digital audio domain and without reference to pre-existing acoustic or perceptual models. It is a special case of breakpoint interpolation synthesis, a family of waveform segment techniques.9 In DSS, the cycle (basic recurring unit) of a quasiperiodic waveform is defined by a series of breakpoints in amplitude-time space. The waveform is produced by linear interpolation between adjacent breakpoints. When a cycle ends, it undergoes a process of stochastic perturbation in which the breakpoints are displaced by random walks. A random walk is a stateful random number generator that produces its value by adding some randomly generated “step” to its previous value. Each breakpoint represents two random walks: one each in the horizontal and vertical dimensions. The horizontal dimension affects pitch, and the vertical dimension affects amplitude; both influence timbre. The displacement of the breakpoints produces successive variations of the cycle, resulting in an evolution of pitch, amplitude, and timbre over time.

The random walks are governed by several parameters that affect the nature and degree of variation between cycles. These are the probability distribution that produces random-walk steps, such as uniform, logistic, or exponential;10 the step size, which is the maximum allowable difference between successive values of a random walk; and the elastic barriers, numerical limits that reflect excessive random-walk values back within a circumscribed range.11 The mature form of DSS, as implemented in GENDY, uses second-order random walks: two random walks in series, in which the value of the first determines the step size of the second.12

Figure 33.1 illustrates the effect of the DSS technique on a waveform. C represents an initial cycle, and C′ represents the subsequent cycle, i.e., the next iteration of the algorithm. Each contains twelve breakpoints and segments.

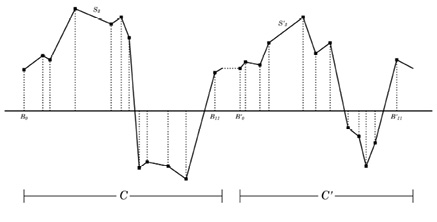
Fig. 33.1 Two contiguous cycles of a waveform generated by DSS. C′ is a variation of C, produced by stochastic displacement of the breakpoints defining its contour. Figure created by author (2024).

The cycles proceed continuously, with B11, the last breakpoint of C, leading directly to B′0, the first breakpoint of C′. However, the breakpoints shift positions between iterations, in both their horizontal and vertical dimensions, as a result of the random walks. The displacements of the breakpoints, constrained by the random-walk step sizes and elastic barriers, account for the differences in contour between C and C′. While these two cycles are clearly similar in form, the effect of random variation on local features is also apparent, e.g., in how the negative slope of segment S3 becomes positive at S′3. Additionally, a greater or lesser sum of breakpoint abscissae varies the wave period; because C′ is not as wide as C, the frequency of this wave would increase. When made audible, these accumulated variations affect the pitch, amplitude, and timbre of the generated tone, producing dynamic sonic behavior in which the degree and rate of change is parametrically controlled.

Assessment of Dynamic Stochastic Synthesis

As his motivation for developing DSS, Xenakis describes a search for a total theory of sound synthesis: a “most economical way” of producing waves in the time domain that encompasses “all possible forms from a square wave to white noise.”13 Generating either of these edge cases is trivial; the challenge lies in creating “waves representing melodies, symphonies, [and] natural sounds.” DSS approaches this problem by injecting periodicities and symmetries into a probabilistically determined wave: it starts from a chaos condition and imposes constraints that induce stability.14

An advantage of DSS is that its parameter space enables interpolation between pitch and noise, and exploration of intervening timbres. Its economy lies in its few interrelated parameters, which afford considerable diversity of musical behavior. With parameters that permit only slight variations of the wave cycle, tones of stable pitch and timbre emerge. Conversely, the more the parameters allow profound dissimilarities between cycles, the more the resultant tone loses its periodicity and tends toward noise.

Xenakis exploits these properties to create scenes of contrasting character in Gendy3, the definitive manifestation of DSS. In his discussion of this work, Sergio Luque identifies three sections that feature similar behaviors in all voices.15 Due to their relative homogeneity, these textures are particularly instructive as to the nature of DSS. Each spectrogram in Figure 33.2 analyzes a fifteen-second excerpt from one of these sections. They all exhibit high levels of energy throughout their spectra, indicating a general brightness of timbre. Figure 33.2a (17:03–17:18) represents the use of fixed pitches to create melodies, chords, and clusters. The horizontal striations indicate sustained voices and their harmonics; the abrupt transitions between regions of spectral coherence mark their sudden entrances and exits. Figure 33.2b (14:25–14:40) represents fluctuating pitch (vibrato) and glissandi. These behaviors are reflected, respectively, in the wavy lines visible in the first half of the spectrogram and the rising diagonals near its end. Figure 33.2c (5:15–5:30) represents noisy DSS timbres. The extreme, sustained density and intensity of the spectrum are immediately apparent. However, the noise retains a faintly pitched quality throughout, as evidenced by the horizontal striations running along the bottom of the spectrogram.

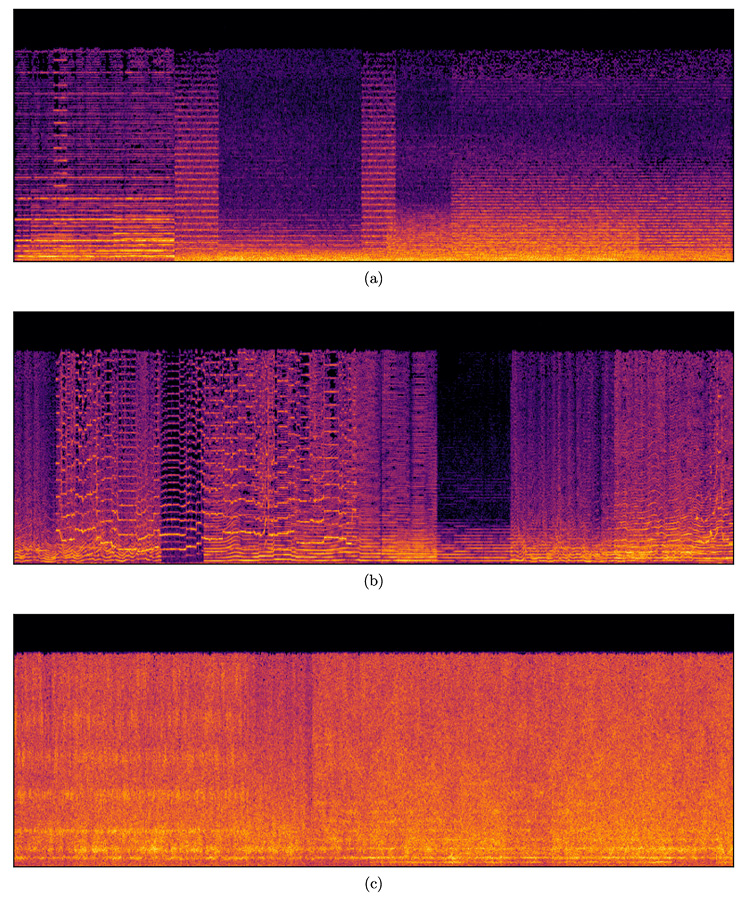
Fig. 33.2 Spectrograms of three homogeneous textures from Gendy3. (a) Fixed pitch. (b) Fluctuation and glissandi. (c) Noise. Figure created by author (2024).

Xenos

DSS produces a variety of compelling sounds but is problematic to control. Lacking basis in acoustic or instrumental models, its pitch and timbral features are emergent, arising from parameters only indirectly connected to perceptual characteristics.16 Indeed, Xenakis described composition with DSS as “a struggle,” likening the process to reining in “wild horses.”17

It should be noted that GENDY was a non-real-time application. Xenakis therefore could not manipulate DSS parameters while listening to the algorithm, which undoubtedly contributed to the challenges he experienced. Furthermore, the parameters of each GENDY voice were static.18 While Xenos is far from the first implementation of DSS to overcome these limitations (this distinction belongs to Peter Hoffmann’s New GENDYN Program),19 real-time operation remains a significant aesthetic departure. Immediate aural feedback facilitates compositional decision-making and promotes proficiency with DSS, while dynamic modification of synthesis parameters affords an additional dimension of control, enabling gestures and textures that evolve in radical ways.

Though unpredictable, DSS is capable of a variety of behaviors with respect to pitch. In his sketchbook, Xenakis annotated parameters with the pitches that they induced,20 indicating his desire to exercise a degree of deterministic control over the harmonic products of the algorithm. The design of Xenos is informed by similar concerns. Xenos makes DSS more practical for general-purpose composition by adjusting the way that it specifies pitch and presents related parameters to the user. It additionally leverages the inherent microtonality of DSS via pitch quantization.

Xenos also aims to encourage composition with DSS through its implementation as a plugin. Since the plugin is arguably the most widely used class of virtual instrument, it offers an attractive medium for preserving and democratizing historical, nonstandard synthesis algorithms and other lesser-known computer music techniques. Packaging DSS in this ubiquitous and long-lived format extends access to a broad group of current and future composers of electronic music, who might find new creative applications for it.

Finally, the Xenos project is motivated by the desire to make a cross-platform and widely compatible DSS instrument available as open-source software. Because Xenos is built with JUCE, an industry-standard C++ framework for audio programming, it is easily modified or extended by interested developers from the community. The Xenos source code includes original implementations of a DSS voice, a frequency quantizer, and a Scala parser, all of which may be incorporated into new projects.

The elastic barriers of the pitch random walk specify the minimum and maximum pitches of a DSS voice. Xenos expresses these via two metaparameters: pitch center, which is a MIDI pitch, and pitch width, which defines a range about the center in equal-tempered semitones. Incoming MIDI note-on messages trigger voices and define their pitch centers; the pitch width is a single parameter affecting all voices. This design more readily fits the model of the traditional musical note, facilitating adaptation of DSS as a MIDI-equipped, polyphonic plugin; it is also more perceptually informative, allowing intuitive reasoning about the range of each voice during composition or performance.

Xenos introduces a pitch quantizer that tunes each wave period to the nearest degree of a user-defined scale. Its effect is to precisely compress or expand the cycle so as to snap the DSS voice to an exact pitch.21 Quantization retunes fixed pitches, converts vibrato into ostinato, transforms glissandi into scalar melodies, and filters noise through specific pitch collections. Table 33.1 describes the fourteen scale presets included in Xenos.

Table 33.1 Scale presets included in Xenos.

The quantizer can also import arbitrary scales in the Scala format. Scala (.scl) files implement a simple, human-readable syntax for specifying original scales and are supported by a long list of commercial and experimental music software.22 Because Scala can represent intervals as either ratios or cents, it is a very flexible and powerful tool for composing xenharmonic music.

Most DSS implementations use either first- or second-order random walks; Xenakis himself employed the former in La Légende d’Eer and the latter in Gendy3.23 The choice is musically consequential: a first-order walk wanders erratically throughout the random-walk space, imposing a noisy quality on any parameter it influences, while a second-order walk swings between the extremities of the range, producing a quasi-pulse shape that engenders a semblance of regularity. Figure 33.3 graphs both a primary walk and the secondary walk it feeds; their juxtaposition highlights the filtering effect of a second random-walk stage. Xenos implements second-order walks but offers first-order walks as an option.24 It thus covers both of Xenakis’s revisions and allows simultaneous use of different orders for the pitch and amplitude random walks.

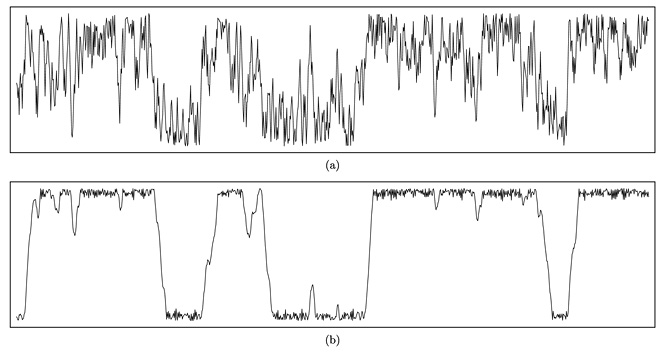
Fig. 33.3 Comparison of characteristic random-walk behaviors. (a) First order. (b) Second order. Where (a) is high, (b) tends toward the upper boundary; likewise, where (a) is low, (b) tends toward the lower boundary. Figure created by author (2024).

Xenos supports varying the number of linear segments in a wave cycle between 2 and 128.25 Using a greater number of segments models the complexity of a composite wave with components at various frequencies, amplitudes, and phases, resulting in a brighter timbre. Figure 33.4 compares the waveforms and spectrograms of DSS with four and sixteen segments. The pronounced frequency banding reflects constrained pitch fluctuation.

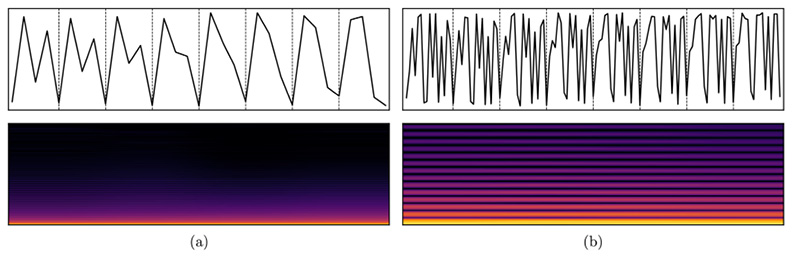
Fig. 33.4 Eight contiguous cycles of a DSS waveform and resulting spectrogram. (a) Four segments. (b) Sixteen segments. Figure created by author (2024).

In GENDY, the amplitude random walk alone shapes the amplitude of an individual voice (“sound field”),26 which thus tends to begin or cease sounding rather instantaneously. Xenos implements an additional per-voice amplitude envelope using a classic, four-stage design. This feature brings DSS more in line with standard synthesizer architectures, enhancing its capacity for practical sound design by enabling a variety of deterministic, time-varying amplitude contours.

Like most nonstandard synthesis techniques, DSS is obscure within the general domain of electronic music and likely opaque to many potential users. The Xenos graphical user interface (GUI), shown in Figure 33.5, thus aims to present all controls clearly and with an apparent logic that makes the instrument easy to learn and rewarding to use.

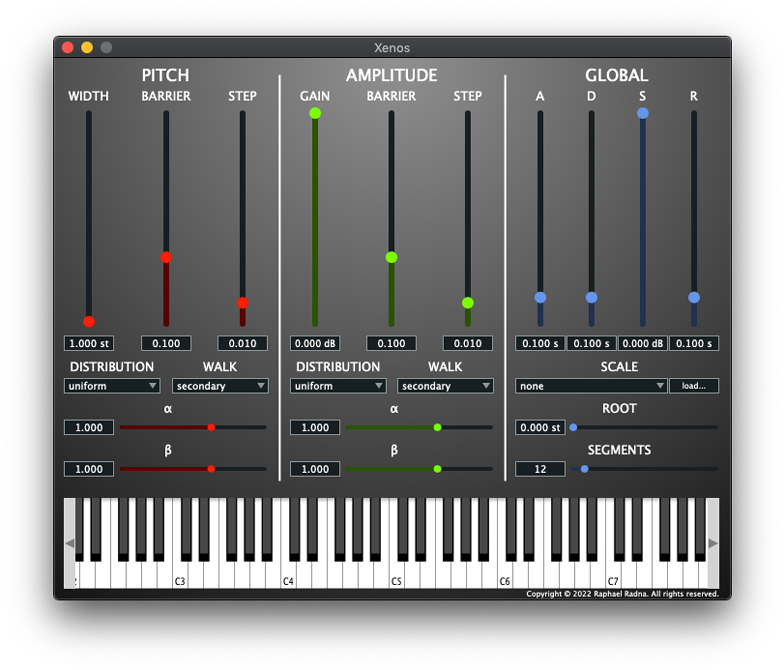
Fig. 33.5 Xenos plugin interface. Figure created by author (2024).

The GUI is divided into three color-coded panels that group related controls: the Pitch panel (left) contains the pitch random-walk parameters; the Amplitude panel (center) contains the amplitude random-walk parameters; and the Global panel (right) contains the parameters affecting the amplitude envelope, the pitch quantizer, and the number of linear segments. Table 33.2 details the parameters of the Xenos instrument.

Table 33.2 Xenos parameters by group.

Xenos acquires much interactive functionality through integration with a plugin host, typically a digital audio workstation (DAW). Using Xenos within such an environment provides benefits such as MIDI sequencing, physical controller mapping, and parameter automation. These affordances are well known and understood by electronic musicians of all backgrounds; applied to Xenos, they offer a familiar and convenient entry point to experimental synthesis.

The DAW routes incoming MIDI data to a track containing a Xenos instance. In addition to note-on and note-off events, Xenos responds to pitch bend messages, enabling an additional, deterministic layer of pitch transposition up to one octave above or below voice pitch. Sustain pedal messages are also implemented.

A suitable DAW will facilitate control of Xenos parameters via physical devices and will typically offer an automatic mapping feature. This allows assignment of external hardware controllers (usually faders and dials, but also wheels, pedals, breath controllers, touch-sensitive surfaces, etc.) to any parameter, a crucial element of many composition and performance workflows.

Finally, using Xenos within a DAW enables automation: the specification of parameter value as a function of time. Any Xenos parameter can be automated, including those that represent a discrete choice, such as the Distribution, Walk, and Scale parameters. Automation curves can be drawn manually, generated algorithmically, or captured from controller gestures.

The unifying principle of these interfaces is the abstraction of the control apparatus from the DSS process. As a result, any interactive or algorithmic composition system that can produce MIDI events can drive one or more Xenos instances. Beginners are thus empowered to explore DSS intuitively via familiar and convenient MIDI control schemes. At the same time, ambitious composer-programmers can define parameterized, time-variant gestures that produce the low-level MIDI instructions needed to realize specific DSS events according to any criteria. Xenos might thus appeal to electronic music composers of diverse aesthetic concerns, technical orientations, and creative practices.

This section considers specific musical applications of Xenos through fourteen sound examples that illustrate characteristic timbres and gestures.29

Media 33.1 demonstrates traditional DSS sounds similar to those heard in Gendy3, including fluctuating pitch, glissando, and noise. These behaviors are attained through various settings of the pitch random-walk parameters. In general, low Barrier and Step values are required to induce behaviors other than noise.

Media 33.1 Typical DSS behaviors in Xenos: fluctuating pitch, glissando, and noise.
https://hdl.handle.net/20.500.12434/6fb46f5c

DSS easily produces noise by applying large step sizes and wide elastic-barrier distances to the random walks. Such settings cause discontinuous motion of the breakpoints, resulting in dissimilarity between adjacent cycles. Because DSS affects pitch and amplitude independently, Xenos can create a variety of noise colors. Many of these exhibit a subtly harmonic quality; only the most extreme settings overcome the periodicity inherent in the algorithm. Media 33.2 demonstrates noise generation, first by increasing the pitch Barrier and Step parameters, then by increasing the amplitude Barrier and Step parameters, and then by both methods combined.

Media 33.2 Noise generation by discontinuous pitch fluctuation, discontinuous amplitude fluctuation, and both techniques simultaneously.
https://hdl.handle.net/20.500.12434/d4b9dc80

The choice of random-walk order asserts additional influence over the instrument’s behavior. Media 33.3 presents a noise texture produced by the amplitude random walk, first using the secondary walk and then the primary walk, with all other parameters held constant. The secondary walk produces greater periodicity, preserving traces of pitch, while the primary walk produces an aperiodic wave with a far noisier timbre.

Media 33.3 Effect of second- and first-order random walks on amplitude. A first-order walk produces a more uniform distribution of values, resulting in a noisier timbre.
https://hdl.handle.net/20.500.12434/0940e955

Perceptually, the most immediate effects of the amplitude random walk concern timbre.30 In Media 33.4, the vertical movements of the breakpoints create gradually drifting peaks and troughs in the waveform, shifting emphasis among harmonics of the pitch period and imparting a sense of continuous spectral evolution.

Media 33.4 Stochastic spectral emphasis among harmonics of the pitch period, produced by the amplitude random walk.
https://hdl.handle.net/20.500.12434/b215e59d

Media 33.5 varies the number of linear segments in the wave cycle from eight to sixty-four and back, affecting spectral brightness. Though dynamically variable, this parameter is, by definition, discrete, and far more sensitive at the lower end of its range.

Media 33.5 Effect of the number of wave-cycle segments on timbre. A greater number of segments increases brightness.
https://hdl.handle.net/20.500.12434/e661056c

The stochastic distributions influence the random walks in various ways. They typically follow one of two general tendencies: symmetrical distributions generate values around a mean, producing a chaotic fluctuation within a range of values, and asymmetrical distributions converge on one of the boundaries of the random-walk space, producing a directed, continuous trajectory toward one elastic barrier or the other. Table 33.3 classifies the available distributions according to this typology.

Table 33.3 Classification of stochastic distributions available in Xenos by behavioral tendency.

However, even within these categories, different distributions produce contrasting behaviors. Media 33.6 compares the effects of the Cauchy and hyperbolic cosine distributions on the pitch random walk, with all other parameters held constant. The Cauchy distribution imparts a frenetic fluctuation, while the relatively smoother slope of the hyperbolic cosine distribution produces a gentler pitch variation.

Media 33.6 Effect of Cauchy and hyperbolic cosine distributions on pitch. While both produce fluctuation, the roughness of the former contrasts the smoothness of the latter.
https://hdl.handle.net/20.500.12434/b6539f51

Application of an asymmetrical distribution to the pitch random walk produces continuous glissandi. Since these begin at a voice’s pitch center and terminate at an interval defined by Width, they can be applied quite deterministically. The other pitch random-walk parameters influence the glissando rate and direction. Media 33.7 demonstrates ascending and then descending one-octave glissandi via the arcsine distribution.

Media 33.7 Ascending and descending one-octave glissandi produced by the arcsine distribution, continuous.
https://hdl.handle.net/20.500.12434/bb02e5db

Because Xenos centers a DSS voice on a MIDI pitch, it can be played like a typical keyboard instrument. Media 33.8 produces deterministic melody and harmony via standard MIDI sequencing. No quantization is applied; a narrow Width (ca. one semitone) simply constrains the voices tightly around their center pitches. The pitch random walk subtly detunes the oscillators within this range, simulating tape wow and flutter effects.

Media 33.8 Deterministic pitch control via MIDI sequencing with constrained pitch width.
https://hdl.handle.net/20.500.12434/b0746e07

Variation of the pitch width thus enables interpolation between determinism and chaos. Media 33.9 demonstrates this technique with four voices that begin in octaves and then split off into wild, independent glissandi before converging once again. The effect recalls the arborescences employed by Xenakis in several of his works: organic, branching structures reminiscent of trees or lightning in form.31 The quasipalindromic morphology of Media 33.9 suggests a particular affinity with Figure 33.6, a section of Xenakis’s graphic score of Mycènes Alpha (1978), for the UPIC graphical synthesis system, featuring an expanding and contracting network of arborescences.32

Media 33.9 Chaos and convergence: varying the pitch width alternately constrains several voices to their center pitches and allows them to fluctuate.
https://hdl.handle.net/20.500.12434/7e472a7b

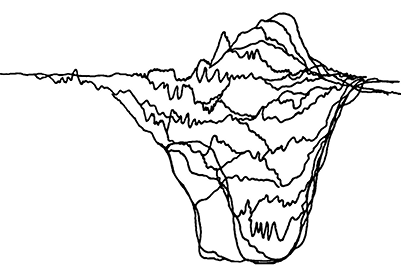
Fig. 33.6 Converging arborescences in Mycènes Alpha by Iannis Xenakis. The traces represent frequency over time; their branching and converging contours thus denote an expansion and subsequent contraction of frequency range. Xenos produces analogous gestures via variation of its Width parameter. © Les Editions Salabert. Used with permission.

Pitch control in Xenos is further refined by its quantization feature. Media 33.10 quantizes a single, meandering glissando to the pentatonic scale, producing a pleasant, folk-like melody.

Media 33.10 Quantization of a single voice to produce melody.
https://hdl.handle.net/20.500.12434/ac4fae7c

With multiple voices, quantization produces counterpoint. Media 33.11 quantizes three voices to a five-limit major scale. The absolute pitch differences between the voices compound with their stochastic fluctuations to create glissandi at different rates and in random directions. Quantization transforms these into stepwise motion; from the interplay between the voices emerges the four types of contrapuntal motion (parallel, similar, oblique, and contrary) and various contrapuntal devices (passing tones, neighbor tones, suspensions, etc.) The pure tuning makes for an especially radiant quasi-chorale texture.

Media 33.11 Quantization of several voices to produce counterpoint.
https://hdl.handle.net/20.500.12434/214cb279

Quantization discretizes a continuous glissando produced by an asymmetrical distribution. Media 33.12 features the same one-octave glissandi of Media 33.7 but quantized to quarter-tones. This quantization highlights the acceleration or deceleration inherent in each glissando, depending on its direction and due to the logarithmic nature of pitch perception.

Media 33.12 Ascending and descending one-octave glissandi produced by the arcsine distribution, discrete.
https://hdl.handle.net/20.500.12434/c568af43

With certain settings of the amplitude random walk, Xenos can simulate granular synthesis. Media 33.13 interpolates between a sustained tone cluster and a quasi-granular texture. As the amplitude Barrier value increases, the smooth dynamic contour gives way to an increasingly iterative and chaotic texture in a manner reminiscent of injecting asynchronicity into a grain stream. Later, increasing the Step parameter results in a much noisier timbre, an effect perceptually analogous to reducing grain size. The turbulent Cauchy distribution is well suited for this application.

Media 33.13 Simulation of granular synthesis with dynamic parameters. Modifying the parameters of the amplitude random walk enables transitions between smooth and iterative textures, and between harmonic and noisy spectra.
https://hdl.handle.net/20.500.12434/4303098d

Applying quantization to such a texture imposes a harmonic character upon it. Media 33.14 presents a single quasi-granular cloud quantized to four different scales: pentatonic, whole-tone, octatonic, and Bohlen–Pierce.

Media 33.14 Harmonic quasi-granular clouds via pitch quantization.
https://hdl.handle.net/20.500.12434/d3477587

Conclusion

Xenos implements and extends DSS in a modern virtual instrument. It aims to:

• Preserve the original sounds and behaviors of DSS.
• Simplify DSS by implementing perceptually informative parameters.
• Enhance DSS with a pitch quantizer that enables xenharmonic exploration.
• Provide access to DSS in a convenient plugin format.
• Facilitate composition and sound design with DSS through an intuitive GUI and standard interfaces.

Although the version of Xenos described here is a viable instrument that realizes these fundamental aims, it can also be considered a starting point, as Xenakis regarded his own work,33 as there remain several directions for continued development that would enhance its creative potential.

One future goal should be further adaptation of traditional synthesizer elements. A general framework for parameter modulation, e.g., the inclusion of supplementary envelopes, low-frequency oscillators, and a matrix for managing their routings to synthesis parameters, would greatly augment the instrument’s sound design capabilities by enabling an additional layer of deterministic, time-variant timbre modification.

The initial state of the wave cycle is another area of interest. A Xenos voice starts with its breakpoints randomized, but since DSS is sensitive to initial conditions, other configurations may yield effective behaviors.34 Alternatively, Dynamic Stochastic Wavetable Synthesis offers a promising method for exploring DSS with complex waves. This technique applies DSS to arbitrary sample data, e.g., the classical waveforms or fragments of recorded audio, enabling the deformation of recognizable timbres by DSS.35

Additionally, visualization should play a larger role in the instrument’s future. While the Xenos GUI aims to present parameters in an appealing and informative layout, it would be enhanced by visualizations of, e.g., the waveform, the random walks, or the stochastic distributions. Visualization presents a real opportunity to create new insight into this unconventional algorithm, its parameter space, and its musical applications.

Finally, Xenos could be made to adapt to multichannel output. Xenakis proposed duplicating the same DSS parameters in multiple voices, using unique random seeds to produce perceptually equivalent but nonidentical waves.36 The ability to route these voices to individual loudspeakers would have compelling implications for spatial electronic music composition.

In Formalized Music, Xenakis criticizes early electronic music for its reliance on the “simplistic sonority” of “pure” electronically generated sound.37 These timbres are deficient, he contends, due to their spectral stasis, unnatural transients, and resistance to pattern recognition. His contrasting approach, which led him to invent Dynamic Stochastic Synthesis, starts from chaos and creates order by introducing constraints. By imposing discrete pitch onto DSS, Xenos takes this principle one step further; in this sense, it proceeds in the same spirit.

HOFFMANN, Peter (2000), “The New GENDYN Program,” Computer Music Journal, vol. 24, no. 2, p. 31–8, https://doi.org/10.1162/014892600559290

HOFFMANN, Peter (2004), “‘Something Rich and Strange:’ Exploring the Pitch Structure of Gendy3,” Journal of New Music Research, vol. 33, no 2, p. 137–44, https://doi.org/10.1080/0929821042000310612

LUQUE, Sergio (2009), “The Stochastic Synthesis of Iannis Xenakis,” Leonardo Music Journal, vol. 19, p. 77–84, https://doi.org/10.1162/lmj.2009.19.77

RADNA, Raphael (2023), “Dynamic Stochastic Wavetable Synthesis,” in S. Serafin, F. Fontana, and S. Willemsen (eds.), Proceedings of the 26th International Conference on Digital Audio Effects, Copenhagen, Aalborg University, p. 343–46, https://dafx23.create.aau.dk/wp-content/uploads/2023/09/DAFX23_Proceedings.pdf

ROADS, Curtis (1996), The Computer Music Tutorial, Cambridge, Massachusetts, MIT Press.

ROBINDORÉ, Brigitte and XENAKIS, Iannis (1996), “Eskhaté Ereuna: Extending the Limits of Musical Thought—Comments On and By Iannis Xenakis,” Computer Music Journal, vol. 20, no 4, p. 11–16, https://doi.org/10.2307/3680410

SERRA, Marie-Hélène (1993), “Stochastic Composition and Stochastic Timbre: GENDY3 by Iannis Xenakis,” Perspectives of New Music, vol. 31, no 1, p. 236–57, https://doi.org/10.2307/833052

VARGA, Bálint András (1996), Conversations with Iannis Xenakis, London, Faber and Faber.

XENAKIS, Iannis (1956), “La Crise de la Musique Sérielle,” Gravesaner Blätter, vol. 1, p. 2–4.

XENAKIS, Iannis (1987), “Mycenae-Alpha 1978,” Perspectives of New Music, vol. 25, no 1/2, p. 12–15.

XENAKIS, Iannis (1992), Formalized Music: Thought and Mathematics in Composition, revised edition with additional material compiled and edited by Sharon Kanach, Stuyvesant, New York, Pendragon.

XENAKIS, Iannis (1994), “Gendy3,” in Aïs—Gendy3—Taurhiphanie—Thalleïn, CD 450–86, St Paul, Minnesota, Neuma Records.