36. Mapping the Influence: Iannis Xenakis’s GENDYN Algorithms as a Means for Creative Explorations in Live Improvised Feedback Music

Thanos Polymeneas-Liontiris1

Introduction

This chapter is written following an autoethnographic perspective.2 It presents one of my most recent creative research projects, aiming to contextualize it within my previous and overall creative practice, while drawing a link between it and its historical relation to Iannis Xenakis’s Generation Dynamic (GENDYN) algorithm.

My creative practice ranges from composition to performance, as well as sound art. Since 2014, the idée fixe in most of my works has been the notion of feedback, a concept I have not ceased to explore in its many different possible manifestations. For example, I have made acoustic and acousmatic compositions based on material deriving from audio feedback processes, such as Sun Bleached (2019), a work for baroque ensemble (flute, violin, viola da gamba, harpsichord) and tape.3 In Sun Bleached, most sounds of the tape were results of feedback processes.

For my live performance practice, I hack acoustic instruments to convert them to feedback instruments (see Figure 36.1). More specifically, through explorations in this field I have made different versions of acoustic feedback resonating double basses.4 The model of feedback in this case is relatively simple: electromagnetic pickups transfer the sound of the instrument’s strings to loudspeakers mounted on the body of the instrument itself, thus exciting the strings, and so on. The concept of feedback in this context might seem simple, but the acoustic and musical results of it are aesthetically extremely rewarding.

Fig. 36.1 Feedback Augmented Acoustic Double Bass. Photos by M. Eugenia Demeglio (2018).

I use these feedback instruments either as a solo performer, or to play with other musicians in a variety of line-ups. Very often, I use the feedback double bass to play in feedback music ensembles. Such ensembles are comprised either by musicians playing on other feedback instruments, such as the Feedback Musicianship Network Ensemble (see Figure 36.2), or by musicians who are interested in the conceptual and creative potential of the notion of feedback, and who employ it in a variety of ways in their practices. In certain cases, these ensembles do operate as larger scale feedback systems, as the audio produced by one instrument might feed into other instruments and vice versa, such as the Brain Dead Ensemble (see Figure 36.3).,5

Fig. 36.2 The Feedback Musicianship Network Ensemble. Photo by Dimitris Kyriakoudis (2022).

Fig. 36.3 The Brain Dead Ensemble. Photo by Matthew Garland (2018).

A very prominent part of my creative practice consists of devising music theater performances. There, the notion of feedback is central, as it takes place between audience, technology, and performers and thus becomes responsible for the musical and dramaturgical development of the work (see Figure 36.4).,6 In these cases, the notion of feedback might extend to human behaviors since it might be manifest as an exchange of information between audience and performers. Feedback processes might include technological interaction, which may cause the production of audio and visual information (sound and/or moving image); or, in other cases, the feedback processes might reside merely in an interpersonal level between audience and performers.

Fig. 36.4 A scene from the performance of my work Quicklime (2016), the design of which was based on feedback processes. Photo by Erin McKinney (2016).

My most recent experimentation in the broad field of feedback, and the one I will present in here, is data feedback using Dynamic Stochastic Synthesis, implemented in the programming language SuperCollider, a process that I use for my live, free improvisation, and noise music performances.7

Coding Feedback

The simplest type of audio feedback happens when one turns a microphone toward the loudspeaker which amplifies it and in turn emits the signal that the same microphone picks up. In this case, the result is a very characteristic high-pitched noise that becomes exponentially louder. A similar effect occurs when one turns an electric guitar towards its own amplifier. Most often the frequency we listen to in these cases is either the resonance frequency of the space or, it is related to the self-resonance, self-noise, and spectral specifications of the equipment used or, a combination of both.

Audio feedback within a computer though may happen in many different manners, and in order to control that feedback and obtain interesting results without letting it get out of hand in terms of loudness, one needs to design “when” feedback will happen, “how” it will happen (“what” will feed back “where”), and “how much” of the original signal will be fed back into the system. The SuperCollider code example written below will reproduce the sound of a sine wave, the frequency of which will be controlled by the mouse cursor within the boundary of 20 Hz to 20 KHz:

Media 36.1 Sine wave example in SuperCollider.
https://hdl.handle.net/20.500.12434/e0c6d5a8

If we wanted to add feedback in the above line of code, then one possible way to do it is to modulate the oscillator’s phase parameter by using the audio output of that same oscillator. We therefore modulate the oscillator of a synthesizer not with another oscillator, but with the synthesizer itself:

Code 36.2 Controlled feedback example.

Media 36.2 Controlled feedback example in SuperCollider.
https://hdl.handle.net/20.500.12434/38e50bc1

The sounding result resembles Frequency Modulation and it is a process called Phase Modulation. The peculiarity though of this case is that the modulator in this process is fed by the output of the entire synthesizer, hence the feedback.

It is most likely that the more composite sounds one creates in the initial process of sound synthesis design, more complex results will be generated once feedback is added to it. For example, in the sound synthesis algorithm below there some reverberation is added, as well as panning for spatialization; and the overall amplitude of the synthesizer is randomly controlled by a low frequency noise generator. These simple additions contribute greatly to the making of a much richer and more intriguing sound result.

Media 36.3 Low frequency noise modulation example in SuperCollider
https://hdl.handle.net/20.500.12434/b71262ba

When one adds feedback to the above sound synthesis algorithm, in a manner similar to the way feedback was added in the first example—by controlling the phase parameter of the oscillator using the sound of the synthesizer itself—one gets a more intricate and interesting result than before. The output of this synthesizer may begin with a sound that resembles the previous example, but very soon, it tends to “break” into noise explosions, surprising the listener. The synthesized sound resembles a sort of walk on a cliff-edge or a tight-rope; it gives the impression of a certain type of unpredictability and fragility. While listening to it, one cannot tell “when” and “how” such loss of “equilibrium” will happen, causing the sound to explode.

  var input, sound, env;

    input = InFeedback.ar(1) * feedbackVol;

  sound = GVerb.ar(Pan2.ar(SinOsc.ar(freq, input, LFNoise2.ar(rate)).fold2(Line.kr(0,1.01,8)),SinOsc.ar(panRate)), 100, 5, 0.1);

Media 36.4 Feedback example in SuperCollider.
https://hdl.handle.net/20.500.12434/99cead12

Feedback music has often been described as the type of music based on the notion of Metacontrol—a process within which one might give away control, to benefit from the influence that the algorithm might reward them with.8 Music making and performing with feedback can also be described as a process of tango dancing, where the two dancers have a dynamic relation of leading and following the cues between them. In that respect, the feedback performer/music maker is required very often let herself be led by the cues of the feedback algorithm. Therefore, feedback music is often a non-linear way of music-making, and it is a matter of playing “with the algorithm” rather than playing “the algorithm.”

Dynamic Stochastic Synthesis

My latest explorations in feedback involve the use of Dynamic Stochastic Synthesis algorithms. Stochastic synthesis emerged in the Centre d’Études de Mathématique et Automatique Musicales (CEMAMu; Research Center for Mathematical and Automated Music) in Paris by Xenakis, assisted by Gérard Marino, Marie-Hélène Serra, and Jean-Michel Raczinski.9 It was first computed by a program called GENDYN (standing for Génération Dynamic) written in BASIC programming language. To write the music generated by such program, Xenakis developed another program called PARAG. The result of the combination of these two programs was first presented to public in October 1991 at the Computer Music Conference, in Montreal as Gendyn301; however, Xenakis subsequently withdrew this work from his catalogue.10 A month later, in November 1991, the work Gendy3 was premiered at the Rencontres Internationales de Musique Contemporaine in Metz. After Gendy3, Xenakis added the possibility of modulating the parameters of the Dynamic Stochastic Synthesis algorithm. With this extended version of GENDYN, in 1994 Xenakis composed S. 709, which was premiered at the Journées UPIC à Radio France that same year.

It is widely recognized that Dynamic Stochastic Synthesis was first used by Xenakis in certain sections of his work La Légende d’Eer (1977), and the process used there may be called the 1977 method. Contrastingly, the composer used the 1991 method for the making of Gendy3 (1991) and S. 709 (1994).11 The difference between these two methods is described in detail in the 2009 article of Sergio Luque: “The Stochastic Synthesis of Iannis Xenakis.”12

Essentially, both Dynamic Stochastic Synthesis methods (1977 and 1991) allow composers to design their music on a sample level using a breakpoint interpolation synthesis method. The positions in time and the amplitude of the samples in such digital sound processing are specified by a process of a probabilistic perturbation called “random walks” (see Figure 36.5).13 The main difference between the two methods is that the 1991 method has two orders (two levels) of random walks, while the 1977 one has only one order.

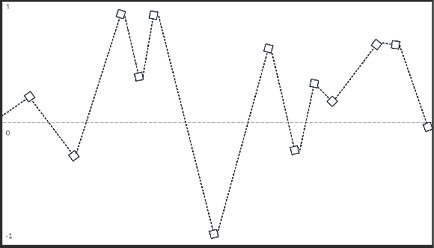
Fig. 36.5 A “random walk” probability perturbation with linear interpolation between the steps © Thanos Polymeneas-Liontiris (2023).

Dynamic Stochastic Synthesis in SuperCollider

In my explorations in SuperCollider I came across few Unit Generators that aim to reproduce—or at least are based on—Xenakis’s Dynamic Stochastic Synthesis algorithms.14 The first three Dynamic Stochastic Synthesis Unit Generators were made by Nick Collins.15 Unit Generator Gendy1 is based on the thirteenth chapter of Formalized Music that describes the 1977 method, while Gendy2 is based on the 1991 algorithm, as it is described in the fourteenth chapter of the same book and in Hoffmann’s 2000 article “The New GENDYN Program.”16 The third stochastic synthesis Unit Generator is called Gendy3 in which, according to Collins, “a desired frequency can be specified and achieved exactly; breakpoints are perturbed, and durations fixed proportionally within the current period.”17 Two more Stochastic Synthesis Unit Generators are to be found in SuperCollider: Gendy4, a cubic-interpolated version of Gendy1; and Gendy5, a non-interpolating version of Gendy1.

Coming across the Gendy Unit Generators in SuperCollider, exploring them and learning to understand them, I was intrigued to find ways to use feedback to drive them. However, the Gendy Unit Generators do not take audio input; therefore, it is not possible to do audio feedback with them. Nonetheless, they have input parameters; therefore, one can do data feedback instead. To do so, I started by analyzing the signal output of a Gendy1 Unit Generator to retrieve its fundamental frequency and its overall dynamics. Then I took these values, I scaled them down to match the range of its input parameters, and finally fed them back to it. The results were immediately rewarding. It was as if one controlled a probability “noise” generator, by its own output: as though one organizes chaos by using chaos to do it. In these explorations I have been using feedback to control different parameters within Gendy1. In other cases, I fed back these values to control external effects applied on Gendy1 such as the parameter of the overall sampling rate of the synthesizer.

Often, the audio results retrieved by these feedback processes resembled sounds characteristic of the original GENDYN, such as “bee-like” sounds, “insect swarms,” etc.; at other times though I came across relatively harsh metallic sounds and uncontrolled noise explosions. A very characteristic sound often produced by this algorithm is a noise with a clear central frequency that moves rapidly and erratically in the spectrum. A sort of classic feedback-like sound, giving the impression that the algorithm is striving to identify itself and trying to imitate it, but then gets lost before it gets back into it.

For demonstration’s sake, the following audio example is the beginning of Xenakis’s work Gendy3 (1991) with the original GENDYN algorithm audio example (Media 36.5), and after that, a short improvisation that I did using data feedback with Gendy1 (Media 36.6), the code of which can be found below.18

Media 36.5 Beginning of Gendy3 (1991) by Iannis Xenakis.
https://hdl.handle.net/20.500.12434/771ba956

(SynthDef(\GendyI, {

  |inbus =0, outbus = 0,

  ampdist = 0, durdist = 1,

  adparam = 0.5, ddparam = 0.4,

  minfreq = 0.095, maxfreq = 0.98878,

  ampscale=0.5, durscale=0.5,

  numcps=24,

  maxdel = 0.5, del= 0.0, pmul = 1,

  pos = 0, bits =24,

  mix = 0,

  vmix = 0.333, vroom = 0.5, vdamp = 0.5|

  var pan, pitch, input, out, crush;

  input = InFeedback.ar(inbus, 1);

  input = DelayC.ar(input, maxdel, del);

  pitch = Pitch.kr(input)[0] * pmul; //we track the pitch

    ampscale, input.fold(0,1),

//we feedback the pitch value here

// we feedback the pitch value also here

Code 36.5 Data feedback example.

Media 36.6 Data feedback example in SuperCollider.
https://hdl.handle.net/20.500.12434/b447e54e

The combination of feedback and Gendy1 Unit Generator offers a great variety of quite harsh, often unstable, and unpredictable spectra of tonal and noisy sounds that call for interaction and playfulness in the context of live improvised music. I have not made an acousmatic piece yet, as I am still experimenting with it and slowly discovering it. Nevertheless, free-improvisation music events are the perfect context to try my ideas and experiment with their potential.

The control parameters of the SuperCollider Unit Generator Gendy1 (the algorithm based on the 1977 method, and the one I use above) are written below, as designed and described by Nick Collins. These parameters control the probability distribution of amplitude, duration, the random walk barriers for amplitude and duration, the minimum and maximum frequency of oscillation, etc… In detail:

• The first parameter is defined as “ampdist” and controls the type of probability distribution that will define the perturbation of the amplitudes’ breakpoints.
• The second parameter is called “durdist” and defines the probability distribution for the duration of random walks.
• The third parameter is called “adparam” and is the coefficient for the probability distribution of the breakpoint amplitude; it requires values in the range 0.0001 to 1.
• The fourth parameter is “ddparam” and is the coefficient for the probability distribution of the breakpoint duration; it requires values in the range 0.0001 to 1.
• The fifth parameter is “minfreq” and is the minimum allowed frequency of oscillation for the Gendy1 oscillator, therefore it gives the largest period, hence the maximum duration of the first random walk.
• The sixth parameter is “maxfreq” and is the maximum allowed frequency of oscillation for the Gendy1 oscillator, therefore it gives the shortest period, hence the minimum duration of the first random walk.
• The seventh parameter “ampscale” defines the primary random walk barriers for amplitude and takes values from 0.0 to 1. An ampscale of 1.0 allows the full range of -1 to 1 for a change of amplitude.
• The eighth parameter “durscale” defines the primary random walk barriers for durations.
• The ninth parameter “numcps” defines the initial number of breakpoints in the buffer.
• The tenth parameter “knum” regards the current number of utilized control points.
• The eleventh parameter “mul” defines the overall amplitude of the Gendy1 algorithm.
• And the twelfth parameter “add” defines its DC offset.

As one can see, there are plenty of parameters for even one instance of the algorithm, something that makes the process of controlling them quite hard, let alone if there are more instances of Gendys within one algorithm. To control so many parameters, I often use a MIDI controller, yet as I need drastic changes in the sound qualities and the materials generated by the processes, I had to find a way to control many parameters at once. I therefore started using a custom trained machine listening application Wekinator, a feed-forward artificial neural network that consists of three layers: the input layer, the hidden layer, and the output.19 It uses a technique called backpropagation to get trained. With it, I gained more control over the different parameters of the algorithm and managed to interact more easily with it during my performances. Essentially, Wekinator gave me the possibility to instantly control many parameters of the synthesizer without having to input all these parameters by myself. In other words, just by operating four MIDI controllers, I was able to instantly control ten parameters of the synthesizer. Lately I have been experimenting with two Gendy1 Unit Generators playing together in SuperCollider. It is important to say here that Hoffmann, in his 2000 article The New GENDYN, explains how the 1991 method was based on sixteen layers of GENDYN algorithms for the making of Gendy3, a level of complexity I have not managed to reach yet with this version of feedback I am using.20 The next step of my experimentation in this domain will be cross feedback between two Gendy1s. Basically, in such experiments, the data output of one Gendy1 Unit Generator will be fed to and therefore drive another Gendy1 Unit Generator, and vice versa.

I admit that I am at the beginning of exploring something very interesting and I have the feeling that I have not even scratched the surface of the possibilities offered by such processes. However, if there is one thing that I am aiming to contribute with this article, it is not the results of my explorations, nor the processes per se, but the desire and urge for experimentation that drive these processes and offer these results. I am aiming to celebrate the spirit of Xenakis, his interest in experimenting and in trying old (and new) processes in new contexts—as he did with stochastics, with cellular automata, with game theory, and with so many other theories and processes that were initially considered “non-musical,” changing the way we understand music computation and music making. Therefore, my essential argument here, aside the technical or aesthetical aspects of it, is that Xenakis’s overall oeuvre has primarily influenced my practice in being musically curious, explorative, daring to try, daring to borrow processes from different practices, and daring to combine concepts, techniques, and technologies to travel to new shores of aesthetics and musical expression.

COLLINS, Nick (2011), “Implementing Stochastic Synthesis for SuperCollider and iPhone,” paper presented at the Proceedings of the Xenakis International Symposium, Southbank Centre, London, 1–3 April, https://composerprogrammer.com/research/stochasticsynthesis.pdf

DE CAMPO, Alberto (2014), “Lose Control, Gain Influence—Concepts for Metacontrol,” in Proceedings of the 2014 International Computer Music Conference, Athens, Greece, p. 217–22, https://quod.lib.umich.edu/cgi/p/pod/dod-idx/lose-control-gain-influence-concepts-for-metacontrol.pdf?c=icmc;idno=bbp2372.2014.034;format=pdf

FIEBRINK, Rebecca, TRUEMAN, Daniel, and COOK, Perry R. (2009), “A Meta-Instrument for Interactive, On-the-fly Machine Learning,” in International Conference on New Interfaces for Musical Expression (NIME), Pittsburgh, Pennsylvania, p. 280–5.

HOFFMANN, Peter (1996), “Implementing the Dynamic Stochastic Synthesis,” Journées d’Informatique Musicale, vol. 4, p. 341–47.

HOFFMANN, Peter (2000), “The New GENDYN program,” Computer Music Journal, vol. 24, no. 2, p. 31–8.

LUQUE, Sergio (2009), “The Stochastic Synthesis of Iannis Xenakis,” Leonardo Music Journal, vol. 19, p. 77–84.

MARINO, Gérard, SERRA, Marie-Hélène, and RACZINSKI, Jean-Michel (1993), “The UPIC System: Origins and Innovations,” Perspectives of New Music, vol. 31, no. 1, p. 258–69.

POLYMENEAS-LIONTIRIS, Thanos (2018), “Low Frequency Feedback Drones: A Non-invasive Augmentation of the Double Bass,” in International Conference on New Interfaces for Musical Expression (NIME), Blacksburg, Virginia, p. 340–1.

POLYMENEAS-LIONTIRIS, Thanos (2019), “Sun Bleached,” in Affect is No Crime: New Music for Old Instruments, Europa Ritrovata, Arcana-Outhere Music, CD A116.

POLYMENEAS-LIONTIRIS, Thanos, and DEMEGLIO, M. Eugenia (2022a), “Cybernetic Performance Ecosystems: The Im-Medea Cycle,” Leonardo, vol. 55, no. 3, p. 272–7, https://doi.org/10.1162/leon_a_02143

POLYMENEAS-LIONTIRIS, Thanos, and DEMEGLIO, M. Eugenia (2022b), “Cybernetic Performance Ecosystems: The Im-Medea Cycle,” ECHO, A Journal of Music, Thought and Technology, vol. 3, https://doi.org/10.47041/xvro7587

POLYMENEAS-LIONTIRIS, Thanos, MAGNUSSON, Thor, KIEFER Chris, and ELDRIDGE, Alice (2018), “The Ensemble as Expanded Interface: Sympoetic Performance in the Brain Dead Ensemble,” in José Alberto Gomes, Miguel Carvalhais, and Rui Penha (eds.), 4th International Conference on Live Interfaces. Inspiration, Performance, Emancipation, Porto, University of Porto, p. 117–25, https://live-interfaces.github.io/2018/pdf/ICLI2018-Liontiris.pdf

WILSON, Scott, COTTLE, David, and COLLINS, Nick (2011), The SuperCollider Book, Cambridge, Massachusetts, The MIT Press.

XENAKIS, Iannis (1992), Formalized Music: Thought and Mathematics in Music, additional material compiled and edited by Sharon Kanach (rev. ed.), Stuyvesant, New York, Pendragon.