38. The Algorithmic Music of Iannis Xenakis—What’s Next?

Bill Manaris1

Introduction

Iannis Xenakis was a pioneer in algorithmic composition of music and art. He combined architecture, mathematics, music, and performance art to create avant-garde compositions and performances that are still being analyzed, performed widely, and discussed.2 The compositions and other artifacts created by him were primarily inspired by his deep appreciation and understanding of algorithms, mathematics, and the use of controlled randomness, i.e., stochastic processes.

Xenakis was awarded a doctorate from the Sorbonne in 1976, for previously published theoretical and creative works.3 Since Xenakis was trained in mathematics, he viewed algorithmic computation through the lens of mathematics. Given the evolution of the field of computer science since that time, Xenakis’s work now clearly falls within the field of algorithmic arts (AlgoArts). Xenakis’s many musical contributions are deeply algorithmic in nature, and his rich and influential output would not have been possible without the ability to implement his processes through different computer programming languages, such as Fortran and BASIC, and the formalization, standardization, and replicability that such programming languages provide.4

This chapter is based on an invited talk-performance for a general audience at the Music Library of Greece, in the context of “Meta-Xenakis”—a transcontinental celebration of the life and work of Iannis Xenakis.5 It navigates the intersection of science and art, introduces some of Xenakis’s computational and algorithmic techniques to a non-technical audience, and explores how the field of stochastic music has advanced in the twenty years since Xenakis’s passing. While ideas and techniques pioneered and employed by Xenakis are now well-understood, today’s music technology has evolved tremendously through the integration of artificial intelligence, advanced computing algorithms, and human-computer interaction—techniques and technologies that were unavailable to Xenakis.

This chapter discusses some of Xenakis’s works in algorithmic and stochastic music, and reimagines the types of music that Xenakis could possibly be making today, having access to the modern technologies of smartphones and computing devices. It spans several of the topics from the Meta-Xenakis call for participation, including the blending of music, science and technology; a performance and retelling of one of Xenakis’s early works, Concret PH (1958) through the use of smartphone technology; UPIC (a system he developed to compose music through the use of computers); Xenakis’s compositional methods and tools, and how these can be enhanced with newer ideas in computational aesthetics and modeling of creativity; how musical gestures can be informed by advances in sensors, data mapping/translation, and human-computer interaction techniques; and how stochastic music and art can be enhanced through other mathematical methods and models that Xenakis did not use, to blend more traditional music theoretic ideas into the body of techniques introduced by him.

Meta-Xenakis—The Algorithm Is the Medium

The word “meta” stems from the Greek “μετά,” which means “transcending” in a theoretical (or structural) sense, i.e., “higher-level”; and “after,” in a temporal (or spatial) sense, i.e., “beyond.”

Many sources on Xenakis are written by and for musicologists, music composers, and performers, and as such focus on the musical output that Xenakis created.6 This is reasonable, as Xenakis was primarily known as a music composer. Fewer works have been written on the meta-level, algorithmic side of Xenakis—i.e., the algorithms or processes he created to generate musical artifacts. However, there are some notable examples of such meta-level analyses.7

In this chapter, I interpret the prompt “Meta-Xenakis” in both senses: (a) by exploring his work at a higher, algorithmic-level, something Xenakis did extensively himself, and (b) by exploring how it is possible to move forward utilizing his algorithmic contributions and innovations, which are a rich part of his intellectual and artistic inheritance.8

The next section focuses on Xenakis’s algorithmic process. It discusses an example of mathematical modeling, sonification, and computer programming he used in musical compositions.

Algorithms–A Brief Definition and History

An algorithm is a formalization of process, or a sequence of steps for performing a task. Algorithms have become prominent through their use in computer science within the last seventy years or so. However, they have existed at least for two thousand years (e.g., Euclid’s algorithm), and possibly longer, e.g., Plimpton 322, the 3,700-year-old, Babylonian clay tablet depicting various Pythagorean triples—numbers that exemplify the Pythagorean theorem and imply a procedure for generating them.9

Another early algorithmic example is the Antikythera mechanism, an ancient computational device surviving at the National Archeological Museum of Greece, constructed approximately 2,100 years ago to replicate movement of celestial bodies.10 The Antikythera mechanism employs gear ratios to implement mathematical relations, similarly to the nineteenth-century Difference and Analytical Engines, designed by Charles Babbage (1791–1871) and Ada Lovelace (1815–52).11 The connection between early algorithms, these machines, and modern computing is undeniable.

In music and art, algorithms appear as early as Guido d’Arezzo (ca. 1000 AD), and in compositions of Johann Sebastian Bach (1685–1750), Wolfgang Amadeus Mozart (1756–91), John Cage (1912–92), and Iannis Xenakis, as well as in the visual works of M. C. Escher (1898–1972), Roman Verostko (1929–2024), Vera Molnár (1924–2023), and Ernest Edmonds (b. 1942), among others.

By focusing on the algorithms used to generate pieces, i.e., the meta-level analysis followed herein, we begin to see the true extent of possibilities that Xenakis introduced to us.

It is important to make the following distinction, between analyzing the music of a particular piece—such as Pithoprakta (1955–56) or ST/10-1, 080262 (1962)—versus analyzing the algorithms created to generate such pieces. For instance, Damían Keller and Brian Ferneyhough (b. 1943) offer a notable meta-level analysis of ST/10-1, 080262:

Xenakis employed his ST (Stochastic Music) program to compose a number of works, including ST/10. The program was coded by M. F. Génuys and M. J. Barraud in FORTRAN IV on an IBM 7090 […] Xenakis utilized ST to generate data in text format which he later transcribed to musical notation. As he declared, the transcription was a delicate step, and required the making of several compositional decisions.12

Xenakis included the complete ST program in his seminal book, Formalized Music: Thought and Mathematics in Music.13 By doing so, he indicated the autonomy, and significance of algorithms in his compositional approach. This program, written in Fortran, was used to compose a number of works, including ST/10-1, 080262.14

In some regards, this Fortran (or other programming language) notation is similar to reading a musical score, for people who are well-versed in it. However, to be precise, this notation is actually a meta-score, i.e., a score (or recipe) for generating musical scores, in a particular musical style. This important observation is usually sidestepped in many sources on Xenakis. This is probably due to the fact that the intersection of people who are well-versed in both notations—computer programming as well as common practice notation—is relatively small, compared to people who can only read/write computer code, and people who can only read/write musical notation.

Input → Process → Output

All artifacts surrounding us (chairs, computers, smartphones) may be analyzed in terms of:

• The process that created them.
• The input to this process.
• The output of this process.

In the case of music and art, the process is usually hidden (or protected) in a veil of mystery (or secrecy)—few artists share their process with the world. On the other hand, the inputs to the process, the source materials (or inspiration) are available to us, usually from conversations with the artists. For instance, Claude Debussy (1862–1918) created harmonic material from gazing at colorful landscapes. Finally, the outputs of the process—the actual artifacts—are always available to experience, inspect, interpret, and evaluate. It is by experiencing these artifacts that people are attracted to a particular composer, or artist, or not—as the case may be with Xenakis, or, say, Jackson Pollock (1912–56).15

Xenakis used algorithms and mathematical models to create much of his music. For instance, he presents a thorough, eight-step process labelled “Fundamental Phases of a Musical Work,” clearly influenced by early software development processes.16

Above, I discussed one of Xenakis’s algorithms, written in the programming language Fortran. Given this algorithm, we can identify input, process, and output:

• The musical output is what most people experience first.17
• The input to the process consists of numerical data.18
• The output generated by the program is a sequence of numbers.19

However, given the program output, there are several possibilities for what to do next. One possibility is data visualization, i.e., take the numerical output and convert it to visual drawings, or charts. Such visualizations may be information preserving, or they may focus more on aesthetic or artistic outcomes, without necessarily preserving accuracy. Another possibility is data sonification, i.e., take the numerical output and convert it to sounds or a musical composition. This is mainly what Xenakis did in his ST works. Yet another possibility is data materialization. The term is relatively recent, and refers to something Xenakis did do, i.e., take the numerical output and convert it to physical form.20

Xenakis produced sonification designs, where he translated numerical data to sound. In the case of the ST program, he used solfege pitches on the Y (vertical) axis, and time on the X (horizontal) axis. The dots are actual numerical outputs, which are mapped to notes. Finally, he draws lines to connect the notes.21 The final output—the musical score—is generated by transcribing the numerical output, using a sonification design, to musical notation. Xenakis chooses to sonify these numerical data as large masses of musical point-notes. There are other possibilities, as will be shown later in the chapter. These point-notes are mapped to string pizzicati, glissandi, and other aleatoric and stochastic microsound events, to be again interpreted by chosen orchestral instruments and performers. This mapping is stochastic, in that some aspects of the performance are approximate (and may be unplayable); these aspects are left to be interpretated (or approximated by) the performers.22

The piece is eventually performed by musicians, who interpret (or approximate) the musical score, adding subtle layers of breathing, hesitation, movement, simplification, and micro-textures to the sonic outcome. This can be heard in specific performances or recordings of the piece.23

The challenging nature of Xenakis’s musical scores is expressed well in the following:24

Of the many pianists who have performed and discussed Evryali, dedicatee Marie-Françoise Bucquet perhaps best expresses the performance issues Xenakis raised, writing, “Supreme challenge: he asks us to take risks and overwhelming responsibilities. I find it wonderful that instead of saying to the performer ‘I have written this piece for you, and you are going to play it,’ he said to me ‘Here is the piece. Look at it, and if you think you can do something with it, play it.’”25

Xenakis himself states:

I do take into account the physical limitations of performers [...] But I also take into account the fact that what is limitation today may not be so tomorrow. [...] Then there are works, such as Synaphai, where it’s up to the soloist whether he plays all the notes or leaves some out. Of course, I prefer it if he plays them all. [...] But as I’ve said before, for all their difficulty, the pieces can be performed. In order for the artist to master the technical requirements he has to master himself. Technique is not only a question of muscles, but also of nerves. [...] In music the human body and the human brain can unite in a fantastic, immense harmony. No other art demands or makes possible that totality. The artist can live during performance in an absolute way. He can be forceful and subtle, very complex or very simple, he can use his brain to translate an instant into sound but he can encompass the whole thing with it also. Why shouldn’t I give him the joy of triumph—triumph that he can surpass his own capabilities?26

One may explore the value this rich interpretive space potentially adds, by listening to Xenakis’s musical scores performed through a computerized (i.e., perfectly accurate) MIDI synthesizer. For instance, one such effort appears in Grossman’s CD release comprising the pieces, Herma (1961), Mists (1980), Khoaï (1976), Evryali (1973), and Naama (1984), for solo piano or harpsichord.27 However, according to Kanach:

[This] recording of Xenakis’s keyboard music realized by computer defeats the purpose of this human, self-surpassing, personal engagement in performance. But it does lift the veil on that which cannot—yet!—be easily performed by human hands. At most then, it could be considered a pedagogical tool.28

Finally, an important point here is that Xenakis chose the way his work sounds—he meticulously crafted his sound aesthetic, through his sonification choices. In other words, his particular sound aesthetic is mainly the result of the second part of his compositional process—the sonification design. The first part—his algorithmic approach—is mostly style-agnostic, and as such it can be used with other sonification choices, bringing possibly broader acceptance, and application of his techniques to other compositional spaces. This will be demonstrated below, through specific musical examples.

Algorithmic Music: Who Is the Composer?

Authorship attribution is a significant question, often arising in algorithmic music composition. Sometimes this may even confuse experts in computer science. So, given the above example (ST/10—1,080262), who is the composer? Possible answers include:

• Carl Friedrich Gauss (1777–1855), the German mathematician who created the probabilities used for input in Xenakis’s work.
• The computer—an IBM 7090—which executed the ST program and produced the output numbers.
• Xenakis who created (a) the process, or algorithm, and (b) the sonification design used to generate the final music score.

In the original talk (upon which this chapter is based), with an audience of about 160 people, three identified Gauss as the composer, three identified the computer as the composer, but the majority identified Xenakis as the composer. Without doubt, the algorithm created the musical output. However, Xenakis wrote the algorithm, therefore, Xenakis is indeed the composer. This is a significant observation.

However, the question of authorship becomes more nuanced when the input to the process becomes statistical probabilities derived from other composers’ musical works, such as those of Bach, Mozart, or Ludwig van Beethoven (1770–1827).29 Recently, this has become a controversial topic, given the availability of software systems trained with statistical probabilities from large language models (LLMs), such as ChatGPT and DALL·E.30

Ultimately, though, this demonstrates the power of the algorithm as a creative medium, and strengthens our appreciation for Xenakis’s vision and pioneering algorithmic work. In summary, algorithms are a powerful compositional tool, as Xenakis demonstrated.31

What’s Next?

Some Xenakis-Inspired Ideas and Examples

The following sections present algorithmic music examples, derived from Xenakis’s work, as well as proposing some ideas on what might come next.

Concret PH (1958) —A Simplified Algorithm

Fig. 38.1 Algorithm for generating a simplified version of Xenakis’s Concret PH (1958), in Python. Figure created by author (2014).

Xenakis coined the term stochastic music (from the Greek stochos, “στόχος,” or target), to describe music that evolves over time within certain statistical tendencies and densities, and has points of origin and destination. Xenakis created stochastic music to react to purely chaotic, random properties of twelve-tone, or serialist music.32 He believed the listener may be aesthetically overwhelmed by the complexity of serialist music—which, although deterministic due to its rules of creation, by definition, over time sounds utterly chaotic (i.e., uniformly distributed). He proposed that statistical mathematics could be used to produce a compositional technique, whose musical outcome is more controllable. This could produce more aesthetically pleasing music, as he went on to demonstrate. His first electroacoustic composition, Concret PH, was composed intuitively (i.e., non-algorithmically, by ear) to demonstrate this.

We have constructed an algorithm to simulate a simplified version of Xenakis’s Concret PH, in Python, as shown in Figure 38.1.33 Concret PH is revisited later in this chapter, to include a probability density function that models more accurately Xenakis’s original.

UPIC—Controlling Musical Parameters through Curves

Xenakis used computer programming to create musical compositions, but also tools to assist in the compositional process. One important example is the Unité Polygogique Informatique de CEMAMu (UPIC) computer system. UPIC was invented in 1977 by Xenakis and his associates to connect visual drawing (e.g., architectural drafting) with musical or sound design, in order to achieve “sonic realization of drawn musical ideas by a computer.”34

UPIC allows a music composer to draw curves (or arcs) via stylus or mouse on a graphical user interface. Curves are converted to sounds automatically, using wave tables and envelopes to form individual sounds. This process can generate arbitrarily complex, evolving timbres, and thus offers immense compositional power to describe new sounds, whose texture unfolds over time.35 UPIC’s system design went through several iterations, over the years, to improve its functionality and usability.

UPISketch is a direct descendant of UPIC, initially developed by the Centre Iannis Xenakis (CIX) at the University of Rouen, and the European University of Cyprus (EUC) in 2018.36 Similarly to UPIC, UPISketch is a drawing sound composition tool. However, it is more advanced technologically (e.g., runs on smartphones and modern computers), and has a more intuitive interface, being geared towards a general audience.37

UPISketch follows Xenakis’s original sonification approach of pitch versus time, and, like UPIC, extends it to the continuous (i.e., frequency) domain. Users draw curves, which then are mapped to frequency, or amplitude contours, used to generate complex sound timbres. Additionally, UPISketch supports importing arbitrary audio recordings, to be used as instruments, through pitch-shifting, and micro (or granular) sampling, which is a powerful feature. UPISketch runs on iOS (iPhones, iPads), Windows, and Mac OSX, making it widely available. As an educational tool, it further promotes Xenakis’s music-pedagogic motivation for developing UPIC. As he stated in 1979:

The pedagogical interest is obvious: with UPIC, music becomes a game for children. They draw. They hear. They have everything at their fingertips. They can correct things immediately. They are not forced to learn instruments. They can imagine timbres. And above all, they can immediately devote themselves to composition.38

My research students and I have also reconstructed a simplified version of UPIC, in Python. To do so, we used JythonMusic, an environment for developing interactive musical experiences, and systems for computer-aided analysis, composition, and performance in music and art.39 JythonMusic has been used for research in music information retrieval and computational musicology, as well as in modeling aesthetics and creativity, sound spatialization, and telematics. It provides various libraries for music representation and composition, image manipulation, graphical user interface development, and interaction with external devices via MIDI and OSC (Open Sound Control), among others. Also, it works with other software, such as Ableton Live, PureData, Max/MSP, and Processing. JythonMusic’s pedagogical goal is to provide a gentle introduction to the powerful medium of algorithms, and computer programming, to musicians and computational artists. It has been used to teach algorithmic music composition, dynamic coding (live coding), and musical performativity to university students for over a decade.40

Our UPIC implementation expands on the original to control various aspects of a musical piece through curves. Although we have implemented a simple graphical user interface for drawing curves and generating sounds in real-time, in our work, we find it more useful to simply output numerical sequences—x and y coordinates of graph points—and then incorporate them algorithmically in other JythonMusic programs. This algorithmic-based UPIC approach has been taught to first-year university students, in the context of introducing algorithmic thinking and computer programming to students with musical and artistic backgrounds and interests, for over a decade.41 For example, here is an early (ca. 2010) implementation of the approach.42 After students were exposed to this approach, they were asked to create their own musical compositions, as semester final projects. Here are videos of these student projects.43 Finally, these student projects were showcased in “Visual Soundscapes,” a month-long exhibit at our university’s library.44

One might argue that embedding UPIC-generated data back into programs reverts back to Xenakis’s original, pre-UPIC approach. However—pedagogically and artistically—this is both desirable and effective, as it combines the best of both worlds: drawing (or capturing existing curves) to represent input data (like Xenakis did), with the readability, learnability, and expressivity of modern programming languages, such as Python, Processing, and Scratch.

Programming languages may be seen as actual user interfaces, and may be evaluated in terms of their usability, defined as specific attributes such as: their learnability, user efficiency, memorability, user error-proneness, and user satisfaction.45 Also, given that some of these programming languages can now fully represent (and play back!) musical data, they have become representationally equivalent to common practice music notation, and can be used as alternative music notations.46 In fact, such languages are supersets of common practice notation, because they may also represent algorithmic processes, and thus connect notation and compositional processes into one powerful and expressive representation.

In our approach, UPIC graphs may describe densities of pitch, dynamic, harmonic probability or consonance, timbre or different instruments, occurrence of arbitrary sonic events, as these unfold over time (or relative to each other). In fact, these graphs can model any musical attribute desired, as long as it can be controlled via algorithmic means. Since this is done in Python, such graphs can also control aspects of other algorithmic artifacts, including parameters of external sound engines (e.g., Ableton Live), visualizations, animation parameters, and arguments to arbitrary Python functions, thus tapping into the full power of a Turing Machine.47

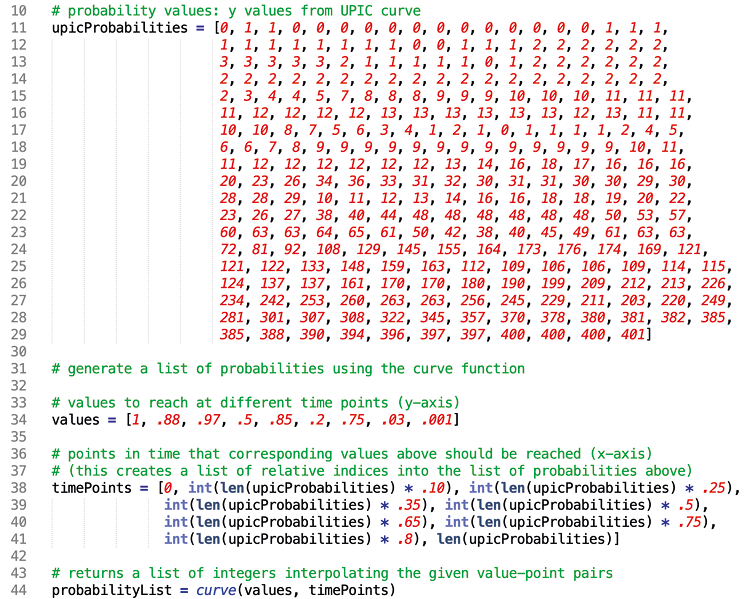
Fig. 38.2 Code excerpt implementing a UPIC-generated probability list, in Python. Figure created by author (2022).

Concret PH—A Retelling (2022)

As mentioned above, Concret PH is an early and influential piece of stochastic music, composed by Xenakis intuitively, to capture mathematical probabilities he was deeply interested in. It was performed in the Philips Pavilion at the 1958 World’s Fair, using approximately four hundred loudspeakers–arranged in five clusters, and ten channels, or sound routes. Special playback machines with a three-track sound tape, and a fifteen-track control tape were used for sound routing. Unfortunately, the Pavilion was demolished, so we cannot experience the piece as it was originally performed.48

Our reinterpretation of Concret PH utilizes speakers on audience smartphones, to recreate the multiplicity and apparent unpredictability of sound sources of the original, as well as audience movement through the performance space. We utilize our UPIC approach to control the density of sound events over time, in order to recreate the unfolding sound densities and textures of the original.

In the original, Xenakis used tape recordings of burning charcoal, partitioned into one-second fragments, pitch-shifted and overlaid, to create granular, unfolding sound textures. Our recreation uses sounds from the original,49 together with hammer-on-anvil sounds, to simulate individual charcoal sound events.

Our code distributes the required number of sound events across all participating audience smartphones. This works regardless of how many smartphones are participating. The piece may be reproduced using a single smartphone, as well as hundreds of them, always maintaining the desired density and sound texture. Participants are asked to move around freely, resembling people moving through the Philips Pavilion in 1958, to create a truly immersive experience.50

Concret PH—A Retelling was performed at the University of Maryland, College Park, USA in April 2022 (see Media 38.1). The performance was captured via a high-quality 3D binaural microphone, so stereo headphones are recommended.51

Media 38.1 Video performance of Concret PH—A Retelling using audience smartphones, at the University of Maryland, College Park, USA, April 2022.
https://hdl.handle.net/20.500.12434/3c3e3f35

Éolienne PH (2022)

Éolienne PH (or Be the Wind) was composed in the context of the 2022 Meta-Xenakis transcontinental celebration. It was performed at the International Symposium on Electronic Art (ISEA 2022) in Barcelona, in June 2022. It was partially inspired by the ISEA 2022 conference themes, “exploring our relationship with nature,” and “transforming/inhabiting our world.”

Éolienne PH is based on Xenakis’s Concret PH (see previous section). It demonstrates the importance of separating the two parts in Xenakis’s compositional process:

1. The algorithmic process used to generate numerical data.
2. The sonification choices mapping these data to sounds.

It should be emphasized that Éolienne PH utilizes the same probability density function as its sister piece, Concret PH – A Retelling—in fact, they share the exact same code. However, the sonification design of Éolienne PH employs natural, soothing sounds, such as flowing water, and birdsong. The piece was composed during COVID-19, and given the ISEA 2022 conference theme, the sonification choices were meant to create a restorative, meditative, and potentially healing experience. Similarly to its sister piece, these sounds are partitioned into small fragments, and then pitch-shifted and overlaid, to create a granular, ever-unfolding sound texture.

Éolienne PH utilizes audience smartphones to deliver its sounds. Participants are asked to move around, creating independent, aleatoric sound trajectories. This is also inspired by Xenakis’s Polytope de Mycènes (1978).52 This free movement creates infinite possibilities for sound texture and placement, as each person traverses a unique and unpredictable sound path.

Finally, the composition allows participants to generate high-quality, binaural sounds of wind-chimes—tuned in C aeolian scale—by tapping on their screens. This makes them active contributors to the unfolding soundscape, and invites (but does not require) deep listening and potentially collaboration.

A video of the ISEA 2022 performance, in Barcelona, Spain (June 2022) is available below (Media 38.2). While identical to Concret PH in terms of algorithmic design, the new sonification design produces a completely different (diametrically opposing?) aesthetic experience, and emotional outcome. This demonstrates the intrinsic value, and independence from sonic outcome, of Xenakis’s algorithmic and stochastic contributions.53

Media 38.2 Video performance of Éolienne PH, at the International Symposium on Electronic Art (ISEA 2022), in Barcelona, Spain, June 2022. It includes photographs from the performance site of Xenakis’s Polytope de Mycènes (1978) taken by author (2022).
https://hdl.handle.net/20.500.12434/6400503c

Nereides/Νηρηΐδες (2023)

As mentioned above, Xenakis was deeply interested in statistical properties of natural phenomena:

[O]ther paths also led to the same stochastic crossroads—first of all, natural events such as the collision of hail or rain with hard surfaces, or the song of cicadas in a summer field. These sonic events are made out of thousands of isolated sounds; this multitude of sounds, seen here as a totality, is a new sonic event. This mass event is articulated and forms a plastic mold of time, which itself follows aleatory and stochastic laws.54

Interestingly, originating in a different (emotional, intuitive, non-mathematical) space, Debussy makes a similar observation, in 1911:

Who will discover the secret of musical composition? The sound of the sea, the curve of the horizon, the wind in the leaves, the cry of a bird, register complex impressions within us. Then suddenly, without any deliberate consent on our part, one of these memories issues forth to express itself in the language of music. It bears its own harmony within it. By no effort of ours can we achieve anything more truthful or accurate. [...] No doubt, this simple musical grammar will jar some people. [...] I foresee that and I rejoice in it. I shall do nothing to create adversaries, but neither shall I do anything to turn enmities into friendships.55

It is intriguing to see how similar Xenakis and Debussy are, both being inspired by statistical properties of natural phenomena, and both being unapologetic about it. Still, they use different compositional tools and techniques: Xenakis, algorithmic and mathematical means; while Debussy, traditional (classical/impressionist) compositional processes.56 We have reached a point, where both Xenakis’s and Debussy’s processes (and those of other composers) can be modeled through algorithmic means and computer programming.57

Xenakis uses mathematical formulas to model natural phenomena. Being mathematical, these formulas are abstractions or generalizations, approximating trends in the actual data. They do not actually account for slight “imperfections” or noise. It should be noted that nature is never exactly ideal.58

This leads to the following compositional idea or “syllogism”: What if, in an attempt to be more precise, we bypassed the intermediate models of mathematical formulas (such as Gaussian or Poisson distributions), used by Xenakis (and others) to describe statistical tendencies of natural phenomena? Instead, what if we captured data directly from the natural phenomenon, since—technologically—we can do that now relatively easily? Thus, we can use the exact distributions or fluctuations of densities in natural phenomena, for instance, through processing of high-quality audio recordings, or high-resolution images.59

Nereides/Νηρηΐδες is an experimental piano miniature piece, which demonstrates this approach. It was composed for the seventieth anniversary celebration of The Friends of Music Society of Greece. It explores the ever-unfolding interplay between sky and sea–the evaporation-condensation-precipitation cycle. It is named after the female spirits of sea waters of Ancient Greece, the Nereides, that personify the cycle of water. I used our UPIC approach to capture trajectories or curves of white light (or luminosity), in the cloudy sky image shown in Figure 38.3. I extracted the distributions of light straight from the source material (an image, in this case), making deliberate choices where trajectories begin and end, and how they spread onto the piece’s timeline—some are lengthier, others shorter, some slower, others faster, some inverted, and so on. This is similar to Xenakis’s choices using UPIC, i.e., where to draw shapes, how long to draw them, etc. Nereides/Νηρηΐδες is then literally, and figuratively, a stochastic study of light in a cloudy sky. Through this process, intuitively, I selected six trajectories, or curves. These were given the following Nereid names: Autonoe/Αὐτονόη, Ianassa/Ἰάνασσα, Eione/Ἠιόνη, Galene/Γαλήνη, Melita/Μελίτη, and Evarne/Εὐάρνη.60

Fig. 38.3 Source of thematic material for Nereides/Νηρηΐδες. Six trajectories, or curves, were selected intuitively (i.e., by ear) to capture the variety of white light distributions and densities (not shown). Photo by author (2022).

Nereides/Νηρηΐδες resembles Xenakis’s Evryali (1973) for solo piano, as it also consists of arborescences, or branching patterns of melodic material (see Figure 38.4). Similar to Evryali, these interweave to create harmonic patterns of varying and unfolding complexity.61 Unlike Evryali, the sonification design resembles Arvo Pärt’s (b. 1935) Tintinnabuli style, used, for example, in Für Alina (1976).

Nereides/Νηρηΐδες has a fractal, or self-similar structure. This is a direct result of the source material (i.e., cloud formations) being fractal.62 Also, the piece may sound deceptively simple. However, under the apparent musical simplicity, hides an intricate interweaving of pitches and rhythmic material that fit harmoniously together.63 It should again be emphasized that the source material originates from a cloudy sky. The trajectories were selected intuitively (i.e., non-algorithmically, by ear) to consist of reflective patterns. These patterns originated in the natural processes that produced these clouds. This image in Figure 38.3 contains unusual, yet very appealing—or aesthetically pleasing—groupings of cloud patterns. The sonification design attempts to preserve this essence, or aesthetic quality, and reflect it (or map it) in the harmonic interweaving of melodic lines. The source material depicts a natural phenomenon—cloudy sky—that is somewhat unpredictable, contrasting, yet relatively stable, non-chaotic. Thus, the extracted probability distributions reflect a natural phenomenon that has reached a plateau of low entropy, or relative balance.64 Some might say it is beautiful.

Fig. 38.4 The arborescences/branching patterns of Nereides/Νηρηΐδες, generated from intuitively combining the six trajectories, in piano roll notation. It is interesting to note the emergent large fractal X, consisting of many, smaller X’s (reminiscent perhaps of Xenakis’s initial on some CDs of his music). Figure created by author (2023).

Nereides/Νηρηΐδες supports the performance approach suggested by Xenakis in his stochastic pieces, such as Evryali (1973) and Synaphaï (1969), which invite the performer to engage their dexterity and decide which notes they may play, and which to omit. Being fractal (due to its source material), Nereides/Νηρηΐδες has the same stochastic quality, i.e., not every note is necessary. In other words, the piece sounds approximately the same, even when some notes are left out. Here is a relevant part of Xenakis’s earlier quote, to emphasize this point:

[T]here are works, such as Synaphai, where it’s up to the soloist whether he plays all the notes or leaves some out. Of course, I prefer it if he plays them all. [...] Why shouldn’t I give him the joy of triumph—triumph that he can surpass his own capabilities?65

Being inspired by both Xenakis’s and Debussy’s perspectives above, here is the composer’s artistic intent, for this piece:

“Only from the heart can you touch the sky” (Rumi). I gazed upon this breathtaking sky […] and then began to translate it to sound. Wrote some code to help. I kept interweaving parts, until I managed to “liberate” the sound I was seeing...

Given its fractal nature, the piece can be played at different levels of abstraction. In its original form, it requires six hands, one for each melodic contour or trajectory. It has also been reduced to be playable by two hands. This version was performed at the Megaron Athens Concert Hall in November 2023, as part of the celebration for the seventieth anniversary of The Friends of Music Society of Greece (see Media 38.3).

Media 38.3 Performance of Nereides/Νηρηΐδες at the Megaron Athens Concert Hall in November 2023, as part of the celebration for the seventieth anniversary of The Friends of Music Society of Greece.
https://hdl.handle.net/20.500.12434/ed314ac8

on the Fractal Nature of Being… (2022)

As a final example, the piece on the Fractal Nature of Being… was also composed in the context the 2022 Meta-Xenakis transcontinental celebration. It was performed at the Music Library of Greece in May 2022. It brings together everything discussed so far, exploring how stochastic and aleatoric techniques introduced by Xenakis may be combined with traditional music theory and modern mathematics/fractal geometry. Also, audience members are invited to participate via their smartphones, contributing to the performance via their speakers and accelerometers.

The piece is modeled after a fractal plant-like structure, or arborescence, known as the golden tree, which incorporates the golden ratio, or φ (0.61803398…). Figure 38.5 shows the code used to generate a golden tree. Figure 38.6 shows one possible output. Following this format, the piece is built from a one-minute-long harmonic theme, shown in Figure 38.7, which serves as the “trunk” of the tree. This theme is expanded and embellished upon, at different levels of granularity, as the piece unfolds.

Fig. 38.5 Code for generating a fractal arborescence, known as golden tree, in Python. This algorithm models the on the Fractal Nature of Being… piece structure. As seen above, the structure incorporates the golden ratio and fractal geometry (i.e., self-similarity through subdivision). Figure created by author (2014).

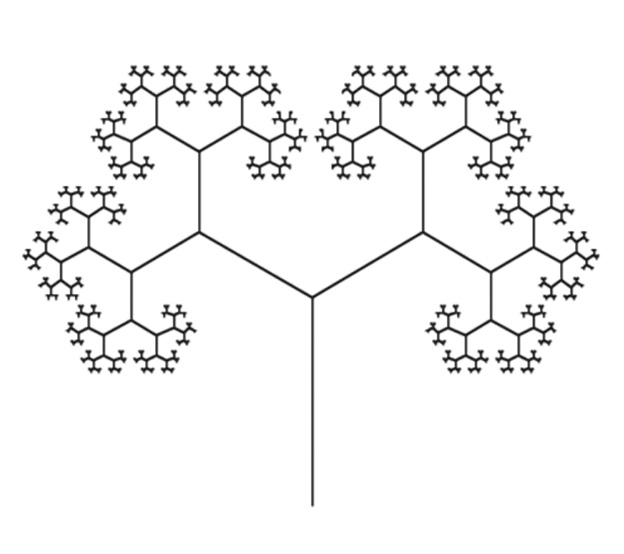
Fig. 38.6 Output of code in Figure 38.5—a golden tree—is a fractal plant-like shape, which incorporates the golden ratio, or φ (0.61803398…). The musical structure of on the Fractal Nature of Being… is based on this shape. Figure created by author (2014).

Fig. 38.7 The musical theme—or fractal trunk—of on the Fractal Nature of Being… The piece unfolds fractally from this theme, following a golden tree structure (see Figure 38.6). Figure created by author (2022).

The fractal structure of the piece begins with the harmonic theme being introduced on the piano. As the piece progresses, this theme is repeated at different levels of granularity, by different instruments, including smartphones, cello, bassoon, and guitar—using tempo (faster), register (higher octaves), and randomness (improvised, aleatoric notes), in order to create musical space for the fractal to unfold, and other instruments to enter.

A UPIC-based probability density function controls the interplay between consonance and dissonance, which is a meta-Xenakian idea (as Xenakis mainly focused on the statistical interplay between sounds and silence). The piece moves through seven phases, each introducing a new instrument, while earlier instruments cyclically move to higher levels of detail (via register and tempo). The fifth phase introduces dissonance utilizing stochastic probabilities from the first minute and a half of Xenakis’s Metastasis (1953–4).66 This phase also uses increased loudness of notes on smartphones, to highlight them. Then, at the piece’s golden ratio, the dissonance ends, and a new phase begins with the bassoon restoring consonance. In the seventh and last phase, instruments go out one by one, ending the piece on an ambiguous interval (a major 2nd). Smartphone sounds are controlled via algorithm, while physical instruments improvise on the theme (in F minor), at different levels of granularity, based on their fractal level in the piece structure at the time. On the visual side, the performance includes fractal images displayed on a screen (see Media 38.4), a new image per phase, whose fractal properties (or entropy) are controlled by the accelerometers of participating audience smartphones. When the audience smartphones are still, the image’s fractal structure is precisely the golden tree.67 As the piece progresses, phase transitions are marked by new fractal images, selected to match the tone or aesthetic of the phase.

Finally, the algorithmic part of the piece—which includes transitioning from one phase of the piece to the next, updating images to be displayed on the venue’s main screen, sending control messages to smartphones with instructions on what sounds to play and when, and adjusting volumes of smartphone speakers in real-time, as needed—is done partially through a specially-designed user interface, running on a dedicated smartphone or tablet. This allows one of the performers to serve in part as a human conductor,68 walking through the venue (among participants and performers), listening to the piece unfold, adjusting volumes in real time, keeping track of time, and deciding when to transition the piece to a new phase, including when to end the piece. For simplicity, human performers are synchronized through transitions of images on the venue’s main screen, and a small visual score.

Media 38.4 Performance of on the Fractal Nature of Being… at the Music Library of Greece, in Athens, Greece (May 2022). The piece utilizes audience smartphones for distributing sounds and controlling aspects of the performance.69
https://hdl.handle.net/20.500.12434/1a7eb5c9

The Algorithmic Arts: Discussion and Closing

The infusion of algorithms in the arts has increased dramatically since the greater availability of computers starting in the 1960s. All areas of art and entertainment, such as graphics, design, animation, sculpture, dance, theater, music, and film, to name a few, have been impacted greatly. At the same time, the inverse infusion of artistic creativity, design, and innovation into computing, engineering, and other STEM fields produces a creative tension, which leads to new ideas, and continues to produce new discoveries:70

Art and science are in a tension that is most fruitful when these disciplines observe and penetrate each other and experience how much of the other they themselves still contain.71

As Xenakis himself said in 1979:

From here nothing prevents us from foreseeing a new relationship between the arts and the sciences, especially between the arts and mathematics: where the arts would consciously “set” problems which mathematics would then be obliged to solve through the invention of new theories.72

In the intersection of music, computing, and engineering, we find significant advances relating to the aesthetic, as well as the algorithmic, mathematical, and technological. In this context, Iannis Xenakis is a prime example of a polymath: an individual who combined mathematics, computing, and technology; with music, architecture, visual arts and performance; and multimedia to produce artifacts existing in this intersection. These contributions should also be seen from an algorithmic arts perspective to be fully and adequately appreciated.

In the United States, where this chapter is written, we have the emergence of a pedagogic movement to promote the combination of the creative-arts and design with science, technology, engineering and math (STEM + Art = STEAM). This movement has also spread to Europe and other parts of the world. For instance, Zeyenp Özer and Rasim Erol Demirbatır present a study of STEAM-inspired computer applications used in music education, including UPISketch (mentioned above), MIT Scratch, earSketch, and iMuSciCA. For more information on these programs, including how to access them, please refer to their article.73 Xenakis might have appreciated this development.

Being funded by both the US National Science Foundation (NSF) and the US National Endowment for the Arts (NEA), an algorithmic arts (AlgoArts) meeting was held in January 2022 to examine the potential for standardizing and bringing greater amalgamation—or synthesis—between the aesthetic sophistication, creativity, and design of the arts; and the technological mastery, mathematical rigor, and theory of computer science, and engineering.

This two-day meeting, entitled “The Arts and the Algorithm – An Amalgamation” was the first of its kind in the United States. It brought together 422 researchers, educators, and practitioners who synthesize, or integrate computing, engineering, and the arts.74

In closing, this chapter argues that we have finally reached a point where the algorithm has become a creative medium, for artists and musicians. As we move forward into the twenty-first century, researchers, composers, artists, and educators are engaging algorithmically, and are interweaving algorithmic thinking and development of technological solutions, into their art theory and creative practice.

Young composers and musicians, who are learning common practice notation, should also learn this new, powerful musical notation, and thus enter the magical world of Xenakis.75 In fact, some may argue that this should be a requirement in a well-rounded musical curriculum, not unlike algebra (which was probably a revolutionary concept in the Renaissance), given the de-facto importance and prevalence of computers in music creation. There is a fundamental difference between a creator of music via an existing program, such as Logic Pro or Ableton Live, and a creator of new musical tools and compositional approaches (notice the shift to the meta-level), like Xenakis with his ST program and UPIC, among others.

This is captured very eloquently, but perhaps a bit polemically by Douglas Rushkoff:

When human beings acquired language, we learned not just how to listen but how to speak. When we gained literacy, we learned not just how to read but how to write. And as we move into an increasingly digital reality, we must learn not just how to use programs but how to make them. In the emerging highly programmed landscape ahead […] it’s really that simple: Program, or be programmed.76

In analyzing Rushkoff’s point, we see that, as students become creators of new digital material (e.g., images, sounds, videos, etc.) through available options in professional software, such as Photoshop and Ableton Live, their creative thinking is limited by what is easily achievable–and ultimately possible–in the specific “sandbox” they use. And, while this is a wonderful way to be introduced to the world of art and music creation, and a powerful motivator to learn more, the future demands “out-of-the-box” thinkers–people who will create new things that have not been done before.

This is precisely what Xenakis did in a pioneering way, given how early he engaged with algorithms and computer programming, for musical and artistic purposes. In essence, Xenakis paved the way. Now, we must follow it…

References

BOUROTTE, Rodolphe and KANACH, Sharon (2019), “UPISketch: The UPIC Idea and Its Current Applications for Initiating New Audiences to Music,” Organised Sound, vol. 24, no. 3, p. 252–60, https://doi.org/10.1017/S1355771819000323

COPE, David (1997), Techniques of the Contemporary Composer, Boston, Massachusetts, Cengage Learning.

COPE, David (2001), Virtual Music: Computer Synthesis of Musical Style, Cambridge, Massachusetts, MIT Press.

DI SCIPIO, Agostino (1998), “Compositional Models in Xenakis’s Electroacoustic Music,” Perspectives of New Music, vol. 36, no. 2, p. 201–43.

FORGETTE, Anna, MANARIS, Bill, GILLIKIN, Meghan, and RAMDSEN, Samantha (2022), “Speakers, More Speakers!!! – Developing Interactive, Distributed, Smartphone-Based, Immersive Experiences for Music and Art,” in Pau Alsina, Irma Vilà, Susanna Tesconi, Joan Soler-Adillon, and Enric Mor (eds.), Proceedings of the 28th International Symposium on Electronic Art (ISEA 2022), Barcelona, Spain, p. 275–81.

GROSSMANN, Daniel (2008), Herma for piano (1961), Mists for piano (1980), Khoaï for harpsichord (1976), Evryali for piano (1973), and Naama for harpsichord (1984), in Iannis Xenakis, Music for Keyboard Instruments—Realized by Computer. MIDI Programming, Munich, Neos CD 10707.

HARLEY, James (2002), “The Electroacoustic Music of Iannis Xenakis,” Computer Music Journal, vol. 26, no. 1, p. 33–57.

HARLEY, James (2004), Xenakis: His Life in Music, London, Routledge, https://doi.org/10.4324/9780203342794

HOFFMANN, Peter (2000), “The New GENDYN Program,” Computer Music Journal, vol. 24, no. 2, p. 31–8.

HOFFMANN, Peter (2009), Music Out of Nothing? A Rigorous Approach to Algorithmic Composition by Iannis Xenakis, doctoral dissertation, Technical University of Berlin.

HOFSTADTER, Douglas R. (1989), Gödel, Escher, Bach: An Eternal Golden Braid, New York, Vintage Books.

KALFF, Louis, TAK, Willem, and DE BRUIN, S. L. (1958), “The ‘Electronic Poem’ Performed in the Philips Pavilion at the 1958 Brussels World Fair,” Philips Technical Review, vol. 20, no. 2/3, p. 37–84.

KANACH, Sharon (ed.) (2010), Performing Xenakis, Hillsdale, New York, Pendragon.

KANACH, Sharon (ed.) (2012), Xenakis Matters: Contexts, Processes, Applications, Hillsdale, New York, Pendragon.

KELLER, Damián and FERNEYHOUGH, Brian (2004), “Analysis by Modeling: Xenakis’s ST/10-1 080262,” Journal of New Music Research, vol. 33, no. 2, p. 161–71, https://doi.org/10.1080/0929821042000310630

KOTZAMANI, Marina (2014), “Greek History as Environmental Performance: Iannis Xenakis’ Mycenae Polytopon and Beyond,” Gramma: Journal of Theory and Criticism, vol. 22, no. 2, p. 163–78, https://doi.org/10.26262/gramma.v22i2.6262

LOMBARDO, Vincenzo, VALLE, Andrea, FITCH, John, TAZELAAR, Kees, WEINZIERL, Stefan, and BORCZYK, Wojciech (2009), “A Virtual-Reality Reconstruction of Poème Électronique Based on Philological Research,” Computer Music Journal, vol. 33, no. 2, p. 24–47.

MANARIS, Bill (2007), “Dropping CS Enrollments: Or the Emperor’s New Clothes?” ACM SIGCSE Bulletin, vol. 39, no. 4, p. 6–10, https://doi.org/10.1145/1345375.1345377

MANARIS, Bill, ROMERO, Juan, MACHADO, Penousal, KREHBIEL, Dwight, HIRZEL, Timothy, PHARR, Walter, and DAVIS, Robert B. (2005), “Zipf’s Law, Music Classification and Aesthetics,” Computer Music Journal, vol. 29, no. 1, p. 55–69.

MANARIS, Bill, ROOS, Patrick, MACHADO, Penousal, KREHBIEL, Dwight, PELLICORO, Luca, and ROMERO, Juan (2007), “A Corpus-Based Hybrid Approach to Music Analysis and Composition,” in Anthony Cohn (ed.) Proceedings of 22nd Conference on Artificial Intelligence (AAAI-07), Vancouver, Canada, p. 839–45.

MANARIS, Bill and BROWN, Andrew R. (2014), Making Music with Computers: Creative Programming in Python, London, Routledge.

MANARIS, Bill, MCCAULEY, Renée, MAZZONE, Marian, and BARES, William (2014), “Computing in the Arts: A Model Curriculum,” in Proceedings of the 45th ACM Technical Symposium on Computer Science Education (SIGCSE 2014), Atlanta, Georgia, Association for Computer Machinery, p. 451–6, https://doi.org/10.1145/2538862.2538942

MANARIS, Bill, JOHNSON, David, and ROURK, Mallory (2015), “Diving into Infinity: A Motion-Based, Immersive Interface for M.C. Escher’s Works,” in Proceedings of 21st International Symposium on Electronic Art (ISEA 2015), Vancouver, Canada, p. 8.

MANARIS, Bill, STEVENS, Blake, and BROWN, Andrew R. (2016), “JythonMusic: An Environment for Teaching Algorithmic Music Composition, Dynamic Coding, and Musical Performativity,” Journal of Music, Technology & Education, vol. 9, no. 1, p. 55–78.

MANARIS, Bill, BROUGHAM-COOK, Pangur, HUGHES, Dana, and BROWN, Andrew R. (2018), “JythonMusic: An Environment for Developing Interactive Music Systems,” in Proceedings of the 18th International Conference on New Interfaces for Musical Expression (NIME 2018), Blacksburg, Virginia, p. 259–62.

MANARIS, Bill and McCAULEY, Renée (eds.) (2022), The Arts and the Algorithm: An Amalgamation—Report on the Algorithmic Arts (AlgoArts) Workshop, co-sponsored by the US National Science Foundation and the US National Endowment for the Arts, p. 67, https://algoarts.org/report

MARINO, Gérard, SERRA, Marie-Hélène, and RACZINSKI, Jean-Michel (1993), “The UPIC System: Origins and Innovations,” Perspectives of New Music, vol. 31, no. 1, p. 258–69.

NATIONAL ENDOWMENT FOR THE ARTS (2019), Arts and Research—Partnerships in Practice: Proceedings from the First Summit of the National Endowment for the Arts Research Labs, Washington, DC, National Endowment for the Arts, https://www.arts.gov/impact/research/publications/arts-and-research-partnerships-practice

ÖZER, Zeynep and DEMIRBATIR, Rasim Erol (2023), “Examination of STEAM-based Digital Learning Applications in Music Education,” European Journal of STEM Education, vol. 8, no. 1, p. 11, https://doi.org/10.20897/ejsteme/12959

PAPARRIGOPOULOS, Kostas (2015), “The Sounds of the Environment in Xenakis’ Electroacoustic Music,” in Makis Solomos (ed.), Iannis Xenakis, La Musique Électroacoustique / The Electroacoustic Music, Paris, Éditions L’Harmattan, p. 201–10.

PAGE, Rex and DIDDAY, Rich (1980), FORTRAN 77 for Humans, Eagan, Minnesota, West Publishing.

STARRETT, Courtney, REISER, Susan, and PACIO, Tom (2018), “Data Materialization: A Hybrid Process of Crafting a Teapot,” Leonardo, vol. 51, no. 4, p. 381–85, https://doi.org/10.1162/leon_a_01647

ROADS, Curtis (2004), Microsound, Cambridge, Massachusetts, MIT Press.

ROBSON, Eleanor (2002), “Words and Pictures: New Light on Plimpton 322,” American Mathematical Monthly, vol. 109, no. 2, p. 105–20.

REYNOLDS, Roger and REYNOLDS, Karen (2021), Xenakis Creates in Architecture and Music—The Reynolds Desert House, London, Routledge.

RILLIG, Matthias C., BONNEVAL, Karine, DE LUTZ, Christian, LEHMANN, Johannes, MANSOUR, India, RAPP, Regine, SPAČAL, Saša, and MEYER, Vera (2001), “Ten Simple Rules for Hosting Artists in a Scientific Lab,” PLoS Computational Biology, vol. 17, no. 2, p. 1–5, https://doi.org/10.1371/journal.pcbi.1008675

ROOSE, Kevin (2022), “The Brilliance and Weirdness of ChatGPT,” New York Times, 5 December, https://www.nytimes.com/2022/12/05/technology/chatgpt-ai-twitter.html

RUSHKOFF, Douglas (2010), Program or Be Programmed: Ten Commands for a Digital Age, New York, OR Books.

SCHAFER, R. Murray (1993), The Soundscape–Our Sonic Environment and the Tuning of the World, Merrimac, Massachusetts, Destiny Books.

SCHROEDER, Manfred R. (1991), Fractals, Chaos, Power Laws: Minutes from an Infinite Paradise, New York, W. H. Freeman.

SPEHAR, Branka, CLIFFORD, Colin W.G., NEWELL, Ben R., TAYLOR, and Richard P. (2003), “Universal Aesthetic of Fractals,” Computers and Graphics, vol. 27, p. 813–20.

SOLOMOS, Makis (2008), Ιάννης Ξενάκης: Το Σύμπαν ενός Ιδιότυπου Δημιουργού, Athens, Alexandria Press.

SOLOMOS, Makis (2021), From Music to Sound—The Emergence of Sound in 20th- and 21st-Century Music, London, Routledge.

TAYLOR, Richard P., MICOLICH, Adam P., and JONAS, David (1999), “Fractal Analysis of Pollock’s Drip Paintings,” Nature, vol. 399, p. 422, https://doi.org/10.1038/20833

VALLAS, Léon (1933), Claude Debussy: His Life and Works, Oxford, Oxford University Press.

VALLE, Andrea, KEES, Tazelaar, LOMBARDO, Vincenzo (2010), “In a Concrete Space. Reconstructing the Spatialization of Iannis Xenakis’ Concret PH on a Multichannel Setup,” in Proceedings of the 7th Sound and Music Computing Conference (SMC 2010), Barcelona, Spain, SMC, p. 271–78.

VINCENT, Nick, LI, Hanlin (2023), “ChatGPT Stole Your Work. So What Are You Going to Do?” Wired Magazine, 20 January, https://www.wired.com/story/chatgpt-generative-artificial-intelligence-regulation

XENAKIS, Iannis (1971), Formalized Music: Thought and Mathematics in Music, Bloomington, Indiana, Indiana University Press, https://issuu.com/markusbreuss1/docs/formalized_music._thought_and_mathe

XENAKIS, Iannis (1985), Arts-Sciences, Alloys: The Thesis Defense of Iannis Xenakis before Olivier Messiaen, Michel Ragon, Olivier Revault d’Allonnes, Michel Serres, and Bernard Teyssèdre, translated by Sharon Kanach, Hillsdale, New York, Pendragon.

XENAKIS, Iannis (2008), Music and Architecture: Architectural Projects, Texts, and Realizations, compilation, translation, and commentary by Sharon Kanach, Hillsdale New York, Pendragon.

VALLIANATOS, Evaggelos (2012), “Deciphering and Appeasing the Heavens: The History and Fate of an Ancient Greek Computer,” Leonardo, vol. 45, no. 3, p. 250–57.

---

1. 1 This work is partially co-sponsored by the US National Science Foundation and the US National Endowment for the Arts, under CNS-2139786, “Computing in the Arts—The Algorithm is the Medium,” http://AlgoArts.org. It is partially based on a talk given at the Music Library of Greece, in May 2022. It also includes materials presented at the International Symposium on Electronic Art (ISEA) 2022 conference (Forgette et al., 2022), and the first Algorithmic Arts workshop (Manaris and McCauley, 2022). The author would like to thank Stephanie Merakos, Director, Music Library of Greece, for her invitation to give the talk upon which this paper is based. The author would also like to acknowledge Anna Forgette and Samantha Ramsden, for their contributions to design, computer programming, and execution of the performances reported herein. Andrew Brown contributed to the implementation of Concret PH in JythonMusic. Meghan Gillikin and Nick Moore helped with the design, programming, and testing of the experiences. Finally, the musicians, Yiannis Bafaloukas (piano), Daniel Brown (cello), and Devon Wyland (bassoon) traveled from the Netherlands, United States, and Germany, respectively, to be part of the performance of the on the Fractal Nature of Being… piece.

2. 2 See Di Scipio, 1998; Kanach, 2008; Kanach, 2010; Kanach, 2012; Lombardo et al., 2009; Reynolds and Reynolds, 2021; Schafer, 1993; Solomos, 2008; Solomos, 2021; Valle et al., 2010.

3. 3 Xenakis, 1985.

4. 4 Hoffmann, 2000; Xenakis, 1971.

5. 5 Meta-Xenakis, https://meta-xenakis.org; “Iannis Xenakis and Algorithmic Music” (31 May 2022), BLOD, https://www.blod.gr/lectures/iannis-ksenakis-kai-algorithmiki-mousiki

6. 6 See for example Solomos, 2008; Solomos, 2021; Roads, 2004.

7. 7 Xenakis, 1971; Reynolds and Reynolds, 2021; Hoffmann, 2009.

8. 8 Cf. Xenakis, 1971.

9. 9 Plimpton 322 does not describe the actual Pythagorean theorem, which was named after the Greek philosopher Pythagoras (c. 570–495 BCE), and which was communicated to us through Book I of Euclid’s Elements (see The Editors of Encyclopaedia Britannica, “Pythagorean Theorem,” Encyclopaedia Britannica, https://www.britannica.com/science/Pythagorean-theorem). However, the existence of Plimpton 322 presupposes the algorithm, or process for generating such numbers. Cf. Robson, 2002.

10. 10 Vallianatos, 2012.

11. 11 Manaris and Brown, 2014, p. 4–5..

12. 12 Keller and Ferneyhough, 2004, p. 162.

13. 13 Xenakis, 1971, p. 145–52.

14. 14 Fortran was the state-of-the-art, high-level programming language, at the time.

15. 15 Jackson Pollock’s process generated artifacts with similar statistical properties to Xenakis’s (Taylor et al., 1999).

16. 16 Compare Xenakis, 1971, p. 22; Page and Didday, 1980, p. 248–9.

17. 17 See first five measures of ST/10-1, 080262 in Xenakis, 1971, p. 154.

18. 18 Fortran, like most programming languages, allows embedding of external data in programs: see Xenakis, 1971, p. 152.

19. 19 Xenakis, 1971, p. 153.

20. 20 This is the case, for example, with the architectural design of the Philips Pavilion: see Kalff et al., 1958; Harley, 2004. For more on data materialization see Starrett et al., 2018.

21. 21 Xenakis, 1971, p. 18–19.

22. 22 For instance, in Evryali (1973), Xenakis overlooks the fact “that the two hands and ten fingers of the pianist can only reach so far … and even includes a high C#, beyond the range of any piano” (Harley, 2004, p. 75).

23. 23 Ryan Power, “Iannis Xenakis—ST/10-1, 080262 (Audio + Full Score)” (09 Nov 2021), YouTube, https://youtu.be/Jtoge5GIa9o

24. 24 One may argue that this contributes to why he is admired by some musicians, while avoided by others.

25. 25 Harley, 2004, p. 74.

26. 26 Kanach, 2010, p. xii.

27. 27 Grossmann, 2008.

28. 28 Kanach, 2010, p. xii.

29. 29 See Cope, 2001; Manaris et al., 2007.

30. 30 Roose, 2022; Vincent and Li, 2023.

31. 31 This raises a forward-thinking, corollary question: Since algorithms are such a creative medium, when should algorithmic music composition, and computer programming, in particular, become part of a well-rounded music education curriculum, and begin to be taught broadly in conservatories?

32. 32 Xenakis, 197, p. 8–9.

33. 33 Manaris and Brown, 2014, p. 166–7.

34. 34 Bourotte and Kanach, 2019, p. 252.

35. 35 Marino et al., 1993.

36. 36 Bourotte and Kanach, 2019.

37. 37 UPISketch was developed under the Creative Europe program, Interfaces, whose goal is to explore innovative ways of introducing audiences to the work of cutting-edge musicians and sound artists (see Interfaces Network, http://www.interfacesnetwork.eu).

38. 38 Xenakis, 1979, p. 96, quoted in Bourotte and Kanach, 2019, p. 253.

39. 39 JythonMusic, http://jythonMusic.org

40. 40 Manaris and Brown, 2014; Manaris et al., 2016; 2018.

41. 41 Manaris et al., 2014; Manaris and Brown, 2014.

42. 42 “Sonifying images,” JythonMusic, https://jythonmusic.me/ch-7-sonification-and-big-data/#Sonifying-images

43. 43 It should be emphasized that these students had not programmed before (for the most part): “Computing in the Arts @CofC,” Vimeo, https://vimeo.com/cofccita

44. 44 This exhibit was funded in part by the US National Science Foundation, under grant “Computing in the Arts: A Model Curriculum” (DUE #1044861).

45. 45 Manaris, 2007.

46. 46 Something that might have given Xenakis immense joy, since this is precisely what he was trying to do with his Fortran and BASIC programs, i.e., represent musical data and processes. This is precisely the reason why programming languages like Max/MSP (and Pure Data) have been invented at Ircam (and elsewhere), and are being used widely by music composers, around the world, to create avant-garde music.

47. 47 Another wonderful alternative, also inspired by UPIC, is the graphical environment IanniX, a sequencer for digital art and real-time control. See Iannix, https://www.iannix.org/

48. 48 Kalff et al., 1958; Lombardo et al., 2009; Valle et al., 2010.

49. 49 See pelodelperro, “Iannis Xenakis - Concret PH” (4 January 2011), YouTube,
    https://youtu.be/XsOyxFybxPY

50. 50 Forgette et al., 2022.

51. 51 Recording courtesy of Ian McDermott, Immersive Media Design, University of Maryland.

52. 52 Kotzamani, 2014.

53. 53 This also suggests that those who possibly dislike Xenakis’s music, may only dislike his sonification choices, but not his algorithmic ones.

54. 54 Xenakis, 1971, p. 8–9.

55. 55 Debussy, cited in Vallas, 1933, p. 226.

56. 56 Cope, 1997.

57. 57 For example, see Manaris and Brown, 2014.

58. 58 For example, the Earth is not spherical, and its orbit is not a perfect ellipsis—there are perturbations not captured by traditional geometrical or mathematical models, which tend to be ideal.

59. 59 This was not an option during Xenakis’s time, since computing and related technologies were at their infancy. Now, this is easy, given advances in computer science (e.g., see Manaris and Brown, 2014, p. 191–240).

60. 60 Fifty Nereid names have survived from antiquity. These six were selected intuitively, to match the musical characteristics of each trajectory, based on what we know about each of the Nereides.

61. 61 Harley, 2004, p. 74.

62. 62 Spehar, et al., 2003; Schroeder, 1991.

63. 63 This is perhaps reminiscent of the deceptive simplicity of Bach’s Trias Harmonica (BWV 1072)—where a single theme is inverted, doubled, and time-shifted in various ways, to create eight independent trajectories (voices), that fit perfectly/harmoniously together (Manaris and Brown, 2014, p. 108–9). It is also perhaps reminiscent of tessellations in M.C. Escher works (Hofstadter, 1989; Manaris et al., 2015).

64. 64 Manaris et al., 2005.

65. 65 Kanach, 2010, p. xii.

66. 66 See jarkkkoo, “Iannis Xenakis – Metastasis” (9 Oct 2006), YouTube, https://youtu.be/SZazYFchLRI

67. 67 This can be seen later in the video of the piece’s performance.

68. 68 The other part is done automatically, through a digital musical score of the piece, which sends control messages to participating smartphones on what sounds to play and when.

69. 69 Incidentally, this performance coincided with the last day of COVID-19 restrictions.

70. 70 STEM is a common acronym in education that stands for science, technology, engineering and mathematics. See National Endowment for the Arts, 2019.

71. 71 Rillig et al., 2001, p. 1.

72. 72 Xenakis, 1979, p. 3.

73. 73 Özer and Demirbatır, 2023.

74. 74 AlgoArts, http://algoarts.org

75. 75 Who learned to read and write the now arcane syntax of Fortran on his own, and created so much with it.

76. 76 Rushkoff, 2010, p. 7.