12. Art and anti-mathematics

Houman Harouni

©2024 Houman Harouni, CC BY-NC 4.0 https://doi.org/10.11647/OBP.0407.12

Scattered across history and cultures, we encounter instances of people trying to limit or reject the expansion and application of mathematics. These actions, which we can refer to as “anti-mathematics”, are particularly common among artists of the modern era. This chapter tries to decipher, through a close reading of a large group of examples, the different motivations and desires that give rise to anti-mathematics across different contexts. The author argues that such actions are attempts at shielding particular ways of life from the encroachment of forces (economic, philosophical, and administrative) that use mathematics as their main instrument. In art, the pain and confusion caused by the uses of mathematics can be hurled back at those uses and expose their underlying violence. Anti-mathematics, however, does not only expose. It always creates new zones, new approaches, new products for thinking and life. The author finally connects these historical examples with the experience of children in contemporary schools and suggests that a study of anti-mathematics might be the key to developing an autonomous and rational relationship to the irrationality of mathematized reason.

Let it not be four: Anti-mathematics and science

“Every prayer”, Ivan Turgenev wrote in 1881, “reduces itself to this: Great God, grant that twice two be not four” (Turgenev, 2015, p. 102). Almost eighty years earlier, in Germany, Novalis had written that “miracles, as facts contrary to nature, are anti-mathematical” (Novalis, 2021, p. 289). Both sayings open, almost immediately, onto a familiar battlefield: the one between the hard rationality of science on one side and the softened allure of religion, occultism, and romanticism on the other. It is a sentiment that energized many in the European eighteenth and nineteenth centuries, as they stood amid the transformation of the world through a power whose surest instrument, beside gunpowder, was mathematics. Almost seventy years earlier, in 1813, Lord Byron had written to his wife-to-be, the mathematician Anne Milbanke: “I know that two and two make four—& should be glad to prove it too if I could—though I must say if by any sort of process I could convert 2 & 2 into five it would give me much greater pleasure” (Byron, 1899, p. 404). In all of these pronouncements on the nature of 2+2 we can hear two ideas, stated simultaneously. The first is a desire for something anti-mathematical, something that breaks the bounds of certainty. The second is a confession that reality has already become fully subject to mathematical models and explanations. 2+2 was not merely a mathematical sentence, but a weapon that could be used to promote or forestall social transformation. Only a few years before and not far from where Turgenev wrote ‘The Prayer’, the revolutionary Mikhail Bakunin had used the formula to dismiss deism, perhaps the last rationalist attempt at a religious perspective, as “a philosophical vinegar sauce of the most opposed systems […] accompanied, of course, by an ignorance, as contemptuous as it is complete, of natural science, and proving just as two times two make five, the existence of a personal god” (Bakunin, 1910, p. 63).

For most of history, whenever a person has been called “anti-mathematical”, or labeled as someone who wants 2+2 to equal a number other than four, the connotation has been purely negative. It has been an epithet reserved for the ignorant, the occultist, or the dimwitted.1 The connotation of being a loser in the game of reality is particularly strong whenever the term “anti-mathematical” is applied to a person or a movement, an adjective purporting to describe a way of being that is out of step with truth itself.² Almost no one has ever applied the term to themselves.³ The only serious exception to the rule happens to be extremely common: I am referring to the many students who proclaim or admit, without self-irony, that they “hate mathematics”. We will have a chance, before the end, to discuss the relationship between this cry of exasperation and the more self-assured statements by those like Byron and Turgenev.

We should suspect that there is more to the prayer that wishes to unmoor the laws of mathematics than mere occultism. After all, religion itself is more than the opiate of masses: Karl Marx saw in religion “the sigh of the oppressed creature, the heart of a heartless world, and the soul of soulless conditions” (1970, p. 11). When Fyodor Dostoevsky has his mouthpiece in Notes from the Underground protest “Two times two is four is no longer life, gentlemen, but the beginning of death!”, he might, on one plane of thought, be militating for that obsolete religious faith that he held on to for most of his painful life. On another level, however, he is arguing on behalf of something new and yet-to-come, a creative project that recedes in the face of numerical certainty. “Gentlemen”, he says, “what sort of will of one’s own can there be if it comes to tables and arithmetic, and the only thing going is two times two is four?” (Dostoevsky, 2011, p. 30).

It is only by looking at the positive, creative aspects of the above examples that we can perceive the real differences between the speakers. Byron, for example, who would “be glad” to partake of the work of proofs, and who respects in his correspondent, Anne Milbanke, her work on mathematics, does not wish merely to uproot numbers, but to search far enough until a zone of chaos can present itself. This is how his letter continues:

The only part [of my mathematical education] I remember which gave me much delight were those theorems (is that the word?) in which after ringing the changes upon A, B and C, D etc., I at last came to “which is absurd”—“which is impossible” and at this point I have always arrived and I fear always shall through life—very fortunate if can continue to stop there. (Byron, 1899, p. 404)

Here Byron, a man who looked for liberty within the discipline of the military or of the strictest rhyme schemes, has greater affinity with a figure like Goethe—also accused of being “anti-mathematical” (e.g., in Read, 1898, p. 216)—who explored within scientific logic itself for pathways that could not be reduced to logic. He is far from, to look at another example, Turgenev’s spiritualized nihilism, the acquiescence to living in a world absolutely bereft of miracles, while nonetheless believing in them. For Turgenev, the only solution, as the ending of ‘Prayer’ suggests, is a defiant resignation:

And so let us eat, drink, and be merry—and say our prayers. (Turgenev, 2015, p. 104)

This kind of quietism, in turn, is alien to Dostoevsky, whose lonely characters often rage against the logic of their surroundings—money, morals, measures—by violent means, doomed to exhaustion and disgust.

In each of these cases, the artist is carrying an opposition to the uses of mathematics on behalf of a form of life. The more a society rationalizes its terrain, the more strictly it defines (i.e., cuts from the infinite) the world by dividing it into manageable zones—then the more likely for various forms of life to become threatened. It is then not unlikely for certain people to take on the burden of illuminating chaos in their actions, in their mode of existence. We do not have to think of this as a modern phenomenon. Highly traditional, small societies, with strict rules of conduct and a willingness to let the unknown be unknown, give rise to the figure of the shaman with his or her chaotic and magical relationship to social norms. It is in very rare instances, such as early medieval Islam, where tremendous diversity and curiosity are allowed to live side-by-side with imposed order, in such a way that the task of engaging with chaos does not become a specialized activity. There, polymaths proliferate, so that an Omar Khayyam can both write the most precise treatises on cubic equations, the theory of parallels, and astronomic calculations, and also compose spiritual poems that render all precision and prediction, other than death, ineffective. At the same time, Khayyam’s doubts as a spiritualist were not exiled from his work on mathematics, which, by doubting the assumptions of the old masters, produced the first inkling of a non-Euclidean geometry (see Smith, 1935). The Islamic Golden Age is a long procession of such complexities: Avicenna, Al-Biruni, Ibn Firnas, Al-Farabi. Everywhere chaos and order mingle, so that the same person, in a single train of thought, moves from science to mysticism to poetry in patterns that define the vastly varying cosmologies of that all-too-brief period.

A major distinction of the modern era is the solidification of science as a separate realm, for which consistent patterns of movement can be devised. At the most decisive moment of this new era, that is at the moment when Philosophiæ Naturalis Principia Mathematica obliterated the need for philosophy in understanding nature, it was still possible for its author, a devout Christian and an alchemist, to think, in all seriousness, that divine intervention might be necessary to keep the machinery of the universe running without a hitch (Newton, 1952, p. 402). But Isaac Newton did not work this hypothesis into the Principia. The axiomatic logic had finally become so tightly bound and so extensible that it left no room for such metaphysical conjectures. Philosophy and art now stood outside the periphery of science. Science did not need them, but they could not ignore it. Of the three (the scientist, the philosopher, and the artist), it was the artist who received most clearly the task of dealing with chaos and uncertainty as they impact the senses. We can say with Gilles Deleuze and Félix Guattari that the “artist brings back from the chaos varieties that […] set up a being of the sensory, a being of sensation, on an anorganic plane of composition that is able to restore the infinite” (1994, pp. 202–203). However, we need to restore to the statement the historical background that Deleuze and Guattari have ignored. What they describe is the artist as the product of a specific, historical division of labor.4 In other words, “restoring the infinite” is neither the artist’s sole vocation, nor is it solely the artist’s burden. Anyone who feels the overwhelming power of the absolutely-defined and the irrevocably-measured also has the opportunity to pose counter-measures to that power.

This is why we are on more secure ground when we think of anti-mathematics as a series of actions (rather than a way of being, as implied by the term “anti-mathematical”) which are scattered across epochs and cultures. Their apparent goal is to either limit the encroachment—the expansion—of mathematics into a way of life, or to encroach on the realm set apart by mathematics. The motivating purposes of these acts, however, are open only to speculation. The evidence for any definitive statement is lacking. Almost everywhere, the actors have held back from disclosing, or even exploring, their own motives at length. Perhaps the opposing force has always remained too powerful, held too overwhelming a claim to truth. Whoever speaks against this force, speaks in the self-doubting voice reserved for prayer.

Beyond a prayer: The larger terrain of anti-mathematics

Not all acts of anti-mathematics are the work of artists per se. Various philosophers have also put up a resistance to the science. We have Zeno of Elea’s paradoxes, which might have been devised to curb the ambitions of the Pythagoreans (Matson, 2001), Augustine of Hippo’s highly influential exhortations in De Doctrina Christiana (1995, p. 123) that the clergy limit their study of mathematics to the most rudimentary topics, Blaise Pascal’s expressions of horror at the idea of a rationalized universe (see Zakai, 2010), and Martin Heidegger’s (1969) vilification of “calculative thought”, to name only a few examples. Elsewhere, I study these instances in detail (Harouni, forthcoming) and so will only pause here to point out two important theses. First, all of the above actors recognize the legitimate claim of mathematics to encroach on what we can call their “domains of interest”. In fact, all of them had a relatively strong command of the mathematics of their time, and, just as in the statement “two plus two does not equal four”, some also use numerical reasoning to bolster their ideas (e.g., Zeno’s paradoxes). Second, in all cases, the opposition, in contrast to what Charles Wolfe (2017) claims regarding his seventeenth-century examples, is not based on some scientific scepticism regarding the utility of mathematics.5 It is purely ideological. The problem is never the instruments of arithmetic and geometry in and of themselves. It is what an opposing ideology is trying to do with those instruments.

It is important to remember that mathematics is not only the instrument of an explanatory (scientific) power. People shape it into a tool for a wide range of activities—for example, commerce, administration, and construction (Harouni, 2015b)—and in turn humanity is shaped by these uses. There are forms of anti-mathematics that do not aim their opposition at a scientific perspective at all, but at certain organizations of social life. Nothing in the examples I have given so far prepares us to understand, for example, the taboo against the counting of human beings that we find among the ancient Israelites (Park, 2013), various communities in Africa (Githuku, 2001), and the Quechua in South America (Urton, 1997). In each case, the taboo appears alongside an administrative or cultural system that obsessively reckons people and their possessions (an opprobrium against counting livestock sometimes accompanies the one against counting humans). It is as if the culture, knowing that it must surrender all its members as units in a giant scheme of reckoning refereed by kings, empires, or avaricious men, tries at the last moment to warn itself of the ultimate consequences. The Torah establishes the ban on counting humans just at the moment that Yahweh demands a military census from Moses (Exodus 30:11–16). Such taboos are not merely outdated superstitions. Contemporary culture still carries forms of aversion to the infringement of numbers on certain aspects of life: A calculating mindset in the context of family or romantic love disgusts us (Belk, 2005). To demand that you be paid back, in equal monetary terms, for a gift you gave out of love does not belong in the harmonious sphere of marriage, but in the explosive zone of divorce. The certainty of mathematical reasoning in the realm of exchange or administration is not in itself a problem; but when extended into other realms, it can pose a formidable challenge to those forms of life that must shirk it to survive.

The nineteenth century, my point of departure in this chapter, marks the era in which money economy and state administration (statistics, the science of the state) finally overtook nearly every arena of life. It also marks the beginning of a widespread awareness of the consequences of such a takeover. Medieval Europe, particularly among its aristocracy, had harbored an opposition to monetary relations and, with them, to the craft that made monetary exchange possible: arithmetic (see Davis, 1960; Harkness, 2007). But this was an issue for the high-handed fringes of society who had access to surplus resources, and to those who built a living around the movement of this surplus through loans and luxuries. The serf, the priest, the craftsman, or the soldier, placed in immutable social positions and exploited or rewarded according to set formula, had very little to do with these concerns. We must travel a long way to arrive at a system that promotes the total fungibility of labor, objects, and values in the manner that, for example, plagued the thinking of Charles Dickens. His books are populated by characters who are, on the one hand, obsessed by money, as it determines their movement through society (upward or downward—Dickens had experienced both in his life), and who, on the other hand, are incapable of comprehending its value when they have it in hand. The incomprehension is essential to the humanity of these characters—the upstart, Pip, for example, in Great Expectations—but they are not heroes fit for their own adventure if they do not give in to the desires that their universe dictates (in the same novel, the saintly blacksmith, Joe, is not a hero, but a pole that attracts or repels young Pip).

Dickens could see the same push and pull in the operations of the state and its agents. To reduce individuals to statistical units both sheds light on social problems and, at the same time, annihilates the individuals within those problems. This is made ham-fistedly clear in a passage from Hard Times. I quote it at length, because it concerns the character with whom this discussion will end: the child who comes to say that he/she hates mathematics. Here we see her in the person of little Sissy, who has come home after receiving a scolding at school and is describing the ordeal to her benefactor:

‘Nothing, Miss—to the relations and friends of the people who were killed. I shall never learn,’ said Sissy. ‘And the worst of all is, that although my poor father wished me so much to learn, and although I am so anxious to learn, because he wished me to, I am afraid I don’t like it.’ (Dickens, 1854, p. 69)

Sissy in the above passage acts as an artist. The sentences she crafts rise, supposedly, from working-class experience, and they twist the utilitarian logic of the schoolmaster (the brutal Mr. Gradgrind, with his motto “the Facts, sir; nothing but Facts”) to express what bourgeois calculations stifle. But these words are an obvious idealization of what real working-class children can usually articulate in schools. Sissy’s tears, her pain, and her confusion are closer to reality than her words. “I am afraid I don’t like it” is anti-mathematics in its most defeated form. A contemporary expression of the sentiment is the exasperated cry of Detective McNulty in the most Dickensian of all-American television series,6 The Wire: “Fuck the fucking numbers already! The fucking numbers destroyed this fucking department” (Simon & Burns, 2008). Each season of The Wire centers on a social institution that, under the pressure of calculated costs and benefits, has lost its capacity to serve its purpose. Almost every time someone makes a calculation in The Wire, it is an act that affirms the supremacy of the economic factor. In one scene (Simon & Burns, 2002), a young girl comes to her older brother to ask for help with a math homework problem. The children live in a dilapidated squat, and the older brother, a very low-level drug dealer, is the breadwinner. It is a simple word problem, about the number of people on a bus after such and such number step in or out at various stations. The girl cannot answer it, and so the brother, frustrated, restates the question in terms of street drug dealing:

Wallace: How the fuck you able to keep the count right and not be able to do the word problem then?

Educational scholars have seen in this very scene (e.g., Dixon-Román, 2014), and ethnographic data like it (e.g., Mesquita et al., 2011), the antidote to working-class children’s resistance to learning school mathematics. If only someone had the wherewithal, Ezekiel Dixon-Román (2014) muses, to take advantage of these “deviantly marked cultural repertoires” (i.e., child labor in the extreme violence of the drug economy) in order “to pedagogically mediate [the children’s] textbook learning experience,” then “the academic mathematics” would “function effectively within the particularities of marginalized communities” (p. 20).

In art, the pain and confusion caused by the uses of mathematics can be hurled back at those uses. The action often relies on an extrapolation of what mathematical models leave out or override. This is, in part, similar to what critical social science tries to do with economic and statistical data (see Harouni, 2015b). Marx’s theory of value, for example, walks back the calculations of commodity exchange until one reaches the element that buying and selling had obscured—that is human labor. In fact, there are entire arenas of art that cannot be distinguished from politically motivated data visualization. The German artist K. P. Brehmer, in 1972, rigged a West German flag so that the sizes of the three colors—black, red, and gold—were determined by the distribution of wealth in the country (Figure 12.1).

Fig. 12.1 K. P. Brehmer, Korrektur der Nationalfarben, Gemessen an der Vermögensverteilung (Version I) [Correction of the National Colours, Measured by Distribution of Wealth (Version I)], 1972, Collection Alexander Schröder, Berlin. Exhibition photo from KP Brehmer. Real Capital-Production, Raven Row, 2014. Photograph by Marcus J. Leith. Reprinted with permission.

The extrapolation here is still thoroughly within the realm of mathematical sense-making and indistinguishable from social science. We can compare the flag to another of Brehmer’s works, the series titled The Soul and Feelings of a Worker, where the artist renders the incalculable elements of the worker’s life (Sissy’s tears and Sissy’s imagination) as precise but nonsensical geometrical constructions arranged on graph paper (Figure 12.2).

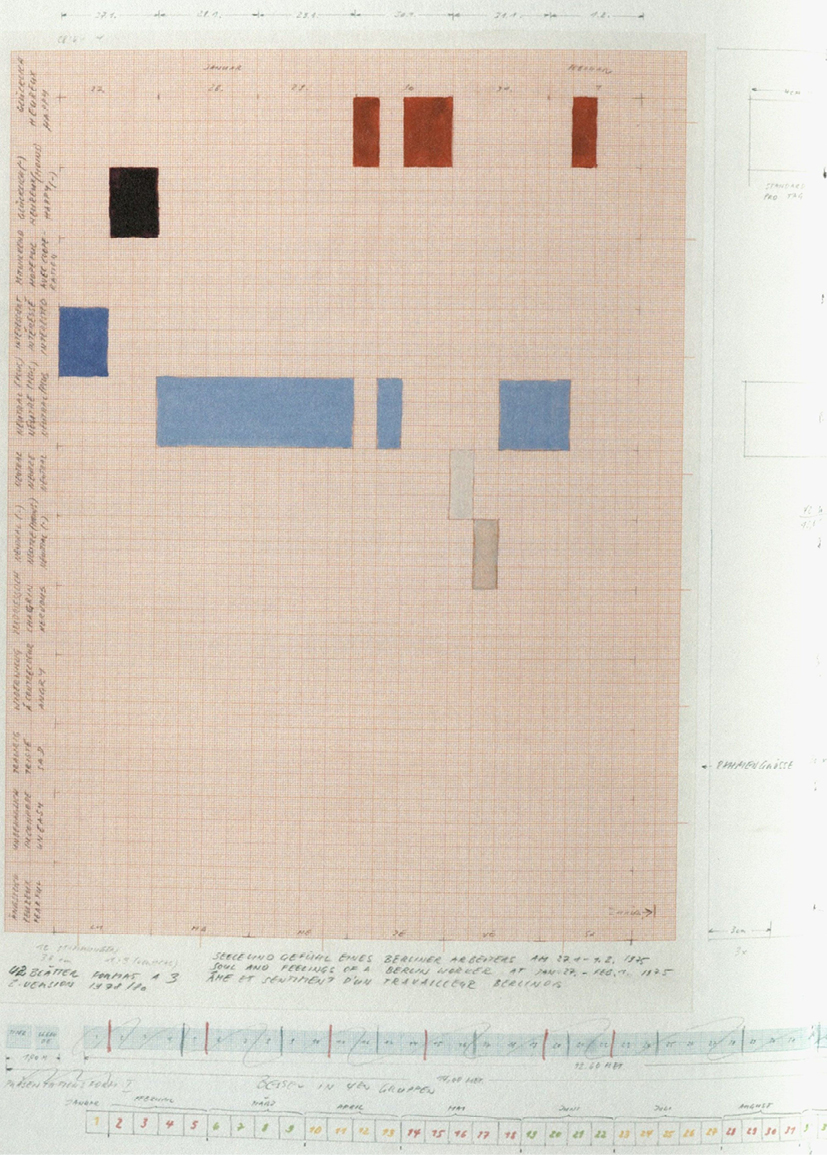
Fig. 12.2 K. P. Brehmer, Seel und Gefühl eines Arbeiters [Soul and Feelings of a Worker] 1980, Photo from K. P. Brehmer, Wie mich die Schlange sieht. Daadgalerie. 1986. Reprinted with permission.

The obvious and intentional failure of Brehmer’s graph to capture “the soul and feelings” illuminates the irreducibility of the inner life of the worker to the products of calculation. Of course, so much of the external life of labor revolves around hard numberings that even social or governmental movements with the expressed aim of improving that life have to return, again and again, to those calculative reductions. By placing itself within this tension, Brehmer’s graph becomes an act of anti-mathematics. In one sense, it is part of a tradition that tries to oppose the administrative function of mathematics through rendering it senseless. The Slovakian artists, Stano Filko, Alex Mlynárčik, and Zita Kostrová, in their 1965 project, HAPPSOC (a mix of “happy,” “happening,” and “socialism”) created census data that pushed against the communist regime’s obsession with representations of its own achievements. “One Danube… six cemeteries”, one piece of data claimed (Hoptman & Pospiszyl, 2002, p. 86). Zhang Huan’s 1995 performance piece in which a group of naked artists piled on top of each other to “Add One Meter to an Anonymous Mountain” can also be seen as a ridicule of Chinese governmental propaganda that constantly recounted the roads, dams, schools, and hospitals built in a year. But, in another sense, Brehmer’s piece differs from these other works in that it contains also a call for taking into account, in the mathematical sense of the phrase, the non-productive aspects of a worker’s life.

Fig. 12.3 Zhang Huan, To Add One Meter to an Anonymous Mountain (1995). Reprinted with permission.

That sophistication may not need to have any impact on the world beyond its own expression. But I would like to suggest at least one potential extension of its impact. Consider Gustave Flaubert’s famous “Age of the Captain” problem, which he invented for his younger sister:

Since you are now studying geometry and trigonometry, I will give you a problem. A ship sails the ocean. It left Boston with a cargo of wool. It grosses 200 tons. It is bound for Le Havre. The mainmast is broken, the cabin boy is on deck, there are 12 passengers aboard, the wind is blowing East-North-East, the clock points to a quarter past three in the afternoon. It is the month of May. How old is the captain? (Flaubert, 1893, p. 39)

The nonsensical little story mounts a small opposition to the way mathematics was, and continues to be, taught in schools. Different versions of it have been used to that effect ever since its composition (see Verschaffel et al., 2000). Its oppositional force, however, only extends to what happens in schools and schoolbooks. It critiques the use of fictional word problems that reduce the complexity of a context such as a merchant ship to a few cliched situations within which a mathematical calculation can find an example. Works like Dickens’s, Brehmer’s, Huan’s, and HAPPSOC, however, go further. They challenge the social systems that made mercantile-administrative mathematics (Harouni, 2015b), with its constant emphasis on calculation and reduction of objects to values, a staple of the modern education system (Harouni, 2015a). They do not stay with the age of the captain, but hint at a challenge to the movement of wool from Boston to Europe in 1841 (the year Flaubert wrote his word problem), and the structures that make such a movement possible or necessary.

We find a stronger version of this challenge in the works of the Chilean poet (and physicist) Nicanor Parra, who simultaneously disrupts our conception of school mathematics and the social activities that give rise to it. The piece titled “Mission Accomplished” (Parra, 2004, pp. 59–61) begins and ends as follows:

In form, Parra (probably unwittingly) returns us to the earliest word problems on record—the little stories that Babylonian scribes created to teach their craft and worldview to the youth who, one day, would take over the duties of accounting and organizing labor on behalf of the state:7

In order for a sum to be gained, all these different objects (ants, birds, corn, people) must lose their identity, even as genera and species, until nothing but an evenly distributable identity—i.e. pure value for accounting—remains to them (see Chapter 5 in this volume). It is such losses and gains that Parra comingles in his writing, acknowledging and discarding both: all kisses, or injuries, or works accomplished, can indeed be summed up—but the final results may be wrong, and in the end both profit and loss will return to that grounding of blood and tears wherein they both draw and lose their meanings. That Parra does not divorce this image from its historical background can be seen in his riff on the 2+2 motif, in the poem “Watch Out for the Gospel of the Times” (p. 5):

For students in today’s math-obsessed schools, a study of anti-mathematics will at least elevate their sense of opposition to the school subject from defeatism to a critical, historical, and artistic stance. It might even help free them from the designs of all those educationalists who conspire to spoon-feed them, day after day and for more than a decade, a set of skills that, should we accept Jacques Ranciére’s (1991) historical examples, one could pick up with a few months of interested and diligent study, paced according to one’s own needs or desires.

The examples I have gathered so far seem to stand at a distance from the work of mathematics itself. They comment on it, impact its role in social or private life, but do not touch it directly. So-called pure, theoretical mathematics might prove immune to the influence of anti-mathematics. As a strictly reasoned discourse, it forces all opposition to express itself in strictly reasoned terms, at which point it has already proven itself victorious. This is what it did to Zeno’s paradoxes, which, in the beginning, might have been posed against the influence of the Pythagoreans on philosophy. The paradoxes were posed in mathematical terms—for example, “that which is in locomotion must arrive at the half-way stage before it arrives at the goal [and so will never reach it]” (Aristotle, 1984, 239b11). Eventually, the paradoxes became part of mathematics itself, rather than any reaction against it. Their arguments fueled not less, but more mathematical exploration and power (Salmon, 2001).

But, as various activities draw on mathematical power to expand their reach, the strict reasoning of mathematics loosens, sometimes to such an extent that it becomes merely a mask for the chaotic desires that try to impose themselves on life. In these instances, anti-mathematics can expose the unreason that masquerades as reason. The false equations and orders break apart under the power of an opposition that through transposition of mathematical terms, expresses their limits. To return to Dickens’s Hard Times:

‘Yes, Miss Louisa, I know it was, now’. (Dickens, 1854, p. 68)

Anti-mathematics, however, does not only expose. It always creates new zones, new approaches, new products for thinking-life. We can see this more clearly if we look at a plastic and three-dimensional example. In his architectural designs, Friedensreich Hundertwasser mounted an opposition to the straight line. According to his own words, he was “against rationalism in architecture” (1958). The straight line, he said, is “something cowardly drawn with a rule, without thought or feeling,” and “any design undertaken with the straight line will be stillborn. Today we are witnessing the triumph of rationalist knowhow and yet, at the same time, we find ourselves confronted with emptiness. An esthetic void, desert of uniformity, criminal sterility, loss of creative power” (as quoted in Peitgen & Richter, 1986, p. v).

In his own buildings, lines undulate and spiral. The floors and stairs are uneven, forcing the inhabitant to think and feel with every step: “An uneven floor is melody to the feet” (quoted in Karberg et al., 1995). The anti-mathematical force of these statements and actions does not destroy mathematics as such: Hundertwasser still needs numbers to erect his buildings. Rather, it disrupts the march of standardization and anonymization that, in modernism, cloaks itself in reasonability—efficiency paraded as justice.

The apartment-house tenant must have the freedom to lean out of his window and as far as his arms can reach transform the exterior of his dwelling space. And he must be allowed to take a long brush and as far as his arms can reach paint everything pink, so that from far away, from the street, everyone can see: there lives a human who distinguishes himself from his neighbors, the pent-up livestock! (Hundertwasser, 1958)

Hundertwasser himself could not clearly grasp the implications of his own work. He confused false reason with reason itself, and in his writings, such as the Mouldiness Manifesto against Rationalism in Architecture (1958), he proposed that it was rationality itself that must be fought. The work, nonetheless, surpasses the words. In his buildings a new rationality survives the onslaught of the fiendish powers that can only rest happy by turning people into objects living within objects.

Belk, R. W. (2005). Exchange taboos from an interpretive perspective. Journal of Consumer Psychology, 15(1), 16–21. https://doi.org/10.1207/s15327663jcp1501_3

Byron, G. G. B. (1899). The works of Lord Byron. J. Murray.

Comte, A. (1876). System of positive polity. Longmans, Green, & Company.

Davis, N. Z. (1960). Sixteenth-century French arithmetics on the business life. Journal of the History of Ideas, 21(1), 18–48.

Deleuze, G., & Guattari, F. (1994). What is philosophy? Columbia University Press.

DeLyria, J., & Robinson, S. M. (2011, March 23). ‘When it’s not your turn’: The quintessentially Victorian vision of Ogden’s ‘The Wire’. Hooded Utilitarian. https://www.hoodedutilitarian.com/2011/03/when-its-not-your-turn-the-quintessentially-victorian-vision-of-ogdens-the-wire

Dickens, C. (1854). Hard times: For these times. Bradbury & Evans.

Dixon-Román, E. J. (2014). Deviance as pedagogy: From nondominant cultural capital to deviantly marked cultural repertoires. Teachers College Record, 116(8), 1–30. https://doi.org/10.1177/016146811411600802

Dostoevsky, F. (2011). Notes from underground. Knopf Doubleday.

Fauvel-Gouraud, F. (1845). Phreno-mnemotechny: Or, the art of memory. Wiley and Putnam.

Flaubert, G. (1893). Correspondance. G. Charpentier.

Friberg, J. (2005). Unexpected links between Egyptian and Babylonian mathematics. World Scientific.

Githuku, S. (2001). Taboos on counting. In M. Getui, K. Holter, & V. Zinkuratire (Eds.), Interpreting the Old Testament in Africa: Papers from the International Symposium on Africa and the Old Testament in Nairobi, October 1999 (pp. 113–118). Peter Lang.

Hansson, S. O. (2018). The rise and fall of the anti-mathematical movement. In S. O. Hansson (Ed.), Technology and mathematics: Philosophical and historical investigations (pp. 305–323). Springer. https://doi.org/10.1007/978-3-319-93779-3

Harkness, D. E. (2007). The Jewel House: Elizabethan London and the scientific revolution. Yale University Press.

Harouni, H. (2015a). Reframing the discussion on word problems: A political economy. For the Leaning of Mathematics, 35(2), 27–32.

Harouni, H. (2015b). Toward a political economy of mathematics education. Harvard Educational Review, 85(1), 50–74.

Harouni, H. (forthcoming). Anti-mathematics: A programmatic study.

Heaviside, O. (1893). Electromagnetic theory. ‘The Electrician’ Printing and Publishing Company.

Heidegger, M. (1969). Discourse on thinking. Harper & Row.

Hoptman, L. J., & Pospiszyl, T. (2002). Primary documents: A sourcebook for Eastern and Central European art since the 1950s. Museum of Modern Art. Distributed by the MIT Press.

Hundertwasser, F. (1958). Mouldiness manifesto against rationalism in architecture. Hundertwasser Archive. https://www.hundertwasser.at/english/texts/philo_verschimmelungsmanifest.php

Karberg, R., Jalving, A., & Jalving, C. (1995). Hundertwasser: The phenomenon. In Hundertwasser, Arken (pp. 15–43). Museum of Modern Art.

Koyré, A. (1966). Études d’histoire de la pensée scientifique [Studies in the history of scientific thought]. Presses Univeritaires de France.

Marx, K. (1970). A contribution to the critique of Hegel’s Philosophy of Right. Cambridge University Press.

Matson, W. (2001). Zeno moves! In A. Preus (Ed.), Essays in Ancient Greek philosophy VI: Before Plato (pp. 87–108). State University of New York Press.

Mesquita, M., Restivo, S., & D’Ambrosio, U. (2011). Asphalt children and city streets: A life, a city and a case study of history, culture, and ethnomathematics in São Paulo. Sense.

Newton, I. (1952). Opticks: Or a treatise of the reflections, refractions, inflections & colours of light. Dover.

Novalis (2021). Mathematical fragments. Symphilosophie International Journal of Philosophical Romanticism, 3, 273–290.

Park, S.-M. S. (2013). Census and censure: Sacred threshing floors and counting taboos in 2 Samuel 24. Horizons in Biblical Theology, 35(1), 21–41.

Parra, N. (2004). Antipoems: How to look better & feel great. New Directions.

Peitgens, H. O., & Richter, P. H. (1986). The beauty of fractals: Images of complex dynamical systems. Springer.

Ranciére, J. (1991) The ignorant schoolmaster: Five lessons in intellectual emancipation.

Stanford University Press.

Read, C. (1898). Logic, deductive and inductive. Simpkin, Marshall, Hamilton, Kent, & Co.

Salmon, N. (2001). The limits of human mathematics. Philosophical Perspectives, 13, 93-117. https://doi.org/10.1111/0029-4624.35.s15.5

Schliesser, E. (2011). Newton’s challenge to philosophy: A programmatic essay. The Journal of the International Society for the History of Philosophy of Science, 1(1), 101–128.

Schliesser, E. (2017). Adam Smith: Systematic philosopher and public thinker. Oxford University Press.

Simon, D., & Burns, E. (Directors). (2002). Lessons (Season 1, Episode 8) [Television series episode]. In The Wire. Blown Deadline Productions; HBO Entertainment.

Simon, D., & Burns, E. (Directors). (2008). Not for attribution (Season 5, Episode 3) [Television series episode]. In The Wire. Blown Deadline Productions; HBO Entertainment.

Smarandache, F. (2012). Aftermath & antimath. Zip.

Smith, D. E. (1935). Euclid, Omar Khayyam, and Saccheri. Scripta Mathematica, 3(1), 5–10.

Sonnenschein, S., et al. (1889, June 5). A first Euclid. Bookseller: A Newspaper of British and Foreign Literature, 577.

Turgenev, I. S. (2015). The novels of Ivan Turgenev: Dream tales and prose poems. BiblioBazaar.

Urton, G. (1997). The social life of numbers: A Quechua ontology of numbers and philosophy of arithmetic. University of Texas Press.

Verschaffel, L., Greer, B., & De Corte, E. (2000). Making sense of word problems. Swets & Zeitlinger.

White, E. C. (1919). Mathematics and anti-mathematics. School Science and Mathematics, 19(1), 20–37.

Wigner, E. (1960). The unreasonable effectiveness of mathematics in the natural sciences. Communications on Pure and Applied Mathematics, 13(1), 1–14. https://doi.org/10.1002/cpa.3160130102

Wolfe, C. T. (2017). Vital anti-mathematicism and the ontology of the emerging life sciences: From Mandeville to Diderot. Synthese, 196(9), 3633–3654. https://doi.org/10.1007/s11229-017-1350-y

Young, T. (1813). An introduction to medical literature, including a system of practical nosology, intended as a guide to students, and an assistant to practitioners. Underwood and Blacks.

Zakai, A. (2010). Jonathan Edwards’s philosophy of nature: The re-enchantment of the world in the age of scientific reasoning. T & T Clark.