16. Globalisation of mathematics education and the world’s first monoculture: Assessment spread’s association with consumerism and human capital

Mark Wolfmeyer

The global spread of mass schooling supports ideologies of human capital and consumerism that we can consider as the world’s first monoculture. Educational organisations with global reaches, such as the International Association for the Evaluation of Educational Achievement and the Organisation for Economic Co-operation and Development, spread particular mathematics education goals that present opportunities for analysis and critique by mathematics educators who seek to advance causes beyond or in opposition to the consumer-industrial complex. In this chapter I utilise Joel Spring’s review of perspectives on globalisation and education to motivate extended analysis of one example of ‘assessment spread’ within mathematics education, namely the Trends in International Mathematics and Science Study. Complementary methods of analysis (historical/contextual and content-based) reveal a strong association between mathematics education assessment spread and the rise of a world culture emphasising human capital and lifelong consumerism.

Introduction

In this chapter I take up themes on the purpose of mathematics education that resonate with other chapters in this volume, in which mathematics education is viewed as relating to global capitalism. I suggest the possibility that mathematics education practices are not just responsive to the context of global capitalism; rather, they are perceived by the world’s power elite as a means to achieve their objectives. In my contribution, I collocate perspectives on globalisation and globalisation of education with phenomena that we, as mathematical enthusiasts and mathematics educators, know all too well: international mathematics educational assessments like the Trends in International Mathematics and Science Study (TIMSS). I argue that such phenomena, what I refer to as ‘assessment spread’ to highlight the historical context of increasing participation, serve as one of many vehicles through which a global culture can permeate the world, creating a first monoculture. Specific tenets of this monoculture include commitments to laissez-faire capitalism, markets dominated by consumerism, and education systems oriented to those ends. In other words, with the global economy as its foundation, the first monoculture’s twin features are increasing the number of people in the world that 1) enter the wage labour market and 2) become lifelong consumers of goods and services in a market-based system. Mathematics education is seen by the power elite as an opportunity to extend this vision for the world.

I begin with the perspectives on globalisation and globalisation of education as reviewed by Joel Spring (2014). Among the options he presents, which include ‘world system’ and ‘culturist’, what he terms ‘the world culture theory’ on globalisation provides the most suitable means for analysing the assessment spread phenomena at the heart of this project. In utilising this framework, I turn the theory on its head by describing the exact nature of this world culture that is spreading: a first monoculture dominated by laissez-faire capitalism and the supports required by it, such as education for human capital. Existing literature from globalisation and mathematics education studies contributes important connections to the theories on globalisation as well as laying the ground for my present inquiry into assessment spread.

In my focus on TIMSS, I begin with a narrative to document this ongoing activity as an example of assessment spread. This includes tracing the growing list of participating countries, with attention paid to their relative engagement with the global economy. Along with this historical narrative, I provide a contextual analysis (similar in goal but different in method from my other projects, e.g., Wolfmeyer, 2014) to describe the motives represented in this project, mostly by analysing the implications presented by the World Bank’s involvement in TIMSS. A primary finding of interest emerges from this historical and contextual analysis: several participating TIMSS countries increased their engagement in the global economy during their periods of participation. Specifically, the vast majority of participating countries maintained high-level income or significantly increased their per-capita income levels during the years of participation in TIMSS. As I will argue, this data presents a perfect instantiation of the World Bank’s vision for a global society with everyone participating in the wage labour market and consumer society. To be sure, I dare not make any claim of causality, that TIMSS participation actually caused countries’ citizens to better engage in the global economy, but suggest that the association displayed by the data carries weight for my argument that TIMSS and assessment spread relate to an emerging world culture of human capital and consumerism.

In the final section, I complement the historical and contextual analysis with content analysis; I engage with Houman Harouni’s (2015) notion of the political economy of mathematics to analyse released mathematics assessment items from a recent implementation of TIMSS. This content analysis again confirms the relationship of TIMSS to the spread of the global economy. The vast majority of content items within TIMSS are associated with mathematical preparation for human capital, with a very limited scattering of alternatives, thereby signifying to users of this assessment that mathematics could not be applied to anything but behaviours relating to wage labour and being a consumer. Thus, taking content and context analyses together, I suggest that the mathematics education assessment spread over time is associated heavily with a global economy of laissez-faire capitalism and human capital existing primarily for a consumerist, profit-driven world culture.

Perspectives on globalisation and education

In this section I review Spring (2014) for a variety of perspectives on globalisation, with specific attention to their relationship to the globalisation of education. This review presents several options for consideration when analysing the assessment spread phenomena in mathematics education and ultimately, what Spring terms the ‘world culture’ perspective seems the most fitting to the spread’s aims and origins. In addition, I also provide some analyses in existing literature regarding globalisation of education as it pertains to the world culture theory as well as a few contributions from among the mathematics education literature that engage the globalisation perspectives as reviewed here.

Spring (2014) reviews existing bodies of scholarship on globalisation of education to produce three broad categories: world culture theorists, world system (postcolonial/critical), and culturist. These reflect his understanding of the ways that scholars engage in the activities of spreading education practices across the globe. World culture theory resonates most closely to the assessment spread of a global mathematics education because it insists ‘all cultures are slowly integrating into a single global culture’ (p. 7). However, review of each is important for understanding the opportunities at play when analysing global phenomena in education.

Clear examples of how educational systems are unifying globally are abundant. For instance, Spring point out that most school systems comprise a sequential ladder from the elementary to middle level to secondary years of schooling, with groupings of students by age and with achievement as indicating progress through the ladder. However, he notes how John Meyer, David Kamens, and Aaron Benavot (1992) suggest that the spread of the nation state required education of the citizenry to ensure political stability and economic growth. The authors argue that ‘the gradual rationalisation of the Western polity, the modern curricular structure became a take-for-granted “model” by the turn of the twentieth century’ (p. 72). As the Western concept of the nation state spread, ‘the standard model of the curriculum has also diffused throughout the world, creating a worldwide homogeneity in the over-all categorical [curriculum categories] system’ (Spring, 2014, p. 8).

The spread of educational practices across the globe corresponded, thus, to the spread of governing people through the structure of the nation-state. A main feature of the globalisation of education is what Spring highlights, from the work of Francisco Ramirez (2003), as the ‘credentialed society’. By tying educational achievements to the opportunity to obtain employment, global education spread commits not only to the needs of a nation’s citizenry but to the capitalist economy and markets that rose alongside it. A key feature of such developments is increasing the number of people engaging in the wage labour structure. The naturally occurring relationship between the nation state and capitalism is well documented in literature. For example, Arun Ghosh (1997) states: ‘At any rate, historically, capitalism and nation states evolved and prospered together’ (p. 683). Furthermore:

Ramirez locates the origins of world cultural theorists in the work of John Boli, Frank Lechner, George Thomas, and Immanuel Wallerstein. These theorists argue that a world culture began with the spread of Western Christian ideas in the late nineteenth century and escalated after the end of World War II. (Spring, 2014, p. 8)

World cultural theorists primarily focus on the relationship between the spread of nation state governing structures and the similar schooling systems set up across these nation states. What appears explicitly absent in a world culture’s emphasis on nation state is the acknowledgment that a modern nation state requires a capitalist economic structure as well. This could be sometimes suggested by those utterances that confuse ‘the development of capitalism with the development of “liberal” thought’ (Ghosh, 1997, p. 683). The suggestion of credentialing as a key feature within world culture’s schooling systems implies this entanglement between capitalism and the modern nation state. My contribution here recognises the entanglement of developing nation states and free-market capitalism, not always going hand in hand, but very often co-developing, as illustrated by analysis of TIMSS and its association with the World Bank.

Spring also describes critiques of globalisation via postcolonial theory, also referring to related scholars as ‘world systems theorists’ who ‘argue that the richest nations legitimise their power by imposing their educational values on other nations. These educational values include schooling for economic growth and developing workers for a free market economy’ (Spring, 2014, p. 10). Specific discussions here include the ways that the World Bank enacts educational programs in its broader mission to enact laissez-faire capitalism across the globe (Spring, 2004). The World Bank and their networked actors put forth the suggestion of a knowledge economy as the key for emerging economies in so-called ‘developing nations’. This policy features in multiple World Bank publications, such as Building Knowledge Economies: Advanced Strategies for Development (World Bank, 2007). Similarly, the global economic elite, as represented by the Organisation for Economic Co-operation and Development (OECD), declares an education for human capital among the wealthy nations as the primary educational imperative (as in Keeley, 2007).

Viewing world culture theory alongside world systems and postcolonialist critiques of globalisation immediately reveals important insights for understanding a globalised mathematics education, as observed through assessment spread phenomena. I will argue that the assessment spread and globalised mathematics education practices are generated from a world culture theory framing: they situate in a movement towards a unified monoculture emphasising the nation state and its concomitant laissez-faire capitalism and consumerism. By asserting this, then, I align with world systems theorists’ portrayal of the state of affairs we have witnessed over the last hundred years. In other words, both theoretical framings engage with my present work and, as a rhetorical strategy, my chapter title and framing assert the dominance of world cultural theory as a perspective for signifying just what is at stake with such assessment spread phenomena, namely the dominance of a unifying world culture emphasising human capital and consumerism.

The remaining theorists on globalisation and education of interest to Spring are worth considering, though they are less significant to this project. The culturist perspective provides a viewpoint suggesting agency across parties in the globalisation of education. Spring points out their rejection of movement towards a unified practice in education and declaration in favour of a concept of ‘educational borrowing and lending’ (Spring, 2014, p. 11). Culturists represent a variety of interpretations; they differ, however, in how helpful they are in understanding assessment spread in mathematics education. One culturist example, as indicated by Spring, occurred with the late 1980s educational fad in the United States that looked to the schooling practices in Japan. Implicit in this discussion, however, is the framing of a quest to perfect a system across the globe in service of nation-state and capitalist economies; the practice was less about borrowing and lending than it was about deepening commitments to capitalism and the nation state.

Other culturist examples provide optimism and balance to the significant and weighty suggestions by world culture theory and the world systems critique. As Spring suggests, culturists argue that there is not just one world education model:

Anderson-Levitt argues that there are two competing world models for education. World culture theorists, she argues, consider the goal of the world education model to be preparing students to be workers in the global economy. She identifies two competing world education models, which I will label ‘Economic Education World Model’ and ‘Progressive Education World Model’. I propose the existence of two other competing global models, which I label ‘Religious Education World Models’ and ‘Indigenous Education World Models’. These last two global models openly reject world models of schooling based on Western education. (Spring, 2014, p. 13)

These competing global models for education are worth considering in mathematics education, as I note below, although will not factor into my discussion of assessment spread. Mathematics education as a global practice, via assessment spread and closely associated curricular convergence, appears to me as a dominant ‘Economic Education World Model’ that seeks to define and claim a particular set of human behaviours that are identified as mathematical.

Concepts relating to this review of globalisation and education have been applied to studies in the globalisation of mathematics education prior to my contributions here. For example, Spring (2014) frames his discussion on globalisation and mathematics education with the dominating discourse of the knowledge economy (in part via the World Bank, as I note above). This appears as a critical world systems approach, as reviewed above, especially when he suggests an ‘export’ of Eurocentric models of education and higher education across the globe and, specific to my focus, a suggested ‘appropriation effect’ via the assessment spread, as in:

[Projects] can also be focused on applying some predetermined framework as in international assessment and comparative studies (e.g., SIMS, TIMSS, PISA) typical of scientific paradigm research. In both of these types of research there is what I shall term the appropriation effect. In this, locally gathered knowledge from ‘developing’ countries is appropriated for academic and other uses in ‘developed’ countries. (Ernest, 2016, p. 40)

As another example, Bill Atweh and Phillip Clarkson (2010) frame inquiries into internationalising mathematics education with an open perspective on globalisation, as somewhat of a commitment to Spring’s culturist perspective, but with clear intentions to be critical of the negative effects, as in the world systems and postcolonial approach:

[Some] internationalization and globalization processes may be good, whereas others may be less desirable and should be contested. Further, what is considered good aspect of internationalization and globalization for a particular group of people may very well be at the expense of other groups. (p. 80)

And in provoking discussions about differing models of global mathematics education systems, perhaps resonating with a culturist approach, I would promote the work of Peter Appelbaum and Susan Gerofsky (2013), with their vision of an alterglobalisation in mathematics education. They suggest ‘another world is possible’ by reviewing the alterglobalisation ‘movements of people who are extremely concerned about the neoliberal agenda of a self-regulating free-market, and the linkage between global cultures and a dominant Western culture that often runs counter to many of the values and principles by which people live their lives’ (p. 27). Asserting a stance that is not quite anti-globalisation, they emphasise a need for global ‘renewal of political citizenship and activism’ and, specific to mathematics education, suggest a world model of mathematics education grounded in the arts and participatory democratic practice.

Finally, recall that the mathematics education community initiated an early critique of the internationally comparative mathematics tests! Hans Freudenthal (1975) provided pointed arguments against the early efforts that ultimately led to the TIMSS, emphasising many points such as that mathematicians and mathematics educators were not involved in the design, and dubious conclusions are often made from the data.

And what could be blunter than the summary by Christine Keitel and Jeremy Kilpatrick (2012) that:

The studies rest on the shakiest of foundations – they assume that the mantel of science can cover all weaknesses in design, incongruous data and errors of interpretation. They not only compare the incomparable, they rationalize the irrational. (p. 254)

In the present project, I aim to take up these conversations critiquing TIMSS yet again, and specifically by associating the project with its broader policy objectives. Providing insights and critique of significant projects like TIMSS (and other examples of mathematics education spread) aims to complement the literature for mathematics educators and enthusiasts who recognise the relationships between mathematics educational practice and social life, such as scholars working among the international Mathematics Education and Society group.

Reviewing perspectives on globalisation and education has uncovered a promising framework for investigating assessment spread in mathematics education across the globe. Situating the phenomena as grounded by a world-culture perspective allows us to consider how dominating and powerful agencies envision a global, unified culture and practice in service of particular elite goals. In this manner I put forth a critical, some might say postcolonial, analysis of the power embedded in assessment spread of mathematics. With this critique, I aim to motivate rejections of the seemingly benign or neutral assessment spread that we witness in mathematics education. My contribution complements the culturist contributions from mathematics education, reviewed above, that provide much-needed optimism when we have such a formidable force in mathematics education with which to contend. I next turn to tracing the history and social context of the TIMSS practice before offering a content analysis of released test items from that assessment’s recent iteration.

From 10 to 60+: TIMSS, the World Bank, and a global economy

In this section I survey the history and context of TIMSS to provide additional material for analysing the global spread of assessment in mathematics education. In its origins, the practice began with only a handful of similar countries, but over time, the entanglement of the World Bank with the main organisation behind TIMSS, IEA (International Association for the Evaluation of Educational Achievement) suggests a new context in line with the world-culture perspective that frames my inquiry. In this section, I will trace this history and context as well as present the data on participating countries and their participation rates in the global economy, as measured by per-capita income levels.

The IEA practices began with their pilot study of twelve countries in 1959, which included subjects beyond mathematics and science. The countries were Belgium, England, Finland, France, (Federal Republic of) Germany, Israel, Poland, Scotland, Sweden, Switzerland, United States, Yugoslavia, and the language that IEA uses to describe the original project suggests a culturist framing:

The founders of the IEA viewed the world as a natural educational laboratory, where different school systems experiment in different ways to obtain optimal results from educating their youth. They assumed that if research could obtain evidence from across a wide range of systems, the variability would be sufficient to reveal important relationships that would otherwise escape detection within a single education system. (IEA, n.d., n.p.)

In other words, although mostly comprising a list of nations powerful at the time, the originators of this practice suggested that there was ‘no one way’ to teach but that there was one way to assess. This would allow for best practices to be shared and analysed for efficacy; the contradiction arises from the assumption that one assessment implies consensus on educational goals. This assumption in the pilot study, albeit framed through a culturist lens, suggests a global objective to unify both the goals and the practices of education. At this point in the history, these goals were less explicit and more open than at later stages, as the assessment spread continued and especially once the World Bank became involved.

The following tables indicate the countries that have been brought into IEA’s assessment practice in mathematics over time. After the pilot study in 1959, we have the FIMS (First International Mathematics Study) of 1964, the SIMS (second) of 1980–1982, the TIMSS (third and including science) of 1995, and finally, the renaming of the practice to TIMSS (Trends in International Mathematics and Science Study) and its iterations via a four-year cycle with the last completed in 2019. Table 16.1 below shows the countries that participated prior to the renaming. Table 16.2 includes the countries participating in the four-year iterative assessments since 1995, with an additional variable presented, namely the World Bank’s analytical classification for each country based on the Gross National Income (GNI) per capita. I will use these classifications to make arguments about the significance of the assessment spread. In Table 16.2, the categories of economic classification are high, upper middle, lower middle, and low income. Thresholds for these categories vary slightly from year to year and increase over time due to inflation of the US dollar. The thresholds for 2019’s analytical classifications were: Low – GNI per capita less than $1035 US, lower middle – between $1036 and $4045, upper middle – between $4046 and $12535, high – above $12535. Sources to create these tables include the IEA (n.d.) website with lists of participating countries and World Bank Group (n.d.), a data set with historical classifications according to the economic groups listed above.

To help illustrate the geographic spread of a globalised mathematics education, I accompany each table with a dymaxion world map indicating participating countries. I chose the dymaxion two-dimensional projection of the world sphere to destabilise typical projections’ assumptions of north-south superiority/inferiority as well as to more accurately represent land mass proportionally. The projection I used is an adaptation of Buckminster Fuller’s Airocean projection (1954), adapted by Visioncarto (2018) and free for all uses. A participating country is indicated by a circle on the dymaxion map. The darker the circle, the earlier the country began participation. In Figure 16.1, to represent the first three iterations, the participating countries have darker circles; accordingly, in Figure 16.2 (to accompany Table 16.2), the additional countries added in the iterations of the assessment occurring from 1995 to 2019 are indicated with lighter gray circles.

Table 16.1 Participating countries in IEA’s early mathematics assessments.

1959 (Pilot)	1964 (FIMS)	1982 (SIMS)
Belgium	Australia	Belgium
England	Belgium	Canada
France	England	England/Wales
W. Germany	Finland	Finland
Israel	France	France
Poland	W. Germany	Hong Kong
Scotland	Israel	Hungary
Sweden	Japan	Israel
Switzerland	Netherlands	Japan
US	Scotland	Luxembourg
	Sweden	Netherlands
	US	New Zealand
		Nigeria
		Scotland
		Swaziland
		Sweden
		Thailand
		USA

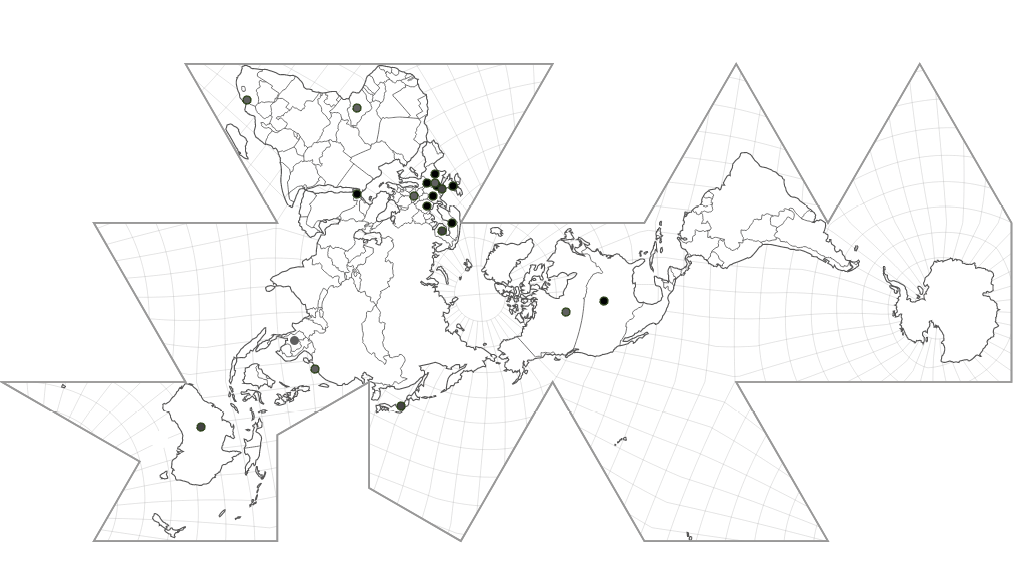
World map indicating participating countries in TIMSS through 1982.

Fig. 16.1 Participating countries through 1982. Adaptation of Buckminster Fuller’s Airocean projection (1954), adapted by Visioncarto (2018).

The next table shows countries of participation from (19)95 to (20)19, with economic classification by the World Bank. (All country names are as stated in the TIMSS reports, and are not necessarily the same as the name used by either the World Bank, the nation state itself, or its people at the time.) The first batch of countries are those with the highest income level per capita. Their years of participation are indicated by 4s in the appropriate column which also signifies their income level. The next batch of countries are those that only participated in one year. Their year of participation is marked in the column of the year and with the income level 1 (low), 2 (lower middle), or 3 (upper middle). Since these countries participated for only one year, we cannot make any conclusions about the relationship between participation and the country’s income level. The next batch of countries in Table 16.2 are those that participated and did not increase income level. It should be noted that for these countries (fifteen plus Palestine, for which income data were not available) they remained at their income level during their years of participation. The last batch of countries in Table 16.2 are those that increased their income levels during TIMSS participation. Twenty-three countries in total are included in this final batch, signifying that the majority of countries with lower income levels who participated in TIMSS did increase their income levels over time.

Table 16.2 Participating countries in TIMSS, years 1995 to 2019, with income level.

	95	99	03	07	11	15	19
Participating countries with high per-capita income levels
Australia	4	4	4	4	4	4	4
Austria	4			4	4
Bahrain				4	4	4	4
Belgium	4	4	4		4	4	4
Canada	4	4	4	4	4	4	4
Chinese Taipei		4	4	4	4	4	4
Cyprus	4	4	4	4		4	4
Denmark	4			4	4	4	4
England	4	4	4	4	4	4	4
Finland		4		4	4	4	4
France	4					4	4
Germany	4			4	4	4	4
Hong Kong SAR	4	4	4	4	4	4	4
Iceland	4
Ireland	4				4	4	4
Israel	4	4	4	4	4	4	4
Italy	4	4	4	4	4	4	4
Japan	4	4	4	4	4	4	4
Korea	4	4	4	4	4	4	4
Kuwait	4			4	4	4	4
Malta				4	4	4	4
Netherlands	4	4	4	4	4	4	4
New Zealand	4	4	4	4	4	4	4
Northern Ireland					4	4	4
Norway	4		4	4	4	4	4
Oman				4	4	4	4
Poland					4	4	4
Portugal	4				4	4	4
Qatar				4	4	4	4
Scotland	4			4
Singapore	4	4	4	4	4	4	4
Spain	4		4	4	4	4	4
Sweden	4		4	4	4	4	4
Switzerland	4
USA	4	4	4	4	4	4	4
Participating countries – only one year of participation
Algeria				2
Azerbaijan					3
Bosnia and Herzegovina				2
El Salvador				2
Estonia			3
Greece	3
Honduras					2
Mexico	3
Mongolia				2
Participating countries – No increase in income level
Argentina	3		3			3	3
Botswana			3	3	3	3	3
Colombia	2			2
Croatia					4	4	4
Egypt			2	2		2	2
Kazakhstan				3	3	3	3
Lebanon			3	3	3	3	3
Malaysia		3	3	3	3	3	3
Moldova		1	1
Palestine			P	P	P	P	P
Philippines	2	2	2
Serbia			P	3	3	3	3
South Africa	3	3			3	3	3
Syria			2	2	2
Ukraine				2	2
United Arab Emirates				4	4
Participating countries – Increase in income level
Armenia			2	2	2	2	3
Bulgaria	2	2	2	3		3	3
Chile		3	3		3	4	4
Czech Republic	3	3		4	4	4	4
Georgia				2	2	3	3
Ghana			1	1	2
Hungary	3	3	3	4	4	4	4
Indonesia	2	1	2	2	2	2	3
Iran	2	2	2	2	3	3	3
Jordan		3	2	2	3	3	3
Latvia	2	2	3	3
Lithuania	2	2	3	3	3	3	3
Macedonia		2	2		3
Morocco		2	1	2		2	2
Romania	2	2	2	3	3
Russian Federation	2	2	2	3	3	3	3
Saudi Arabia			3	4	4	4	4
Slovak Republic	2	3	3	4	4	4	4
Slovenia	3	4	4	4	4	4	4
Thailand	2	2		2	3	3	3
Tunisia		2	2	2	3
Turkey		2		3	3	3	3
Yemen			1	1	2

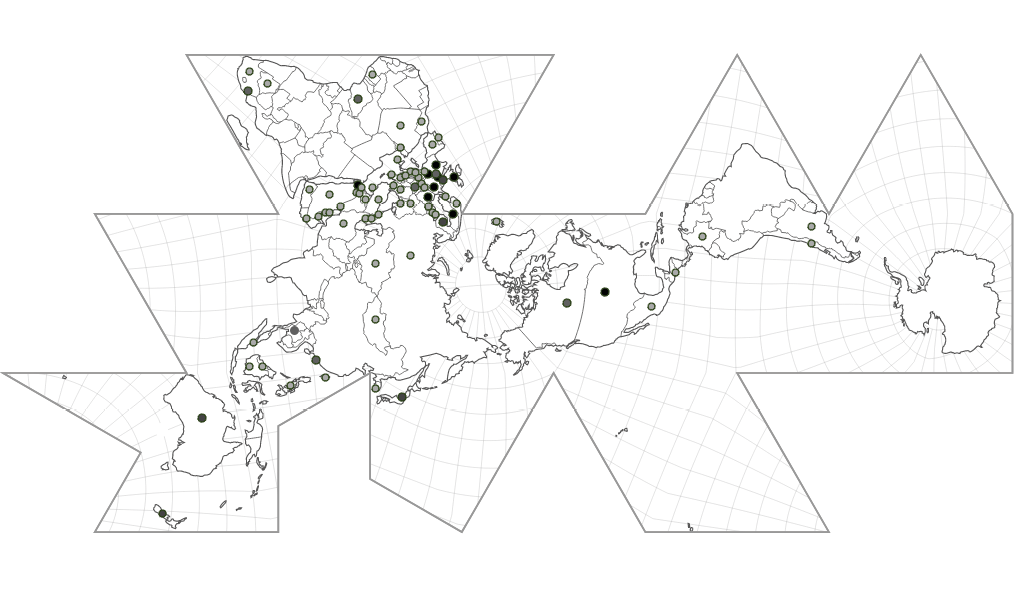
World map indicating participating countries in TIMSS through 2019.

Fig. 16.2 Participating countries in TIMSS through 2019. Adaptation of Buckminster Fuller’s Airocean projection (1954), adapted by Visioncarto (2018).

The tables reveal several interesting phenomena after careful consideration of the years and involvement over time. The simple and clear statement that this assessment has spread across the globe throughout the years cannot be understated and is best viewed when looking back and forth between Figures 16.1 and 16.2. What began as an initial pilot study to compare a handful of countries is now a consistent practice with about sixty-one countries participating on average in the last four iterations. Looking geographically, what began as eight European countries, the United States and Israel, now also routinely includes several countries from North, Central and South America, the Middle East, Asia, Oceania, and Africa. And economically, what began as a group of predominantly wealthy nations has expanded to include a diverse group of lower, lower middle, upper middle, and higher-income countries. The phenomenon of mathematics education assessment spread is laid bare by these tables; providing them in their complete form is a clear method to capture the spread.

However, the significance of the spread moves beyond the increasing geographic diversity and simple glimpse at economic diversity. To the latter, I first offer further consideration of the World Bank’s economic classifications for each country by relating more details and analysis regarding the World Bank’s involvement with TIMSS and education in general. The World Bank is a regular funding source for IEA and is regularly listed as a funding partner for each cycle of TIMSS. The first year that this was displayed on their reports and/or websites was in the 1999 TIMSS cycle. The significance of World Bank’s involvement in TIMSS is best understood by considering the World Bank’s involvement in global education generally.

Earlier, I pointed to the World Bank’s push for a global economy of human capital. Spring (2004) offers poignant analysis to the framing in which World Bank takes educational action:

[Their] educational ideology contains a particular vision about how society should be organized. For many people, this vision is just assumed to be a necessary part of the advancement of world societies. It is an image of the good society that is often unquestioned because of its promise of economic abundance for all […] As envisioned by the World Bank, a good society is one based on the mass production of consumer goods within a global economy. Each region or nation contributes to mass production through factory and agricultural goods. The production of agricultural goods is done on large corporate farms or plantations. Small family agricultural units are replaced by large units with factory-like organization. Workers in these larger units are trained for specialized roles and work in corporate teams. Those who previously worked on family farms either work on corporate agricultural units or move to urban centers. […] From the viewpoint of the World Bank, the problem is that many countries have not reached a high enough level of economic development to participate in the mass consumer society. The role of education is to help them make this leap. (pp. 40–41)

As Spring continues, he provides examples of the types of educational activities that the World Bank has enacted over time. These include a variety of curricula, funding and loans, and assessment programs. In this chapter, I am pointing to specifically one of these, namely the World Bank’s funding of and entanglement with TIMSS. It’s clear that TIMSS has been enacting the World Bank’s educational ideology since at least 1999 when they acknowledged the World Bank as a significant funding source. With deeper analysis, however, by returning to the economic data from Tables 16.1 and 16.2, the participating countries and their economic classifications are a perfect instantiation of the World Bank’s vision for the globe. The data speak volumes especially for their connections to the vision for a monoculture of human capital and consumerism.

The countries with increased income levels over the years were Armenia, Bulgaria, Chile, Czech Republic, Georgia, Ghana, Hungary, Indonesia, Iran, Jordan, Latvia, Lithuania, Macedonia, Morocco, Russia, Romania, Saudi Arabia, Slovak Republic, Slovenia, Thailand, Tunisia, Turkey, and Yemen.

The increase in income level corresponds exactly to Spring’s description of the World Bank’s global vision. A country that increases its per-capita income levels over time means that more people in the country are entering the wage labour market and have the ability to consume goods and services in market economies. When the World Bank looks at data for countries like these, it sees its vision realised: more people entering the global marketplace as both the human capital that markets need and as consumers in an ever-increasing demand for products.

Looking specifically at the TIMSS participating countries, we see an increase in GNI per capita for these twenty-three countries equating to about one quarter of all participating countries in TIMSS. Furthermore, all twelve high-income countries hold steady at the high-income level. These are remarkable data; the World Bank is surely pleased to see that countries participating in its activities are increasing the numbers of people entering the wage labour market, or at the very least increasing their salaries by engaging in global capitalism, and increasing demands for global consumption. The World Bank and IEA might even make a leap in suggesting that the TIMSS mathematics assessment, in close association with converging curricula, causes new mathematics education practices that in turn enables a country’s citizens to enter the global economy more readily. However, such an assertion would be poor mathematics. In other words, I am not pointing to any cause-and-effect relationship between TIMSS participation and the increase in income levels of participating countries; I am pointing to the association between the two. A nation state’s choice to participate is likely indicative of several other actions they are taking, many of them additionally with support of the World Bank, to increase their engagement with the global economy. At the very least, participating in TIMSS represents a country’s willingness to engage in the ideology that Spring describes and it should come as no surprise, then, that the majority of countries who could increase their income levels actually did. Although there can be no suggestion of cause and effect between TIMSS and increasing global economic activity, it will serve useful to indicate further how the two are associated. This appears in the next section when I lay out the content of TIMSS and how it clearly accords with the world’s first monoculture.

The commercial-administrative mathematics of TIMSS

Given TIMSS’s history within the context of the World Bank, which is clearly linked to the goals of increasing human capital and consumerism, as argued above, I next offer content analysis of TIMSS material to further explicate the association between mathematics assessment spread and the global economy. Although I am careful not to suggest a cause-and-effect relationship here, at the very least my content analysis below displays that TIMSS practice is very much in line with global capitalism. The discussion here will reveal that the majority of mathematical activities referred to in TIMSS material displays a narrow-minded view of the opportunities within the array of mathematical behaviour. To do so, I first review Harouni’s (2015) categories of mathematics, since I use these as a tool to code the contents of test items released by TIMSS.

Harouni (2015) traces the history of mathematics/mathematics education in terms of its direct correspondence to engagement in the political economy. Thus, the categorisation of mathematical behaviours he provides are highly relevant to the nature of my present inquiry. His four categories of mathematical behaviour are commercial-administrative, artisanal, philosophical, and social-analytical.

Commercial-administrative mathematics centres on the mathematical activity of counting and always implies the market economy’s use of currency, even when not made explicit. He writes: ‘Ultimately, in modern curricula, when a textbook question talks about apples and oranges, it does not mean apples and oranges. It means money’ (p. 62). Furthermore, explicit examples of this type abound in mathematics education; very often, mathematics students practice problems to do with interest rates, buying and selling, breaking even, and the like.

Artisanal mathematics, as Harouni suggests, centres on the mathematics of measurement and uses numbers and geometry to engage in the three-dimensional world as creators and doers.

Philosophical mathematics, centring on patterns, is ‘the one corresponding to the math practiced in universities. This type of math stands neither inside nor beside productive labour. Its product is neither an object nor an interaction in the world but an order in the mind’ (p. 64). For example, mathematics students sometimes engage in creative discovery of mathematical concepts, like determining a pattern about the three sides of any right triangle.

Finally, social-analytical mathematics takes the materials and tools from among the three others and engages the social world for understanding patterns and making group decisions. Harouni clarifies that in some ways, this category can be used to extend the objectives in the commercial-administrative category, such as in a corporation making decisions based on big data. However, Harouni also points to the traditions in critical mathematics education as examples of the category that move in a different social-analytical direction (e.g., Frankenstein, 1983; Gutstein, 2006).

Harouni’s categories emerge from his discussion of the political economy’s relationship with mathematics education. In associating mathematical practice to the ways that the political economy emerged over the course of history, these categories provide an opportunity to classify mathematical practices that exist in the current historical moment. For this reason, I located TIMSS-released items from their grade 8 assessment in 2011 (IEA, 2013) and used these categories to analyse the types of problems that appear in the document; in all there were seventy-seven mathematical tasks to code. The document organised the mathematical tasks according to content strands, including Number, Algebra, Geometry, and Data and Chance. As I refer to specific problems as examples, I will use the code for each problem as it appears in the document, typically the letter M followed by a six-digit number.

I first split the tasks into two lists, those mathematical tasks that were situated in context versus those that had no context. The total number of tasks with no context, that is, no relationship to a real-world situation or scenario, was fifty-four. For example, one mathematical task that is without a context asks the test-taker to find a fraction equivalent to a given decimal (item M042059). As another example, test-takers are asked to determine the largest value that can be obtained when the product of any pair of two-digit numbers is found using the digits 3, 5, 7, and 9 exactly once (item M042002). There were twenty-three mathematical tasks that had an explicit context to relate to the mathematical action to be performed. Examples of these kinds of tasks included calculating the area of a garden (item M052173), using a histogram to interpret data about soda sales (item M032701), and calculating the cost of a taxi trip (item M032477).

I chose to start with context because of the implications of mathematical purpose that context can reveal. The scenarios that test-takers read for uses of mathematics suggest the types of mathematical behaviour that TIMSS promotes. I will return to the no-context problems later but will continue for now with the twenty-three items coded as in-context. For these, I next used Harouni’s insights (2015) to specify the explicit connections to the real world and purposes for mathematics that are displayed by the task. For the twenty-three context-driven mathematical tasks, I coded nine as commercial-administrative, eight as artisanal, and six as social-analytic. However, in working with the data it became immediately obvious that a second round of coding was needed for several items because of implications towards commercial-administrative, as suggested by Harouni. For example, the social-analytic can be used for commercial-administrative means. It will be helpful to look at an example item to make transparent these coding decisions that I made.

Figure 16.3 reproduces item M032695, a task denoted as ‘Make a pie chart with labels’ and with the topic paraphrased as ‘Where people go after secondary school’. I coded the task as social-analytic because the mathematics requires the test-taker to look at counts of people in relation to the whole and make a visual display to present details, with the potential that a viewer could make inferences about some social data. To be clear, the task does not require this kind of critical thinking (making inferences from data) and amounts to not much more than a test-taker’s recall of the procedures in making a pie chart. However, as seen in the example, notice the categories of people to be analysed. Students in a school are grouped by their next choices in life with a small percentage attending university, a greater percentage going immediately into the workforce, and over half attending either business or trade school. There is not any other option or any ‘other’ category. The options for after school are all in keeping with a human capital and consumerist vision for every individual. With the aims of the World Bank and their motives in entangling with TIMSS as laid out in the previous section, it is almost as if the World Bank itself wrote this mathematical task.

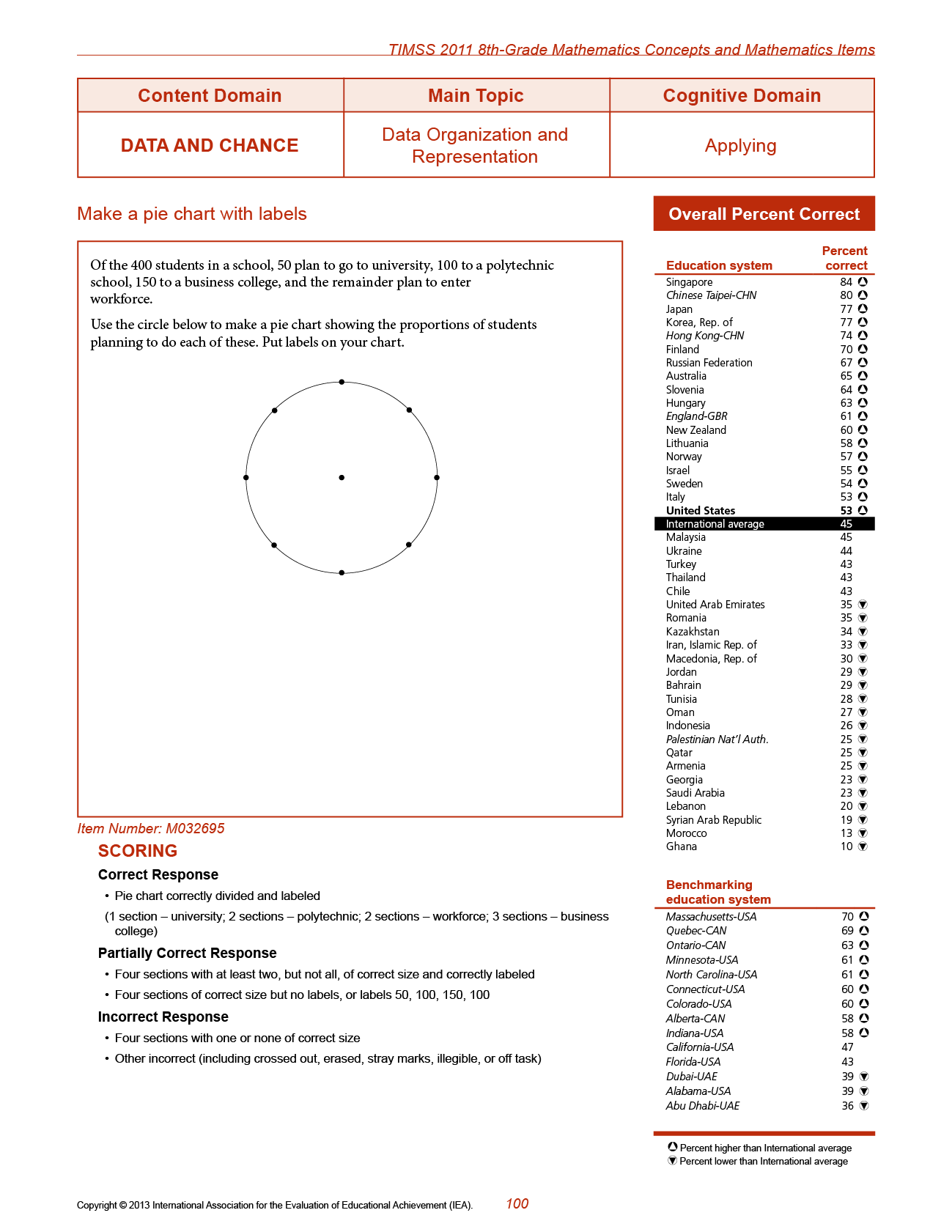
Facsimile of Item M032694 “Make a pie chart with labels” from TIMSS exam.

Fig. 16.3 Item M032695, ‘Make a pie chart with labels’. SOURCE: TIMSS 2011 Assessment. Copyright © 2013 International Association for the Evaluation of Educational Achievement (IEA). Publisher: TIMSS & PIRLS International Study Center, Lynch School of Education, Boston College, Chestnut Hill, MA and International Association for the Evaluation of Educational Achievement (IEA), IEA Secretariat, Amsterdam, the Netherlands.

Table 16.3 TIMSS Released items with context, coded by type.

Commercial-administrative	9
Artisanal (2^nd: Commercial-administrative)	5
Social analytic (2^nd: Commercial-administrative)	6
Artisanal	3

Therefore, TIMSS-released items indicate that, where overt displays of mathematical behaviour are connected to the real world, these are most likely to be related to commercial-administrative goals.

However, what can be said about the remaining tasks, those that do not display a connection to the real world? For these, the items that I coded with ‘no context’, I relied on Harouni’s notion of philosophical mathematics, what he describes as the mathematics of universities and researchers in the field. For many of the fifty-four tasks that had no context, however, this immediately proved to be controversial. Coding a mathematical task that requires the test-taker to convert a decimal to a fraction (as in item M042032) seemed hardly to be what Harouni imagines for philosophical mathematics. For help in distinguishing what I could code as truly philosophical, I turned to literature in mathematics education that distinguishes between procedural mathematics and ‘doing mathematics’ like that of research mathematicians. Mary Kay Stein and Margaret Schwan Smith (1998) offer clarity in comparing procedural mathematics with non-routine tasks that require higher order thinking by students, making connections, noticing patterns, etc.

Thus, to further code the problems with no context in the TIMSS-released items, I clarified which problems were 1) procedural problems that (when considering mainstream middle school textbooks) are often taught to be routines that students memorise and without connections to mathematical concepts and 2) problems that were not routine and required activating either conceptual connections and/or deductive approaches. As examples, the two items I mentioned earlier as no-context tasks provide an example of the two types. Item M042032 (decimal to fraction) is a typical routine that students practice ad nauseum in the classroom. On the other hand, M042002 requires test-takers to use their understanding of place-value and problem-solve by carefully considering some cases to determine which product will be greatest. While the solution can be found by a routine (trying out each case), this is not a typical problem like converting from a decimal.

With this coding scheme in hand, I could then distinguish within the fifty-four TIMSS-released items that were devoid of context. Exactly forty-seven of them were coded as procedural problems with no conceptual connections and only seven remained as nonroutine problems requiring problem solving, deductive reasoning, and/or conceptual connections. I argue that these tasks overwhelmingly represent routine mathematics requiring speed and memorisation rather than analytical, higher cognitive demand mathematics. I argue these forty-seven routine, no-context tasks resonate strongly with a mathematics education for human capital and consumerism. Recall Harouni’s argument that counting oranges and apples is a stand-in for counting money. In the same way, the emphasis on procedural mathematics, devoid of context, devoid of meaning, implies a context that is yet again commercial-administrative. By emphasising the automatic processes in mathematics, the lack of thought and connection, these tasks commit to mathematical practices that wage labourers need to perform quickly and without critical thought.

Taking all the codes and implications thereof together, TIMSS mathematics items from 2011’s grade 8 test contain sixty-seven items with overt and/or implied connections to the commercial-administrative purpose for mathematics with only ten that fit outside this norm. Three items are purely artisanal and seven items are purely philosophical. The exhaustive coding process I have detailed thus indicates a content analysis to complement the context analysis earlier in this chapter. The content of assessment spread is commercial-administrative, the increased use of these materials across the globe also increases the suggested associations between mathematical behaviour and corporate-profit, competition, and consumerism. Although it is far too big a leap to suggest that the content in TIMSS caused the increased income levels of participating countries, revealing this content analysis does suggest how such participation, one among likely many other actions taken by participating countries, at the very least resonates heavily with the goal that said country engages more fully with the world’s emerging monoculture of the global economy, of human capital and consumerism.

Assessment spread in mathematics education is not unique to TIMSS. A similar analysis could focus on the Program for International Student Assessment (PISA) created by the Organisation for Economic Co-operation and Development (OECD). As an assessment spread that initially focused its reach on elite countries and now has extended its spread to include ‘developing countries’ as well, future research areas can consider how contextual analysis and content analysis, as above, might reveal the extent to which assessment spread via PISA provides a complementary understanding of assessment spread.

In this chapter, I have articulated via two research methods that TIMSS as a phenomenon of assessment spread is concomitant with the spread of the global economy. I conclude that a dominant global mathematics education associates with the twin goals of increasing the number of people who enter the wage labour market and become lifelong consumers. On the one hand, critical mathematics educators must develop clear arguments, as presented here, to assert their claims about these entanglements rather than passively accepting the reports from TIMSS, PISA, and the like (as dramatically conveyed in Chapter 15 of this volume). On the other hand, we can use these analyses to motivate culturist perspectives in mathematics education, such as an alter-globalisation mathematics education (Appelbaum & Gerofsky, 2013), that would resist a global and dominating mathematics education solely dedicated to support human capital and consumerism.

References

Appelbaum, P., & Gerofsky, S. (2013). Performing alterglobalization in mathematics education: Plenary in the form of a jazz standard. Quaderni di Ricerca in Didattica (Mathematics), 23, 23–48.

Atweh, B., & Clarkson, P. (2010). Internationalization and globalization of mathematics education: Toward an agenda for reseach/action. In B. Atweh, H. Forgasz, & B. Nebres (Eds.), Sociocultural research on mathematics education: An international perspective (pp. 77–94). Routledge. https://doi.org/10.4324/9781410600042-12

Ernest, P. (2016). Mathematics education ideologies and globalization. In P. Ernest, B. Sriraman, & N. Ernest (Eds.), Critical mathematics education: Theory, praxis, and reality (pp. 35–79). Information Age.

Frankenstein, M. (1983). Critical mathematics education: An application of Paulo Freire’s epistemology. Journal of Education, 165(4), 315–339. https://doi.org/10.1177/002205748316500403

Freudenthal, H. (1975). Pupils’ achievements internationally compared: The IEA. Educational Studies in Mathematics, 6(2), 127–186. https://doi.org/10.1007/BF00302542

Ghosh, A. (1997). Capitalism, nation state, and development in a globalised world. Economic and Political Weekly, 32(14), 683–686.

Gutstein, E. (2006). Reading and writing the world with mathematics: Toward a pedagogy for social justice. Taylor & Francis.

Harouni, H. (2015). Toward a political economy of mathematics education. Harvard Educational Review, 85(1), 50–74. https://doi.org/10.17763/haer.85.1.2q580625188983p6

International Association for the Evaluation of Educational Achievement (IEA). (2013). TIMSS 2011 Assessment. TIMSS & PIRLS International Study Center.

International Association for the Evaluation of Educational Achievement (IEA). (n.d.). History. IEA. https://www.iea.nl/about/org/history

Keeley, B. (2007). Human capital: How what you know shapes your life. OECD publishing.

Keitel, C., & Kilpatrick, J. (2012). The rationality and irrationality of international comparative studies. In I. Huntley, G. Kaiser, & E. Luna (Eds.), International comparisons in mathematics education (pp. 241–255). Falmer. https://doi.org/10.4324/9780203012086-19

Meyer, J., Kamens, D., & Benavot, A. (1992). School knowledge for the masses: World models and national primary curricular categories in the twentieth century. Falmer. https://doi.org/10.4324/9781315225173

Ramirez, F. (2003). Toward a cultural anthropology of the world? In K. Anderson-Levitt (Ed.), Local meanings, global schooling: Anthropology and world culture theory (pp. 239–254). Palgrave Macmillan. https://doi.org/10.1057/9781403980359_12

Spring, J. (2004). How educational ideologies are shaping global society: Intergovernmental organizations, NGOs, and the decline of the nation-state. Routledge.

Spring, J. (2014). Globalization of education: An introduction (2^nd ed.). Routledge.

Stein, M. K., & Smith, M. S. (1998). Mathematical tasks as a framework for reflection: From research to practice. Mathematics teaching in the middle school, 3(4), 268–275.

Visioncarto. (2018). Buckminster Fuller’s Airocean projection (1954) [Map]. Visionscarto. https://visionscarto.net/base-maps#&gid=1&pid=1

Wolfmeyer, M. (2014). Math education for America? Policy networks, big business, and pedagogy wars. Routledge.

World Bank. (2007). Building knowledge economies: Advanced strategies for development. World Bank.

World Bank Group. (n.d.). Historical classification by income in XLS format [Data set]. Databank. http://databank.worldbank.org/data/download/site-content/OGHIST.xls