19. Gender, mathematics, and mathematics education

David Kollosche, Daniela Steflitsch, and
Kora Maria Deweis-Weidlinger

©2024 David Kollosche et al., CC BY-NC 4.0 https://doi.org/10.11647/OBP.0407.19

This chapter approaches the discipline of mathematics from the perspective of gender studies. It provides an overview of the gendering of mathematics and mathematics education based on aspects such as images of mathematics, achievement, representation, biology, cognition, learning preferences, classroom interaction, and belonging. These aspects are then critically addressed from a post-structural perspective on gender and mathematics. Special attention is paid on moral dilemmas in dealing with gender inequality in mathematics and on the question how the perspective of gender studies can enrich our understanding of mathematics.

Why bother to look at mathematics and mathematics education from the perspective of gender? At a first glance, the political struggles for the recognition and non-discrimination of different genders seem to be very far away from the presumably objective and logical shores of mathematics. Daring a closer look, we might be surprised that we have entered a rose garden of thorny questions and paradoxes: Why is mathematics commonly regarded as a male domain? Why is there only one female winner of the Fields Medal, the highest decoration for success in mathematics research? Why is there a clear male majority of university professors of mathematics? And why are far fewer women than men pursuing mathematics-intensive careers? These are examples for persistent inequalities, while school achievement in mathematics differs only slightly between girls and boys, while some countries even show higher achievements among girls, and while female mathematicians are just as successful as their male counterparts.

These differences between men and women in the field of mathematics demand an explanation for different reasons. Politically, they raise the question whether women in mathematics are being systematically discriminated against. Economically, motivating more women to pursue mathematics-intensive careers is often believed to be beneficial for a country’s economic development. Didactically, we might want to ask if girls and boys have different resources and needs in the mathematics classroom and should be taught differently. Even for the sake of mathematics, an investigation into gender aspects of mathematics and mathematics education might be illuminating: Would not an answer to the question why mathematics is commonly regarded a male domain deepen our understanding of mathematics? Might not the hypothetical result that women do mathematics differently but are systematically excluded from higher mathematics call for a different way of doing mathematics? We shall return to these questions.

We know no other field of inquiry into mathematics education which would include as many theoretical perspectives and interest-based positions as the gender-and-mathematics discourse. For an intense experience of that variety, see the forty-two divergent peer commentaries on Camilla Persson Benbow’s (1988) contribution to the topic in the journal Behavioral and Brain Sciences; and even further perspectives have been developed since. The questions that Betty Johnston (1995) raised give a quick taste of this melange:

Noteworthy of this research field is the nearly exclusive reliance on a men-versus-women dichotomy. There is hardly any research, especially nothing that we found to be a useful reference, about gender issues in mathematics and mathematics education, that would transcend that dichotomy and focus on non-binary identities. We think that it is an urgent research desideratum to open up the gender concepts used in mathematics education research, but we will not be able to achieve that in this chapter.

The next part of this chapter will deal with the concept of gender, which has proven to be an important concept for explaining and problematising differences between men and women. In the third part of this chapter, we will address differences and explanations regarding mathematics. We dedicate a separate part to post-structural perspectives on gender and mathematics, as we consider them to be extremely powerful but also surprisingly alien to common thinking. In the fifth part, we allow ourselves to place a critique of the common discourses on mathematics and gender by proposing a closer focus on a possible gender bias of mathematics itself. In the last part, we turn to moral questions in asking what could and should be done in mathematics and mathematics education as a consequence of the provided insights.

The concept of gender

The concept of gender has been developed as a counterpart to the concept of sex. The first section of this part of the chapter presents the gender concept and addresses how it can help us understand certain aspects of differences between men and women. The second section problematises the concept of gender from a post-structural perspective.

Sex and gender

The distinction between the concepts sex and gender has been established to point out that some differences between men and women are biological in nature while many others are social constructions and open to change. The term ‘gender’ has presumably been introduced to academia in the above sense by John Money (1955). His perspective on the cultural conditions of the differences between men and women became of wider academic and public interest to describe socially created inequalities.

We are usually able to assign the sex of a person with quite a certainty by detecting the external sexual organs, and we start doing so even before a baby is born. However, when it comes to the attribution of gender, it is usually more difficult or less clear. What we can perceive are gendered signs and forms of behaviour, for example a certain stature, shape of a face, haircut, dress code, certain ways of moving and talking, also interests in certain activities, such as in mathematics. In rare cases, we might be puzzled by seemingly conflicting signs and wonder in which pigeonhole to put that person, but in most cases, we easily assign a gender and, by doing that, activate certain expectations or gender-specific role models. These stereotypes can be clearly visible and obvious, as for example in a group photo of the all-male staff of a fire station. They can also be more subliminal, for example in television advertisements for cough syrup, when the image of the caring and nurturing mother and wife is implicitly conveyed in the marketing of medical products that are equally suitable for both sexes.

In the United States, an early influence in academia had been anthropologist Margaret Mead (1949) who showed that different societies ascribed different social roles to the sexes. Michael N. Friedan’s (1963) The Feminine Mystique, documenting the dissatisfaction of housewives, became a bestseller and made feminism an issue of the general public in the US and beyond. Such contributions opened an intellectual space in which alternative roles for women in society could be envisioned and expressed. The analysis and change of gender roles were at the heart of the subsequent women’s right movement in the second half of the twentieth century. This movement included not only political struggle for women’s suffrage, equal access to education and professions and sexual autonomy, it also led to a critique of theories that positioned women as inferior to men and motivated research on femininity.

Janet Saltzman Chafetz (2006) provides an impressive overview of the variety of theoretical approaches to gender theory. Among this variety, social learning theories have become widely used to describe gender as a social role one is educated into. As Jennifer Marchbank and Gayle Letherby (2014) put it, social learning theories assume ‘that girls and boys learn gender-appropriate behaviour from birth as we are all surrounded by gender socialisation messages from our families, peers and the media’, and they have ‘been the basis of most sociological work on masculinity and femininity, mainly focused on determining how we learn, internalise, and then recreate gender stereotypical roles’ (p. 9). Social learning theories make us aware that, having undergone education in a gender-biased society, we are always-already part of this social structure.

Problematising gender

The gender discourse has been fundamentally criticised from a post-structural perspective. This perspective is closely connected to the French philosopher Michel Foucault, who worked out the discursive constitution of reality in such fields as mental illness (Foucault, 1961), delinquency (Foucault, 1975), sexuality (Foucault, 1976), or patterns of thought more generally (Foucault, 1966). The main line of argumentation is that reality is not just out there in a pre-structured form but constructed by humans in discourse. Reality, therefore, is not objective but ambiguous, constituted differently from different perspectives in different times and places, and a product of interests and power. To take the example of mental illness, Foucault (1961) worked out how the idea of mental illness is the product of a modern discourse which is designed to exclude from society any forms of behaviour deviating from the modern rationalist ideal and tempting us to fall back to a pre-rationalist existence by abandoning our self-discipline. Thereby, the construction of reality does not only include the assertion of a certain discourse, it also includes the organisation of social practices and institutions, the legitimisation of specific arguments, and the validity of a certain body of knowledge. In the case of mental illness, institutions such as asylums, academic discourses such as psychology, the distinction of experts on mental illness, and practices of removing the mentally ill from the public sphere work together in a complex web that constitutes what mental illness means for us today.

In his later work, Foucault (1982) investigated how power is executed on people by discourses. He explained that discourses do not simply direct and forbid, rather they create temptations and design rooms in which to position the self. People then make these discourses their own by filling them out individually within the given boundaries, thus becoming an accomplice of the discourse itself. As an example, consider speaking in your mother tongue: sure enough, you have a distinct style of expressing yourself in it, but there are also certain boundaries you would not cross, certain rules you will stick to, rules you would even demand others to follow. Foucault (2007) stressed the possibility of resistance against discourses that govern us and understood critique as the art ‘not the be governed like that, by that, in the name of those principles, with such and such an objective in mind and by means of such procedures, not like that, not for that, not by them’ (p. 33, original emphasis). Now, from this post-structural perspective, it would seem promising to direct one’s attention at the discursive constitution of women, men and gender.

In Gender Trouble and her later Undoing Gender, Judith Butler (1999, 2004) approached the gender discourse from a post-structural perspective. With traditional feminism she shared the assumption that gender roles are cultural constructs and designed in a way to secure the social privilege of men. However, Butler’s view differed from traditional feminism in some crucial points. Foremost, studies asking for the nature of femininity, for example with the goal of a more girls-friendly organisation of education, reproduce the idea that we are born into our roles as males and females. In contrast to that assumption, Butler argues that even sex is discursively constructed. As Penelope Eckert and Sally McConnell-Ginet (2003) pointed out, ‘there is no obvious point at which sex leaves off and gender begins, partly because there is no single objective criterion for male or female sex’ (p. 10). For example, the configuration of genitals is sometimes ambiguous, and controversially discussed medical procedures are systematically being undertaken to adjust the configuration of genitals to social expectations. In the light of the variety of possibly inconsistent biological features used to determine sex, including anatomical, genetical and hormonal features, and in the light of the sometimes ambiguous nature of these features, the decision which sex to assign to a person is ultimately social.

Butler (1999) problematised that traditional feminist studies, by adhering to the dichotomy of the two genders, proved unable to explain cases of third, mixed, and changing gender. Further, neither biology nor social learning theory can explain the different varieties of masculinity and femininity. Neither can they explain instances of individual resistance to gender roles, of testing their boundaries, playing with them, maybe even redefining them.

Post-structural theories redirect our attention from the question what could typically count as masculine or feminine to the question how the necessarily political discourses on gender interact with the constitution of our identities, with the goals we deem approachable, the roles we feel comfortable in, and the expectations directed at us. Our various discourses often include gender roles and direct men and women to specific positions within the discourse, for example to positions of ability or disability. Deviations from such discursively set roles are difficult to accept for others sharing that discourse, but they may also lead to conflict within the respective person. For instance, it may be difficult to position oneself as a loving mother and well-organised housewife and simultaneously as following a professional career. Heather Mendick (2005) calls the inner negotiation of the different discourses ‘identity work’.

At the same time, the post-structural perspective points out that we are not only inevitably educated into gender discourses, but, from that position within the discourse, always-already accomplices of gender discourses and ‘doing gender’ (Butler, 1999, p. 41). This perspective does not present women as passive victims of gender stereotypes but assumes an active role of women in positioning themselves in gender discourses. This shift is not meant to reassign the blame for gender inequalities to women. Instead, it is meant to highlight the ways in which we could do gender differently. Eventually, the benefit of understanding gender as a product of discourse is that gender differences are not inescapable but open to change. From a post-structural perspective, promoting such change begins with a deconstruction of dominant discourses and a search for possibilities to think differently. At least in academia, though not that easily in the social pressures of daily life, we are not reduced to the decision where to position us in given gender discourses but can eventually decide ‘not to be governed like that’.

How do men and women differ at all concerning mathematics? Before we give a short presentation of gender differences in mathematics, we want to address the question whether investigating such differences bears dangers. In her insightful book Sex Differences in Cognitive Abilities, Diane F. Halpern (2012) explained:

Roberto Ribeiro Baldino (2000) was surprised by the acceptance and tolerance for his conference presentations where he explained that a gene had been identified which allowed for higher mathematical understanding in the first place, and for which ‘it has been possible do determine that only 10 to 15 per cent of men and 5 to 8 per cent of women are […] carriers’, explaining among other inequalities ‘why the majority of mathematicians are men’ (p. 145). The whole theory was bogus, the presentation an experiment conducted with a clueless audience of researchers in mathematics education, but, aside from much else, it showed that seemingly scientific explanations for differences are often too uncritically accepted, maybe even welcomed, and eventually set to use in the legitimisation of inequalities. We assume that any contestation of differences is dialectical in nature, on the one hand assisting in the explanation of inequalities, while on the other hand forming a basis for their legitimisation. We will have to bear in mind this twofold nature of stated differences if we seek to avoid being trapped by explanations that, from a different perspective, turn out to be questionable and problematic.

Paul Ernest (2007) warned against taking up a one-dimensional perspective in which we assume that there is one gender problem in mathematics. He found that what is addressed when discussing gender and mathematics is a whole array of different inequalities, and that authors often talk about rather different issues under similar headings. Ernest claimed that what poses a gender-related problem is eventually a question of perspective and interest. We can conclude that talking about the gender problem in mathematics is diffusing the discussion and may even be proposing that gender itself is the problem, rather than facing a range of different problems, which shine up from different perspectives and become problematic for people with specific interests. Here, we decided to distinguish the following perspectives on gender differences in mathematics:

1. Gender differences in images of mathematics.
2. Gender differences in achievement.
3. Gender differences in representation.
4. Gender differences in biology.
5. Gender differences in cognition.
6. Gender differences in learning preferences.
7. Gender differences in classroom interaction.
8. Gender differences in belonging.

These areas can serve as an explanatory basis for each other, but they are not easily brought into a linear order of cause and effect. For example, gender differences in learning preferences can explain differences in achievement and demand an explanation themselves. Consequently, gender-oriented studies in mathematics education need to navigate through a complex web of interrelating issues, which shine up with different intensity when different interests come to play. Ernest (1995) proposed to understand gender inequality in mathematics as a vicious cycle of mutually reinforcing phenomena. We will address this idea in the section titled ‘Where is mathematics?’. On the following pages, we wish to address the various perspectives on gender differences in their own right. Afterwards, we will revisit these discourses more critically from a post-structuralist perspective.

For a long time and in many places, mathematics had been considered to be male. Even today, mathematics and mathematics-related domains are still stereotyped as masculine and are therefore difficult to reconcile with female gender roles. Public images are influences by role models, with whom people can identify more or less easily. In mathematics, the names and faces of such role models are predominantly male (and White, one might add). There are several reasons for that. One reason is that the successes of female mathematicians have often been withheld in the history writing of predominantly male historians. The most outstanding ancient example is Hypatia of Alexandria, whose story has only recently become a vivid field of historical study. A more recent example is the controversy around the impact of Albert Einstein’s wife Mileva Marić on her spouse’s work in theoretical physics.

However, the number of published contributions of women to mathematics have indeed been few compared to those of men. The reason here is not necessarily that women are less interested in mathematics. Teri Perl (2010) examined an annual magazine published in England from 1704 to 1841, which contained enigmas, queries, and mathematical questions and was aimed specifically at women. Its existence over decades suggests that there was a wide market for such publications among women and that women were indeed interested in mathematics. The main explanation rather seems to be that, until fairly recently in human history, patriarchal structures in society have not allowed or at least strongly hindered women to appear as an independent intellectual, to receive the necessary education and formal qualification, to have their voices heard and their work published, and to secure paid positions in mathematics. In this vein, Reuben Hersh and Vera John-Steiner (2011) tell the stories of Sophie Germain, Sofya Kovalevskaya and Emmy Noether. Today, as we shall see in a later section on ‘Representation’, female mathematicians are no longer the exception but still a minority.

Stereotypical images about mathematics and mathematicians are transported through popular media. Gilah Leder (1995) analysed articles of well-known newspapers in Australia and Canada regarding gender equity. These articles confirmed the prevailing stereotypical views about male-dominated power structures much more often than they questioned them. She concluded that ‘it appears that the subtle messages conveyed in the popular press are consistent with small but consistent differences in the ways females and males perceive and value mathematics and related careers as appropriate for themselves’ (p. 125).

Mendick (2005) analysed movies presenting mathematics and mathematicians and stated: ‘This dominant discourse around mathematicians in popular culture depicts them as boring, obsessed with the irrelevant, socially incompetent, male and unsuccessfully heterosexual’ (p. 214). Movies with mathematical contents (e.g., A Beautiful Mind, Enigma, Good Will Hunting, Pi) make use of such stereotypical images and at the same time shape our image of a ‘typical’ mathematician. In all films, the protagonists struggle with mental illness that is directly or indirectly related to mathematics. In these movies, mathematics is presented as something where femininity does not fit in. However, in a later analysis of fictions published after the financial crises of 2008, Mendick (2017) finds that mathematics has been portrayed in more diverse and critical ways. Hidden Figures, a movie about a group of female Afro-American mathematicians contributing crucial work to NASA projects, was too new to find its way in Mendick’s paper but serves as an outstanding example for that shift.

Stereotypical images about mathematics and mathematicians are also reproduced in and influence education. Natthapoj Vincent Trakulphadetkrai (2017) analysed the representation of girls and women in sixty-four Anglophone mathematical picture books produced for private education and entertainment. He found that girls and women were considerably underrepresented. In a study on images of mathematics in the mathematics classroom, Mary Schatz Koehler (1990) concluded that the image of mathematics as a male domain was reinforced by the portrayal of mostly male mathematicians and the use of mostly masculine context in test questions.

In a mathematics course designed for re-entry into science and technology fields, Zelda Isaacson (1990) explored the reasons why the attending women (all in their twenties and thirties) chose to opt out of mathematics somewhen in their school career. Some explained that as a woman you are considered weird if you like maths. One example of a conversation with colleagues about what course one of these women is in, shows this clearly: ‘They look at you in absolute horror, and that’s the end of the conversation’ (p. 24). Within these conversations, the impact of stereotype-based family pressure and peer influence crystallised. Another woman described mathematics as a subject where competences such as creativity or imagination are not used and thus women who are more likely to show such skills (in her view) cannot connect with mathematics. While we will return later to the question of how women negotiate their identities in the light of such images of mathematics, Isaacson’s study showed that images of mathematics do have an impact on women’s choices. Other evidence, which we will only mention here, comes from a statistical analysis of gender-science stereotypes and sex differences in science and math achievement in thirty-four countries, which established ‘that nation-level implicit stereotypes predicted nation-level sex differences in 8th-grade science and mathematics achievement’ (Nosek et al., 2009, p. 10593).

Mathematics is often considered a discipline in which men show higher proficiency than women. Statistical data reveals that this is the case in some environments but no general phenomenon. As an illustration, we can look at the results of large-scale assessment regimes such as PISA. In PISA 2012, the latest PISA run with an emphasis on mathematics when we wrote this chapter, boys had significantly higher mean scores than girls in mathematics performance in thirty-seven of the participating sixty-five countries, reaching differences in the mean scores of boys and girls as high as 22 score points in Austria and 25 in Colombia and Chile (OECD, 2014, p. 305). However, there were also six countries in which girls performed significantly better than boys, including Iceland, where girls on average scored 6 points more than boys, and Jordan, where the difference amounted to 21 points. Summing up the data from the thirty-four participating OECD states (the only average values provided by the study), the mean score of boys is 12 points higher than that of girls. What do these numbers tell us? First, the PISA score is normalised with a standard deviation of 100. 12 score points amount to only 12% of that deviation in score points. Second, the mean scores between comparable countries often differ more drastically than between girls and boys in the countries. For example, Belgium scored 20 points higher than neighbouring France, Switzerland scored 25 points higher than neighbouring Austria, and Finland scored 40 points higher than neighbouring Sweden. On average, Finnish girls scored 37 points higher than Swedish boys. Other comparative assessments yield similar patterns (e.g., Hanna 1989, 1994; Ernest 2007). We conclude that differences in mathematics achievement in favour of boys can be detected but appear to be very small and possibly negligible when compared to other variations.

Countries in which girls perform significantly better than boys prove that higher performance by boys is no general phenomenon and indicate that local factors such as culture and school systems must play a crucial role. Obviously, it would be difficult to explain these differences between countries by biological theories, which claim universal validity, alone (Nosek et al., 2009). In a study with 2300 school leavers in England, Geoffrey Driver (1980) compared the mathematical achievement of students with English descent with that of students with West Indian descent. It was not very surprising that boys of English descent slightly outperformed girls of English descent. However, West Indian girls outperformed English boys and West Indian boys performed at the level of English girls. Driver explained these gender differences in performance between students of English and students of West Indian descend by the different social roles of men and women in both societies.

Admittedly, one might contend that the mathematical literacy defined and measured by PISA and school mathematics as assessed in Driver’s study are something different than higher secondary or even tertiary mathematics, where gender differences could show differently. This is why we compared the number of enrolments in tertiary education programs (including Bachelor, Master and doctoral studies) in mathematics and statistics with the number of graduations in these programs within the European Union as documented by the European Statistical Office Eurostat. In 2014, the latest year for which we have union-wide data, there were 117064 women and 147901 men enrolled, while 25074 women and 27871 men graduated in these programs (Eurostat, 2019a, 2019b). That yields 0.214 female graduates per female enrolments, whereas the ratio is only 0.188 for men. Although the statistics include no information about the obtained grades, women appear to be more successful students of mathematics than men. We conclude that there is no evidence that men would generally achieve better in tertiary mathematics either.

When we look at academic positions, the proportion of women, depending on the ascending level of qualification, ranges from 35% (lower level) to 15% (highest level) in STEM fields compared to 46% and 24% across all scientific fields in the European Union (European Commission, 2019). In the US, an average of 30% of PhDs in mathematics were awarded to women between 2005 and 2008 and in 2005 only 9% of all full-time tenured professors in doctoral-level mathematics departments were women (Popejoy & Leboy, 2012). Even more severe underrepresentation of women is reported from African countries (Gerdes, 2006; Masanja, 2010). Apart from some exceptions, this list could easily be extended further. In summary, both horizontal and vertical segregation can be observed. This means that not only the proportion of women is significantly lower in mathematics-related areas than in other areas, but also that women are less frequently represented in higher status areas than in lower status areas.

The underrepresentation of women in mathematics can partly be explained historically. Isolde Kinski (1994) studied the history of the underrepresentation of women in mathematics from a German perspective. Until the last century, education was reserved for only a few people and a privilege of men. The distribution of tasks between the sexes and the societal roles associated to the sexes restricted women to the domestic sphere and thus excluded them from higher education. It was argued that dealing with science or mathematics was against women’s nature. Even when, from around 1820 onwards, bourgeois daughter schools became more common in the German-speaking world and elsewhere, these were limited to teach girls only elementary arithmetic necessary for keeping the household.

At the beginning of the twentieth century, there were initial discussions about girls’ access to school-leaving examinations and thus access to universities. Even though women were officially admitted to study in German countries from 1900 onwards, they had to fight different obstacles for decades. In those days it was unthinkable for many universities to award doctorates to women. For example, Christine Ladd, who was the first American woman to fulfil all formal requirements for a PhD in 1883, was not officially recognised until forty-three years later (Green, 2001). Even in 1981, only about 6% of the thousand speakers at the meetings of the American Mathematical Society were women (Kenschaft, 1982). Nevertheless, with the admission of women to the universities, the contents of the higher girls’ schools changed. Curricula for girls’ and boys’ schools were unified and coeducation was introduced in the course of the twentieth century. Since then, representational inequalities have decreased but they still exist to a considerable extent.

Sapna Cheryan (2012) suggested that ‘seeking out math-related careers is still a gender role violation for women’ (p. 184, without original emphasis). She explained that the public image of mathematics as a male domain and activity remained an obstacle for the perusal of mathematical careers by women. However, there are other possible explanations for the underrepresentation of women in mathematics which we will address in the following sections.

Biological explanations for gender differences in mathematics often focus on abilities in spatial visualisation. Three different approaches are repeatedly found in the literature: a cerebral explanation, a hormonal explanation, and a genetic explanation. The cerebral explanation refers to the neuropsychological effect of lateralisation. This describes the unequal distribution of individual functions between the two halves of the brain. Studies show that an asymmetrical organisation of the brain is more pronounced among men (Halpern, 2012). Therefore, women tend to use both brain hemispheres when solving exercises requiring spatial abilities while men particularly use the right brain half, to which skills such as spatial thinking and numerical reasoning are attributed. However, there is no evidence that one way of using the brain for spatial ability tasks is more successful than the other. Other studies show that the level of certain hormones might have an impact on the performance in spatial ability tests (Hampson, 1990; Hampson & Rovet, 2015). Approaches which linked spatial ability to specific genes have been found unconvincing (Boles, 1980), but the assumption that men and women might have different genetical dispositions for spatial ability as a result of their archaic roles as hunters and fighters persists among some scholars (Geary, 1998; Halpern et al., 2007).

Despite these attempts to explain sex-related differences biologically, different meta-studies on biological differences between men and women concluded that, in most areas, differences are minimal, if not negligible. That includes fine motor skills, mental rotations, spatial perception and visualisation, mathematical ability, computational skills and understanding of mathematical concepts (Hines, 2010) but also general intelligence (Colom et al., 2000) as well as language skills, communication behaviour, computer use, self-esteem, aggression, helpfulness, leadership skills and sexual behaviour (Hyde, 2005). Consequently, Janet Shibley Hyde (2005) proposed ‘that males and females are similar on most, but not all, psychological variables’ (p. 581). Obviously, biology appears not to explain much.

Some scholars argue that gender differences in academia derive from the fact that men and women think differently. One of the most provocative studies in this direction is Mary Field Belenky, Blythe McVicker Clinchy, Nancy Rule Goldberger, and Mattuck Jull Tarule’s Women’s Ways of Knowing (for a similar study resulting in a somewhat different categorisation see Magolda, 1992). Belenky and colleagues (1997) argued that women think differently than men and that academia is usually organised in a way that values only masculine ways of thinking with the effect of silencing women. The psychologists conducted interviews with a wide variety of US-American women to learn about ‘the way they perceived themselves and the world around them’ (p. 4):

Belenky and colleagues (1997) described received knowledge, which relied solely on authorities and was the main form of knowledge organisation for many women before they developed subjective knowledge. The latter form of knowledge is the first step towards building confidence in oneself and includes a drastic refusal of authoritarian truth claims:

Some women in the study felt a need to abandon purely subjectivist positions for the sake of universal perspectives which would, for example, fulfil the requirement of academic or other interpersonal debate. However, the way of knowing adopted by women differed from that of men in what Belenky and colleagues (1997) termed procedural knowledge. Procedural knowledge focused not on how things are but on how something can be done, including an appreciation of different perspectives on situations. Here, objectivity was gained not by assuming that there is one true way but by leaving subjective positions and opening up for a variety of perspectives. However, the authors stressed that the adopted procedures are most often man-made and might bear in them a gender bias, which allows for answering questions relevant for men rather than questions relevant for women. Such a bias might be found in a very specific example, but it was also identified on a very general level: Belenky and colleagues reported men to strive for separate knowing, which positions the learner in a distance to the object of learning and looks for procedures for its manipulation, whereas women are found to strive for connected knowing, which is a very personal endeavour to find ever new procedures to understand the object in question. Women, especially those engaged in academia, were found to also perform separate knowing, but they often reported to find it meaningless or to have turned to connected knowing later. A last way of knowing, termed constructed knowledge, assumes the post-structuralist position that knowledge is but a construction. Constructers of their own knowledge embark on the mission to unify valuable input and subjective positions into a narrative that personally makes sense and still meets the requirements of successful communication with others.

Discussing the relevance of women’s ways of knowing to mathematics education, Olive Chapman (1993) argued that a positivist ‘view of mathematics tends to dehumanize or objectify it, thus limiting it to a framework with characteristics that are more compatible with separate knowing than connected knowing’ and that ‘all of the circumstances that could facilitate connected knowing are stripped away’ in traditional teaching settings with the result of silencing connected and mostly female knowers (pp. 208–209). She demanded ‘that mathematics be reconceptualized to reflect its humane features and mathematics classroom processes revised to facilitate the characteristic ways of knowing of both males and females’ (p. 209), a demand that we will return to. We recommend Joanne Rossi Becker’s (1995) more detailed account of what it might mean to allow for connected knowing in the classroom.

The work of German mathematics educator Inge Schwank departs from different theoretical frameworks but could be interpreted as an application of the insights presented above. In her analysis of problem-solving strategies in Information Technology studies and mathematics, Schwank (2002) identified two typical cognitive approaches, which she terms predicative and functional thinking:

The label predicative was used to characterize a problem solving behaviour highly orientated at and sensible for features, relations and judgements, whereas the label functional was used to characterize a problem solving behaviour highly orientated at and sensible for courses, modes of actions and effects. (p. 489, original emphasis)

We find it striking that predicative thinking as described by Schwank aims at understanding very much in the sense of what Belenky and colleagues (1997) called procedural knowledge, while functional thinking as described by Schwank aims at manipulation very much in the sense of what Belenky et al. called separate knowing. Given that analogy, it does not come as a surprise that Schwank (1994) reported that women tend to think mostly in a predicative way, while the majority of men seems to apply a functional way of thinking. A small proportion of men was found to prefer predicative thinking but functionally thinking girls seem to be a real exception. However, there are people who cannot be assigned to either one or the other way of thinking.

Through the analysis of problem-solving behaviour, electroencephalogram (EEG) patterns, and eye movement in experiments, Schwank (1999, 2002) showed that the way of solving a task within logical reasoning differs greatly with the method of thinking. There are tasks where one method of thinking is more successful than the other, depending on the way the task is presented. Broken down to mathematics classes, it also seems to be decisive how the teacher articulates help when students have problems in solving tasks. In contrast to the functional thinker, who likes to elaborate solutions step by step with active trying, it will not be quite helpful for a predicative thinker to tell him or her to ‘just give it a try’ (Bischof-Köhler, 2002/2011). Students who are using a predicative strategy tend to think about the whole problem with all its aspects before they start working on it. Teachers largely attributed this approach of solving problems to the female students in their class and therefore often characterised the girls as being insecure. Hence, we can imagine that the way of thinking might also explain why girls and boys differently participate in class. While boys as a part of their way of thinking just try to find solutions to the problem and accept wrong answers along the way without being discouraged, girls might need some time to grasp a problem in its entirety and to build up the relations between single elements. The reason why boys and girls act differently in mathematics lessons could, therefore, be partly due to different ways of thinking.

Halpern and colleagues (2007) suggested that there might be sex differences within the underlying cognitive processes, as there seem to be specific tasks where females perform better than males and vice versa. Examples where women tend to excel men are language production, reading, writing, and algebra. These are all tasks requiring fast retrieval of information stored in long-term memory and the use of language to create connections. Males, on the other hand, seem to use strategies focusing on the maintenance and manipulation of mental representation in working memory, letting them outperform females in mathematical problem solving, mental rotation or spatial perception tasks. This approach seems to largely coincide with that of Schwank, suggesting that girls and boys might just use different strategies for solving problems. However, it is not possible to say with certainty to what extent these findings really influence performance in mathematics class. The step from cognitive psychology to mathematics teaching and learning does not seem to have been sufficiently explored and one can only speculate to what extent the different cognitive processes lead to gender differences in mathematics achievement or cause different degrees of interest in mathematics.

The idea that people use different styles of thinking and that these styles are used with different frequency among men and women, quickly leads to the question of how far classrooms are organised in a way that welcomes both styles. Jo Boaler (1997) took up that question. She followed the cohorts moving from school years 9 to 11 in two schools over the course of three years and used ethnographic methods, including classroom observations as well as questionnaires and interviews with students and teachers, to learn how students experience mathematics education.

One issue Boaler pointed out is that addressing a ‘lack of understanding of the mathematics they encountered in class […] was particularly acute for the girls, not because they understood less than the boys, but because they appeared to be less willing to relinquish their desire for understanding’ (p. 112). For example, in an interview, a student called Marsha explained that ‘you have to work it out and you get the right answers but you don’t know what you did, you don’t know how you got them’ (p. 114), whereas a student called Gary explained that ‘once you know how to do it, you’re away’ (p. 115). Apparently, students such as Marsha strive for what Belenky and colleagues (1997) called connected knowing, while students such as Gary strive for separate knowing.

Boaler (1997) pointed out that the use of different ways of knowing interacts with teaching styles. Textbook work, which offers only one perspective on the mathematical content and usually one approach to performing procedures, is usually preferred by boys. In contrast to that, girls preferred working with individualised booklets and in groups:1

The reasons that the girls liked these approaches were related to the freedom they experienced to use their own ideas, work as a group or work at their own pace. All these practices, the girls claimed, gave them access to a depth of understanding that textbook work denied them. (p. 114)

Boaler also discussed the desire expressed by many boys to solve problems quickly. This competitive desire to excel in speed and number, or at least not to fall behind, reduced the need for knowledge to knowing how to solve the involved problems and stands in opposition to a wish for understanding. Teachers quickly pacing through the mathematical contents are then clearly meeting the desires of separate knowers and disregarding the needs of connected knowers.

Some of Boaler’s findings had already been reported by Jacquelynne Eccles (1989), who stated that competitive activities, drills, and practices are attributes of classrooms that produce high sex differences, while classrooms with low sex differences in mathematics tend to be more co-operative and supportive. In her course for re-entrants, which was attended only by women, Isaacson (1990) worked mainly in the form of group work, which most women reported to be the decisive difference to mathematics lessons at school. The participants acknowledged the importance of this form for building deeper understanding through explaining contents to other group members and discussing their answers until all agree. Boaler’s study coincided with a German study by Sylvia Jahnke-Klein (2001). She obtained similar results and posed the question whether boys, who seek technical understanding and want to move on faster, appear more gifted or higher achieving than girls, who want to dwell on contents to understand them thoroughly.

It becomes apparent that different styles of teaching are to a different extent able to meet the desire for learning of connected knowers. Boaler (1997) reported a number of cases where girls with a high potential in mathematics hardly participate in mathematics lessons for reasons closely associated with unfitting ways of knowing. As this ‘disparity […] was most acute for the highest ability girls’ (p. 123), Boaler raised the question if unfitting teaching styles could be responsible for unequal achievement and representation of girls in high-ability environments.

On the other hand, Boaler reported of boys in reform-oriented classrooms with open teaching approaches, who complained that ‘they wanted more structure in their work, they wanted someone to tell them what to do’ (p. 120). Obviously, there are also teaching styles that do not meet the wishes of separated knowers. However, Boaler added that these boys were able to adjust to the different teaching styles within one- or two-years’ time.

There are numerous studies on the behaviour of both teachers and pupils in mathematics lessons. Many of these studies show that teachers treat boys more favourably than girls and that boys act differently from girls. This may not only lead to the conclusion that girls are disadvantaged by the interactions, structure, and climate in the classroom, but might also have an impact on the performance, the choice of course, and also on the motivation and self-image of students.

While different treatment can already be found in interactions with children who do not yet attend school (Olson et al., 2010), most studies have been conducted with students in secondary school education. Becker (1981) reported that classroom environment seems to be more supportive of males than of females both academically and emotionally. Interactions on a non-academic level such as joking are much more common between teachers and male students. Females do not seem to have an active role during class and seem to react to teachers’ bonding with boys by becoming even more passive. Becker observed that teachers seemed to reinforce the traditional view of mathematics as a male domain, for example through language or examples used for explanations. Therefore, the identified class environment was not considered as a positive way to stimulate girls to continue their study in mathematics. In contrast, it seemed to have led girls to behave in ways that reinforce teachers’ expectations of male superiority.

Koehler (1990) confirmed that boys receive more help from teachers than girls, they are more often involved in conversation with teachers, they receive more feedback on their behaviour from teachers, and they are provided more critical feedback on their work outcomes by teachers. Joachim Tiedemann (2002) documented that teachers attributed higher mathematical abilities and higher effort-resources to boys than to girls. Elizabeth Fennema, Penelope L. Peterson, Thomas P. Carpenter, and Cheryl A. Lubinski (1990) argued that the potential in mathematics of boys is usually overestimated, while that of girls is rather underestimated. By examining teacher perceptions about their students’ mathematical ability by letting them classify if they consider maths classes as too easy or too hard for them, Catherine Riegle-Crumb and Melissa Humphries (2012) found that especially on mid-level classes, White females are more likely to be judged as being in a course too difficult for them.

Helga Jungwirth (1991) investigated how boys and girls interact in teacher-centred classroom conversations, which are still widely found in everyday school life in the German-speaking part of the world. Jungwirth does not refer to the work of Belenky and colleagues (1997), but analogies in the results are obvious. She found that boys are more likely to respond to open and ambiguous questions or to give fragmentary answers, on which this teaching method basically thrives, while girls hardly respond at all to ambiguous questions or try to answer questions completely. This tends to disrupt the structure of this method and might, therefore, let them appear less competent. Furthermore, boys tend to hide their lack of knowing by dismissing it as a little mistake, taking up the teacher’s advice and corrections, while girls tend to emphasise their lack of knowing by sticking to their solution in a desire for thorough understanding. However, this mismatch of conversational expectations might give the impression that girls are less competent than boys. Jungwirth stressed that girls adjust to such classroom cultures, so that changing classroom culture without addressing the role expectations of girls might be futile.

Jessica Brooke Ernest, Daniel L. Reinholz, and Niral Shah (2019) put on record that men appear more competent in mathematics than women also in student-centred post-secondary education in mathematics. They were able to show that women prove their mathematical competence in small-group discussions and in side talk and that they participate in these discussions almost equally as men. However, in many cases their ideas do not find their way into public plenary discussions, which means that these discussions are not only dominated by men, but also that women’s mathematical competence remains invisible.

Regarding the gender-specific treatment of women and men in higher education in mathematics, studies by Irene Pieper-Seier (2009) not only showed that women report more experiences of discrimination as their level of qualification increases. Moreover, personal support within the academic community is found to be particularly decisive for success but more often offered to men than to women, possibly due to a culture of self-sex support.

Experiences based on the dimensions of gender and mathematics discussed above add up to very different feelings of belonging to mathematics, often to the disadvantage of girls and women. Catherine Good, Aneeta Rattan, and Carol S. Dweck (2012) pointed out that the sense of belonging acts as a contributory factor when it comes to choosing maths courses or a career in this field. They found that the sense of belonging to maths is a strong predictor of the intent to pursue maths and to remain in the discipline. Feelings of belonging are more than changing the perspective from the structural effects of the dimensions of gender and mathematics discussed above to individual manifestations of gender inequalities. They are very personal answers to situations in which mathematics, gender and the self interact in complex ways.

Women’s sense of belonging seems to be quite vulnerable to the perceptions of their academic environment. Stereotype threat – the effect of explicitly or implicitly believing a negative stereotype about a social group – seems to trigger psychological processes leading to a weaker performance. Steven J. Spencer, Claude M. Steele, and Diane M. Quinn (1999) found that when female students believe the stereotype that they are not as able as males to do good at maths, their test performances decline. Sian L. Beilock, Elizabeth A. Gunderson, Gerardo Ramirez, and Susan C. Levine (2010) showed that female teachers’ maths anxiety correlated with negative self-concepts and low achievement among female primary students. These finding might be just the tip of the iceberg, and stereotype threat might influence women’s feelings of belonging to mathematics more widely. Consequently, this could well lead to less interest to become a member of this community, even among high-achieving women. This is especially likely to be the case if the surrounding environment of women underlays the fixed-ability concept. Good, Rattan, and Dweck (2012) showed that, in environments with malleable ability attitudes, even high gender stereotypes did not harm women’s sense of belonging to maths. Therefore, it appears to be crucial if the surrounding community of women holds mathematical ability to be fixed or developable, and how it sees women’s maths ability relative to the ones of men.

A special research focus has been laid on the interplay of feelings of belonging and the personal attribution of success and failure. Bettina Hannover (1991) documented that female students of German grammar schools are likely to assume less competence and expect less success than male students with comparable mathematical achievement – an effect that did not show for the subject of German language. Their self-assessment of their mathematical abilities is therefore much less favourable than their actual performance (Ludwig, 2010). Alternatively, one could speak of overestimation among boys, as they tend to judge their mathematical achievements higher than their grades are.

The issue of confidence in the own mathematical ability also shows up on university level. In a project on students’ experiences of undergraduate mathematics, Melissa Rodd and Hannah Bartholomew (2006) conducted interviews to ask female students for their experiences studying mathematics. As at earlier educational levels, the women showed patterns of doubting their own mathematical abilities. Two keywords came up again and again during these interviews: specialness and invisibility. The stories of the women drew a picture of still being special when studying mathematics as a woman. In their observations of a lecture, Rodd and Bartholomew found that women showed a higher attendance rate than men, were the higher attaining group but mostly men were participating in it. Even high attaining women felt uncomfortable when they were asked to contribute. Consistent with the studies on the different roles of boys and girls in mathematics lessons, it seems that women choose different ways to acquire knowledge and that traditional forms of university teaching do not meet women’s learning preferences. Jillian M. Knowles (2010) took up these insights when she noticed that her female mathematics students made considerably less use of tutoring than male students, identified underlying organisational structures as obstacles for the female students, and introduced a gender-friendly support system for students of mathematics. In a study at a US university, Abbe H. Herzig (2004) found that even female mathematics staff were troubled by feelings of not belonging and chose to abandon mathematics on these grounds.

Dweck and N. Dickon Reppucci (1973) introduced the concept of learned helplessness to explain the effect of the way in which success and failure are dealt with on a learner’s motivation and self-image. Men often attribute failure externally to certain circumstances or other person’s fault or simply talk about having had bad luck. On the other hand, they usually attribute success to personal skill. This means that even in the case of failure there is no reduction in self-confidence, while self-confidence is boosted in the light of success. Women often show exactly the opposite pattern. They blame themselves for failure and attribute success to external factors. This tends to lead to a lower level of self-confidence (Dweck et al., 1978). Leder (1980) suggested that learned helplessness at least partly explains gender differences in mathematics education, as they stand in the way of feelings of belonging.

Another explanation is that girls deny any belonging to mathematics by underestimating their abilities for tactical reasons (Bischof-Köhler, 2002/2011). Matina Horner (1968) caused some controversy with her fear-of-success theory, according to which women are reluctant to prove their abilities because they fear that performing well within male domains will cause them to be rejected by society. Therefore, lower self-confidence within this area might act as a kind of self-protection to meet the stereotypical expectations of society. Although not all subsequent studies came to the same results, some did reach the same conclusion: women in non-traditional careers were the least popular within both sexes (Pfost & Fiore, 1990). Men still seem to tend to react critically when women enter traditionally male domains, and women reflect this attitude. So, the fear of success is not without reason, even though it may not be as severe a problem today as it was in the days of Horner’s study.

A different line of explanation locates the problem rather in environmental conditions than in the individual. Dweck (2007) argued that the combination of the mindsets that success in mathematics required talent rather than work and that this talent was more common among men than among women led to a loss of confidence when challenges occur. Especially in mathematics, it adds to the problem that effort is not valued as high as giftedness. She stated:

A talent-focused mindset is therefore especially harming girls, as they might easily believe the negative stereotype that boys show more mathematical ability and hence are more likely to not deepen their mathematical knowledge. A change to mindsets in which mathematical ability is not a fixed thing but a consequence of work might protect women from such stereotypical views and might increase their confidence within mathematical tasks. Studies showed that the gender gap in mathematical achievement nearly disappeared when only looking at the students with such more beneficial mindsets (Dweck, 2007). It seems like girls who believe that mathematical abilities can be developed and are not something unchangeable are doing just as good as boys do. This would indicate the need for some change within cultural values in the educational environment. Instead of believing that one is smart only if things come easily, a greater belief in the power of effort and the appreciation of it will lead to more confidence among all students.

Problematising the discourse on mathematics and gender

Earlier, we introduced a post-structural perspective, which assumes that our reality is constituted through discourse, and that such discourse is necessarily ambiguous and interest-driven. We stressed that we are necessarily part of such discourses and reproduce them, positioning us as accomplices of such discourses. But we also stressed that we can step out of such discourses and deconstruct them by analysing the way the discourses present reality, how they allow to interpret what is happening, which social roles they arrange, which forms of conduct they demand. Here, we will first attempt to deconstruct the discourses on mathematics and gender presented above. Then we will outline how a post-structural approach to mathematics and gender can help us build new ways of understanding.

• The idea that different images of mathematics compete, and that they represent the interests of different groups, is no post-structural insight. From a post-structural perspective, we have however become aware that images of mathematics are closely intertwined with more general ideas of rationality, objectivity, and government, and that they usually direct at deprivileged positions for women. Valerie Walkerdine and the Girls and Mathematics Unit (1989) draw on Foucault (1975) to argue that rationalism has constructed modern academia as a truth-seeking and masculine enterprise, relegating women to household work. This idea is deeply rooted in contemporary discourses on how and by whom academic work should be approached and creates struggles for women who want to unite mathematical success and femininity in their identity work.
• Much effort is being laid in the measurement and comparison of achievement in mathematics. From a post-structural perspective, objective achievement does not exist and the very idea of achievement and differences in achievement are inseparably linked to the practices through which discourses on achievement are constituted. Most assessment programs on the basis of which performance is compared by gender use batteries of short and one-ended tasks. As shown in our discussion on cognition, learners differ in how quickly and technically instead of carefully and holistically they want to understand issues, in how much they enjoy racing through competitive situations, and in whether they share the style of thinking in which a problem is presented. Pamela L. Paek (2010) tested a group of 122 Californian high school students once with a timed pen-and-paper test and then with an untimed online computer system. She found that boys showed better achievements in the timed pen-and-paper test while girls performed better in the untimed online test. How far can the small differences in national and international assessments between boys and girls then be said to indicate differences in mathematical ability, and how far do they only indicate that the assessment instruments serve rather male than female expectations and strengths?
• As the often-documented underrepresentation of girls and women in mathematics addresses limited educational options and limited access to socio-economically prestigious careers, such underrepresentation is usually considered a problem that has to be challenged. However, we propose to also critically address the social environment in which such underrepresentation can be constituted as a problem. For example, from a perspective in which uncritical use of mathematics and science is held responsible for the technological devastation of our planet, the overrepresentation of boys and men in mathematics might be seen as a social problem. Such a change of perspective does not change the socio-economic consequences of underrepresentation, but it might help to understand and question the system in which women deciding against mathematics come to be seen as a problem.
• Biological attempts to explain inequalities between men and women in mathematics depart from an uncritical understanding of biology. From a post-structural perspective, biology itself is not objective, but necessarily a political discourse. This becomes obvious when revisiting historical biological theories that were intended to prove the superiority of a specific gender, ethnicity or race, and it is still effective today as becomes obvious in the often-practiced dichotomic definition of gender or the assumption that body and mind are widely separated entities. Alternative positions, which are just as scientifically sound, propose that body and mind are closely interwoven, that our experiences and discourses can influence the composition of the body, and that bodily differences between the sexes, at least those deemed to affect our relationship to mathematics, may well be produced discursively. For example, visuospatial skills are not biological invariants but can be improved through training (Marulis et al., 2007; Sorby & Baartmans, 2000).
• Cognitive explanations suggest that there are innate differences in the ways men and women think. Studies such as Women’s Ways of Knowing (Belenky et al. 1986/1997) had a historical function in claiming a distinct female identity instead of regarding femininity merely as an inferior version of masculinity, but they also carry the message that there are ways of knowing closely connected with being a woman in a biological sense. From a post-structural perspective, we contend that there are different meta-discourses that regulate how knowledge is valued, connected, structured and communicated. Again, such meta-discourses are ambiguous and interest-driven. Cognitive studies show that different styles of thinking are not used exclusively by one gender but cross gender boundaries. Gender differences appear because a majority of men prefers a certain style amongst the alternatives they have, while most women prefer a different style. Such preferences need not be natural; instead, they can be assumed to result from other gender-biased cultural influences. Therefore, it would be short-sighted to uncritically take different ways of knowing as a departure of a differentiated organisation of mathematics education. Instead, the different cognitive approaches deserve closer analysis as to how they organise our relationship to the world. Such an analysis might come to the conclusion that education in a specific way of knowing is crucial for our society and that it is legitimate to form students’ thinking accordingly. Such an analysis might also come to the conclusion that it is paramount to introduce all students to a plurality of ways of knowing, and to critically address the position of mathematics within this cognitive field.
• Just like ways of knowing, learning preferences clearly differ between men and women, but do not allow to draw clear lines between the genders. Boaler (1997) documented that a few girls have the same preferences as the majority of boys, that some boys have the same preferences as the majority of girls, and that some preferences are shared by both genders. Anna Llewellyn (2012) raises the question if such preferences are formed by the discourses of what it means for girls and boys to be a good student. Again, it would be short-sighted to take the discourses which say that women need to be taught in one way and men in another way for granted. These attempts to change classroom interaction, which has already been identified as a source of gender inequality in mathematics education, can easily produce new inequalities and reinforce the assumption that boys and girls are different species in the mathematics classroom.
• While it has been established that feelings of belonging and not belonging influence students’ educational and vocational choices, it would be dangerous to search for the reasons for different feelings in the individuals or in a specific gender alone. Indeed, psychological work on stereotype threat, learned helplessness, and fear of success depart from an analysis of the individual. Interventions based on such theories usually attempt to change the mindset of the individual. However, all these theories already acknowledge that feelings of not belonging result from an interplay of individuals and their social environment. Consequently, the social environment and the interplay mechanisms, which allow for structural exclusion by feelings of not belonging in the first place, should receive just as much attention as the psyche of the individual.

Post-structural analysis investigates how gender is incorporated when learners construct discourses that explain their relationship to mathematics. Thereby, gender is seen as a problematic discourse itself, rather than as the safe grounds from which to engage in further analysis. Walkerdine and the Girls and Mathematics Unit (1989) stated that dominant views tend to present possible causes of such differences as something real and true. Contrary to that, their way of dealing with the gender problem is ‘one which treats truth not as something easily empirically verifiable but as slippery stuff created out of fantasies and fictions which have been made to operate as fact’ (p. 19).

They pointed out that there is the trap of thinking mathematics and gender in patriarchal patterns formed by society, trying to prove the assumption that there is a gap between girls and boys and then finding ways to put right what was found wrong. They argued that research about gender tends to focus on searching for differences, whereas similarities are often neglected and seen as a failure to show significant differences. The interpretation of results, they wrote, often indicated that the approach of the study was to show that girls lack something that boys have (e.g., competence, confidence, spatial abilities) or to show that girls are different. The problem with this approach, however, is that with a search for deficits, one group is always portrayed as a problem and bears the blame. Walkerdine and the Girls and Mathematics Unit questioned if such a perspective can help women in any way.

Just as much as gender discourses influence the discourses we relate to when making sense of us in relation to mathematics, our relation to mathematics influences how we constitute ourselves as gendered people. Thereby, identity work on gender cannot be reduced to deciding whether we are male or female. Rather, identity work on gender requires a positioning in discourses that describe gender roles differently, in combining different discourses, maybe in rejecting and reauthoring them. In this sense, although we have evidence of women who do not combine discourses of mathematical success and femininity and consequently abandon mathematics when they have the chance to (Herzig, 2004), mathematical success can also be the source of a new kind of femininity (Foyn et al., 2018, addressed below).

In her analysis of case studies, Mendick (2006) documented how identity work negotiates among divergent discourses on gender and mathematics. She found that the students positioned themselves and others within binary oppositions such as talent vs. hard work or real understanding versus rote learning. Thereby, both sides of the oppositions are unequally valued with higher-valued sides associated with masculinity and lower-valued sides associated with femininity. This is the discursive minefield in which girls and women have to build an identity as a learner of mathematics.

After Mendick (2006) had documented the gendered identity work of school students in mathematics, further case studies resulted in similar findings and deeper insights, also in different environments. Trine Foyn, Yvette Solomon, and Hans Jørgen Braathe (2018) presented case studies of high-achieving girls in mathematics and presented how they identified as a ‘nerd’ and how they had to renegotiate their social roles. Elizabeth de Freitas (2008) authored a fictional biography of a girl obsessed with mathematics and illuminated possible connections between the epistemology of mathematics and gender stereotypes. Jennifer Hall (2010) reported how female high school and university students of mathematics dealt with the feeling of not belonging to mathematics. A longitudinal study by Fiona Walls (2010) traced the identity work of both male and female students of mathematics from primary to secondary school and illustrated how identity work in mathematics relates to the gendered discourses that adolescents are subjected to. Yvette Solomon, Darinka Radovic, and Laura Black (2016) presented a retrospective on the identity work of a female mathematician within a field of experienced contradictions.

It is astonishing how little reference is made to mathematical contents and methods when gender differences in mathematics and mathematics education are discussed. Our argument here is that an important perspective on gender and mathematics is missing in the current literature. We will show this shortcoming in the discussion of a text by Ernest, only to later express some initial thoughts on how mathematics might come into play.

One would assume that the discourse called mathematics would have an impact on gender differences in mathematics and mathematics education. How then is mathematics addressed in gender-oriented research in mathematics education? We already saw that the relationship between gender and mathematics can be located in different dimensions, but none of these address mathematics as a discourse in itself.

Public images of mathematics might be the closest to an analysis of the discourse of mathematics, as the suitability of such images is usually evaluated by their suitability to certain philosophies of mathematics. Ernest (1995) presented one of the most profound discussions of images of mathematics in connection to the philosophy of mathematics. He indicated analogies between absolutist philosophies of mathematics, traditional teaching styles, and a masculine style of thought on the one hand and fallibilist philosophies of mathematics, reform teaching styles, and a feminine style of thought. On this basis, which would itself be worthy of discussion, he postulated that ‘such values, stereotypes and beliefs end up as a vicious cycle denying women equal opportunities’ (p. 456).

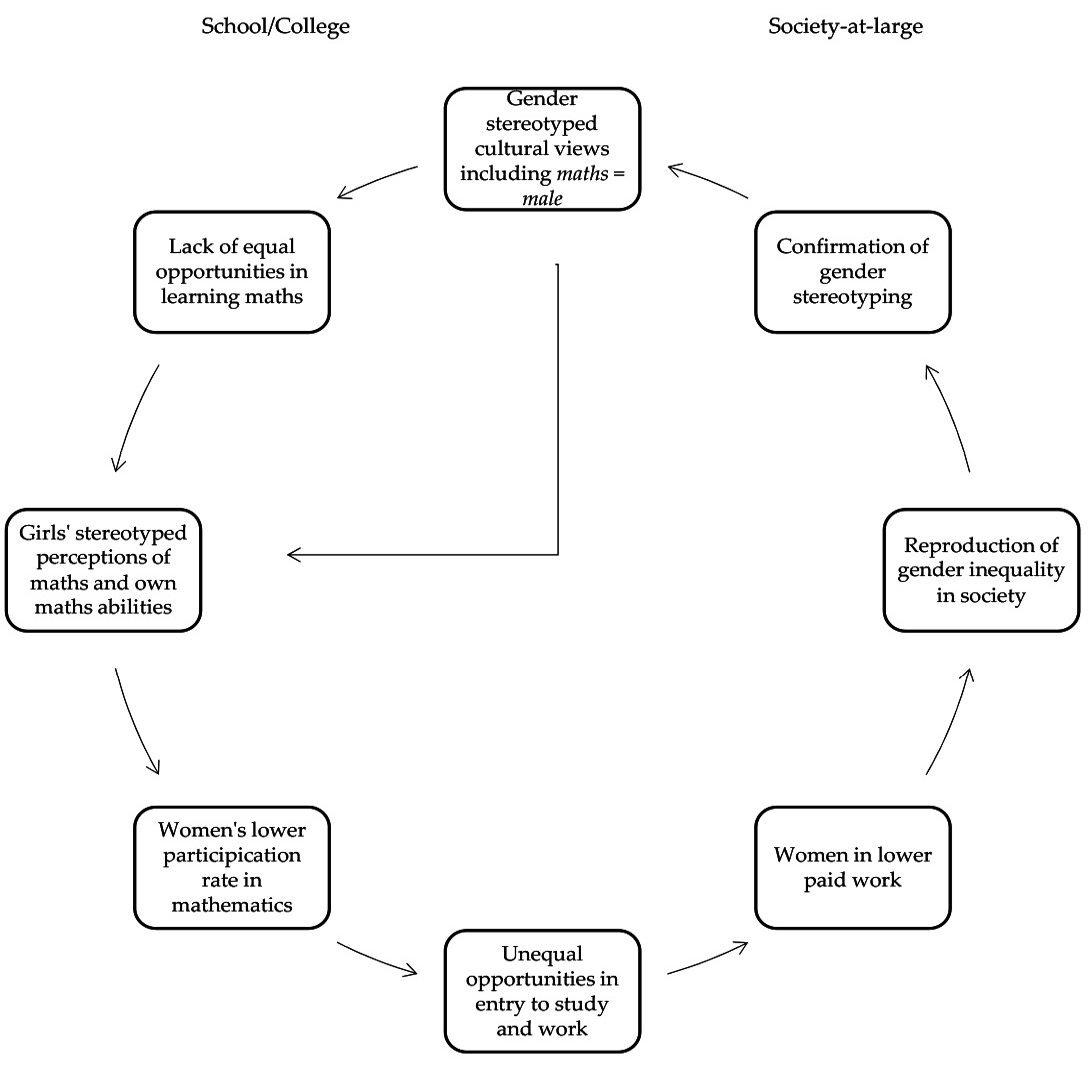
Fig. 19.1 The reproductive cycle of gender inequality in mathematics education (after P. Ernest, 1995, p. 457).

Ernest’s vicious cycle, presented in Figure 19.1, is powerful indeed. However, what role does mathematics play in this explanation? Where in the cycle does the specificity of mathematics come into play? What is special about mathematics so that this vicious cycle works for mathematics as it would for chemistry but not for psychology? If we do not want to make ourselves believe that gender inequalities in mathematics are a mere coincidence or historical artefact, we will have to look for the reasons in mathematics.

Ernest’s argument that a fallibilistic philosophy of mathematics is associated with reformist teaching styles and that it approaches mathematics in line with feminine ways of thinking assumes that mathematics itself has no gender-bias so that the image of mathematics could be changed towards a more gender-inclusive form. This assumption is shared by many, both in studies on gender and mathematics (e.g., Chapman, 1993) and beyond (e.g., Skovsmose, 2011). In his Invitation to Critical Mathematics Education, Ole Skovsmose (2011) sees ‘mathematics education as being undetermined’, ‘without “essence”’, able to ‘be acted out in many different ways and come to serve a grand variety of social, political, and economic functions and interests’ (p. 2). In this spirit, Leone Burton (1995) proposed ‘that the perceived male-ness of mathematics is equally an artefact of its production and its producers’ (p. 215). Critical and feminist research in mathematics education is then supposed to find a way of teaching mathematics that allows for equality. Here also, critique is reduced to the teaching methods and does not cover the discourse of mathematics.

We deem it possible that the social turn in the philosophy of mathematics, which allowed to understand mathematics as a social construction, left the impression that this construction was fully open to change and could be adjusted to social interests. Pat Rogers and Gabriele Kaiser (1995) assumed that a gender-inclusive form of mathematics ‘will involve a fundamental shift in what we value in mathematics, in how we teach it, in how mathematics is used, and in the relationship of mathematics to the world around us’ (p. 9). Obviously, such a change of mathematics might mean that mathematics would no longer be able to play the role it plays in society today, that we create something completely different. Here, we do not talk about what we approach as mathematics today, but about a fiction called mathematics, without any idea of how much both ideas would overlap.

With reference to the distinction between separate and connected knowing presented by Belenky and colleagues (1997), Chapman (1993) warned us that ‘the traditional view of mathematics as a value-free, purely cognitive endeavour […] tends to dehumanize or objectify it, thus limiting it to a framework with characteristics that are more compatible with separate knowing than connected knowing’ (p. 208). She demanded that ‘mathematics be reconceptualised to reflect its humane features and mathematics classroom processes revised to facilitate the characteristic ways of knowing of both males and females’ (p. 209). In ‘Moving Towards a Feminist Epistemology of Mathematics’, Burton (1995) drew on conceptualisations of mathematics as a social practice, refused the myth of objectivity, and stressed that mathematics is open to error, never fixed, and requires different perspectives and exchange – all in line with connected knowing.

We argue that this discourse still does not advance to the issue of mathematics. Admittedly, these philosophical attitudes try to make sense of mathematics and can align more to separate or connected ways of knowing. However, this tells us more about these attitudes than about the social practice of mathematics. Ian Hacking (2014) argued that usually mathematicians neither participate in these philosophical discussions nor do they find them enlightening of their practice. The work of Davis and Hersh (1980) was composed in this spirit. They dedicated only one chapter of their The Mathematical Experience to these philosophical debates and far more to reflections of doing mathematics. They further noted ‘that the typical working mathematician is a Platonist [assuming mathematics to be objective and truth to be recognisable] on weekdays and a formalist [assuming mathematics to be ambiguous constructions and knowledge related to such constructions] on Sundays’ (p. 321). It is telling that such a view constitutes a paradox for the philosopher but does not hinder the work of the mathematician. We propose that, while it is clear that mathematical work is partly subjective, open to debate, and in need of different perspectives, objectivity is an ideal that mathematicians strive for. On weekdays they have a Platonist attitude when working towards this ideal, while on Sundays they can lean back and admit that mathematics stays messy and the ideal has not been reached. Platonist attitudes can then be considered one form of describing that ideal, while alternative attitudes, which argue that such an ideal cannot be fully realised, do not hinder anyone on holding these ideals.

We also propose that this ideal permeates the whole mathematical discourse. David Kollosche, in Chapter 5 of this volume, argues that calculation and logic, two practices present in any area of mathematics, are explicitly directed at such objectification, at separating mathematics from us rather than connecting it to a plurality of meanings. This disconnectedness of mathematics is what constitutes it as a discipline in its own right and establishes it in opposition to applied disciplines such as physics. From this perspective, mathematics is not waiting to be humanised or to open up for connective knowing. Rather, separated knowing is the very ideal of mathematics. Changing that ideal would require mathematics to become something very different, something that might not be assigned the same cultural value. We think that before asking mathematics to change, we should direct our attention more closely to the social situatedness of mathematics and its connection to separated knowing. That does not mean that the teaching and learning of mathematics cannot be changed to more gender-inclusive forms, nor do we think that the separated nature of mathematical knowledge necessarily excludes women. Instead, we should endeavour towards a transparent, explicit, and unbiased discussion of the importance, potential, limits, and dangers of mathematical forms of knowledge. Making the gendering of mathematics and connected styles of thinking explicit should constitute a vital step towards rejecting presupposed gender-roles and finding new ways of identifying with mathematics.

Another feature of the discourse of mathematics which is closely related to gender issues is the analogy between logical hierarchies and patriarchal social systems as discussed in detail by Kollosche in Chapter 5 of this volume. While communities before did not know fatherhood and private property, patriarchal societies connected the ideas of property and father-son relationship through the idea of inheritance. In this logic of inheritance, one’s position in the net of relationships is static as you always stay your father’s son. Further, you either are somebody’s son or you are not – this dichotomy does not allow for mixed or third identities. Eventually, you are defined by whose household you will inherit. This logic of inheritance can be found again in the organisation of the military and in the organisation of the world of polytheistic gods. Eventually, a logic of thought has been developed in patriarchal Ancient Greece, which shows the same organisation: the meaning of its objects is static through definition, its subsumption under other objects is either true or false, and its features can be deduced from objects under which it is subsumed.

We find it hard to disregard the structural analogy between the patriarchal organisation of society and the logic that some Ancient Greek philosophers and rationalists celebrated as its purest expression. It seems unlikely that the development of logic as a very distinct organisation of thought in Ancient Greece was completely independent from the development of patriarchy in the same culture only a few centuries earlier. We propose reconsidering to what extent the ideas that meaning is static, can be expressed through dichotomies, and is inherited through directed bipolar relationships represent gender-biased assumptions. These assumptions, we argue, lie at the heart of mathematics and present it as a patriarchal project for making sense of our world. Thereby, understanding mathematics as a patriarchal project does not mean that women are excluded from mathematics or less able to do mathematics. Instead, it means that mathematics mirrors a social organisation which reproduces male hegemony, thereby possibly reinforcing the latter and provoking sentiments differing by gender.

The documentation of inequalities in the education system and beyond is often accompanied by demands to take action. But, as might be guessed from the deconstruction of gender, what might seem to be a good intervention from one perspective may raise serious concerns from a different perspective on mathematics and gender. Sue Willis (1996) differentiated between four perspectives on mathematics and gender, identifying either women, classroom practices, the mathematics curriculum, or social inequality itself as the main problem. We will address some of the moral paradoxes invoked by these perspectives in this last part of our chapter with the hope of further elaborating the grounds on what can be done.

Since the 1960s, programs have been installed around the globe to positively influence the achievements, career choices and self-images of girls and women in mathematics. Burton (1990), Rogers and Kaiser (1995), as well as Lynda R. Wiest (2010) included reports about various such programs. However, many of these programs have been criticised, as they tend to ignore feminist approaches to mathematics and seek to adjust feminine intellect, choices, and attitudes to a masculine norm, thus installing masculine approaches to mathematics as normality and portraying feminine approaches as inferior. For example, Olive Fullerton (1995), who taught mathematics methodology for prospective primary school teachers at university, stated:

One of the barriers to understanding mentioned frequently by the teacher candidates working with me, was that, for them, mathematics was neither relevant nor meaningful. They did not appreciate that mathematics permeated their lives, that their every action was in some way connected to mathematics, that the beauty and harmony of their world was due in large measure to mathematics. (pp. 44–45)

In her statement, Fullerton assumed that there is a truth about the role mathematics plays and should play in our world, and that her female students require assistance to recognise this truth. As Willis (1996) framed it from a deficit perspective, ‘the problem lies with the children, who, because of their gender, race, ethnicity, social class or disability, lack the knowledge, skills or motivations necessary for access to, and success in, school mathematics’ (p. 44). Boaler (1997) criticised how such a perspective is not interested in the girls’ experiences and in the reasons for their action; it is only interested in changing the girls so that they can reach the achievements and representation of boys.

There are, however, many programs that opened up for feminine approaches to mathematics. For instance, Charlene Morrow and James Morrow (1995) repeatedly organised summer schools for female high-school students in the United States. These included classes in problem solving, in fundamental mathematics concepts, and in programming. The organisers wrote that they laid special foci on allowing for women’s ways of knowing, on increasing self-confidence in mathematics, and on developing a voice in mathematics. From the student feedback presented by the organisers, it becomes clear that such opportunities can have an empowering effect for the participants. Such feedback is reassuring and documents that this approach is worth considering.

While programs that take place independently from school can be assumed to usually meet the interests of the girls and women who choose to participate, programs interacting with schools, for example by working in schools, inviting classes, or providing teaching materials, approach girls who might have no desire to renegotiate their relationship to mathematics. No matter how well-intentioned, sensitive, and open such obligatory programs might be, they are still forms of manipulation. Is it really emancipation to encourage women to pursue mathematics, even when they have valid reasons not to? If the environment in which women learnt not to identify with mathematics does not change, would not fostering enthusiasm for mathematics, especially in secure environments, only create a deeper conflict of identity for these women when they return to their original environments? May there even be good reasons not to be too enthusiastic about mathematics as a way to approach our world? It seems fair to conclude that programs, which offer women a safe space to investigate their relationship to mathematics, are important. However, they should be open to the possibility that women might have good reasons not to pursue mathematics, and they should be accompanied by gender-inclusive changes of the mathematics classroom and the mathematics curriculum.

Besides, it is an interesting thought experiment to consider whether boys, rather than girls, should change their relationship to mathematics. This is not to suggest that boys should aim for lower achievements in mathematics to achieve equal outcomes. However, given the critique that assessment instruments usually benefit a masculine approach to mathematics, instruments favouring women might put men in a deficit position and demand them to change in order to fill that gap. Concerning the didactical shift from mastering mathematical procedures, which now can be outsourced to computers, to a critical understanding of mathematics, connected knowers might indeed be advantaged over separated knowers. Eventually, it might turn out that a separated and therewith uncritical approach to mathematics laid the basis for devastating applications in modernity. Such a perspective might explicitly position mathematics as a problem of masculinity.

Changing the teaching and learning of mathematics in order to challenge gender inequality in mathematics leads to moral dilemmas as well. The work of Boaler (1997) shows clearly that the preferred ways of teaching and learning differ between boys and girls. Does that mean that the organisation of teaching and learning should be adjusted to meet the wishes of all learners? Is that even possible? Or is the implication that students should be allowed to choose from mathematics courses that differ in their styles of teaching and learning, even if that led to something close to single-sex education in mathematics? If we followed this latter plan to approach mathematics in such safe havens, what would that mean for our students’ abilities to approach mathematics once they leave our safe havens and engage with mathematics in their future lives? Do we risk that our students fall back into old patterns because they had no chance to learn how to navigate in an environment with divergent approaches to mathematics? In the end, does meeting students’ gender-sensitive learning preferences actually reproduce gender inequalities?

A more general question is whether teaching styles should be chosen on the basis of students’ learning preferences at all. Educational theory might present well-founded arguments on why to teach mathematics in specific ways. For example, if mathematics education was meant to produce technocrats who are able to technically master mathematics without asking many why questions, would it not be only natural to rely on exposition and individual exercise, irrespective of how boys and girls reacted to this orientation? If, on the other hand, mathematics education was meant to allow for a critical and multifaceted perspective on mathematics, would it not be only natural to allow for diverse approaches to mathematics and to facilitate discussions on these approaches, again irrespective of how boys and girls reacted to that orientation? What causes gender inequalities here is that specific ways of teaching and learning are gendered and not equally accessible for or valued by all genders.

We conclude that there are no clear answers on how to change classroom practice to combat gender inequalities in mathematics education. The overall problem is that the teaching of mathematics is embedded in a complex social system. Even if we know that specific measures have the potential to fight gender inequalities, they might produce gender inequalities of a different kind and further problems or radical changes regarding the teaching and learning of mathematics. A pragmatic approach here, in order to avoid getting stuck in the midst of these paradoxes, is to promote changes to the best of our knowledge and to deal with upcoming problems as they arise. The awareness that there are no easy answers for classroom interventions may help us to see such problems coming and to meet them with open eyes.

Willis (1996) reminded us that ‘the choices made in developing school mathematics curricula will reflect the values, priorities and lifestyles of the dominant culture’ (p. 45). She continues that, with respect to gender, school mathematics could privilege characteristics of mathematics which are identified more closely with the masculine over characteristics more closely identified with the feminine, such as the logical over the intuitive, the context-free over the context-bounded, the rational and abstract over the personal and social, the unambiguous over the ambiguous, or the absolute over the relative (ibid.).

Indeed, many of the curriculum reforms undertaken in many countries in the last decades can be interpreted as pointing in this direction. The mastery of standard techniques for calculation and proof, together with a desire to accumulate truths, which were dominant in traditional mathematics curricula, are well aligned to what Belenky and colleagues (1997) termed the more masculine separate knowing. The corresponding activities made room for more connected knowing in the sense of a multi-faceted understanding: individual approaches in problem solving and modelling, appreciation of different voices in group work and classroom discussions, productive ways of dealing with seemingly wrong ideas, even critical reflections on the use of mathematics. Aside from questioning how far this shift from viewing mathematics as a product to seeing it as a social activity (see Chapter 1 in this volume) has affected the mathematics classrooms, could it be that the prescribed mathematics curriculum has already opened up for more diverse and especially connected approaches to the subject? We see two problems here.

First, it is unclear how far such reforms indeed affect schools. Kollosche (2018) proposes that many reform initiatives in mathematics education fail because they disregard the social expectations directed at schools. Contributions in the so-called math-war discussions in the US, where some mathematicians expressed their interest in preserving a conservative conception of mathematics (summarised in J. R. Brown, 2008, pp. 207–217), lay bare such expectations, but we can expect that this is just the tip of the iceberg and that most expectations are communicated through more subtle channels. Tony Brown and Olwen McNamara (2005) captured how the growing industry of standard testing with its focus on test items, which can be answered unambiguously and quickly, has caused teachers to direct their teaching away from the reform curricula and back to teaching mathematical techniques and truths. Consequently, we wonder how far curriculum reforms that would open up mathematics for various ways of knowing is still nothing but an aspiration.

Second, it is unclear how far the mathematics curriculum can open up at all. Curriculum change has addressed the methods through which the mathematical contents are approached. We agree that it is possible to allow for other ways of knowing here. However, the mathematical contents remain widely untouched. The triangle stays a triangle; the Pythagoras theorem stays the Pythagoras theorem. As we concluded earlier in this chapter, mathematics as a body of knowledge is closely related to a distinct way of knowing, and it is questionable how far it can be altered at all.

Socio-critical scholars proposed that gender inequalities in mathematics are an active part of a larger problem, and that they should be addressed as such. Paul Dowling (1991) stressed that the inequalities are actually functional in reproducing social advantages of men. The mathematics classroom then appears as a mere part in a larger system which aims at securing and reproducing discourses that position men in superior social positions. From such a perspective, it seems questionable how far gender equity in mathematics education can be achieved while the discourses reproducing inequality survive throughout society. In short, does it make sense to fight gender inequalities in the mathematics classroom, or would it be necessary to become a gender activist with a general agenda?

We would argue that change has to start somewhere and in many places before social systems can be said to have changed as a whole. It would be unethical to tolerate structural disadvantages for girls and women while waiting for global answers to gender inequality. Pending further research and without a global solution, change has to be promoted by us, mathematics educators or not, concerning the ways mathematics is publicly perceived, the ways we understand mathematical achievement, the ways of knowing that we accept for approaching mathematics, the styles in which we teach and learn, how we treat each other as teachers and learners of mathematics, and the stories we tell about our and others’ relations to mathematics. These goals are unlikely to be achieved through a few interventions alone. We assume that they will provide challenges for generations of teachers and students of mathematics to come. Eventually, these changes may alter our understanding of mathematics and ourselves as mathematical beings in ways that cannot yet be imagined.

Baldino, R. R. (2000). Neurone-Z, philosophy of the mind and symptom. In J. F. Matos & M. Santos (Eds.), Proceedings of the 2nd international mathematics education and society conference (pp. 143–157). Universidade de Lisboa.

Becker, J. R. (1981). Differential treatment of females and males in mathematics classes. Journal for Research in Mathematics Education, 12(1), 40–53. https://doi.org/10.2307/748657

Becker, J. R. (1995). Women’s ways of knowing to mathematics. In P. Rogers & G. Kaiser (Eds.), Equity in mathematics education: influences of feminism and culture (pp. 164–175). Falmer. https://doi.org/10.4324/9780203990087-29

Becker, J. R. (2001). Single-gender schooling in the public sector in California: Promise and practice. In B. Atweh, H. Forgasz, & B. Nebres (Eds.), Sociocultural research on mathematics education: an international perspective (pp. 367–378). Lawrence Erlbaum. https://doi.org/10.4324/9781410600042-31

Beilock, S. L., Gunderson, E. A., Ramirez, G., & Levine, S. C. (2010). Female teachers’ math anxiety affects girls’ math achievement. Proceedings of the National Academy of Sciences of the United States of America, 107(5), 1860–1863. https://doi.org/10.1073/pnas.0910967107

Belenky, M. F., Clinchy, B. M., Goldberger, N. R., & Tarule, M. J. (1997). Women's ways of knowing: The development of self, voice, and mind. Basic Books. (Original work published 1986)

Benbow, C. P [Camilla Persson] (1988). Sex differences in mathematical reasoning ability in intellectually talented preadolescents: Their nature, effects, and possible causes. Behavioral and Brain Sciences, 11(2), 169–183. https://doi.org/10.1017/S0140525X00049244

Bischof-Köhler, D. (2011). Von Natur aus anders: Die Psychologie der Geschlechtsunterschiede [Different by nature: The psychology of gender differences]. Kohlhammer. (Original work published 2002)

Boaler, J. (1997). Experiencing school mathematics: Teaching styles, sex, and setting. Open University.

Boles, D. B. (1980). X-linkage of spatial ability: A critical review. Child development, 51(3), 625–635. https://doi.org/10.2307/1129448

Brown, J. R. (2008). Philosophy of mathematics: A contemporary introduction to the world of proofs and pictures. Routledge.

Brown, T., & McNamara, O. (2005). New teacher identity and regulative government: The discursive formation of primary mathematics teacher education. Springer. https://doi.org/10.1007/b104107

Burton, L. (Ed.). (1990). Gender and mathematics: An international perspective. Cassell.

Burton, L. (1995). Moving towards a feminist epistemology of mathematics. In P. Rogers & G. Kaiser (Eds.), Equity in mathematics education: Influences of feminism and culture (pp. 211–227). Falmer.

Butler, J. (1999). Gender trouble: Feminism and the subversion of identity. Routledge.

Chafetz, J. S. (2006). The varieties of gender theory in sociology. In J. S. Chafetz (Ed.), Handbook of the sociology of gender (pp. 3–23). Springer. https://doi.org/10.1007/0-387-36218-5_1

Chapman, O. (1993). Women’s voice and the learning of mathematics. Journal of Gender Studies, 2(2), 206–222. https://doi.org/10.1080/09589236.1993.9960539

Cheryan, S. (2012). Understanding the paradox in math-related fields: Why do some gender gaps remain while others do not? Sex Roles, 66(3-4), 184–190. https://doi.org/10.1007/s11199-011-0060-z

Colom, R., Juan-Espinosa, M., Abad, F., & García, L. F. (2000). Negligible sex differences in general intelligence. Intelligence, 28(1), 57–68. https://doi.org/10.1016/S0160-2896(99)00035-5

Davis, P. J., & Hersh, R. (1980). The mathematical experience. Birkhäuser.

Delon, F. (1995). The French experience: The effects of de-segration. In P. Rogers & G. Kaiser (Eds.), Equity in mathematics education: influences of feminism and culture (pp. 142–153). Falmer.

Dowling, P. (1991). Gender, class, and subjecivity in mathematics: A critique of Humtpy Dumpty. For the Learning of Mathematics, 11(1), 2–8.

Driver, G. (1980). Beyond underachievement: Case studies of English, West Indian, and Asian school-leavers at sixteen plus. Commission for Racial Equality.

Dweck, C. S. (2007). Is math a gift? Beliefs that put females at risk. In S. J. Ceci & W. M. Williams (Eds.), Why aren't more women in science? Top researchers debate the evidence (pp. 47–55). American Psychological Association.

Dweck, C. S., Davidson, W., Nelson, S., & Enna, B. (1978). Sex differences in learned helplessness: II. The contingencies of evaluative feedback in the classroom and III. An experimental analysis. Developmental Psychology, 14(3), 268–276. https://doi.org/10.1037/0012-1649.14.3.268

Dweck, C. S., & Reppucci, N. D. (1973). Learned helplessness and reinforcement responsibility in children. Journal of Personality and Social Psychology, 25(1), 109–116. https://doi.org/10.1037/h0034248

Eccles, J. S. (1989). Bringing young women to math and science. In M. Crawford & M. Gentry (Eds.), Gender and thought: Psychological perspectives (pp. 36–58). Springer. https://doi.org/10.1007/978-1-4612-3588-0_3

Eckert, P., & McConnell-Ginet, S. (2003). Language and gender. Cambridge University Press.

Ernest, J. B., Reinholz, D. L., & Shah, N. (2019). Hidden competence: Women’s mathematical participation in public and private classroom spaces. Educational Studies in Mathematics, 102(2), 153–172. https://doi.org/10.1007/s10649-019-09910-w

Ernest, P. (1995). Values, gender and images of mathematics: A philosophical perspective. International Journal of Mathematical Education in Science and Technology, 26(3), 449–462. https://doi.org/10.1080/0020739950260313

Ernest, P. (2007). Questioning the gender problem in mathematics. Philosophy of Mathematics Education, 20. https://www.exeter.ac.uk/research/groups/education/pmej/pome20/index.htm

European Commission. (2019). She figures 2018. Publications Office of the European Union.

Eurostat. (2019a). Graduates by education level, programme orientation, sex and field of education. Eurostat. https://ec.europa.eu/eurostat/databrowser/view/educ_uoe_grad02/default/table?lang=en

Eurostat. (2019b). Students enrolled in tertiary education by education level, programme orientation, sex and field of education. Eurostat. https://data.europa.eu/data/datasets/tvoyfp236pvctmgfqyudca?locale=en

Fennema, E., Peterson, P. L., Carpenter, T. P., & Lubinski, C. A. (1990). Teachers’ attributions and beliefs about girls, boys, and mathematics. Educational Studies in Mathematics, 21(1), 55–69. https://doi.org/10.1007/BF00311015

Foucault, M. (1961). Histoire de la folie à l'âge classique: Folie et déraison [Madness and civilization: A history of insanity in the Age of Reason]. Plon.

Foucault, M. (1966). Les mots et les choses: Une archéologie des sciences humaines [The order of things: An archaeology of the human sciences]. Gallimard.

Foucault, M. (1975). Surveiller et punir: Naissance de la prison [Discipline and punish: The birth of the prison]. Gallimard.

Foucault, M. (1976). Histoire de la sexualité: La volonté de savoir [The history of sexuality: The will to knowledge]. Gallimard.

Foucault, M. (1982). How is power exercised? In H. L. Dreyfus & P. Rabinow (Eds.), Michel foucault: beyond structuralism and hermeneutics (pp. 216–226). Harvester.

Foucault, M. (2007). What is Critique? In S. Lotringer (Ed.), The politics of truth (pp. 41–81). Semiotext(e). (Original work published 1990)

Foyn, T., Solomon, Y., & Braathe, H. J. (2018). Clever girls’ stories: The girl they call a nerd. Educational Studies in Mathematics, 5(1), 77–93. https://doi.org/10.1007/s10649-017-9801-4

Freitas, E. de (2008). Mathematics and its other: (Dis)locating the feminine. Gender and Education, 20(3), 281–290. https://doi.org/10.1080/09540250801964189

Friedan, B. (1963). The feminine mystique. Norton.

Fullerton, O. (1995). Who wants to feel stupid all of the time? In P. Rogers & G. Kaiser (Eds.), Equity in mathematics education: Influences of feminism and culture (pp. 38–49). Falmer.

Geary, D. C. (1998). Male, female: The evolution of human sex differences. American Psychological Association.

Gerdes, P. (2006). African women with a doctorate in mathematics. Newsletter of the African Mathematical Union Commission on the History of Mathematics in Africa, 33. http://africanwomeninmath.org/women-in-math/report/african-women-doctorate-in-mathematics

Good, C., Rattan, A., & Dweck, C. S. (2012). Why do women opt out? Sense of belonging and women’s representation in mathematics. Journal of Personality and Social Psychology, 102(4), 700–717. https://doi.org/10.1037/a0026659

Green, J. (2001). How many women mathematicians can you name? Math Horizons, 9(2), 9–14. https://doi.org/10.1080/10724117.2001.12021856

Hacking, I. (2014). Why is there philosophy of mathematics at all? Cambridge University Press. https://doi.org/10.1017/CBO9781107279346

Hall, J. (2010). The influence of high school and university experiences on women’s pursuit of undergraduate mathematics degrees in Canada. In H. J. Forgasz, J. R. Becker, K.-H. Lee, & O. B. Steinthorsdottir (Eds.), International perspectives on gender and mathematics education (pp. 365–390). Information Age.

Halpern, D. F. (2012). Sex differences in cognitive abilities. Psychology Press.

Halpern, D. F., Benbow, C. P., Geary, D. C., Gur, R. C., Hyde, J. S., & Gernsbacher, M. A. (2007). The science of sex differences in science and mathematics. Psychological Science in the Public Interest, 8(1), 1–51. https://doi.org/10.1111/j.1529-1006.2007.00032.x

Hampson, E. (1990). Variations in sex-related cognitive abilities across the menstrual cycle. Brain and Cognition, 14(1), 26–43. https://doi.org/10.1016/0278-2626(90)90058-v

Hampson, E., & Rovet, J. F. (2015). Spatial function in adolescents and young adults with congenital adrenal hyperplasia: clinical phenotype and implications for the androgen hypothesis. Psychoneuroendocrinology, 54, 60–70. https://doi.org/10.1016/j.psyneuen.2015.01.022

Hannover, B. (1991). Zur Unterrepräsentanz von Mädchen in Naturwissenschaften und Technik: Psychologische Prädiktoren der Fach- und Berufswahl [On the underrepresentation of girls in science and technology: Psychological predictors of subject and career choice]. Zeitschrift für Pädagogische Psychologie, 5, 169–186.

Hersh, R., & John-Steiner, V. (2011). Loving and hating mathematics: Challenging the myths of mathematical life. Princeton University Press.

Herzig, A. H. (2004). ‘Slaughtering this beautiful math’: Graduate women choosing and leaving mathematics. Gender and Education, 16(3), 379–395. https://doi.org/10.1080/09540250042000251506

Hiddleston, P. (1995). The contribution of girls-only schools to mathematics and science education in Malawi. In P. Rogers & G. Kaiser (Eds.), Equity in mathematics education: influences of feminism and culture (pp. 148–153). Falmer.

Hines, M. (2010). Sex-related variation in human behavior and the brain. Trends in Cognitive Science, 14(10), 448–456. https://doi.org/10.1016/j.tics.2010.07.005

Horner, M. (1968). Sex differences in achievement motivation and performance in competitive and non-competitive situations [Doctoral dissertation, University of Michigan].

Hyde, J. S. (2005). The gender similarities hypothesis. The American psychologist, 60(6), 581–592. https://doi.org/10.1037/0003-066X.60.6.581

Isaacson, Z. (1990). ‘They look at you in absolute horror’: Women writing and talking about mathematics. In L. Burton (Ed.), Gender and mathematics: an international perspective (pp. 20–28). Cassell.

Jahnke-Klein, S. (2001). Sinnstiftender Mathematikunterricht für Mädchen und Jungen [Meaningful mathematics education for girls and boys]. Schneider.

Johnston, B. (1995). Mathematics: An abstracted discourse. In P. Rogers & G. Kaiser (Eds.), Equity in mathematics education: Influences of feminism and culture (pp. 228–236). Falmer.

Jungwirth, H. (1991). Interaction and gender: Findings of a microethnographical approach to classroom discourse. Educational Studies in Mathematics, 22(3), 263–284. https://doi.org/10.1007/BF00368341

Kenschaft, P. C. (1982). Women in mathematics around 1900. Journal of Women in Culture and Society, 7(4), 906–909.

Kinski, I. (1994). Mädchenmathematik kontra Knabenmathematik [Girls’ mathematics versus boys’ mathematics]. Mitteilungen der Deutschen Mathematiker-Vereinigung, 2(3), 13–24. https://doi.org/10.1515/dmvm-1994-0308

Knowles, J. M. (2010). Recognizing gender in mathematics relationships: A relational counseling approach helps teachers and students overcome damaging perceptions. In H. J. Forgasz, J. R. Becker, K.-H. Lee, & O. B. Steinthorsdottir (Eds.), International perspectives on gender and mathematics education (pp. 421–450). Information Age.

Koehler, M. S. (1990). Classrooms, teacher and gender differences in mathematics. In E. Fennema & G. C. Leder (Eds.), Mathematics and gender (pp. 128–148). Teachers College, Columbia University.

Kollosche, D. (2018). Social functions of mathematics education: A framework for socio-political studies. Educational Studies in Mathematics, 98(3), 287–303. https://doi.org/10.1007/s10649-018-9818-3

Leder, G. (1980). Bright girls, mathematics and fear of success. Educational Studies in Mathematics, 11(4), 411–422. https://doi.org/10.1007/BF00231214

Leder, G. (1995). Equal or different? Cultural influences on learning mathematics. In P. Rogers & G. Kaiser (Eds.), Equity in mathematics education: Influences of feminism and culture (pp. 118–126). Falmer.

Lee, K., & Anderson, J. (2015). Gender differences in mathematics attitudes in coeducational and single sex secondary education. In M. Marshman, V. Geiger, & A. Bennison (Eds.), Mathematics education in the margins: proceedings of the 38th annual conference of the mathematics education research group of australasia (pp. 357–364). MERGA.

Llewellyn, A. (2012). Unpacking understanding: The (re)search for the Holy Grail of mathematics education. Educational Studies in Mathematics, 81(3), 385–399. https://doi.org/10.1007/s10649-012-9409-7

Ludwig, P. H. (2010). Schulische Erfolgserwartungen und Begabungsselbstbilder bei Mädchen: Strategien ihrer Veränderung [Expectations of success at school and self-image of talent in girls: Strategies for change]. In M. Matzner & I. Wyrobnik (Eds.), Handbuch Mädchen-Pädagogik (pp. 145–158). Beltz.

Magolda, M. B. B. (1992). Knowing and reasoning in college: Gender-related patterns in students’ intellectual development. Jossey-Bass.

Marchbank, J., & Letherby, G. (2014). Introduction to gender: Social science perspectives. Pearson.

Marulis, L. M., Lui, L. L., Warren, C. M., Uttal, D. H., & Newcombe, N. S. (2007). Effects of training or experience on spatial cognition in children and adults: A meta-analysis. Annual Meeting of the American Educational Research Association, Chicago, IL.

Masanja, V. G. (2010). Increasing women’s participation in science, mathematics and technology education and employment in Africa. https://www.un.org/womenwatch/daw/egm/gst_2010/Masanja-EP.8-EGM-ST.pdf

Mead, M. (1949). Male and female: A study of the sexes in a changing world. Morrow.

Mendick, H. (2005). A beautiful myth? The gendering of being/doing ‘good at maths’. Gender and Education, 17(2), 203–219. https://doi.org/10.1080/0954025042000301465

Mendick, H. (2006). Masculinities in mathematics. Open University.

Mendick, H. (2017). Mathematical futures: Discourses of mathematics in fictions of the post-2008 financial crisis. In A. Chronaki (Ed.), Mathematics education and life at times of crisis (Vol. 1, pp. 74–89). University of Thessaly Press.

Money, J. (1955). Hermaphroditism, gender and precocity in hyperadrenocorticism: Psychologic findings. Bulletin of the Johns Hopkins Hospital, 96(6), 253–264.

Morrow, C., & Morrow, J. (1995). Connecting women with mathematics. In P. Rogers & G. Kaiser (Eds.), Equity in mathematics education: Influences of feminism and culture (pp. 13–27). Falmer.

Nosek, B. A., Smyth, F. L., Sriram, N., Lindner, N. M., Devos, T., Ayala, A., Bar-Anan, Y., Bergh, R., Cai, H., Gonsalkorale, K., Kesebir, S., Maliszewski, N., Neto, F., Olli, E., Park, J., Schnabel, K., Shiomura, K., Tulbure, B. T., Wiers, R. W., … Greenwald, A. G. (2009). National differences in gender-science stereotypes predict national sex differences in science and math achievement. Proceedings of the National Academy of Sciences of the United States of America, 106(26), 10593–10597. https://doi.org/10.1073/pnas.0809921106

OECD. (2014). PISA 2012 results: What students know and can do: Student performance in mathematics, reading and science. OECD Publishing.

Olson, M., Olson, J., Okazaki, C., & La, T. (2010). Conversations of parents and children working on mathematics. In H. J. Forgasz, J. R. Becker, K.-H. Lee, & O. B. Steinthorsdottir (Eds.), International perspectives on gender and mathematics education (pp. 33–54). Information Age.

Peak, P. L. (2010). Factors contributing to gender differences in mathematics performance of United States high school students. In H. J. Forgasz, J. R. Becker, K.-H. Lee, & O. B. Steinthorsdottir (Eds.), International perspectives on gender and mathematics education (pp. 203–224). Information Age.

Perl, T. (2010). The Ladies’ Diary or Woman’s Almanack, 1704–1841. In H. J. Forgasz, J. R. Becker, K.-H. Lee, & O. B. Steinthorsdottir (Eds.), International perspectives on gender and mathematics education (pp. 15–32). Information Age.

Pfost, K. S., & Fiore, M. (1990). Pursuit of nontraditional occupations: Fear of success or fear of not being chosen? Sex Roles, 23(1–2), 15–24. https://doi.org/10.1007/BF00289875

Pieper-Seier, I. (2009). Studentinnen und Professorinnen in der Mathematik [Female students and female professors of mathematics]. Gender, 1(1), 59–72. http://dx.doi.org/10.25595/76

Popejoy, A. B., & Leboy, P. S. (2012). Is math still just a man’s world? Journal of Mathematics and System Science, 2, 292–298.

Prendergast, M., & O’Donoghue, J. (2014). Influence of gender, single-sex and co-educational schooling on students’ enjoyment and achievement in mathematics. International Journal of Mathematical Education in Science and Technology, 45(8), 1115–1130. https://doi.org/10.1080/0020739X.2014.904530

Riegle-Crumb, C., & Humphries, M. (2012). Exploring bias in math teachers’ perceptions of students’ ability by gender and race/ethnicity. Gender & Society, 26(2). https://doi.org/10.1177/0891243211434614

Rodd, M., & Bartholomew, H. (2006). Invisible and special: Young women’s experiences as undergraduate mathematics students. Gender and Education, 18(1), 35–50. https://doi.org/10.1080/09540250500195093

Rogers, P., & Kaiser, G. (Eds.). (1995). Equity in mathematics education: Influences of feminism and culture. Falmer.

Schwank, I. (1994). Zur Analyse kognitiver Mechanismen mathematischer Begriffsbildung unter geschlechtsspezifischem Aspekt [On the analysis of cognitive mechanisms of mathematical concept formation from a gender-specific perspective]. Zentralblatt für Didaktik der Mathematik, 26(2), 31–40.

Schwank, I. (1999). On predicative versus functional cognitive structures. In I. Schwank (Ed.), European research in mathematics education: proceedings of the first conference of the European society in mathematics education (Vol. 2, pp. 84–96). Forschungsinstitut für Mathematikdidaktik.

Skovsmose, O. (2011). An invitation to critical mathematics education. Sense. https://doi.org/10.1007/978-94-6091-442-3

Solomon, Y., Radovic, D., & Black, L. (2016). ‘I can actually be very feminine here’: Contradiction and hybridity in becoming a female mathematician. Educational Studies in Mathematics, 91(1), 55–71. https://doi.org/10.1007/s10649-015-9649-4

Sorby, S. A., & Baartmans, B. J. (2000). The development and assessment of a course for enhancing the 3-D spatial visualization skills of first year engineering students. Journal of Engineering Education, 89(3), 301–307. https://doi.org/10.1002/j.2168-9830.2000.tb00529.x

Spencer, S. J., Steele, C. M., & Quinn, D. M. (1999). Stereotype threat and women’s math performance. Journal of Experimental Social Psychology, 35(1), 4–28. https://doi.org/10.1006/jesp.1998.1373

Thompson, D. R. (1995). The METRO achievement program: Helping inner-city girls excel. In P. Rogers & G. Kaiser (Eds.), Equity in mathematics education: influences of feminism and culture (pp. 28–37). Falmer.

Tiedemann, J. (2002). Teachers’ gender stereotypes as determinants of teacher perceptions in elementary school mathematics. Educational Studies in Mathematics, 50(1), 49–62. https://doi.org/10.1023/A:1020518104346

Trakulphadetkrai, N. V. (2017). Where are the girls and women in mathematical picture books? Mathematics Teaching, 258, 23–25.

Walkerdine, V., & The Girls and Mathematics Unit. (1989). Counting girls out. Virago.

Walls, F. (2010). Freedom to choose? Girls, mathemaitcs and the gendered construction of mathematical identity. In H. J. Forgasz, J. R. Becker, K.-H. Lee, & O. B. Steinthorsdottir (Eds.), International perspectives on gender and mathematics education (pp. 87–110). Information Age.

Wiest, L. R. (2010). Out-of-school-time (OST) programs as mathematics support for females. In H. J. Forgasz, J. R. Becker, K.-H. Lee, & O. B. Steinthorsdottir (Eds.), International perspectives on gender and mathematics education (pp. 55–86). Information Age.

Willis, S. (1996). Gender justice and the mathematics curriculum: Four perspectives. In L. H. Parker, L. J. Rennie, & B. J. Fraser (Eds.), Gender, science and mathematics: shortening the shadow (pp. 41–51). Springer. https://doi.org/10.1007/978-94-011-0143-1_4