Problem 14:  Sketching subsets of the plane ($✓$ $✓$) 1999 Paper I

Sketch the following subsets of the $x$-$y$ plane:

(i)

$\left|x\right|+\left|y\right|\le 1$ ;

(ii)

$|x-1|+|y-1|\le 1$ ;

(iii)

$|x-1|-|y+1|\le 1$ ;

(iv)

$\left|x\right||y-2|\le 1$ .

Comments

Often with modulus signs, it is easiest to consider the cases separately, so for example in part (i), you would first work out the case $x>0$ and $y>0$, then $x>0$ and $y<0$, and so on. Here there is a simple geometric understanding of the different cases: once you have worked out the first case, the other three can be deduced by symmetry.

Another geometric idea should be in your mind when tackling this question, namely the idea of translations in the plane.

Post-mortem

There was no room for a post-mortem over the page, because the diagrams take up so much space.

Don’t read this until you have tried the question!

There are two key learning points, if you will excuse this horrible expression.

The first is that if you want to sketch a region, it is often best to draw the curves that define the boundary of the region, then just work out whether you want the interior or exterior of the boundary by choosing one interior point and seeing whether it satisfies the inequalities.

The second is that quite complicated inequalities can sometimes be much simplified by translating or rotating the axes.

Solution to problem 14

The way to deal with the modulus signs in this question is to consider first the case when the things inside the modulus signs are positive, and then get the full picture by symmetry, shifting the origin as appropriate.

For part (i), consider the first quadrant $x\ge 0$ and $y\ge 0$. In this quadrant, the inequality is $x+y\le 1$. Draw the line $x+y=1$ and then decide which side of the line is described by the inequality. It is obviously (since $x$ has to be smaller than something) the region to the left of the line; or (since $y$ also has to be smaller than something) the region below the line, which is the same region.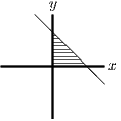     

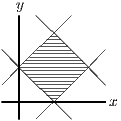
Similar arguments could be used in the other quadrants, but it is easier to note that the inequality $\left|x\right|+\left|y\right|\le 1$ is unchanged when $x$ is replaced by $-x$, or $y$ is replaced by $-y$, so the sketch should have reflection symmetry in both axes, as shown in the diagram on the right.

    

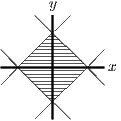
Part (ii) is the same as part (i), except for a translation. The origin of (i) is now at $\left(1,1\right)$.    

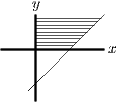
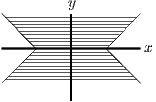
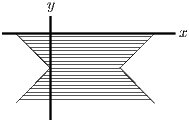
For part (iii), consider first $x-y\le 1$, instead of $|x-1|-|y+1|\le 1$. For $x>0$ and $y>0$, this gives a region that is infinite in extent in the positive $y$ direction, as shown in the first diagram below. Then reflect this in both axes and translate one unit down the $y$ axis and 1 unit along the positive $x$ axis as shown in the second and third diagrams below.

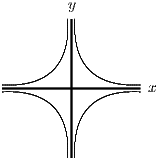
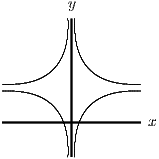
For part (iv), consider first the rectangular hyperbola $xy=1$ reflected in both axes to give four hyperbolas, as in the first diagram below. Then translate the four hyperbolas translated 2 units up the $y$ axis as in the final diagram. The region required is enclosed by the four hyperbolas.