Problem 15:  More sketching subsets of the plane ($✓$ $✓$) 1995 Paper I

(i)

Show that

$$x^2-y^2+x+3y-2=\left(x-y+2\right)\left(x+y-1\right)$$

and hence, or otherwise, indicate by means of a sketch the region of the $x$-$y$ plane for which

$$x^2-y^2+x+3y>2.$$

(ii)

Sketch also the region of the $x$-$y$ plane for which $$x^2-4y^2+3x-2y<-2.$$

(iii)

Give the coordinates of a point for which both inequalities are satisfied or explain why no such point exists.

Comments

This question gets a $✓$ $✓$difficulty rating because inequalities always need to be handled with care.

For the very first part, you could either factorise the left hand side to obtain the right hand side, or multiply out the right hand side to get the left hand side. Obviously, it is much easier to do the multiplication than the factorisation. But is that ‘cheating’ or taking a short cut that might lose marks? No, it is not cheating: it doesn’t matter if you start from the given answer and work backwards — it is still a mathematical proof and any proof will get the marks. (But note that if there is a ‘hence’ in the question, you will lose marks if you do not use the result or results that you have just proved.)

In part (ii), you have to do the factorisation yourself, so you should look carefully at where the terms in the (very similar) first part came from. It will help to spot the similarities between $x^2-y^2+x+3y-2$ and $x^2-4y^2+3x-2y+2$.

Since no indication is given as to what detail should appear on the sketch, you have to use your judgement: it is clearly important to know where the regions lie relative to the coordinate axes.

Post-mortem

As in the previous sketching question, the solution is so long that there is no room for a post-mortem after the answer.

Don’t read this before having tried the question!

The answer given overleaf is inadequate in two ways, each of which would have probably lost me marks. First, as in the previous question, the answer should definitely have referred to the boundaries. Here, the inequalities are strict, which means that the boundary lines are excluded from the required regions. Second, justification should have been provided for the claim that the point $\left(1,2\right)$ satisfies both inequalities. This could be provided either by simply indicating the position of the point on both sketches or algebraically by substitution into the inequalities.

Solution to problem 15

To do the multiplication, it pays to be systematic and to set out the algebra nicely:

$$\begin{array}{rcll}\left(x-y+2\right)\left(x+y-1\right)& =& x\left(x+y-1\right)-y\left(x+y-1\right)+2\left(x+y-1\right)& \\ & =& x^2+xy-x-yx-y^2+y+2x+2y-2& \\ & =& x^2+x-y^2+3y-2& \end{array}$$

as required.

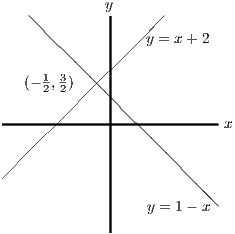
For the first inequality, we need both $x-y+2$ and $x+y-1$ either to be positive or to be negative. To sort out the inequalities (or inequations as they are sometimes horribly called), the first thing to do is to draw the lines corresponding to the corresponding equalities. These lines divide the plane into four regions and we then have to decide which regions are relevant.

The diagonal lines $x-y=-2$ and $x+y=1$ intersect at $\left(-\frac{1}{2},\frac{3}{2}\right)$; this is the important point to mark in on the sketch. The required regions are the left and right quadrants formed by these diagonal lines (since the inequalities mean that the regions are to the right of both lines or to the left of both lines).

For part (ii), the first thing to do is to factorise $x^2-4y^2+3x-2y+2$. The key similarity with the first part is the absence of ‘cross’ terms of the form $xy$. This allows a difference-of-two-squares factorisation of the first two terms: $x^2-4y^2=\left(x-2y\right)\left(x+2y\right)$. Following the pattern of the first part, we can then try a factorisation of the form

where $ab=2$. Considering the terms linear in $x$ and $y$ gives $a+b=3$ and $2a-2b=-2$ which quickly leads to $a=1$ and $b=2$. Note that altogether there were three equations for $a$ and $b,$ so we had no right to expect a consistent solution (except for the fact that this is a STEP question for which we had every right to believe that the first part would guide us through the second part).

Alternatively, we could have completed the square in $x$ and in $y$ and then used difference of two squares:

$$\begin{array}{rcll}{x}^2-4y^2+3x-2y+2& =& {\left(x+\frac{3}{2}\right)}^2-\frac{9}{4}-{\left(2y+\frac{1}{2}\right)}^2+\frac{1}{4}+2& \\ & =& {\left(x+\frac{3}{2}\right)}^2-{\left(2y+\frac{1}{2}\right)}^2=\left(x+\frac{3}{2}-2y-\frac{1}{2}\right)\left(x+\frac{3}{2}+2y+\frac{1}{2}\right).& \end{array}$$

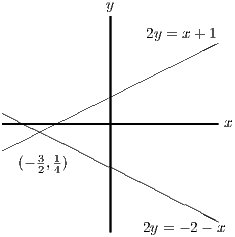
As in the previous case, the required region is formed by two intersecting lines; this time, they intersect at $\left(-\frac{3}{2},-\frac{1}{4}\right)$ and the upper and lower regions are required, since the inequality is the other way round. It is easy to see from the sketches that there are points that satisfy both inequalities: for example $\left(1,2\right)$.