Problem 17:  Inequalities ($✓$ $✓$) 2001 Paper I

Solve the inequalities

(i)

$1+2x-x^2>\frac{2}{x}$       ($x\ne 0$) ,

(ii)

$\sqrt{3x+10}>2+\sqrt{x+4}$       ($x\ge -10∕3$) .

Comments

The two parts are unrelated (unusually for STEP questions), except that they deal with inequalities. Both parts need care, having traps for the unwary.

In part (i) you have to watch out when you multiply an inequality: if the thing you multiply by is negative then the inequality reverses. You might find sketching a graph helpful.

In part (ii) you have to consider the possibility that your algebraic manipulations have created extra spurious solutions. It is worth (after you have finished the question) sketching the graphs of $\sqrt{3x+10}$ and $2+\sqrt{x+4}$ just to see what is going on. You can get the latter graph by translations of $\sqrt{x}$ (and you can get $y=\sqrt{x}$ by reflection $y=x^2$ in the line $y=x$). I would have drawn them for you in the post-mortem overleaf had there been room.

In fact, a solution relying on sketches for part (ii) is probably preferable to my solution. With the sketches to hand, you only have to solve the equation $\sqrt{3x+10}=2+\sqrt{x+4}$ and then look at your sketches to see to see what range of values of $x$ you need, thereby saving much anguish.¹⁸

Solution to problem 17

(i) We would like to multiply both sides of the inequality by $x$ in order to obtain a nice cubic expression. However, we have to allow for the possibility that $x$ is negative (which would reverse the inequality). One way of dealing with this is to consider the cases $x>0$ and $x<0$ separately.

For $x>0$, we multiply the whole equation by $x$ without changing the direction of the inequality:

$$\begin{array}{llll}\hfill 1+2x-x^2>\frac{2}{x}& \Rightarrow x+2x^2-x^3>2& \hfill & \\ \hfill & \Rightarrow x^3-2x^2-x+2<0& \hfill & \\ \hfill & \Rightarrow \left(x-1\right)\left(x+1\right)\left(x-2\right)<0& \hfill & \\ \hfill & \Rightarrow 1<x<2,& \hfill \text{(}\ast \text{)}\end{array}$$

discarding the possibility $x<-1$, since we have assumed that $x>0$.

The easiest way of obtaining the result $\left(\ast \right)$ from the previous line is to sketch the graph of $\left(x-1\right)\left(x+1\right)\left(x-2\right)<0$. For $x<0$, we must reverse the inequality when we multiply by $x$ so in this case, $\left(x-1\right)\left(x+1\right)\left(x-2\right)>0$, which gives $-1<x<0$. In the sketch on the right, the values of $x$ for which the inequality holds are shown as bold lines.  

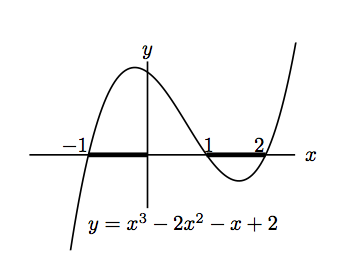
The smart way to do $x>0$ and $x<0$ in one step is to multiply by $x^2$ (which is never negative and hence never changes the direction of the inequality) and analyse
$x\left(x-1\right)\left(x+1\right)\left(x-2\right)<0$. Again, a sketch is useful.  

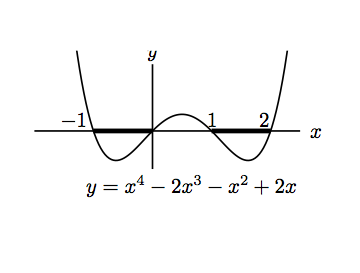
(ii) First square both sides the inequality $\sqrt{3x+10}>2+\sqrt{x+4}$:

Note that the both sides of the original inequality are positive or zero (i.e. non-negative), so the direction of the inequality is not changed by squaring. Now consider the new inequality $x+1>2\sqrt{x+4}$. If both sides are non-negative, that is if $x>-1$, we can square both sides again without changing the direction of the inequality. But, if $x<-1$, the inequality cannot be satisfied since the right hand side is always non-negative. Squaring gives

Thus, $x>5$ or $x<-3$. However, we must reject $x<-3$ because of the condition $x>-1$. Therefore the inequality holds for $x>5$.

Post-mortem

The spurious result $x<-3$ at the end of part (ii) arises through loss of information in the process of squaring: if you square an expression, you lose its sign. After squaring twice, the resulting inequality is the same as would have resulted from $\surd \left(3x+10\right)<2-\surd \left(x+4\right)$ and it is to this inequality that $-\frac{10}{3}\le x<-3$ is a solution.