Problem 18

Problem 18: Inequalities from cubics ( $✓$ $✓$ )

2001 Paper

(i)

Sketch, without calculating the stationary points, the graph of the function

f (x)

given by

f (x) = (x - p) (x - q) (x - r),

where $p < q < r$ . By considering the quadratic equation $f^{'} (x) = 0$ , or otherwise, show that

{(p + q + r)}^{2} > 3 (q r + r p + p q) .

(ii)

By considering

(x^{2} + g x + h) (x - k)

, or otherwise, show that

g^{2} > 4 h

is a sufficient condition but not a necessary condition for the inequality

{(g - k)}^{2} > 3 (h - g k)

to hold.

Comments

The idea behind the ﬁrst part is to obtain an inequality by considering a certain graph. In the second part, we again use graphs to obtain an inequality, which this time holds subject to a different inequality.

For the sketch in the ﬁrst part it is not necessary to do more than think about the behaviour for $x$ large and positive, and for $x$ large and negative, and the points at which the graph crosses the $x$ -axis.

For the second part, you should also have a sketch or sketches in mind. The argument is very similar to that of the ﬁrst part, except that it also tests understanding of the meaning of the terms necessary and sufficient. For this, it is probably best to use $\Rightarrow$ notation.

To show that $g^{2} > 4 h$ is not a necessary condition for the inequality ${(g - k)}^{2} > 3 (h - g k)$ to hold, you just have to give an example (the simpler the better) for which ${(g - k)}^{2} > 3 (h - g k)$ but $g^{2} \leq 4 h$ .

Solution to problem 18

From the sketch, we see that

f (x)

has two turning points, so the equation

f^{'} (x) = 0

has two real roots.

Now

\begin{array}{l} f (x) & = (x - p) (x - q) (x - r) \\ = x^{3} - (p + q + r) x^{2} + (q r + r p + p q) x - p q r \end{array}

so at a turning point

f^{'} (x) = 3 x^{2} - 2 (p + q + r) x + (q r + r p + p q) = 0 .

Using the condition ‘ $b^{2} > 4 a c$ ’ for this quadratic to have two real root gives the required result:

4 {(p + q + r)}^{2} > 12 (q r + r p + p q) .

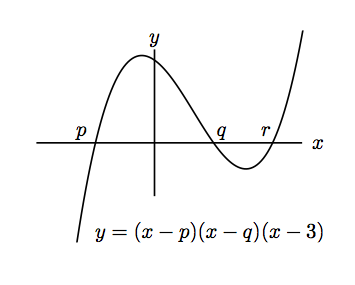
For the second part, we can use a similar argument. First note that if the quadratic equation $x^{2} + g x + h = 0$ has two distinct real roots then the cubic equation $(x^{2} + g x + h) (x - k) = 0$ has three roots, at least two of which are distinct. Thus

\begin{array}{l} g^{2} > 4 h & \Rightarrow (x^{2} + g x + h) (x - k) = 0 has at least two distinct roots \\ \Rightarrow (x^{2} + g x + h) (x - k) has at least two distinct turning points (draw graphs!) \\ \Rightarrow x^{3} + (g - k) x^{2} + (h - g k) x - h k has at least two distinct turning points \\ \Rightarrow 3 x^{2} + 2 (g - k) x + (h - g k) = 0 has two distinct roots \\ \Rightarrow 4 {(g - k)}^{2} > 12 (h - g k) as required. \end{array}

Thus $g^{2} > 4 h$ is a sufficient condition for this inequality to hold.

Why is it not necessary? That is to say, why is it too strong a condition? The reason is that both turning points could be above the $x$ –axis or both could be below (not one on either side which was the origin of the inequality). Saying this would get all the marks. Or you could give a counterexample: for example, $g = 2$ , $h = 1$ and $k = 1000$ .

Post-mortem

When I set this question, I got considerable satisfaction from the way that seemingly obscure inequalities are derived from understanding simple graphs and the quadratic formula. It was only when preparing this book that I realised that they are, disappointingly, not at all obscure.

The inequality of the ﬁrst part is equivalent to ${(q - r)}^{2} + {(r - p)}^{2} + {(p - q)}^{2} > 0$ , the inequality coming from the fact the squares of real numbers are non-negative and in this case the given condition $p < q < r$ means that the expression is strictly positive (not equal to zero).

If we rewrite the second inequality as ${(k + \frac{1}{2} g)}^{2} + 3 (\frac{1}{4} g^{2} - h) > 0$ we see that it certainly holds if $(\frac{1}{4} g^{2} - h) > 0$ , as expected. This is not a necessary condition: it also holds if $(\frac{1}{4} g^{2} - h) < 0$ provided $k$ is large enough.