Problem 24:  Sketching $x^m{\left(1-x\right)}^n$ ($✓$ $✓$ $✓$) 2002 Paper I

Let $\mathrm{f}\left(x\right)=x^m{\left(x-1\right)}^n$, where $m$ and $n$ are both integers greater than 1. Show that

Show that the curve $y=\mathrm{f}\left(x\right)$ has a stationary point in the interval $0<x<1$. By considering $\mathrm{f}{}^{″}\left(x\right)$, show that this stationary point is a maximum if $n$ is even and a minimum if $n$ is odd.

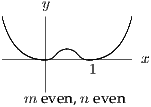
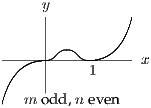
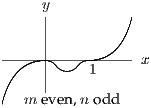
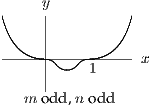
Sketch the graphs of $\mathrm{f}\left(x\right)$ in the four cases that arise according to the values of $m$ and $n$.

Comments

There is quite a lot in this question, but it is one of the best STEP questions on basic material that I came across.

First, you have to find ${\mathrm{f}}^{\prime }\left(x\right)$. The very first part (giving a form of ${\mathrm{f}}^{\prime }\left(x\right)$) did not occur in the original STEP question. This particular expression is extremely helpful when if comes to finding the value of ${\mathrm{f}}^{″}\left(x\right)$ at the stationary point. In the actual exam, a handful of candidates successfully found a general expression for ${\mathrm{f}}^{″}\left(x\right)$ in terms of $x$ then evaluated it at the stationary point: first class work.

You should find that the value of ${\mathrm{f}}^{″}\left(x\right)$ at the stationary point can be expressed in the form $\left(\cdots \right)\mathrm{f}\left(x\right)$, where the factor in the brackets is quite simple and always negative, so that the nature of the stationary point depends only on the sign of $\mathrm{f}\left(x\right)$. Actually, this is intuitively obvious: $\mathrm{f}\left(0\right)=\mathrm{f}\left(1\right)=0$ so the one stationary point with $0<x<1$ must be, for example, a maximum if $\mathrm{f}\left(x\right)>0$ for $0<x<1$.

For the sketches, you really have only to think about the behaviour of $\mathrm{f}\left(x\right)$ when $\left|x\right|$ is large and the sign of $\mathrm{f}\left(x\right)$ between $x=0$ and $x=1$. That allows you to piece together the graph, knowing that there is only one stationary point between $x=0$ and $x=1$. You should then be able to identify the four cases referred to.

Note that, very close to $x=0$, $\mathrm{f}\left(x\right)\approx x^m{\left(-1\right)}^n$ so it is easy to see how the graph there depends on $n$ and $m$; you can use this to check that you have got the graphs right.

Post-mortem

Don’t read this until you have worked through the question!

You may have noticed a little carelessness in the first line of the solution: what happens in the logarithmic differentiation if any of $\mathrm{f}\left(x\right)$ or $x$ or $x-1$ are negative? The answer is that it doesn’t matter. One way to deal with the problem of logs with negative arguments is to put modulus signs everywhere using the correct result

If you are not sure of this, try it on $\mathrm{f}\left(x\right)=x$ taking the two cases $x>0$ and $x<0$ separately.

A more sophisticated way of dealing with logs with negative arguments is to note that $ln\left(-\mathrm{f}\left(x\right)\right)=lnf\left(x\right)+ln\left(-1\right)$. We don’t have to worry about $ln\left(-1\right)$ because it is a constant (of some sort) and so won’t affect the differentiation. Actually, a value of $ln\left(-1\right)$ can be obtained by taking logs of Euler’s famous formula ${\mathrm{e}}^{i\pi }=-1$ giving $ln\left(-1\right)=i\pi$.

Solution to problem 24

The first result can be established by differentiating $\mathrm{f}\left(x\right)$ directly, but the neat way to do it is to start with $ln\mathrm{f}\left(x\right)$:

as required. Writing this as ${\mathrm{f}}^{\prime }\left(x\right)=m{x}^{m-1}-n{\left(x-1\right)}^{n-1}$, we see that $\mathrm{f}\left(x\right)$ has stationary points at $x=0$ and $x=1$ (since $m-1>0$ and $n-1>0$) and when

i.e. when $m\left(1-x\right)-nx=0$. Solving this last equation for $x$ gives $x=\frac{m}{m+n}$, which lies between $0$ and $1$ since $m$ and $n$ are positive.

Next we calculate ${\mathrm{f}}^{″}\left(x\right)$. Starting with

we obtain

At a stationary point, the second of these two terms is zero because ${\mathrm{f}}^{\prime }\left(x\right)=0$, leaving

The bracketed expression is negative so at a stationary point ${\mathrm{f}}^{″}\left(x\right)<0$ if $\mathrm{f}\left(x\right)>0$ and ${\mathrm{f}}^{″}\left(x\right)>0$ if $\mathrm{f}\left(x\right)<0$.

The sign of $\mathrm{f}\left(x\right)$ for $0<x<1$ is the same as the sign of ${\left(x-1\right)}^n$, since $x^m>0$ when $x>0$. For the stationary point in the interval $0<x<1$, ${\left(x-1\right)}^n>0$ if $n$ is even and ${\left(x-1\right)}^n<0$ if $n$ is odd. Thus ${\mathrm{f}}^{″}\left(x\right)<0$ if $n$ is even and ${\mathrm{f}}^{″}\left(x\right)>0$ if $n$ is odd, which is the required result.

The four cases to sketch are determined by whether $m$ and $n$ are even or odd. The easiest way to understand what is going on is to consider the graphs of $x^m$ and ${\left(x-1\right)}^n$ separately, then try to join them up at the stationary point between $0$ and $1$. If $m$ is odd, then $x=0$ is a point of inflection, but if $m$ is even it is a maximum or minimum according to the sign of ${\left(x-1\right)}^n$. You should also think about the behaviour for large $\left|x\right|$. All the various bits of information (including the nature of the turning point investigated above) should all piece neatly together.