Problem 25

Problem 25: Inequalities by area estimates ( $✓$ $✓$ $✓$ ) 2002 Paper I

Give a sketch of the curve $y = \frac{1}{1 + x^{2}}$ , for $x \geq 0$ .

Find the equation of the line that intersects the curve at $x = 0$ and is tangent to the curve at some point with $x > 0$ . Prove that there are no further intersections between the line and the curve. Draw the line on your sketch.

By considering the area under the curve for $0 \leq x \leq 1$ , show that $π > 3$ .

By considering the volume formed by rotating the curve about the $y$ axis, show also that $ln 2 > \frac{2}{3}$ .

Note: $\int_{0}^{1} \frac{1}{1 + x^{2}} d x = \frac{π}{4} .$

Comments

There is quite a lot to this question, so $✓$ $✓$ $✓$ even though none of it is particularly difficult (very surprising to ﬁnd it on Paper I). The most common mistake in ﬁnding the equation of the tangent is to muddle the $y$ and $x$ that occur in the equation of the line ( $y = m x + c$ ) with the coordinates of the point at which the tangent meets the curve, getting ‘constants’ $m$ and $c$ that depend on $x$ . I’m sure you wouldn’t make this rather elementary mistake normally, but it is surprising what people do under examination conditions.

The reason for sketching the curve lies in the last parts: the shape of the curve relative to the straight line provides the inequality.

The note at the end of the question had to be given because integrals of that form (giving inverse trigonometric functions) are not in the core A-level syllabus.

Solution to problem 25

Your sketch should show a graph which has gradient $0$ at $(0, 1)$ and which asymptotes to the $x$ -axis for large $x$ . The extra line in my sketch is the tangent to the graph from the point $(0, 1)$ which is required later.

PICT

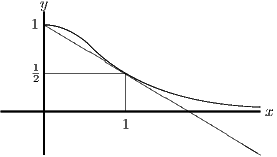
First we ﬁnd the equation of the tangent to the curve $y = {(1 + x^{2})}^{- 1}$ at the point $(p, q)$ . The gradient of the curve at the point $(p, q)$ is $- 2 p {(1 + p^{2})}^{- 2}$ , i.e. $- 2 p q^{2}$ , so the equation of the tangent is

y = - 2 p q^{2} x + c

where $c$ is given by $q = - 2 p q^{2} p + c .$ This line is supposed to pass through the point $(0, 1)$ , so $1 = c$ . Thus $1 = q + 2 p^{2} q^{2}$ , or (replacing $q$ with $1 ∕ (1 + p^{2})$ )

1 = \frac{1}{1 + p^{2}} + \frac{2 p^{2}}{{(1 + p^{2})}^{2}}

which simpliﬁes to

{(1 + p^{2})}^{2} = 1 + 3 p^{2} i.e. p^{4} = p^{2} .

The only positive solution is $p = 1$ , so the equation of the line is $y = - \frac{1}{2} x + 1 .$

We can check that this line does not meet the curve again by solving the equation

- \frac{x}{2} + 1 = \frac{1}{1 + x^{2}} .

Multiplying by ${(1 + x)}^{2}$ gives

(1 - \frac{1}{2} x) (1 + x^{2}) = 1 i.e. x^{3} - 2 x^{2} + x = 0 .

Factorising shows that $x = 1$ and $x = 0$ satisfy this equation (these are the known roots, $x = 1$ being a double root corresponding to the tangency) and that there are no more roots.

The area under the curve for $0 \leq x \leq 1$ is $\frac{1}{4} π$ as given. The sketch shows that this area is greater than the area under the tangent line for $0 \leq x \leq 1$ , which is $\frac{1}{2} + \frac{1}{4}$ (the area of the rectangle plus the area of the triangle above it). Comparing with with $\frac{1}{4} π$ gives the required result.

The volume formed by rotating the curve about the $y$ axis is

\int_{0}^{1} 2 π y x d x = π \int_{0}^{1} \frac{2 x}{1 + x^{2}} d x = π ln 2 .

This is greater than the volume formed by rotating the line about the $y$ axis, which is

\int_{0}^{1} 2 π y x d x = 2 π \int_{0}^{1} (1 - \frac{1}{2} x) x d x = \frac{2}{3} π .

Comparison gives the required result.

Post-mortem

As I said before, no step of this question is particularly difficult, but lots of different ideas are required. The last part is very challenging, because you have to do and compare two separate volume integrals without any intermediate steer at all. You should be very pleased if you made good progress with it.

The important lesson to learn from this is that perseverance will eventually pay off.