Problem 49:  Areas and volumes ($✓$ $✓$) 1987 Paper II

The function f satisfies the condition ${\mathrm{f}}^{\prime }\left(x\right)>0$ for $a\le x\le b$, and $\mathrm{g}$ is the inverse of $\mathrm{f}$.

(i)

By making a suitable change of variable, prove that

$${\int \; <!--nolimits-->}_a^b\mathrm{f}\left(x\right)\mathrm{d}x=b\beta -a\alpha -{\int \; <!--nolimits-->}_{\alpha }^{\beta }\mathrm{g}\left(y\right)\mathrm{d}y,$$

(1)

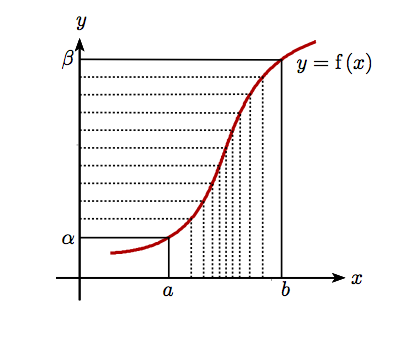
where $\alpha =\mathrm{f}\left(a\right)$ and $\beta =\mathrm{f}\left(b\right)$. Interpret this formula geometrically, by means of a sketch, in the case where $\alpha$ and $a$ are both positive.

Verify the result (1) for $\mathrm{f}\left(x\right)=e^{2x}$, $a=0$, $b=1$.

(ii)

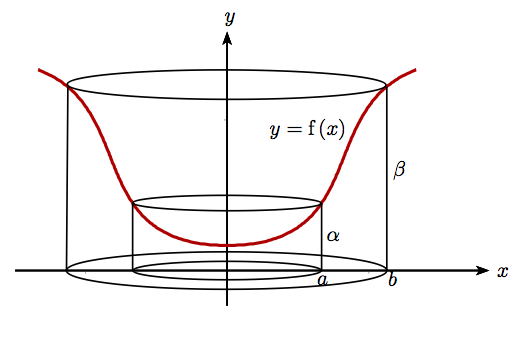
Prove similarly and interpret the formula

$$2\pi {\int \; <!--nolimits-->}_a^{b}x\mathrm{f}\left(x\right)\mathrm{d}x=\pi \left(b^2\beta -a^2\alpha \right)-\pi {\int \; <!--nolimits-->}_{\alpha }^{\beta }\left[\right.\mathrm{g}\left(y\right){\left]\right.}^2\mathrm{d}y.$$

(2)

Comments

As is often the case, the required change of variable for part (i) can be worked out by inspection of the limits.

To find the inverse function (note: inverse, not reciprocal) of the function f, it is often best to try to think of the function $\mathrm{g}$ such that $\mathrm{g}\left(\right.\mathrm{f}\left(x\right)\left)\right.=x$, though making $x$ the subject of $y=\mathrm{f}\left(x\right)$ is perhaps safer with an unfamiliar function.

The condition ${\mathrm{f}}^{\prime }\left(x\right)>0$ ensures that $\mathrm{f}$ has a unique inverse; a function such as sin which has maximum and minimum points has a unique inverse only on restricted ranges of its argument which do not contain the turning points. (This is obvious from a sketch). The condition ${\mathrm{f}}^{\prime }\left(x\right)<0$ would do equally well.

The geometrical interpretations of these formulae are exceptionally pleasing, though the second one needs some artistic skill to make it convincing.

Solution to problem 49

(i) The limits of the integral on the right hand side of equation (1) are $\mathrm{f}\left(a\right)$ and $\mathrm{f}\left(b\right)$, which suggests the change of variable $y=\mathrm{f}\left(x\right)$. Making this change, so that $\mathrm{d}y={\mathrm{f}}^{\prime }\left(x\right)\mathrm{d}x$, gives

$${\int \; <!--nolimits-->}_{\alpha }^{\beta }\mathrm{g}\left(y\right)\mathrm{d}y={\int \; <!--nolimits-->}_a^b\mathrm{g}\left(\right.\mathrm{f}\left(x\right)\left)\right.{\mathrm{f}}^{\prime }\left(x\right)\mathrm{d}x={\int \; <!--nolimits-->}_a^{b}x{\mathrm{f}}^{\prime }\left(x\right)\mathrm{d}x.$$

For the last equality, we have used the definition of g as the inverse of f, i.e. $\mathrm{g}\left(\right.\mathrm{f}\left(x\right)\left)\right.=x$. This last integral is begging to be integrated by parts:

$${\int \; <!--nolimits-->}_a^{b}x{\mathrm{f}}^{\prime }\left(x\right)\mathrm{d}x={x\mathrm{f}\left(x\right)\left|\right.}_a^b-{\int \; <!--nolimits-->}_a^b\mathrm{f}\left(x\right)\mathrm{d}x,$$

which gives the required result after evaluating $x\mathrm{f}\left(x\right)$ at $a$ and $b$. The first sketch below shows these areas: the area between the large and small rectangles is $\left(b\beta -a\alpha \right)$, which is split into the areas represented by the two integrals of equation (1), hatched vertically and horizontally, respectively.

Setting $\mathrm{f}\left(x\right)={\mathrm{e}}^{2x}$ and $a=0$, $b=1$ in the left hand side of (1) gives ${\int \; <!--nolimits-->}_0^1{\mathrm{e}}^{2x}\mathrm{d}x=\frac{1}{2}\left(\right.{\mathrm{e}}^2-1\left)\right..$ For the right hand side of (1), we have $\alpha =1$ and $\beta ={\mathrm{e}}^2$ so $b\beta -a\alpha ={\mathrm{e}}^2$. The inverse of ${\mathrm{e}}^{2x}$ is $\frac{1}{2}lny$ so the integral becomes

$${\int \; <!--nolimits-->}_1^{{\mathrm{e}}^2}\frac{1}{2}lny\mathrm{d}y=\frac{1}{2}\left(ylny-y\right){\left|\right.}_1^{{\mathrm{e}}^2}=\frac{1}{2}\left(2{\mathrm{e}}^2-{\mathrm{e}}^2\right)-\frac{1}{2}\left(0-1\right)=\frac{1}{2}{\mathrm{e}}^2+\frac{1}{2}.$$

Thus the left hand side of (1) agrees with the right hand side.

(ii) We can use the same method (change of variable followed by integration by parts):

$${\int \; <!--nolimits-->}_{\alpha }^{\beta }\left[\right.\mathrm{g}\left(y\right){\left]\right.}^2\mathrm{d}y={\int \; <!--nolimits-->}_a^b{x}^2{\mathrm{f}}^{\prime }\left(x\right)\mathrm{d}x={x^2\mathrm{f}\left(x\right)\left|\right.}_a^b-{\int \; <!--nolimits-->}_a^{b}2x\mathrm{f}\left(x\right)\mathrm{d}x=\left(b^2\beta -a^2\alpha \right)-2{\int \; <!--nolimits-->}_a^{b}x\mathrm{f}\left(x\right)\mathrm{d}x,$$

which gives the required formula (2) on multiplication by $\pi$.

The first of the integrals in (2) is the volume of the solid body under the surface formed by rotating the curve $y=\mathrm{f}\left(x\right)$ round the $y$-axis; this volume is thought of as a set of concentric cylindrical shells of height $\mathrm{f}\left(x\right)$ with internal radius $x$ ($a\le x\le b$), and thickness $\mathrm{d}x$. The second integral is the volume inside the surface formed by rotating the curve $y=\mathrm{f}\left(x\right)$ round the $y$-axis; this volume is thought of as a pile of infinitesimally thin discs of radius $\mathrm{g}\left(y\right)$ ($\alpha \le y\le \beta$) and thickness $\mathrm{d}y$. The sum of the two integrals is equal to the difference between the volumes of the two concentric cylinders (of radii $a$ and $b$, heights $\alpha$ and $\beta$, respectively) as shown in the second sketch below.