Problem 56:  A chocolate orange ($✓$) 1987 Specimen Paper II

A chocolate orange consists of a sphere of delicious smooth uniform chocolate of mass $M$ and radius $a$, sliced into segments by planes through a fixed axis. It stands on a horizontal table with this axis vertical and it is held together by a narrow ribbon round its equator. Show that the tension in the ribbon is at least $\frac{3}{32}Mg$.

[You may assume that the centre of mass of a segment of angle $2𝜃$ is at distance $\frac{3\pi asin𝜃}{16𝜃}$ from the axis.]

Comments

This question can be done by the usual methods (resolving forces and taking moments about a suitably chosen point). Since the chocolate is smooth, there is no friction. The ribbon may be elastic, so it could be tighter than is needed just to keep the orange together. At the lowest tension possible the orange is on the point of falling apart, so there are no forces between the faces of the segments, except at the point of contact with the table.

The ribbon is said to be thin, but actually this has to be interpreted as massless as well as thin; a ribbon with mass would simply drop off the equator of the orange.

Notice that the question does not say that the segments are all the same size. That suggests that we should look at just one segment, expecting to find that the tension required for that segment is independent of the angle of the segment.

When I set this question originally on a 1985 examination paper (pre-dating STEP, which started in 1987), I gave the wrong formula for the distance of the centre of mass of the segment, and the answer for the tension was also incorrect, but consistent with the incorrect formula. Not surprisingly, no one pointed it out, either at the time or afterwards. With a bit of luck, it is correct now.

I sent a copy of the examination paper to a well-known manufacturer of high quality chocolate confection³¹ and was rewarded with a puzzled letter and a parcel; not as large a parcel as I had hoped for (perhaps they spotted the incorrect formula), but better than nothing. It seemed worth including the question in this book in case they wanted an opportunity to make amends $\dots$ .

Solution to problem 56

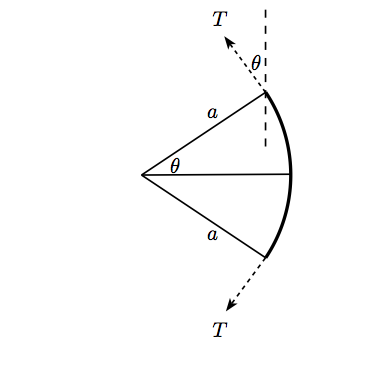
The above diagram shows a horizontal cross-section of a segment of the orange.

Resolving the tension $T$ in the ribbon as shown gives a horizontal component of force due to tension on the segment of $2Tsin𝜃$ towards the left of the diagram.

The volume of the segment is a fraction $2𝜃∕\left(2\pi \right)$ of the volume of the sphere, so the segment has mass $M\left(2𝜃\right)∕\left(2\pi \right)$. The weight of the segment gives a force of $Mg𝜃∕\pi$ acting downwards through the centre of mass as shown in the diagram below, which is a vertical cross-section of a segment.

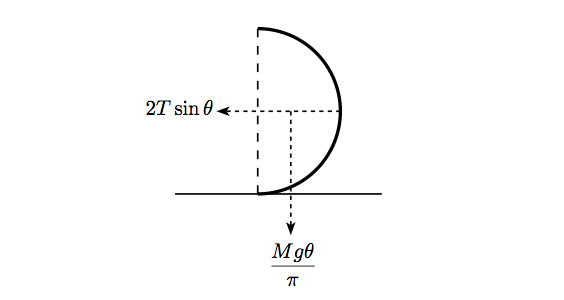
Taking moments about the point of contact of the table and the segment gives

which gives the required answer.

Post-mortem

Another way of tackling this sort of problem is to use the principle of virtual work, for which you imagine that the system relaxes a very small amount (in this case, by allowing the ribbon to stretch) and equate the work done against the constraints (here, tension times extension) to the change of potential energy of the system, to obtain a formula for the constraint force (here, the tension). In many cases, this method is simpler, but here it turns out to be very difficult: not recommended at all. The difficulty is that if the orange relaxes so that each segment is now inclined at a small angle $\alpha$ to the vertical, quite a lot of work is needed to calculate how far the centre of mass has fallen, even working to lowest order in $\alpha$.