Problem 57:  Lorry on bend ($✓$) 2002 Paper I

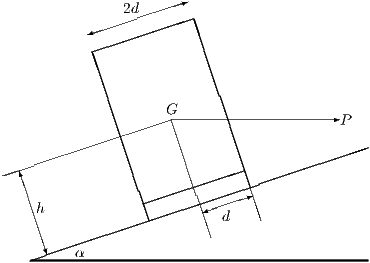
A lorry of weight $W$ stands on a plane inclined at an angle $\alpha$ to the horizontal. Its wheels are a distance $2d$ apart, and its centre of gravity $G$ is at a distance $h$ from the plane, and halfway between the sides of the lorry. A horizontal force $P$ acts on the lorry through $G$, as shown.

(i)

If the normal reactions on the lower and higher wheels of the lorry are equal, show that the sum of the frictional forces between the wheels and the ground is zero.

(ii)

If $P$ is such that the lorry does not tip over (but the normal reactions on the lower and higher wheels of the lorry need not be equal), show that

$$Wtan\left(\alpha -\beta \right)\le P\le Wtan\left(\alpha +\beta \right),$$

where $tan\beta =d∕h$.

Comments

There is not much more to this than just resolving forces and taking moments about a suitable point.

You might think it a bit odd to have a force that acts horizontally through the centre of gravity of the lorry: it is supposed to be centrifugal. The first draft of the question was intended as a model of a lorry going round a bend on a cambered road. The idea was to relate the speed of the lorry to the angle of camber: the speed should be chosen so that there is be no tendency to skid. However, the modelling part of the question was eventually abandoned.

You can do the second part algebraically (using equations derived from resolving forces and taking moments), but there is a more direct approach.

There was a slight inaccuracy in the wording of the question, which I have not corrected here. Maybe you will spot it in the course of your solution. The diagram is correct.

Solution to problem 57

Let the normal reactions at the lower and upper wheels be $N_1$ and $N_2$, respectively, and let the frictional forces at the lower and upper wheels be $F_1$ and $F_2$, respectively, (both up the plane).

(i) Taking moments about $G$, we have

so if $N_1=N_2$ the sum of the frictional forces is zero.

(ii) The condition for the lorry not tip over down the plane is $N_2\ge 0$, which is the same as saying that the total moment of $W$ and $P$ about the point of contact between the lower wheel and the plane in the clockwise sense is positive. This gives $P\le Wtan\left(\alpha +\beta \right)$ after a bit of geometry. Actually, working out the shortest distance between the line of action of the forces and the wheels requires a bit of thought. You find that $\alpha +\beta$ is the angle between the vertical and the lines joining $G$ to the wheels. This is obvious, at least in retrospect: if the plane were not tilted, the angle would be $\beta$ and tilting just increases this by the angle of tilt.

The other inequality comes from a similar calculation using the other wheel.

Post-mortem

I expect that you found that really clear and BIG diagrams made the question much easier: that is nearly always the case with mechanics.

The slight inaccuracy in the question occurs because if the line of action of $P$ passes between the wheels of the lorry (not, as shown in the diagram, higher than the higher wheel), then the lorry cannot tip over up the plane however large $P$ is. The given inequality is not correct in this case, which corresponds to $\alpha +\beta >\frac{1}{2}\pi$ and therefore $tan\left(\alpha +\beta \right)<0$.

An alternative way of obtaining the inequalities of part (ii) is to work with the resultant of $P$ and $W$. The direction of this resultant force must be such that its line of action passes between the wheels. The line of action makes an angle of ${tan}^{-1}\left(P∕W\right)$ with the vertical through $G$ and the inequalities follow after the same geometry as in the answer to part (ii) above.