Problem 62: Particle on wedge ( ) 1998 Paper II
A wedge of mass rests on a smooth horizontal surface. The face of the wedge is a smooth plane inclined at an angle to the horizontal. A particle of mass slides down the face of the wedge, starting from rest. At a later time , the speed of the wedge, the speed of the particle and the angle of the velocity of the particle below the horizontal are as shown in the diagram.
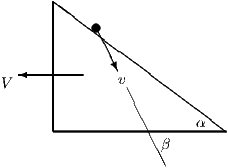
Let be the vertical distance descended by the particle. Derive the following results, stating in (ii) and (iii) the mechanical principles you use:
- (i)
- ;
- (ii)
- , where ;
- (iii)
- .
Hence show that , where and . Deduce that .
Comments
I was surprised at the difficulty of this problem, compared with a particle on a fixed wedge. There is an easier method (just using forces and Newton’s second law) but the route suggested here uses basic principles, the outcomes of which are the numbered parts of the question. For a fixed wedge, the horizontal component of momentum is not conserved, because of the force required to hold the wedge; but (i) and (iii) are just what you would use in the fixed case.
Part (ii) is used only (apart from the very last result) to show that the angle is constant. This is a bit at first sight surprising: it means that the particle moves in a straight line.
Most of the important intermediate results are given to you, but it is still very good discipline to check that they hold in special cases: for example, corresponding to a massless particle or equivalently a fixed wedge; and or corresponding to a horizontal or vertical wedge face. You should check that you understand what should happen in these special cases and that your understanding is consistent with the formulae.
Solution to problem 62
(i) This equation follows immediately from the constraint placed on the particle: it remains in contact with the plane so components of the velocities of the particle and the wedge perpendicular to the face must be equal.
(ii) Horizontal momentum is conserved, so . Substitution for using (i) gives
which leads immediately to the required result. Note that the angle remains constant in the motion.
(iii) Conservation of energy gives
Thus .
The next step is to write in terms of to obtain the differential equation. The vertical component of velocity is , so
Now using the result of (iii) gives
| () |
Squaring gives the required result, and we can use part (ii) to obtain the expression for in terms of and .
Now, at last, we use the hard-won result that , and hence , is constant. The equation
is exactly the same as the equation of conservation of energy for a particle falling vertically in a gravitational field of strength . For such a particle, we have , as required.
Post-mortem
The basic principles behind this solution are conservation of momentum and energy, together with the constraint that the particle moves on the surface of the face of the wedge. The benefit of using conservation of energy is that you do not have to worry about the normal reaction force, because it does no work.
Of course, we could obtain the final result by integrating the differential equation , which takes only a few lines.
Problem 62: Particle on wedge ( ) 1998 Paper II
A wedge of mass rests on a smooth horizontal surface. The face of the wedge is a smooth plane inclined at an angle to the horizontal. A particle of mass slides down the face of the wedge, starting from rest. At a later time , the speed of the wedge, the speed of the particle and the angle of the velocity of the particle below the horizontal are as shown in the diagram.
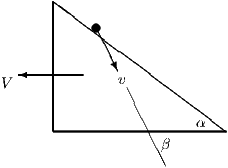
Let be the vertical distance descended by the particle. Derive the following results, stating in (ii) and (iii) the mechanical principles you use:
-
(i) - ;
-
(ii) - , where ;
-
(iii) - .
Hence show that , where and . Deduce that .







