Problem 63: Sphere on step () 1997 Paper II
A uniform solid sphere of radius and mass is drawn very slowly and without slipping from horizontal ground onto a step of height by a horizontal force of magnitude which is always applied to the highest point of the sphere and is always perpendicular to the vertical plane which forms the face of the step. Find the maximum value of in the motion, and prove that the coefficient of friction between the sphere and the edge of the step must exceed .
Comments
This is quite straightforward once you have realised that very slowly means so slowly that the sphere can be considered to be static at each position. You just have to solve a statics problem with the usual tools: resolving forces and taking moments about suitably chosen points.
It seems odd to have a force that always acts at the highest point of the sphere. The idea is that there is a string wrapped round the sphere and it is being pulled horizontally to get the sphere up the step.
Solution to problem 63
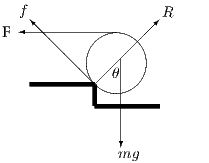
Let the angle between the radius to the point of contact with the step and the downward vertical be , as shown. At the point of contact, let the frictional force, which is tangent to the sphere, be and the reaction (along the radius of the sphere).
To investigate , we take moments about a point cunningly chosen to eliminate other unknown forces. Since the lines of action both and pass through the point of contact of the sphere with the step, we can eliminate both forces by taking moments about this point:
so
This takes its maximum value when is largest, i.e. when the sphere just touches the horizontal ground. At this position, and and .
Taking moments about the centre of the sphere (to eliminate the normal reaction and weight) gives , and resolving forces parallel to the radius at the point of contact gives
Now
so . We therefore
need , as
required.
Post-mortem
Should we have known that (in the last line of the solution)? It doesn’t look obvious from the diagram. However, if we follow the principle, used twice already, of taking moments about a point that eliminates unwanted forces, the result drops out. To relate and directly, we need to eliminate and . We therefore need to take moments about the intersection of the lines of action of these two forces, which is shown in the diagram (call it ). Moments must balance about any point: it doesn’t matter whether the point is inside the body, or outside it as in the case of . It is easy to see from the geometry ( and act along tangents to the sphere) that the distances from to the lines of action of and are equal, which means that the two forces are equal.
To be precise about the meaning of slow in this context, you have to compare the dynamic forces connected with the motion of the sphere with the static forces. The motion of the sphere is rotation about the fixed point of contact with the step. If we assume that the centre moves with constant speed, the only extra force due to the motion is an additional reaction at the point of contact with the step. This reaction is centrifugal in nature and so is roughly of the form , which is to be small compared with . The static approximation (‘very slowly’) is therefore valid if .







